REGRESI DAN INTERPOLASI

(1)

REGRESI DAN INTERPOLASI

Curve Fitting

http://istiarto.staff.ugm.ac.id

Universitas Gadjah Mada

Departemen Teknik Sipil dan Lingkungan Prodi Sarjana Teknik Sipil

(2)

Curve Fitting

2

¨

Acuan

¤ Chapra, S.C., Canale R.P., 1990, Numerical Methods for Engineers,

2nd Ed., McGraw-Hill Book Co., New York.

(3)

Curve Fitting

3

¨

Mencari garis/kurva yang mewakili serangkaian titik data

¨

Ada dua cara untuk melakukannya, yaitu

¤ Regresi ¤ Interpolasi

¨

Aplikasi di bidang enjiniring

¤ Pola perilaku data (trend analysis) ¤ Uji hipotesis (hypothesis testing)

(4)

Curve Fitting

4

¨

Pemakaian regresi

¤ Apabila data menunjukkan tingkat kesalahan yang cukup signifikan

atau menunjukkan adanya noise

¤ Untuk mencari satu kurva tunggal yang mewakili pola umum perilaku

data

(5)

Curve Fitting

5

¨

Interpolasi

¤ Diketahui bahwa data sangat akurat

¤ Untuk mencari satu atau serangkaian kurva yang melewati setiap titik

data

¤ Untuk memperkirakan nilai-nilai di antara titik-titik data ¨

Extrapolasi

¤ Mirip dengan interpolasi, tetapi untuk memperkirakan nilai-nilai di luar

(6)

Curve Fitting terhadap Data Pengukuran

6

¨

Analisis pola perilaku data

¤ Pemanfaatan pola data (pengukuran, experimen) untuk melakukan

perkiraan

¤ Apabila data persis (akurat): interpolasi

¤ Apabila data tak persis (tak akurat): regresi ¨

Uji hipotesis

¤ Pembandingan antara hasil teori atau hasil hitungan dengan hasil

(7)

Beberapa Parameter Statistik

¨

Rata-rata aritmatik, mean

¨

Deviasi standar, simpangan

baku, standard deviation

¨

Varian (‘ragam’), variance

¨

Coefficient of variation

7

1

2

-=

n

S

s

t y

å

=

y

_i

n

y

1

1 -=

n

S

s

t y

=

å

(

-

)

2

y

S

_t _i

%

100 .

.

y

s

v

c

=

y m er ep res en ta si ka n se b a ra n d a ta

(8)

Distribusi Probabilitas

8

X

frek

_{Distribusi Normal}

salah satu distribusi/sebaran data yang sering dijumpai adalah distribusi normal

(9)

Regresi linear

Regresi non-linear

Regresi

9

(10)

Regresi: Metode Kuadrat Terkecil

10

¨

Mencari satu kurva atau satu fungsi (pendekatan) yang sesuai

dengan pola umum yang ditunjukkan oleh data

¤ Datanya menunjukkan kesalahan yang cukup signifikan ¤ Kurva tidak perlu memotong setiap titik data

¨

Regresi linear

¨

Regresi persamaan-persamaan tak-linear yang dilinearkan

¨

Regresi tak-linear

(11)

Regresi: Metode Kuadrat Terkecil

11

¨

Bagaimana caranya?

¤ Program komputer

(12)

Regresi Linear

12

¨ Mencari suatu kurva lurus yang cocok menggambarkan pola serangkaian

titik data: (x₁,y₁), (x₂,y₂) … (x_n,y_n) ¨ Microsoft Excel ¤ INTERCEPT(y₁:y_n;x₁:x_n) ¤ SLOPE(y₁:y_n;x₁:x_n) y_reg = a₀ + a₁x a₀ : intercept a₁ : slope

(13)

Regresi Linear

13

¨

Kesalahan atau residu (e) adalah perbedaan antara nilai y

sesungguhnya (data y) dan y nilai pendekatan (y

_reg

) menurut

persamaan linear a

₀

+ a

₁

x.

¨

Minimumkan jumlah kuadrat residu tersebut

x

a

y

e

=

-

₀

-

₁

[ ]

=

[

_å

]

=

[

_å

(

- -

)

2

]

1 0 2 min min min S_r e_i y_i a a x_i

(14)

Regresi Linear

¨

Bagaimana cara mencari

koefisien a

₀

dan a

₁

?

¤ Diferensialkan persamaan

tersebut dua kali, masing-masing terhadap a₀ dan a₁.

¤ Samakan kedua persamaan

hasil diferensiasi tersebut dengan nol. 14

(

)

(

)

0 2 0 2 1 0 1 1 0 0 = -= ¶ ¶ = -= ¶ ¶

å

i i i r i i r x x a a y a S x a a y a S

(15)

Regresi Linear

15

¤ Selesaikan persamaan yang didapat untuk mencari

a₀ dan a₁

¤ dalam hal ini, dan masing-masing adalah nilai y rata-rata dan

x rata-rata a₁= n

∑

xiyi −

∑

xi

∑

yi n

_∑

x_i2 ₋

(

_∑

x_i

)

2 a₀ _{= y − a}₁x y x

(16)

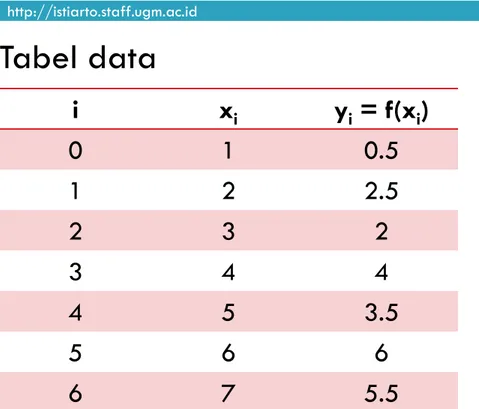
Contoh Regresi Linear

i x_i y_i = f(x_i) 0 1 0.5 1 2 2.5 2 3 2 3 4 4 4 5 3.5 5 6 6 6 7 5.5 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 y = f( x) X 16

(17)

Hitungan regresi linear

17

i xi yi xi yi xi2 yreg (yi−yreg)2 (yi−ymean)2

0 1 0.5 0.5 1 0.910714 0.168686 8.576531 1 2 2.5 5 4 1.75 0.5625 0.862245 2 3 2.0 6 9 2.589286 0.347258 2.040816 3 4 4.0 16 16 3.428571 0.326531 0.326531 4 5 3.5 17.5 25 4.267857 0.589605 0.005102 5 6 6.0 36 36 5.107143 0.797194 6.612245 6 7 5.5 38.5 49 5.946429 0.199298 4.290816 ∑ = 28 24.0 119.5 140 ∑ = 2.991071 22.71429

(18)

Hitungan regresi linear

18 a₁ = n

∑

xiyi −

∑

xi

∑

yi n x_i2

∑

−

(

∑

x_i

)

2 = 7 119.5

(

)

− 28 24

( )

7 140

₍

₎

_{− 28}

_{( )}

2 = 0.839286

( )

4

0 .

071429

839286

.

0

4 .

3

4

7

28

4 .

3

7

24

0

=

-

=

a

x

y

(19)

Hitungan regresi linear

19 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 Y X data regresi

(20)

Regresi Linear

20

¨

Kuantifikasi kesalahan

¤ Kesalahan standar

¤ Perhatikan kemiripannya dengan simpangan baku

2 -=

n

S

s

r x y

1 -=

n

S

s

t y

=

å

(

-

)

2

y

S

_t _i

(

)

å

-

-=

2 1 0 i i r

y

a

x

S

(21)

Regresi Linear

21

¨

Beda antara kedua kesalahan tersebut menunjukkan

perbaikan atau pengurangan kesalahan

r2 = St − Sr S_t r = n

∑

xiyi −

(

∑

xi

)

(

∑

yi

)

n

_∑

x_i2 −

(

∑

x_i

)

2 n

∑

y_i2 −

(

∑

y_i

)

2 koefisien determinasi (coefficient of determination) koefisien korelasi (correlation coefficient)

(22)

Hitungan regresi linear

22

(

)

(

)

22.71429 991071 . 2 2 2 1 0 = -= = -=

å

y y S x a a y S i t i i r 931836 . 0 868318 . 0 71429 . 22 991071 . 2 71429 . 22 2 = = -= -= r S S S r t r t

(23)

Regresi Linear

23

¨

Linearisasi persamaan-persamaan tak-linear

¤ Logaritmik menjadi linear

¤ Eksponensial menjadi linear

¤ Pangkat (polinomial tingkat n > 1) menjadi linear (polinomial tingkat 1) ¤ Dll.

(24)

Linearisasi persamaan non-linear

24 x y ln y 1 ln a₁ x b

e

a

y

1 1

=

x

b

a

y

ln

₁ ₁

ln

=

+

x b₁

(25)

Linearisasi persamaan non-linear

25 1 x y log y log x b₂ 2 2 b

x

a

y =

x

b

a

y

log

=

₂

+

₂ 2

logb

(26)

Linearisasi persamaan non-linear

26 1/y 1

x

b

x

a

y

+

=

3 3 1/x y x

x

a

b

a

x

a

x

b

y

1

3 3 3 3 3

+

=

+

=

3

1 a

3 3

a

b

(27)

Metode Newton

Metode Lagrange

Interpolasi

27

(28)

Interpolasi

28

(29)

Interpolasi

29

¨

Penyelesaian persamaan polinomial tingkat n membutuhkan

sejumlah n + 1 titik data

¨

Metode untuk mencari polinomial tingkat n yang merupakan

interpolasi sejumlah n + 1 titik data:

¤ Metode Newton ¤ Metode Lagrange

(30)

Interpolasi Linear: Metode Newton

30 x f(x) f(x₁) f₁(x) f(x₀) x₀ x x₁

( ) ( ) ( ) ( )

( ) ( ) ( ) ( )(

₀

)

0 1 0 1 0 1 0 1 0 1 0 0 1 x x x x x f x f x f x f x x x f x f x x x f x f -+ = -=

(31)

-http://istiarto.staff.ugm.ac.id

Interpolasi Kuadratik: Metode Newton

31

( )

(

)

(

)(

)

(

) (

) ( )

_!

2 2 1 2 0 2 1 1 0 2 0 1 0 1 2 0 2 1 0 2 2 2 0 1 1 0 1 0 2 0 1 0 2 2 1 0

x

b

x

b

x

b

x

b

x

b

xx

b

xx

b

x

b

x

b

x

b

x

b

x

b

x

b

x

f

a a a

+

-+

+

-=

-+

+

-+

=

-+

=

"

" #

"

" $

%

"

" #

"

" $

%

( )

2 2 1 0 2

x

a

x

a

x

f

=

+

ï

î

ï

í

ì

=

-=

+

-=

2 2 1 2 0 2 1 1 1 0 2 0 1 0 0

b

a

x

b

x

b

a

x

b

x

b

a

(32)

Interpolasi Kuadratik: Metode Newton

32

( )

₀ 0

f

x

b =

( ) ( )

_[

_]

0 1 0 1 0 1 1

f

x

, x

x

f

x

f

b

=

-=

b₂ ₌ f x

( )

₂ − f x

( )

₁ x₂ − x₁ − f x

( )

₁ − f x

( )

₀ x₁− x₀ x₂ − x₀ = f x⎡⎣ 2,x1,x0⎤⎦ = f x⎡⎣ ₂,x₁⎤⎦ − f x⎡⎣ ₁,x₀⎤⎦ x₂ − x₀

(33)

Interpolasi Polinomial: Metode Newton

33

( )

=

0

+

1

(

-

0

)

+

...

+

n

(

-

0

)(

-

1

) (

...

-

n-1

)

n

x

b

x

b

x

f

( )

[

]

[

]

[

₁ ₁ ₀

]

0 1 2 2 0 1 1 0 0 , ,..., , . . . , , , x x x x f b x x x f b x x f b x f b n n n = -= = =

(34)

Interpolasi Polinomial: Metode Newton

34

[ ]

( )

[

] [ ] [

]

[

] [

]

0 0 2 1 1 1 0 1 1 ,..., , ,..., , , ,..., , , , , , , x x x n x f x x x f x x x x f x x x x f x x f x x x f x x x f x f x x f n n n n n n n k i k j j i k j i j i j i j i -= -= -=

(35)

-http://istiarto.staff.ugm.ac.id

Interpolasi Polinomial: Metode Newton

35

( ) ( ) (

)

[

]

(

)(

)

[

]

(

1 0 ₀

)(

₁

) (

0 1 ₁

)

2

[

1 0₁ ₀

]

0 0

,...,

,

...

,

x

f

x

f

x

f

x

f

x

f

n n n n

-+

+

-+

=

(36)

Interpolasi Polinomial: Metode Newton

36

i x_i f(x_i) langkah hitungan

ke-1 ke-2 ke-3

0 x₀ f(x₀) f[x₁,x₀] f[x₂,x₁,x₀] f[x₃,x₂,x₁,x₀] 1 x₁ f(x₁) f[x₂,x₁] f[x₃,x₂,x₁]

2 x₂ f(x₂) f[x₃,x₂]

(37)

Interpolasi Polinomial: Metode Lagrange

37

f

_n

_{( )}

x

₌

L

_i

_{( )}

x

f x

_{( )}

_i i=0 n

∑

f

₃

_{( )}

x

=

x − x

1

x

₀

− x

₁

x − x

₂

x

₀

− x

₂

x − x

₃

x

₀

− x

₃

⎡

⎣

⎢

⎤

⎦

⎥

f x

( )

0

+

x − x

₀

x

₁

− x

₀

x − x

₂

x

₁

− x

₂

x − x

₃

x

₁

− x

₃

⎡

⎣

⎢

⎤

⎦

⎥

f x

( )

1

+...

+

x − x

0

x

₂

− x

₀

x − x

₁

x

₂

− x

₁

x − x

₃

x

₂

− x

₃

⎡

⎣

⎢

⎤

⎦

⎥

f x

( )

2

+

x − x

₀

x

₃

− x

₀

x − x

₁

x

₃

− x

₁

x − x

₂

x

₃

− x

₂

⎡

⎣

⎢

⎤

⎦

⎥

f x

( )

3

L

_i

_{( )}

x

=

x − x

k

x

_i

− x

_k k=0 k≠i n

∏

Contoh interpolasi polinomial order 3:

(38)

Contoh interpolasi

i x_i f(x_i) 0 1 1.5 1 4 3.1 2 5 6 3 6 2.1 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 f( x) X 38

(39)