Soal soal dan Pembahasan Matematika IPA SBMPTN SNMPTN 2009

(1)

w w w .pur w antow ahyudi.com Hal - 1

Soal-Soal dan Pembahasan Matematika IPA SNMPTN 2009

1. Jika a, b  0, maka pernyataan di bawah ini yang benar adalah…

A.

2 b a

ab   C.

2 ab

ab E. ab ab

B. ab b a D. ab b a

Jawab:

karena pada jawaban terdapat ab maka selesaikan soal sbb:

)

( a  b 2  0

a + b – 2 ab  0

a + b  2 ab



2 b a _

ab

 ab 

2 b a

Jawabannya adalah A

2. Diketahui segitiga ABC. Titik P di tengah AC dan Q pada BC, sehingga BQ = QC. Jika

AB

=

c

,

AC

=

b

dan

BC

=

a

, maka

PQ

= ….

A.

(

)

2

1

b

a





_C.

(

)

2

1

c

a





_E.

(

)

2

1

c

b



B.

(

)

2

1

b

a



_D.

(

)

2

1

c

b





Jawab: C

b a P Q

(2)

PQ

=

Q

-

P

=

AQ

-

AP

= (c+ 2 1

a) – ( 2 1

b)

= c+ 2 1

a – 2 1

b

= (b- a)+ 2 1

a – 2 1

b

= 2 1

b - 2 1

a

= 2 1

(-a + b)

Jawabannya adalah A

3. Diberikan balok ABCD.EFGH dengan AB = 2cm, 2BC = 2cm, 2AE = 2cm. Panjang AH adalah……

A. 2 1

cm C. 2 cm E. 3 cm

B. 1 cm D. 2 cm

Jawab:

2BC = 2cm  BC = 1 cm, 2AE = 2cm  AE = 1 cm

H G E F

1 cm

D C 1 cm A B

2 cm

AH = 2 2

DH AD  = 2 2

1 1  = 2 cm

(3)

w w w .pur w antow ahyudi.com Hal - 3 4. Jika pada integral



 2 1

0 1 x

x

dx disubstitusikan x = sin y, maka menghasilkan :

A.



2 1

0 2

sin x dx C.



4

0 2

sin 2



dx

x E.



6

0 2

sin 2



dx x

B.



2 1

0 2

cos sin

dy y

y

D.



4

0 2

sin



dy y

Jawab:

x = sin y  dikuadratkan x = sin2_y

dx = 2 sin y cos y dy

batas integral:

untuk x = 0 maka :

0 = sin y

0 = sin y  y = 0

untuk x = 2 1

2 1

= sin y

2 1

. 2 2

= sin y

2 1

2 = sin y

y = 450₌

4





2 _

1

0 1 x

(4)







4

0 1 sin2

sin



y y

2 sin y cos y dy ; sin2_{y + cos}2_{y = 1}__cos2_{y = 1 - sin}2_y





4 0 cos2

sin



y y

2 sin y cos y dy =



4

0 cos

sin



y y

2 sin y cos y dy





4 0

2

sin 2



ydy =



4

0 2

sin 2



xdx

Jawabannya adalah C

5. Misalkan Un menyatakan suku ke n suatu barisan geometri. Jika diketahui U5 = 12 dan

log U₄ + log U₅ - log U₆ = log 3, maka nilai U₄ adalah …

A. 12 C. 8 E. 4 B. 10 D. 6

Jawab:

barisan geometri:

U₄, U₅, U₆  U₅ = 12

log U₄ + log U₅ - log U₆ = log 3 ditanya U₄= ..?

r =

5 6

U U

= 12

6

U

 U₆ = 12r

log U₄ + log U₅ - log U₆ = log 3 log U₄ + log U₅ = log 3 + log U₆ log U₄ . U₅ = log 3 . U₆

U₄ . U₅ = 3 . U₆ 12 . U₄ = 3 . 12r

U₄ = 12 36r

= 3r

U₅ = U₄. r U₅ = 3r. r 12 = 3r2

r2_{= 4}

(5)

w w w .pur w antow ahyudi.com Hal - 5 U₄ = 3 .r = 3. 2 = 6

Jawabannya adalah D

6. Suatu rumah dibangun pada sebidang tanah berbentuk persegi panjang dengan lebar 24 m dan panjang 40 m seperti pada gambar berikut.

Keliling bangunan rumah tersebut adalah…..

A. 30 m C. 40 m E. 64 m B. 32 m D. 56 m

Jawab:

20 m

d a e b 12 m

f c

a + b + c = 20 m d + e + f = 12 m

keliling rumah = 20 m + 12 m + (a + b+c)+(d+e+f) = 20 m + 12 m + 20 m + 12 m = 64 m

Jawabannya adalah E

7. Diketahui fungsi f dan g dengan f(x) = x2_{+ 4x + 1 dan g}'_{(x) =} 2

10x dengan g'

menyatakan turunan pertama fungsi g. Nilai turunan pertama g  f di x = 0 adalah

(6)

w w w .pur w antow ahyudi.com Hal - 6 Jawab:

f(x) = x2_{+ 4x + 1}

f'_{(x) =2x + 4}

(g  f)'(x) = g'(f(x)) . f'(x) = 2 2

) 1 (

10 x x .(2x+4)

untuk x = 0

(g  f)'_{(x) =} 2

) 1 0 0 (

10   .(0+4)

= 101 . 4 = 9 . 4 = 3 . 4 = 12

Jawabannya adalah D

8. Diberikan fungsi f memenuhi persamaan 3 f(-x) + f(x-3) = x + 3 untuk setiap bilangan real x. Nilai 8 f(-3) adalah …..

A. 24 C. 20 E. 15 B. 21 D. 16

Jawab:

untuk x = 0 :

3 f(-0) + f(-3) = 3 …..(1)

untuk x = 3 :

3 f(-3) + f(0) = 6 ……(2)

dari (1) dan (2) :

3 f(0) + f(-3) = 3 x 1  3 f(0) + f(-3) = 3 f(0) + 3 f(-3) = 6 x 3  3 f(0) + 9f(-3) = 18 - - 8 f(-3) = - 15 8 f(-3) = 15 Jawabannya adalah E

9. Jika f(3x+2) = x x1 dan f' adalah turunan pertama fungsi f, maka 12 f'(11) = …

A. 9 C. 12 E. 15 B. 11 D. 14

(7)

f(3x+2) = x x1

f(3x+2) = 3 2

x

x  = (x3_{+ x}2₎2 1

3 . f'_{(3x+2) =} ₂ 1 2 3

) (

2

1 _ 

x

x =

2 3 2

2

2 3

x x

 

agar f'_{(3x+2) menjadi f}'_{(3x+2) maka x = 3}

untuk x = 3 :

3 f'_{(11) =}

9 27 2

3 . 2 9 . 3

 

= 36 2

33 =

12 33

12 f'(11) = 3 33

= 11

Jawabannya adalah B

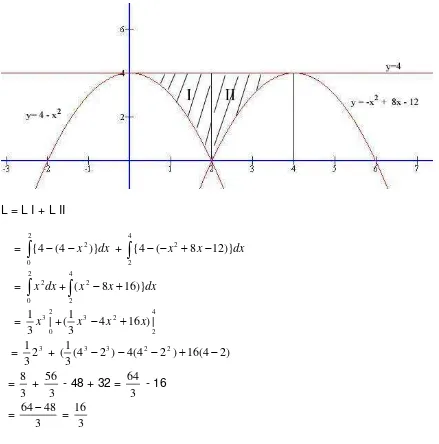
10. Jika f(x) = x2, maka luas daerah yang dibatasi kurva y = 4 – f(x), y = 4 - f(x-4) dan garis y = 4 adalah…..

A. 12 C. 5 E. 3 11

B. 3 16

D. 4

Jawab:

f(x) = x2

Kurva:

* y = 4 – f(x)  y = 4 - x2

* y = 4 - f(x-4)  y = 4 – (x-4)2

= 4 – (x2 - 8x + 16) = - x2_{+ 8x – 12}

(8)

w w w .pur w antow ahyudi.com Hal - 8 grafik :

L = L I + L II

=



 

2

0

2

)} 4

( 4

{ x dx +



   

4

2

)} 12 8 (

4

{ x x dx

=



2

0 2

dx

x +



 

4

2 2

)} 16 8

(x x dx

= 2

0 3

| 3 1

x + 4

2 2

3

| ) 16 4

3 1

( x  x  x

= 3

2 3 1

+ (4 2 ) 4(4 2 ) 16(4 2) 3

1

( 3  3  2  2  

= 3 8

+ 3 56

- 48 + 32 = 3 64

- 16

= 3

48 64

= 3 16

Jawabannya adalah B

11. Luas daerah yang diarsir pada lingkaran besar adalah 4 kali luas daerah lingkaran kecil.

Jika jari-jari lingkaran besar adalah



5

, maka keliling lingkaran kecil adalah ….

A.



5

C. 2 5 E. 5 2

B. 5 D. 5

(9)

Luas lingkaran = r2

Keliling = 2 r

ditanya keliling lingkaran kecil = …?

misal:

Lb = Luas Lingkaran besar Lk = Luas Lingkaran kecil

rb = jari-jari lingkaran besar =



5

rk = jari-jari lingkaran kecil

Lb – Lk = 4 Lk Lb = 5 Lk

 (



5

)2_{= 5}_rk2

(



5

)2_{= 5 rk}2



25

= 5 rk2

rk2 =



5 25

=



5

rk =



5

keliling lingkaran kecil = 2



5 = 2

 2

5

= 2 5

Jawabannya adalah C

12. Jika F _

  

 

sin2 x 4

6

= tan x,   x  2, maka F(3) = ….

A. 0 C. 2



E. 2

(10)

F _

  

 

sin2x 4

6

= F(3)

 _

  

 

sin2 x 4

6

= 3

 4sin2 x =

3 6

= 2 ; dikuadratkan

4 + sin2x_{= 4}

 sin2x = 0 x = 

maka:

F _

  

 

sin2x 4

6

= tan x

F _

  

 

 2

sin 4

6

= tan 

F(3) =

 

cos sin

= 1 0  = 0

Jawabannya adalah A

13. Salah satu faktor suku banyak x3_{+ kx}2_{+ x – 3 adalah x – 1. Faktor yang lain adalah ….}

A. x2_{+ 3x + 3 C. x}2_{+ 3x - 3 E. x}2_{- 7x + 3}

B. x2_{+ x - 3 D. x}2_{+ 2x + 3}

Jawab:

Metoda Horner

x -1  x = 1

x = 1 1 k 1 -3

1 k+1 k+2

1 k+1 k+2 k – 1 sisa

k – 1 = 0  k = 1

sehingga faktor yang lainnya adalah : x2+ (k+1) x + k+ 2 k = 1  x2 + 2x + 3

(11)

w w w .pur w antow ahyudi.com Hal - 11 14. Diberikan tiga pernyataan:

1. Jika



b

a

dx x

f( ) 1, maka f(x) 1 untuk semua x dalam [a,b]

2. 4 1

+

2

4 1      

+

3

4 1      

+ …+

2009

4 1      

< 3 1

3.









3

2009

0

sin

xdx

A. 1 dan 2 C.2 dan 3 E.Tidak ada B. 1 dan 3 D. 1, 2 dan 3

Jawab:

1. Misal persamaan garis sembarang : f(x) =2x + 6

6

-3 0



b

a

dx x

f( ) =







0

3

) 6 2

( x dx = 0

3 2

| 6

  x

x = -9 + 6(0+3) = 9 1

apakah benar f(x) 1 untuk semua x dalam [a,b]

untuk x dalam [-3,0]

untuk x = -3  y = 0 untuk x = 0  y = 6

hasilnya  0 f(x)  6 syarat tidak berlaku

(12)

w w w .pur w antow ahyudi.com Hal - 12 2. merupakan deret geometri dengan a =

4 1

; r = 4 1

dan n = 2009

S_n = r r a n   1 ) 1 (

untuk r <1

S₂₀₀₉ =

4 1 1 ) ) 4 1 ( 1 ( 4 1 ₂₀₀₉   = 4 1 (1-( ) 4 1 2009 ) . 3 4 = 3 1 (1-( ) 4 1 2009

) < 3 1

pernyataan benar

3.







  3 3 2009

0

sin

xdx

dengan n = 2009 dan n 2 gunakan rumus reduksi:



sinn xdx = x x

n

cos sin

1 1

 + 



 xdx

n

n n 2

sin 1







  3 3

sin

n

xdx

x x

n

cos sin

1 ₁

   3 3 |  + _



    3 3 2 sin 1 xdx n n n

= 0 +



     3 3 2 sin 1 xdx n n n maka :







  3 3 2009

sin

xdx

...

2006 2004 2008 2006 2009 2008 x x

x x



   3 3 sin 3 2 xdx = ... 2006 2004 2008 2006 2009 2008 x x x x 3 2

. (– cos x)

  3 3 |  = ... 2006 2004 2008 2006 2009 2008 x x

x x 0 = 0

pernyataan benar

(13)

w w w .pur w antow ahyudi.com Hal - 13 15. Fungsi f(x) =

x 2 cos 2 1

12

 dalam selang 0 < x < 2mencapai nilai maksimum a pada

beberapa titik x₁. Nilai terbesar a +

1

4x

adalah…

A. 13 C. 16 E. 20 B. 15 D. 18

Jawab:

f(x) =

x 2 cos 2 1

12

 = 12 (1-2cos2x)

1



syarat mencapai nilai maksimum jika f'_{(x) = 0}

f'_{(x) = -12(1 – 2cos2x)}2_{. 4 sin2x}

=

2

) 2 cos 2 1 (

2 sin . 48

x x



 = 0

sin 2x = 0 atau sin 2x = 180

2x = 0 + k . 2 2x = 180 + k . 2 x = k.  x = 90 + k. 

untuk k = 0 didapat: x = 90

untuk k = 1 didapat x = 180 dan 270

x f(x) =

x 2 cos 2 1

12 

90 4 180 -12

(14)

w w w .pur w antow ahyudi.com Hal - 14 grafik:

terlihat bahwa - 12 adalah nilai maksimum berarti a = -12

didapat x₁ = 180 atau  sehingga nilai terbesar a +

1

4x

adalah:

-12 +

 

. 4

= -12 + 4 = -8