81 Bab 6 Ruang Hasilkali Dalam

(1)

81 Bab 6 ● Ruang Hasilkali Dalam

Bab 6

R

U

A

N

G

H

A

S

I

L

K

A

L

I

D

A

L

A

M

Ruang hasil kali dalam merupakan ruang vektor yang dilengkapi dengan operasi hasil kali dalam. Seperti halnya ruang vektor, ruang hasilkali dalam bermanfaat dalam beberapa metode optimasi, seperti metode least square dalam peminimuman error dalam berbagai bidang rekayasa.

5.1 HASIL KALI DALAM

Misalnya V adalah suatu ruang vektor, dan u, v∈V maka notasi < , > dinamakan hasil kali dalam jika memenuhi keempat aksioma sebagai berikut:

(i)

<

u ,

v

>

=

<

v ,

u

>

(Simetris)

(ii)

<

u

+

v

,

w

>

=

<

u

,

w

>

+

<

v

,

w

>

(Aditivitas)

(iii) untuk suatu k∈R, berlaku

<k ,u v> = <u,kv>= k< vu, > (Homogenitas) (iv) <u,u >≥0, untuk setiap u dan

<

u

,

u

>

=

0

⇔ u =0 (Positifitas) Ruang vektor yang dilengkapi dengan hasil kali dalam dinamakan ruang hasilkali dalam (RHD). Jika V merupakan suatu ruang

hasil kali dalam, maka norm (panjang) sebuah vektor u

dinyatakan oleh u yang didefinisikan oleh :

=

u

<

_u

,

_u

>

12

≥

0

Contoh 6.1 :

(2)

82 Bab 6 ● Ruang Hasilkali Dalam Misalkan, u , v ∈ Rn maka

<

u

,

v

>=

u

₁

v

₁

+

u

₂

v

₂

+

...

+

u

_n

v

_n maka

u

=

<

_u

,

_u

>

12

≥

0

_{= (u}₁₂_{+ u}₂₂_{+ …..+u}_n2₎1/2 Contoh 6.2 :

Misalnya W ⊆ R3 _{yang dilengkapi dengan operasi hasil} kali berbentuk :

= 2u1v1 + u2v2 + 3u3v3, ∀ u , v ∈ W

Buktikan bahwa W adalah ruang hasilkali dalam ( RHD). Jawab : Misalnya u,v,w∈W (i) <u ,v> = 2u1v1 + u2v2 + 3u3v3 = 2 v1u1 + v2 u2+ 3 v3u3 = < v , u > (terbukti simetris) (ii) <u+v,w> = < (u1+v1 , u2+v2, u3+v3), (w1 , w2 , w3)> = 2(u1+ v1)w1 + (u2+v2) w2 + 3(u3+v3) w3 = 2u1w1 + 2v1w1 + u2w2 + v2w2 + 3u3 w3 + 3v3w3 = 2u1w1+u2 w2 + 3u3w3+ 2v1w1 + v2w2 + 3v3w3 = + < v,w> (terbukti aditivitas)

(iii) untuk suatu k∈R,

<k ,u v > = <(ku1, ku2, ku3), (v1,v2, v3)> = 2ku1v1 + ku2v2 + 3ku3v3 = k.2u1v1 + ku2v2 + k.3u3v3 = k<u,v> <k ,u v> = <(ku1, ku2, ku3), (v1,v2, v3)> = 2ku1v1 + ku2v2 + 3ku3v3 = 2u1kv1 + u2kv2 + 3u3kv3 = <u ,kv > (terbukti homogenitas) (iv)

<

u,

u

>

= 2u12 + u22 + 3u32

(3)

Aljabar Linear Elementer – Adiwijaya 83 Jelas bahwa < u, u > ≥ 0, untuk setiap u, dan

< u, u > = ⎯0 ⇔ u = ⎯0 terbukti memenuhi sifat

positifitas.

Contoh 6.3:

Tunjukan bahwa < u, v > = u1v1 + 2u2v2 – 3u3v3 bukan merupakan hasil kali dalam

Jawab :

Misalkan u= (u1, u2, u3) ∈ W

Perhatikan < u, u > = u12 + 2u22 – 3u32

Jelas bahwa saat : 3u32 > u12 + 2u22 maka < 0

Ini menunjukan tidak memenuhi sifat positifitas

Jadi < u, v > = u1v1 + 2u2v2 – 3u3v3 bukan merupakan hasil kali dalam.

Contoh 6.4 :

Diketahui = ad + cf

dimana u = (a, b, c) dan v = (d, e, f),

Apakah <u,v> merupakan hasil kali dalam? Jawab : 1. Sifat Simetris <u,v> = ad + cf = da + fc =<v,u>……….(terpenuhi) 2. Sifat Aditivitas Misalkan w = ( g, h, i ) <u+ v,w> = <( a + d, b + e, c + f ), ( g, h, i )> = ( a + d )g + ( c + f )i = (ag + ci ) + (dg + fi ) = + <w,v> …….….(terpenuhi)

(4)

84 Bab 6 ● Ruang Hasilkali Dalam 3. Sifat Homogenitas <ku,v> = ( kad + kcf) = k (ad + cf) = k <u ,v>…………..………(terpenuhi) 4. Sifat Positivitas

>

<

u,

u

= ( a2_{+ c}2₎

≥

₀

Tetapi ada u ≠0 sedemikian hingga

<

u

,

u

>

=

0

Karena saat u = ( 0, 2, 0 ) diperoleh < u, u > = 0.

Aksioma terakhir tidak terpenuhi.

Jadi

<

u ,

v

>

=

ad + cf bukan merupakan hasil kali

dalam.

5.2 HIMPUNAN ORTONORMAL DAN PROSES GRAMM- SCHMIDT

Sebuah himpunan vektor pada ruang hasil kali dalam dinamakan himpunan ortogonal jika semua pasangan vector yang berbeda dalam himpunan tersebut adalah orthogonal (saling tegak lurus). Sebuah himpunan orthogonal yang setiap vektornya memiliki panjang (normnya) satu dinamakan himpunan ortonormal.

Agar lebih memudahkan dalam pemahaman, misalkan

{

c

n

T

=

₁

,

₂

,...,

}

pada suatu RHD.

1. T dikatakan himpunan vektor ortogonal jika : Semua vektor didalam T yaitu <c_i,c_j > = 0 Untuk setiap i ≠ j , i, j = 1,2,3,…n 2. T dikatakan himpunan ortonormal jika :

T merupakan himpunan ortogonal dan untuk setiap ci ∈ T, maka

c

_i

=

1

(setiap vektor di T merupakan vektor satuan) Contoh 6.5 : 1. ⎭ ⎬ ⎫ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎩ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 0 1 -0 1 , A

(5)

Aljabar Linear Elementer – Adiwijaya 85 2. ⎪⎩ ⎪ ⎨ ⎧ ⎭ ⎬ ⎫ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 1 0 0 1 , B

Pada RHD Euclides, B merupakan himpunan ortonormal.

Misal S =

{

d₁,d₂, _K d_n

}

merupakan basis bagi suatu RHD V dan

merupakan himpunan ortonormal, maka S dinamakan Basis Ortonormal.

Jika S=

{

v1,v2,...,vn

}

adalah basis ortonormal untuk ruang hasil

kali dalam V, dan u adalah sembarang vektor di ruang vektor V, maka : n nv k v k v k u = ₁ ₁+ ₂ ₂ +...+ (6.1)

Perhatikan bahwa, untuk suatu i ∈ 1, 2, … n, maka berlaku : > + + + < = > <u,vi k1v1 k2v2 ... knvn,vi

Dengan menggunakan sifat aditifitas dan homogenitas hasilkali dalam maka

<u,v_i >=k1<v1,v_i >+k2 <v2,v_i >+...+k_i <v_i,v_i >+...k_n<v_n,v_i > Karena S merupakan himpunan ortonormal, yaitu

i v

v_i, _i >=1 untuk setiap

<

dan

Jadi, untuk setiap i berlaku < ,u v_i >=k_i

j i v

v_i _j >= ≠

< , 0 untuk setiap

Sehingga kombinasi linear (6.1) dapat ditulis dalam bentuk :

n n v v u v v u v v u u =< , ₁> ₁+< , ₂ > ₂ +...+< , > Contoh 6.6 :

Tentukan kombinasi linear vektor

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 2 1 a

(6)

86 Bab 6 ● Ruang Hasilkali Dalam ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 2 1 2 1 u dan ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = 2 1 2 1 v Jawab :

Terlihat bahwa vektor pembangun bidang merupakan basis ortonormal bagi bidang tersebut, sehingga kombinasi linear dapat ditulis menjadi :

v v a u u a a=< , > +< , > v u a _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 2 1 2 1 2 1 2 1 , 2 1 , 2 1 2 1

(

)

v u a 1 ₂ 2 1 + − =

Misal S =

{

c₁,c₂, _K c_n

}

merupakan basis bagi suatu RHD V dan bukan merupakan himpunan Ortonormal, maka S dapat ditransformasi menjadi Basis Ortonormal dengan suatu proses yang dinamakan proses Gramm-Schmidt.

Misal B=

{

w1, w2,...,wn

}

merupakan basis ortonormal hasil proses

Gramm-Schmidt dari basis S.

1. Misalkan

w

₁ merupakan perubahan dari vektor

c

₁ maka

1 1 1 c c w = , dimana w1 =1.

2. Misal

w

₂adalah hasil perubahan dari

c

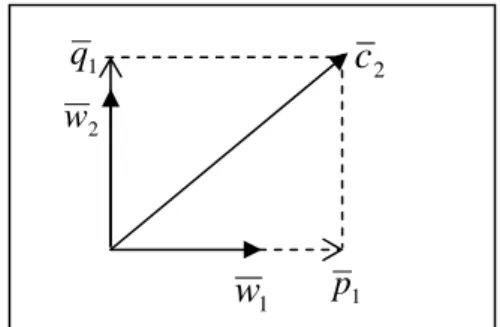
₂. Agar dapat memahami lebih jauh, berikut adalah ilustrasi pembentukan vektor

w

₂ Vektor

c

₂ diproyeksikan pada pada vektor

w

₁, terlihat pada gambar bahwa hasil proyeksi berupa vektor

p

₁. Selanjutnya ambil komponen

c

₂ yang tegak lurus terhadap

w

₁, yaitu

q

1. Sehingga diperoleh

2

w

, yaitu vektor yang searah dengan

q

₁ dan normnya sama dengan satu.

(7)

Aljabar Linear Elementer – Adiwijaya 87 Berikut ini adalah ilustrasi perhitungan nilai vektor yang ada pada gambar diatas :

1 q 1

w

2

c

1 p 2 w

Gambar 6.1 Ilustrasi gram Schmidt di Bidang

1

p

merupakan proyeksi vektor

c

₂ terhadap

w

₁ (vektor ortonormal), sehingga : 1 1 2 1 1 1 2 2 1 , , 1 c w w w w w c c proy p = _w =< > =< >

Karena

q

1 merupakan komponen

c

2 yang tegak lurus

terhadap

w

₁maka

1 2 1

c

p

q

=

−

Akhirnya diperoleh vektor

w

₂, yaitu : 1 1 2 q q w = atau 2 1 2 2 1 1 2 2 2 , , , w w c c w w c c w > < > < − =

(8)

88 Bab 6 ● Ruang Hasilkali Dalam 3. Misalkan

w

₃ adalah hasil perubahan dari

c

₃. Agar dapat

memahami lebih jauh, berikut adalah ilustrasi pembentukan vektor

w

₃ adalah sebagai berikut:

2 q 3

c

3

w

2 w 1 w

W

2 p

Gambar 6.1 Ilustrasi gram Schmidt di Ruang

Vektor

c

₃ diproyeksikan pada pada bidang W =

span(

w

₁,

w

₂), artinya W dibangun oleh dua vektor yang ortonormal. Terlihat pada gambar bahwa hasil proyeksi berupa vektor

p

2. Ambil komponen

c

3 yang tegak lurus terhadap bidang W, yaitu

q

₂. Selanjutnya diperoleh

w

₃, yaitu vektor yang searah dengan

q

2 dan normnya sama dengan satu.

Berikut ini adalah ilustrasi perhitungan nilai vektor yang ada pada gambar diatas :

2

p

merupakan proyeksi vektor

c

₃ terhadap bidang W

yang dibangun oleh dua vektor ortonormal

w

₁ dan

w

₂, sehingga : 2 2 3 1 1 3 3 2 proy c c ,w w c ,w w p = _W =< > +< >

Karena

q

₂ merupakan komponen

c

₃ yang tegak lurus

(9)

Aljabar Linear Elementer – Adiwijaya 89

2 3 2 c p

q = −

Akhirnya diperoleh vektor

w

₃, yaitu

2 2 3 q q w = atau 2 2 3 1 1 3 3 2 2 3 1 1 3 3 3 , , , , w w c w w c c w w c w w c c w > < + > < − > < + > < − =

Secara umum, proses Gramm Schmidt untuk mentransformasi basis

S

=

{

c

1

,

c

2

,

K

c

n

}

pada suatu

RHD V menjadi basis ortonormal

B

=

{

w

1

,

w

2

,

...

,

w

n

}

.

1 1 1 1 1 1 1 1 , ... , , ... , − − − − > < + + > < − > < + + > < − = i i i i i i i i i i i w w c w w c c w w c w w c c w , untuk setiap i = 1, 2, 3, … n. Contoh 6.7 :

Diketahui R3 _{merupakan ruang vektor dengan hasil kali} dalam Euclides. Misalkan

⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = = 1 0 0 , 1 1 0 , 1 1 1 3 2 1 u u u B

merupakan basis pada ruang vektor tersebut.

Dengan proses Gram Schmidt transformasikan basis tersebut menjadi basis Ortonormal!

Jawab :

(10)

90 Bab 6 ● Ruang Hasilkali Dalam 1 1 1 u u v =

(

)

3 1 , 1 , 1 = ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 3 1 3 1 3 1 Langkah 2. 2 2 2 2 2 1 1 u proy u u proy u v v v − − = Sementara itu,

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = − = − 3 1 , 3 1 , 3 2 3 1 , 3 1 , 3 1 3 2 1 , 1 , 0 , ₁ ₁ 2 2 2 2 proy ₁u u u v v u _v Karena itu, 3 6 9 1 9 1 9 4 2 2 −proy₁u = + + = u v sehingga : ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − = 6 1 6 1 6 2 2 v Langkah 3. 3 3 3 3 3 u proy u u proy u v W W − − = ,

dimana W merupakan bidang yang dibangun oleh v1 dan 2

(11)

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = − − = − 2 1 , 2 1 , 0 6 1 , 6 1 , 6 2 6 1 3 1 , 3 1 , 3 1 3 1 1 , 0 , 0 , , ₁ ₁ ₃ ₂ ₂ 3 3 3 3 proy u u u v v u v v u W sehingga :

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

−

=

2 1 2 1 3

0 v

Dengan demikian,

{

v1,v2,v3

}

=

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

−

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛−

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

2 1 2 1 6 1 6 1 6 2 3 1 3 1 3 1

₀

,

merupakan basis ortonormal untuk ruang vektor R3 dengan hasil kali dalam Euclides.

Contoh 6.8 :

Diketahui bidang yang dibangun oleh merupakan

subruang dari RHD Euclides R . Tentukan proyeksi orthogonal dari vektor

⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ 1 1 0 , 1 0 1 3 ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 1 1

(12)

92 Bab 6 ● Ruang Hasilkali Dalam Jawab : Diketahui ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 1 0 , 1 0 1 2 1 v

v membangun subruang pada

RHD tersebut.

Jelas bahwa

{

v1, v2

}

merupakan basis bagi subruang pada

RHD tersebut, karena v1 dan v2 saling bebas linear (terlihat bahwa ia tidak saling berkelipatan).

Basis tersebut akan ditransformasikan menjadi basis ortonormal.

(

)

( ) ( ) ( )

(

)

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = = + + = = 2 1 , 0 , 2 1 2 1 , 0 , 1 1 0 1 1 , 0 , 1 2 2 2 1 1 1 v v w 1 1 2 2 1 1 2 2 2 , , w w v v w w v v w − − = Perhatikan bahwa :

(13)

(

)

2 1 2 1 0 0 2 1 , 0 , 2 1 1 , 1 , 0 , ₁ 2 = + + = > ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ < = w v Sehingga: ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 2 1 , 0 , 2 1 2 1 , 0 , 2 1 2 1 , ₁ ₁ 2 w w v

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛− = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = − 2 1 , 1 , 2 1 2 1 , 0 , 2 1 1 , 1 , 0 , ₁ ₁ 2 2 v w w v

( )

6 2 1 4 6 4 1 1 4 1 2 1 1 2 1 , 2 2 2 1 1 2 2 = = + + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− = − v w w v ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛₋ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− = − − = 6 1 , 6 2 , 6 1 6 2 1 2 1 , 1 , 2 1 , , 1 1 2 2 1 1 2 2 2 w w v v w w v v w

Jadi Basis Orthonormal bagi bidang tersebut adalah : ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛₋ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 6 1 6 2 6 1 , 2 1 0 2 1

(14)

94 Bab 6 ● Ruang Hasilkali Dalam

Proyeksi Orthogonal Vektor

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 1 1

u pada bidangwadalah:

u oy_W Pr = u,w₁ w₁+ u,w₂ w₂ Perhatikan bahwa :

(

)

2 2 2 2 1 0 2 1 2 1 , 0 , 2 1 1 , 1 , 1 , 1 = = + + = > ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ < = w u Sehingga

(

1 , 0 , 1

)

2 1 , 0 , 2 1 2 , 1 1 ⎟= ⎠ ⎞ ⎜ ⎝ ⎛ = w w u

(

)

6 2 6 1 6 2 6 1 6 1 , 6 2 , 6 1 1 , 1 , 1 , ₂ = + + − = > ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛₋ < = > < wu ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛− = ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛− = ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛₋ = 3 1 3 2 3 1 6 1 6 4 6 2 6 1 6 2 6 1 6 2 ,w₂ w₂ u Dengan demikian, Proy_Wu = u,w₁ w₁+ u,w₂ w₂ = ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛− + ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ 3 1 3 23 1 1 0 1 ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 3 43 2 3 2

(15)

Latihan Bab 6

1. Periksa apakah operasi berikut merupakan hasil kali dalam a.

<

u

,

v

>

= u12v1 + u2v22 di R2

b.

<

u

,

v

>

= u1v1 + 2u2v2 – u3v3 di R3 c.

<

u

,

v

>

= u1v3 + u2v2 + u3v1 di R3

2. Tentukan nilai k sehingga vektor (k, k, 1) dan vektor (k, 5, 6 ) adalah orthogonal dalam ruang Euclides !

3. Diketahui {u1 = u ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ 1 1 1 1 = , u ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − 0 1 1 1 = } basis bagi R ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ 1 2 1

3 _{dengan hasil kali dalam Euclides. Gunakan proses} Gram Schmidt untuk mentransformasikan basis tersebut menjadi basis ortonormal !

4. W merupakan subruang ruang hasilkali dalam euclides di

ℜ3 _{yang dibangun oleh} _dan _{. Tentukan}

proyeksi orthogonal pada W ! ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ 0 1 1 ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − 1 0 1 ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − 2 1 1