Relasi dan Fungsi dalam Matematika Diskr (2)

Tugas Matematika Diskrit

“Relasi & Fungsi Serta Penerapannya”

OLEH

Albert Ch. Soewongsono

JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNIK

UNIVERSITAS NUSA CENDANA

KATA PENGANTAR

Puji syukur penulis panjatkan ke hadirat Tuhan Yang Maha Esa, karena atas berkat dan rahmatnya makalah Matematika Diskrit mengenai Relasi dan Fungsi ini dapat terselesaikan.

Penulis menyadari bahwa makalah ini masih jauh dari kesempurnaan. Oleh karena itu, penulis senantiasa mengharapkan masukan dan kritik yang membangun dari pembaca demi penyempurnaan makalah ini. Akhir kata, semoga makalah ini dapat bermanfaat bagi yang membacanya..

Kupang, 23 Juni 2015

DAFTAR ISI

BAB I. PENDAHULUAN

1.1 . Latar Belakang...1

1.2. Tujuan...1

BAB II. ISI 2.1. Pengertian Relasi... 2

2.2. Representasi Relasi... 2

2.3. Sifat-Sifat Relasi Biner...6

2.4. Operasi Dalam Relasi Biner...9

2.4.1. Relasi Inversi...9

2.4.2. Komposisi Relasi...9

2.4.3. Mengkombinasikan Relasi...11

2.5. Relasi Ekivalen, Kompatibel dan Poset...12

2.5.1. Relasi Ekivalen...12

2.5.2. Relasi Kompatibel...12

2.5.3. Poset (Partially Ordered Set)...13

2.6. Pengertian Fungsi... 13 2.7. Representasi Fungsi ... 14

2.8 .Jenis-Jenis Fungsi...15

2.9. Fungsi-Fungsi Khusus...18

BAB III. PENUTUP

3.1. Kesimpulan... 22

BAB I

PENDAHULUAN

1.1 Latar Belakang

Matematika diskrit adalah salah satu cabang dari matematika yang membahas segala sesuatu yang bersifat diskrit. Diskrit disini artinya tidak saling berhubungan (lawan dari kontinu). Beberapa hal yang dibahas dalam ilmu matematika ini adalah teori himpunan, teori kombinatorial, permutasi, relasi, fungsi, rekursif, teori graf, dan lain-lain.

Hubungan antara elemen-elemen dalam suatu himpunan sering dijumpai dalam kehidupan sehari-hari, misalnya hubungan antara mahasiswa dengan mata kuliah yang diambil, hubungan antara lama waktu tidur dengan peningkatan prestasi belajar dan lain-lain. Di dalam bidang ilmu komputer, dapat dicontohkan hubungan antara program komputer dengan peubah yang digunakan, hubungan antara bahasa pemrograman dengan pernyataan (statement) yang sah, hubungan antara plaintext dan chipertext pada bidang kriptografi dan sebagainya (Munir,2001). Hubungan tersebut dinamakan relasi. Di dalam matematika terdapat banyak jenis-jenis relasi seperti, relasi dalam himpunan, relasi dalam matriks dan relasi dalam suatu graf berarah.

Fungsi merupakan suatu bentuk khusus dari relasi. Suatu fungsi merupakan relasi akan tetapi suatu relasi belum tentu merupakan fungsi. Agar suatu relasi dapat disebut sebagai fungsi, ada syarat yang harus dipenuhi yaitu setiap anggota dalam suatu himpunan harus dipasangkan dengan tepat satu anggota dari himpunan lain. Di dalam matematika terdapat banyak jenis-jenis fungsi antara lain, fungsi injektif, fungsi surjektif dan fungsi bijektif.

1.2 Tujuan

 Mengetahui pengertian relasi dan fungsi

 Mengetahui sifat-sifat relasi

 Mengetahui jenis-jenis relasi dan fungsi

 Mengetahui representasi-representasi dari relasi dan fungsi

BAB II ISI

2.1 Pengertian Relasi

Relasi adalah hubungan antara elemen himpunan dengan elemen himpunan yang lain. Cara paling mudah untuk menyatakan hubungan antara elemen 2 himpunan adalah dengan himpunan pasangan terurut. Himpunan pasangan terurut diperoleh dari perkalian kartesian.

 Definisi 1

Perkalian kartesian (Cartesian products) antara himpunan A dan B ditulis: A x B didefinisikan sebagai semua himpunan pasangan terurut dengan komponen pertama adalah anggota himpunan A dan komponen kedua adlah anggota himpunan B. Notasi : A x B = { (x,y) / x A dan y B}ϵ ϵ

 Definisi 2

Relasi biner R antara A dan B adalah himpunan bagian dari A x B. A disebut daerah asal dari R (domain) dan B disebut daerah hasil (range) dari R.

Notasi: R (AB)

 Definisi 3

Relasi pada A adalah relasi dari A ke A.

Contoh 1 : Misalkan P = {2, 3, 4} dan Q = {2, 4, 8, 9, 15}. Jika kita definisikan relasi R dari

P ke Q dengan (p, q) R jika p habis membagi q maka kita peroleh R = {(2, 2), (2,4), (4,4), (2,8), (4,8), (3,9), (3,15)}

Contoh 2 : Misal R adalah relasi pada A = {2,3,4,8,9} yang didefinisikan oleh (x,y)ÎR jika x

adalah faktor prima dari y, maka: R = {(2,2), (2,4), (2,8), (3,3), (3,9)}

2.2 Representasi Relasi

Dalam penerapannya suatu relasi dalam direpresentasikan dalam berbagai bentuk, sebagai berikut :

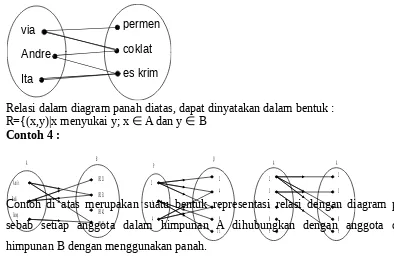
 Representasi Relasi dengan Diagram Panah

via

Relasi dalam diagram panah diatas, dapat dinyatakan dalam bentuk : R={(x,y)|x menyukai y; x ∈ A dan y ∈ B

Contoh 4 :

Contoh di atas merupakan suatu bentuk representasi relasi dengan diagram panah sebab setiap anggota dalam himpunan A dihubungkan dengan anggota dalam himpunan B dengan menggunakan panah.

 Representasi Relasi dalam Sistem Koordinat

Suatu relasi dapat direpresentasikan ke dalam sistem koordinat, sebagai contoh : R = {(Microsoft, Windows), (IBM, OS/2), ( Macintosh, MacOS)}

Relasi tersebut dapat dibuat dalam suatu sistem koordinat, sebagai berikut :

Gambar 1

Tanda titik pada gambar di atas menjelaskan bahwa pasangan tersebut termasuk dalam relasi.

 Representasi Relasi dengan Tabel

Suatu relasi juga dapat direpresentasikan ke dalam bentuk tabel, sebagai contoh : Diberikan suatu relasi :

R={(Via,permen) , (Via,coklat) , (Andre,coklat) , (Andre,es krim) , (Ita,es krim)}, relasi di atas dapat dibuat dalam bentuk tabel, sebagai berikut :

Via Permen

Via Coklat

Andre Coklat

Andre Es Krim

Ita Es Krim

dimana, kolom pertama pada tabel tersebut menyatakan daerah asal sedangkan kolom kedua menyatakan daerah hasil.

 Representasi Relasi pada Himpunan

Definisi :

Suatu relasi pada himpunanA adalah relasi dariA ke A.

Definisi :

Relasi pada himpunan A adalah subhimpunan dari A×A.

Contoh 5 :

Misalkan A = {1, 2, 3, 4}. Himpunan terurut manakah yang terdapatdalam relasi R = {(a, b) | a < b} ?

Jawab :

(1, 2),(2),(1, 3),(3),(1, 4),(4),(2, 3),(3),(2, 4),(4),(3, 4)}(4)}

Bentuk yang diperoleh di atas merupakah salah satu contoh penerapan relasi dalam himpunan.

Banyaknya subhimpunan yang dapat dibentuk dari suatu himpunan dengan m anggota adalah 2m_{. Sehingga, terdapat} 2n2_{subhimpunan yang dapat dibentuk dari AxA.}

Definisi:

Sebagai contoh penerapan relasi dalam matriks, diberikan relasi :

R={(Via,permen) , (Via,coklat) , (Andre,coklat) , (Andre,es krim) , (Ita,es krim)} Relasi tersebut dapat diubah ke dalam bentuk matriks, sebagai berikut :

Permen Coklat Es krim

Via 1 1 0

Andre 0 1 1

Ita 0 0 1

Dimana, baris merupakan domainnya dan kolom merupakan kodomainnya.

 Representasi Relasi dengan Graf Berarah

Graf berarah merupakan gambaran yang paling tepat untuk relasi RX2 dengan aturan-aturan, sebagai berikut :

a. Setiap anggota himpunan X digambarkan dengan lingkaran

b. Graf berarah antara lingkaran menggambarkan adanya relasi antar anggota himpunan, jadi pasangan-pasangan anggota himpunan tersebut termasuk dalam relasi

Contoh 6 :

Via

Andre

Ita

[

a1 prasyarat untuk semua bagian lain

a3 prasyarat untuk a5 dan a6

a6 bukan prasyarat untuk semua bagian lain

Gambar 2

Contoh 7 :

Misalkan R = {(a, a), (a, b), (b, a), (b, c), (b, d), (c, a), (c, d), (d, b)} adalah relasi pada himpunan {a, b, c, d}.

R direpresentasikan dengan graf berarah sbb:

Gambar 3

2.3 Sifat-Sifat Relasi Biner

Suatu relasi biner yang didefinisikan dalam sebuat himpunan mempunyai beberapa sifat, sebagai berikut :

a. Sifat Refleksif dan Irrefleksif

Definisi : (Sifat Refleksif)

Relasi R pada himpunan A disebut refleksif jika (a, a) R untuk setiap aA.

Kontraposisi : (Sifat Irrefleksif)

Relasi R pada himpunan A tidak refleksif jika ada aA sedemikian sehingga (a, a)

R.

a

b

Contoh 8 :

Relasi “kenal dengan” bersifat refleksif Relasi “mengagumi” bersifat irrefleksif

Contoh 9 :

Misalkan A = {1, 2, 3, 4}, dan relasi R di bawah ini didefinisikan pada himpunan A, maka relasi R = {(1, 1), (1, 3), (2, 1), (2, 2), (3, 3), (4, 2), (4, 3), (4, 4) } bersifat refleksif karena terdapat elemen relasi yang berbentuk (a, a), yaitu (1, 1), (2, 2), (3,3), dan (4, 4).

b. Sifat Simetrik dan Asimetrik

Definisi : (Sifat Simetrik)

 Relasi yang bersifat simetrik mempunyai matriks yang elemen-elemen di bawah diagonal utama merupakan pencerminan dari elemen-elemen di atas diagonal utama, atau mij = mji= 1, untuk i = 1, 2, …, n.

Gambar 5

c. Sifat Anti-simetrik

 Matriks dari relasi anti-simetrik mempunyai sifat yaitu jika mij = 1 dengan i  j,

maka mji= 0. Dengan kata lain, matriks dari relasi anti-simetrik adalah jika salah

satu dari mij = 0 atau mji = 0 bila ij.

Gambar 6

 Sedangkan graf berarah dari relasi yang bersifat anti-simetrik dicirikan oleh: jika dan hanya jika tidak pernah ada dua busur dalam arah berlawanan antara dua simpul berbeda.

Sifat transitif pada graf berarah ditunjukkan oleh: jika ada busur dari a ke b dan dari b ke c, maka juga terdapat busur berarah dari a ke c.

R–1 _{adalah invers dari relasi R, yaitu relasi dari Q ke P dengan (q, p) R–1 jika q}

adalah kelipatan dari p, maka kita peroleh:

R–1 _{= {(2, 2), (4, 2), (4, 4), (8, 2), (8, 4), (9, 3), (15, 3) }}

Definisi : (Komposisi dalam Matriks)

Jika relasi R1 dan R2 masing-masing dinyatakan dengan matriks MR1 dan MR2,

maka matriks yang menyatakan komposisi dari kedua relasi tersebut adalah : MR2 R1 = MR1 MR2, yang dalam hal ini operator “.” sama seperti pada perkalian

matriks biasa, tetapi dengan mengganti tanda kali dengan “” dan tanda tambah dengan “”.

Contoh 15 :

2.5 Relasi Ekivalen, Kompatibel dan Poset 2.5.1 Relasi Ekivalen

Definisi :

Suatu relasi pada himpunan A dikatakan sebagai relasi ekivalen jika relasi tersebut bersifat refleksif, simetris, dan transitif. Dua anggota A yang berelasi oleh suatu relasi ekivalen dikatakan ekivalen.

Contoh 17 :

Misalkan A himpunan string yang memuat alfabet dan l(x) panjang dari string x. Jika R relasi pada A dengan aRb jika dan hanya jika l(a) = l(b), apakah R suatu relasi ekivalen ?

Solusi:

R refleksif, karena l(a) = l(a) dan karenanya aRa untuk setiap string a.

R simetris, karena jika l(a) = l(b) maka l(b) = l(a), sehingga jika aRb maka bRa.

R transitif, karena jika l(a) = l(b) dan l(b) = l(c), maka l(a) = l(c), sehingga aRb dan bRc mengakibatkan aRc.

Jadi, R adalah suatu relasi ekivalen.

2.5.2 Relasi Kompatibel Definisi :

Suatu relasi biner dikatakan kompatibel bila memenuhi sifat refleksi dan simetri, tetapi tidak harus transitif.

Contoh 18 :

Berdasarkan tabel di atas, dapat dibuat relasi kompatibel, sebagai berikut :

Gambar 8

2.5.3 Poset (Partially Ordered Set)

Definisi :

Sebuah relasi biner R pada himpunan semesta S dikatakan poset, jika relasi R tersebut bersifat: refleksi, antisimetri, dan transitif.

Poset sering dinyatakan dengan “mendahului” atau “didahului”, seperti : ; a mendahului b

; a langsung mendahului b ; b didahului a

; b langsung didahului a

/ / ; a tidak dapat dibandingkan dengan b a b

Poset seringkali dipaparkan dengan diagram Hess.

Contoh 19 :

Misalkan relasi R adalah hubungan dalam himpunan A = {1,2,3,4,5,6} yang didefinisikan oleh : “x membagi y”

Gambar 9

2.6 Pengertian Fungsi Definisi :

Fungsi adalah sebuah relasi biner dimana masing-masing anggota dalam himpunan A (domain) hanya mempunyai 1 bayangan pada himpunan B (kodomain).

Notasi fungsi : :

f AB_,

dibaca, f adalah fungsi dari A ke dalam B atau f memetakan A ke dalam B.

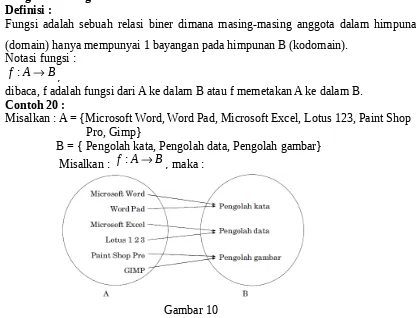
Contoh 20 :

Misalkan : A = {Microsoft Word, Word Pad, Microsoft Excel, Lotus 123, Paint Shop Pro, Gimp}

B = { Pengolah kata, Pengolah data, Pengolah gambar} Misalkan : :f AB, maka :

Gambar 10

Pengolah kata adalah bayangan dari Microsoft Word dan Word Pad, dan dinyatakan oleh: f(Microsoft Word) dan f(Word Pad). Jangkauan (Range) dari f adalah {Pengolah kata, Pengolah data, Pengolah gambar}.

2.7 Representasi Fungsi

a) Himpunan Pasangan Terurut

Suatu fungsi dapat ditulis dalam bentuk himpunan pasangan terurut, sebagai contoh : Misalkan fungsi kuadrat pada himpunan {1, 2, 3, 4, 5, 6, 7, 8, 9,10} maka fungsi itu dapat dituliskan dalam bentuk : f = {(2, 4), (3, 9)}

b) Formula Pengisian Nilai (assignment)

Suatu fungsi dapat ditulis dalam bentuk formula, sebagai contoh : f(x) = x2 _{+ 10,}

c) Kata-Kata

Suatu fungsi juga dapat ditulis dalam bentu kata-kata, sebagai contoh : “f adalah fungsi yang memetakan jumlah bit 1 di dalam suatu string biner”

d) Kode Program (Source Kode)

Suatu fungsi juga dapat ditulis ke dalam bentuk program komputer, sebagai contoh : Fungsi menghitung |x|.

function abs(x:integer):integer;

begin

b. Fungsi Surjektif (Pada) Definisi :

Fungsi f: A → B disebut fungsi pada (surjektif) jika dan hanya jika untuk sembarang b dalam kodomain B terdapat paling tidak satu a dalam domain A sehingga berlaku f(a) = b.

c. Fungsi Bijektif (Korespondensi Satu-Satu) Definisi :

Fungsi f: A → B disebut disebut fungsi bijektif jika dan hanya jika untuk sembarang b dalam kodomain B terdapat tepat satu a dalam domain A sehingga f(a) = b, dan tidak ada anggota A yang tidak terpetakan dalam B. Dengan kata lain, fungsi bijektif adalah fungsi injektif sekaligus fungsi surjektif.

Gambar 13

Fungsi invers merupakan kebalikan dari fungsi itu sendiri

f : A  B di mana f(a) = b f –1_{: B  A di mana f} –1_{(b) = a}

Catatan: f dan f –1 _{harus bijektif.}

Fungsi yang bijektif sering dinamakan juga fungsi yang invertible (dapat dibalikkan), karena kita dapat mendefinisikan fungsi balikannya. Sebuah fungsi dikatakan not invertible (tidak dapat dibalikkan) jika ia bukan fungsi yang bijektif, karena fungsi balikannya tidak ada. elemen himpunan B yang menjadi bayangan dari seluruh elemen himpunan A.

Contoh 26 :

A = Himpunan software aplikasi B = Himpunan sistem operasi

Gambar 14

2.9 Fungsi – Fungsi Khusus

Selain jenis-jenis fungsi yang umum diatas, terdapat juga beberapa fungsi khusus, antara lain :

a. Fungsi Floor dan Ceiling

Definisi :

Misalkan x adalah bilangan riil, berarti x berada di antara dua bilangan bulat. Fungsi floor dari x:

x menyatakan nilai bilangan bulat terbesar yang lebih kecil atau sama dengan x Fungsi ceiling dari x:

x menyatakan bilangan bulat terkecil yang lebih besar atau sama dengan x. Contoh 27 :

Definisi :

Misalkan a adalah sembarang bilangan bulat dan m adalah bilangan bulat positif. a mod m memberikan sisa pembagian bilangan bulat bila a dibagi dengan m a mod m = r sedemikian sehingga a = mq + r, dengan 0 r < m.

Contoh 28 :

Beberapa contoh fungsi modulo : 25 mod 7 = 4

Fungsi rekursif tersusun atas 2 bagian, yaitu : a) Basis

Bagian yang berisi nilai awal yang tidak mengacu pada dirinya sendiri. Bagian ini juga sekaligus mengehentikan definisi rekursif.

b) Rekurens

Bagian ini mendefinisikan argumen fungsi dalam terminologi dirinya sendiri. Setiap kali fungsi mengacu pada dirinya sendiri, argumen dari fungsi harus lebih dekat ke nilai awal (basis)

Contoh 29 :

n! = 1  2  …  (n – 1) n = (n – 1)! n.

2.10. Operasi – Operasi Pada Fungsi

Contoh 30 :

f(x) = x2 _{+ 1}

g(x) = x + 6

(f+g)(x) = f(x)+g(x)

= (x2 _{+ 1) + (x + 6)}

= x2 _{+ x +7}

b.Perkalian 2 Buah Fungsi Definisi :

(f.g)(x) = f(x).g(x)

Contoh 31 :

f(x) = x2 _{+ 1}

g(x) = x + 6 (f.g)(x) = f(x).g(x)

= (x2 _{+ 1).( x + 6)}

= x3_+6x2_+x+6

c. Komposisi Fungsi Definisi :

Komposisi fungsi dari fungsi f dan g dinyatakan oleh (g fo )atau g.f Jika f : AB dan g : B  C, maka :

( ) :

( )( ) ( ( ))

g f A C g f a g f a

  o

o

Contoh 32 :

Contoh 33 :

Diberikan fungsi g = {(1, u), (2, u), (3, v)} yang memetakan A = {1, 2, 3} ke B = {u, v, w}, dan fungsi f = {(u, y), (v, x), (w, z)} yang memetakan B = {u, v, w} ke C = {x, y,

BAB III PENUTUP

3.1. Kesimpulan

 Relasi adalah hubungan antara elemen himpunan dengan elemen himpunan yang lain. Cara paling mudah untuk menyatakan hubungan antara elemen 2 himpunan adalah dengan himpunan pasangan terurut. Himpunan pasangan terurut diperoleh dari perkalian kartesian.

 Fungsi adalah sebuah relasi biner dimana masing-masing anggota dalam himpunan A (domain) hanya mempunyai 1 bayangan pada himpunan B (kodomain).

Notasi fungsi : :

f AB_,

 Sifat-sifat relasi biner, antara lain: a. Refleksif dan Irrefleksif b. Simetrik dan Asimetrik c. Anti-Simetrik

d. Transitif

 Suatu relasi dapat dikategorikan ke dalam beberapa jenis, antara lain:

 Relasi Ekivalen

 Relas Kompatibel

 Poset (Partially Ordered Set)

 Suatu fungsi dapat dikategorikan ke dalam beberapa jenis, antara lain :

 Fungsi Injektif (Satu-Satu)

 Fungsi Surjektif (Pada)

 Fungsi Bijektif (Korespondensi Satu-Satu)

 Fungsi Invers

 Suatu relasi dapat direpresentasikan ke dalam :

 Diagram Panah



Suatu fungsi dapat direpresentasikan ke dalam :



Himpunan Pasangan Terurut



Formulas Pengisian Nilai (Assignment)



Kata-Kata



Kode Program (Source Code)



Relasi Inversi



Komposisi Relasi



Mengkombinasikan Relasi

 Operasi-operasi dalam suatu fungsi, antara lain :

 Penjumlahan dan Pengurangan 2 Buah Fungsi

 Perkalian 2 Buah Fungsi

 Komposisi Fungsi

DAFTAR PUSTAKA

Jonhsonbaugh, Ricard.2001.”Discrete Mathematics”.New Jersey:Prentice Hall Int. Munir, Rinaldi.2001.“Matematika Diskrit”.Bandung:Informatika.

Munir, Rinaldi.2003.“Materi Kuliah Matematika Diskrit”.Bandung :Informatika-ITB. Rosen, Kenneth H.2003.”Discrete Mathematics and Application to Computer Science 5th

Edition”: Mc Graw-Hill.

Witala, Stephen A.1987.”Discrete Mathematics A Unified Approach”.Singapore:McGraw Hill Int.

http://www.academia.edu/7150505/05_FUNGSI (diakses pada tanggal 22 Juni 2015)

http://haryanto-harrybae61gmailcom.blogspot.com/2012/06/representasi-relasi-kedalam-graf-dan.html (diakses pada tanggal 22 Juni 2015)

http://matdis06141.blogspot.com/2012/10/fungsi.html (diakses pada tanggal 22 Juni 2015) http://matdisglutton.blogspot.com/2012/09/relasi-matematika-diskrit.html (diakses pada

tanggal 22 Juni 2015)

http://sulistiawan03.blogspot.com/2012/09/relasi_524.html (diakses pada tanggal 22 Juni

2015)

http://www.slideshare.net/biangreen/materi-1-matriks-relasidanfungsi (diakses pada

tanggal 22 Juni 2015)