UJI CHI SQUARE (X2).pdf

1

UJI CHI SQUARE (X

2

₎

FUNGSI

• Menguji hasil penelitian

dalam bentuk data

kategori/diskrit

• Jumlah kategori ≥ 2

METODE

• Untuk menguji perbandingan

antara data yang diamati ( fo)

dgn data yang diharapkan

(fh), dgn menentukan nilai

data yang diharapkan utk

tiap kategori berdasar Ho.

X

2

( Chi Square )

Digunakan :

• Stat non parametrik • Pengujian Hipotesis :

A. 1 sampel

B. 2 sampel bebas (tdk berkorelasi ) C. komparatif k sampel

1. Sampel berkorelasi 2. Sampel tdk berkorelasi • Ketentuan :

Data berskala nominal/kategori • Keputusan Hipotesis : X2_{hitung < X}2_{(tabel,α) : Ho} diterima Ha ditolak X2hitung ≥ X2(tabel,α) : Ho ditolak Ha diterima

3 UJI CHI SQUARE (X2₎

RUMUS 1. k X2 =

∑ (

fo-fh

)

2 atau i=1 fh Ket: X2_{= chi square} fo = frekuensi observasi ( 0) fh = frekuensi harapan ( E ) Pendekatan tabel silang

Ktgr 1 2 3 1 O11, E11 O12, E12 O13 E13 2 O12, E12 O22, E22 O23 E33 3 O13, E13 O22, E22 O33 E33 Variabel 1 V a r i a b e l 2 ∑ ∑ = = = r i k 1 j Eij 2 ) 0,5 -| Eij -ij 0 | ( X2 1 4 UJI CHI SQUARE (X2₎

RUMUS

2. Pendekatan Koreksi Yate

X2 = n(|ad-bc| -½ n)2

(a+b)(a+c)(b+d)(c+d)

KATE

GORI Pengaruh perlakuan Jml Kelompok Berpengaruh Tdk berpengaruh Eksp Kontrol a c b d a+b c+d Jumlah a+c b+d N Syarat :

•Pada tabel 2x2 , sampel > 40 •Pada tabel r x k ( r atau k > 2 ), nilai fh < 5 ( tdk lebih 20%), tdk ada nilai fh <1, lakukan penggabungan kategori

5

A. X

2

1 sampel

1. Digunakan :

• Menguji hipotesisi 1 sampel • Populasi terdiri dr ≥ klas/kategori 2. Pengujian Hipotesis : dk (derajat kebebasan) = 1 Rms : k

X

2

=

∑ (

fo-fh

)

2 i=1 _fh Ket: X2 = chi square fo = frekuensi observasi fh = frekuensi harapan

Contoh :

• Hasil survei untuk mengetahui bagaimana kemungkinan PUS dlm memilih alat kontrasepsi yaitu IUD & implant. Sampel diambil secara random sebanyak 300 PUS Dari sampel tsb ternyata 200 memilih IUD & 100 PUS memilih Implant.

• Hipotesis yg diajukan adl: Ho : Kemungkinan PUS memilih

alkon IUD & implant sama besarnya ( tdk ada beda) Ha : Kemungkinan PUS memilih

alkon IUD & implant tdk sama besarnya ( ada beda)

• Langkah pembuktian hipotesis :

7 Rms : k

X

2

=

∑ (

fo-fh

)

2 i=1 _fh fh = 50% x N • Keputusan Hipotesis X2hitung= 33,34 X2 tabel ( α=5%,dk=1) = 3,841 X2

hitung> X2tabel : Ho ditolak

Kesimp. : Ada perbedaan pemilihan alkon pd PUS

Pilihan alkon

fo fh fo-fh (fo-fh)2 (fo-fh)2 fh IUD 200 150 50 2500 16,67 Impl 100 150 -50 2500 16,67 Juml 300 300 0 5000 33,34 8

B. X

2

2 sampel

1. Digunakan :

• Menguji hipotesis komparatif 2 sampel bebas maupun berpasangan

• Menguji hip komparatif : menguji ada tdknya perbedaan/ kesamaan nilai-nilai variabel yg ada pada 2 sampel utk diberlakukan dlm populasi/tdk • Sampel berpasangan :

Umumnya digunakan pd desain penet. Eksperimen ( membandingkan keadaan sebelum dan sesudah perlakuan atau membandingkan kelp perlakuan & kontrol)

• Aturan umum:

a. Jml N (fo) > 40 ( fh tdk ada syarat –gunakan koreksi yates)

b. Bila 20 ≤ N ≤ 40 maka semua fh ≥ 5

c. Bila fh ≤ 5 gunakan fisher exact test

2. Pengujian Hipotesis :

Menggunakan tabel kontingensi 2 X 2 dk = (b-1)(k-1)

9

Pola tabel :

Rms : (Pendekatan koreksi Yates) X2 = n(|ad-bc| -½ n)2

(a+b)(a+c)(b+d)(c+d) 3. Keputusan hipotesis

Kelompok Pengaruh perlakuan Jml Berpengaruh Tdk berpengaruh Eksp Kontrol a c b d a+b c+d Jumlah a+c b+d N X2_{hitung < X}2_{(tabel,α) : Ho} diterima Ha ditolak X2hitung ≥ X2(tabel,α) : Ho ditolak Ha diterima Contoh:

• Suatu penelitian dilakukan utk mengetahui perbedaan diklat thd peningkatan pengetahuan peserta . Kelompok yg diberi penyuluhan sebanyak 80 org yg tdk diberi penyuluhan 70 org.

Pada akhir diklat, sebanyak 60 org meningkat pengetahuannya sedangkan yg tdk 20 org. Dari kelompok yg tdk diberi diklat ada perbedaan (kel kontrol) yg pengetahuannya meningkat sebanyak 30 org & yg tdk meningkat 40 org.

• Hipotesis :

Ho : Tidak ada perbedaan peningkatan pengetahuan Ha : Ada perbedaan peningkatan pengetahuan

11

Langkah pembuktian hipotesis

X2 = n(|ad-bc| -½n)2 (a+b)(a+c)(b+d)(c+d) X2 = 150(|60.40- 20.30| -½.150)2 (60+20)(60+30)(20+40)(30+40) X2 = 14,76 X2 tabel ( α= 5%, dk=1) = 3,841

X2_hitung >X2_tabel : Ho ditolak, Ha diterima

Kesimp : Ada perbedaan pengetahuan sebelum dan sesudah mengikuti diklat Kelompok Pengaruh perlakuan

Jml Berpengaruh Tdk berpengaruh Eksp Kontrol 60 30 20 40 80 70 Jumlah 90 60 150 12

SOAL2 LATIHAN

1. Suatu penelitian ingin menguji

efektifitas serum jenis A dan B

thd kesembuhan ( +) atau (-) dr

penyakit X. Dari hasil uji

diperoleh data sbb :

Jenis (+) (-) Total

Serum A 75 25 100

Serum B 65 35 100

Total 140 60 200

Buktikan apakah terdapat perbedaan efektifitas serum A dan B ( α = 1% )

13

SOAL2 LATIHAN

2. Suatu perusahaan farmasi ingin

mengevaluasi efektifitas pil X

yang dikembangkan sebagai obat

anti pusing. Sekelompok pasien

penderita pusing diberi pil X,

sebagai kelompok kontrol diberi

placebo. Hasil pengamatan sbb :

Efektifitas Pil X Placb Total

Pusing ↓ 30 40 70

Pusing ↑ 4 10 14

Total 34 50 84

Buktikan apakah pil X efektif terhadap penyembuhan penyakit ? ( α = 5% )

SOAL2 LATIHAN

3. Suatu penelitian dilakukan untuk mengetahui pengaruh pemberian obat Y terhadap kesembuhan pasien hipertensi. Kelompok yang diberi obat Y sebanyak 24 orang dan yang tidak diberi sejumlah 23 org. Setelah beberapa waktu siperoleh hasil bahwa pasien yang diberi obat dan sembuh sebanyak 14 dan yang belum sembuh sebanyak 10 orang sedangkan kelompok yang tidak diberi obat dan sembuh sebanyak 11 orang yang tidak sembuh 12

Buatlah hipotesis dari pernyataan diatas dan ujilah hipotesis sdr !

15

SOAL2 LATIHAN

15

4. Perhatikan tabel berikut :

Tabel 1. Hubungan antara tingkat pendidikan dengan keikutsertaan KB

KB Pend. dasar SMA Jml

Ikut 9 8 17

Tdk 9 5 14

Jml 18 13 31

Pendidikan

Buatlah hipotesis dari pernyataan diatas dan ujilah hipotesis sdr ! ( α= 1%

16

C. X

2

_{k sampel}

1. Digunakan

• Menguji hipt komparatif > 2 sampel • Data berskala diskrit/nominal

2. Pengujian hipotesis = komparatif 2 sampel bebas Rumus :

k

X2 ₌

∑ (

_fo-fh

₎

2

i=1

fh

3. Keputusan hipotesis= komparatif 2 sampel bebas 4. Contoh :

Dilakukan survei utk mengetahui ada/tdknya perbedaan umur harapan hidup antara penduduk di 5 propinsi di Indonesia.

Umur harapan hdp dikelompokkan menjadi 2 yaitu : ≥ 70 th dan < 70 th.

17 Tabel 1 • Persentase umur ≥ 70 th = 300 + 700 + 800 + 700 + 600X 100% 5800 = 53,45 % • Prosentase umur < 70 th = 800 + 600 + 500 + 500 + 300X 100% 5800 = 46,55 % Propinsi Umur fo DKI ≥ 70 th < 70 th 300 800 Jabar ≥ 70 th < 70 th 700 600 Jateng ≥ 70 th < 70 th 800 500 Jatim ≥ 70 th < 70 th 700 500 DIY ≥ 70 th < 70 th 600 300 Jumlah 5800

X2_{utk menguji hipotesis komparatif}

rata-rata 2 sampel bebas, dimana tiap kelas terdiri dr beberapa kategori

Contoh :

Suatu penelitian dilakukan untuk mengetahui apakah ada perbedaan antara kelompok pegawai negeri dengan pegawai swasta dalam memilih Rumah Sakit. Untuk menjwab

pertanyaan tersebut dilakukan pengumpulan data pada kedua

kelompok tersebut secara random. Dari 150 pegawai negeri yg diambil, 70 org menyatakan pertimbangan memilih Rumah Sakit karena tersedianya dokter yang lengkap, 50 org karena tersedia alat-alat yang canggih, dan 30 org memilih karena biaya murah. Sedangkan dari kelompok pegawai swasta 40 org memilih Rumah Sakit karena tersedianya dokter yang lengkap, 30 org karena tersedia

alat-19

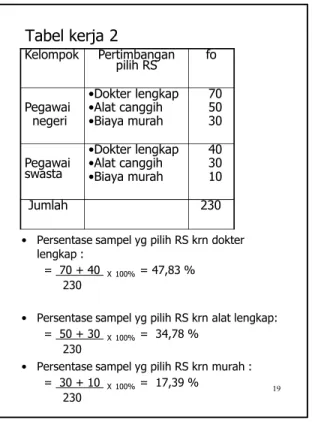
Tabel kerja 2

• Persentase sampel yg pilih RS krn dokter lengkap :

= 70 + 40 _{X 100%} = 47,83 % 230

• Persentase sampel yg pilih RS krn alat lengkap: = 50 + 30 _{X 100%} = 34,78 %

230

• Persentase sampel yg pilih RS krn murah : = 30 + 10 X 100% = 17,39 % 230 Kelompok Pertimbangan pilih RS fo Pegawai negeri •Dokter lengkap •Alat canggih •Biaya murah 70 50 30 Pegawai swasta •Dokter lengkap •Alat canggih •Biaya murah 40 30 10 Jumlah 230 20

• Fh yg pilih RS krn dokter lengkap : Pegneg = 150 X 47,83 % = 71,74 Pegswa = 80 X 47,83 % = 38,26

• Fh yg pilih RS krn alat lengkap : Pegneg = 150 X 34,78 % = 52,17 Pegswa = 80 X 34,78 % = 27,82

• Fh yg pilih RS krn alat lengkap : Pegneg = 150 X 17,39 % = 26,08 Pegswa = 80 X 17,39 % = 13,91

Masukkan rumus :

X

2 =

∑ (

fo-fh

)

2 fh Buat tabel kerja : Buat hipotesis :

21 Kelp Pilih RS fo fh (fo-fh) (fo-fh)2 (fo-fh) 2 fh P N PS Jml Dokter Alat Murah Dokter Alat Murah 70 50 30 40 30 10 230 71,74 52,17 26,10 38,26 27,82 13,91 230 -1,74 -2,17 3,92 1,74 2,18 -3,91 0 3,02 4,70 15,37 3,03 4,75 15,29 0,04 0,09 0,59 0,08 0,17 1,90 2,87

Ho : Tidak terdapat perbedaan

antara pegneg dan

pegswas dlm memilih RS

Ha : Terdapat perbedaan antara

pegneg dan pegswas dlm

memilih RS

dk = (b-1)(k-1)

α = 5%

= (2-1)(3-1)

23

Koefisien Kontingensi C

• Untuk mengetahui kekuatan

hubungan antara variabel bebas

dengan variabel terikat

• Rumus :

C =

C maks =

2 2

x

x

+

N

(

m

1)

m

−

24

ATURAN UMUM & KESIMPULAN

•

Rms 1 : k X2 = ∑ ( fo-fh)2 i=1 _fh Rms 2 : X2 = n ( |ad-bc| )2 (a+b)(a+c)(b+d)(c+d) Rms 3 : Pendekatan koreksi Yates

X2 = n(|ad-bc| -½n)2

(a+b)(a+c)(b+d)(c+d) Keterangan :

1. Rms 1 bila tabel > 2x2 dgn syarat : fh < maksimal 20 % & tidak ada fh < 1

2. Rms 3 dipakai bila tabel 2x2 : * N>40 (fh tdk ada syarat ), * 20 ≤ N ≤ 40 persyaratan :

semua fh ≥ 5, bila fh < 5 gunakan fisher exact

25

Kesimpulan :

•

X2 _{hanya dpt utk menganalisis}

data hasil penghitungan (frekuensi)

• Utk pengetesan korelasi hanya dpt menunjukkan apakah ada korelasi/tidak antara 2

gejala/lebih, namun tdk bisa menghitung besar-kecilnya korelasi

• X2_{paling tepat dipakai utk data}

kategorik/diskrit/nominal, bila dipakai utk data kontinyu maka menggunakan pendekatan koreksi Yates.

Fisher Exact Probability Test

Digunakan utk :

• Menguji sign hipt komparatif 2 sampel kecil ( <= 20)

• Data berskala nominal Tabel kerja :

Keterangan :

• X dan Y menunjukkan adanya klasifikasi. Misal : lulus/tdk, baik/buruk

• A,B,C,D : data nominal berbentuk frekuensi Rumus : P = (A+B)! (C +D )! (A +C )! ( B+D )! Kelompok X Y Jml I A B A+B II C D C+D Jumlah N

27

Penerimaan hipotesis :

Ho diterima, Ha ditolak : p_hitung> α

Contoh:

• Hasil pengamatan terhadap ibu hamil di desa X secara random, diperoleh data bahwa ibu hamil pertamakali

(primigravida) lebih menyukai periksa ke bidan swasta sedangkan ibu hamil lebih dari 1 lebih menyukai di

Puskesmas

.

• Hipotesis :

Pilihan tempat periksa hamil pada ibu hamil 1 sama dgn ibu hamil lebih dari 1.

• Data :Kelompok _Swasta Pusk Jml

Bumil 1 5 3 5+3 Bumil >1 2 5 2+5 Jumlah 7 8 15 28

Penggunaan Aplikasi

SPSS

• Langkah kerja :

• Aktifkan data sheet yang akan diolah ,misal : nonparametric .sav

• Klik menu analize, lalu Descriptive , pilih Crosstab

• Akan muncul kotak dialog , pindahkan variabel yang hendak diuji ke kotak row dan coloumn , semisal hendak diuji variabel pendidikan menurut jenis kelamin, maka letakkan pendidikan di Coloumn, dan Jenis kelamin di Row.

• Klik Statistic, berikan tanda check pada Chi Square( apabila mencari hubungan klik juga pada Contingency Coefficient ), lalu klik Continue

31