19. Fungsi Komposisi dan Fungsi Invers

2. F(x) = f(x)

g(x) _{, DF semua bilangan R, dimana g(x)  0}

B. Komposisi Fungsi dan Invers Fungsi 1. (f ∘ g)(x) = f(g(x))

2. (f ∘ g ∘ h)(x) = f(g(h(x)))

3.

(f ∘ g)– 1 (x) = (g– 1 ∘ f– 1)(x)

4.

f(x) =

ax

+

b

cx

+

d

_{, maka f}– 1_(x)=

−

dx

+

b

cx

−

a

5.

f(x) = a_{log x, maka f}– 1_{(x)= a}x

6.

f(x) = ax_{, maka f}– 1_(x)= a_{log x}

SOAL PENYELESAIAN

1. UN 2012/B25

Diketahui fungsi g(x) = x + 1 dan

f(x) = x2 _{+ x – 1. komposisi fungsi (fg)(x)} = ...

A. x2 _{+ 3x + 3} B. x2 _{+ 3x + 2} C. x2 _{– 3x + 1} D. x2 _{+ 3x – 1} E. x2 _{+ 3x + 1} Jawab : E

2. UN 2012/E52

Diketahui fungsi f(x) = 2x + 1 dan g(x) = x2 _{– 4x. Komposisi (fg)(x) =…..} A. 2x2 _{+ 8x + 2 D. 2x}2 _{– 8x –2} B. 2x2 _{– 8x + 2 E. 2x}2 _{– 8x –1} C. 2x2 _{– 8 + 1 Jawab : C}

3. UN 2011 PAKET 12

Diketahui f(x) = 2x + 5 dan g(x) =

x

−

1

x

+

4

, x

≠−

4

_{, maka (fg)(x) = …}

A.

7

x

+

2

x

+

4

,x

≠−

4

_D.

7

x

+

18

x

+

4

,x

≠−

4

B.

2

x

+

3

x

+

4

, x

≠−

4

_E.

7

x

+

22

C.

2

x

+

2

x

+

4

, x

≠−

4

_{Jawab : d}

4. UN 2009 PAKET A/B

Diketahui fungsi-fungsi f : R  R

didefinisikan dengan f(x) = 3x – 5, g : R  R

didefinisikan dengan g(x) =

x

−

1

2

−

x

, x

≠

2

_.

Hasil dari fungsi (f ∘ g)(x) adalah …

a.

2x+13 x+8 , x≠−8

b.

2x+13 x+2 , x≠−2

c.

−2x−13

−x+2 , x≠2

d.

8x−13

−x+2 , x≠2

e.

8x+7

−x+2, x≠2

Jawab : d

5. UN 2007 PAKET A

Diketahui f : R  R, g : R  R dirumuskan oleh f(x) = x2 _{– 4 dan g(x) = 2x – 6. Jika (f}

∘ g)(x) = –4, nilai x = …

A. –6 D. 3 atau –3

B. –3 E. 6 atau –6

C. 3 Jawab : C

6. UN 2007 PAKET B

Diketahui f : R  R, g : R  R dirumuskan oleh f(x) = x – 2 dan g(x) = x2 _{+ 4x – 3. Jika} (g ∘ f)(x) = 2, maka nilai x yang memenuhi

adalah … a. –3 atau 3 b. –2 atau 2 c. –1 atau 2 d. 1 atau –2 e. 2 atau –3 Jawab : a

7. EBTANAS 2002

√

x

−

1

_{, maka fungsi g adalah g(x) = …}

a. 2x – 1 b. 2x – 3 c. 4x – 5 d. 4x – 3 e. 5x – 4 Jawab : c 8. UN 2005

Diketahui g(x) = 2x + 5 dan

(f  g) = 4x2 _{+ 20x + 23. Rumus fungsi f(x)} adalah …

a. x2 _{– 2} b. 2x2 _{– 1}

c.

1

2 x2 _{– 2}

d.

1

2 _x2 _{+ 2}

e.

1

2 x2 _{– 1} Jawab : c 9. UN 2004

Suatu pemetaan f : R  R, g : R  R dengan (g  f)(x) = 2x2 _{+ 4x + 5 dan g(x) = 2x + 3,} maka f(x) = …

a. x2 _{+ 2x + 1} b. x2 _{+ 2x + 2} c. 2x2 _{+ x + 2} d. 2x2 _{+ 4x + 2} e. 2x2 _{+ 4x + 1} Jawab : a 10. UN 2006

Jika g(x) = x + 3 dan (f ∘ g)(x) = x2 – 4,

maka f(x – 2) = …

a. x2 _{– 6x + 5} b. x2 _{+ 6x + 5} c. x2 _{– 10x + 21} d. x2 _{– 10x – 21} e. x2 _{+ 10x + 21} Jawab : c

11. UN 2012/A13

Diketahui fungsi f(x) = 3x – 1, dan

g(x) = 2x2 _{– 3. Komposisi fungsi (gf)(x) = …}

A. 9x2 _{– 3x + 1}

B. 9x2 _{– 6x + 3}

C. 9x2 _{– 6x + 6}

D. 18x2 _{– 12x – 2}

Jawab : E

12. UN 2012/D49

Diketahui fungsi f(x) = 2x – 3 dan g(x) = x2 _{+ 2x – 3. Komposisi fungsi} (gof)(x) = ..

A. 4x2 _{+ 4x – 9} B. 4x2 _{+ 4x – 3} C. 4x2 _{+ 6x – 18} D. 4x2 _{+ 8x} E. 4x2 _{– 8x} Jawab : E

13. UN 2011 PAKET 46

Fungsi f dan g adalah pemetaan dari R ke R yang dirumuskan oleh f(x) = 3x + 5 dan

g(x) =

2

x

x

+

1

, x

≠−

1

_{. Rumus (gf)(x)} adalah …

a.

6

x

x

+

6

, x

≠−

6

_d.

6

x

+

5

3

x

+

6

,x

≠−

2

b.

5

x

+

5

x

+

1

,x

≠−

1

_e.

5

x

+

5

3

x

+

6

,x

≠−

2

c.

6

x

+

10

3

x

+

6

,x

≠−

2

_{Jawab : c}

14. UN 2010 PAKET A

Diketahui fungsi f(x) = 3x – 5 dan

g(x) =

4x−2 6−4x, x≠

3

2 _{. Nilai komposisi} fungsi

(g  f)(2) adalah … a.

1 4

b.

2 4

d. 1 e. 8 Jawab : d

15. UN 2010 PAKET B

Diketahui fungsi f(x) = x+1

x−3, x≠3 _{, dan} g(x) = x2 _{+ x + 1. Nilai komposisi fungsi} (g  f)(2) = …

a. 2 b. 3 c. 4 d. 7 e. 8 Jawab : d

16. UAN 2003

Ditentukan g(f(x)) = f(g(x)). Jika f(x) = 2x + p dan g(x) = 3x + 120, maka nilai p = …

a. 30

b. 60

c. 90

d. 120

e. 150

Jawab : b

17. UN 2008 PAKET A/B

Fungsi f : R  R didefinisikan dengan

f(x) =

3x+2 2x−1, x≠

1 2 _.

Invers dari f(x) adalah f – 1 _{(x) = …}

A. x−2 2x+3, x≠−

3

2 _D.

x+2 2x−3, x≠

3 2

B. x−2 2x+3, x≠

3

2 _E.

x+2 2x+3, x≠−

3 2

C. x+2 3−2x, x≠

3

2 _{Jawab : d}

18. UAN 2003

Fungsi f : R  R didefinisikan sebagai

f(x) = 2x−1 3x+4

, x

≠

−4

3 _.

Invers dari fungsi f adalah f-1_{(x) = …}

a.

4x−1 3x+2

, x

≠

−2 3

b.

4x+1 3x−2

,x

≠

2 3

c.

4x+1 2−3x

,x

≠

0

y = 2– x

Y

X d.

4x−1 3x−2

, x

≠

2 3

e.

4x+1 3x+2

, x

≠

−2 3

Jawab : c

19. UN 2010 PAKET A

Jika f – 1_{(x) adalah invers dari fungsi}

f(x) = 2x−4

x−3 , x≠3 _{. Maka nilai f} – 1_{(4) = …} a. 0

b. 4 c. 6 d. 8 e. 10 Jawab : b

20. UN 2010 PAKET A

Dikatahui f(x) = 1−5x

x+2 ,x≠−2 _{dan f} – 1_(x) adalah invers dari f(x). Nilai f – 1 _{( –3 ) = …}

a.

4 3

b. 2

c.

5 2

d. 3

e.

7 2

Jawab : e

21. UN 2010 PAKET A/B

Perhatikan gambar grafik fungsi eksponen berikut ini!

Persamaan grafik fungsi invers pada gambar adalah….

A. y = 2_{log x D. y = –2 log x}

B. y =

1 2

log

x

E. y = –

1 2 _{log x}

C. y = 2 log x Jawab : b

22. UN 2009 PAKET A/B

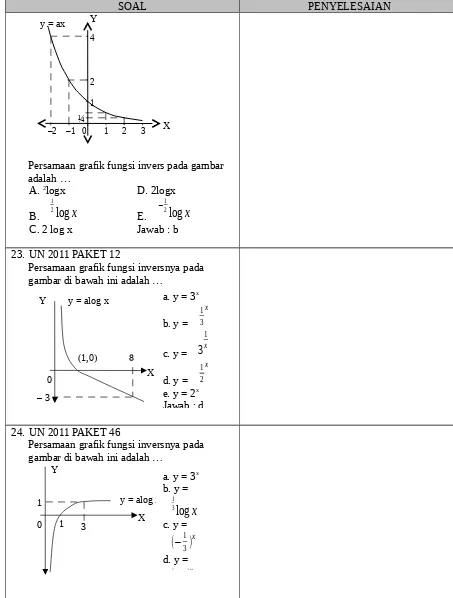
1 2 4

–2 –1 0 1 2 3

¼

y = ax Y

X

0

(1,0) 8

– 3

y = alog x Y

X

0 1

1

3

y = alog x Y

X

Persamaan grafik fungsi invers pada gambar adalah …

A. 2_{logx D. 2logx}

B.

1 2

log

x

E.

−1₂

log

x

C. 2 log x Jawab : b

23. UN 2011 PAKET 12

Persamaan grafik fungsi inversnya pada gambar di bawah ini adalah …

24. UN 2011 PAKET 46

Persamaan grafik fungsi inversnya pada gambar di bawah ini adalah …

a. y = 3x

b. y =

1 3

x

c. y =

3

1

x

d. y =

1 2

x

e. y = 2x Jawab : d

a. y = 3x b. y =

1 3

log

x

c. y =

(−

1₃

)

x

d. y =

(−

3

)

x