FUNGSI KOMPOSISI DAN FUNGSI INVERS
1. Relasi dan Fungsi 2. Fungsi Khusus
3. Fungsi Surjektif, Injektif, dan Bijektif 4. Aljabar Fungsi
5. Fungsi Komposisi
LEMBAR KERJA SISWA 1
Mata Pelajaran : Matematika Uraian Materi Pelajaran : Relasi dan Fungsi
Kompetensi Dasar Menggunakan sifat dan aturan fungsi komposisi dalam pemecahan masalah
Kelas / Semester : XI IA
Waktu : 3 x 45 menit
MATERI :
I. Pengertian produk Cartesius, Relasi dan Fungsi A. Pengertian Produk Cartesius
Jika A dan B adalah dua himpunan yang tidak kosong, maka produk Cartesius himpunan A dan himpunan B adalah himpunan semua pasangan terurut (x,y) dengan x A dan y B dan ditulis AxB = {(x,y) | x A dan y B}.
Contoh :
Misal A : {a, b, c} dan B : {1, 2}, tentukan : a. A x B c. A x A
b. B x A d. B x B Jawab :
a. A x B = {(a,1), (b,1), (c,1), (a,2), (b,2), (c,2)} b. B x A = {(1,a), (1,b), (1,c), (2,a), (2,b), (2,c)}
c. A x A = {(a,a), (a,b), (a,c), (b,a), (b,b), (b,c), (c,a), (c,b), (c,c)} d. B x B = {(1,1), (1,2), (2,1), (2,2)}
B. Relasi Misal :
a. Himpunan ordinat pertama dari pasangan terurut (x,y) disebut daerah asal (domain).
b. Himpunan B, disebut daerah kawan (kodomain).
c. Himpunan bagian dari B yang bersifat Ry dengan y B disebut
daerah hasil (range) relasi R.
Suatu relasi R = {(x,y) | x A dan x B} dapat ditulis dengan menggunakan :
a. Diagram panah
b. Grafik pada bidang Cartesius Contoh :
Relasi dari himpunan A : {1,2,3,4} ke himpunan B : {0,1,2,3,4} ditentukan oleh f : {(1,0), (2,1), (3,2), (4,3)} dapat dituliskan rumus fungsi f : {(x,y) | y = x-1, x A, y B}.
Fungsi f disajikan dalam diagram panah sebagai berikut : Domain : Df : {1,2,3,4}
Kodomain : Kf : {0,1,2,3,4}
Range : Rf : {0,1,2,3}
Relasi f
Fungsi f dapat digambarkan grafik pada bidang kartesius : y
3
2 1 2 3 4
1
1 2 3 4 x
C. Fungsi atau Pemetaan
Relasi dari himpunan A ke himpunan B disebut fungsi atau pemetaan, jika dan hanya jika tiap unsur dalam himpunan A berpasangan tepat hanya dengan sebuah unsur dalam himpunan B.
f adalah suatu fungsi dari himpunan A ke himpunan B, maka fungsi f dilambangkan dengan f : A B
jika x A dan y B, sehingga (x,y)
f, maka y disebut peta atau bayangan dari x oleh fungsi f dinyatakan dengan lambang y : f (x)
(ditunjukkan dalam gambar disamping)
A B
y = f (x) : rumus untuk fungsi f x disebut variabel bebas y disebut variabel tak bebas Contoh :
Diketahi f : A B dan dinyatakan oleh rumus f (x) = 2x – 1.
Jika daerah asal A ditetapkan A : {x | 0 x 4. x R} a. Tentukan f (0), f (1), f (2), f (3) dan f (4).
b. Gambarkan grafik fungsi y : f (x) = 2x – 1 dalam bidang kartesius. f : x y = f (x)
c. Tentukan daerah hasil dari fungsi f. Jawab :
a. f (x) = 2x – 1, maka : f (0) = -1
f (1) = 1 f (2) = 3 f (3) = 5 f (4) = 7
b. Grafik fungsi y : f (x) = 2x – 1
8 y = f (x) = 2x – 1
7
5
1
1 2 3 4 5
-1 Daerah
asal
c. Daerah hasil fungsi f Rf = {y | -1 y 7, y R}
Jika daerah asal dari suatu fungsi f tidak atau belum ditentukan, maka dapat diambil daerah asalnya himpunan dari semua bilangan real yang mungkin, sehingga daerah hasilnya merupakan bilangan real. Daerah asal yang ditentukan dengan cara seperti itu disebut daerah asal alami (natural domain).
Contoh :
Tentukan daerah asal alami dari fungsi berikut :
1. f (x) = 1 x
4
Jawab :
f (x) = 1 x
4
, supaya f (x) bernilai real maka x + 1 0 atau x -1 Jadi Df : {x | x R, dan x -1}
2. g (x) = 4 x2
Jawab :
g (x) = 4 x2 , supaya g (x) bernilai real maka :
4 – x2 0
(x-2) (x+2) 0 -2 x 2 Jadi Dg = {x | -2 x 2, x R}
Latihan 1
1. Relasi-relasi himpunan A : {a,b,c,d} ke himpunan B : {1,2,3,4} berikut ini manakah yang merupakan fungsi / pemetaan (gambarkan terlebih dulu diagram panahnya).
a. f = {(a,1), (b,2), (c,3), (d,4)} b. g = {(a,2), (b,2), (c,3), (d,3)} c. h = {(a,4), (b,1), (b,3), (c,2), (d,4)} d. i = {(a,1), (a,2), (a,3), (a,4)}
e. j = {(a,1), (b,1), (c,1), (d,1)}
2. Relasi-relasi yang disajikan dalam bentuk grafik kartesius manakah yang merupakan pemetaan atau fungsi ?
a. b.
y y
c. d.
y y
0 x 0 x
3. Diketahui fungsi f : R R dinyatakan dengan rumus f (x) = x2 – 1.
Jika daerah asal f adalah Df : {x | -3 x 3, x R}
a. Tentukan f (-3), f (-2), f (0), f (1), f (2), f (3).
b. Gambarkan grafik fungsi f (x) = x2 – 1 dalam bidang kartesius.
c. Tentukan daerah hasil fungsi f.
d. Tentukan nilai a jika diketahui f (a) = 3. 4. Tentukan daerah asal alami pada fungsi berikut !
a. f (x) = 5x 2
b. g (x) =
3 x 4
1
c. f (x) =
2 x 3 x
3
2
d. g (x) =
1 x
LEMBAR KERJA SISWA 2 Mata Pelajaran : Matematika
Uraian Materi Pelajaran : Fungsi Khusus
Kompetensi Dasar : Menggunakan sifat dan aturan fungsi komposisi Dalam pemecahan masalah
Kelas / Semester : XI IPA / I
Waktu : 3 x 45 menit
MATERI :
I. Beberapa Fungsi Khusus
Beberapa fungsi khusus meliputi : A. Fungsi konstan
Fungsi konstan : semua anggota dalam himpunan A dihubungkan hanya dengan sebuah unsur dalam himpunan B.
Ditulis dengan : f : x k, k : konstanta
Disajikan dalam :
a. Diagram panah b. Grafik pada bidang kartesius y
y = f (x) = k (0,k)
x
B. Fungsi identitas
Fungsi identitas : semua unsur dalam himpunan A dihubungkan dengan dirinya sendiri.
Ditulis dengan : f : x I (x) = x
Disajikan dalam :
a. Diagram panah b. Grafik pada bidang kartesius
C. Fungsi genap dan fungsi ganjil
Fungsi f : x f (x) disebut fungsi genap jika f (-x) = + f (x)
Fungsi f : x f (x) disebut fungsi ganjil jika f (-x) = - f (x)
Jika ada fungsi yang tidak memenuhi kedua pernyataan di atas disebut fungsi tidak genap dan tidak ganjil.
Contoh :
1. Tentukan fungsi genap atau fungsi ganjil di antara fungsi berikut : a. f (x) = x2 + 1
b. f (x) = x3
c. f (x) = x3 – 1
Jawab :
a. f (x) = x2 + 1
f (-x) = (-x)2 + 1 = x2 + 1 = + f (x)
Jadi f (x) = x2 + 1 adalah fungsi genap
b. f (x) = x3
f (-x) = (-x)3 = -x3 = - f (x)
Jadi f (x) = x3 adalah fungsi ganjil
c. f (x) = x3 – 1
f (-x) = (-x)3 – 1 = -x3 – 1
f (-x) + f (x) dan f (-x) -f (x)
Jadi f (x) = x3 – 1 bukan fungsi genap dan bukan fungsi ganjil.
Contoh penyajian dalam grafik bidang kartesius Fungsi genap Fungsi ganjil
y y = f(x) = x2+1 y y = f(x) = x3
(0,1) 0
x -1 1 x
D. Fungsi Linier
Fungsi linier ditentukan dengan rumus f (x) = mx + n, m dan n adalah
konstanta, m 0.
Disajikan dalam grafik bidang kartesius :
Grafiknya berupa garis lurus yang memotong dengan sumbu x di
x = m
n
dan memotong sumbu y
di y = n.
Nilai m adalah koefisien arah atau gradien dan m = tg .
E. Fungsi Kuadrat
Fungsi kuadrat ditentukan dengan rumus f (x) = ax2 + bx + c.
a, b, c = konstanta dan a 0.
Grafik fungsi kuadrat disebut parabola.
F. Fungsi Modulus (fungsi mutlak)
Fungsi modulus disajikan dalam f : x |x| didefinisikan sebagai :
+ x, jika x > 0 |x| = 0, jika x = 0 - x, jika x < 0
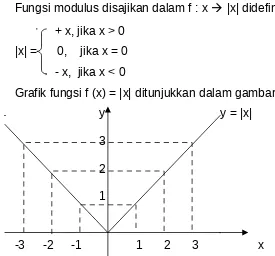
Grafik fungsi f (x) = |x| ditunjukkan dalam gambar :
y y = |x|
3
2
1
-3 -2 -1 1 2 3 x
)
(o,n)
Contoh :
Diketahui fungsi f : x |x-1| dengan x R
a. Ditentukan f (-3), f (-2), f (-1), f (0), f (1), f (2), f (3) b. Tentukan p, jika f (p) = 10
c. Tentukan q, jika f (q) = 4
d. Gambarkan grafik fungsi f dalam bidang kartesius Jawab :
a. f (x) = |x-1|
f (-3) = |-3-1| = |-4| = 4 f (0) = |0-1| = |-1| = 1 f (-2) = |-2-1| = |-3| = 3 f (1) = |1-1| = |0| = 0 f (-1) = |-1-1| = |-2| = 2 f (2) = |2-1| = |1| = 1 f (3) = |3-1| = |2| = 2 b. f (p) = |p-1| = 10
p –1 = 10 atau p – 1 = -10 p = 11 atau p = -9 c. f (q) = |q-1| = 4
q –1 = 4 atau p – 1 = -4 p = 5 atau p = -3 d. Gambar grafik
y
G. Fungsi Tangga atau Fungsi Nilai Bulat Terbesar
Fungsi nilai bulat terbesar disajikan dengan f : x [[x]], yaitu suatu
nilai bulat terbesar yang kurang dari atau sama dengan x.
Grafik fungsi y : f (x) = [[x]], x R diperlihatkan dalam gambar sebagai berikut :
Contoh :
-2 x < -1 [[x]] = -2 -1 x < 0 [[x]] = -1 0 x < 1 [[x]] = 0
1 x < 2 [[x]] = 1 2 x < 3 [[x]] = 2
y
3
2
1
-2 -1 1 2 3
-1
-2
Karena grafiknya menyerupai tangga, maka f (x) = [[x]] sering disebut fungsi tangga.
Latihan 2
1. Gambarkan grafik fungsi berikut pada bidang kartesius a. f : x 4
c. f : x x2 + 5x
d. f : x |4x-1|
2. Diantara fungsi-fungsi berikut mana yang merupakan fungsi ganjil dan mana yang merupakan fungsi genap.
a. f (x) = 3x + 1 b. f (x) = x2 – 6
c. f (x) =
3 x
1 x
2 2
d. f (x) = x21
3. Gambar grafik fungsi modulus f (x) = |x| - 1 pada bidang kartesius. 4. Gambarkan grafik fungsi g (x) = [[2x-1]] dengan x R pada bidang
LEMBAR KERJA SISWA 3
Mata Pelajaran : Matematika
Uraian Materi Pelajaran : Fungsi Surjektif, Fungsi Injektif, dan Fungsi Bijektif Kompetensi Dasar : Menggunakan sifat dan aturan fungsi komposisi dalam pemecahan masalah.
Kelas / Semester : XI IPA / I
Waktu : 2 x 45 menit
MATERI :
A. Fungsi Surjektif
Suatu fungsi f : A B disebut fungsi surjektif atau fungsi onto atau fungsi
Contoh dalam diagram panah
A : {1,2,3,4} , B : {a,b,c}
Fungsi f : A B dinyatakan dalam pasangan
terurut : f = {(1,a), (2,c), (3,b), (4,c)}.
Tampak bahwa daerah hasil fungsi f adalah Rf
: {a,b,c} dan Rf = B maka fungsi f adalah
fungsi surjektif atau fungsi onto atau fungsi kepada.
Fungsi f : A B disebut fungsi into atau fungsi ke dalam jika dan hanya
jika daerah hasil fungsi f merupakan himpunan bagian murni dari
himpunan B atau Rf B.
Contoh :
A : {1,2,3,4} , B : {a,b,c}
fs f : A B dinyatakan dalam pasangan
terurut f : {(1,a), (2,b), (3,a), (4,b)}.
Tampak bahwa daerah hasil fs f : Rf : {a,b} dan Rf B, maka fungsi f adalah fungsi into atau fungsi ke dalam.
A f B
1
2
3
4
a b c
1
2
3
4
a b c
B. Fungsi Injektif
Fungsi f : a B disebut fungsi injektif (fungsi satu-satu) jika dan hanya jika
untuk tiap a1, a2 A dan a1 a2 berlaku f (a1) f (a2).
Contoh :
A : {1,2,3} , B : {a,b,c}
f : A B dinyatakan dalam pasangan
terurut f : {(1,a), (2,b), (3,c)}.
Tampak bahwa tiap anggota A yang berbeda mempunyai peta yang berbeda di B
Fungsi f adalah fungsi injektif atau satu-satu.
C. Fungsi Bijektif
Fungsi f : A B disebut fungsi bijektif jika dan hanya jika fungsi f sekaligus
merupakan fungsi surjektif dan fungsi injektif. Contoh :
A : {1,2,3} , B : {a,b,c}
fs f : A B, dinyatakan dalam pasangan
terurut f : {(1,a), (2,c), (3,b)}.
Tampak bahwa fungsi f adalah fungsi surjektif sekaligus fungsi injektif.
fungsi f adalah fungsi bijektif atau korespondensi satu-satu.
Latihan 3
1. Fungsi-fungsi berikut adalah fungsi-fungsi dari himpunan A : {p,q,r} ke himpunan B : {a,b,c}. Manakah yang merupakan fungsi surjektif.
2. Fungsi-fungsi berikut adalah fungsi-fungsi dari himpunan A : {1,2,3,4} B : {a,i,u,e,o}, manakah yang merupakan fungsi injektif.
a. f : {(1,a), (2,e), (3,i), (4,o)}
b. g : {(1,a), (1,e), (1,i), (1,o), (1,u)} c. h : {(1,a), (2,e), (3,i), (4,u)} d. k : {(,a), (2,a), (3,e), (4,e)}
3. Diantara fungsi-fungsi berikut, manakah yang merupakan fungsi injektif ? a. y : f (x) = 2x – 1
b. y : f (x) = x2
c. y : f (x) = x3
4. Fungsi-fungsi berikut adalah fungsi-fungsi dari himpunan A : {0,2,4,6} ke himpunan B : {a,b,c,d}, manakah yang merupakan fungsi bijektif.
LEMBAR KERJA SISWA 4
Mata Pelajaran : Matematika Uraian Materi Pelajaran : Aljabar Fungsi
Kompetensi Dasar : Menggunakan sifat dan aturan fungsi komposisi dalam pemecahan masalah.
Kelas / Semester : XI IPA / I
Waktu : 2 x 45 menit
MATERI :
Jenis operasi aljabar sering dijumpai dalam himpunan bilangan real, seperti penjumlahan, pengurangan, perkalian, pembagian dan perpangkatan. Operasi aljabar pada bilangan real dapat diterapkan pada aljabar fungsi, yaitu jika diketahui fungsi f (x) dan g (x), dan n bilangan rasional.
Operasi aljabar pada fungsi ditetapkan sebagai berikut : 1. Jumlah fungsi f (x) dan g (x) ditulis (f + g) (x) = f (x) + g (x)
Diketahui fungsi-fungsi f dan g ditentukan dengan rumus f (x) = 2x – 10 dan g (x) = 2x 1
Tentukan nilai fungsi-fungsi berikut, kemudian tentukan domain alaminya.
Jawab :
b. Selisih fungsi f (x) dan g (x) adalah
(f – g) (x) = f (x) – g (x) = 2x – 10 - 2x 1
Domain alami fs (f – g) (x) = Df – g = {x | x ½ , x R}
c. Perkalian fungsi f (x) dan g (x) adalah
(f x g) (x) = f (x) x g (x) = (2x – 10) ( 2x 1) = 2x 2x 1 - 10 2x 1
Domain alami fs (f x g) (x) = Df x g = {x | x ½ , x R}
d. Pembagian fungsi f (x) dengan g (x) adalah
Karena bagian penyebut tidak boleh nol, maka domain alami fungsi
e. Perpangkatan fungsi f (x)
f3 (x) = {f (x)}3 = (2x – 10)3 = 8x3 – 160x2 + 800x – 1000
Dari contoh di atas, terlihat bahwa jika Df adalah domain alami fungsi f, dan
Dg adalah domain alami fungsi g maka domain alami dari fungsi-fungsi f + g, f
– g, f x g, gf adalah irisan dari Df dan Dg ditulis Df Dg.
Latihan 4
f (x) = x2 + 1 dan g (x) =
2. Fungsi f dan fungsi g ditentukan oleh rumus
f (x) =
Tentukan fungsi-fungsi berikut, kemudian tentukan domain alaminya.
LEMBAR KERJA SISWA 5
Mata Pelajaran : Matematika Uraian Materi Pelajaran : Fungsi Komposisi
Kompetensi Dasar : Menggunakan sifat dan aturan fungsi komposisi dalam pemecahan masalah.
Kelas / Semester : XI IPA / I
Waktu : 3 x 45 menit
MATERI :
1. Pengertian komposisi fungsi
Dari dua buah fungsi f (x) dan g (x) dapat dibentuk fungsi baru dengan menggunakan operasi komposisi. Operasi komposisi dilambangkan dengan o (dibaca : komposisi atau bundaran).
Fungsi baru yang dapat dibentuk dengan operasi komposisi itu adalah : a. (f o g) (x) dibaca : f komposisi gx atau fgx
b. (g o f) (x) dibaca : g komposisi fx atau gfx
1) Misal fungsi
g : A B ditentukan dengan y = g (x)
f : B C ditentukan dengan y = f (x)
Fungsi komposisi f dan g ditentukan dengan : h (x) = (f o g) (x) = f (g(x))
2) Misal fungsi
f : A B ditentukan dengan y = f (x)
g : B C ditentukan dengan y = g (x)
Fungsi komposisi g dan f ditentukan dengan : h (x) = (g o f) (x) = g (f (x))
Contoh :
Misal fungsi f : R R dan g : R R ditentukan dengan rumus f (x) =
3x – 1 dan g (x) = 2x.
Jawab :
2. Syarat Komposisi Fungsi Contoh 1
Misal fungsi f dan g dinyatakan dalam pasangan terurut : f : {(-1,4), (1,6), (2,3), (8,5)}
b. (g o f) = {(-1,1), (1,2), (2,8), (8,-1)}
f g
(g o f) c. (f o g) (4) = 6
d. (f o g) (2) tidak didefinisikan e. (g o f) (1) = 2
f. (g o f) (4) tidak didefinisikan
Contoh 2
Dari contoh 1 dan 2 dapat disimpulkan syarat fungsi komposisi (f o g) adalah :
Hasil irisan antara daerah hasil fungsi g dengan daerah asal fungsi f bukan himpunan kosong.
Rg Df
Daerah asal fungsi komposisi (f o g) adalah himpunan bagian dari daerah asal fungsi g.
D(f o g) Dg
Daerah hasil fungsi komposisi (f o g) adalah himpunan bagian dari daerah hasil fungsi f.
R(f o g) Rf
Contoh :
Diketahui fungsi f : R R dan g : R R ditentukan dengan rumus :
f (x) = 2x + 1 dan g (x) = x
Tentukan : a. (f o g) (x) b. (g o f) (x)
c. Daerah asal (f o g) (x) dan daerah hasil (f o g) (x) d. Daerah asal (g o f) (x) dan daerah hasil (g o f) (x) Jawab :
f (x) = 2x + 1
Daerah asal Df : {x | x R} daerah hasil Rf : {y | y R}
g (x) = x
Daerah asal Dg : {x | x 0, x R}, daerah hasil Rg : {y | y 0, y R}
a. (f o g) (x) = f (g (x)) = f ( x ) = 2 x + 1
b. ( g o f) (x) = g (f (x)) = g (2x + 1) = 2x1
c. Daerah asal (f o g) (x) = D(f o g) = {x | x 0, x R}
Daerah hasil (f o g) (x) = R(f o g) = {y | y 1, y R}
d. Daerah asal (g o f) (x) = D(g o f) = {x | x ½ , x R}
Daerah hasil (g o f) (x) = R(g o f) = {y | y o, y R}
Tampak bahwa D(g of) Df dan R(g o f) = Rg
Latihan 5
1. Fungsi f dan g berikut adalah pemetaan dari R ke R. Tentukan rumus untuk fungsi komposisi (f o g) (x) dan (g o f) (x).
a. f (x) = 4x – 2 dan g (x) = x2
b. f (x) = 5x + 2 dan g (x) = 4 – 2x c. f (x) = x2 + x dan g (x) = x – 1
d. f (x) = x3 + x dan g (x) = 2x2
2. Fungsi f dan g dinyatakan dalam bentuk pasangan terurut sebagai berikut f : {(2,-2), (4,-3), (5,0), (7,-1)}
g : {(-3,2), (-2,4), (-1,5), (0,7)}
Nyatakan fungsi-fungsi komposisi berikut dalam pasangan terurut a. f o g d. f o g (6)
b. g o f e. g o f (-3) c. f o g (5) f. g o f (0)
3. Fungsi f : R R dan g : R R ditentukan dengan rumus :
f (x) = x2 + 3 dan g (x) =
2 x
2
a. Tentukan daerah asal fungsi f dan fungsi g b. Tentukan rumus (f o g) (x) dan (g o f) (x)
c. Tentukan daerah asal dan daerah hasil fungsi (f o g) (x) d. Tentukan daerah asal dan daerah hasil fungsi (g o f) (x) 4. Diketahui fungsi f : R R ditentukan dengan rumus
f (x) = 2x2 – 1 , jika x 1
5x , jika x > 1
a. Hitung f (-2), f (-1), f (0), f (1) dan f (2)
5. Fungsi f dan g adalah fungsi dari R ke R ditentukan dengan rumus
f (x) = x 1 dan f (x) =
3 x 2
2
LEMBAR KERJA SISWA 6
Mata Pelajaran : Matematika
Uraian Materi Pelajaran : - Sifat-sifat komposisi fungsi
- Menentukan fungsi jika fungsi komposisi dan fungsi lain diketahui
Kompetensi Dasar : Menggunakan sifat dan aturan fungsi komposisi dalam pemecahan masalah
Kelas / Semester : XI IPA / I
Waktu : 3 x 45 menit
MATERI :
A. Sifat-sifat Komposisi Fungsi
Sifat-sifat operasi komposisi pada fungsi-fungsi dapat disimpulkan dengan menggunakan beberapa contoh di bawah ini.
Contoh 1
Fungsi f : R R ditentukan oleh rumus f (x) = 3x – 5 dan g (x) = 2x2 – 1
Tentukan :
a. (f o g) (x) dan (g o f) (x)
b. dari hasil di atas apakah (f o g) (x) = (g o f) (x) ? Jawab :
a. (f o g) (x) = …… (g o f) (x) = ……
b. (f o g) (x) ………… (g o f) (x) Kesimpulan : ………….
Contoh 2
Fungsi f : R R dan g : R R, h : R R ditentukan dengan rumus :
f (x) = x + 1 , g (x) = 3x dan h (x) = x2
Tentukan :
a. ((f o g) o h) (x) dan (f o (g o h)) (x)
Jawab :
a. Misal k (x) = (f o g) (x) = f (g (x)) = ……… ((f o g) o h) (x) = ( k o h) (x) = k (h (x)) = ………
Misal l (x) = (g o h) (x) = g (h (x)) = g (………) = ……… (f o (g o h)) (x) = (f o l) (x) = f (l (x)) = f (………) = …… b. ((f o g) oh) (x) …………. (f o (g o h)) (x)
Kesimpulan :
………. ……….
Contoh 3
Fungsi f : R R dan I : R R ditentukan dengan rumus f (x) = x2 – 2x +
1 dan I (x) = x Tentukan :
a. (f o I) (x) dan (I o f) (x)
b. dari hasil di atas apakah (f o I) (x) = (I o f) (x) ? Jawab :
a. (f o I) (x) = f (I (x)) = f (………) = ……… (I o f) (x) = I (f (x)) = I (………) = ……… b. (f o I) (x) ……… (I o f) (x)
Kesimpulan :
………. ……….
Dari ketiga contoh di atas, beberapa sifat operasi komposisi pada fungsi-fungsi dapat disimpulkan sebagai berikut :
2. Operasi komposisi pada fungsi bersifat …… ((f o g) o h) (x) ……… (f o (g o h)) (x)
3. Dalam operasi komposisi pada fungsi-fungsi ada sebuah unsur identitas yaitu fungsi identitas I (x) = x sehingga
(f o I) (x) ……… (I o f) (x) ……… f (x)
B. Menentukan fungsi jika fungsi komposisi dan fungsi yang lain diketahui
Misal fungsi f dan fungsi komposisi (f o g) atau (g o f) sudah diketahui maka fungsi g dapat ditentukan, demikian juga fungsi g dan fungsi komposisi (f o g) atau (g o f) diketahui maka fungsi f dapat ditentukan. Contoh 1
Misal fungsi komposisi (f o g) (x) = -2x + 3 dan f (x) = 2x + 1. Tentukan fungsi g (x).
Jawab :
(f o g) (x) = -2x + 3 f (g (x)) = -2x + 3 2 (g (x)) + 1 = -2x + 3 2 g (x) = -2x + 2
g (x) = 2
2 x 2
g (x) = -x + 1 Jadi fungsi g (x) = -x + 1
Contoh 2
Diketahui fungsi komposisi (f o g) (x) = 4 – 2x dan fungsi g (x) = 2x + 2. Tentukan fungsi f (x).
Jawab :
(f o g) (x) = 4 - 2x f (g (x)) = 4 – 2x f (2x + 2) = 4 – 2x
= 4 – (2x + 2) + 2 f (2x + 2) = 6 – (2x + 2) f (x) = 6 – x
Latihan 6
1. Misal fungsi f, g dan h dinyatakan dalam bentuk pasangan terurut sebagai berikut :
f : {(-6,4), (3,3), (2,5), (8,1)} g : {(-4,-6), (2,3), (3,2), (7,8)} h : {(0,-4), (1,2), (2,3), (3,7)}
Tentukan fungsi-fungsi komposisi berikut dalam bentuk pasangan terurut : a. (g o h) c. (f o (g o h))
b. (f o g) d. ((f o g) o h)
2. Diketahui fungsi f, g dan h adalah pemetaan dari R ke R ditentukan
dengan rumus f (x) = 1 x
x
, g (x) = x 1
dan h (x) = 3x – 1.
Tentukan : a. (f o (g o h)) (x) b. ((f o g) o h) (x)
3. Tentukan rumus untuk fungsi g (x), jika diketahui : a. f (x) = 4x + 1 dan (f o g) (x) = x2 – x – 1
b. f (x) = x2 – x + 4 dan (f o g) (x) = 3 – 2x
4. Tentukan rumus untuk fungsi f (x), jika diketahui a. g (x) = 2x + 1 dan (f o g) (x) = x2 + x
b. g (x) = x + 3 dan (f o g) (x) = 2x – 4
5. Diketahui g (x) = 2 – x dan h (x) = x + 4 dan (f o (g o h)) (x) = x2 + 10x – 2,
LEMBAR KERJA SISWA 7 Mata Pelajaran : Matematika
Uraian Materi Pelajaran : Fungsi Invers
Kompetensi Dasar : Menggunakan sifat dan aturan fungsi invers dalam Pemecahan masalah
Kelas / Semester : XI IPA / I
Waktu : 3 x 45 menit
MATERI :
A. Pengertian Invers Fungsi
Jika fungsi f : A B dinyatakan dalam pasangan terurut
f : {(a,b) | a A dan b B} maka invers dari fungsi f adalah f-1 : B A
ditentukan oleh :
f-1 : {(b,a) | b B dan a A}
Invers suatu fungsi tidak selalu merupakan fungsi. Jika invers suatu fungsi merupakan fungsi maka invers fungsi itu disebut fungsi invers.
Contoh :
1. Misal A : {-2, -1, 0, 1} , B : {1, 3, 4}.
Fungsi f : A B ditentukan oleh f : {(-2,1), (-1,1), (0,3), (1,4)}.
Carilah invers fungsi f, dan selidiki apakah invers fungsi f merupakan fungsi.
Jawab :
Invers fungsi f adalah f-1 = B A ditentukan oleh :
f-1 : {(1,-2), (1,-1), (3,0), (4,1)}.
Fungsi f dan f-1 disajikan dalam gambar diagram panah
f f-1
A B B A
Terlihat bahwa f-1 adalah relasi biasa (bukan fungsi).
-2. Misal A : {1,2,3} B : {2,4,6,8}. Fungsi g : A B ditentukan oleh
g : {(1,2), (2,4), (3,6)}.
Tentukan invers fs g, dan selidiki apakah invers fungsi g merupakan fungsi ?
Jawab : kerjakan sebagai latihan.
g g-1
A B B A
Terlihat bahwa g-1 adalah ………
3. Misal A : {a,b,c,d} dan B : {1,2,3,4}, fungsi h : A B ditentukan oleh
h : {(a,2), (b,1), (c,3), (d,4)}.
Carilah invers fungsi h dan seilidiki apakah invers fungsi h merupakan fungsi ?
Jawab : kerjakan sebagai latihan
h h-1
A B B A
Fungsi h-1 adalah ……
Suatu fungsi f : A B mempunyai fungsi invers f-1 = B A jika dan
hanya jika f merupakan fungsi ……
B. Menentukan rumus fungsi invers
Beberapa langkah untuk menentukan rumus fungsi invers f-1(x) jika f (x)
1. Ubah persamaan y = f (x) dalam bentuk f sebagai fungsi y. 2. Bentuk x sebagai fungsi y pada langkah 1 dinamai dengan f-1(y).
3. Ganti y pada f-1(y) dengan x untuk memperoleh f-1(x). Maka f-1(x)
adalah rumus fungsi invers fungsi f (x). Contoh :
2. Fungsi f ditentukan dengan rumus f (x) = x 1
x
a. Tentukan rumus untuk f-1(x)
x = f-1(y) =
1. Tentukan rumus fungsi invers f-1(x), fungsi berikut :
a. f (x) = 3x – 1 b. f (x) = - ½ x + 5 c. f (x) = 1/
5 (x – 3)
d. f (x) = 3 (x – 2)
2. Tentukan rumus fungsi invers f-1(x) dan daerah asal alami fungsi f (x) dan
fungsi f-1(x) pada fungsi berikut.
a. f (x) =
3. Tentukan rumus fungsi invers f-1(x) dan daerah asal fungsi f (x) agar fungsi
f (x) mempunyai invers dan tentukan rumus fungsi inversnya, pada fungsi berikut :
a. f (x) = (x – 1)2
b. f (x) = x2 – 4x + 2
c. f (x) = x2 – 3x + 1
SOAL-SOAL LATIHAN
1. Jika f(x) = x – 3 , maka f(x2) – 2 f(x) + {f(x)} 2 = ……
a. x2 – 6x + 9
b. x2 – 8x
c. 2x2 – 8x + 12
d. 2x2 – 4x + 12
e. 2x2 – 4x + 9
2. Jika f(x) = x2 – 2x – 17 , maka f(5) – 3f(2) = ….
a. -36 b. -10 c. 25 d. 49 e. 52
3. Jika f(x + 2) = x2 + 2x , maka f(x) = …..
a. 2x + x2
b. 2x - x2
c. –x2 + 2x
d. –x2– 2x
e. x2 – 2x
4. Diketahui f(x) = log x , g(x) = 3x – 2 dan h(x) = sin x , maka f o g o h (x) = .. a. log sin 3x -2
b. log sin (3x -2) c. 3x 2logsin x
d. sinxlog 3x 2
e. sinxlog(3x 2)
5. Jika f :R R , g, R R ,f(x) = x 7
dan g(x) = x2 maka f o g (3 ½) = …
c. 0 d. -1 e. -2
6. Jika g(x) = 3x + 1 dan g(f(x)) = 5x2 + x – 3 ,maka f(x) = …..
a. 1/3 (x2 – x - 4)
b. 1/3 (x2 – x + 4)
c. 1/3 ( x2 – x – 2)
d. 1/3 (5x2 + x + 4)
e. 1/3 (5x2+ x – 4)
7. Jika f(x) = (2x + 1) 2 dan g(x) = 8x2 + 8x + 5 , maka g(x) = ….
a. x +3 b. x – 3 c. 2x + 3 d. 2x – 3 e. 2x + ½
8. Fungsi berikut yang tidak memiliki fungsi invers adalah …. a. y = x +1
b. y = x3
c. y = log x d. y = x2 + 1000
e. y = 1 – 100 x
9. Jika diketahiu f(x) = sin x dan g(x) = x2 – 4x – 6 dan g o f (x) = 1 , maka
nilai sin 2x adalah …… a. -2
c. 0 d. 1 e. 2
10. Invers dari y 2logx adalah …..
a. y = x2
b. y = 2x c. y = log x d. y = 2x

![Grafik fungsi y : f (x) = [[x]], x R diperlihatkan dalam gambar sebagai](https://thumb-ap.123doks.com/thumbv2/123dok/3297671.1748577/14.595.133.469.119.585/grafik-fungsi-y-f-x-r-diperlihatkan-gambar.webp)