1 2 3
–2 –1 0 1 2 3
(1,3) (0,2)
X Y
1. Jika af(x) = ap, maka f(x) = p 2. Jika af(x) = ag(x), maka f(x) = g(x) 3. Jika af(x) = bf(x), maka f(x) = 0 4. Jika {h(x)}f(x) = {h(x)}g(x), maka
a) f(x) = g(x) b) h(x) = 1
c) h(x) = 0 untuk f(x) > 0 dan g(x) > 0
d) h(x) = – 1 untuk f(x) dan g(x) keduanya ganjil atau keduanya genap
5. Jika
A
{
a
f(x)}
2
+
B
{
a
f(x)}
+
C
=
0
, maka dapat diselesaikan secara persamaan kuadrat.SOAL PENYELESAIAN
1. UN 2012/B25
Fungsi eksponen yang sesuai dengan grafik berikut adalah ...
A. f(x) = 2x D. f(x) = 3x + 1 B. f(x) = 2x+1 E. f(x) = 3x C. f(x) = 2x + 1 Jawab : C
2. UN 2012/C37
Fungsi yang sesuai dengan grafik berikut adalah …
A. f(x) = 2x – 1 D. f(x) = 2log (x – 1) B. f(x) = 2x – 1 E. f(x) = 2x – 2 C. f(x) = 2log x Jawab : B
−
1
2 4 10
–2 –1 0 1 2 3
Y
X
1 2 3
–2 –1 0 1 2 3
X Y
SOAL PENYELESAIAN
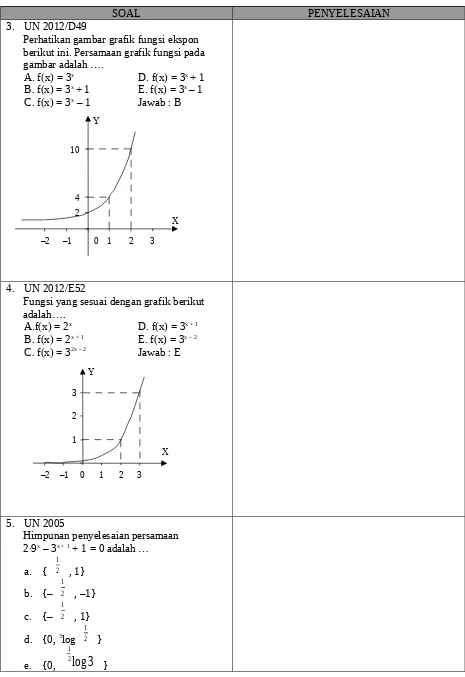
3. UN 2012/D49
Perhatikan gambar grafik fungsi ekspon berikut ini. Persamaan grafik fungsi pada gambar adalah ….
A. f(x) = 3x D. f(x) = 3x + 1 B. f(x) = 3x + 1 E. f(x) = 3x – 1 C. f(x) = 3x – 1 Jawab : B
4. UN 2012/E52
Fungsi yang sesuai dengan grafik berikut adalah….
A.f(x) = 2x D. f(x) = 3x + 1 B. f(x) = 2x + 1 E. f(x) = 3x – 2 C. f(x) = 32x – 2 Jawab : E
5. UN 2005
Himpunan penyelesaian persamaan 2·9x – 3x + 1 + 1 = 0 adalah …
a. {
1 2 , 1}
b. {–
1 2 , –1}
c. {–
1 2 , 1}
d. {0, 3log
1 2 }
e. {0, 1 2
log 3
SOAL PENYELESAIAN Jawab : d
6. EBTANAS 2002
Nilai x yang memenuhi
√
3
2x+1 = 9x – 2 adalah …a. 2 b. 2½ c. 3 d. 4 e. 4½
Jawab : e
7. UN 2009 PAKET A/B
Akar–akar persamaan 2x + 23 – x = 9 adalah dan . Nilai + = …
a. 3 b. 4 c. 6 d. 8 e. 9 Jawab : a
8. UN 2007 PAKET A
Diketahui x1 dan x2 akar–akar persamaan
9x – 10
3 ·3x + 1 = 0. Nilai x1 + x2 = … a. 2
b.
3 2
c. 1 d. 0 e. – 2 Jawab : d
9. UN 2007 PAKET B
Akar–akar persamaan 32 + x + 31 – x = 12, adalah x1 dan x2. Nilai 2x1 + 2x2 = … a. –4
b. –2 c. –1
d.
4 9
e.
2 3
SOAL PENYELESAIAN
10. UAN 2003
Penyelesaian persamaan
√
8
x2−4x+3=
1
32
x−1adalah p dan q, dengan p > q. nilai p + 6q = …
a. –17 b. –1 c. 3 d. 6 e. 19
Jawab : b
11. UN 2008 PAKET A/B
Akar–akar persamaan 4x – 12 2x + 32 = 0 adalah x1 dan x2. nilai x1 x2 = …
B. Pertidaksamaan Eksponen
Untuk a > 1
1. Jika af(x) > ag(x), maka f(x) > g(x) 2. Jika af(x) < ag(x), maka f(x) < g(x)
Jika 0 < a < 1
1. Jika af(x) > ag(x), maka f(x) < g(x) 2. Jika af(x) < ag(x), maka f(x) > g(x)
SOAL PENYELESAIAN
1. UN 2012/A13
Nilai x yang memenuhi pertidaksamaan 32x + 1 + 9 – 283x > 0, x R adalah…
A. x > –1 atau x > 2 B. x < –1 atau x < 2 C. x < 1 atau x > 2 D. x < –1 atau x > 2 E. x > –1 atau x < –2 Jawab : D
2. UN 2012/C37
Nilai x yang memenuhi pertidaksamaan 92x – 109x + 9 > 0, x R adalah …
A. x < 1 atau x > 9 B. x < 0 atau x > 1 C. x < –1 atau x > 2 D. x < 1 atau x > 2 E. x < –1 atau x > 1 Jawab : B
3. UN 2012/D49
Nilai x memenuhi pertidaksamaan 52x – 65x+1 + 125 > 0, x R adalah….
A. 1 < x < 2 B. 5 < x < 25 C. x < – 1 atau x > 2 D. x < 1 atau x > 2 E. x < 5 atau x > 25 Jawab : D
SOAL PENYELESAIAN 4. UN 2012/E52
Penyelesaiyan pertidak samaan 22x+1 – 52x+1 + 8 0 adalah…. A. x 0 atau x 2
B. x 1 atau x 4 C. x 2 atau x 4 D. 0 x 2 E. 1 x 4 Jawab : A
5. UN 2006
Nilai x yang memenuhi pertidaksamaan
(
√
5
)
x3<
25
x2−3 4x
adalah … a. 1 < x < 3 atau x > 4
b. 0 < x < 1 atau x > 2 c. 0 < x < 3 atau x > 4 d. x < 0 atau 1 < x < 3 e. 0 < x < 1 atau x > 3
Jawab : d
6. UN 2008 PAKET A/B
Himpunan penyelesaian pertidaksamaan
(
13
)
3x−1≤
9
x2+3x−2adalah …
A.
{
x|−5≤x≤12}
B.{
x|−1
2≤x≤5
}
C.
{
x|x≤−5 atau x≥12}
D.{
x|x≤−1
2 atau x≥5
}
E.{
x|x≤12 atau x≥5}
A. Persamaan Logaritma
Untuk a > 0, a
1; f(x) > 0, g(x) > 0
1. Jika alog f(x) = alog p, maka f(x) = p 2. Jika alog f(x) = alog g(x), maka f(x) = g(x)SOAL PENYELESAIAN
1. UN 2009 PAKET A/B
Untuk x yang memenuhi 2
log 16
2x−1 4
=
8
, maka 32x = …
a. 19 b. 32 c. 52 d. 144 e. 208 Jawab : d
2. UN 2004
Himpunan penyelesaian dari persamaan
x
2+2logx=
8
adalah …
a. {
1 3 , 1}
b. {
1 4 , 2}
c. {
1 8 , 1}
d. {
1 8 , 2}
e. {2} Jawab : D
3. UN 2011 PAKET 12
Nilai x yang memenuhi persamaan
1
2
log
(
x
2−
3
)−
12
log
x
=−
1
adalah … a. x = –1 atau x = 3
b. x = 1 atau x = –3 c. x = 1 atau x = 3 d. x = 1 saja e. x = 3 saja Jawab : a
4. UN 2011 PAKET 46
Nilai x yang memenuhi persamaan
2
log
2(
2
x
−
2
)−
2log
(
2
x
−
2
)=
2
adalah …
SOAL PENYELESAIAN e. x = 4 atau x = 6
Jawab : a
5. UN 2008 PAKET A/B
Akar–akar persamaan logaritma
3log2x – 3 3log x + 2 = 3log 1 adalah x1 dan x2. nilai x1 + x2 = ….
a. 2 b. 3 c. 6 d. 9 e. 12 Jawab : E
6. UN 2006
Akar–akar persamaan 4log(2x2 – 3x + 7) = 2 adalah x1 dan x2. Nilai 4x1· x2 = …
a. –6 b. –18 c. 10 d. 18 e. 46 Jawab : B
7. UAN 2003
Jika x1 dan x2 adalah akar–akar persamaan (3log x)2 – 3 3log x + 2 = 0, maka x1· x2 = …
A. 2 D. 24
B. 3 E. 27
C. 8 Jawab : E
8. EBTANAS 2002
Jika 6x – 1 =
(
2 3
)
x+1
, maka x = … a. 2log3
b. 3log2
c. 1 2
log 3
d. 3log6
B. Pertidaksamaan Logaritma
Untuk a > 1
1. Jika alog f(x) > alog g(x), maka f(x) > g(x) 2. Jika alog f(x) < alog g(x), maka f(x) < g(x)
Jika 0 < a < 1
1. Jika alog f(x) > alog g(x), maka f(x) < g(x) 2. Jika alog f(x) < alog g(x), maka f(x) > g(x)
SOAL PENYELESAIAN
1. UN 2004
Himpunan penyelesaian pertidaksamaan 1
2
log
(
x
2−
8
)>
0
adalah … A. {x | –3 < x < 3
B. {x | –
2
√
2
< x <2
√
2
} C. {x | x < –3 atau x < 3D.
{x | x < –2
√
2
atau x <2
√
2
} E. {x | –3 < x < –2
√
2
atau2
√
2
< x <3} Jawab : E
2. EBTANAS 2002
Himpunan penyelesaian pertidaksamaan xlog9 < xlog x2 adalah …
a. {x | x 3} b. {x | 0 < x < 3} c. {x | 1 < x < 3} d. {x | x > 3} e. {x | 1 < x 3} Jawab : D