VI. FUNGSI EKSPONEN DAN FUNGSI LOGARITMA
6.1 Pendahuluan A. Tujuan
Setelah mempelajari bagian ini diharapkan mahasiswa dapat:
1. menuliskan bentuk umum fungsi eksponen;
2. menggambar grafik fungsi eksponen;
3. menuliskan bentuk umum fungsi logaritma;
4. menggambar grafik fungsi logaritma.
B. Deskripsi Singkat Isi Bab
Bab ini berisi uraian tentang:
1. fungsi eksponen;
2. fungsi logaritma.
Kata kunci: fungsi, eksponen, logaritma
6.2 Fungsi eksponen Bentuk Umum
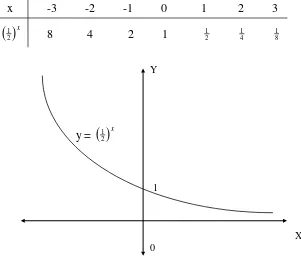
Grafik fungsi konstan dibedakan menjadi dua yaitu untuk 0 < a < 1 dan untuk a > 1.
b) jika x bernilai kecil sekali dan bertanda negatip maka y besar sekali dan bertanda
positip;
c) jika x bernilai besar sekali dan bertanda positip maka y bernilai mendekati nol
2 Grafik y = ax, untuk a > 1
Dipelajari salah satu kasus yaitu y = 2x.
Fungsi y = 2x memiliki sifat-sifat:
a) terdefinisi untuk semua x R;
b) jika x bernilai kecil sekali dan bertanda negatip maka y mendekati nol dan
bertanda positip;
c) jika x bernilai besar sekali dan bertanda positip maka y bernilai besar sekali dan
bertanda positip;
d) untuk x = 0 y = 1.
Dari uraian di atas, ditambah dengan tabel yang berisi beberapa nilai fungsi
berikut ini, grafik y = 2x dapat digambarkan seperti di bawah ini.
6.3 Fungsi Logaritma Bentuk Umum
Jika ay = x dengan a 0 dan a 1 maka yalog x
Grafik fungsi logaritma dibedakan menjadi dua yaitu untuk 0<a<1 dan untuk a > 1.
1. Grafik yalogx, untuk 0 < a < 1
Dipelajari salah satu kasus yaitu y = 12logx.
Fungsi y = 21logxmemiliki sifat-sifat:
a) terdefinisi untuk semua x >0;
b) jika x mendekati nol maka y besar sekali dan bertanda positip;
c) untuk x = 1, y = 0
d) untuk x lebih besar dari 1, y berharga negatip. Jika x semakin besar, maka y
semakin kecil;
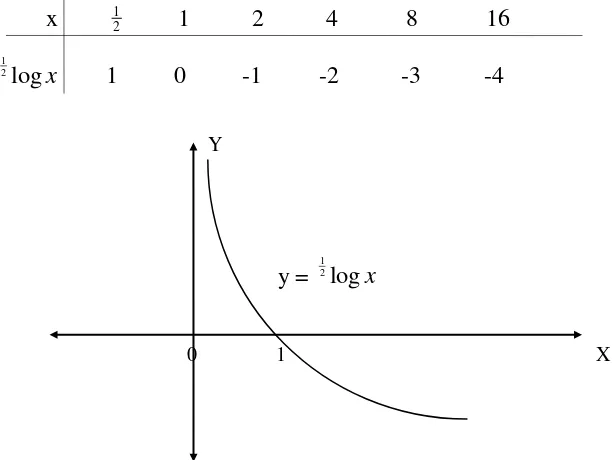
Dari uraian di atas, ditambah dengan tabel yang berisi beberapa nilai fungsi
berikut ini, grafik y = 12logx dapat digambarkan seperti di bawah ini.
x 12 1 2 4 8 16
1
2logx 1 0 -1 -2 -3 -4
Y
y = 12logx
0 1 X
b) jika x mendekati nol maka y kecil sekali dan bertanda negatip;
c) untuk x = 1, y = 0
d) untuk x lebih besar dari 1, y berharga positip. Jika x semakin besar, maka y
semakin besar pula;
Dari uraian di atas, ditambah dengan tabel yang berisi beberapa nilai fungsi
berikut ini, grafik y = 2logx dapat digambarkan seperti di bawah ini.
x 12 1 2 4 8 16
bilangan pokok e, yang disebut logaritma Napier, disingkat ln (dibaca len). Jadi
Rangkuman
1. Bentuk umum fungsi eksponen adalah y = ax, dengan a 0 dan a 1
2. Grafik fungsi eksponen dibedakan menjadi dua yaitu untuk 0<a<1 dan untuk a>1
3. Jika ay = x dengan a 0 dan a 1 maka yalog . x
4. Grafik fungsi logaritma dibedakan menjadi dua yaitu untuk 0<a<1 dan untuk a>1.
5. Dalam fungsi logaritma dikenal satu fungsi khusus yaitu fungsi logaritma de-
ngan bilangan pokok e, yang disebut logaritma Napier, disingkat ln (dibaca
Latihan
1. Tuliskan bentuk umum fungsi eksponen!
2. Gambarkan grafik fungsi berikut ini:
a) y =
1 3x
b) y = 3x
c) y =
14 x1 d) y = 2x13. Tuliskan bentuk umum fungsi logaritma
4. . Gambarkan grafik fungsi berikut ini:
a) y = 13logx
b) y = 3logx
c) y = 13log(x1)
Rangkuman Keseluruhan I. Tinjauan Umum
1. Fungsi digunakan dalam teknik sipil untuk menyatakan hubungan antara variabel
bebas dengan variabel terikat.
2. Fungsi-fungsi tersebut digunakan dalam berbagai kajian bidang teknik sipil se-
perti struktur, mekanika tanah, teknik keairan dan lain-lain.
3. Grafik fungsi digunakan untuk mempresentasikan fungsi secara grafis.
II. Fungsi
1. Diketahui A dan B adalah dua himpunan yang tidak kosong. Suatu fungsi dari A
ke B adalah suatu aturan yang memetakan setiap elemen di A dengan tepat satu
elemen di B.
2. Daerah definisi fungsi y = f(x) adalah himpunan semua nilai x sehingga nilai y
ada.
3. Daerah definisi fungsi y = f(x) adalah himpunan semua nilai y dengan x berasal
dari daerah definisi.
III. Fungsi Polinomial
1. Bentuk umum fungsi polinomial adalah,
p x( )a0 a x1 a x2 2 a x3 3...a xn n, dengan ao, a1, a2, a3, …, an adalah
konstanta dan disebut koefisien fungsi polinomial.
IV. Fungsi Rasional
2. Fungsi rasional sejati yaitu jika derajat p(x) lebih rendah dari derajat q(x).
3. Fungsi rasional tidak sejati yaitu jika derajat p(x) lebih tinggi atau sama dengan
derajat q(x).
2. Bentuk umum fungsi sinus adalah f(x) = sin x, dengan x adalah satuan ukuran
sudut.
3. Bentuk umum fungsi cosinus adalah f(x) = cos x, dengan x adalah satuan ukuran
sudut.
4. Bentuk umum fungsi tangen adalah f(x) = tan x, dengan x adalah satuan ukuran
sudut.
5. Jika x = sin y, maka fungsi invers dari sinus didefinisikan dengan y = arc sin x.
Dengan cara yang sama, jika x = cos y maka inversnya adalah y = arc sin x;
x = tan y maka inversnya adalah y = arc tan x.
1. Bentuk umum fungsi eksponen adalah y = ax, dengan a 0 dan a 1
2. Grafik fungsi eksponen dibedakan menjadi dua yaitu untuk 0<a<1 dan untuk a>1
3. Jika ay = x dengan a 0 dan a 1 maka yalog . x
4. Grafik fungsi logaritma dibedakan menjadi dua yaitu untuk 0<a<1 dan untuk a>1.
5. Dalam fungsi logaritma dikenal satu fungsi khusus yaitu fungsi logaritma de-
ngan bilangan pokok e, yang disebut logaritma Napier, disingkat ln (dibaca
len). Jadi logaritma dengan bilangan pokok e adalah y = e
x
log = ln x.
Croft, A., Davison, R., Hargreaves, M., 1995, Introduction to Engineering Mathema- tics, Addison-Wesley, New York.
Frick, H., 1979, Mekanika Teknik I Statika dan Kegunaanya, Penerbit Yayasan kanisius, Yogyakarta.
Henderson, F.M., 1966, Open Chanel Flow, Macmillan Publishing CO. INC., New York
Karyadi, 2002, Analisis Nonlinier Geometri Struktur Frame-Truss 3D dengan Meto- de Elemen Hingga, Tesis Program Pasca Sarjana, UGM Yogyakarta.
Martono, K., 1985, Kalkulus dan Ilmu Ukur Analitik I, Penerbit Angkasa, Bandung.
Smith, M.J., 1981, Mekanika Tanah, Penerbit Erlangga, Jakarta.
Soemartojo, N., 1985, Kalkulus, Penerbit Erlangga, Jakarta.