9. Mengaplikasikan Konsep Fungsi - Fungsi

(1)

9. M engaplikasikan Konsep Fungsi

Tujuan Pembelajaran

Setelah mempelajari kegiatan belajar pada modul ini diharapkan siswa dapat :

1. Menjelaskan pengertian relasi dan fungsi serta sifat-sifatnya 2. Menjelaskan bentuk umum fungsi linear

3. Menggambar grafik fungsi linear

4. Menentukan persamaan garis lurus yang melalui satu titik dengan gradien tertentu 5. Menetukan persamaan garis lurus yang melalui dua titik

6. Menentukan titik potong dua buah garis lurus yang diketahui persamaannya

7. Menentukan persamaan garis lurus yang melalui sebuah titik dan berpotongan tegak lurus dengan garis lain yang diketahui persamaannya.

8. Menentukan persamaan garis lurus yang melalui sebuah titik dan sejajar garis lain yang diketahui persamaannya.

9. Menentukan invers fungsi linear

10. Menjelaskan bentuk umum fungsi kuadrat

11. Menentukan titik potong grafik fungsi dengan sumbu koordinat 12. Menentukan sumbu simetri dan nilai ekstrim suatu fungsi 13. Menggambar grafik fungsi kuadrat

14. Menentukan persamaan fungsi kuadrat jika diketahui grafik atau unsur-unsurnya

Kegiatan Belajar 1. M endeskripsikan perbedaan konsep relasi dan fungsi

Tujuan Kegiatan Belajar 1

Setelah mempelajari uraian kegiatan belajar ini, siswa diharapkan : 1. Menentukan notasi dari suatu fungsi.

2. Menyatakan suatu fungsi dengan diagram panah.

3. Menyatakan diagram panah dengan himpunan pasangan berurutan.

Uraian M ateri Kegiatan Belajar 1

1.1 Definsi dan Notasi Fungsi

Fungsi atau pemetaan dari himpunan A ke himpunan B adalah relasi yang memasangkan

setiap x∈ A dengan tepat satu y∈ B.

Fungsi f dari himpunan A ke himpunan B dapat dinyatakan sebagai :

a. Diagram panah

• • •

3 2 1

6 5 4 2

• • ••

b. Himpunan pasangan berurutan

F : {(1,4) (2,5) (3,6)}

A {1, 2, 3} disebut domain/ daerah adal (Df)

B {2, 4, 5, 6} disebut kodomain/ daerah kawan (Kf) C {4, 5 , 6} disebut daerah hasil/ range (Rf)

A B

f w

w

.docu-track.com ww

(2)

c. Diagram Cartesius

d. Rumus fungsi

f : A → B dari pemisalan di atas dapat dinyatakan secara rumus f(x) = x + 3.

1.2 Macam-macamFungsi

a. Fungsi konstan

Fungsi konstan dapat dirumuskan f(x) = C, untuk setiap x∈ Domain fungsi.

(C = konstanta) b. Fungsi identitas

Fungsi identitas memetakan setiap x∈ Df ke dirinya sendiri dan dirumuskan f(x) = x.

c. Fungsi Linier d. Fungsi Kuadrat

e. Fungsi Eksponen

f. Fungsi Logaritma

g. Fungsi Trigonometri

Uraian mengenai macam-macam fungsi di atas akan dibahas lebih lanjut pada kegiatan belajar berikutnya.

1.3 Sifat-sifat Fungsi

a. Fungsi f : x ∈ A → y ∈ B adalah fungsi Into

jika ada y∈ B bukan peta dari x∈ A.

Perhatikan gambar di samping, dimana y2, y4∈ B bukan peta dari x∈ A.

f : { (1 , a) (2 , a) (3 , c) }

b. Fungsi f : x∈ A → y∈ B adalah fungsi Injektif

jika setiap y ∈ B yang mempunyai kawan

tunggal di x∈ A.

f : { (1 , a) (2 , d) (3 , b) (4 , c) } y

x

6 5 4 2

3 2 1

A B

f

•• •

3 2 1

d c b a

•• ••

A B

f

• • • •

4 3 2 1

d c b a

•• •• Click to buy NOW!

w w

w

.docu-track.com

Click to buy NOW! w

w w

(3)

33

c. Fungsi f : x ∈ A → y ∈ B adalah fungsi

Surjektif (Onto) jika setiap y ∈ B mempunyai

peta x∈ A.

f : { (1 , a) (2 , c) (3 , b) (4 , c) }

d. Fungsi f : x∈ A→ y ∈ B adalah fungsi Bijektif

jika fungsi tersebut injektif sekaligus surjektif ( korespondensi satu-satu ) dengan indikator n(A ) = n(B)

f : { (1 , c) (2 , b) (3 , a) }

Lembar Kerja Siswa KB 1

1. Dari fungsi-fungsi yang disajikan dalam diagram panah berikut ini manakah yang merupakan fungsi onto, injektif atau bijektif ?

a. b.

3. Suatu Relasi R dinyatakan dalam himpunan pasanagan berurutan R : { (a,1) (b,2) (c,2) (a,6) }.

a. Tentukan domain dari R !

b. Tentukan Kodomain dari R !

c. A pakah R merupakan fungsi ?

c.

(4)

4. Suatu Relasi R dinyatakan dengan diagram panah di samping :

a. A pakah R merupakan fungsi ?

b. Jika R fungsi, nyatakan R sebagai rumus f(x) !

5. Sebuah fungsi f : A → B, A = { 1, 3, 4, 6 } ditentukan oleh f(x) = 2x – 1.

a. Tentukan Range dari f (Rf) !

b. Nyatakan fungsi f pada bidang kartesius !

6. Fungsi g : R→ R ditentukan oleh g(x) = x2_{+ 3}

a. Tentukan g(-3), g(-2), g(-1), g(0), g(1), g(2), g(3) !

b. Tentukan m jika g(m) = 19

7. Pemetaan f didefinisikan seperti pada diagram berikut : a. Nyatakan f sebagai himpunan pasangan berurutan ! b. Carilah f(a), f(b) dan f(d) !

c. Bila f(x) = 4 maka carilah x ! d. Bila f(y) = 2 maka carilah y !

8. Diketahui f : x→ 3x - 5

a. Tuliskan f dalam bentuk rumus !

b. Carilah f(0), f(3), f(-2), f(a), f(2x) dan f(x+3) ! c. Jika f(y) = -14 maka carilah nilai y !

9. Tuliskan Range fungsi dari f(x) = 2x – 4 jika : a. Domain fungsi Df : {-3, -2, -1, 0, 1, 2, 3 }

b. Domain fungsi Df : { x- 3 x 3 }

c. Domain fungsi Df : { xx∈ Real }

10. Gambarkan grafik fungsi dari f(x) = x2_{– 4 dengan domain fungsi sebagai berikut :}

a. Df : { -2, -1, 0, 1, 2 } b. Df : { x - 2 x 2 }

c. Df : { xx∈ Real }

Kegiatan Belajar 2. M enerapkan konsep fungsi linier

Setelah mempelajari uraian kegiatan belajar ini, siswa diharapkan : 1. Menggambarkan grafik fungsi linier.

2. Mengintepretasikan gradien.

3. Menentukan persamaan garis yang melalui titik dengan gradien m. 4. Menentukan titik potong dua garis.

2.1 Grafik Fungsi Linear

Secara umum persamaan fungsi linear ditulis :

y = ax + b , dengan a dan b∈ R.

Click to buy NOW!

w w

w

.docu-track.com

w w

(5)

Contoh : Gambarlah grafik yang persamaannya y = 4x – 2.

Untuk menggambar grafik fungsi linear dapat digunakan 2 cara, yaitu dengan : a. dengan tabel

b. dengan menentukan titik potong terhadap sumbu x dan sumbu y. a. dengan tabel

y = 4x - 2

x y titik

-1 - 6 (-1 , -6)

0 - 2 (0 , -2)

1 2 (1 , 2)

2 6 (2 , 6)

3 10 (3 , 10)

b. dengan titik potong sb-x dan sb-y

1. perpotongan dengan sumbu-x maka syarat : y =0 y = 4x – 2

0 = 4x – 2 4x = 2

x = ½ Jadi koordinat titik potongnya : ( ½ , 0) 2. perpotongan dengan sumbu-y maka syarat : x = 0

y = 4x – 2 y = 4.0 – 2

y = - 2 Jadi koordinat titik potongnya : (0 , -2)

Titik potong sumbu-x dan titik potong sumbu-y dihubungkan, maka terbentuklah garis y = 4x – 2

2.2 Gradien

Gradien adalah angka kemiringan grafik yaitu kemiringan terhadap sumbu- x positif. Gradien dinotasikan dengan huruf m.

Jika sudut yang dibentuk antara garis terhadap sumbu-x positif adalah tgα=m , maka :

x komponen komponen y m

tgα= =

Sifat-sifat grafik fungsi linear :

a. Jika m = 0 maka grafik sejajar sumbu-x.

b. Jika m > 0 maka grafik condong ke kanan ( 0° < α < 90°).

c. Jika m < 0 maka grafik condong ke kiri (90° < α < 180°).

2.3 Persamaan Garis

1. Persamaan garis melalui satu Titik dengan Gradien m

Persamaan garis melalui satu titik P (x1,y1) dan mempunyai gradient m, dapat ditentukan

dengan persamaan : y – y1 = m (x – x1)

Contoh :

Tentukan persamaan garis yang melalui P (2 , 3) dan mempunyai gradien 2. Penyelesaian :

x y

1 2 3 6 10

-2 2

w w

(6)

y – y1 = m (x – x1)

y – 3 = 2. ( x – 2) y = 2x – 4 + 3 y = 2x -1

2. Menentukan Persamaan Garis yang Melalui Dua Titik

Persamaan garis yang melalui dua titik P (x1,y1) dan Q (x2,y2) dapat ditentukan dengan

Tentukan persamaan garis yang melalui titik P (3, -2) dan Q (-4 , 5)! Penyelesaian :

2.3 Menentukan Sudut yang Dibentuk oleh Grafik Fungsi

Untuk menentukan sudut yang dibentuk oleh grafik fungsi terhadap sumbu-x positif dapat

ditentukan dengan gradiennya. (tgα=m )

Contoh :

Tentukan sudut yang dibentuk oleh garis 2 3x – 2y = 1!

Penyelesaian : 3x – 2y = 1

- 2y = 1 - 2 3x y = 3x - ½

Dengan melihat hasil akhir persamaan, maka m = 3

tg α = 3

α = 60°

2.4 Menentukan Titik Potong Dua Garis

Untuk menentukan titik potong dapat digunakan cara eliminasi, substitusi atau determinan.

Contoh :

w w

w

.docu-track.com

w w

(7)

2x = -1 + 5

2x = 4 maka nilai x = 2

Jadi kedua garis berpotongan di koordinat (2 , 1). 2.5 Hubungan Dua Garis Berpotongan Tegak Lurus.

Dua buah garis berpotongan tegak lurus jika : m1 . m2 = -1

Contoh :

Tentukan persamaan garis yang melalui titik (-2 , 3) dan tegak lurus terhadap garis 2y - 4x + 8 = 0 !

Penyelesaian :

Mengubah persamaan garis 2y - 4x + 8 = 0 ke bentuk umum persamaan garis :

ke bentuk y = mx + c , yaitu : 2y - 4x + 8 = 0

y = 2x – 4 . gradien garis 1 (m1) = 2

Tegak lurus berlaku : m1 . m2 = -1

2 . m2 = -1 maka m2 = - ½

Persamaan garis yang dicari adalah : y – y1 = m (x – x1)

y – 3 = - ½ (x – (-2)) y = - ½x - 1 + 3

y = - ½x + 2 atau 2y = - x + 4

2.5 Hubungan Dua Buah Garis yang Sejajar

Dua buah garis dikatakan sejajar jika : m1 = m2

Contoh :

Sebuah garis melalui titik (6 , -4) dan sejajar dengan garis -3y + 9x +12 = 0. Tentukan persamaan garis tersebut !

Penyelesaian :

Mengubah persamaan garis -3y + 9x +12 = 0 ke bentuk umum persamaan garis :

ke bentuk y = mx + c , yaitu : -3y + 9x +12 = 0

-3y = -9x – 12

y = 3x + 4 gradien garis 1 (m1) = 3

Dua buah garis sejajar berlaku : m1 = m2

Maka gradien m2 = 3

Persamaan garis yang dicari adalah : y – y1 = m (x – x1)

y – (-4) = 3(x – 6) y = 3x – 18 – 4 y = 3x – 22

2.6 Invers Fungsi Linear

a. Pengertian invers suatu fungsi. Perhatikan gambar !

Jika fungsi f: A → B maka peta setiap x ∈ A adalah y ∈ B

ditulis y = f(x) jika g : B→ A, maka peta setiap y∈ B adalah

x ∈ A dan ditulis x = g(y). Maka dikatakan f dan g saling

invers.

x y

g(y) f(y)

A g B

f

w w

(8)

g invers dari f ditulis : g = f-1_{dan f invers g ditulis f = g}-1_{. Jadi}

invers dari f dinyatakan dengan f-1_.

b. Cara menentukan fungsi invers 2.7 Memisalkan f(x) = y

2.8 Nyatakan nilai x dalam y yang dinamai dengan f-1_(y).

2.9 Gantilah y pada f-1_{(y) dengan x untuk mendapatkan f}-1_(x).

Contoh :

1. Diberikan garis k : y = 2x + 1 dan m : y = 2x – 3. a. Tentukan gradient masing-masing garis !

b. Gambarkan masing-masing garis ! Dan amatilah hasilnya !

c. Buatlah persamaan garis baru p yang melalui titik A (5, 2) dengan gradient m = 2 ! d. Simpulkan hasil pengamatamu !

2. Diketahui persamaan garis g1 : y = ½ x + 4 dan garis g2 : y = - 2x + 3.

a. Tentukan gradient masing-masing garis !

b. Gambarkan masing-masing garis tersebut dan amatilah hasilnya !

c. Ukur besar sudut antara garis g1 dan garis g2 dengan menggunakan busur derajat !

d. Simpulkan pengamatanmu ! 3. Diberikan fungsi f(x) = 3x - 6

a. Tentukan invers dari f(x) !

b. Tentukan komposisi fungsi fof−1(x) ( tanyakan kepada Guru Pendamping )

c. Tentukan pula f−1of(x) !

d. Perhatikan jawaban b dan c untuk mengambil kesimpulan ! 4. Tentukan persamaan garis yang melalui titik :

a. (1 , 2) dan (0 , 0) b. (2 , 1) dan (3 , 5) c. (3 , 2) dan (-1 , -6)

5. Tentukan titik potong dua garis dengan persamaan berikut :

w w

w

.docu-track.com

w w

(9)

a. 4x + 5y = 18 dan x – 3y = - 4 b. 2x – 5y = 4 dan x + 2y = 3

3. Tentukan sudut yang dibentuk antara garis yang persamaannya di bawah ini terhadap sumbu-x positif!

a. y = - x + 2 b. 2y = 2x + 3

4. Tentukan sebuah titik pada y =x2_{+ 1 sehingga garis singgung pada titik tersebut sejajar}

dengan garis y = 4x + 1!

5. Tentukan gradian persamaan grafik fungsi berikut, kemudian gambarkan grafiknya !

a. f(x) = 2x + 4 c. f(x) = ½ x – 4 e. f(x) = - 3x

b. f(x) = 3x – 6 d. f(x) = - x + 2 f. f(x) = 2x

6. Gambarkan grafik fungsi berikut dalam suatu bidang koordinat

a. f(x) = 4x + 3 c. f(x) = 4x – 2

b. f(x) = ½ x + 6 d. f(x) = 10 – 2x

Amati mana yang saling sejajar dan mana yang saling tegak lurus.

7. Tentukanlah persamaan garis yang melalui titik A (3, -2) dan sejajar garis y = 5x – 3 ! 8. Tentukan persamaan garis yang melalui titik P (2 , 5) dan tegak lurus garis y = 8x + 5 !

9. Tentukan persamaan garis yang melalui titik Q (1 , 7) dan titik perpotongan garis y = 3x – 2 dan garis y = x – 1 !

10. Tentukan fungsi invers dari fungsi-fungsi berikut ini !

a. f(x) = ½x + 3 c. f(x) = 4 – 3x e. f(x) = 4x – ₃2

b. f(x) = 2x – 7 d. f(x) = 6 – 2x f. f(x) = 2x + ½

Kegiatan Belajar 3. M enggambar fungsi kuadrat

Setelah mempelajari uraian kegiatan belajar ini, siswa diharapkan :

1. Menginterpretasikan sifat-sifat fungsi kuadrat.

2. Menentukan sumbu simetri dari fungsi kuadrat.

3. Menentukan koordinat puncak dari fungsi kuadrat.

4. Menentukan titik potong grafik dengan sumbu koordinat.

5. Mencari persamaan fungsi kuadrat jika diketahui unsur-unsurnya

3.1 Grafik Fungsi Kuadrat

Bentuk umum fungsi kuadrat :f(x) = ax2_{+ bx + c}_{, dengan a, b, dan c bilangan real a}≠_0.

D = b2_{– 4ac disebut diskriminan.}

f(x) = ax2_{+ bx + c}_{dapat juga ditulis}_{y = ax}2_{+ bx + c.} w

w

(10)

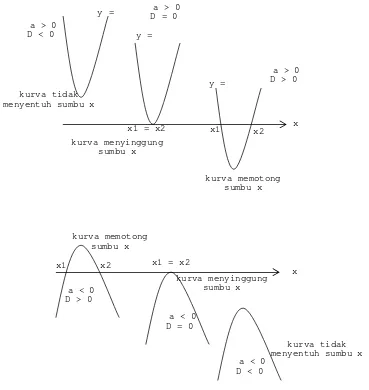
Perhatikan kedudukan dan bentuk kurva di bawah ini :

Grafik fungsi kuadrat berrbentuk parabola dengan sifat :

(i) Jika a > 0 maka parabola terbuka ke atas dan mempunyai nilai balik minimum

(ii) Jika a < 0 maka parabola terbuka ke bawah dan mempunyai nilai balik minimum

(iii) Jika D > 0 maka parabola memotong sumbu x di dua titik

(iv) Jika D = 0 maka parabola memotong sumbu x di satu titik (menyinggung sumbu x)

(v) Jika D < 0 maka parabola tidak memotong sumbu x

3.2 Langkah-langkah Menggambar Grafik Fungsi Kuadrat

a. Menentukan sumbu simetri yaitu

a 2

b

x=−

b. Menentukan titik puncak yaitu P (x,y) dengan

a 2

b

x=− dan

a 4

D

y=−

c. Menentukan titik potong dengan sumbu y untuk x = 0

d. Bila D > 0 tentukan titik potong dengan sumbu x untuk y = 0

Bila D≤ 0 tentukan beberapa titik di sekitar sumbu simetri.

Contoh 2. a :

kurva tidak menyentuh sumbu x

kurva menyinggung sumbu x

x1 = x2 x1 _x2

a > 0 D < 0

a > 0 D = 0

a > 0 D > 0 y =

y =

x

kurva memotong sumbu x

a < 0 D < 0 x1 = x2

kurva menyinggung sumbu x kurva memotong

sumbu x

kurva tidak menyentuh sumbu x

x

a < 0 D = 0 a < 0

D > 0

x1 x2

w w

w

.docu-track.com

w w

(11)

Gambarlah grafik dari y = - x2_{+ 2x}

Penyelesaian :

y = - x2_{+ 2x} →_{a = -1, b = 2, c = 0}

D = b2_{– 4ac}

D = (2)2_{– 4(-1) (0) = 4}

Sumbu simetri→

a 2

b

x= − = 1

) 1 ( 2

2

= − −

a 4

D

y=− = 1

) 1 ( 4

4

= −

− _→ _{Nilai balik maksimum : 1}

Jadi titik puncak (1 , 1)

Titik potong dengan sumbu-x, y = 0

- x2_{+ 2x = 0}

- x.(- x + 2) = 0

- x = 0 atau x = 2

Jadi titik potong sumbu-x adalah : (0 , 0) dan (2 , 0).

Titik potong dengan sumbu-y, x = 0

y = - (0)2_{+ 2 (0) = 0}

Jadi titik potong dengan sumbu y adalah (0 , 0).

Contoh 2. b :

Tentukan persamaan parabola melalui titik (0, -5) dan titik puncak (3 , 4)!

Penyelesaian :

y = a.( x – p )2_{+ q} →_{p dan q : titik puncak}

→ x dan y : titik yang dilalui

- 5 = a.( 0 – 3)2_{+ 4}

- 5 = 9a + 4

9a = 9→ a = - 1

maka persamaan parabola : y = - 1 ( x – 3)2_{+ 4}

y = - 1 ( x2_{– 6x + 9) + 4}

y = - x2_{+ 6x - 5}

1. Gambarkan grafik fungsi kuadrat f(x) = x2_{– 4 , jika :}

a. Domain fungsi Df : { -2, -1, 0, 1, 2 }

b. Domain fungsi Df : { x -2 x 2 }

c. Domain fungsi Df : { x x∈ Real }

2. Gambarkan grafik fungsi kuadrat berikut :

a. f(x) = x2_{+ 2 x – 24}

b. f(x) = x2_{- 3 x + 20}

c. f(x) = x2_{- 4 x + 4}

Amatilah hasil sketsa grafik, kesimpulan apa yang dapat ditarik antara grafik dan nilai D

(diskriminan ) untuk masing-masing soal ?

x y

2

0 ₁

1 y = - x2 + 2x

w w

(12)

3. Diketahui y = - x2_{– x + 2 dengan Df = { x / -4}≤_x≤_{3 }}

Tentukan :

a. Titik potong dengan sumbu x dan y

b. Sumbu simetri

c. Koordinat puncak

4. Gambarkan grafik f(x) = x2_{– 8x + 12 dengan terlebih dahulu menentukan :}

a. Titik potong grafik dengan sumbu-x dan sumbu-y.

b. Persamaan sumbu simetris.

c. Koordinat titik balik.

d. Titik Bantu yang akan dilalui grafik.

5. Sebuah fungsi kuadrat mempunyai maksimum –3 untuk x = 2 , sedangkan untuk x = –2 fungsi berharga –11, tentukan fungsi tersebut!

6.Tentukan persamaan suatu fungsi kuadrat yang memotong sumbu X di titik (–4, 0) dan (3, 0)

serta melalui titik (0, –12)

7. Tentukan persamaanfungsiy = ax2 + bx + c yang memotong sumbu x di titik-titik yang

absisnya 0 dan 2, dan puncaknya di titik (1,1).

8. Tentukan persamaan fungsi kuadratf(x) yang mempunyai nilai maksimum 5 untukx = 2, dan nilai f(4)

= 3.

9. Suatu fungsi kuadrat mempunyai maksimum –3 untuk x = 2 , sedangkan untuk x = –2 fungsi berharga –11, tentukan persamaan fungsi tersebut.

10. Sebuah benda dilambungkan ke atas setinggi h meter dengan persamaan tinggi benda h(t) =

500t – 5t 2. Setelah berapa detik benda itu mencapai tinggi maksimum dan berapa tingginya ?

Kegiatan Belajar 4. M enerapkan konsep fungsi eksponen

Setelah mempelajari uraian kegiatan belajar ini siswa diharapkan :

1. Siswa dapat menerapkan konsep fungsi eksponen

2. Siswa dapat menggambar grafik fungsi eksponen.

4.1 Bentuk Umum fungsi eksponen

f : x→ ax atau f(x) = ax atau y = ax

keterangan : a > 0 dan a≠ 1

Untuk fungsi eksponen bentuk f(x) = ax_{berlaku :}

o x disebut peubah dan daerah asal f(x) (domain) dari fungsi eksponen adalah himpunan

bilangan Real. Df : { x-∼ < x < +∼ , x∈ R }.

o a disebut bilangan pokok fungsi dengan syarat a > 0 dan a 1.

Jadi boleh : 0 < a < 1 atau a >1.

Untuk menyelesaikan permasalahan fungsi eksponen perlu diingat kembali sifat-sifat operasi

bilangan berpangkat, antara lain :

1. am.an =am+n Click to buy NOW!

w w

w

.docu-track.com

w w

(13)

2. _n m n

m

a a

a ₌ −

3.

( )

am n =am.n

4.

( )

m m m

b . a b .

a =

5. _m

m m

b a b a

=      

6. m _m

a 1 a− =

4.2 Menggambar grafik fungsi eksponen

Contoh 2. a : Gambarlah grafik fungsi eksponen f(x) = 4x ! Penyelesaian :

x _{f(x) =} ₄x

- 1 ₄−1 _{= ¼}

- ½ ₂1

4− =

2 1 4

1 ₌ 4 1 _{= ½}

0 0

4 = 1

½

2 1

4 =√ 4 = 2

1 1

4 = 4

2 2

4 = 16

Contoh 2. b :

Gambarlah grafik fungsi y=3.2x

Penyelesaian :

x _y₌₃_.₂x

-2 3 . 2-2_{= 3/ 4}

-1 3 . 2-1_{= 3/ 2}

0 3 . 20_{= 3}

1 3 . 21_{= 6}

2 3 . 22_{= 12}

1. Gambarlah grafik fungsi eksponen di bawah ini :

a. y=2x c. y=2.3x e. _y₌₍₄1₎x

b. y=3x d. y=2.4x f. _y₌₍₂1₎x

2. Dengan mengingat sifat-sifat eksponen, sederhanakan bentuk-bentuk berikut :

a. (x3.x5):x4 =... c. a :a4 ...

5 4 1

=

b. (3p.5p):152 =... d. (x .y ) 2 ...

1

7 7 − ₌

3. Sederhanakan bentuk berikut menjadi eksponen positif. w

w

(14)

a. ...

4. Tentukan batas-batas nilai x yang memenuhi :

a. 53x−4 >5x+2 b. 2x2−2x ≤16x−2 c.

Tentukanlah : a. nilai dari f(2) dan f(-2)

b. nilai k jika f(k) = 96

6. Gambarkan dalam satu bidang koordinat grafik-grafik berikut :

a. f(x) = 3x b. f(x) =

8. Gambarkan dalam satu bidang koordinat grafik fungsi berikut !

a. f(x) = 2x+1

b. f(x) = 2x−1

c. f(x) = 2x+1

d. f(x) = 2x−1

9. Gambarkan dalam satu bidang kartesius grafik fungsi f(x) = 2x dan f(x) =

x

10. Amati apakah kedua grafik pada soal nomor 9 berpotongan?

Kegiatan Belajar 5. M enerapkan konsep fungsi logaritma

Setelah mempelajari uraian kegiatan belajar ini diharapkan siswa dapat:

1. menggambar grafik fungsi logaritma

2. menerapkan konsep fungsi logaritma

5.1 Bentuk Umum Fungsi Logarithma

f : x→ alogx atau f(x) = alogx atau y = alogx

dimana a > 0, a 1 dan x∈ Real.

Dari bentuk umum di atas dapat diambil pengertian sebagai berikut :

i. Daerah asal (domain) fungsi logagaritma adalah Df : { x x > 0, x∈ R }

w w

w

.docu-track.com

w w

(15)

ii. a adalah bilangan pokok (basis) logaritma dengan syarat a > 0 dan a 1 berarti boleh

0 < a < 1 atau a >1.

iii. Daerah hasil (Range) dari fungsi log adalah Rf : { y  -∼ < y < +∼ , y∈ R}

5.2 Menggambar Grafik Fungsi Logarithma

Contoh 2. a : Gambarlah grafik fungsi logarithma y = 3logx ! Penyelesaian :

x _{y =} 3_log_x

3 1

3_log _{= - 1}

1 3log1 = 0

3 3log3 = 1

9 3log9 = 2

Contoh 2. b : Gambarlah grafik fungsi logarithma y = 2log(x−1) ! Penyelesaian :

x _{y =} 2_log(_x₋₁₎

1½ log(1 1)

2 1

2 ₋ _{= -1}

2 2log(2−1) = 0

3 2log(3−1) = 1

5 2log(5−1) = 2

9 2log(9−1) = 3

1. Gambarkan fungsi grafik di bawah ini :

a. y=2logx b. y 2logx

1

= c. y=2log(x−2) d. y=3log(x+2)

2. Gambarkan dalam satu bidang koordinat untuk fungsi f(x) = 2logx dan f(x) = 2x ! Dengan

melihat sketsa gambar kedua grafik tersebut maka jawablah pertanyaan-pertanyaan di

bawah ini !

a. Apakah kedua grafik fungsi tersebut saling berpotongan ? Jika berpotongan tentukan

koordinat titik potongnya !

b. Tentukan titik potong grafik tersebut terhadap sumbu koordinat !

c. Bagaimana kedudukan kedua grafik fungsi tersebut satu terhadap yang lain (simpulkan

bersama Guru Pendamping).

3. Diketahui f(x) = 4log(x+1), tentukanlah :

a. f(0) = … b. f(3) = … c. f(-₄3_{) = …} _d.

f(-64

63_{) = …} _{e. f(15) = …}

4. Tentukan titik potng grafik fungsi f(x) dengan sumbu-x jika diketahui :

a. f(x) =3logx b. f(x) =3log(x+1)c. f(x) =2logx d. f(x) =2log(x−1) e. f(x) =2logx

1

5. Tentukan batas-batas x yang memenuhi : w

w

(16)

a. 2logx>3 b. 3log(x−2)>1 c. 14log(x2−x−6)≤1 d. log(x2 +4x+ 4)≤log(5x+10) 6. Gambarkanlah grafik fungsi f(x) = 2 _x1

log dengan Df : {x₁₆1 _{x 16 }}

Dengan melihat hasil sketsa grafik, apakah memotong sumbu-x ? Tentukan titik potongnya !

7. Gambarkanlah grafik fungsi f(x) = 2logx

1

dengan : {x₁₆1 _{x 16 }}

Dengan melihat hasil sketsa grafik, apakah memotong sumbu-x ? Tentukan titik potongnya !

Bandingkan dengan sketsa grafik no. 1

8. Tentukan batas-batas x yang memenuhi :

a. log(x−1)<log(2x−5) b. 5logx+5log(x−4)≥1 c. 3log(x−5)+3log(x+3)<2

Kegiatan Belajar 6. M enerapkan konsep fungsi trigonometri

Setelah mempelajari uraian kegiatan belajar ini siswa diharapkan dapat :

1. menggambar grafik fungsi trigonometri

2. menerapkan konsep trigonometri.

Fungsi tirgonometri merupakan fungsi periodik (berulang) jika fungsi f(x) berlaku f(x) = f(x+p)

untuk setiap x, maka nilai positif terkecil dari p disebut periode fungsi f(x) tersebut.

6.1 Periode fungsi sin

Jika f(x) = sin x° = sin (x° + k . 360°) dinyatakan sebagai f(x+p) dengan p = k . 360° maka nilai

positif terkecil dari p adalah 360° untuk k = 1.

Jadi periode f(x) = sin x ° adalah 360° artinya nilai f(x) akan berulang mempunyai nilai yang

sama setiap bertambah 360° atau 2π ( dalam satuan radian).

6.2 Periode fungsi cos

Jika f(x) = cos x° = cos (x°+ k . 360°) dinyatakan sebagai f(x+p) dengan p = k . 360° maka nilai

Jadi periode f(x) = cos x° adalah 360° artinya nilai f(x) akan berulang mempunyai nilai yang

sama setiap bertambah 360° atau 2π ( dalam satuan radian).

6.3 Periode fungsi tg

Jika f(x) = tg x° = tg (x° + k . 180°) dinyatakan sebagai f(x+p) dengan p = k . 180° maka nilai

Jadi periode f(x) = tg x° adalah 180° artinya nilai f(x) akan berulang mempunyai nilai yang

sama setiap bertambah 180° atauπ ( dalam satuan radian).

Menggambar grafik fungsi trigonometri.

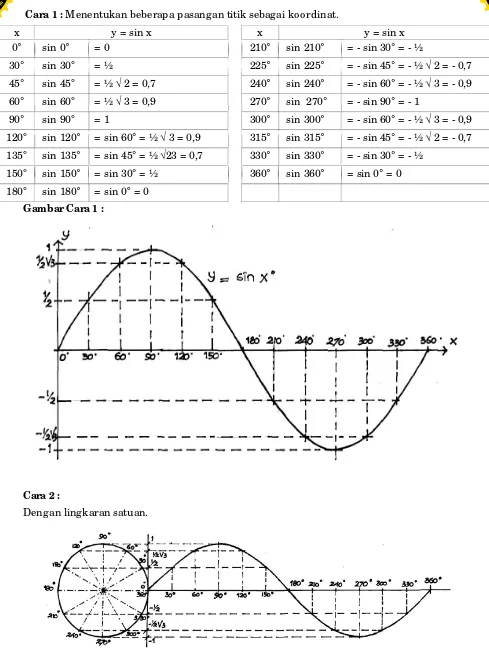
Contoh b. 1 :

Gambarlah grafik fungsi y = sin x dengan 0° ≤ x≤ 360° !

Penyelesaian :

w w

w

.docu-track.com

w w

(17)

Cara 1 : Menentukan beberapa pasangan titik sebagai koordinat.

x y = sin x x y = sin x

0° sin 0° = 0 210° sin 210° = - sin 30° = - ½

30° sin 30° = ½ 225° sin 225° = - sin 45° = - ½√ 2 = - 0,7

45° sin 45° = ½√ 2 = 0,7 240° sin 240° = - sin 60° = - ½√ 3 = - 0,9

60° sin 60° = ½√ 3 = 0,9 270° sin 270° = - sin 90° = - 1

90° sin 90° = 1 300° sin 300° = - sin 60° = - ½√ 3 = - 0,9

120° sin 120° = sin 60° = ½√ 3 = 0,9 315° sin 315° = - sin 45° = - ½√ 2 = - 0,7

135° sin 135° = sin 45° = ½√23 = 0,7 330° sin 330° = - sin 30° = - ½

150° sin 150° = sin 30° = ½ 360° sin 360° = sin 0° = 0

180° sin 180° = sin 0° = 0

Gambar Cara 1 :

Cara 2 :

Dengan lingkaran satuan. w

w

(18)

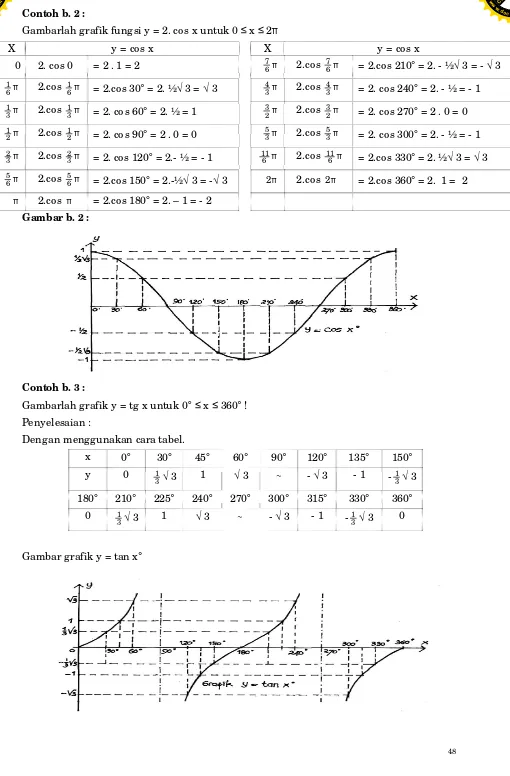
Contoh b. 2 :

Gambarlah grafik fungsi y = 2. cos x untuk 0≤ x≤ 2π

X y = cos x X y = cos x

0 2. cos 0 = 2 . 1 = 2 ₆7π 2.cos 7₆π _{= 2.cos 210}_°_{= 2. - ½}_√_{3 = -}_√₃

π

6

1 _2.cos _π

6

1 _{= 2.cos 30}_°_{= 2. ½}_√_{3 =}_√₃ _π

3

4 _2.cos _π

3

4 _{= 2. cos 240}_°_{= 2. - ½ = - 1}

π

3

1 _2.cos _π

3 1

= 2. cos 60° = 2. ½ = 1 ₂3π 2.cos ₂3π = 2. cos 270° = 2 . 0 = 0

π

2

1 _2.cos _π

21 = 2. cos 90° = 2 . 0 = 0 3π

5 _2.cos _π

3 5

= 2. cos 300° = 2. - ½ = - 1

π

3

2 _2.cos _π

3 2

= 2. cos 120° = 2.- ½ = - 1 11₆ π 2.cos 11₆ π = 2.cos 330° = 2. ½√ 3 =√ 3

π

6

5 _2.cos _π

6 5

= 2.cos 150° = 2.-½√ 3 = -√ 3 2π 2.cos 2π = 2.cos 360° = 2. 1 = 2

π 2.cos π = 2.cos 180° = 2. – 1 = - 2

Gambar b. 2 :

Contoh b. 3 :

Gambarlah grafik y = tg x untuk 0° ≤ x≤ 360° !

Penyelesaian :

Dengan menggunakan cara tabel.

x 0° 30° 45° 60° 90° 120° 135° 150°

y 0

3

1√₃ ₁ √₃ ∼ _-√₃ _{- 1}

-3 1√₃

180° 210° 225° 240° 270° 300° 315° 330° 360°

0

3

1√₃ ₁ √₃ ∼ _-√₃ _{- 1}

-3

1√₃ ₀

Gambar grafik y = tan x°

w w

w

.docu-track.com

w w

(19)

1. Gambarlah grafik fungsi trigonometri berikut untuk nilai batas x yang diberikan !

a. y = 2 sin x untuk 0° ≤ x≤ 360°

b. y = cos x untuk 0° ≤ x≤ 2π

c. y = tan 2x untuk 0° ≤ x≤ 180°

d. y = cos 2x untuk 0° ≤ x≤ 180°

e. y = sin (x + 45°) untuk 90° ≤ x≤ 270°

f. y = 2 tg 3x untuk 0° ≤ x≤ π

g. y = cos (x + 30°) untuk 0° ≤ x≤ π

h. y = cos (2x + 30°) untuk 0° ≤ x≤ 180°

i. y = 2 cos 2x + 3 untuk 0° ≤ x≤ 360°

j. y = 2 sin 3x +2 untuk 0° ≤ x≤ 180°

2. Tentukan nilai dari fungsi trigonometri berikut :

a. sin 850°= … b. cos 13₆ π_{= …} _{c. tg 225}°_{= …}

3. Jika f(x) = 3 sin (2x + 30°) tentukanlah nilai f(x) jika :

a. f(30°) = … b. f(5a) = … c. f(x+p) = …

4. Tentukan periodesitas dari fungsi trigonometri berikut :

a. f(x) = sin 5x° b. f(x) = cos 3x° c. f(x) = tg 4x°

d. f(x) = sin ½ x° e. f(x) = cos ₄3_x° _{f. f(x) = tg ¼ x}°

5. Tentukan periodesitas dari fungsi trigonometri berikut :

a. f(x) = 2 . sin (3x – 15°) b. f(x) = 3 cos (2x + 45°) c. f(x) = 5 . tg (₂1_{x – 30}°₎

6. Tentukan nilai maksimum dan minimum dari fungsi trigonometri barikut :

a. f(x) = 4 . cos (4x + 60°) b. f(x) = 2 . sin x° c. f(x) = ½ . sin (5x – 40°)

7. Nyatakan fungsi trigonometri berikut dalam sudut lancip, kemudian tentukanlah nilai-nilai

periodenya.

a. sin 1020° b. cos 700° c. tg 520° d. tg ₃5π

8. Jika f(x) = 2 . cos (3x – 15°), tentukanlah :

a. f(20°) b. f(-25°) c. f(2a) d. f(x+a)

9. Tentukan nilai periode dari fungsi f(x) = (2x + 30°)

10. Tentukan nilai maksimum dan minimum dari fungsi f(x) = 2 sin (x – 30°) adalah … …

w w

(20)

UJI KOMPETENSI

Pilihlah Jawaban yang paling tepat!

1. Invers dari f(x) =

8. Persamaan garis lurus yang melalui titik (-2,-4) dan sejajar garis 8x – 2y + 3 = 0 adalah … A . y = 4x + 4 C. y = 2 x – 1 E. x – y = 4

B. y = 4x – 4 D. 2y = -4x + 2

9. Persamaan garis lurus yang melalui titik A.(2,-3) dan sejajar garis g : 2y–x+ 6= 0 adalah..

A . y = ½ x + 4 C. y = ½ x – 2 E. y = ½ x – 6 B. y = ½ x + 2 D. y = ½ x – 4

10. Persamaan garis yang melalui titik potong garis 2x + 5y = -1 dengan garis 3x – 2y = 8 serta sejajar dengan garis 2x – y + 5 = 0 adalah …

w w

w

.docu-track.com

w w

(21)

13. Persamaan garis yang melalui titik A (3 , 2) dan tegak lurus dengan persamaan 3x + y = - 2 adalah … (no. 10, Uan. 99-00)

A . 3x – 3y – 1 = 0 B. 3x – y + 10 = 0 C. 3x – y – 3 = 0 D. x – 3y + 3 = 0 E. x – 3y – 3 = 0

14. Koordinat titik balik grafik fungsi f(x) = x2_{– 6x + 8 adalah … (no. 11, Uan. 99-00)}

A. (3 , -1) B. (-3 , -1) C. (4 , -2) D. (6 , 8) E. (-6 , -8)

15. Persamaan garis yang melalui titik potong garis dengan persamaan 2x + 5y = 1 dan x – 3y = - 5 serta tegak lurus pada garis dengan 2x – y + 5 = 0 adalah … (no. 8, Uan. 00-01)

A . y + x = 0 B. 2y + x = 0 C. y = -2x + 2 D. y + 2x + 2 = 0 E. y = - ½ x + 2

16. Nilai m agar grafik fungsi y = (m - 1) x2_{– 2mx + (m – 3) selalu berada di bawah sumbu-x (definit negatif)}

adalah … (no. 9, Uan. 00-01)

A . m = 1 B. m > 1 C. m < 1 D. m > 3/ 4 E. m < 3/ 4

17. Grafik dari fungsi f(x) = - x2_{+ 4x – 6 akan simetris terhadap garis adalah …(no. 10, Uan. 00-01)}

A . x = 3 B. x = 2 C. x = -2 D. x = -3 E. x = -4

18. Grafik fungsi f(x) = x3_{+ 3x}2_{– 9x, turun pada interval …(no. 37, Uan. 00-01)}

A . – 3 < x < 1 B. – 1 < x < 3 C. 1 < x < 3 D. x <-3 atau x> 1 E. x< -1 atau x > 3

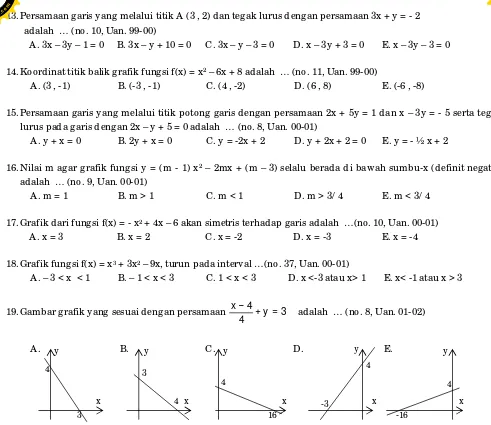
19. Gambar grafik yang sesuai dengan persamaan y 3 4

4 x

= + −

adalah … (no. 8, Uan. 01-02)

A . B. C. D. E.

20. Sebuah peluru ditembakkan vertikal dengan persamaan lintasan h(t) = 150 t – 5t2_{. Tinggi maksimum peluru}

aadalah … (No. 29, Uan. 01-02)

A . 925 m B. 1015 m C. 1025 m D. 1125 m E. 1225 m

21. Fungsi f: R R dan g : R R , dengan f(x) = 2x2_{– 1 dan g(x) = 3x + 2. Nilai dari (fog) (x) = … (no. 36,}

Uan. 01-02)

A . 18x2_{– 24 X + 7 B. 18x}2_{+ 24 X + 7} _{C. 18x}2_{– 24 X - 7} _{D. 6x}2_{+ 12 X + 7} _{E. 6x}2_{– 12 X + 7}

22. Diketahui f(x) =

1 x

1

− dan g(x) = x – 2, maka (gof)–1 (x) = … (no. 37, Uan. 01-02)

A .

2 x

3 x

− +

B.

2 x

3 x

− −

C.

2 x

3 x

+ +

D.

2 x

− +

E. (X+3) (X+2)

23. Grafik fungsi y = 4x2_{– 8x – 21 memotong sumbu x, sumbu y dan mempunyai titik balik P}

berturut-turut adalah … (no. 8, Uan. 02-03)

A . x = - 3/ 2, x = 7/ 2, y = 21 dan P (1 , 25) D. x = 3/ 2, x = - 7/ 2, y = - 21 dan P (1 , - 25) B. x = 3/ 2, x = - 7/ 2, y = 21 dan P (- 1 , 25) E. x = 3/ 2, x = - 7/ 2, y = - 21 dan P (- 1 , - 25) C. x = - 3/ 2, x = 7/ 2, y = - 21 dan P (1 , - 25)

y y y y

x y

x 4

3

x 4 3

x 4

16

4

-3 x

4

-16 w

w

(22)

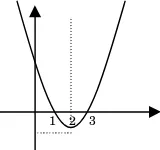
24. Grafik di samping adalah grafik dari …

A. y =x2_{– 3}_x_{+ 4} _{D. y}_{= 2}_x2_{– 8}_x_{+ 3} B. y =x2_{– 4}_x_{+ 3} _{E. y}_{= 2}_x2_{– 3}_x_{+ 3} C. y =x2_{+ 4}_x_{+ 3}

25. Grafik fungsiy =ax2₊_bx_{– 1 memotong sumbu}_x_{di titik-titik (}

2 1

,0) dan (1,0). Fungsi ini mempunyai nilai ekstrim ….

A . maksimum

8 3

C. maksimum

8 1

E. maksimum

8 5

B. minimum –

8 3

D. minimum –₈1

1 2 3

w w

w

.docu-track.com

w w