BAB IV FUNGSI LINEAR
Fungsi : hubungan antara satu variable dengan variable lain yang masing-masing variable tersebut saling mempengaruhi.
Variable / peubah : suatu besaran yang didalam suatu permasalahan nilainya dapat berubah-ubah.
Variable bebas ( independent variable ) : peubah yang nilainya tidak tergantung pada peubah lain dan nilai peubah ini akan menentukan nilai fungsi yang bersangkutan.
Variable tergantung ( dependent variable ) : peubah yang nilainya tergantung pada peubah yang lainnya.
Fungsi Linear
Merupakan fungsi yang pangkat tertinggi dari variable bebasnya adalah 1. Bentuk umumnya adalah :
y = ax + b Dimana a = koefisien arah
b = konstanta yang merupakan titik potong pada sumbu y x = variable bebas
y = variable tergantung Penggambaran Fungsi Linear 1. cara daftar
digunakan untuk melihat perubahan nilai angka dari peubah bebas dan peubah tergantungnya. Contoh :
y = 2x + 10
X 0 1 2 3 4 5 6 7
Y 10 12 14 16 18 20 22 24
24 21 18 15 12 10 6 3
0 1 2 3 4 5 6 7 x
2. cara matematis
Dengan cara mencari ciri matematis dari persamaan yang bersangkutan. Y = 2x + 10
Titik potong sumbu y apabila x = 0 maka y = 2 (0) + 10 = 10
Sehingga titik potong pada sumbu y = ( 0,10 )
Titik potong sumbu x apabila y = 0 maka 0 = 2x + 10 - 2x = 10 x = - 5 sehinnga titik potong pada sumbu x = ( -5,0 )
y = 2x + 10 (0,10)
a. metode dua titik (dwi koordinat )
merupakan metode pembentukan persamaan linear ( garis lurus ) dari dua buah titik yang diketahui
( Y – Y1) = ( X – X1 ) (Y 2 – Y1) (X2 – X1)
Contoh buatlah persamaan garis lurus yang melalui titik A (4,2) dan B (2,6) Titik A (4,2) X1 = 4 Y1 = 2
Titik B (2,6) X2 = 2 Y2 = 6 (Y - 2) = (X - 4)
(6 - 2) ( 2 – 4) 10
(Y – 2) = (X – 4) y = -2x + 10 (4) (-2)
-2y + 4 = 4x – 16 -2y = 4x – 20 y = -2x + 10
0 5 x
b. metode titik potong sumbu
digunakan untuk kasus tertentu, yaitu jika suatu titik A (x1,y1) merupakan titik potong sumbu Y, misalnya pada titik (0,b) dan titik B (x2,y2) merupakan titik potong sumbu x misalnya pada (a,0) maka persamaan garisnya dapat dibentuk sbb:
y / b + x / a = 1
apabila diketahui suatu garis dengan titik potong sumbu y adalah (0,6) dan titik potong sumbu x adalah (4,0), carilah persamaan garisnya
y / b + x / a = 1
y / 6 + x / 4 = 1 x 12 12y / 6 + 12x / 4 = 12
2y + 3x = 12 2y = -3x + 12 y = -3/2 x + 6
c. metode kemiringan garis dan titik
apabila diketahui suatu titik A (x1,y1) dan dilalui oleh suatu garis lurus yang memiliki kemiringan m, maka persamaannya adalah :
y – y1 = m (x – x1) persamaan garis yang melalui titik (x1,y1) dengan kemiringan sebesar m. contoh
carilah persamaan garis yang melalui suatu titik (4,2) dan kemiringan -3 y – y1 = m(x – x1)
y – 2 = -3(x – 4 ) = -3x + 12 y = -3x + 14
d. metode kemiringan garis dan titik potong sumbu
apabila diketahui suatu titik yang berkoordinat (0,b) merupakan titik potong dengan sumbu y sebuah garis lurus yang memiliki kemiringan garis m, maka persamaan garis tersbut adalah y = mx + b, merupakan persamaan garis yang melalui titik potong sumbu y dengan kemiringan m, contoh :
apabila suatu garis memiliki titik potong dengan sumbu y pada (0,-4) dan kemiringannya 5 maka bagaimana persamaan garisnya :
y = 5x – 4
cara mencari titik potong y1 = 2x + 4
y2 = x + 5
garis pertama y1 = 2x + 4
titik potong dengan sumbu y pada (0,4) titik potong dengan sumbu x pada (-2,0) garis kedua y2 = x + 5
titik potong dengan sumbu y pada (0,5) titik potong dengan sumbu x pada (-5,0)
garis pertama (y1) akan berpotongan dengan garis kedua (y2) saat y1 = y2, maka :
2x + 4 = x + 5, x = 1 y = 2x + 4 y = 2(1) + 4
Y = 6
Jadi titik potong garis pertama dan garis kedua (1,6) 6
5 4
Penerapan dalam ekonomi fungsi permintaan
dalam fungsi permintaan ini sumbu y diganti dengan P sebagai sumbu harga dan sumbu x diganti dengan Q sebagai sumbu jumlah (Quantitas) produksi. Bentuk umum :
Q = -aP + b Dimana
Q = jumlah barang yang diminta P = harga barang yang bersangkutan a = koefisien fungsi permintaan
b = konstanta fungsi permintaan yang bersangkutan contoh :
diketahui bahwa permintaan suatu barang apabila harga jualnya Rp 160 jumlah barang yang diminta konsumen sebanyak 20 buah, sedangkan apabila harga jualnya diturunkan menjadi Rp. 120, maka jumlah barang yang diminta sebanyak 40 buah. Tentukan :
a. bagaimanakah fungsi permintaannya
b. apabila barang tersebut dibagi secara gratis kepada konsumen, berapa jumlah barang tersebut yang diminta
c. berapa harga maksimum barang tersebut sehingga tidak ada yang membelinya.
a. P1 = 160, P2 = 120, Q1 = 20, Q2 = 40 P – P1 / P2 – P1 = Q – Q1 / Q2 – Q1 P – 160 / 120 – 160 = Q – 20 / 40 – 20 P – 160 / -40 = Q – 20 / 20
b. apabila dibagi secara gratis, maka P = 0 P = -2Q + 200
0 = -2Q + 200 2Q = 200 Q = 100
c. apabila barang tersebut tidak ada yang membeli (Q = 0) maka harga maksimum :
P = -2Q + 200 P = -2 (0) + 200 P = 200
Harga max Rp. 200 P
200 160 120
P = -2Q + 200
Keadaan permintaan barang diketahui bahwa ketika harga jualnya Rp. 400 tidak ada barang yang diminta, sedangkan apabila barang tersebut dibagikan secara cuma-cuma, maka jumlah barang tersebut yang diminta hanya 100 unit. Bagaimanakah persamaan fungsi permintaannya.
y / b + x / a = 1 P / b + Q / a = 1
P = Rp. 400 maka Q = 0 unit titik potong (0,400) P = Rp. 0 maka Q = 100 unit titik potong (100,0) P / 400 + Q / 100 = 1 x 400
P + 4 Q = 400
P = -4Q + 400 atau Q = -1/4 P + 100 400
P = -4Q + 400
100 Fungsi Penawaran
Bentuk umum fungsi penawaran Q = aP + b
Q = jumlah barang yang ditawarkan P = harga barang yang bersangkutan a = koefisien fungsi penawaran
contoh
sebuah perusahaan konveksi menjual salah satu produknya sebanyak 500 unit dengan harga Rp 1000 perunit. Apabila harganya naik menjadi Rp. 1.200 perunit, maka jumlah barang yang ditawarkan menjadi 900 unit. Tentukan :
a. bagaimana fungsi penawarannya
b. berapa harga minimal yang ditawarkan produsen a. persamaan fungsi penawaran.
P1 = 1000, P2 = 1200, Q1 = 500, Q2 = 900 P – P1 / P2 – P1 = Q – Q1 / Q2 – Q1
Maka
P – 1000 / 1200 – 1000 = Q – 500 / 900 – 500 P – 1000 / 200 = Q – 500 / 400
400 P – 400.000 = 200 Q – 100.000 400 P = 200 Q + 300.000
P = 1/2Q + 750 atau Q = 2P – 1500 P
750
-1500 0 Q
keseimbangan pasar (market equilibrium)
merupakan keadaan dimana pada tingkat harga tertentu jumlah barang yang diminta (Qd) sama dengan jumlah barang yang ditawarkan (Qs)
contoh
fungsi permintaan (Qd) P : -1/2Q + 40 fungsi penawaran (Qs) P : 1/2Q + 10 carilah keseimbangan pasar :
Qd = Qs
-1/2 Q + 40 = 1/2 Q + 10 Q = 30 unit P = ½ Q + 10
= ½ (30) + 10 = Rp 25
Berarti harga keseimbangan pasar pada saat harga Rp 25 perunit dengan kuantitas 30 unit.
P
40
(30,25) 25
Pengaruh pajak
Didalam matematika ekonomi, pajak yang dibicarakan adalah pajak tidak langsung yaitu pajak penjualan. Dasar pengenaannya atas dasar perunit atau dasar prosentase.
1. Pajak perunit.
Yaitu pajak yang besarnya tetap untuk setiap unit penjualan. Pajak ini langsung dibebankan pada harga jualnya. Fungsi penawaran akan akan bergerak dengan adanya pajak.
Ex. Diketahui Qs = P : 1/4Q + 4 Qd = P : -1/4Q + 25
Pajak perunit Rp 6
a. hitunglah harga dan kuantitas pada keseimbangan pasar sebelum pajak b. hitung harga dan kuantitas pada keseimbangan pasar sesudah pajak c. besarnya total pajak diterima pemerintah, pajak ditanggung konsumen
dan pajak ditanggung produsen. a. MEQ.
Qs = Qd
1/4 Q + 4 = -1/4 Q + 25
1/2Q = 21
b. MEQ ‘
Qs ‘ = P : 1/4Q + 4 + 6 : 1/4Q + 10
Qs ‘ = Qd
1/4Q + 10 = -1/4Q + 25
1/2Q = 15
Q’ = 30 unit
P’ = 1/4Q + 10 P’ = 1/4 (30) + 10
= Rp. 17,5
c. Pajak yang ditanggung konsumen (tk) = (P1 – P0)
Pajak yang ditanggung produsen (tp) = (t – tk) atau
(tp) = t – (P1 – P0)
Pajak yang diterima pemerintah (tg) = (t x Q1)
Dimana t = besarnya pajak perunit
P1 = harga keseimbangan setelah pajak
P0 = harga keseimbangan sebelum pajak
Q1 = kuantitas / jumlah keseimbangan setelah pajak
tg = Rp 6 x 30
= Rp 180
tk = (17,5 – 14,5) x 30
= Rp 3 x 30 = Rp 90
tp = Rp 180 – Rp 90
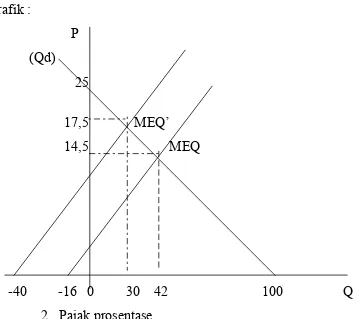
Grafik :
P (Qd) 25
17,5 MEQ’ 14,5 MEQ
-40 -16 0 30 42 100 Q 2. Pajak prosentase.
Adalah pajak yang dikenakan sebesar prosentase tertentu dari penerimaan penjualan produk
Fungsi penawaran bergeser sebesar prosentase tersebut untuk setiap jumlah produk yang ditawarkan.
Qs ‘ = Qs (1 + r) Contoh
Diketahui Qs = P : 1/4 Q + 10 Qd = P : -1/2 Q + 30 Pajak 20 %
Jawab a. MEQ
Qs = Qd
1/4Q + 10 = -1/2Q + 30
3/4Q = 20
Q = 80/3 = 26,67 unit
P = 1/4Q + 10
= 1/4 x 80/3 + 10 = 50/3 = Rp. 16,67 b. MEQ’
(Qs’) P = (1/4Q + 10) (1 + 20%) = (1/4Q + 10) (1 + 0,2) = (1/4Q + 10) (1,2) = (1/4Q + 10) (6/5) (Qs’) P = 3/10 Q + 12
Qs’ = Qd
3/10Q + 12 = -1/2Q + 30 8/10Q = 18
Q’ = 180/8 = 22,5 unit P = 3/10Q + 12
= 3/10 x 180/8 + 12 P’ = Rp. 18,75
c. Pajak/unit = P’ x % Pajak
Qs 30
18,75 MEQ ‘
16,75 MEQ 12
10
II. Subsidi
Yaitu bantuan yang diberikan pemerintah kepada produsen atau distributor barang agar harga jual produk menjadi lebih murah daripada harga sebelumnya. Subsidi hanya berpengaruh terhadap fungsi penawaran.
Contoh :
Qs P = 1/4Q + 10 Qd P = -1/4Q + 25 Subsidi perunit Rp 6
Ditanya : a. keseimbangan pasar sebelum subsidi b. keseimbangan pasar setelah subsidi c. subsidi pemerintah
d. grafik a. MEQ
Qs = Qd
1/4Q + 10 = -1/4Q + 25 1/2Q = 15
Q = 30 unit
P = 1/4Q + 10 = 1/4x30 + 10
= Rp 17,5
b. MEQ’
(QS’) - P = 1/4Q + 10 – 6 = 1/4Q + 4
QS’ = Qd
Q’ = 42 unit P = 1/4Q + 4
= 1/4x(42) + 4 P’ = Rp 14,5
c. Sg = Q’ x Rp
= 42 x Rp 6,-= Rp
Sk = (Rp 17,5 – Rp 14,5) x 42
= Rp Sp = Rp 252 – Rp 126
= Rp 126,-
Qs
Qd Qs’ 25
17,5 14,5
Break Event Point (BEP)
Adalah suatu keadaan yang menunjukkan bahwa perusahaan tidak memperoleh laba maupun rugi.
Manfaat BEP :
Dapat digunakan sebagai alat perencanaan laba
Dapat digunakan untuk mendeteksi faktor-faktor yang menyebabkan perusahaan menderita kerugian.
Unsur-unsur BEP :
1. Fixed cost (FC) = Biaya Tetap
Yaitu biaya yang jumlahnya tetap untuk seluruh jumlah barang yang dihasilkan.
2. Variable cost (VC) = Biaya Variable
Yaitu biaya yang berubah sesuai dengan perubahan jumlah barang produksi.
3. Total cost (TC) = total biaya ---- TC = FC + VC
4. Total revenue (TR) = total pendapatan --- TR = P x Q Syarat analisis BEP
1. biaya produksi didalam perusahaan harus dapat digolongkan kedalam biaya tetap dan biaya variable.
2. biaya variable secara total berubah sebanding dengan volume produksi, tetapi biaya variable perunit tetap
Contoh :
Diket FC = Rp
12.200.000,-VC/unit = Rp 14.000,-P/unit = Rp 18.000,-Ditanya a. jumlah unit untuk BEP
b. Bila jumlah barang 10.000 unit, tentukan rugi atau laba c. Grafik
jawab :
a. TC = TR
FC + VC = P x Q
12.200.000 + 14.000Q = 18.000Q 12.200.000 = 4.000Q
Q = 3050 unit BEP unit : 3050
BEP (Rp) = BEP unit x P/u
= 3050 x 18.000
=
Rp.54.900.000,-b. TC = FC + VC
= 12.200.000 + (14.000 x 10.000) = 12.200.000 + 140.000.000 = Rp. 152.200.000
TR = P x Q
= 18.000 x 10.000 = 180.000.000 TR > TC = Laba
Laba = 180.000.000 – 152.200.000
TR TC 54,9 juta
BEP dalam rupiah
VC
12,2 juta FC BEP dalam unit