PPT MATH VIIIA_edt2 PPT MATH VIIIA_edt2

Daftar Isi Disklimer

MATEMATIKA

Disusun Oleh:

• Powerpoint _Powerpoint pembelajaran ini dibuat sebagai pembelajaran ini dibuat sebagai alternatif guna membantu Bapak/Ibu Guru

alternatif guna membantu Bapak/Ibu Guru

melaksanakan pembelajaran.

melaksanakan pembelajaran.

• Materi _Materi powerpoint powerpoint ini mengacu pada Kompetensi ini mengacu pada Kompetensi Inti (KI) dan Kompetensi Dasar (KD) Kurikulum 2013.

Inti (KI) dan Kompetensi Dasar (KD) Kurikulum 2013.

• Dengan berbagai alasan, materi dalam Dengan berbagai alasan, materi dalam powerpoint powerpoint ini disajikan secara ringkas, hanya memuat

ini disajikan secara ringkas, hanya memuat

poin-poin besar saja.

poin besar saja.

• Dalam penggunaannya nanti, Bapak/Ibu Guru dapat _{Dalam penggunaannya nanti, Bapak/Ibu Guru dapat}

mengembangkannya sesuai kebutuhan.

mengembangkannya sesuai kebutuhan.

• Harapan kami, dengan Harapan kami, dengan powerpoint powerpoint ini Bapak/Ibu ini Bapak/Ibu Guru dapat mengembangkan pembelajaran secara

Guru dapat mengembangkan pembelajaran secara

kreatif dan interaktif.

kreatif dan interaktif.

Daftar Isi

BAB IPola Bilangan

BAB IIKoordinat Kartesius

BAB IIIRelasi dan Fungsi

BAB IV Persamaan Garis Lurus

BAB I

Pola Bilangan

A.

Pola Barisan Konfigurasi Objek

B.

Pola dan Suku-Suku Barisan Bilangan

C.

Barisan dan Deret Aritmetika

D.

Barisan dan Deret Geometri

A. Pola Konfigurasi

Objek

1. Pengertian Pola Barisan Bilang an

2. Barisan Bilangan Khusus dan P olanya

1. Pengertian Pola Barisan Bilangan

Barisan bilangan dapat diartikan sebagai susunan bilangan yang memiliki keteraturan

Contoh:

Batang-batang korek api disusun seperti berikut.

Banyak batang korek api yang dibutuhkan adalah 3, 5, 7, 9.

2. Barisan Bilangan Khusus dan Polanya

a. Barisan Bilangan Asli

Barisan bilangan asli adalah 1, 2, 3, 4, 5, 6, · · · . Barisan asli dapat ditampilkan dengan gambar berikut

b. Barisan Bilangan Ganjil

c. Barisan Bilangan Genap

Barisan bilangan genap adalah 2, 4, 6, 8, 10, 12, 14, · · · .

Barisan ini dapat ditampilkan dengan gambar berikut

d. Barisan Bilangan Segitiga

e. Barisan Bilangan Persegi Panjang

Salah satu barisan bilangan persegi panjang adalah 2, 6, 12, 20, · · · .

Barisan ini dapat ditampilkan dengan gambar berikut.

f. Barisan Bilangan Persegi

Barisan bilangan persegi adalah 1, 4, 9, 16, 25, · · · .

g. Barisan Bilangan pada Segitiga Pascal

Beberapa sifat barisan bilangan pada segitiga Pascal sebagai berikut. 1) Pada setiap baris diawali dan diakhiri dengan bilangan 1.

2) Setiap bilangan diperoleh dengan menjumlah dua bilangan di atasnya kecuali bilangan pada baris pertama dan kedua.

3) Bilangan-bilangan dalam satu diagonal membentuk suatu barisan, misalkan: diagonal pertama : 1, 1, 1, 1, 1, · · · (barisan bilangan konstan)

diagonal kedua : 1, 2, 3, 4, · · · (barisan bilangan asli)

CONTOH SOAL

Perhatikan pola berikut ini.

Berapa banyaknya persegi pada pola ke-7 dan ke-12?

Jawaban:

Banyaknya persegi pada

pola ke-1 = 5 = 5 + 0 = 5 + 3 × 0 pola ke-2 = 8 = 5 + 3 = 5 + 3 × 1 pola ke-3 = 11 = 5 + 6 = 5 + 3 × 2 Dari pola di atas maka:

pola ke-7 = 5 + (3 × 6) = 23 pola ke-12 = 5 + (3 × 11) = 38

B. Pola dan Suku-Suku Barisan

Bilang

1.

Pengertian Barisan Bilangan

2.

Beberapa Contoh Aturan Barisan

Bilangan

3.

Menemukan Rumus Suku Ke-n (Un

)

1. Pengertian Barisan Bilangan

Perhatikan pola bilangan-bilangan berikut. a. 1, 3, 5, 7

b. 2, 4, 6, 8, 10

c. 3, 6, 9, 12, 15, . . .

Jika kamu perhatikan, bilangan-bilangan pada a, b, dan c disusun dengan pola tertentu. Bilanganbilangan tersebut disebut barisan bilangan. Adapun setiap bilangan dalam barisan bilangan disebut

suku barisan. Suku ke-n suatu barisan bilangan ditulis dengan Un.

Pada barisan bilangan: 1, 3, 5, 7 diperoleh: Suku ke-1 = U1 = 1

Suku ke-2 = U2 = 3 Suku ke-3 = U3 = 5 Suku ke-4 = U4 = 7

2. Beberapa Contoh Aturan Barisan Bilangan

a. Barisan dengan Aturan Ditambah 1) Barisan Bertingkat Satu

Barisan bilangan 1, 3, 5, 7, · · · merupakan barisan bertingkat satu.

2) Barisan Bertingkat Dua

Barisan bilangan 0, 1, 3, 6, · · · merupakan barisan bertingkat dua.

3) Barisan Bertingkat Tiga

b. Barisan dengan Aturan Dikali

d. Barisan fibonacci

1, 1, 2, 3, 5, 8, 13, . . . Aturannya: mulai suku

ketiga, setiap suku diperoleh dengan menjumlahkan dua suku sebelumnya.

3. Menemukan Rumus Suku Ke-n

(U

_{Prinsip dasar menentukan rumus suku ke-n adalah n}

)

mencari kaitan antara bilangan satu dengan suku kesatu, bilangan dua dengan suku kedua, bilangan tiga dengan suku ketiga, dan seterusnya.

Contoh:

Barisan bilangan 2, 4, 8, 16, · · · U₁ = 2 = 21

U₂ = 4 = 22

U₃ = 8 = 23

U₄ = 16 = 24, dan seterusnya

C. Barisan dan Deret

Aritmetika

1. Barisan Aritmetika

2. Deret Aritmetika

1. Barisan Aritmetika

a. Pengertian Barisan

Aritmetika_{Barisan aritmetika adalah barisan bilangan yang selisih}

antara dua suku barisan yang berurutan nilainya selalu tetap atau sama

b. Rumus-Rumus pada Barisan Aritmetika





t 1 n

1

U = U +U 2

1) Rumus Suku Ke-n (U_n) U_n = a + (n – 1)b

2) Beda (b)

b = U_n – (U_{n – 1})

3) Rumus Suku Tengah (U_t)

c. Jenis-Jenis Barisan Aritmetika

Deret aritmetika adalah nilai yang diperoleh dari penjumlahan suku-suku barisan bilangan aritmetika.

Jika U₁, U₂, U₃, · · · , U_{n – 1}, U_n membentuk barisan aritmetika, bentuk penjumlahan U₁ + U₂ + U₃ + · · · + U_{n – 1} + U_n disebut deret aritmetika.

2. Deret Aritmetika

Rumus penjumlahan n suku pertama deret aritmetika dapat dituliskan sebagai berikut.

Dengan : S_n = jumlah n suku pertama n = banyak suku

a = suku pertama b = beda suku

Contoh Soal

Setiap Minggu Dina menyimpan uang di laci. Pada

minggu pertama Dina menyimpan Rp500,00,

minggu

kedua

Rp700,00,

minggu

ketiga

Rp900,00, minggu keempat Rp1.100,00, begitu

seterusnya setiap minggu bertambah Rp200,00.

a.Tentukan besar uang yang disimpan Dina pada

minggu ke-20.

D. Barisan dan Deret Geometri

1. Barisan Geometri

2. Deret Geometri

1. Barisan Geometri

a. Pengertian Barisan

Geometri_{Barisan geometri adalah barisan bilangan yang}

perbandingan setiap dua suku barisan yang berurutan nilainya selalu tetap atau sama.

b. Rumus-Rumus pada Barisan Aritmetika

1) Rumus Suku Ke-n (U_n) Un _{= ar}n – 1

2) Rasio (r)

3) Rumus Suku Tengah (U_t)





n n 1

U

r

U



�

t 1 n

Deret geometri adalah penjumlahan dari suku-suku barisan geometri.

Jika U₁, U₂, U₃, · · · , U_{n – 1}, U_n membentuk barisan geometri, bentuk penjumlahan U₁ + U₂ + U₃ + · · · + U_{n – 1} + U_n disebut deret geometri.

2. Deret Geometri

Rumus penjumlahan n suku pertama deret geometri dapat dituliskan sebagai berikut.

Dengan : S_n = jumlah n suku pertama n = banyak suku

Contoh Soal

1. Tentukan suku ke-8 dari setiap barisan

geometri berikut.

a. 1, 3, 9, 27, · · ·

b. 3, –6, 12, –24, · · ·

2. Berdasarkan pengamatan diketahui bahwa

setiap bakteri berkembang biak menjadi dua

kali lipat dalam waktu dua menit. Semula ada

50 sel bakteri untuk pengamatan.

a. Berapa banyak bakteri setelah 10 menit?

BAB II

Koordinat Kartesius

A.

Letak Benda pada Koordinat Kar

tesius

B.

Posisi Relatif Benda Menggunak

an Koordinat Kartesius

A.Letak Benda pada Koordinat Kartesius

Kembali ke BAB II

1.

Jarak Tempat/Benda terhadap Garis Su

mbu

2.

Membaca Letak Benda Menggunakan Si

stem Koordinat

1. Jarak Tempat/Benda terhadap Garis

Sumbu

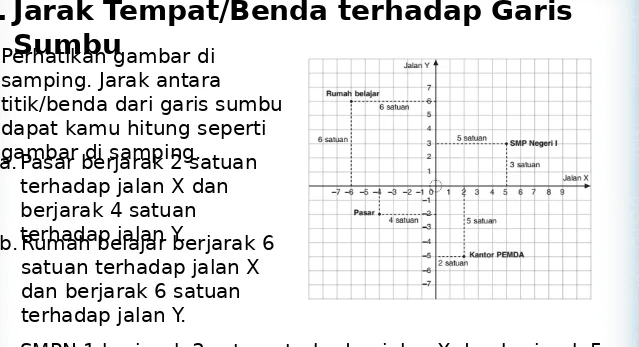
Perhatikan gambar di samping. Jarak antara

titik/benda dari garis sumbu dapat kamu hitung seperti gambar di samping.

a. Pasar berjarak 2 satuan terhadap jalan X dan berjarak 4 satuan terhadap jalan Y.

b.Rumah belajar berjarak 6 satuan terhadap jalan X dan berjarak 6 satuan terhadap jalan Y.

2. Membaca Letak Benda Menggunakan Sistem

Koordinat

Perhatikan gambar di samping. Letak tempat-tempat pelayanan tersebut dapat ditunjukkan dengan sistem koordinat secara sederhana. Sumbu mendatar diberi kode huruf abjad dan sumbu tegak diberi kode bilangan.

Letak tempat-tempat layanan tersebut dapat ditulis sebagai berikut.

Hotel terletak pada koordinat (C, 5).

Bank terletak pada koordinat (F, 5). Pasar terletak pada koordinat (F, 10).

Kantor Pos terletak pada koordinat (J, 3).

3. Membaca dan Menuliskan Letak

Titik/Benda pada Sistem Koordinat

Kartesius

_{Cara membaca letak titik pada}

sistem koordinat kartesius sebagai berikut.

a.Gunakan titik acuan (0, 0) untuk menentukan titik A(x, y).

b.x menunjukkan banyak langkah/satuan untuk arah

mendatar (arah ke kanan bernilai positif, arah ke kiri bernilai

negatif).

c.y menunjukkan banyak

langkah/satuan untuk arah tegak (arah ke atas bernilai positif, arah ke bawah bernilai negatif).

Contoh Soal

Jajargenjang ABCD terletak pada bidang koordinat

dengan koordinat titik A(–2, –4), B(6, –4), dan C(9,

2).

Tentukan:

a. koordinat titik D dengan bantuan gambar;

b. panjang AB;

B. Posisi Relatif

Benda

Menggunakan

Koordinat

Kartesius

Contoh Soal

Perhatikan gambar berikut.

Dengan sistem koordinat

kartesius, tentukan koordinat tempat-tempat di pada gambar di samping dengan titik acuan yang diberikan.

a. Posisi kampus dan stasiun dengan titik acuan balai kota. b. Posisi toko buku dan apotek

dengan titik acuan stasiun. c. Posisi toko buku dan stasiun

dengan titik acuan kampus

BAB III

Relasi dan Fungsi

A.

Relasi dan Fungsi

B.

Rumus Fungsi, Nilai Fungsi, dan Gr

afik Fungsi

A.Relasi dan

Fungsi

1.

Relasi

2.

Fungsi

1. Relasi

Relasi dari himpunan A ke himpunan B adalah suatu

hubungan (pengaitan) yang memasangkan (mengawankan) anggota-anggota himpunan A dengan anggota-anggota

himpunan B.

a. Pengertian Relasi

b. Menyajikan Relasi

1) Relasi Berbentuk Tabel

2) Relasi Berbentuk Diagram Panah

3) Relasi Berbentuk Himpunan Pasangan Berurutan

a. Pengertian Fungsi

Fungsi disebut juga pemetaan.

Fungsi dari himpunan A ke himpunan B adalah relasi khusus yang memasangkan setiap anggota himpunan A dengan

tepat satu anggota himpunan B.

Notasi Fungsi: f : x  y atau f : x  f(x) atau f : x  y = f(x)

Tepat satu artinya tidak boleh lebih dan tidak boleh kurang dari satu.

Syarat suatu relasi merupakan fungsi atau pemetaan sebagai berikut.

1) Setiap anggota A mempunyai pasangan di B.

2) Setiap anggota A dipasangkan dengan tepat satu anggota B.

b. Domain, Kodomain, dan Range

Fungsi f memetakan anggota himpunan A ke anggota himpunan B.

A = {1, 2, 3, 4} disebut daerah asal (domain).

B = {3, 5, 7, 9, 11} disebut daerah kawan (kodomain).

Dari diagram panah di samping diperoleh himpunan pasangan berurutan

f = {(1, 3), (2, 5), (3, 7), (4, 9)}.

(1, 3) dibaca bayangan 1 oleh fungsi f adalah 3.

(1, 3) juga dapat dituliskan dengan f(1) = 3 dibaca nilai dari f(1) adalah 3.

Himpunan dari anggota kodomain yang mempunyai pasangan dengan

c. Banyak Fungsi yang Mungkin dari

Dua Relasi

Jika banyak anggota himpunan A = n(A) dan banyak

anggota himpunan B = n(B) maka:

1) banyak fungsi yang mungkin dari A ke B =

n(B)

n(A)

dan

d. Fungsi Korespondensi Satu-Satu

Suatu fungsi dikatakan korespondensi satu-satu jika setiap anggota domain dipasangkan dengan tepat satu anggota kodomain dan sebaliknya setiap anggota kodomain

dipasangkan dengan tepat satu anggota domain.

Jika terdapat himpunan A dan B dengan n(A) = n(B) = n,

B. Rumus Fungsi, Nilai Fungsi, dan

Grafik Fungsi

1.

Rumus Fungsi dan

Nilai Fungsi

2.

Grafik Fungsi pad

a Bidang Koordina

t Kartesius

1. Rumus Fungsi dan Nilai

Fungsi

Fungsi f : x  y = f(x) dari himpunan A ke himpunan B jika

digambarkan dalam bentuk diagram panah seperti gambar di bawah.

y merupakan peta atau bayangan x atau nilai fungsi dari x, ditulis y = f(x).

x merupakan prapeta dari f(x) atau x merupakan prapeta dari y.

Dalam bentuk pasangan berurutan, f : x  y = f(x) dituliskan sebagai (x, y) atau (x, f(x)).

Contoh Menentukan Nilai Fungsi

Suatu fungsi f : x  3x + 5 dapat dinyatakan dengan rumus fungsi f(x) = 3x + 5. Berdasarkan rumus fungsi ini, dapat ditentukan nilai fungsi untuk setiap nilai x pada domain {x | –2 ≤ x ≤ 1, x  bilangan bulat} sebagai berikut.

Nilai fungsi untuk x = –2 adalah f(–2) = 3 × (–2) + 5 = –6 + 5 = –1

Nilai fungsi untuk x = –1 adalah f(–1) = 3 × (–1) + 5 = –3 + 5 = 2

Nilai fungsi untuk x = 0 adalah f(0) = 3 × 0 + 5 = 0 + 5 = 5

Nilai fungsi untuk x = 1 adalah f(1) = 3 × 1 + 5 = 3 + 5 = 8

Himpunan pasangan berurutan f : x  3x + 5 pada domain {x | –2 ≤ x ≤ 1, x  bilangan bulat} adalah {(–2, –1), (–1, 2), (0, 5), (1, 8)}.

Range f = {–1, 2, 5, 8}.

Prapeta dari –1 adalah f–1_{(–1) = –2.}

Prapeta dari 2 adalah f–1_{(2) = –1.}

Prapeta dari 5 adalah f–1_{(5) = 0.}

2. Grafik Fungsi pada Bidang Koordinat

Kartesius

a.

Grafik Fungsi Konsta

n

b.

Grafik Fungsi Identit

as

c.

Grafik Fungsi Linear

a.Grafik Fungsi Konstan

Fungsi konstan dinyatakan dengan rumus f(x) = c, c



bilangan real.

Grafik fungsi f(x) = 3 pada domain {x | –3 ≤ x ≤ 3} dapat

digambar sebagai berikut.

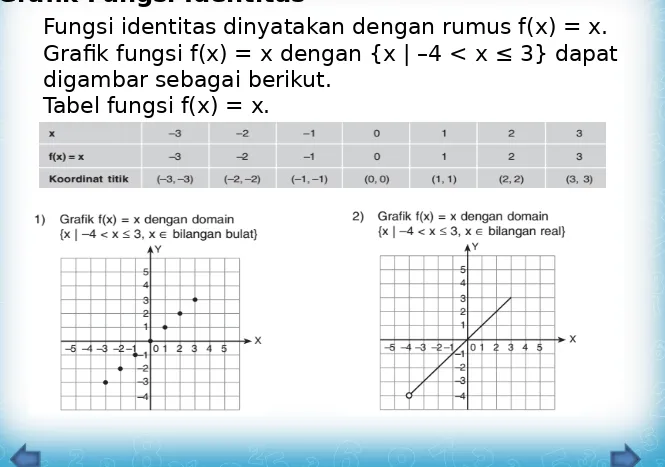
b. Grafik Fungsi Identitas

Fungsi identitas dinyatakan dengan rumus f(x) = x.

Grafik fungsi f(x) = x dengan {x | –4 < x ≤ 3} dapat

digambar sebagai berikut.

c. Grafik Fungsi Linear

d. Grafik Fungsi Kuadrat

Fungsi kuadrat dinyatakan dengan rumus f(x) = ax

2

Kembali ke Daftar Isi

BAB IV

Persamaan Garis Lurus

A.Grafik Garis Lurus B.Gradien Garis Lurus

C. Persamaan Garis Lurus D.

Kembali ke BAB IV

A. Grafik Garis Lurus

1.

Persamaan Garis Lu

rus

2.

Syarat Titik Terleta

k pada Garis

1. Persamaan Garis Lurus

Bentuk umum persamaan garis lurus dalam variabel x dan y sebagai berikut.

y = mx +

n

atau

Ax + by = c

Contoh:

y = –2x + 4 dan 4x + 2y = 8 merupakan persamaan garis lurus.

Perhatikan cara mengubah persamaan garis lurus menjadi bentuk

2. Syarat Titik Terletak pada Garis

Sebuah titik terletak pada suatu garis jika nilai absis dan ordinat titik tersebut memenuhi persamaan garisnya . Titik (x₁, y₁) terletak pada garis y = mx + n jika y₁ = mx₁ + n bernilai benar.

Contoh:

Langkah-langkahnya sebagai berikut.

1) Menentukan beberapa titik bantu yang terletak pada garis lurus.

2) Menggambar titik-titik bantu tersebut pada bidang koordinat kartesius.

3) Menghubungkan titik-titik bantu pada bidang koordinat kartesius dengan garis lurus.

a. Menggambar Grafik Garis Lurus Menggunakan Beberapa Titik Bantu

Contoh Soal.

Diketahui titik A(0, 15), B(5, 25), C(10, 35), dan D(30, 75).

1. Gambarlah garis yang melalui titik A dan B. 2. Gambarlah garis yang melalui titik A dan C. 3. Gambarlah garis yang melalui titik A dan D. 4. Gambarlah garis yang melalui titik B dan C.

Apakah keempat grafik garis tersebut merupakan grafik garis yang sama? Selidikilah!

b. Menggambar Grafik Garis Lurus Menggunakan

Pertolongan Titik Perpotongan Garis dengan

Sumbu Koordinat

_{Langkah-langkahnya sebagai berikut.}

1) Menentukan titik potong garis dengan sumbu X.

Garis memotong sumbu X di y = 0. Substitusikan y = 0 ke dalam persamaan garis untuk menentukan titik potong garis dengan sumbu X.

2) Menentukan titik potong garis dengan sumbu Y.

Garis memotong sumbu Y di x = 0. Substitusikan x = 0 ke dalam persamaan garis untuk menentukan titik

potong garis dengan sumbu Y.

3) Menggambar titik potong dengan sumbu X dan sumbu Y tersebut pada bidang koordinat kartesius.

4) Menghubungkan kedua titik potong dengan garis lurus. 5) Menuliskan persamaan garisnya pada salah satu ujung

B. Gradien Garis

Lurus

1.

Gradien Garis

2.

Menentukan Gradien Garis

3.

Sifat-Sifat Gradien Suatu Garis

1. Gradien Garis

Gradien garis

adalah nilai

kemiringan atau

kecondongan suatu garis.

Gradien biasanya

2. Menentukan Gradien Garis

Langkah-langkah menentukan gradien garis yang diketahui grafiknya. Misalkan diketahui grafik garis g. 1)Menentukan dua titik sembarang pada grafik garis g. 2)Membuat garis lurus putus-putus mendatar dari kiri ke kanan dimulai dari titik yang terletak di sebelah kiri.

Misalkan garis putus-putus tersebut garis a.

3)Dari garis a, membuat garis yang tegak lurus dengan garis a dan memotong titik yang terletak di sebelah

kanan. Misalkan garis putus-putus tersebut garis b. 4)Garis g, garis a, dan garis b membentuk segitiga dengan:

panjang sisi mendatar segitiga = perubahan nilai x dan

panjang sisi tegak segitiga = perubahan nilai y. 5)Menentukan gradien garis tersebut menggunakan rumus berikut.

b. Menentukan Gradien Garis Jika Diketahui Persamaannya

1) Gradien garis dengan persamaan y = mx + n

Gradien garis dengan persamaan y = mx + n adalah m.

2) Gradien garis dengan persamaan ax + by = c

C. Persamaan Garis Lurus

1.

Persamaan Garis yang Diketahui Gradien

dan Salah Satu Titik yang Dilalui Garis

2.

Persamaan Garis yang Melalui Dua Titik

1.Persamaan Garis yang Diketahui Gradien dan

Salah Satu Titik yang Dilalui Garis

a. Persamaan Garis yang Bergradien m dan Memotong Sumbu Y di (0, n)

CONTOH SOAL

1. Tentukan persamaan garis yang melalui titik (2, –3) dan bergradien:

a. 5

b.

D. Kedudukan Dua Garis Lurus

1. Dua Garis Sejajar

2. Dua Garis Berimpit

3. Dua Garis Berpotonga

n

1. Dua Garis Sejajar

Dua garis dikatakan sejajar jika jarak kedua garis tersebut

selalu sama atau kedua garis tersebut tidak pernah

berpotongan.

Dua garis yang sejajar

2. Dua Garis Berimpit

Dua garis dikatakan berimpit jika semua titik-titik yang dilalui kedua garis tersebut berimpit. Dengan kata lain, kedua garis tersebut merupakan garis yang sama.

Dua garis berimpit mempunyai persamaan garis yang

ekuivalen.

3. Dua Garis

Berpotongan

a. Kedudukan Dua Garis Berpotongan

1) Dua Garis Berpotongan Tegak Lurus

2) Dua Garis Berpotongan Tidak Tegak Lurus

b. Titik Potong Dua Garis Berpotongan

Titik potong dua garis berpotongan dapat ditentukan dengan cara menggambar kedua garis dalam satu bidang koordinat kartesius.

CONTOH SOAL

1. Diketahui persamaan garis g adalah y = 3x – 10.

Garis

l

sejajar dengan garis g sedangkan garis k

tegak lurus dengan garis

g

. Tentukan gradien garis

l

dan garis

k

.

2. Tentukan persamaan garis yang tegak lurus dengan

garis

y = –2x – 5 dan melalui titik (3, 4).

3. Apakah garis dengan persamaan y = –3x + 14 akan

berpotongan dengan garis –4y + 3x – 4 = 0?

BAB V

SISTEM PERSAMAAN

LINEAR DUA V ARIABEL

A.

Mengenal Sistem Persamaan Linear Dua V ar

iabel (SPLDV )

B.

Menyelesaikan Sistem Persamaan Linear Du

a V ariabel

C.

Menyelesaikan Masalah yang Berkaitan den

gan Sistem Persamaan Linear Dua V ariabel

A. Mengenal Sistem Persamaan Linear Dua

V ariabel (SPLDV )

1.

Persamaan Linear

2.

Sistem Persamaan Linear Dua V ariabel

1. Persamaan Linear

Persamaan linear adalah persamaan yang mengandung

variabel dengan syarat setiap variabel tersebut berpangkat satu.

a. Persamaan Linear Satu V ariabel (PLSV )

Persamaan linear satu variabel adalah persamaan linear yang hanya mempunyai satu variabel.

Contoh: y + 4 = 12  Variabelnya satu, yaitu y

b. Persamaan Linear Dua V ariabel (PLDV )

Persamaan linear dua variabel adalah persamaan linear yang mempunyai dua variabel.

Contoh: y + 4x = 12  Variabelnya dua, yaitu x dan y

c. Sistem Persamaan Linear Dua V ariabel (SPLDV )

2. Sistem Persamaan Linear Dua V ariabel

b. Penyelesaian dan Bukan Penyelesaian SPLDV

Nilai pengganti yang memenuhi SPLDV sehingga persamaan bernilai benar disebut penyelesaian atau akar. Sebaliknya, nilai pengganti yang tidak memenuhi SPLDV sehingga

persamaan bernilai salah disebut bukan penyelesaian atau

bukan akar

c. Perbedaan Antara PLDV dengan SPLDV

PLDV hanya terdiri atas satu persamaan. Penyelesaiannya merupakan nilai pengganti dari variabel-variabel yang

memenuhi persamaan tersebut.

SPLDV terdiri atas dua persamaan. Penyelesaian SPLDV merupakan nilai pengganti dari variabel-variabel yang memenuhi kedua persamaan tersebut

a. V ariabel dan Koefisien PLDV

Pada persamaan 3x – 4y = 23, bilangan 3 disebut koefisien dari x, bilangan –4 disebut koefisien dari y, bilangan 23

B. Menyelesaikan Sistem Persamaan Linear

Dua V ariabel

1.

Metode Substitusi

2.

Metode Eliminasi

(Penghilangan)

3.

Metode Grafik

1. Metode Substitusi

2x – 3y = –10

 2(2 – 2y) – 3y = –10

 4 – 4y – 3y = –10

 4 – 7y = –10  –7y = –14  y = 2

Substitusikan y = 2 ke dalam persamaan (3).

x = 2 – 2y

 x = 2 – 2(2)  x = –2

Jadi, penyelesaiannya x = –2 dan y = 2.

Contoh:

Tentukan penyelesaian SPLDV berikut menggunakan metode substitusi. 2x – 3y = –10 . . . (1)

x + 2y = 2 . . . (2)

Jawaban:

Cara 1: mensubstitusikan x

Nyatakan variabel x dalam y pada persamaan (2).

x + 2y = 2  x = 2 – 2y . . . (3)

Substitusikan persamaan (3) ke dalam persamaan (1).

Penyelesaian SPLDV menggunakan metode substitusi dilakukan dengan cara berikut.

a.Ambil satu variabel pada salah satu persamaan.

Selanjutnya, nyatakan variabel tersebut dalam variabel lain. Dengan begitu akan diperoleh persamaan dalam bentuk baru.

2. Metode Eliminasi

(Penghilangan)

Penyelesaian SPLDV dengan metode eliminasi dilakukan dengan cara menghilangkan salah satu variabelnya.

Contoh:

Tentukan penyelesaian SPLDV berikut menggunakan metode eliminasi.

2x – 3y = –10 . . . (1) x + 2y = 2 . . . (2)

Jawaban:

3. Metode Grafik

Penyelesaian SPLDV menggunakan metode grafik dilakukan dengan menggambar grafik dari kedua persamaan yang

diketahui pada satu bidang kartesius. Koordinat titik potong kedua grafik merupakan penyelesaian dari sistem persamaan tersebut.

Contoh:

Tentukan penyelesaian SPLDV berikut menggunakan metode grafik.

2x – 3y = –10 . . . (1) x + 2y = 2 . . . (2)

Jawaban:

Menggambar garis 2x – 3y = –10.

Menggambar garis x + 2y = 2 .

Kedua garis tersebut

digambar dalam satu bidang kartesius berikut.

Tampak bahwa kedua garis

tersebut berpotongan di titik (–2, 2).

C. Menyelesaikan Masalah yang Berkaitan

dengan Sistem Persamaan Linear Dua

V ariabel

Untuk menyelesaikan masalah sehari-hari kamu harus mampu mengubah masalah menjadi SPLDV.

Secara garis besar langkah-langkah mengubah

permasalahan sehari-hari menjadi SPLDV dilakukan sebagai berikut.

1.Tentukan variabel-variabelnya, lalu lakukan pemisalan. 2.Terjemahkan permasalahan tersebut ke dalam model matematika berbentuk SPLDV.

3.Selesaikan model matematika yang diperoleh pada langkah 2.

4.Selanjutnya, nilai-nilai variabel yang telah diperoleh

Contoh Soal

1.

Pak Maman membeli buku tulis dan buku gambar untuk

anak-anak panti asuhan. Jumlah buku-buku tersebut

160 buah. Harga setiap buku gambar Rp2.400,00,

sedangkan harga setiap buku tulis Rp3.500,00. Jika Pak

Maman harus membayar sebanyak Rp494.000,00,

tentukan banyak setiap jenis buku tersebut.

2.

Bu Sita mempunyai persediaan 4 kotak penghapus dan

15 rautan. Setiap kotak berisi 12 buah penghapus. Jika

terjual semua, Bu Sita akan memperoleh uang

Rp59.400,00. Pada suatu hari terjual 10 buah

penghapus dan 3 rautan. Hasil penjualan tersebut

Rp12.200,00. Tentukan hasil penjualan jika terjual 8

penghapus dan 10 rautan.