Materi Matematika Kelas VIII

BAB 4

PERSAMAAN LINEAR DUA VARIABEL (SPLDV) A. Perbedaan PLSV, PLDV dan SPLDV

Persamaan Linear Satu Variabel (PLSV) adalah persamaan yang hanya memiliki satu variabel berpangkat satu. Bentuk umum PLSV, yaitu : ax + c1 = c2 dengan a ≠0 variabelnya berpangkat satu.

Bentuk umum PLDV, yaitu : ax + by = c dengan a dan b ≠0

Contoh : 1) x + 3y = -2 2) 3a – 2b = 4 3) 2p + q – 6 = 0

Sistem Persamaan Linear Dua Variabel (SPLDV) adalah gabungan dari dua buah atau lebih PLDV yang membentuk satu kesatuan.

B. Metode Penyelesaian SPLDV

Contoh :

Tentukan penyelesaian dari sistem persamaan berikut : 4x + y = 2 dan x – 2y = 5

Adapun metode yang dapat digunakan untuk menyelesaikan soal di atas adalah dengan 3 metode, yaitu :

1. Subtitusi

Langkah-langkah penyelesaiannya, yaitu :

a. Tulis salah satu persamaan menjadi y = ... atau x = ... x – 2y = 5

x = 2y + 5

b. Subtitusikan ke persamaan lainnya

 x = 2y + 5 disubtitusikan

 Nilai y = -2 disubtitusikan ke salah satu persamaan, misal ke persamaan: 4x + y = 2

Jadi, penyelesaian sistem persamaan tersebut adalah x = 1

dan y = -2, sehingga himpunan penyelesaiannya, yaitu (1, -2).

2. Eliminasi

Merupakan penyelesaian SPLDV dengan cara menghilangkan salah satu variabel.

Langkah-langkah penyelesaiannya, yaitu :

a. Mengeliminasi (menghilangkan) variabel x dengan menyamakan koefisien variabel x kemudian menjumlahkan atau mengurangi kedua persamaan sehingga variabel x hilang (koefisien x = 0)

Jadi, penyelesaian sistem persamaan tersebut adalah x = 1

dan y = -2, sehingga himpunan penyelesaiannya, yaitu (1, -2).

3. Grafik

Merupakan penyelesaian SPLDV dengan cara menggambar grafik dari kedua buah atau lebih persamaan kemudian menentukan titik potongnya.

Langkah-langkah penyelesaiannya, yaitu :

a. Menentukan titik potong dari persamaan 4x + y = 2

 Titik potong sumbu x

b. Menentukan titik potong dari persamaan x – 2y = 5

 Titik potong sumbu x

c. Menggambar grafik kedua persamaan tersebut, kemudian menentukan titik potongnya

Jadi, himpunan penyelesaian sistem persamaan tersebut adalah (1, -2)

C. Penggunaan SPLDV dalam Kehidupan Sehari-hari

Contoh :

Diketahui harga 3 buku tulis dan 2 pulpen adaah Rp 11.500,- sedangkan harga 2 buku tulis dan 5 pulpen adalah Rp. 15.000,-. Hitunglah :

a. Harga masing-masing

b. Harga 5 buku tulis dan 7 pulpen Jawab :

Misal : Harga 1 buah buku tulis = x

Harga 1 buah pulpen = y

Sehingga : Harga 3 buku tulis dan 2 pulpen dinyatakan dengan 3x + 2y = 11.500

Harga 2 buku tulis dan 5 pulpen dinyatakan dengan 2x + 5y = 15.000

Model matematikanya yaitu 3x + 2y = 11.500 dan 2x + 5y = 15.000

a. Harga masing-masing

 Mengeliminasi variabel x

3x + 2y = 11.500 dikali 2 6x + 4y = 23.000

 Subtitusikan nilai y = 2.000 ke salahsatu persamaan, misal ke persamaan : harga 1 buah pulpen adalah Rp.

a. Nilai x dan y b. Nilai 6x + 4y

2. Harga 8 buah pensil dan 6 buah penghapus Rp. 14.400,-sedangkan harga 6 buah pensil dan 5 buah penghapus Rp. 11.200,-. Hitunglah :

a. Harga masing-masing pensil dan penghapus

b. Jumlah harga 5 buah pensil dan 8 buah penghapus

GARIS SINGGUNG LINGKARAN A. Pengertian

Dari gambar berikut, manakah yang termasuk garis singgung lingkaran? Jelaskan!

1) Garis p bukan merupakan garis singgung, karena garis p saling lepas (tidak berpotongan sama sekali dengan lingkaran).

2) Garis q bukan merupakan garis singgung, karena garis q

berpotongan di dua titik pada lingkaran.

3) Garis r bukan merupakan garis singgung, karena jika garis r

diperpanjang akan berpotongan di dua titik pada lingkaran.

4) Garis s merupakan garis singgung, karena garis s berpotongan tepat di satu titik pada lingkaran dan akan tegak lurus dengan jari-jari melalui titik singgungnya.

Garis singgung lingkaran adalah garis yang apabila diperpanjang akan memotong lingkaran hanya pada satu titik.

Sifat-sifat garis singgung lingkaran, yaitu: 1) Memotong lingkaran hanya pada satu titik.

O B

L M

L M

3) Garis yang tegak lurus dengan garis singgung pada titik singgungnya pasti melalui titik pusat lingkaran.

4) Garis yang tegak lurus dengan diameter dan melalui titik ujungnya adalah garis singgung lingkaran.

B. Melukis Garis Singgung Lingkaran

1) Melukis Garis Singgung Melalui Satu Titik pada Lingkaran

 Gambarlah lingkaran dengan titik pusat O!

 Buatlah sebuah titik B pada lingkaran tersebut!

 Hubungkan OB!

 Tarik sebuah garis singgung lingkaran sehingga menyinggung

titik B dan tegak lurus dengan OB!

2) Melukis Garis Singgung Melalui Titik di Luar Lingkaran

 Gambarlah lingkaran dengan titik pusat O!

 Buatlah sebuah titik B di luar lingkaran tersebut!

 Hubungkan OB, kemudian jadikan OB sebagai diameter

lingkaran baru!

 Buatlah lingkaran baru dengan pusat P dan berjari-jari PA dan

PB. Lingkaran baru tersebut akan memotong lingkaran sebelumnya di titik M dan N.

 Tarik B ke M dan N! BM dan BN adalah garis singgung lingkaran.

C. Kedudukan Dua Buah Lingkaran

L M

L M

lingkaran bersinggungan di luar

3) LM < r1 + r2 → kedua lingkaran berpotongan

4) LM = r1 - r2 → kedua

lingkaran bersinggungan di dalam

5) LM < r1 - r2 → lingkaran kecil berada di dalam lingkaran besar

6) LM = 0 → kedua lingkaran

sepusat (memiliki titik pusat yang sama)

D. Panjang Garis Singgung Lingkaran

1) Garis Singgung yang Melalui Satu Titik di Luar Lingkaran

AC2 _{= BC}2 _{= PC}2 _{– PB}2 AC = BC = √ PC2 _{– PB}2

AC = BC = Garis singgung dari titik di luar lingkaran

PC = Jarak titik pusat dengan titik di luar lingkaran

PB = PA = Jari-jari lingkaran

Contoh :

Diketahui AB adalah garis singgung lingkaran dengan panjang 12 cm dan berjari-jari 5 cm, hitunglah panjang OB!

P

2) Garis Singgung Persekutuan Dalam Dua Lingkaran

gd2 = PQ2 = AT2 =

AB = Jarak antara kedua titik pusat lingkaran r1 = AP = TQ = Jari-jari lingkaran besar r2 = BQ = Jari-jari lingkaran kecil

3) Garis Singgung Persekutuan Luar Dua Lingkaran

gℓ2 = PQ2 = TQ2 – TP2 gℓ2 = AB2 – (AP - AT)2 gℓ2 = AB2 – (AP - QB)2 gℓ2 = AB2 – (r1 - r2)2 gℓ = √ AB2 – (r1 - r2)2

gℓ = PQ = Garis singgung persekutuan luar dua lingkaran

AB = TQ = Jarak antara kedua titik pusat lingkaran

r1 = AP = Jari-jari lingkaran besar r2 = QB= AT = Jari-jari lingkaran kecil

Contoh :

C

A _B

P Q

R

Jika jarak titik pusat kedua lingkaran 20 cm, hitunglah:

a) Panjang garis singgung persekutuan dalam dua lingkaran b) Panjang garis singgung persekutuan luar dua lingkaran Jawab :

1) Diketahui dua buah lingkaran memiliki jari-jari 13,5 cm dan 6,5 cm. Jika jarak titik pusat kedua lingkaran 25 cm, hitunglah:

a) Panjang garis singgung persekutuan dalam dua lingkaran b) Panjang garis singgung persekutuan luar dua lingkaran

2) Panjang garis singgung persekutuan dalam dua lingkaran 15 cm dan jari-jarinya masing-masing 3 cm dan 5 cm. Hitunglah jarak titik pusat kedua lingkaran tersebu!

3) Panjang garis singgung persekutuan luar dua lingkaran 24 cm. Jika jarak titik pusat kedua lingkaran tersebut 26 cm dan jari-jari lingkaran besar 15 cm. Hitunglah jari-jari lingkaran kecil!

LINGKARAN DALAM DAN LUAR SEGI-TIGA A. Pengertian

Lingkaran dalam Segi-tiga adalah lingkaran yang menyinggung bagian dalam ketiga sisi suatu Segi-tiga.

Lingkaran luar Segi-tiga adalah lingkaran yang melalui ketiga titik sudut suatu Segi-tiga.

B. Melukis Lingkaran Dalam Segi-tiga

1) Gambarlah ∆ ABC!

2) Lukislah garis bagi AP, BQ dan CR dari ketiga sudut ∆ ABC!

3) Tulislah perpotongan ketiga garis bagi tersebut sebagai titik pusat (titik O)!

P O Q

R

ABC dengan jari-jari OP, OQ dan OR!

Garis bagi adalah garis yang membagi setiap sudut ∆ menjadi dua sama besar.

Panjang jari-jari Lingkaran Dalam Segi-tiga :

rd =

C. Melukis Lingkaran Luar Segi-tiga

1) Gambarlah ∆ ABC!

2) Lukislah garis sumbu AP,

BQ dan CR dari ketiga sisi ∆ ABC!

3) Tulislah perpotongan ketiga garis sumbu tersebut sebagai titik pusat (titik O)! 4) Buatlah lingkaran luar ∆ ABC

dengan jari-jari AO, BO dan CO!

Garis sumbu adalah garis yang membagi setiap sisi ∆ menjadi dua sama panjang.

Panjang jari-jari Lingkaran Luar Segi-tiga :

rℓ =

a) Panjang jari-jari lingkaran dalam Segi-tiga b) Panjang jari-jari lingkaran luar Segi-tiga Jawab :

a

L∆ =

1) Buatlah lingkaran dalam Segi-tiga dan lingkaran luar Segi-tiga dari

∆ ABC dengan panjang sisi AB = 6 cm, BC = 8 cm dan AC = 10 cm! Kemudian tentukan :

a) L ∆ ABC

b) K ∆ ABC

c) Panjang jari-jari lingkaran dalam Segi-tiga

d) Panjang jari-jari lingkaran luar Segi-tiga

2) Perhatikan gambar di samping!

Panjang PQ = 15 cm dan QR = 8 cm dan RP = 17 cm

Hitunglah :

a) L ∆ PQR

b) Panjang jari-jari lingkaran dalam

Segi-tiga

c) L lingkaran

d) L daerah yang diarsir

Dari gambar di atas manakah yang termasuk bangun ruang sisi datar dan manakah yang termasuk bangun ruang sisi lengkung?

Yang termasuk bangun ruang sisi datar adalah gambar (i) korek api berbentuk balok, (ii) dadu berbentuk kubus, (iii) piramida berbentuk

limas, dan (v) paping blok berbentuk prisma Segi-enam.

Yang termasuk bangun ruang sisi lengkung adalah gambar (iv) nasi tumpeng berbentuk kerucut, (vi) kaleng cat berbentuk tabung, dan (vii) bola sepak berbentuk bola.

kongruen

Kubus adalah suatu bangun ruang yang dibatasi oleh 6 bidang (sisi) yang kongruen berbentuk persegi.

 Jaring-jaring Kubus

 Luas Permukaan Kubus

Kubus terdiri atas ... buah sisi yang sama ... dan ... (kongruen). Sisi-sisi kubus tersebut berbentuk ...

Karena : L Persegi = ... x ...

. Unsur-unsurBalok Nama Unsur-unsurBalok Keterangan

AH = DE = BG = CF =

Balok adalah suatu bangun ruang yang dibatasi oleh 3 pasang bidang (sisi) yang kongruen berbentuk persegi panjang.

 Jaring-jaring Balok

 Luas Permukaan Balok

Misal p adalah panjang balok, l adalah lebar balok dan t adalah tinggi balok, maka:

p = AB = ... = ... = ...

l = BC = ... = ... = ...

t = EA = ... = ... = ...

Balok terdiri dari ... pasang sisi yang berbentuk ..., yaitu:

ABCD = ... sehingga L ABCD = L ... = ... x ... = ... ABFE = ... sehingga L ABFE = L ... = ... x ... = ... BCGF = ... sehingga L BCGF = L ... = ... x ... = ... Berdasarkan uraian di atas, maka:

1) Prisma tegak, yaitu prisma yang rusuk-rusuknya tegak lurus terhadap bidang alasnya.

2) Prisma miring, yaitu prisma yang rusuk-rusuknya tidak tegak lurus (condong) terhadap bidang alasnya.

No. Bentuk Bidang_{Alas Prisma} rusuknya terhadapKedudukan

Rusuk-Bidang Alas Nama Prisma

(i) Segi-empat Tegak lurus Prisma Tegak Segi-_empat

(ii) Segi-tiga Tegak lurus Prisma Tegak Segi-_tiga

(iii) Segi-enam Tegak lurus Prisma Tegak Segi-_enam

(iv) Segi-empat Condong / miring Prisma Miring Segi-_empat

(v) Segi-tiga Condong / miring Prisma Miring Segi-_tiga

(vi) Segi-enam Condong / miring Prisma Miring Segi-_enam (vii

) Segi-lima Tegak lurus Prisma Tegak Segi-lima

 Unsur-Unsur Prisma

Ada 9 buah rusuk

∑

rusuk prisma

❑

¿3n

3. Bidang / sisi ABC = DEF = alas & tutup

ABED, BCFE, ACFD =

sisi tegak

Ada 5 buah sisi

∑

Prisma adalah suatu bangun ruang yang dibatasi oleh 2 buah bidang (alas dan tutup) Segi- banyak yang sejajar dan kongruen dibatasi oleh sisi-sisi tegak yang berbentuk Segi-empat.

Tugas :

 Luas Permukaan Prisma

c adalah sisi 3 alas prisma (Segi-tiga), maka: c = CA Berdasarkan uraian di atas, maka:

L Permukaan Prisma = L ... + L ... + L ...

Berdasakan ukuran sisi-sisi alasnya dan bentuk sisi-sisi tegaknya, maka limas dibagi menjadi 2 macam, yaitu :

1) Limas Segi-n beraturan, yaitu limas yang sisi-sisi alasnya sama panjang dan sisi-sisi tegaknya berbentuk Segi-tiga yang kongruen. 2) Limas Segi-n sembarang, yaitu limas yang sisi-sisi alasnya tidak

sama panjang dan sisi-sisi tegaknya berbentuk Segi-tiga yang tidak kongruen.

No

. Bentuk AlasLimas Panjang SisiAlas Bentuk SisiTegak Nama Limas

(i) Segi-tiga Tidak sama _panjang Tidak kongruen Limas Segi-tiga_sembarang

(ii) Segi-tiga sama sisi Sama panjang Kongruen Limas Segi-tiga_beraturan

(iii) Segi-empat sama _sisi Sama panjang Kongruen _{empat beraturan}Limas Segi-(iv

sembarang (v) Segi-lima Tidak sama _panjang Tidak kongruen Limas Segi-lima_sembarang (vi

) Segi-enam sama sisi Sama panjang Kongruen Limas Segi-enamberaturan

 Unsur-Unsur Limas

No. Limas Segi-empatUnsur-Unsur Beraturan

3. Bidang / sisi ABCD

ATB = BTC = CTD = DTA Ada 5 buah sisi

bidang yang sama panjang

5. Bidang diagonal BTD = ATC Ada 2 buah diagonal bidang yang kongruen Limas adalah suatu bangun ruang yang sisi-sisi alasnya dibatasi oleh sebuah segi-n (segi-banyak) dan sisi-sisi tegaknya berbentuk segi-tiga.  Jaring-jaring Limas

 L Permukaan Limas

Tinggi sisi tegak (apotema) = t’ = ... = ... = ...

= ... = √1

2s2+t2

Dari gambar di atas kita ketahui bahwa: Limas Segi-empat terdiri dari::

1) Alas yang berbentuk ... , yaitu ...

Dari uraian di atas, kita dapat mengambil kesimpulan bahwa:

L Permukaan Limas = L Alas +

BANGUN RUANG SISI LENGKUNG A. Pengertian

Dari gambar di atas manakah yang termasuk bangun ruang sisi lengkung bentuk tabung, kerucut dan bola?

Sisi Alas

Jarak antara titik pusat dengan titik pada lingkaran.

2. Diameter AB = CD = d = 2r Ruas garis yang

menghubungkan dua titik pada lingkaran melalui titik pusat.

3. Tinggi EI = t

4. Sisi atas /

tutup Sisi yang menutupi tabung

5. Sisi bawah /

alas Sisi sebagai alas tabung

6. Selimut

tabung

Sisi (segiempat) yang menyelimuti tabung

Tabung adalah bangun ruang yang dibatasi sebuah sisi lengkung berbentuk segiempat dengan sisi alas dan atas berbentuk lingkaran yang kongruen.

 Jaring-jaring Tabung

 Luas Permukaan Tabung

Permukaan tabung terdiri dari alas, tutup dan selimut tabung. Alas dan tutup tabung berbentuk lingkaran yang kongruen, sehingga :

L Alas = L Tutup = L Lingkaran = π r2

s = Garis Pelukis

Berdasarkan uraian di atas, maka :

L Permukaan Tabung = L Alas + L Tutup +L Selimut

Jarak antara titik pusat dengan titik pada lingkaran.

2. Diameter BC = d = 2r Ruas garis yang

menghubungkan dua titik pada lingkaran melalui titik pusat.

3. Tinggi AD = t

4. Garis pelukis

(apotema) AB = AC = √ t2+r2 s =

5. Sisi alas Sisi sebagai alas kerucut

6. Selimut

kerucut Sisi yang menyelimuti kerucut

Kerucut dapat dipandang sebagai limas yang alasnya berbentuk lingkaran.

Selimut Kerucut = Juring Lingkaran r2 = s

 Luas Permukaan Kerucut

Permukaan kerucut terdiri dari alas, dan selimut kerucut. Alas kerucut berbentuk lingkaran (kecil), sehingga :

L Alas = L Lingkaran (Kecil) = π r2

Selimut kerucut merupakan juring lingkaran (besar) dengan :

p Busur = K Lingkaran (Kecil) = 2πr K Lingkaran (Besar) = 2πs

L Lingkaran (Besar) = π s2

sehingga :

L Selimut Kerucut =

Berdasarkan uraian di atas, maka :

No

. unsur BolaUnsur- Nama Unsur-unsur Bola Definisi

1. Jari-jari

r =

1

2d Jarak antara titik pusat dengan titik pada lingkaran.

2. Diameter d = 2r Ruas garis yang

menghubungkan dua titik pada lingkaran melalui titik pusat.

Suatu lingkaran diputar setengah putaran dengan diameter sebagai sumbu putarnya akan diperoleh bangun ruang yang disebut bola dengan jari-jari bola r dan tinggi d.

 Luas Permukaan Bola

Sebuah bola yng dapat masuk kedalam tabung dengan tepat, berarti :

a. diameter bola = diameter tabung b. tinggi tabung = diameter bola = diameter tabung

Dalam keadaan ini Archimedes merumuskan hubungan berikut :

E. Glosarium

 Titik sudut adalah titik pertemuan dari tiga buah rusuk yang berdekatan.  Rusuk adalah ruas garis yang merupakan perpotongan dua buah bidang sisi.  Bidang / sisi adalah suatu bidang yang membatasi bangun ruang.

 Diagonal bidang adalah ruas garis yang menghubungkan dua titik sudut sebidang yang saling berhadapan.

 Diagonal ruang adalah ruas garis yang menghubungkan dua titik sudut tidak sebidang yang saling berhadapan.

 Bidang diagonal adalah bidang di dalam bangun ruang yang dibuat melalui dua buah rusuk yang sejajar tetapi tidak terletak pada satu sisi.

 Jaring-jaring suatu bangun ruang adalah penyusunan beberapa bangun datar, sehingga ketika dirangkaikan membentuk bangun ruang.

PERSAMAAN GARIS LURUS

A. Pengertian Persamaan Garis Lurus

selalu digambarkan dalam koordinat Cartesius. Untuk itu, pelajarilah uraian berikut.

1. Koordinat Cartesius

Pada bab sebelumnya, kamu telah mengenal tentang bidang Cartesius. Coba kamu perhatikan Gambar 3.1 dengan seksama. Gambar tersebut menunjukkan bidang koordinat Cartesius yang memiliki sumbu mendatar (disebut

sumbu-x) dan sumbu tegak (disebut sumbu-y). Titik potong kedua sumbu tersebut dinamakan titik asal atau titik pusat koordinat. Pada Gambar 3.1, titik pusat koordinat Cartesius ditunjukkan oleh titik O (0, 0). Sekarang, bagaimana menggambar titik atau garis pada bidang koordinat Cartesius?

a. Menggambar Titik pada Koordinat Cartesius

b. Menggambar Garis pada Koordinat Cartesius

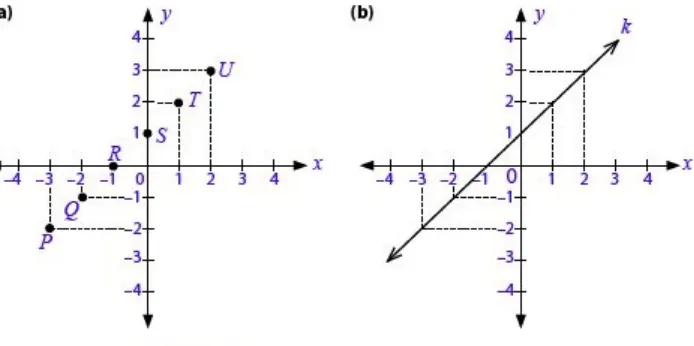
Kamu telah memahami bagaimana menggambar titik pada bidang koordinat Cartesius. Sekarang bagaimana menggambar garis lurus pada bidang yang sama? Coba perhatikan Gambar 3.3

Perlu diingat, garis lurus adalah kumpulan titik-titik yang letaknya sejajar. Dari Gambar 3.3(a) , terlihat bahwa titik-titik P, Q, R, S, T, dan U memiliki letak yang sejajar dengan suatu garis lurus, misalkan garis k, seperti yang

digambarkan pada Gambar 3.3(b). S ebuah garis lurus dapat terbentuk dengan syarat sedikitnya ada dua titik pada bidang koordinat Cartesius.

2. Menggambarkan Persamaan Garis Lurus

Setelah kamu mempelajari materi sebelumnya, apa yang dapat kamu ketahui tentang persamaan garis lurus? Persamaan garis lurus adalah suatu persamaan yang jika digambarkan ke dalam bidang koordinat Cartesius akan membentuk sebuah garis lurus. Cara menggambar persamaan garis lurus adalah dengan menentukan nilai x atau y secara acak. Perlu diingat bahwa dua titik sudah cukup untuk membuat garis lurus pada bidang koordinat Cartesius.

B. Gradien

Dari Gambar 3.4 terlihat suatu garis lurus pada bidang koordinat Cartesius. Garis tersebut melalui titik A(–6, –3), B(–4, –2), C(–2, –1), D(2, 1), E(4, 2), dan F(6, 3). Perbandingan antara ordinat (y) dan absis (x) untuk masing-masing titik tersebut adalah sebagai berikut.

Perhatikan perbandingan ordinat dengan absis untuk setiap titik tersebut. Semua titik memiliki nilai perbandingan yang sama, yaitu 1_/

2. Nilai tetap atau konstanta dari perbandingan ordinat dan absis ini disebut sebagai gradien. Biasanya gradien dilambangkan dengan m. Apa sebenarnya yang dimaksud dengan gradien? Coba kamu pelajari uraian berikut ini.

1. Pengertian Gradien

Pernahkah kamu mendaki gunung? Jika ya, kamu pasti akan menyusuri lereng gunung untuk dapat sampai ke puncak. Lereng gunung memiliki kemiringan tanah yang tidak sama, ada yang curam ada juga yang landai. Sama halnya dengan garis yang memiliki kemiringan tertentu. Tingkat kemiringan garis inilah yang disebut gradien. Perhatikan kembali garis lurus pada Gambar 3.4,

gradien garis tersebut adalah 1_/

2.

2. Perhitungan Gradien

Ada berbagai cara untuk menghitung gradien dari suatu persamaan garis. Hal ini bergantung pada letak titik koordinat dan bentuk persamaan garis yang

diberikan. Berikut ini akan diuraikan cara menghitung gradien berdasarkan titik koordinat atau bentuk persamaan garis.

a. Menghitung Gradien pada Persamaan Garis y = mx

Seperti yang telah dijelaskan sebelumnya, gradien suatu garis dapat ditentukan melalui perbandingan antara ordinat dan absis sehingga dapat ditulis sebagai berikut.

Dari uraian ini terlihat bahwa nilai gradien dalam suatu persamaan garis sama dengan besar nilai konstanta m yang terletak di depan variabel x, dengan syarat, persamaan garis tersebut diubah terlebih dahulu ke dalam bentuk y = mx.

b. Menghitung Gradien pada Persamaan Garis y = mx + c

Sama halnya dengan perhitungan gradien pada persamaan garis y = mx, perhitungan gradien pada garis y = mx + c dilakukan dengan cara menentukan nilai konstanta di depan variabel x.

c. Menghitung Gradien pada Persamaan Garis ax + by + c = 0

Sama seperti sebelumnya, gradien pada persamaan garis ax + by + c = 0 dapat ditentukan dengan cara mengubah terlebih dahulu persamaan garis tersebut ke dalam bentuk y = mx + c. Kemudian, nilai gradien diperoleh dari nilai konstanta m di depan variabel x.

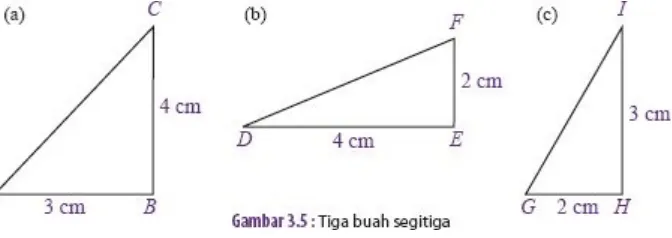
Gambar 3.5 menunjukkan tiga buah Segi-tiga ABC, DEF, dan GHI yang

memiliki sisi miring dengan tingkat kemiringan atau gradien yang berbedabeda. Dengan menggunakan perbandingan ordinat dan absis, gradien untuk masing-masing Segi-tiga dapat dihitung sebagai berikut.

Dengan menggunakan perbandingan ordinat dan absis, akan diperoleh gradien garis yang melalui titik P dan R, yaitu:

Jadi, gradien garis yang melalui P(1, 3) dan R(7, 6) pada Gambar 3.6 adalah 1_/ 2. Dari uraian tersebut diperoleh rumus umum untuk mencari gradien pada garis yang melalui dua titik, sebagai berikut.

3. Sifat-Sifat Gradien

Ada beberapa sifat gradien yang perlu kamu ketahui, di antaranya adalah gradien garis yang sejajar dengan sumbu-x, gradien garis yang sejajar dengan sumbu-y, gradien dua garis yang sejajar, dan gradien dua garis yang saling tegak lurus. Berikut ini akan diuraikan sifat-sifat gradien tersebut.

Pada Gambar 3.7 , terlihat garis k yang melalui titik A(–1, 2) dan B(3, 2). Garis tersebut sejajar dengan sumbu-x. Untuk menghitung gradien garis k, gunakan cara sebagai berikut.

Untuk titik A(–1, 2) maka x1 = –1, y1 = 2. Untuk titik B(3, 2) maka x2 = 3, y2 = 2.

Coba kamu periksa titik-titik lain pada garis k dan hitunglah gradiennya. Apakah nilai gradiennya sama dengan 0? Uraian tersebut memperjelas tentang gradien garis yang sejajar dengan sumbu-x, yaitu sebagai berikut.

Jika garis sejajar dengan sumbu- x maka nilai gradiennya adalah nol.

Pada Gambar 3.8 , garis l yang melalui titik C(1, 3) dan D(1, –1). letaknya sejajar dengan sumbu-y. Gradien garis tersebut adalah sebagai berikut. Untuk titik C(1, 3) maka x1 = 1, y1 = 3.

Untuk titik D(1, –1) maka x2 = 1, y2 = –1.

Perhitungan di atas, memperjelas sifat gradien berikut.

Jika garis sejajar dengan sumbu-y maka garis tersebut tidak memiliki gradien.

c. Gradien Dua Garis yang Sejajar

Garis k dan l merupakan dua garis yang sejajar. Bagaimana gradien kedua garis tersebut? Perhatikan uraian berikut.

• Garis k melalui titik A(–2, 0) dan B(0, 2). Untuk titik A(–2, 0) maka x1 = –2, y1 = 0. Untuk titik B(0, 2) maka x2 = 0, y2 = 2.

• Garis l melalui titik C(0, –1) dan D(1, 0). Untuk titik C(0, –1) maka x1 = 0, y1 = –1. Untuk titik D(1, 0) maka x2 = 1, y2 = 0.

Dari uraian tersebut terlihat bahwa garis k dan l memiliki gradien yang sama.

Setiap garis yang sejajar memiliki gradien yang sama.

d. Gradien Dua Garis yang Tegak Lurus

Gradien kedua garis tersebut dapat dihitung dengan cara sebagai berikut. • Garis k melalui titik C(3, 0) dan D(0, 3).

Untuk titik C(3, 0) maka x1 = 3, y1 = 0. Untuk titik D(0, 3) maka x2 = 0, y2 = 3.

• Garis l melalui titik A(–1, 0) dan B(0, 1). Untuk titik A(–1, 0) maka x1 = –1, y1 = 0. Untuk titik B(0, 1) maka x2 = 0, y2 = 1.

Hasil kali kedua gradien tersebut adalah

mAB × mCD = 1 × –1 = –1

Uraian tersebut memperjelas hal berikut:

C. Menentukan Persamaan Garis Lurus

Pada subbab sebelumnya, kamu telah mempelajari bagaimana menggambar persamaan garis lurus pada bidang koordinat Cartesius dan menentukan gradien dari suatu persamaan garis. Sekarang, bagaimana menentukan persamaan garis dari suatu titik atau gradien? Masih ingatkah kamu tentang gradien yang

diperoleh dari perbandingan ordinat dan absis? Bentuk tersebut dapat dituliskan sebagai berikut.

Bentuk y = mx merupakan bentuk persamaan garis lurus sederhana. Dikatakan sebagai bentuk sederhana karena garis yang dibentuk oleh persamaan garis tersebut selalu melalui titik pusat koordinat. Untuk lebih jelasnya, perhatikan Contoh Soal

Contoh Soal :Tentukan persamaan garis untuk garis yang melalui titik O (0, 0) dan memiliki:

a. gradien 2, b. gradien –3, c. gradien 1.

Jawab :

y = 2xa. y = mx maka y = (2)x y = –3xb. y = mx maka y = (–3)x y = xc. y = mx maka y = (1)x

Persamaan garis ini hampir sama dengan bentuk sederhananya, namun diberi tambahan konstanta (diberi lambang c). Hal ini menunjukkan bahwa garis yang dibentuk oleh persamaan garis tersebut tidak akan melalui titik O(0, 0).

Setelah kamu memahami bentuk sederhana dan bentuk umum persamaan garis, berikut ini akan diuraikan bagaimana menentukan sebuah persamaan garis dari titik koordinat atau gradien.

1. Menentukan Persamaan Garis dari Gradien dan Titik Koordinat

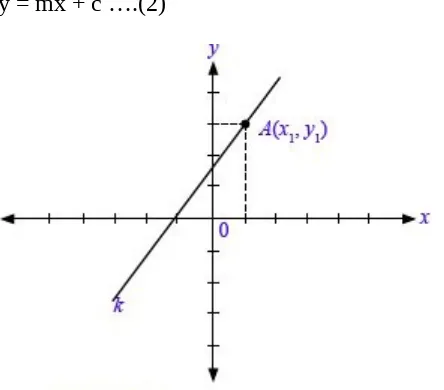
Sekarang, coba kamu perhatikan Gambar 3.1. Gambar tersebut menunjukkan sebuah garis k pada bidang koordinat Cartesius. Garis tersebut melalui titik A(x1, y1) dan tidak melalui titik pusat koordinat sehingga persamaan garis pada

Gambar 3.11 dapat dituliskan: y1 = mx1 + c ….(1)

Adapun bentuk umum persamaan garis yang tidak melalui titik pusat koordinat dituliskan:

y = mx + c ….(2)

Selanjutnya diperoleh rumus umum untuk menentukan persamaan garis jika diketahui gradien dan titik koordinat, yaitu:

2. Menentukan Persamaan Garis yang Melalui Dua Titik

Pada bagian sebelumnya, kamu telah mempelajari cara menentukan persamaan garis yang melalui satu titik koordinat dan gradiennya diketahui. Sekarang, kamu akan mempelajari bagaimana menentukan persamaan garis yang melalui dua titik. Caranya hampir sama dengan rumus umum yang telah dipelajari sebelumnya.

Coba kamu perhatikan uraian berikut :

• y – y1 = m (x – x1) adalah rumus umum persamaan garis dari gradien dan titik koordinat.

3. Menentukan Koordinat Titik Potong dari Dua Garis Lurus

Coba kamu perhatikan Gambar 3.12

Dari Gambar 3.12 , terdapat dua garis dalam bidang koordinat, yaitu garis k dan l. Dalam Gambar 3.12(a) , kedua garis tersebut sejajar. Adapun pada Gambar 3.12(b) , kedua garis tersebut tidak sejajar sehingga keduanya berpotongan di suatu titik, yaitu titik A (x1, y1). Jadi, koordinat titik potong dapat dicari dari dua garis yang tidak sejajar.

Sekarang, bagaimana cara menentukan koordinat titik potong dari dua persamaan garis yang diketahui? Ada dua cara yang dapat digunakan, yaitu cara menggambar (cara grafik) dan cara substitusi. Untuk itu, pelajari uraian berikut.

a. Cara Grafik

Dengan cara ini, dua persamaan garis digambar ke dalam bidang koordinat Cartesius sehingga koordinat titik potong kedua garis tersebut dapat dilihat dari gambar.

b. Cara Substitusi

yang diketahui dimasukkan (disubstitusikan) ke dalam variabel yang sama dari persamaan garis yang lain.

4. Aplikasi Persaman Garis Lurus

Dalam kehidupan sehari-hari, banyak sekali bidang-bidang yang menggunakan aplikasi persamaan garis lurus. Misalnya, perhitungan kecepatan-jarak-waktu dalam fisika dan perhitungan harga barang dan titik impas dalam ekonomi. Coba kamu pelajari Contoh Soal. Aplikasi Persaman Garis Lurus Dalam kehidupan sehari-hari, banyak sekali bidang-bidang yang menggunakan aplikasi persamaan garis lurus. Misalnya, perhitungan kecepatan-jarak-waktu dalam fisika dan perhitungan harga barang dan titik impas dalam ekonomi.

Pengertian Gradien

1. Definisi Gradien

Gradien suatu garis lurus adalah : Perbandingan antara komponen y (ordinat) dan komponen x (absis) antara dua titik pada garis itu. Gradien suatu garis biasanya dinotasikan dengan huruf kecil m. Perhatikan gambar di bawah ini !

komponen y dari garis AB = y2 - y1 ; komponen x dari garis AB = x2 - x1, maka :

Catatan : gradien sebuah garis sering disebut kecondongan sebuah garis atau koefisien arah sebuah garis.

a. Gradien bernilai positif

Garis l condong ke kanan , maka mlbernilai positif

Garis k condong ke kiri , maka mkbernilai negatif

Gradien dari sebuah persamaan garis

Jika sebuah garis mempunyai persamaan ax + by = c, maka gradien

persamaan garis itu ialah :

Garis l melalui pangkal koordinat (0,0) maka

Dua garis yang sejajar mempunyai gradien yang sama, garis l dan garis k sejajar, maka ml = mk

Dua garis yang saling tegak lurus perkalian gradiennya adalah -1.Garis l dan garis k saling tegak lurus, maka ml x mk = -1.

1.2. Contoh-Contoh Soal

Contoh 1 :

Tentukanlah gradien garis :

1. melalui titik P(2,-5) dan titik Q(-9,3)

2. melalui pangkal koordinat dan titik A(-2,-8)

Penyelesaian :

P(2,-5) berarti x1 = 2 , y1 = -5

Q(-9,3) berarti x2 = -9 , y2 = 3

Jadi gradient melalui titik P(2,-5) dan titik Q(-9,3) adalah

b. Melalui pangkal koordinat dan titik A(-2,-8)

A(-2,-8) berarti x = -2 , y1 = -8

Contoh 2 :

Tentukanlah gradient sebuah garis :

1. yang sejajar dengan garis 4x + 2y = 6

2. yang tegak lurus dengan garis x - 4y = 10

Penyelesaian :

1. Persamaan garis 4x + 2y = 6, maka a = 4, b = 2

Dua garis yang sejajar : m1 = m2 , maka m2 = - 2

2. Persamaan garis x - 4y = 10, maka a = 1, b = -4

Dua garis yang tegak lurus : m1 x m2 = -1 , maka

02. Persamaan Garis Lurus Melalui 1 Titik

Pada garis l terdapat titik A dengan koordinat (x1, y1) dan titik B dengan koordinat bebas, yaitu (x , y), bila gradien garis l dinyatakan dengan m, maka AB terdiri atas semua titik (x,y) dengan hubungan berikut ini :

y - y1 = m (x - x1)

Kesimpulan :

Persamaan garis dengan gradien m dan melalui sebuah titik (x1 , y1), adalah :

y - y1 = m (x - x1)

Contoh 1 :

Tentukanlah persamaan garis melalui titik A(-3,4) dan bergradien -2.

Penyelesaian :

Titik A(-3,4), berarti x1 = -3 , y1 = 4 dan bergradien -2, berarti m = -2

Persamaan garis dengan gradient m dan melalui sebuah titik (x1,y1) adalah :

y - y1 = m ( x - x1 )

y - 4 = -2 {x - (-3)}

y - 4 = -2 (x + 3 )

y - 4 = -2 x - 6

y = -2x - 6 + 4

y = -2x - 2

Jadi persamaan garis melalui titik A(-3,4) dan bergradien -2 adalah y = -2x - 2

Tentukanlah persamaan garis melalui titik B(6,2) dan sejajar dengan garis yang melalui titik P(2,-5) dan Q(-6, 3)

Penyelesaian :

Garis yang melalui titik P(2,-5) dan (-6, 3)

P(2,-5) berarti x1 = 2 , y1 = -5

Q(-6,3) berarti x2 = -6 , y2 = 3

Gradien yang melaui titik P(2,-5) dan Q(-6, 3) adalah mPQ

Misal mPQ = m1, maka m1 = m2 = -1 ( dua garis sejajar )

Titik B(6, 2), berarti x1 = 6 , y1 = 2

Persamaan garis dengan gradien -1 dan melalui titik (6, 2) adalah :

y - y1 = m ( x - x1 )

y - 2 = -1 (x - 6)

y - 2 = -x + 6

y = -x + 6 + 2

y = -x + 8

Jadi persamaan garis melalui titik B(6,2) dan bergradien -1 adalah y = -x + 8

03. Persamaan Garis Lurus Melalui 2 Titik

Gradien garis yang melalui titik (x1, y1) dan (x2, y2) yaitu seperti

Selanjutnya dengan menggunakan rumus persamaan garis dengan gradient m dan melalui sebuah titik (x1 , y1), yaitu y - y1 = m ( x - x1 ) dapat diperoleh rumus berikut :

y - y1 = m ( x - x1 )

y - y1

y - y1 = y2 - y1

Kesimpulan :

1. Persamaan garis yang melalui titik (x1, y1) dan (x2, y2) yaitu :

Contoh 1

Perhatikan gambar di bawah ini !

Tentukanlah persamaan garisl !

Penyelesaian :

Garis l melalui titik A(3,4) dan titik B(5,8).

P(3,4) berarti x1 = 3 , y1 = 4

Q(5,8) berarti x2 = 5 , y2 = 8

Persamaan garis l yang melalui titik A(3,4) dan titik B(5,8) adalah :

2y - 8 = 4x - 12

2y - 4x = 8 - 12

2y - 4x = -4

y - 2x = -2