Informasi Dokumen
- Penulis:
- Ir. Parseno, MT.
- Ir. Nurrohmat Widjajanti, MT., Ph.D.
- Dwi Lestari, ST., ME.
- Ir. Sri Narni, MT.
- Pengajar:
- Ir. Djurdjani, MSP., M.Eng., Ph.D.
- Sekolah: Universitas Gadjah Mada
- Mata Pelajaran: Teknik Geodesi dan Geomatika
- Topik: Matematika Geodesi
- Tipe: bahan ajar
- Tahun: 2013
- Kota: Yogyakarta
Ringkasan Dokumen
I. Pendahuluan dan Review Aljabar Vektor
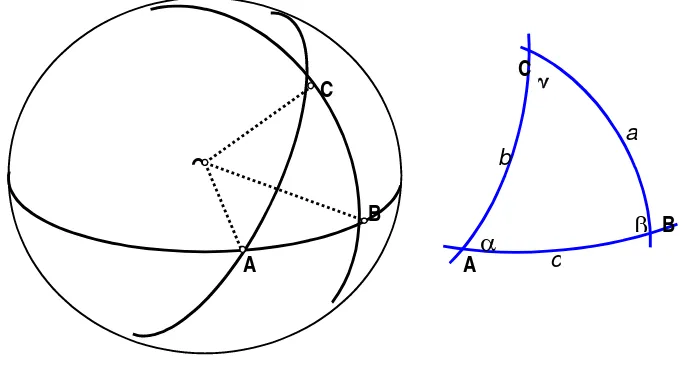
Bab ini memperkenalkan konsep dasar aljabar vektor yang sangat penting dalam geodesi. Melalui pemahaman tentang penggunaan vektor dan segitiga bola, mahasiswa diharapkan dapat mengaitkan konsep matematika dengan aplikasi praktis dalam geodesi. Penjelasan mengenai jenis dan sifat-sifat vektor, serta letak relatif vektor, memberikan landasan yang kuat untuk memahami hubungan antara berbagai vektor dalam ruang dua dan tiga dimensi. Dengan demikian, mahasiswa dapat memanfaatkan pengetahuan ini dalam studi lanjut di bidang fotogrametri dan geodesi.
1.1. Deskripsi Singkat
Vektor adalah besaran yang memiliki arah dan nilai. Dalam konteks geodesi, pemahaman tentang vektor sangat penting karena dapat digunakan untuk menjelaskan fenomena alam seperti gaya gravitasi. Konsep koplanaritas dan kolinieritas vektor juga menjadi kunci dalam memahami hubungan antara berbagai vektor yang digunakan dalam analisis geodesi.
1.2. Manfaat
Mahasiswa akan memahami pentingnya medan vektor dan segitiga bola dalam model bumi teoritik. Pengetahuan ini mendukung pembelajaran di bidang fotogrametri, di mana azas kolinieritas dan koplanaritas diterapkan untuk membentuk peta dari citra udara.
1.3. Relevansi
Bab ini memperkenalkan mahasiswa pada ruang lingkup geodesi dan keterkaitannya dengan disiplin ilmu lain, sehingga mereka dapat memahami bagaimana dasar matematika berfungsi dalam aplikasi geodesi.
1.4. Learning Outcome
Setelah mengikuti kuliah ini, mahasiswa mampu menjelaskan ruang lingkup Matematika Geodesi, pengertian dan jenis vektor, serta letak vektor dan dalil-dalil yang berlaku dalam aljabar vektor.
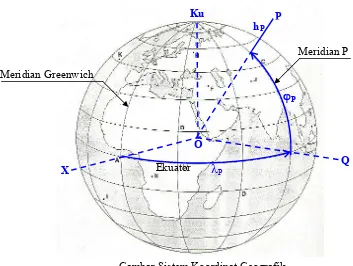
II. Sistem Koordinat Vektor
Bab ini membahas tentang sistem koordinat yang digunakan untuk menentukan posisi titik dalam ruang. Pemahaman tentang komponen vektor dalam bidang dan ruang menjadi penting untuk aplikasi di bidang geodesi. Mahasiswa diajarkan cara menghitung vektor satuan dan menerapkan operasi vektor dalam hitungan, yang merupakan keterampilan dasar dalam analisis geospasial.
2.1. Pendahuluan
Sistem koordinat vektor adalah kerangka yang digunakan untuk menentukan posisi titik dalam ruang. Pengetahuan ini sangat penting dalam penentuan posisi di permukaan bumi, terutama dalam teknologi ruang angkasa.
2.2. Komponen Vektor dalam Bidang dan Ruang
Vektor letak digunakan untuk menentukan posisi titik di ruang. Dalam sistem koordinat R2 dan R3, mahasiswa belajar bagaimana mengekspresikan posisi titik dengan menggunakan vektor basis yang independen.
2.3. Vektor Satuan
Vektor satuan digunakan untuk menyatakan arah dan magnitude dari vektor dalam sistem koordinat. Pemahaman ini penting dalam berbagai aplikasi di bidang geodesi dan pemetaan.
2.4. Operasi Vektor
Bab ini menjelaskan berbagai operasi vektor, termasuk penjumlahan, pengurangan, dan perkalian skalar. Mahasiswa juga diperkenalkan pada dot product dan cross product, yang merupakan operasi penting dalam analisis geometri.
III. Aplikasi Vektor dalam Geometri Analitik
Dalam bab ini, mahasiswa belajar menerapkan konsep vektor untuk menyelesaikan persoalan geometri analitik, seperti menentukan persamaan garis dan bidang. Aplikasi ini sangat relevan untuk pengukuran dan survei dalam geodesi, di mana pemahaman tentang geometri analitik diperlukan untuk menginterpretasikan data.
3.1. Pendahuluan
Aplikasi vektor dalam geometri analitik membantu mahasiswa memahami hubungan antara vektor dan persamaan garis atau bidang. Hal ini penting untuk analisis geometris dalam survei dan pemetaan.
3.2. Persamaan Garis AB
Mahasiswa diajarkan cara menentukan persamaan garis menggunakan vektor letak. Pemahaman ini sangat penting untuk menghitung jarak dan sudut antara garis dalam ruang.
3.3. Persamaan Garis melalui A Sejajar Vektor b
Konsep ini menjelaskan bagaimana garis dapat ditentukan berdasarkan titik dan arah tertentu, yang merupakan aplikasi langsung dalam perhitungan geodesi.
3.4. Persamaan Garis/Bidang Tegak Lurus
Mahasiswa belajar bagaimana menentukan persamaan garis atau bidang yang tegak lurus terhadap vektor lain, yang merupakan konsep penting dalam analisis geometri dan survei.
IV. Diferensial Vektor
Bab ini membahas penerapan kaidah diferensial pada vektor, yang sangat penting dalam menyelesaikan persoalan vektor fungsi. Mahasiswa diajarkan bagaimana menerapkan diferensial dalam konteks geodesi, yang sering melibatkan fungsi vektor dengan beberapa variabel.
4.1. Pendahuluan
Pemahaman tentang diferensial vektor diperlukan untuk menyelesaikan berbagai persoalan dalam geodesi yang melibatkan perubahan dalam fungsi vektor.
4.2. Fungsi dengan Perubah Bebas
Mahasiswa belajar bagaimana mendefinisikan fungsi vektor yang bergantung pada satu atau lebih variabel, serta cara menghitung derivatifnya.
4.3. Fungsi Lebih dari Satu Perubah
Dalam konteks ini, mahasiswa diperkenalkan pada konsep derivatif parsial dan aplikasinya dalam fungsi vektor yang melibatkan lebih dari satu variabel.
V. Medan Vektor dan Medan Skalar
Bab ini menjelaskan konsep medan vektor dan medan skalar, serta aplikasi diferensial vektor dalam konteks ini. Mahasiswa diharapkan dapat memahami penggunaan gradien, divergensi, dan curl dalam analisis medan, yang sangat relevan dalam studi geodesi.
5.1. Pendahuluan
Medan vektor dan medan skalar adalah konsep kunci dalam analisis geodesi. Pemahaman ini membantu mahasiswa dalam memahami fenomena fisik yang terjadi di bumi.
5.2. Pengertian Medan Vektor dan Medan Skalar
Mahasiswa belajar tentang definisi dan karakteristik medan vektor dan skalar, serta cara membedakan antara keduanya dalam konteks geodesi.
5.3. Gradien, Divergensi, dan Curl
Konsep ini sangat penting dalam analisis medan. Mahasiswa diajarkan bagaimana menggunakan rumus-rumus ini untuk menghitung berbagai parameter dalam medan.
Referensi Dokumen
- Theory and Problems of Plane and Spherical Trigonometry ( Ayres, F. Jr. )
- Penentuan Asimut dengan Pengamatan Matahari ( Basuki K.S. )
- Spherical Trigonometry ( Donnay, J.D.H. )
- Matematika Geodesi ( Narni, S. dan Muryamto, R. )
- Linear Algebra, Geodesy and GPS ( Strang, G dan K. Borre )
- Spherical Trigonometry with Numerous Examples ( Todhunter, M.A.F.R.S )