Catatan Kuliah
MA4081
PENGANTAR PROSES STOKASTIK
“Orang Pintar Belajar Stokastik”disusun oleh
Khreshna I.A. Syuhada, MSc. PhD.
Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung
Tentang MA4081 Pengantar Proses Stokastik
A. Jadwal kuliah:
• Selasa; 13-14.40; R.9231
• Kamis; 13-14.40; R.9307
B. Silabus:
• Peluang, peubah acak dan distribusi (2 minggu)
• Peluang dan ekspektasi bersyarat (1 minggu)
• Rantai Markov (4 minggu)
• Distribusi Eksponensial (3 minggu)
• Proses Poisson (2 minggu)
C. Buku teks:
• Sheldon Ross, 2010, Introduction to Probability Models, 10th ed., Aca-demic Press.
• Taylor dan Karlin, 1998, An Introduction to Stochastic Modelling, 3rd ed., Academic Press.
E. Penilaian:
• Ujian 1,2,3 (90%):
18 September 2012 (20%) 18 Oktober 2012 (35%) 4 Desember 2012 (35%)
Matriks kegiatan perkuliahan
Table 1: Materi kuliah MA5181 Proses Stokastik.
Minggu- Materi Keterangan
1 Pengantar Penjelasan kuliah
2 Peluang, peubah acak dan distribusi 3 Peluang dan ekspektasi bersyarat
4 Ujian 1 18 September 2012
5-8 Rantai Markov*
8 Ujian 2 18 Oktober 2012
9
-10-12 Distribusi Eksponensial*
13-14 Proses Poisson*
Daftar Isi
1 Peluang, Peubah Acak dan Distribusi 1
1.1 Peluang . . . 1
1.2 Peubah acak dan distribusi . . . 4
1.3 Ekspektasi bersyarat . . . 7
2 Rantai Markov 1 2.1 Ilustrasi . . . 1
2.2 Definisi . . . 2
2.3 Peluang n-langkah . . . 7
2.4 Jenis Keadaan . . . 9
BAB 1
Peluang, Peubah Acak dan
Distribusi
1.1
Peluang
Peluang adalah suatu konsep berpikir, bukan sekadar angka (walaupun wu-judnya adalah angka diantara nol dan satu). Peluang berkaitan dengan meny-atakan alasan atas suatu kejadian. Peluang, secara implisit, mengajak kita un-tuk mempersiapkan diri menghadapi kejadian yang tidak terjadi (yang memi-liki peluang kecil).
Contoh:
Setiap hari Laila pergi ke kampus dan berharap perkuliahan terjadi (untuk setiap mata kuliah Laila sudah memiliki dugaan peluang terjadinya perkulia-han tersebut). Jika suatu hari Laila tidak pergi ke kampus, akankah sebuah perkuliahan benar-benar tidak terjadi?
Contoh:
Ini kisah masa lalu Tiani yang sempat diceritakan sesaat sebelum Tiani menikah. Katanya “Ayahku meninggal waktu usiaku tiga tahun. Lalu Ibu kawin lagi. Dengan ayah tiriku, Ibu mendapat dua orang anak tiri dan melahirkan tiga orang anak. Ketika usiaku lima belas tahun, Ibu pun meninggal. Ayah tiriku kawin lagi dengan seorang janda yang sudah beranak dua. Ia melahirkan dua orang anak pula dengan ayah tiriku”. Adakah sosok seperti Tiani?
Catatan:
• Percobaan adalah kegiatan yang menghasilkan keluaran/hasil yang mungkin secara acak.
• Ruang sampel S adalah himpunan dari semua hasil yang mungkin dari suatu percobaan. Anggota dari S disebut kejadian elementer.
• Kejadian adalah himpunan bagian dari ruang sampel atau koleksi dari kejadian-kejadian elementer.
• Peluang kejadian A adalah
P(A) = lim n→∞
n(A)
n
P(A) = n(A)
n(S)
Contoh:
Direktur perusahaan mengundang para karyawan yang memiliki setidaknya satu anak laki-laki (L) ke acara syukuran khitanan. Seorang karyawan memi-liki dua anak. Berapa peluang bahwa kedua anak karyawan adalah laki-laki, diberikan bahwa karyawan tersebut diundang ke acara syukuran?
Solusi: Misalkan L kejadian memiliki anak laki-laki; LK kejadian memiliki dua anak laki-laki; U kejadian diundang ke acara syukuran. Jadi,
P(LK|U) = P(LK∩U)
P(U)
= P({{LL} ∩ {LL, LL
c, LcL}})
P({LL, LLc, LcL})
= P({LL})
P({LL, LLc, LcL}) = (1/4)/(3/4) = 1/3
Seringkali dibutuhkan nilai (awal) peluang suatu kejadian, untuk kemudian dapat dihitung peluang kejadian berikutnya. Menentukan nilai awal peluang merupakan masalah yang menarik dan menantang (challenging).
Contoh:
i= 1,2,3. Misalkan Dien mengecek kotak surat 1 dan tidak menemukan surat. Berapa peluang kejadian itu akan terjadi? Jika diketahui Dien mengecek kotak surat 1 dan tidak menemukan surat, berapa peluang bahwa surat itu ada di kotak surat 1?
Solusi: Misalkan Ki, i= 1,2,3 adalah kejadian surat berada di kotak surat i. Misalkan T kejadian mengecek kotak surat 1 dan tidak mendapatkan surat. Peluang kejadian itu akan terjadi adalah
P(T) = P(T|K1)P(K1) +P(T|K2)P(K2) +P(T|K3)P(K3) = (1−p1)(1/3) + 1/3 + 1/3
Jika diketahui Dien mengecek kotak surat 1 dan tidak menemukan surat, maka peluang bahwa surat itu ada di kotak surat 1 adalah
P(K1|T) =
P(T|K1)P(K1)
P(T|K1)P(K1) +P(T|K2)P(K2) +P(T|K3)P(K3)
= (1−p1)(1/3) (1−p1)(1/3) + 1/3 + 1/3
Contoh:
B dan G secara bersamaan menembak sasaran tertentu. Peluang tembakan B mengenai sasaran adalah 0.7 sedangkan peluang tembakan G (bebas dari tembakan B) mengenai sasaran adalah 0.4. Jika sebuah tembakan menge-nai sasaran, berapa peluang bahwa itu tembakan G? Berapa peluang bahwa, jika sasaran tertembak, kedua tembakan mengenai sasaran? Berapa peluang bahwa, jika sasaran tertembak, tembakan G mengenai sasaran?
Solusi: Misalkan B kejadian B menembak sasaran. Misalkan G kejadian G menembak sasaran. Misalkan T kejadian sebuah tembakan mengenai sasaran. Misalkan S kejadian sasaran tertembak
P(G|T) = P(G∩T)
P(T)
= P(G∩B
c)
P(G∩Bc) +P(B ∩Gc)
P(G∩B|S) = P(G∩S)P(B ∩S)
P(S)
= P(G)P(B) 1−P(Gc∩Bc)
= (0.4)(0.7) 1−(0.6)(0.3)
P(G|S) = P(G∩S)
P(S)
= P(G∩S) 1−P(Gc∩Bc)
= 0.4
1−(0.6)(0.3)
1.2
Peubah acak dan distribusi
Peubah acak (p.a.) adalah alat untuk “memudahkan” kita dalam “menyeder-hanakan” hitungan peluang; p.a. membuat kita bekerja dalam bilangan riil. Catatan: Peubah acak berbeda dengan peubah!
P.a. berkaitan dengan distribusi atau, secara khusus, fungsi distribusi (kumu-latif) (f.d.). Melalui f.d., p.a. akan makin memiliki makna dan aplikatif. Con-toh, suatu p.a. menyatakan waktu tunggu seorang lulusan mendapat peker-jaan. P.a. tersebut mengikuti distribusi eksponensial. Kita dapat memahami perilaku p.a. (secara probabilistik) tersebut melalui f.d.
Misalkan X suatu p.a.; F.d. untuk X adalah
FX(x) = F(x) =P(X ≤x)
dengan sifat-sifat:
(a) F fungsi tidak turun (b) limx→∞ F(x) = 1
(c) limx→−∞ F(x) = 0
(d) F fungsi kontinu kanan
Catatan:
Jika X p.a. diskrit,
• P(X ≤b)̸=P(X < b)
Tentukan fungsi peluang dari f.d. berikut:
F(x) =
MisalkanXp.a dengan f.d. FX(x). Kita dapat membentuk p.a. baru (menurut konsep Transformasi Peluang) yaitu
U =FX(X)∼U nif(0,1),
Jika X berdistribusi Uniform pada selang (-1,1), tentukan (a) P(|X|>1/2)
(b) fungsi peluang dari |X|. Solusi:
Contoh:
untuk menjual 52 tiket penerbangan pada pesawat dengan kapasitas duduk 50 orang. Berapa peluang akan ada kursi yang tersedia untuk setiap pemesan tiket yang datang?
Solusi:
Contoh:
Misalkan X p.a. berdistribusi Poisson dengan mean λ. Parameter λ berdis-tribusi eksponensial dengan mean 1. Tunjukkan bahwa
P(X =n) = (1/2)n+1
Solusi:
Misalkan X peubah acak dengan f.d. F dapat diturunkan. Fungsi peluang (f.p.) f adalah turunan dari f.d.,
fX(x) =
d
dxFX(x)
atau, dengan kata lain,
FX(x) = ∫ x
−∞
fX(t)dt
Jika X p.a. sedemikian hingga f.p.-nya ada (turunan dari f.d.) maka X
dikatakan sebagai peubah acak kontinu.
Catatan:
1 = FX(∞) = ∫ ∞
−∞
fX(t)dt
P(a≤X ≤b) = FX(b)−FX(a) = ∫ b
a
fX(t)dt
P(X =a) = ∫ a
a
fX(t)dt= 0
Salah satu contoh distribusi kontinu adalah distribusi eksponensial dengan parameter θ yang memiliki f.d.
F(x) = 1−e−θx, x≥0,
Seperti apakah “bentuk” data berdistribusi eksponensial? Untuk membangk-itkan datanya, contoh X ∼ exp(1/3), serta bentuk distribusinya (dalam his-togram) kita gunakan kode berikut:
Kita dapat pula membangkitkan data dengan menggunakan teknik simulasi stokastik yaitu “Invers Transformation Method”. Misalkan U peubah acak Uniform(0,1). Untuk setiap f.d. kontinu F, jika kita definisikan peubah acak
X sbb:
X =F−1(U)
maka peubah acak X memiliki f.d. F. Contoh: Jika F(x) = 1−e−x maka
F−1(u) adalah nilai x sedemikian hingga
1−e−x =u
atau
x=−log(1−u)
Jadi, jika U adalah p.a. Uniform(0,1) maka
F−1(U) =−log(1−U)
adalah p.a. eksponensial dengan mean 1 (parameter 1).
1.3
Ekspektasi bersyarat
Distribusi Bersama
Misalkan X dan Y p.a. dengan f.d. berturut-turut FX dan FY. Kita dapat membangun f.d. dan f.p. bersama dari kedua peubah acak tersebut dari infor-masi distribusi marginal dan sifat kebebasan. Distribusi bersama untuk dua atau lebih p.a. sangat membantu dalam membangun model yang lebih rumit. Hubungan antara f.d. marginal dan f.d. bersama adalah sebagai berikut: f.d. marginal mungkin dapat membangun f.d. bersama; dengan f.d. bersama kita dapat menentukan f.d. marginal.
Misalkan X dan Y ada peubah acak-peubah acak diskrit yang terdefinisi di ruang sampel yang sama. Fungsi peluang bersama dari X dan Y adalah
pX,Y(x, y) =P({X =x, Y =y})
Perhatikan bahwa (i) kondisi bahwa X dan Y terdefinisi pada ruang sampel yang sama berarti dua p.a. tsb memberikan informasi secara bersamaan ter-hadap keluaran (outcome) dari percobaan yang sama, (ii) {X = x, Y = y}
adalah irisan kejadian {X = x} dan {Y = y}; kejadian dimana X bernilai x
Proposisi
Misalkan X dan Y p.a. diskrit yang didefinisikan pada ruang sampel yang sama. Maka,
pX(x) = ∑
y
pX,Y(x, y), x∈R
dan
pY(y) = ∑
x
pX,Y(x, y), y ∈R
adalah f.p. marginal dari X dan f.p. marginal dari Y.
Contoh:
Diberikan data ttg jumlah kamar tidur dan kamar mandi dari 50 rumah yang akan dijual sbb (X kamar tidur, Y kamar mandi):
X\Y 2 3 4 5 Total
2 3 0 0 0
3 14 12 2 0 28
4 2 11 5 1
Total 23 50
a. Hitung pX,Y(3,2)
b. Tentukan f.p. bersama dari X dan Y
Solusi:
Contoh:
Misalkan kita punyai 2 komponen elektronik yang identik. Misalkan juga X
danY adalah waktu hidup (jam, diskrit). Asumsikan f.p. bersama dariX dan
Y adalah
pX,Y(x, y) =p2(1−p)x+y−2, x, y ∈ N
dimana 0< p < 1. Tentukan f.p. marginal dariX dan Y. Solusi:
Contoh:
Perhatikan soal diatas. Tentukan peluang bahwa kedua komponen elektronik tsb bertahan lebih dari 4 jam. Tentukan peluang bahwa salah satu komponen bertahan setidaknya 2 kali dari komponen yang lain.
Solusi:
Contoh:
peluang bersama dari X dan Y adalah
fX,Y(x, y) =λ µ exp(−λx+µy), x, y >0
dimana λ > 0, µ > 0. Tentukan peluang bahwa kedua komponen berfungsi pada saat t. Tentukan peluang bahwa komponen A adalah komponen yang pertama kali rusak
Solusi:
Ekspektasi Bersyarat
Ilustrasi - Seorang narapidana terjebak dalam suatu sel penjara yang memiliki tiga pintu. Pintu pertama akan membawanya ke sebuah terowongan dan kem-bali ke sel dalam waktu dua hari. Pintu kedua dan ketiga akan membawanya ke terowongan yang kembali ke sel dalam waktu masing-masing empat dan satu hari. Asumsikan bahwa sang napi selalu memilih pintu 1, 2, dan 3 den-gan peluang 0.5, 0.3 dan 0.2, berapa lama waktu rata-rata (expected number of days) yang dibutuhkan untuk dia agar selamat?
Definisi:
Misalkan X dan Y adalah p.a. kontinu dengan f.p. bersama fX,Y(x, y). Jika
fX(x)>0 maka ekspektasi bersyarat dari Y diberikan X =x adalah ekspek-tasi dari Y relatif terhadap distribusi bersyarat Y diberikan X =x,
E(Y|X =x) = ∫ ∞
−∞
y fX,Y(x, y) fX(x)
dy= ∫ ∞
−∞
y fY|X(y|x)dy
Proposisi
Misalkan X dan Y adalah peubah acak-peubah acak kontinu dengan fungsi peluang bersama fX,Y(x, y). Misalkan ekspektasi dariY hingga. Maka
E(Y) = ∫ ∞
−∞
E(Y|X =x)fX(x)dx
atau
E(Y) = E(E(Y|X =x))
Definisi:
Misalkan X dan Y adalah p.a. kontinu dengan f.p. bersama fX,Y(x, y). Jika
fX(x) > 0 maka variansi bersyarat dari Y diberikan X = x adalah variansi dari Y relatif terhadap distribusi bersyarat Y diberikan X =x,
V ar(Y|X =x) = E((
Y −E(Y|X =x))2 X =x
Proposisi
Misalkan X dan Y adalah peubah acak-peubah acak kontinu dengan fungsi peluang bersama fX,Y(x, y). Misalkan variansi dariY hingga. Maka
V ar(Y) =E(V ar(Y|X =x)) +V ar(E(Y|X))
Contoh:
Misalkan X dan Y peubah acak kontinu dengan fungsi peluang bersama
f(x, y) =e−x(y+1), 0≤x,0≤y≤e−1
(a) Hitung P(
X >1|Y = 1 2 )
(b) Hitung E(
X|Y = 12) Solusi:
Contoh:
Febri meninggalkan kantor setiap hari kerja antara pukul 6-7 malam. Jika dia pergi t menit setelah pukul 6 maka waktu untuk mencapai rumah adalah peubah acak berdistribusi Uniform pada selang (20,20 + (2t)/3). Misalkan
Y adalah banyak menit setelah pukul 6 dan X banya menit untuk mencapai rumah, berapa lama waktu mencapai rumah?
Solusi:
Contoh:
Zarudd saat ini berada di penjara Markas Brimob di Kelapa Dua, Depok. Dia ingin melarikan diri (katanya sih ingin ke Bogota atau manalah) namun hal ini tidak mudah. Fakta yang ada menunjukkan bahwa kalau Zarudd hendak keluar dari penjara dia akan menghadapi tiga pintu. Pintu pertama akan membawanya ke sebuah lorong dan kembali ke penjara dalam waktu dua jam. Pintu kedua pun demikian, akan membawanya ke sebuah lorong dan kembali ke penjara dalam waktu tiga jam. Sedangkan pintu ketigalah yang membawa Zarudd langsung bebas. Jika Zarudd memilih pintu-pintu, yang belum di-gunakannya, secara acak, berapa lama waktu rata-rata (expected number of hours) yang dibutuhkan Zarudd untuk bebas?
BAB 2
Rantai Markov
2.1
Ilustrasi
(Ilustrasi 1) Perilaku bunuh diri kini kian menjadi-jadi. Hesti (nama sebe-narnya) adalah sebuah contoh. Dia pernah melakukan percobaan bunuh diri, namun gagal. Menurut pakar, kalau pada suatu waktu seseorang melakukan percobaan bunuh diri maka besar kemungkinan dia akan melakukannya lagi di masa mendatang. Jika seseorang belum pernah melakukan percobaan bunuh diri, di masa mendatang orang tersebut akan mungkin melakukan percobaan bunuh diri. Deskripsikan fenomena diatas sebagai model peluang (probability model).
(Ilustrasi 2) Loyalitas konsumen terhadap suatu merek barang. Wilkie (1994) mendefinisikan “brand loyalty as a favorable attitude toward and consistent purchase of a particular brand”. Lyong (1998): “brand loyalty is a function of a brands’ relative frequency of purchase in both independent and time-dependent situations”. Seorang konsumen pembeli merek barang A diharap-kan adiharap-kan terus membeli barang A. Mungkinkah ini terjadi? Apakah model statistika yang dapat dengan tepat (atau mendekati tepat) merinci peluang terjadinya hal ini? Apakah model ini membantu dalam strategi pemasaran suatu barang?
(Ilustrasi 3) Akhir-akhir ini, hujan dan panas (baca: tidak hujan) datang silih berganti tanpa bisa diduga. Kalau hari ini hujan, besok mungkin hu-jan mungkin juga panas. Tentu saja peluang besok huhu-jan akan lebih besar dibanding peluang besok akan panas. Begitu pula jika hari ini panas. Besok akan lebih mungkin panas dibandingkan hujan. Jika hari Senin hujan, berapa peluang bahwa hari Selasa akan hujan? Berapa peluang bahwa hari Kamis akan hujan?
untuk berlari pagi. Laila akan pergi lewat pintu depan atau belakang den-gan peluang sama. Ketika meninggalkan rumah, Laila memakai sepatu olah raga atau bertelanjang kaki jika sepatu tidak tersedia di depan pintu yang dia lewati. Ketika pulang, Laila akan masuk lewat pintu depan atau belakang dan meletakkan sepatunya dengan peluang sama. Diketahui bahwa Laila memiliki 4 pasang sepatu olah raga. Berapa peluang bahwa Laila akan sering berolah raga dengan bertelanjang kaki?
2.2
Definisi
Proses stokastik {Xn} adalah Rantai Markov:
• n = 0,1,2, . . .
• nilai yang mungkin adalah hingga atau terhitung
•
P(
Xn+1 =j|Xn=i, Xn−1 =in−1, . . . , X1 =i1, X0 =i0 )
=Pij (∗)
• distribusi bersyaratXn+1, diberikan keadaan-keadaan lampau (past states)
X0, X1, . . . , Xn−1dan keadaan sekarang (present state)Xn, hanya bergan-tung pada keadaan sekarang (“Sifat Markov”)
• keadaan-keadaan (states): i0, i1, . . . , in−1, i, j
Pij peluang bahwa proses akan berada di keadaan j dari keadaani;
Pij ≥0, i, j ≥0;
∞
∑
j=0
Pij = 1, i= 0,1, . . .
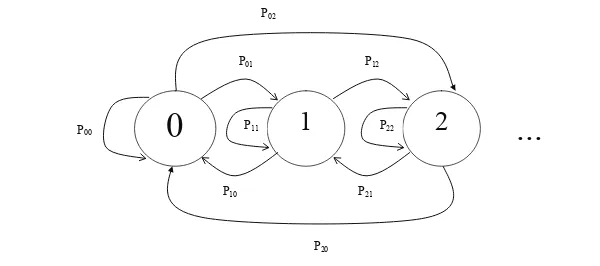
Matriks peluang transisi Pij adalah
P=
P00 P01 P02 · · ·
P10 P11 P12 · · · ... ... ...
Pi0 Pi0 Pi0 · · · ... ... ...
P02
...
P20
0
1
2
P00
P01 P12
P10 P21
P11 P22
Figure 2.1: Diagram transisi keadaan atau state transition diagram
Perhatikan (*):
P(
Xn+1 =j|Xn=i, Xn−1 =in−1, . . . , X1 =i1, X0 =i0 )
=P(
Xn+1 =j|Xn =i )
=Pij,
yang disebut sebagai peluang transisi 1-langkah atauone-step transition prob-ability.
Peluang bersama
P(
Xn=i, Xn−1 =in−1, . . . , X1 =i1, X0 =i0 )
dapat dihitung dengan sifat peluang bersyarat berikut.
P(
Xn=i, Xn−1 =in−1, . . . , X1 =i1, X0 =i0 )
=P(
Xn−1 =in−1, . . . , X1 =i1, X0 =i0 )
×P(
Xn =i|Xn−1 =in−1, . . . , X1 =i1, X0 =i0 )
=P(
Xn−1 =in−1, . . . , X1 =i1, X0 =i0 )
×P(
Xn=i|Xn−1 =in−1 )
=· · ·
=pi0 · · · Pin −1,in
Contoh/Latihan:
adalah... ’0’ tidak mengajukan klaim ’1’ mengajukan klaim
2. Keadaan hujan pada suatu hari bergantung pada keadaan hujan dalam dua hari terakhir. Jika dalam dua hari terakhir hujan maka besok akan hujan dengan peluang 0.7; Jika hari ini hujan dan kemarin tidak hujan maka besok akan hujan dengan peluang 0.5; jika hari ini tidak hujan dan kemarin hujan maka besok akan hujan dengan peluang 0.4; jika dalam dua hari terakhir tidak hujan maka besok hujan dengan peluang 0.2. Matriks peluang transisinya adalah...
P=
’0’ (00) = hari ini dan kemarin hujan
’1’ (10) = hari ini hujan, kemarin tidak hujan ’2’ (01) = hari ini tidak hujan, kemarin hujan ’3’ (11) = hari ini dan kemarin tidak hujan
3. Tiga item produk A dan tiga item produk B didistribusikan dalam dua buah paket/kotak sedemikian hinga setiap paket terdiri atas tiga item produk. Dikatakan bahwa sistem berada dalam keadaan i, i = 0,1,2,3 jika dalam paket pertama terdapat i produk A. Setiap saat (langkah), kita pindahkan satu item produk dari setiap paket dan meletakkan item produk tersebut dari paket 1 ke paket 2 dan sebaliknya. Misalkan Xn menggambarkan keadaan dari sistem setelah langkah ke-n. Matriks pelu-ang transisinya adalah...
’1’ terdapat 1 produk A di paket pertama ’2’ terdapat 2 produk A di paket pertama ’3’ terdapat 3 produk A di paket pertama
4. Menurut Kemeny, Snell dan Thompson, Tanah Australia diberkahi den-gan banyak hal kecuali cuaca yang baik. Mereka tidak pernah memiliki dua hari bercuaca baik secara berturut-turut. Jika mereka mendapatkan hari bercuaca baik maka esok hari akan bersalju atau hujan dengan pelu-ang sama. Jika hari ini mereka mengalami salju atau hujan maka be-sok akan bercuaca sama dengan peluang separuhnya. Jika terdapat pe-rubahan cuaca dari salju atau hujan, hanya separuh dari waktu besok akan menjadi hari bercuaca baik. Tentukan matriks peluang transisi dari Rantai Markov yang dibentuk dari keadaan-keadaan diatas.
P=
5. Suatu rantai Markov dengan keadaan-keadaan “0, 1, 2” memiliki matriks peluang transisi:
Hitung
P(X2 = 1, X3 = 1|X1 = 0)
dan
P(X1 = 1, X2 = 1|X0 = 0)
Solusi: 0.12; 0.12
7. Sebagai calon atlet, setiap pagi Laila meninggalkan rumahnya untuk berlari pagi. Laila akan pergi lewat pintu depan atau belakang den-gan peluang sama. Ketika meninggalkan rumah, Laila memakai sepatu olah raga atau bertelanjang kaki. Ketika pulang, Laila akan masuk lewat pintu depan atau belakang dan meletakkan sepatunya dengan peluang sama. Diketahui bahwa Laila memiliki 4 pasang sepatu olah raga. Ben-tuklah suatu Rantai Markov dari proses diatas.
P=
3/4 1/4 0 0 0 1/4 1/2 1/4 0 0 0 1/4 1/2 1/4 0 0 0 1/4 1/2 1/4 0 0 0 1/4 3/4
dengan keadaan-keadaan:
’0’ (4,0) = 4 sepatu didepan, 0 dibelakang ’1’ (3,1) = 3 sepatu didepan, 1 dibelakang ’2’ (2,2) = 2 sepatu didepan, 2 dibelakang ’3’ (1,3) = 1 sepatu didepan, 3 dibelakang ’4’ (0,4) = 0 sepatu didepan, 4 dibelakang
8. Lena akan melantunkan koin terus menerus hingga diperoleh keluaran
B, B, M (2 keluaran Belakang berturut-turut yang kemudian diikuti oleh keluaran Muka). Bentuklah rantai Markov yang mungkin. Perhatikan bahwa jika lantunan Lena adalah M, laluB, laluM artinya adalah Lena harus mengulang lantunan dari awal.
hingga hanya 1 komputer yang dapat ditangani setiap waktu. Bentuklah rantai Markov yang dapat memodelkan situasi diatas...
10. Ani tinggal tidak jauh dari kampus. Cukup berjalan kaki saja dari tem-pat kos ke kampus dan sebaliknya. Akhir-akhir ini hujan datang hampir setiap hari. Mau tidak mau, Ani menggunakan payung dalam perjalanan kos-kampus atau kampus-kos. Jika hari hujan dan payung ada ditem-pat Ani berada maka Ani akan menggunakan payung tersebut. Jika hari tidak hujan, Ani selalu lupa untuk membawa payung. Misalkanθ adalah peluang hujan setiap kali Ani akan menuju kampus atau kos. Jika Ani memiliki 3 buah payung, bentuklah suatu rantai Markov dari proses di-atas!
’0’, ’1’, ’2’, ’3’ yang menyatakan jumlah payung
11. Dua tim futsal wanita di MA-ITB akan memainkan tujuh rangkaian per-tandingan. Hasil setiap pertandingan saling bebas. Setiap pertandingan akan dimenangkan oleh tim A dengan peluang α dan oleh tim B den-gan peluang 1 −α. Misalkan keadaan suatu sistem direpresentasikan oleh pasangan (a, b) dimana a menyatakan banyak pertandingan yang dimenangkan A dan b banyak pertandingan yang dimenangkan B. Ben-tuklah rantai Markov untuk masalah tersebut. Catatan: a+b ≤7 dan rangkaian pertandingan akan berakhir apabila a= 4 atau b = 4.
2.3
Peluang
n
-langkah
Persamaan Chapman-Kolmogorov
Misalkan Pn
ij menyatakan peluang transisi n-langkah suatu proses di keadaan
i akan berada di keadaan j,
Pijn=P(Yk+n=j|Yk =i), n ≥0, i, j ≥0.
untuk semua n, m ≥ 0 dan semua i, j. Pn
ikPkjm menyatakan peluang suatu proses dalam keadaaniakan berada di keadaanj dalamn+mtransisi, melalui keadaan k dalam n transisi/langkah.
Contoh/Latihan:
1. Jika hari ini hujan maka besok akan hujan dengan peluangα = 0.7; jika hari ini tidak hujan maka besok akan hujan dengan peluang β = 0.4. Matriks peluang transisi 4 langkah adalah...
P4
2. Keadaan hujan pada suatu hari bergantung pada keadaan hujan dalam dua hari terakhir. Jika dalam dua hari terakhir hujan maka besok akan hujan dengan peluang 0.7; Jika hari ini hujan dan kemarin tidak hujan maka besok akan hujan dengan peluang 0.5; jika hari ini tidak hujan dan kemarin hujan maka besok akan hujan dengan peluang 0.4; jika dalam dua hari terakhir tidak hujan maka besok hujan dengan peluang 0.2. Matriks peluang transisinya adalah sbb:
P=
Jika hari Senin dan Selasa hujan, berapa peluang bahwa hari Kamis akan hujan?
Peluang hujan pada hari Kamis adalah P2
00+P012 = 0.49 + 0.12 = 0.61
Peluang Transisi Tak Bersyarat
Misalkan
αi =P(X0 =i), i≥0,
dimana ∑∞
i=0 αi = 1. Peluang tak bersyarat dapat dihitung dengan men-syaratkan pada keadaan awal,
Contoh/Latihan:
Pandang soal yang lalu dengan matriks peluang transisi:
P= (
0.7 0.3 0.4 0.6
)
Jika diketahui α0 = P(X0 = 0) = 0.4 dan α1 = P(X0 = 1) = 0.6, maka peluang (tak bersyarat) bahwa hari akan hujan 4 hari lagi adalah...
P(X4 = 0) = 0.4P004 + 0.6P104
= (0.4)(0.5749) + (0.6)(0.5668) = 0.57
2.4
Jenis Keadaan
Keadaan j dikatakan dapat diakses (accessible) dari keadaan i jika Pn ij > 0 untuk suatu n ≥ 0. Akibatnya, keadaan j dapat diakses dari keadaan i jika dan hanya jika dimulai dari keadaan i proses akan masuk ke keadaan j. Jika keadaan j tidak dapat diakses dari keadaanimaka peluang masuk ke keadaan
j dari keadaan i adalah nol. Catatan:
Sifat-sifat:
1. Keadaani berkomunikasi dengan keadaan iuntuk semua i≥0
2. Jika keadaani berkomunikasi dengan keadaan j maka keadaanj berko-munikasi dengan keadaan i
3. Jika keadaaniberkomunikasi dengan keadaanj dan keadaanj berkomu-nikasi dengan keadaank maka keadaaniberkomunikasi dengan keadaan
k
Dua keadaan yang berkomunikasi dikatakan berada dalam kelas (class) yang sama. Setiap dua kelas dari keadaan-keadaan dapat ‘identik’ (identical) atau ‘saling asing’ (disjoint). Rantai Markov dikatakan tidak dapat direduksi (irre-ducible) jika hanya terdapat sebuah kelas dan semua keadaan berkomunikasi satu sama lain.
Contoh/Latihan:
1. Tentukan kelas keadaan dari rantai Markov dengan peluang transisi berikut:
2. Diketahui matrik peluang transisi:
Apakah rantai Markov dengan peluang transisi diatas tidak dapat dire-duksi (irreducible)?
3. Apakah yang dapat anda katakan tentang rantai Markov dengan matriks peluang transisi berikut:
P=
0.5 0.5 0 0 0.5 0.5 0 0 0.25 0.25 0.25 0.25
0 0 0 1
Sifat-sifat KEADAAN - Recurrent dan Transient
Untuk setiap keadaan i, misalkan fi peluang bahwa dimulai dari keadaan i proses akan pernah kembali ke keadaan i. Keadaan idikatakan recurrentjika
fi = 1. Dikatakan transient jika fi <1.
• Jika keadaan i recurrent maka proses akan terus kembali ke keadaan i
dengan peluang satu. Dengan definisi rantai Markov, proses akan dimulai lagi ketika kembali ke keadaani, dan seterusnya, sehingga keadaaniakan dikunjungi lagi. Jika keadaan i recurrent maka dimulai dari keadaan i
maka proses akan kembali ke keadaan i terus dan terus sebanyak tak hingga kali.
• Misalkan keadaan i transient. Setiap kali proses kembali ke keadaan
i, terdapat kemungkinan (peluang yang positif) sebesar 1 −fi bahwa proses tidak pernah kembali ke keadaan i. Dengan demikian, dimulai dari keadaan i, peluang bahwa proses berada di i sebanyak tepat n pe-riode/kali adalah fn−1
i (1−fi), n ≥ 1. Jika keadaan i transient maka, dimulai dari keadaan i, banyak periode/kali bahwa proses akan berada di keadaan i adalah peubah acak geometrik dengan parameter 1−fi.
“Keadaanirecurrentjika dan hanya jika, dimulai dari keadaani, maka banyak periode/kali yang diharapkan (expected number of time periods) bahwa proses akan berada di keadaan iadalah tak hingga”
Misalkan
In = {
1, Yn =i; 0, Yn ̸=i. Misalkan∑∞
keadaan i, dan
• Pada rantai Markov dengan keadaan hingga, tidak semua keadaan bersi-fat transient (Mengapa?)
• “Jika keadaan i recurrent dan keadaan i berkomunikasi (communicate) dengan keadaan j maka keadaan j recurrent” (Bagaimana jika keadaan
i transient?)
• Semua keadaan pada rantai Markov (hingga) yang tidak dapat direduksi adalah recurrent(PENTING!)
Contoh/Latihan:
1. Misalkan rantai Markov dengan keadaan 0,1,2,3 memiliki matriks pelu-ang transisi:
Tentukan keadaan mana yang recurrent dan keadaan mana yang tran-sient!
P=
3. Misalkan rantai Markov dengan keadaan 0,1,2,3 memiliki matriks pelu-ang transisi:
Tentukan keadaan mana yang recurrent dan keadaan mana yang tran-sient!
4. Model penyebaran penyakit memiliki matriks peluang transisi sebagai berikut:
Tentukan sifat keadaan dari rantai Markov diatas.
2.5
Limit Peluang Transisi
Misalkan ‘0’ keadaan belum pernah juara dan ‘1’ keadaan pernah juara. Ma-triks peluang transisi yang dapat dibentuk adalah
P= (
0.9 0.1 0.3 0.7
)
Matriks peluang transisi 8 dan 12 langkahnya:
P12
= (
0.7505 0.2495 0.7484 0.2516
)
...dst.
MatriksP12 hampir identik denganP8 (benar-benar identik dengan P16). Se-lain itu, setiap baris dari P12 memiliki unsur yang identik. Nampaknya, Pn ij konvergen ke suatu nilai, untuk n → ∞, yang sama untuk semua i. Dengan kata lain, terdapat limit peluang (limiting probability) bahwa proses akan be-rada di keadaanj setelah sekian/banyak langkah/transisi. Nilai limit ini saling bebas dengan nilai pada keadaan awal.
Perhatikan 2 sifat keadaan berikut:
Keadaan idikatakan memiliki periode djikaPn
ii = 0 untuk nyang tidak dapat dibagi oleh d (d suatu integer). Contoh, suatu proses dimulai dari keadaan i
akan kembali ke i pada waktu 2,4,6,8, . . ., maka keadaan i memiliki periode 2. Suatu keadaan yang memiliki periode 1 disebut aperiodik. Jika keadaan
i memiliki periode d dan keadaan i berkomunikasi dengan keadaan j maka keadaan j juga memiliki perioded.
Jika keadaan i recurrent, maka keadaan tersebut akan dikatakan positive re-current jika, dimulai dari keadaan i, waktu harapan hingga proses kembali ke i adalah hingga. Pada rantai Markove yang memiliki keadaan hingga, se-mua keadaan yang recurrent adalah positive recurrent. Suatu keadaan yang positive recurrent dan aperiodik disebut ergodik.
Teorema
Untuk rantai Markov yang ergodik dan tidak dapat direduksi,
lim n→∞ P
n ij
ada dan saling bebas dari i. Misalkan
πj = lim n→∞ P
n
ij, j ≥0,
maka πj adalah solusi nonnegatif tunggal dari
πj =
∞
∑
i=0
πiPijn, j ≥0,
dengan ∑∞
Catatan:
• Perhatikan bahwa
P(Xn+1 =j) =
∞
∑
i=0
P(Xn+1 =j|Xn=i)P(Xn=i) =
∞
∑
i=0
PijP(Xn=i)
• Limit peluangπj adalah peluang jangka panjang (long-run proportion of time) bahwa suatu proses akan berada di keadaan j
• Jika rantai Markov tidak dapat direduksi, maka terdapat solusi untuk
πj = ∑
i
πiPij, j ≥0,
dengan ∑
j πj = 1, JIKA dan HANYA JIKA rantai Markov bersifat positive recurrent. Jika solusinya ada maka solusi tersebut tunggal dan
πj adalah proporsi jangka panjang bahwa rantai Markov berada dalam keadaan j. Jika rantai Markov aperiodik maka πj adalah limit peluang bahwa rantai akan berada di keadaan j.
Contoh/Latihan:
1. Jika hari ini hujan maka besok akan hujan dengan peluang α; jika hari ini tidak hujan maka besok akan hujan dengan peluangβ. Jika′0′ adalah
keadaan hujan dan ′1′ adalah keadaan tidak hujan maka peluang hujan
dan tidak hujan untuk jangka adalah...
Matriks peluang transisi:
P= (
α 1−α β 1−β
)
,
dan kita punyai persamaan-persamaan:
π0 =α π0+β π1
π1 = (1−α)π0+ (1−β)π1
π0+π1 = 1
Kita peroleh peluang hujan dan tidak hujan pada jangka panjang:
π0 =
β
dan
π1 =
1−α
1 +β−α
2. Percobaan-percobaan dilakukan secara berurutan. Jika dalam dua per-cobaan terakhir SUKSES maka peluang SUKSES pada perper-cobaan berikut adalah 0.8. Dalam keadaan YANG LAIN, peluang SUKSES adalah 0.5. Hitung peluang percobaan sukses untuk jangka panjang.
3. Pandang pelantunan-pelantunan sebuah koin (dengan peluang muncul MUKA adalah θ) yang saling bebas. Berapa banyak lantunan dibu-tuhkan yang diharapkan (expected number of tosses needed) agar pola
HT HT muncul? (Perhatikan catatan dibawah)
Catatan:
• Peluang jangka panjang πj, j ≥ 0, disebut juga peluang stasioner (sta-tionary probability). Jika keadaan awal dipilih berdasarkan peluang
πj, j ≥ 0, maka peluang akan menjadi keadaan j pada setiap waktu
n adalah sama dengan πj.
• Untuk keadaan j, definisikanmjj yaitu banyak transisi yang diharapkan (expected number of transitions) hingga suatu rantai Markov, dimulai dari keadaan j akan kembali ke keadaan tersebut:
πj = 1