Statistik Inferensi

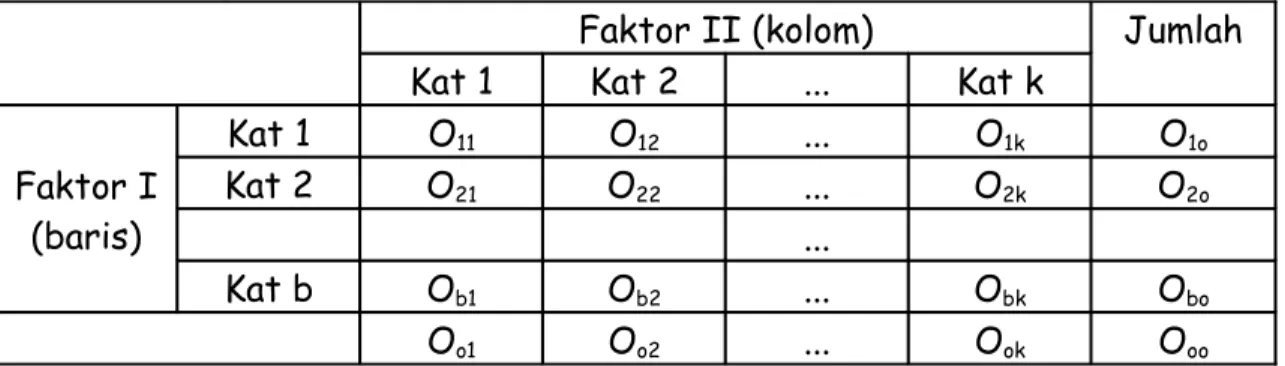
RENCANA MATAKULIAH STATISTIK EKONOMI INFERENSI Materi Kuliah No Materi Pertemua n 1. Distribusi Normal 1 2. Distribusi Binomial 1

3. Distribusi Chi Square 1

4. Distribusi Sampling 2

5. Teori Penaksiran 2

6. Uji Hipotesis 2

7. Uji Chi Square 1

8. Analisis Regresi & Korelasi 1

9. Statistik Non Parametrik 1

JUMLAH 12 Penilaian : 1. UTS 30% 2. UAS 40% 3. TUGAS 20% 4. QUIZ / Latihan 10% 5. Absensi Buku sumber :

1. Sudjana, Statistika Jilid II

2. Anto Dajan, Metode Statistika 08172314131

M. RIZAL : 085222399218 ROHANA 085224952995

PELUANG

Ruang sampel

• Himpunan semua hasil yang mungkin dari suatu

percobaan statistik disebut ruang sampel, biasanya dinyatakan dengan lambang S. Contoh:

Percobaan melantunkan satu keping uang logam menghasilkan S={Muka, Belakang}

Percobaan melantunkan satu buah diadu menghasilkan

S={1,2,3,4,5,6}

• Kejadian adalah himpunan bagian dari ruang sampel • Suatu kejadian yang mengandung satu unsur ruang

sampel disebut kejadian sederhana, suatu kejadian yang dapat dinyatakan sebagai gabungan beberapa kejadian sederhana disebut kejadian majemuk.

• Ruang nol atau ruang hampa adalah himpunan bagian

ruang sampel yang tidak mengandung unsur.

Menghitung titik sampel

• Bila suatu operasi dapat dilakukan dengan n1 cara dan

bila untuk tiap cara ini operasi kedua dapat dikerjakan dengan n2 cara maka kedua operasi itu dapat

dikerjakan bersama-sama dengan n1 x n2 cara. Contoh :

Pelantunan satu keping koin mata uang memberikan dua hasil kemungkinan yaitu S={M, B}. Apabila dua keping mata uang dilantunkan sekaligus akan memberikan hasil 4 hasil kemungkinan yaitu S={MM, MB, BM, BB}. Berapa kemungkinan hasil dari pelantunan satu keping koing dengan satu dadu bersisi 6?

• Suatu permutasi adalah susunan yang dapat dibentuk

dari kumpulan benda-benda yang diambil sebagian atau seluruhnya. Banyaknya permutasi n benda yang berlainan adalah n!. Banyak permutasi n benda berlainan bila diambil r sekaligus adalah :

)!

(

!

r

n

n

P

_r n

−

=

• Jumlah kombinasi dari n benda yang berlainan bila

diambil sebanyak r adalah :

)!

(

!

!

r

n

r

n

r

n

−

=









Peluang suatu kejadian

• Peluang suatu kejadian A adalah jumlah bobot semua

titik sampel yang termasuk A, Jadi :

0

≤

P

(

A

)

≤

1

,

P

(

S

)

=

1

• Bila suatu percobaan dapat menghasilkan N macam

hasil yang berkemungkinan sama dan bila tepat sebanyak n dari hasil berkaitan dengan kejadian A, maka peluang kejadian A adalah :

N

n

A

P

(

)

=

• Contoh bila satu kartu ditarik dari satu kotak kartu

bridge (berisi 52), hitunglah peluang bahwa kartu itu heart (heart ada 13). Jawab : Jumlah hasil yang mungkin adalah 52, dan 13 di antaranya adalah heart. Jadi peluang kejadian A menarik satu kartu heart adalah P(A)=13/52=1/4. Berapakah peluang kejadian menarik kartu As ? Berapakah peluang kejadian menarik kartu bukan As ?

• Dua kejadian saling ekslusif jika terjadinya kejadian

yang satu menyebabkan tidak terjadinya terjadinya kejadian yang lain.

• Jika A dan B adalah dua kejadian yang saling ekslusif

maka berlaku : P(A atau B) = P(A) + P(B). Rumus ini mengatakan jika A dan B dua kejadian yang saling ekslusif maka peluang terjadinya A dan B adalah jumlah peluang A dan peluang B.

• Dua kejadian dikatakan bebas atau independen jika

terjadinya atau tidak terjadinya peristiwa yang satu tidak mempengaruhi atau dipengaruhi oleh kejadian lainnya. Jika A dan B dua peristiwa bebas, maka berlaku :

P(A dan B)= P(A) x P(B). Rumus ini mengatakan bahwa jika A dan B bebas maka peluang terjadinya kejadian A dan B adalah hasil kali peluang A dan B.

• Ekspektasi atau nilai harapan adalah hasil kali antara

peluang dan kejadiannya. Sebagai contoh : Apabila kita melakukan undian dengan melantunkan sebuah uang logam, maka apabila muncul muka kita membayar Rp.1.000 kepada lawan sedangkan apabila muncul belakang kita tidak membayar apa-apa. Maka Ekspektasi dari kejadian tersebut adalah :

E = P(Muka) x - Rp. 1.000 +P(Belakang) x Rp.0,- = 0.5(Rp.1.000) + 0.5(Rp.0)

= - Rp. 500

QUIZ :

Dalam satu buah kantung terdapat 3 bola berwarna hijau, 5 bola berwarna putih 2 bola berwarna biru. Misalkan dari kantung tersebut dilakukan pengambilan bola tiga kali tanpa pengembalian, tentukan peluang terambil bola berwarna hijau pada pengambilan pertama, terambil bola berwarna putih pada pengambilan kedua dan terambil bola berwarna

Peubah Acak (Random Variable)

• Peubah acak adalah suatu fungsi bernilai real yang

harganya ditentukan oleh tiap anggota dalam ruang sampel. Contoh : Pada pelantunan uang logam kita tahu bahwa peluang muncul muka dan belakang masing-masing adalah ½ . Misalnya hasil dari percobaan 1000 kali percobaan pelantunan uang logam diperoleh data sebagai berikut : Nampak Muka Frekuensi Sebenarnya Frekuensi diharapkan 0 480 500 1 520 500

Secara teoritis, digunakan notasi x sebagai lambang dari kejadian dan

f

(x

)

sebagai lambang untuk menyatakan peluang bagi harga x yang bersangkutan. Maka diperoleh :

x

f

(x

)

0 ½ 1 ½ atau

,

2

1

)

(

x

=

f

x

=

0

,

1

• Pada percobaan pelantunan dadu, maka masing-masing

sisi memiliki peluang yang sama yaitu 1/6. Maka percobaan pelantunan dadu tersebut memiliki peubah acak :

,

6

1

)

(

x

=

f

x = 1,2,3,4,5, dan 6

• Latihan : coba tentukan peubah acak (random

variable) dari hasil percobaan pelantunan 2 uang logam sekaligus, pelantunan 3 uang logam sekaligus, serta hasil percobaan pelantunan satu uang logam bersamaan dengan pelantunan satu buah dadu !

• Sifat peubah acak :

∑

=

n

x

f

1

1

)

(

• Jika suatu ruang sampel mengandung titik yang berhingga banyaknya atau suatu deretan anggota

yang banyaknya sama dengan banyaknya bilangan bulat, maka ruang sampel tersebut disebut ruang

sampel diskret, dan peubah acak yang didefinisikan

pada ruang sampel tersebut adalah peubah acak

diskret, contoh peubah acak distribusi binomial.

• Jika suatu ruang sampel mengandung titik sampel yang tak berhingga banyaknya dan sama banyaknya

dengan banyak titik pada sepotong garis maka ruang sampel itu disebut ruang sampel kontinu dan peubah acak yang didefinisikan di atasnya disebut peubah

acak kontinu, contoh : peubah acak distribusi normal. Distribusi Normal N~(_µ,_σ2)

Satu diantara distribusi kontinyu adalah distribusi normal atau distribusi Gauss, sebagai penghargaan kepada seorang matematikawan Carl Gauss yang telah berperan banyak menyelidiki hal ini pada akhir abad ke 18 di samping peneliti pertama Piere de Laplace dan Abraham de Moivre.

Distribusi normal disebut sebagai distribusi paling penting dalam statistika karena pada pekerjaan selanjutnya ternyata banyak teori yang didasarkan pada distribusi normal.

Persamaan distribusi normal :

2 2 1

2

1

)

(

     − −

=

σ µ

π

σ

X

e

x

f

Keterangan :

π

= nilai konstan yang besarnya = 3,1416

e

= tetapan bilangan pokok logaritma natural = 2,7183

σ

= parameter, simpangan baku (standar deviasi) distribusi normal

X

= peubah acak kontinu, harganya _{−∞ <} X _{< +∞}

Distribusi normal memiliki memiliki dua parameter yakni rata-rata

µ

dan simpangan baku (standar deviasi)

σ

. Sehingga lambang umum untuk distribusi normal adalah N(

µ

,

σ

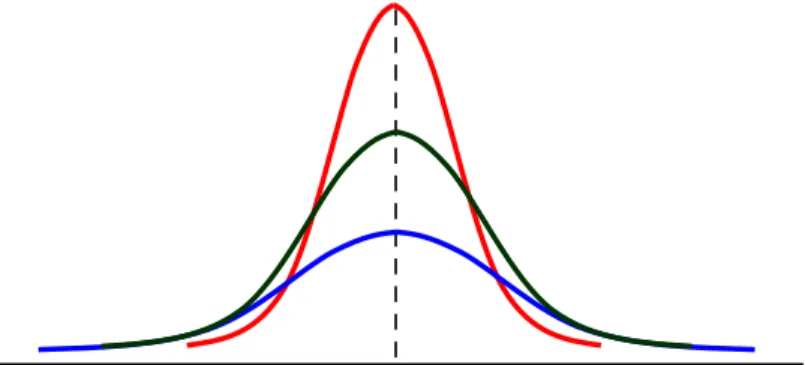
) . Kedua parameter ini akan mempengaruhi bentuk grafik distribusi normal. Grafik distribusi normal menyerupai genta/bel sehingga disebut dengan Bell Curve.

Gambar Bell Curve distribusi normal N~(_µ,_σ2)

Pengaruh besar kecilnya simpangan baku alpa (

σ

):

Grafik berwarna merah (paling runcing) memiliki simpangan baku (

σ

) alpa paling besar sedangkan grafik berwarna biru memiliki simpangan baku alpa (

σ

) paling kecil.

1

µ

µ

₂

Untuk menentukan peluang sebuah kejadian X yang berdistribusi normal secara teoritis, karena melibatkan integral yang kompleks jadi proses penghitungannya sangat sulit dilakukan. Tapi karena hasil perhitungan integral adalah sama dengan dengan menentukan luas dibawah kurva, berarti menentukan peluang sebuah kejadian X sama saja dengan dengan menghitung luas daerah dibawah kurva distribusi normal tersebut.

Untuk menyederhanakan distribusi normal, digunakan sebuah konsep yang disebut ditribusi normal baku (normal standard) yaitu distribusi normal yang memiliki rata-rata 0 dan simpangan baku =1. Hal ini dapat dilakukan menggunakan transformasi yang mengubah peubah acak X yang berdistribusi normal ke dalam peubah acak Z yang berdistribusi normal baku dengan menggunakan rumus :

σ

µ

−

=

X

Z

Apabila hal ini dilakukan maka persamaan distribusi normal baku adalah : 2 2 1

2

1

)

(

z

e

z

f

=

−

π

σ

Secara grafis transformasi dari N(

µ

,

σ

) menjadi N(0,1) adalah sebagai berikut :

σ

σ =1

µ µ=0

Normal Umum Normal Baku

σ µ

−

= X

Tabel luas dibawah kurva normal Z dan penggunaannya : Lihat buku Sudjana Jilid II halaman 46 sampai 56.

Contoh :

Bila X merupakan peubah acak yang memiliki distribusi normal dengan rata-rata µ = 24 dan standar deviasi σ=12, berapakah peluang (17,4<X<58,8) ?

Jawab :

Pengubahan peubah acak normal 17,4 dan 58,8 masing-masing ke dalam peubah acak normal baku diperoleh :

55

,

0

12

24

4

,

17

1

=

−

−

=

Z

90

,

2

12

24

8

,

58

2

=

−

=

Z

Dengan demikian P(17,4<X<58,8) = P(-0,55<Z<2,90) Dengan menggunakan tabel distribusi normal diperoleh : P(-0,55<Z<2,90) = 0,9980 - 0,2912 = 0,7069 atau 70,69 %

Contoh :

Dari pengiriman sebanyak 1.000 rim kertas berat 60gram diketahui bahwa rata-rata tiap rimnya terisi dengan 450 lembar dengan standar deviasi 10 lembar. Jika distribusi jumlah kertas per rim tersebut dapat didekati dengan kurva normal, berapa persen dari rim kertas diatas yang terisi dengan 455 lembar atau lebih?

Jawab :

Dalam soal diatas diketahui bahwa rata-rata µ = 450 dan standar deviasi σ= 10. Transformasi peubah acak normal ke dalam peubah acak standar memperoleh :

Maka P(X>455) = P(Z>0,5) dengan menggunakan tabel distribusi normal diperoleh : P(Z>0,5) = P(1-0,6915) = 0,3085

Contoh :

Angka ujian statistik sebagian besar mahasiswa memiliki rata-rata µ = 34 dan simpangan baku/standar deviasi σ = 4. Jika distribusi angka-angka ujian tersebut mendekati distribusi normal, dibawah angka ujian statistik berapakah akan diperoleh 10 persen terendah dari seluruh distribusi angka-angka tersebut?

Jawab :

Dalam soal diatas diketahui bahwa bahwa rata-rata µ = 34 dan standar deviasi σ = 4. Maka dengan menggunakan tabel distribusi normal luas dibawah kurva normal yang sesuai dengan 10% adalah -1,28, sehingga :

88 , 28 4 34 28 , 1 = − = − X X

Jadi diperoleh keterangan bahwa 10% dari seluruh mahasiswa memperoleh nilai ujian statistik 28,8 atau kurang.

Contoh :

Sebuah sampel mesin cuci memiliki diameter rata-rata sebesar 0,502m dan standar deviasi sebesar 0,005m. Mesin cuci yang demikian dianggap tidak memenuhi syarat jika memiliki spesifikasi diameter di luar 0,496m dan 0,508m. Coba tentukan persentase mesin cuci yang tidak memenuhi syarat jika diketahui bahwa diameter mesin cuci tersebut memiliki distribusi normal?

Jawab :

Dalam soal diatas diketahui bahwa bahwa rata-rata µ = 0,502m dan standar deviasi σ = 0,005m.

2 , 1 005 , 0 502 , 0 496 , 0 1 = − − = Z 2 , 1 005 , 0 502 , 0 508 , 0 2 = − = Z P(Z<-1,2)= 0,1151 P(Z>1,2)=P(1-0,8849)= 0,1151

Jadi persentase mesin cuci yang tidak memenuhi syarat adalah 11,51%+11,51%=23,02%.

DISTRIBUSI BINOMIAL

Suatu percobaan sering terdiri atas beberapa usaha, tiap usaha dengan dua kemungkinan dapat diberi nama sukses

dan gagal. Hal ini terjadi misalnya pada pengujian barang

hasil produksi dengan tiap pengujian atau usaha dapat menunjukkan apakah suatu barang cacat atau tidak cacat. Kita dapat menentukan atau memilih salah satu hasil sebagai sukses. Percobaan seperti ini disebut percobaan

binomial.

Suatu percobaan binomial adalah :

1. Percobaan terdiri atas n usaha yang berulang (tertentu).

2. Tiap usaha memberikan hanya 2 jenis hasil yang dapat ditentukan dengan sukses atau gagal.

3. Peluang sukses dinyatakan dengan p, tidak berubah dari usaha yang satu ke yang berikutnya.

4. Tiap usaha bebas dengan usaha lainnya (tidak dipengaruhi oleh usaha lain).

Distribusi binomial : Bila suatu usaha binomial dapat menghasilkan sukses dengan peluang

p

dan gagal dengan peluang

q

=

1

−

p

, maka distribusi peluang peubah acak binomial X, yaitu banyaknya sukses dalam n usaha bebas adalah : x n x

_q

p

x

n

p

n

x

b

−









=

)

,

;

(

, x = 0,1,2, ... , n dengan

)!

(

!

!

x

n

x

n

x

n

−

=









Contoh : Hitunglah peluang distribusi binomial untuk p=¾ , x=2, n=4

Jawab : P(X=2) = 2 2

4

1

4

3

2

4

)

4

3

,

4

;

2

(

_































=

b

=

128

27

4

3

.

!

2

!

2

!

4

4 2

=

=

0,21

Jadi peluang kita mendapatkan 2 item sukses dari 4 item yang masing-masing memiliki peluang sukses ¾, adalah 0.21

Contoh : Misalnya kita melantunkan 10 dadu sebanyak satu kali, berapa peluangnya akan muncul tepat 8 kali munculnya sisi mata dadu 6?

Jawab : Diketahui p=1/6, n=10, x=8 P(X=8) = 2 8

6

5

6

1

8

10

6

1

,

10

;

8

_































=













b

₀

_,

₀₀₀₀₁₅

6

5

6

1

45

2 8

=

























=

Contoh : Sebuah mesin produksi menghasilkan suatu produk dengan peluang menghasilkan produk cacat adalah 15%. Diambil secara acak dari produk mesin tersebut sebanyak 30 buah untuk diselidiki. Berapa peluang dari produk yang diambil itu akan terdapat :

a. Semuanya bagus (tidak cacat) b. Satu rusak

Jawab :

a. Diketahui q=0,15 maka p=0,85, n=30 dan x=30. Sehingga : P(X=30)=

(

)

(

0

,

85

) (

0

,

15

)

0

,

0076

30

30

85

,

0

;

30

;

30

30 0

=









=

b

Jadi peluang semua produk yang diambil sebanyak 30 bagus semua (tidak ada yang cacat) adalah 0,0076

b. Diketahui q=0,15, p=0,85, n=30 dan x=29. Sehingga :

P(X=29)=

(

)

(

0

,

85

) (

0

,

15

)

0

,

0404

29

30

85

,

0

;

29

;

30

29 1

=









=

b

Jadi peluang dari produk yang diambil sebanyak 30 ternyata hanya 1 yang rusak adalah 0,0404.

c. Diketahui p=0,85, n=30 dan x=2 . Sehingga :

P(X=2)=

(

)

(

0

,

85

) (

0

,

15

)

0

2

30

85

,

0

;

2

;

30

2 28

=









=

b

Jadi peluang dari produk yang diambil sebanyak 30 ternyata hanya 2 yang rusak adalah 0.

Contoh :

Setelah diadakan penelitian terhadap suatu mesin fotocopy, maka diketahui bahwa pada setiap 1450 lembar hasil fotocopy akan terjadi kerusakan sebanyak 145 lembar. Apabila dilakukan fotocopy sebanyak 5 lembar, berapakah peluang untuk menemukan 0, 1, 2, ... , 5 lembar kerusakan ?

Jawab :

Misalkan X adalah kejadian menemukan lembar kertas tidak rusak • n=5, x=5 q=1/10

(

)

( ) ( )

0

,

9

0

,

1

0

,

59049

5

5

9

,

0

;

5

;

5

5 0

=









=

b

• n=5, x=4 q=1/10

(

)

( ) ( )

0

,

9

0

,

1

0

,

32805

4

5

9

,

0

;

5

;

4

=

_



_



4 1

=

b

• n=5, x=3, q=1/10

(

)

( ) ( )

0

,

9

0

,

1

0

,

0729

3

5

9

,

0

;

5

;

3

3 2

=









=

b

• n=5, x=2, q=1/10

(

)

( ) ( )

0

,

9

0

,

1

0

,

0081

2

5

9

,

0

;

5

;

2

2 3

=









=

b

• n=5, x=1, q=1/10

(

)

( ) ( )

0

,

9

0

,

1

0

,

00045

1

5

9

,

0

;

5

;

1

1 4

=









=

b

• n=5, x=0, q=1/10

(

)

( ) ( )

0

,

9

0

,

1

0

,

00001

0

5

9

,

0

;

5

;

0

0 5

=









=

b

Contoh :

Seorang penderita penyakit darah yang jarang terjadi memiliki peluang 0,4 untuk sembuh. Bila diketahui ada 15 orang yang telah mengidap penyakit tersebut, berapakah peluang :

a. Paling sedikit 10 akan sembuh b. Antara 3 sampai 8 yang sembuh c. Tepat 5 akan sembuh

Jawab :

a. Misalnya X menunjukkan banyaknya yang sembuh, maka peluang paling sedikit 10 akan sembuh adalah : P(X=10)+P(X=11)+ P(X=12)+ P(X=13)+ P(X=14)+ P(X=15) =P(X ≥10)

)

10

(

1

)

10

(

X

_≥

₌

₋

P

X

_≤

P

∑

=

−

=

9 0

)

4

,

0

;

15

;

(

1

x

x

b

= 1 – 0,9662 = 0,0338

Jadi peluang paling sedikit 10 dari 15 orang penderita penyakit tersebut akan sembuh adalah 0,00338

b.

∑

∑

∑

= = = − = = ≤ ≤ 8 3 8 0 2 0 ) 4 , 0 ; 15 ; ( ) 4 , 0 ; 15 ; ( ) 4 , 0 ; 15 ; ( ) 8 3 ( x x x x b x b x b X P = 0,9050 – 0,0271 = 0,8779

Jadi peluang antara 3 sampai 8 dari 15 penderita penyakit tersebut akan sembuh adalah 0,8779

c.

∑

∑

= =

−

=

=

=

4 0 5 0

)

4

,

0

;

15

;

(

)

4

,

0

;

15

;

(

)

4

,

0

;

15

;

(

)

5

(

x x

x

b

x

b

x

b

X

P

=0,4032 – 0,2173 = 0,1859

Jadi peluang tepat 5 orang dari 15 penderita penyakit tersebut akan sembuh adalah 0,1859

PR: Untuk mengelabui petugas pabean, seorang pelancong menaruh enam tablet narkotik dalam sebuah botol yang berisi sembilan vitamin yang sama bentuk dan warnanya. Bila petugas pabean memeriksa tiga tablet secara acak untuk dianalisis, berapakah peluang pelancong tersebut akan ditahan karena membawa narkotik?

TUGAS :

KERJAKAN SOAL-SOAL BAB II NOMOR 24, 26, 27, 30, 31, DAN 32

SAMPLING

Populasi :

Adalah kumpulan keseluruhan obyek yang diteliti.

Sampel :

Adalah sebagian dari populasi yang diambil dengan menggunakan cara-cara tertentu.

Berdasarkan banyak obyek yang ada di dalam populasi, populasi dapat dibedakan menjadi :

1. Populasi tak hingga

Yaitu populasi yang memiliki tak terhingga/tak terbatas banyak obyek. Sebagai contoh :

a. Volume air hujan b. Volume udara/gas c. Kepuasan konsumen

d. Prestasi atau kinerja karyawan 2. Populasi terhingga /terbatas

Yaitu populasi yang memiliki terhingga/terbatas banyaknya obyek. Sebagai contoh :

a. Banyaknya perusahaan di suatu daerah b. Banyaknya karyawan di suatu perusahaan

c. Banyak pesanan sebuah perusahaan selama 10 tahun terakhir

d. Banyaknya produksi dalam satu bulan e. dll

Statistika bertujuan untuk mengambil kesimpulan dari populasi. Untuk itu diperlukan data-data yang lengkap mengenai populasi tersebut. Cara mengambil data dari populasi antara lain :

1. Sensus ; yaitu pengambilan data populasi dari keseluruhan obyek yang ada pada populasi tersebut. 2. Sampling ; yaitu pengambilan sebagian data populasi

Pengambilan data secara sampling lebih banyak dilakukan dibandingkan dengan pengambilan data secara sensus, karena berbagai alasan seperti berikut ini :

1. Faktor biaya dan faktor ekonomis

Data yang diambil secara sampling jumlahnya kurang dari data yang diambil secara sensus sehingga lebih hemat 2. Faktor ketelitian dalam penelitian

Karena pengambilan data secara sensus melibatkan obyek yang lebih banyak, sehingga memungkinkan timbul lebih banyak kesalahan dalam pencatatan, pendokumentasian dan pengolahan.

3. Faktor penghematan waktu

Pengambilan data secara sampel yang lebih sedikit, jelas akan mempercepat proses statistik.

4. Percobaan yang sifatnya merusak

Dalam beberapa contoh kasus penelitian, pengambilan data dilakukan dengan cara merusak obyek yang diteliti. Sehingga lebih banyak obyek yang diteliti akan mengakibatkan lebih banyak obyek yang dirusak.

5. Populasi tak terhingga

Pada populasi tak terhingga tidak mungkin dilakukan pengambilan data secara sensus.

Beberapa teknik sampling

Dalam pengambilan sampel terdapat dua cara yang dapat dilakukan, yaitu :

a. Pengambilan data dengan cara pengembalian (with

replacement)

b. Pengambilan data dengan cara tanpa pengembalian (without replacement)

Terdapat beberapa untuk melakukan pengambilan data : a. Sampling seadanya

b. Sampling dengan pertimbangan

c. Sampling peluang atau sampling acak

• Sampling acak dari populasi tak hingga

Kesalahan pada pengambilan data

Pengambilan data secara statistik harus bebas dari kesalahan dan keragu-raguan karena data-data tersebut akan menjadi bahan pengambilan kesimpulan yang harus bisa dipertanggungjawabkan. Beberapa kesalahan dalam pengambilan data statistik antara lain :

1. Kesalahan sampling :

• Kesalahan mengambil sampel/responden

• Jumlah sampel kurang 2. Kesalahan non-sampling:

• Ketidakjelasan populasi

• Pertanyaan yang tidak tepat, membingungkan, atau jawaban yang tidak lengkap.

DISTRIBUSI SAMPLING

Distribusi yang telah dipelajari yaitu distribusi Binomial dan distribusi Normal adalah distribusi teoritis yang dikembangkan dari penurunan rumus matematika.

Sedangkan distribusi yang langsung diperoleh dari data aktual pada populasi yang akan diteliti adalah distribusi sampling.

Jika informasi yang dikumpulkan dari data aktual itu adalah berupa rata-rata hitung untuk semua sampel yang mungkin dapat diambil dari sebuah populasi, maka diperoleh distribusi sampling rata-rata hitung.

Jika informasi yang dikumpulkan dari data aktual itu adalah berupa semua simpangan baku (standar deviasi) untuk semua sampel yang mungkin dapat diambil dari sebuah populasi akan diperoleh distribusi sampling simpangan baku.

Parameter Populasi Statistik Sampel Rata-rata (mean)

µ

_x

Simpangan baku (standar deviasi)

σ

s

Cara pengambilan sampel

Untuk melakukan pengambilan data sampel dari populasi yang berukuran N, dapat digunakan cara permutasi atau kombinasi data sehingga diperoleh kelompok-kelompok data sampel yang masing-masing berukuran n.

Sebagai contoh suatu populasi memiliki lima anggota yaitu A,B,C,D dan E, maka kemungkinan pengambilan sampel adalah :

Sampel terdiri dari 2 obyek : 1. A,B 2. A,C 3. A,D 4. A,E 5. B,C 6. B,D 7. B,E 8. C,D 9. C,E 10. D,E

Sampel terdiri dari 3 obyek : 1. A,B,C 2. A,B,D 3. A,B,E 4. A,C,D 5. A,C,E 6. A,D,E 7. B,C,D 8. B,C,E 9. B,D,E 10.C,D,E

Distribusi sampling rata-rata

Jika terdapat sebuah populasi yang terhingga berukuran N, memiliki parameter rata-rata

µ

dan simpangan baku

σ

, dilakukan pengambilan sampel secara acak yang masing-masing berukuran

n

sehingga memiliki kumpulan rata-rata hitung

x

. Dalam hal ini kita telah membentuk distribusi sampling rata-rata

x

.

PopulaPsi

(rata-rata µ)

Jadi distribusi sampling rata-rata hitung

x

adalah kumpulan dari bilangan-bilangan yang masing-masing merupakan rata-rata hitung.

Hubungan antara rata-rata hitung sampel dan rata-rata hitung populasi adalah :

Sampel 1 X₁, X₂, ……… X _n Sampel 2 X₁, X₂, ……… X _n Sampel 3 X₁, X₂, ……… X _n Rata-rata sampel X₁ Rata-rata sampel X₂ Rata-rata sampel X₃

Sekelompok rata-rata sampel

µ

µ

_x

=

Artinya : rata-rata untuk distribusi sampling rata-rata sama dengan rata-rata populasinya.

Hubungan antara simpangan baku sampel ddan simpangan baku populasi : 1 − − = N n N n X

σ

σ

, untuk sampel kecil atau terbatas :

n

X

σ

σ = , untuk sampel besar atau tidak terbatas

Kesimpulan :

Jika dari sebuah populasi yang memiliki rata-rata

µ

dan simpangan baku

σ

, diambil sampel acak yang masing-masing berukuran

n

maka distribusi sampling rata-rata akan mempunyai rata-rata

µ

dan simpangan baku

1

−

−

=

N

n

N

n

X X

σ

σ

(jika sampel kecil) atau

n

X X

σ

σ

=

(jika sampel besar).

Kita dapat menentukan berapa ukuran sampel paling sedikit apabila kita mengharapkan perbedaan nilai ratra-rata sampel yang satu dan yang lainnya ditentukan. Jika dikehendaki selisih rata-rata setiap dua sampel tidak lebih dari

d

, maka berlaku hubungan :

d

n

≤

σ

Sebagai contoh : kita menginginkan perbedaan nilai rata-rata setiap dua sampel sebesar

d

=0,5 maka dengan

σ

=6 diperoleh :

5

,

0

6

_≤

n

atau

n

≥

144

Ternyata paling sedikit harus diambil 144 data untuk setiap sampel agar perbedaan nilai rata-rata setiap dua sampel sebesar

d

=0,5.

Contoh :

Jika sebuah sampel acak sebesar n=10 dipilih dari populasi normal sebesar N=40 dengan rata-rata µ = 5,5 dan standar deviasi σ =2,9155 berapakah rata-rata dan standar deviasi distribusi sampelnya?

5

,

5

=

X

µ

dan

0

,

80861421

1

40

10

40

10

9155

,

2

=

−

−

=

X

σ

Contoh :

Diketahui bahwa distribusi kecepatan maksimal dari 1.000 mobil Mazda memiliki rata-rata 148,2km/jam dengan standar deviasi sebesar 5,4km/jam. Jika sebuah sampel yang terdiri dari 100 unit mobil Mazda dipilih secara acak dari populasi diatas berapakah peluang kecepatan rata-rata dari 100 mobil tersebut lebih besar dari 149km/jam?

Jawab :

Dalam hal ini sampel dianggap terbatas dengan N=1000, dan n=100, rata-rata µ=148,2 dan standar deviasi σ =5,4. Maka kita peroleh : µ_X =148,2

dan 0,5125 1 1000 100 1000 100 4 , 5 = − − = X σ 56097561 , 1 5125 , 0 2 , 148 149− ₌ = Z Jadi P(X>149)=P(Z>1,56)=0,0594 atau 5,94%=6% Contoh :

Pelat baja yang diproduksi oleh sebuah pabrik memiliki daya regang rata-rata 500kg dan standar deviasi sebesar 20 kg. Jika sampel acak yang terdiri dari 100 pelat sedemikian dipilih dari populasi yang terdiri dari 100.000 pelat, berapakah rata-rata sampelnya akan kurang dari 496 kg?

Jawab :

Dalam hal ini N dianggap tidak terbatas dan n=100, rata-rata µ=500 dan standar deviasi σ =20.

Maka kita peroleh : µ_X =500

dan

2

100

20

=

=

X

σ

2

2

500

496

−

₌

₋

=

Z

P(X<496)=P(Z<-2)=0,0228=2,28%

Suatu mesin minuman diatur sedemikian rupa sehingga banyaknya minuman yang dikeluarkan secara hampiran berdistribusi normal dengan rata-rata 207ml dan simpangan baku 15ml. Secara berkala, mesin diperiksa dengan mengambil sampel sembilan buah dan dihitung rata isinya. Bila rata-rata sampel jatuh pada selang 177 s.d 237 ml maka mesin dianggap bekerja dengan baik. Jika tidak mesin harus di atur lagi. Tindakan apa yang seharusnya diambil bila rata-rata sampel 219ml ?

Dalil Limit Pusat

Apabila kita melakukan pemilihan sampel yang tidak berdistribusi normal, bagaimana penghitungannya?

Secara matematis distribusi rata-rata sampel akan mendekati distribusi normal jika besarnya sampel n bertambah tanpa batas, hal ini didasarkan oleh suatu dalil matematis yang sangat terkenal dan sangat berguna dalam analisis statistik :

Dalil limit pusat : Jika sampel acak dipilih dari populasi

dengan rata-rata µX dan standar deviasi σX dan jika besarnya

sampel n berukuran besar maka rata-rata sampelnya akan memiliki distribusi pemilihan sampel mendekati distribusi normal dengan rata-rata µ =X µX dan standar deviasi

n

X X

σ

σ = .

Jika populasinya terbatas maka rata-rata sampelnya akan memiliki distribusi pemilihan sampel dengan rata-rata

X X µ

µ = dan standar deviasi

1 − − = N n N n X X σ σ , jika populasinya

Distribusi Sampling Perbandingan (Proporsi)

Misalkan kita memiliki sebuah populasi berukuran N dengan perbandingan atau proporsi populasi untuk peristiwa tertentu sama dengan

p

dan simpangan baku p(1− p).

Dari populasi tersebut kita ambil sampel berukuran

n

. Dari setiap sampel yang diperoleh hitunglah perbandingan sampelnya untuk peristiwa yang menjadi perhatian kita, perbandingan dari sampel-sampel yang diperoleh pada umumnya akan berbeda-beda harganya. Kumpulan atau distribusi semua perbandingan sampel-sampel ini dinamakan Distribusi sampling perbandingan atau

Distribusi sampling perbandingan proporsi.

Rata-rata dan simpangan baku untuk distribusi sampling perbandingan masing-masing diberi simbol µp dan

p

σ . Bila dinyatakan dalam parameter populasi

p

adalah :

p p = µ n p p p ) 1 ( − =

σ , (jika sampel besar yaitu >5%

N n ) 1 ) 1 ( − − − = N n N n p p p

σ , (jika sampel kecil yaitu ≤5%

N n

)

Untuk menentukan peluang nilai perbandingan peristiwa yang dikehendaki dari sebuah sampel berukuran

n

terletak antara batas-batas tertentu, dapat berlaku dalil limit pusat asalkan ukuran sampel

n

cukup besar.

Jika ukuran sampel acak

n

cukup besar maka distribusi sampling perbandingan p = x/n ternyata mendekati distribusi normal. Distribusi normal yang didekati oleh distribusi sampling p = x/n ini mempunyai rata-rata

p

dan simpangan baku n p p p ) 1 ( − = σ atau 1 ) 1 ( − − − = N n N n p p p σ bergantung pada >5% N n atau ≤5% N n .

Selanjutnya untuk menentukan bagian-bagian luas dari lengkungan normal standar digunakan transformasi :

n p p p n x z ) 1 ( / − − =

(jika sampel besar yaitu >5%

N n ) atau 1 ) 1 ( / − − − − = N n N n p p p n x z

(jika sampel kecil yaitu ≤5%

N n

Dari kekeliruan baku perbandingan yaitu σp kita dapat

menentukan nilai minimum ukuran sampel

n

bila perbandingan tiap sampel yang diharapkan terjadi diketahui. Nilai

n

tersebut dihitung dari :

d n p p ≤ − ) 1 ( Contoh :

Dari suatu proses produksi semacam barang, ternyata 90% dari produksi tanpa cacat dan 10% lagi dalam keadaan cacat. Setiap hari kerja, selama proses berlangsung diambil sampel acak terdiri dari 100 barang.

Tentukan :

a. Rata-rata persentase barang yang rusak dan simpangan bakunya

b. Peluang barang rusak dari sebuah sampel berukuran 100 paling kecil 15%.

c. Berapa ukuran sampel paling sedikit agar jika kita mengambil sampel cukup banyak dengan ukuran tersebut, persentase kerusakannya diharapkan akan berbeda tidak lebih dari 2%.

Jawab :

Misalkan kita definsikan p=proporsi barang yang rusak. Dari soal diatas dapat diketahui p=0,1_, n=100, populasi dianggap tak hingga. a. µp = p =0,1 b. 0,03 100 ) 1 , 0 1 ( 1 , 0 ) 1 ( = − = − = n p p p σ P(X>15%) = 0,03 1,67 1 , 0 100 / 15 ) 1 ( / ₌ − ₌ − − = n p p p n x z

P(X>15%) =P(Z>1,67)=0,0475 jadi peluang akan memperoleh barang rusak paling sdkt 15% dari sampel berukuran 100 adalah 0,0475

Untuk menentukan n terkecil dengan p=0,1_, d =0,02

225 02 , 0 ) 1 , 0 1 ( 1 , 0 ) 1 ( ≥ ⇒ ≤ − ⇒ ≤ − _d n d n p p

Dalil Limit Pusat

Apabila kita melakukan pemilihan sampel yang tidak berdistribusi normal, bagaimana penghitungannya?

Secara matematis distribusi rata-rata sampel akan mendekati distribusi normal jika besarnya sampel n bertambah tanpa batas, hal ini didasarkan oleh suatu dalil matematis yang sangat terkenal dan sangat berguna dalam analisis statistik :

Dalil limit pusat : Jika sampel acak dipilih dari populasi

dengan rata-rata µX dan varians σ2dan jika besarnya sampel

n bertambah besar maka rata-rata sampelnya akan memiliki

distribusi pemilihan sampel mendekati distribusi normal dengan rata-rata µ =X µX dan standar deviasi _n

X X

σ

σ = _{. Jika}

populasinya terbatas maka rata-rata sampelnya akan memiliki distribusi pemilihan sampel dengan rata-rata

X X µ

µ = dan standar deviasi

1 − − = N n N n X X σ σ , jika populasinya

normal maka distribusi pemilihan sampelnya akan normal.

Distribusi Sampling Selisih Rata-Rata

Dalam penelitian kita sering ingin ketahui apakah antara rata-rata dua sample mempunyai perbedaan yang berarti ataukah kita bisa mengambil kesimpulan bahwa kedua sample itu berasal dari populasi dengan rata-rata sama.

Misalkan terdapat dua populasi yang berukuran cukup besar memiliki rata-rata

µ

₁dan

µ

₂ sedangkan simpangan bakunya

σ

₁ dan

σ

₂. Dari kedua populasi tersebut diambil sampel yang masing-masing berukuran

n

₁ dan

n

₂ . Dari setiap sampel yang diambil tentukanlah rata-ratanya, sehingga diperoleh x11,x12,,x1n1,x21,x22,,x2n2 Misalkan diperoleh

rata-rata untuk sampel dari populasi pertama

x

₁dan rata-rata untuk sampel dari populasi kedua adalah

x

₂. Kumpulan dari

x

₁dan

x

₂dinamakan dengan distribusi sampling selisih rata-rata. Bila distribusi ini dicari rata-ratanya diberi simbol

sr

µ

dan simpangan baku σsr, maka :

2 1 µ µ µsr = − 2 2 2 1 2 1 n n sr σ σ σ = +

Jika ukuran sample

n

₁ dan

n

₂ cukup besar maka distribusi sampling selisih rata-rata akan mendekati distribusi normal dengan rata-rata

µ

_sr dan simapngan baku

sr

σ

. Untuk membuatnya menjadi normal maka diperlukan transformasi :

(

) (

)

2 2 2 1 2 1 2 1 2 1 n n x x z σ σ µ µ + − − − = Contoh :

Misalkan sebuah pabrik memproduksi dua jenis lampu pijar A dan B masing-masing diperkirakan daya pakainya mencapai rata-rata 1.400 jam dan 1.200 jam, sedangkan simpangan bakunya 200 jam dan 100 jam. Jika dari tiap jenis diambil sampel acak masing-masing terdiri atas 125 lampu dan kemudian diuji, berapakah peluang lampu jenis A akan mempunyai rata-rata daya pakai paling sedikit 250 jam lebihnya dari rata-rata daya pakai lampu jenis B?

Jawab :

Misalkan xAdan xBadalah masing-masing rata-rata daya

pakai dari lampu-lampu yang berada dalam sampel-sampel yang diambil dari populasi A dan B. Maka yang dinyatakan adalah peluang (xA- xB) paling sedikit 250 jam. Jika

digunakan indeks A dan B yang sesuai maka diperoleh :

125 100 125 2002 2 2 2 2 1 2 1 _{+ = +} = n n sr σ σ σ = 20 jam Sehingga z 20 ) 200 . 1 400 . 1 ( 250− − = 2,5 20 200 250 = − = P(Z>2,5)= 0,621%

Besi baja yang diproduksi PT. A memiliki daya regang rata-rata 4.500kg dan simpangan baku 200kg. Sedangkan besi baja yang diproduksi PT. B memiliki daya regang rata-rata 4.000kg dan simpangan baku 300kg. Andaikan sampel acak sebesar 50 dipilih dari besi baja hasil produksi PT.A dan sampel acak sebesar 100 dipilih dari besi baja hasil produksi PT. B. Berapa peluang daya regang rata-rata besi baja perusahaan PT.A akan lebih besar 600kg dari pada daya regang rata-rata besi baja PT.B ?

Jawab : 500 000 . 4 500 . 4 2 1− = − = =µ µ µsr kg n n sr 41,23 100 000 . 90 50 000 . 40 2 2 2 1 2 1 _{+ = + =} = σ σ σ

.. 425 , 2 23 , 41 500 600− ₌ = Z P(Z>2,425)=0,75%

Distribusi Sampling Selisih Perbandingan

Jika terdapat dua populasi, populasi pertama memiliki perbandingan p1dan simpangan baku p1(1−p1)dan populasi

kedua memiliki perbandingan p2 dan simpangan baku

) 1 ( ₂

2 p

p − . Kemudian diam

bil semua sampel acak yang masing-masing berukuran

1

n _dan n_{2. Kemudian dibentuk semua selisih perbandingan}

sampel-sampelnya :     − 2 2 1 1 n x n x

maka akan diperoleh distribusi sampling selisih perbandingan : 2 1 p p sp = − µ 2 2 1 1 1 1(1 ) (1 ) n p p n p p sp = − + − σ

Jika perbandingan dari kedua populasi tidak diketahui tetapi dianggap sama, jadi p1 = p2 = p maka diambil perbandingan

gabungan : 2 1 2 1 n n x x p + +

= _{sehingga diperoleh simpangan bakunya :}

    + − = 2 1 1 1 ) 1 ( n n p p sp σ

Jika sampel berukuran besar maka distribusi selisih perbandingan inipun akan mendekati distribusi normal. Angka standar yang digunakan untuk membuatnya menjadi normal standar adalah :

(

)

2 2 1 1 1 1 2 1 2 2 1 1 ) 1 ( ) 1 ( n p p n p p p p n x n x z − + − − −     ₋ = Jika p1= p2 = p :     + −     ₋ = 2 1 2 2 1 1 1 1 ) 1 ( n n p p n x n x z

Contoh :

Ada semacam barang yang dihasilkan oleh dua pengusaha A dan B. Barang yang dihasilkan oleh A biasa terjadi kerusakan 5% sedangkan barang yang dihasilkan B terjadi kerusakan 4%. Dari barang-barang yang dihasilkan kedua pengusaha ini diambil sampel masing-masing 100 barang. Berapakah peluang selisih perbandingan kerusakan barang yang dihasilkan oleh A terhadap kerusakan barang yang dihasilkan oleh B akan berbeda dalam interval 0,5% ? (halaman 103, buku Sudjana)

(

)

_{0,1706 0,43227} 029309 , 0 % 05 , 0 100 %) 4 1 %( 4 100 %) 5 1 %( 5 % 4 % 5 % 5 , 0 ₌ − _{=− =} − + − − − = z

PENDUGAAN SECARA STATISTIK DAN PENDUGAAN PARAMETER

• Pada umumnya kita tidak melakukan observasi atau pengamatan yang menyeluruh meliputi seluruh unsur populasi, kita tidak akan tahu dengan tepat nilai-nilai parameter rata-rata populasi

µ

_X dan simpangan baku

X

σ

dari distribusi sampel yang kita pilih.

• Persoalan yang penting adalah menentukan sampel yang harus kita gunakan untuk menduga kuantitas populasi yang tidak diketahui tersebut. Kuantitas sampel yang kita pergunakan untuk pengujian bagi tujuan sedemikian itu dianggap sebagai penduga (estimator). Jadi fungsi nilai sampel yang digunakan untuk menduga parameter tertentu dinamakan penduga parameter yang bersangkutan. Sedangkan nilai-nilai yang dinyatakan dengan angka dan yang kita peroleh dengan jalan mengevaluasi penduga di atas dinamakan dugaan secara statistik (statistical

estimate). Misalnya rata-rata sampel X merupakan

penduga bagi rata-rata populasi

µ

_X , jika rata-rata sampel adalah 10 maka kita katakan bahwa 10 merupakan dugaan kita secara statistik tentang parameter

µ

_X .

• Dalam pemilihan secara alternatif terhadap berbagai kemungkinan penduga yang dapat dianggap sebagai penduga parameter yang paling baik, kita perlu meneliti ciri-ciri dari berbagai distribusi pemilihan sampel khususnya rata-rata dan variansi.

Ciri-ciri penduga yang baik : 1. Tidak bias (unbiased)

2. Efisien 3. Konsisten

Pendugaan parameter distribusi normal

Misalkan X1,X2,X3,,Xn menyatakan unsur-unsur dari suatu

sampel acak sebesar n yang dipilih dari suatu populasi normal dengan rata-rata dan variansi yang tidak diketahui.

• Penduga rata-rata populasi yang paling baik adalah rata-rata sampel yang dirumuskan sebagai :

∑

= = n i i X n X 1 1 . Rata-rata sampel ini bersifat tidak bias, efisien, dan konsisten.

• Pendugaan variansi populasi

σ

2_X dapat dilakukan dengan variansi sampel yang dirumuskan :

∑

= − − = n n i X X n s 1 2 2 _{( )} 1 1 . Pendugaan interval

• Jika kita menginginkan suatu pengukuran yang obyektif tentang derajat kepercayaan kita terhadap kepastian dugaan, maka sebaiknya kita menggunakan pendugaan interval (interval estimation).

• Dengan menggunakan pendugaan interval kita dapat menyatakan berapa besar kepercayaan kita bahwa interval di atas betul-betul mencakup parameter yang kita duga.

• Pendugaan interval dapat dirumuskan :

st st parameter st Z

Z

st − _α/2σ < < + _α/2σ

st = statistik sampel atau penduga

2 /

α

Z _{= standar deviasi statistik sampel}

st

σ _{= koefisien yang sesuai dengan interval keyakinan yang}

digunakan

Pendugaan interval sampel besar :

Jika kita menggunakan interval keyakinan 95% dengan

σ

_X sudah diketahui maka interval keyakinannya dapat diberikan sebagai : X X X

X

Z

Z

X

−

_0,025

σ

<

µ

<

+

_0,025

σ

n X n X X X X µ σ σ _1,96 96 , 1 < < + −

Untuk menggambarkan luas dugaan itu secara peluang, interval keyakinan

µ

_X dapat dinyatakan sbb :

(

X −Z_0,025σ_X <µ_X < X +Z_0,025σ_X

)

=1−α P 95 , 0 96 , 1 96 , 1 =      _{− < < +} n X n X P X X X µ σ σ • Statistik n

zα/2 σ disebut dengan ukuran kekeliruan dari

penaksiran parameter rata-rata populasi

µ

_X yang ditaksir berdasarkan X .

• Untuk menentukan banyaknya minimum sampel yang harus diambil agar memenuhi persamaan diatas dapat digunakan rumus : 2 2 / . _      ≥ k z

n α α _{dengan k =batas kekeliruan}

yang diinginkan.

Contoh :

Sebuah biro pariwisata di Jakarta mengadakan suatu penelitian tentang kepariwisataan di Indonesia dan ingin memperkirakan pengeluaran rata-rata para wisatawan asing per kunjungannya di Indonesia. Guna keperluan di atas dipilih sampel acak sebanyak 100 wisatawan asing untuk diwawancarai. Hasil wawancara dapat diketahui bahwa rata-rata pengeluaran per kunjungannya adalah $800 per wisatawan. Jika standar deviasi pengeluaran semua wisatawan dianggap konstan sebesar $120, maka buatlah interval keyakinan sebesar 95% guna menduga rata-rata pengeluaran para wisatawan per kunjungannya di Indonesia Jawab : n = 100, X =$800, σX=$120, α =0,05, 1−α =0,95, Z0,025 =1,96 Sehingga $12 100 120 = = X σ

(

800−1,96(12)< _X <800+1,96(12)

)

=0,95 P µ

(

776,48<µX <823,53

)

=0,95

Jadi rata-rata pengeluaran para wisatawan per orang per kunjungan dalam selang kepercayaan 95% berkisar antara $776,48 hingga $823,52.

Contoh :

Sebuah rumah makan ingin menduga rata-rata pengeluaran para konsumennya untuk makan siang yang dijual oleh rumah makan itu. Sebuah sampel acak dipilih dari populasi yang dianggap tidak terhingga. Dari ketiga puluh enam konsumen, diketahui bahwa rata-rata pengeluarannya adalah Rp.12.000,-. Andaikan standar deviasi dianggap konstan sebesar Rp.2.400,- buatlah interval keyakinan sebesar 95% untuk menduga rata-rata pengeluaran seluruh konsumen. Jawab : n = 36, X =$Rp.12.000, σX =$2.400, α=0,05, 1−α =0,95, 96 , 1 025 , 0 = Z Sehingga 400 36 2400 = = X σ dan P

(

12000−1,96(400)<µ_X <12000+1,96(400)

)

=0,95

(

11216<µX <12784

)

=0,95

Jadi dapat diduga dengan keyakinan 95% bahwa pengeluaran konsumen di rumah makan tersebut sekitar Rp.11.216 dan Rp.12.784.

Pendugaan parameter populasi kecil/terbatas.

Pada bahasan sebelumnya telah diketahui bahwa untuk sampel yang terbatas rata-rata standar deviasi dari sampel adalah 1 − − = N n N n X X

σ

σ

. N=banyaknya populasi n=banyaknya sampel

Dengan keyakinan sebesar 95% dan σX diketahui maka

interval keyakinan

µ

_X untuk sampel terbatas adalah :

95 , 0 1 96 , 1 1 96 , 1 =     − − + < < − − − N n N n X N n N n X P X X X _µ σ σ Contoh :

Sampel acak sebesar n=64 dan X =0,1165dipilih dari populasi yang terbatas sebesar N=300 dan diketahui σX =0,012, maka pendugaan secara parameter

µ

_X dengan interval keyakinan 95,45% adalah sebagai berikut :

00134 , 0 299 236 8 012 , 0 1 300 64 300 8 012 , 0 = = − − = X σ

(

0,1165−2(0,00134)< X <0,1165+2(0,00134)

)

=0,9545 P µ

(

0,11382< X <0,11918

)

=0,9545 P µ

Pendugaan parameter

µ

_X , dengan

σ

_X tidak diketahui

Apabila taksiran dilakukan berdasarkan pada sampel yang dengan

µ

_X dan σX tidak diketahui, penggunaan distribusi

normal akan mengakibatkan kekeliruan yang cukup besar. Oleh karena itu digunakan pendekatan distribusi

t

(atau distribusi student). Secara umum pendugaan parameter

µ

_X jika

σ

_X tidak diketahui adalah dengan sampel tidak terbatas adalah sebagai berikut :

α

µ

_α α



=

−











₋

_<

_<

₊

₁

) . , 2 / ( ) . , 2 / (

n

s

t

X

n

s

t

X

P

_{d f X d f} d.f. = derajat kebebasan = n-1

pendugaan parameter

µ

_X jika

σ

_X tidak diketahui dengan sampel terbatas adalah sebagai berikut :

α

µ

_α α



=

−







−

−

+

<

<

−

−

−

1

1

1

( /2, . ) ) . , 2 / (

N

n

N

n

s

t

X

N

n

N

n

s

t

X

P

_{d f X d f} Contoh :

Di suatu pabrik telah diukur 16 buah kayu untuk dasar penaksiran panjang rata-rata tekstil. Dari 16 kayu yang diukur tadi ternyata rata-rata panjangnya 54,5m dan simpangan bakunya 0,8m. Apabila sampel dianggap kecil, tentukan interval kepercayaan panjang rata-rata yang sebenarnya untuk setiap kayu yang dihasilkan dengan α =5% .

Jawab :

Diketahui n_=16, x =54,5m dan s=0,8_m

Dengan α =5% dan derajat kebebasan n_{-1=16-1=15 maka}

dari tabel distribusi t diperoleh t=2,1315.

%

95

16

8

,

0

1315

,

2

5

,

54

16

8

,

0

1315

,

2

5

,

54



=











₋

_<

_<

₊

X

P

µ

% 95 ) 9 , 54 1 , 54 ( < _X < = P

µ

Penaksiran Perbandingan (Proporsi)

• Terdapat dua cara untuk menaksir perbandingan

p

, yaitu taksiran titik dan taksiran interval. Sebagai penaksir

p

diambil perbandingan dari sampel. Jika untuk sebuah sampel yang

berukuran n terdapat peristiwa

_A

sebanyak

x

buah

) 0

( _≤ x _≤n dan dalam populasinya terdapat perbandingan

peristiwa itu sama dengan

p

(

p

belum diketahui), maka titik

taksiran p untuk peristiwan A adalah

p

=

x

/

n

.

• Kita ketahui bahwa jika terdapat sebuah populasi berukuran N

dengan perbandingan populasi untuk peristiwa tertentu sama

dengan

p

memiliki simpangan baku

n p

p(1− ) _{. Dari populasi}

tersebut kita ambil sampel berukuran

n

.

• Jika ukuran sampel acak

n

cukup besar maka distribusi

sampling perbandingan p = x/n ternyata mendekati distribusi

normal. Penaksir interval dari sampling perbandingan dirumuskan sebagai berikut :

α α α  = −    ₋ + < < − − (1 ) (1 ) 1 2 2 n p p Z p p n p p Z p P α α α = −             − + < < − − 1 ) 1 ( ) 1 ( 2 2 n n x n x Z n x p n n x n x Z n x P

• Rata-rata dan simpangan baku untuk distribusi sampling perbandingan: p p = µ n p p p ) 1 ( − =

σ , (jika sampel besar yaitu >5%

N n ) 1 ) 1 ( − − − = N n N n p p p

σ , (jika sampel kecil yaitu ≤5%

N n

)

• Selanjutnya untuk menentukan bagian-bagian luas dari

lengkungan normal standar digunakan transformasi : Contoh :

Dinas kesehatan kota ingin sekali meneliti persentase penduduk kota dewasa yang merokok paling tidak satu bungkus sehari. Sebuah sampel acak sebesar n=300 dipilih dari populasi yang terdiri dari penduduk kota yang telah dewasa dan ternyata 36 orang merokok paling sedikit satu bungkus sehari. Buatlah

interval keyakinan sebesar 95% guna menduga proporsi penduduk kota dewasa yang merokok paling sedikit satu bungkus perharinya. Jawab : p=X/n=36/300=12 % 5 1 300 ) 12 , 0 1 ( 12 , 0 12 , 0 300 ) 12 , 0 1 ( 12 , 0 12 , 0 2 % 5 2 % 5 = −     ₋ + < < − −Z p Z P % 95 300 ) 12 , 0 1 ( 12 , 0 96 , 1 12 , 0 300 ) 12 , 0 1 ( 12 , 0 96 , 1 12 , 0 =     ₋ + < < − − p P

(

0

,

12

−

0

,

037

<

p

<

0

,

12

+

0

,

037

)

=

95

%

P

Jadi jika kita gunakan interval keyakinan 95% maka dugaan bahwa proporsi penduduk dewasa yang merokok paling sedikit satu bungkus perharinya akan terletak antara 8,3% hingga 15,7%

• Kita dapat menentukan nilai minimum ukuran sampel

n

bila

perbandingan tiap sampel yang diharapkan terjadi diketahui.

Nilai

n

tersebut dihitung dari : d

n p p ≤ − ) 1 ( _.

PENGUJIAN HIPOTESIS

• Salah satu kegunaan dari ilmu statistik adalah sebagai alat untuk pengambilan kesimpulan atau keputusan mengenai suatu populasi. Pengambilan kesimpulan atau keputusan tersebut menggunakan sifat-sifat atau karakteristik sampel yang diambil dari populasi.

• Pengambilan keputusan dari suatu populasi tersebut hendaknya dilakukan cukup alasan dan dapat dipertanggungjawabkan secara ilmiah.

• Dalam usaha untuk memperoleh kesimpulan, biasanya didahului oleh adanya dugaan, atau pengandaian atau asumsi mengenai populasi yang bersangkutan. Pengandaian ini mungkin betul mungkin juga tidak betul, disebut dengan hipotesis statistik atau disingkat hipotesis. Hipotesis inilah yang akan diteliti kebenarannya dengan menggunakan karakteristik sampel yang diambil dari populasi. Sehingga sampailah kita pada kesimpulan menerima hipotesis (artinya hipotesisnya benar) atau tidak menerima hipotesis (artinya hipotesisnya salah).

• Apabila kita memiliki sebuah hipotesis mengenai sebuah populasi, maka kita akan selalu memiliki sebuah hipotesis alternatif yang berlawanan dengan hipotesis tadi. Hipotesis yang berlawanan tersebut disebut dengan hipotesis tandingan.

• Pada pengambilan kesimpulan dari suatu populasi, yaitu dengan cara menerima hipotesis atau menolak hipotesis tentu saja dapat terjadi pengambilan kesimpulan yang “benar” atau pengambilan keputusan yang “salah”. Berikut ini adalah berbagai kemungkinan yang dapat terjadi :

1. Jika hipotesis benar, dan kita menerima hipotesis tersebut. Maka pengambilan keputusan tersebut adalah langkah benar.

2. Jika hipotesis yang dibuat adalah salah, dan kita menolak hipotesis tersebut. Maka pengambila keputusan tersebut adalah langkah yang benar. 3. Jika hipotesis yang dibuat adalah benar, tetapi

berdasarkan penelitian yang dilakukan kita menolaknya. Maka pengambilan keputusan tersebut adalah langkah yang keliru. Kekeliruan tersebut disebut dengan kekeliruan jenis I atau kekeliruan

α

. Jadi kekeliruan

α

adalah kekeliruan yang terjadi waktu mengambil kesimpulan yang seharusnya diterima tetapi kita menolaknya.

4. Jika hipotesis yang dibuat adalah salah, tetapi berdasarkan penelitian yang dilakukan kita menerimanya. Maka pengambilan keputusan tersebut adalah langkah yang keliru. Kekeliruan tersebut disebut dengan kekeliruan jenis II atau kekeliruan beta. Jadi kekeliruan beta adalah kekeliruan yang terjadi pada waktu kita menolak sesuatu yang seharusnya diterima.

Kesimpulan Keadaan sebenarnya

Hipotesis benar Hipotesis salah Hipotesis diterima Kesimpulan benar Kekeliruan jenis II Hipotesis ditolak Kekeliruan jenis I Kesimpulan benar

• Jadi untuk melakukan pengujian hipotesis harus dilakukan dengan perencanaan sedemikian rupa sehingga kekeliruan-kekeliruan

α

dan

β

dapat ditekan hingga sekecil mungkin untuk menghindari kesalahan pengambilan keputusan.

• Besar kecilnya risiko membuat kekeliruan (

α

atau

β

) biasanya dinyatakan dalam bentuk peluang. Peluang melakukan kekeliruan jenis I (yaitu peluang peluang menolak hipotesis benar) dinamakan taraf signifikan atau taraf nyata atau taraf arti, peluang ini sering dinyatakan dengan

α

. Arti dari nilai

α

adalah kita merasa yakin sebesar (1-

α

)% bahwa kita telah membuat kesimpulan yang benar. Nilai

α

dapat ditentukan sebelum penelitian dilakukan.

• Salah satu tahap yang penting dalam prosedur pengujian hipotesis adalah menentukan kriteria menerima atau menolak hipotesis (yaitu menentukan nilai statistik sampel yang dianggap sebagai alasan dasar guna menerima atau menolak hipotesis). Nilai statistik demikian itu disebut dengan daerah kritis (critical region).

s Titik kritis

Daerah penerimaan H0

Daerah kritis

Salah satu tahap yang penting dalam prosedur pengujian hipotesis adalah menentukan kriteria menerima atau menolak H0 (menentukan nilai statistik sampel yang dianggap sebagai alasan dasar guna menerima atau menolak H0 di atas). Nilai statistik demikian itu disebut dengan daerah kritis (critical region).

• Langkah-langkah yang harus dipersiapkan dalam melakukan pengujian hipotesis adalah :

1. Merumuskan hipotesis dan hipotesis alternatif

Hipotesis statistik adalah suatu pernyataan atau dugaan mengenai satu atau dua populasi.

a. Hipotesis yang mengandung pengertian sama :

0

:

µ

=

µ

o

H

0 1:

µ

≠

µ

H

b. Hipotesis yang mengandung pengertian maksimum :

0

:

µ

≤

µ

o

H

0 1:

µ

>

µ

H

c. Hipotesis yang mengandung pengertian minimum :

0

:

µ

≥

µ

o

H

0 1:

µ

<

µ

H

2. Menentukan alat uji hipotesis

n

x

z

/

σ

µ

−

=

n

s

x

t

/

µ

−

=

Uji z digunakan apabila simpangan baku populasi (sigma) ketahui

3. Menentukan kriteria penerimaan atau penolakan hipotesis, termasuk didalamnya menentukan taraf signifikan

α

.

Taraf signifikansi dari pengujian hipotesis statistik adalah peluang dari kekeliruan jenis I, yaitu peluang menolak hipotesis nol yang benar.

4. Melakukan penarikan kesimpulan

Menguji rata-rata

Contoh 1 :

Dari pengalaman yang cukup meyakinkan ternyata pada umumnya masa pakai semacam lampu pijar sekitar 800 jam. Akhir-akhir ini timbul dugaan bahwa masa pakai lampu itu telah mengalami perubahan (belum diketahui apakah menjadi lebih baik atau menjadi lebih buruk). Untuk menentukan apakah memang kualitas telah berubah atau masih sama seperti yang lalu, pengusaha menguji sebanyak 50 buah lampu. Kelima puluh buah lampu tersebut dinyalakan terus menerus hingga mati kemudian untuk setiap lampu dicatat berapa lama bisa menyala, dan akhirnya ditentukan rata-ratanya. Andaikan diperoleh untuk kelima puluh buah lampu yang dicoba tadi rata-rata masa pakainya 792 jam dan simpangan baku untuk populasi lampu itu 60 jam. Apabila pengujian dugaan ini risiko α =5%, ambilah kesimpulan bahwa kualitas lampu tersebut masih tetap atau sudah berubah.

2

/

α

2

/

α

α

_α