Aljabar Himpunan Dan Fungsi

DIKTAT KULIAH - ANALISIS

ANALISIS REAL

(Real Analysis)

Siti Lailiyah, M.Si.

e-mail:siti.lailiyah@sunan-ampel.ac.id http://blog.sunan-ampel.ac.id/sitilailiyah

ALJABAR HIMPUNAN DAN FUNGSI

A. PENDAHULUAN

Sebelum mempelajari analisis real, diperlukan sekali konsep-konsep dasar dari aljabar himpunan dan fungsi. Dua konsep ini merupakan alat yang penting untuk belajar analisis, karena konsep himpunan dan fungsi tersebut akan digunakan dalam pembicaraan sistem bilangan real, barisan, limit fungsi, kontinuitas maupun pendiferensian.

Untuk selanjutnya, kita anggap sama kata “himpunan” dengan kata “klas”, ”koleksi”, atau ”keluarga”. Demikian juga dengan kata “fungsi” kita anggap sama dengan “pemetaan”. Untuk himpunan, kita akan membahas mengenai aljabar himpunan, operasi himpunan, hasil kali ganda dan beberapa sifat yang terkait dengan operasi himpunan. Dengan pengertian hasil kali ganda ini, akan dikembangkan pengertian fungsi. Fungsi akan dijelaskan melalui definisi yang tepat maupun grafik. Metode khusus yang disebut induksi matematika juga dibicarakan dalam bagian ini. Metode induksi matematika tersebut merupakan sifat dasar dari sistem bilangan asli.

B. URAIAN DAN CONTOH

Himpunan dapat dipandang sebagai koleksi (himpunan) obyek-obyek yang ditentukan oleh beberapa sifat khusus. Obyek-obyek yang terdapat dalam himpunan disebut anggota atau elemen dari himpunan tersebut. Himpunan juga dapat didefinisikan dengan mendaftar elemen-elemennya. Sedangkan fungsi atau pemetaan dapat dipandang sebagai himpunan khusus/spesial, yaitu hasil pengembangan dari pengertian hasil kali ganda dua himpunan. Lebih lanjut, definisi fungsi yang tepat serta tipt-tipe khusus dari fungsi akan dibahas dalam bagian ini.

1. Aljabar Himpunan

Jika A sebarang himpunan, dan x anggota A maka ditulis . Jika x bukan

anggota A, ditulis . Himpunan yang tidak mempunyai anggota disebut himpunan

kososng (empty set/null set), dinotasikan 0

A x∈ A

x∉

/ . Sekarang, jika A dan B himpunan sehingga

. Berakibat maka dikatakan bahwa A himpunan bagian B, dinotasikan

atau . Jika dan terdapat anggota B yang bukan anggota A, maka A

dikatakan himpunan bagian sejati dari B.

A

x∈ x∈B B

A⊆ B⊇ A A⊆B

Selanjutnya dua himpunan A dan b sama jika A dan B memuat elemen yang sama, ditulis A=B. Jadi, untuk membuktikan bahwa himpunan A dan B sama, maka harus ditunjukkan bahwa A⊆B dan B⊆A.

Sekarang kembali pada definisi himpunan. Pernyataan ”sifat khusus” pada definisi himpunan ternyata tidak mudah didefinisikan secara tepat, tetapi kita tidak perlu ragu menggunakannya. Jika P menyatakan sifat yang mempunyai arti dan kejelasan untuk koleksi elemen-elemen, maka di tulis

{

x:P(x)

}

untuk himpunan semua elemen x yang memenuhi sifat P. Namun, jika kita mengingkan kekhususan yang elemen-elemennya memenuhi sifat P, maka ditulis

{

x∈S:P(x)

}

, untuk himpunan semua elemen x yang memenuhi sifat P.

Pendefinisian Himpunan

Untuk mendefinisikan himpunan digunakan 4 cara, yaitu : 1. Mendaftarkan semua anggotanya.

Contoh:

- A = {a,e,i,o,u}

- B = {2,3,5,7,11,13,17,19}

2. Menyatakan sifat yang dimiliki anggotanya Contoh:

Perhatikan himpunan pada contoh 1 di atas dan bandingkan dengan pendefinisian di bawah ini

- A = Himpunan vokal dalam abjad latin

- B = Himpunan bilangan prima yang kurang dari 20

3. Menyatakan sifat dengan pola Contoh:

- P = {0,2,4,8,10,…,48} - Q = {1,3,5,7,9,11,13,15,…}

Awas dalam kasus: R = { 2,3,5,7,…,19}. Penulisan himpunan seperti ini bukan merupakan well-defined karena memunculkan ambigu, yaitu R dapat diartikan sebagai himpunan bilangan ganjil yang lebih besar dari 1 dan kurang dari 20. Sementara itu R dapat diartikan pula sebagai himpunan bilangan prima yang kurang dari 20. Oleh karena itu pendefinisian himpunan dengan menyatakan pola seperti ini harus sangat hati-hati agar tidak menimbulkan tafsiran lain.

4. Menggunakan notasi pembentuk himpunan Contoh:

- P = {x | x himpunan bilangan asli antara 7 dan 15}(Maksudnya P = {8,9,10,11,12,13,14})

- Q = { t | t bilangan asli} (Maksudnya Q = {1,2,3,4,5,6,7,8,9,10,…} -R = { s | s2-1=0, s bilangan real}(Maksudnya R = {-1,1})

Contoh lain:

a. Himpunan

{

x∈N:x2 −3x+2=0

}

. Karena penyelesaian dari persamaan kuadrat

adalah atau

0 2 3

2 − x+ =

x x=1 x=2 , maka himpunan ini dapat dinotasikan

dengan {1,2}. Dengan demikian himpunan dapat didefinisikan dengan mendaftar elemen-elemennya.

b. Kadang-kadang suatu rumus dapat digunakan untuk mendeskripsikan himpunan, misalnya himpunan semua bilangan asli genap dapat dinotasikan sebagai

{

2x:x∈N

}

atau

{

y∈N:y =2x,x∈N

}

2. Operasi Himpunan

Definisi 1.1.1

(i) Jika A dan B himpunan, maka irisan dari A dan B, dinotasikan A∩B adalah

himpunan dari semua anggota A dan B. Dengan kata lain:

{

x x A x B

}

B

A∩ := ; ∈ dan ∈

(ii) Jika A dan B himpunan maka gabungan A dan B, dinotasikan A∪B adalah

himpunan semua anggota A atau B. Dengan kata lain:

{

x x A x B

}

B

A∪ := ; ∈ atau ∈

(iii)Jika A dan B himpunan, A∩ B=0/ , maka A dan B dikatakan saling asing.

Teorema 1.1.1

Jika A, B dan C sebarang himpunan, maka:

a. A∩A= A, A∪A= A (sifat idempoten)

b. A∩B= B∩A, A∪B=B∪A (sifat komutatif)

c.

(

A∩B

)

∩C= A∩

(

B∩C

) (

, A∪B

)

∪C = A∪

(

B∪C

)

(sifat assosiatif) d. A∩

(

B∪C

) (

= A∩B

) (

∪ A∩C

)

, (sifat distribusi irisan terhadap gabungan)

)

, (sifat distribusi gabungan terhadap irisan)

(

B C

) (

A B

) (

A C A∪ ∩ = ∪ ∩ ∪

Bukti:

a. A∩A:=

{

x;x∈Adan x∈A

}

= ;

{

x x∈A

}

= A

Begitu juga untuk A∪A= A caranya analog. b. A∩B:=

{

x;x∈Adan x∈B

}

=

{

x;x∈Bdan x∈A

}

=B∩A

Pembuktian untuk c dan d ditinggalkan sebagai latihan

Catatan:

{

x x A j j n

}

A A A A= ₁∪ ₂ ∪_K∪ _n := : ∈ _j untuk suatu , =1,2,_K,

{

x x A j j n

}

A A A B= ₁∩ ₂ ∩_K∩ _n := : ∈ _j untuk semua , =1,2,_K, Definisi 1.1.2

Jika A dan B himpunan, maka komplemen dari B relatif terhadap A adalah himpunan

semua anggota A yang tidak menjadi anggota B, dan dinotasikan (dibaca ” A

minus B”). Kadang-kadang dinotasikan

B A \

B

A− atau A ~B atau C(B). Jadi A\B:=

{

x/x∈Adan x∉B

}

Dibawah ini akan diberikan sebuah teorema tentang operasi himpunan yang berkaitan dengan A \B dan pembuktiannya ditinggalkan sebagai latihan.

Teorema 1.1.2

Jika A, B, C sebarang himpunan, maka :

(

B C

) (

A B

) (

A C A\ ∪ = \ ∩ \

)

)

(

B C

) (

A B

) (

A C A\ ∩ = \ ∪ \

Hasil Kali Ganda (Cartesian Product)

Definisi 1.1.3

Jika A dan B dua himpunan tidak kosong, AxB hasil kali ganda (Cartesian Product) dari A dan B adalah himpunan dari semua pasangan terurut (a,b) dengan a∈A dan b∈B. (lihat Gambar 1.1) A AxB (a,b) a b B

Gambar 1.1 Hasil Kali Ganda AxB

Contoh 1.1.2

1) Misalkan A={1, 2, 3} dan B={4, 5} maka AxB adalah himpunan yang anggotanya adalah pasangan terurut (1,4), (1,5), (2,4), (2,5), (3,4), (3,5)

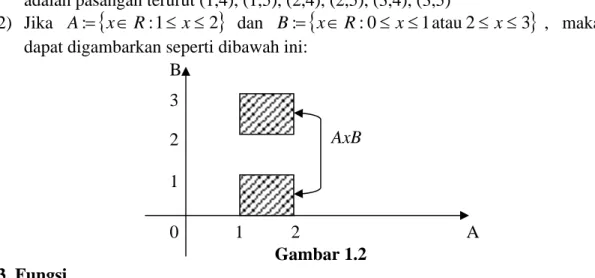
2) Jika A:=

{

x∈R:1≤x≤2

}

dan B:=

{

x∈R:0≤x≤1atau 2≤ x≤3

}

, maka AxB dapat digambarkan seperti dibawah ini:

Gambar 1.2 A B 1 AxB 3 2 0 2 1 3. Fungsi

Pada bagian ini akan dibahas pengertian fungsi atau pemeteaan dan tipe-tipe khusus dari fungsi. Para ahli matematika abad yang lampau, kata ”fungsi” diartikan untuk mendefinisikan rumus, seperti f

( )

x =x2 −6x+8 yang mengkaitkan setiap bilangan real x dengan bilangan real yang lain f

( )

x . Dalam perkembangannya, diberikan definisi

fungsi yang lebih umum, sehingga lebih jelas perbedaan fungsi itu sendiri dengan nilai dari fungsi tersebut. Perhatikan definisi berikut:

Definisi 1.1.4

Fungsi f dari himpunan A ke himpunan B adalah suatu aturan yang mengawankan setiap anggota a∈A dengan tunggal anggota B, dinotasikan f

( )

a .

Himpunan A disebut domain dari f dinotasikan D(f) dan B disebut target dari f. Range dari f, R(f), adalah himpunan f

( ) {

A = f(a)∈B:a∈A

}

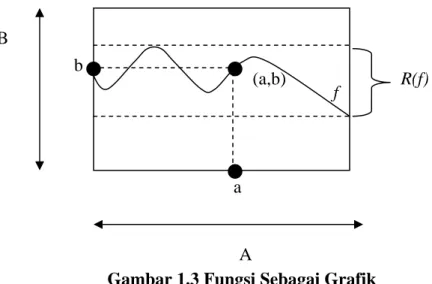
yang merupakan himpunan bagian dari B. Dibawah ini akan diberikan definisi fungsi sebagai himpunan khusus, yaitu dari perkembangan pengertian hasil kali ganda dua himpunan.

Definisi 1.1.5 (Fungsi Sebagai Grafik)

Misalkan A, B himpunan fungsi dari A ke B adalah himpunan f dari pasangan berurutan

dalam AxB sehingga untuk setiap a∈ terdapat dengan tunggal A , dengan

, artinya jika

( )

dan

B b∈

( )

a,b ∈ f a,b ∈ f

( )

a,b1∈ f maka b=b1.

( )

a,b ∈ f dapat ditulis b= f(a). (Lihat Gambar 1.3)

b a (a,b) f B R(f) A

Gambar 1.3 Fungsi Sebagai Grafik

Sekarang kita berikan fungsi dengan domain A dan range di dalam B.

Jika f fungsi dengan D(f) dan , didefinisikan fungsi baru dengan domain

oleh . Fungsi ini disebut fungsi yang dibatasi oleh f pada

himpunan (Restriction of f to the set ). Jadi

B A f : → ) ( 1 D f D ⊆ f₁ 1 D f₁(x):= f(x),∀x∈D₁ f₁ 1 D D₁ f₁(x):=

{

(a,b)∈ f,a∈D₁

}

atau

. Jika g fungsi dengan domain D(g) dan

1 1 f | D

f = D₂ ⊇D(g), maka sebarang fungsi

dengan domain sehingga

2

g D₂ g₂(x)=g(x),∀x∈D(g). Fungsi disebut perluasan

fungsi g pada himpunan (Extension of g to the set ).

2

g

2

Diberikan fungsi , maka bayangan (direct image) dari E terhadap fungsi f

adalah himpunan bagian dari b yang diberikan oleh

B A f : → ) (E f f(E):=

{

f(x):x∈E

}

. Jika B

H ⊂ , maka bayangan invers (invers image) dari H terhadap fungsi f adalah himpunan bagian dari A yang diberikan oleh f1(H) f−1(H):=

{

x∈A: f(x)∈H

}

.

Contoh 1.1.3:

Misalkan f :R→ R dengan f(x):=x2 . Direct image dari E:=

{

x:0≤ x≤2

}

adalah himpunan f(E):=

{

y:0≤ y≤4

}

. Jika G:=

{

y:0≤ y≤4

}

, maka inverse image dari G adalah himpunan f −1(G):=

{

x:−2≤ x≤2

}

. Terlihat bahwa f−1(f(E))≠ E.

Tipe-Tipe Khusus dari Fungsi

1. Fungsi Injektif

Fungsi f : A Æ B disebut fungsi injektif (fungsi satu-satu) jika dan hanya jika untuk tiap a1, a2 ∈ A dan a1 ≠ a2 berlaku f (a1) ≠ f (a2).

Contoh : A : {1,2,3} , B : {a,b,c} 1 y 2 y 3 y y a y b y c A B Fungsi f

f : A Æ B dinyatakan dalam pasangan terurut f : {(1,a), (2,b), (3,c)}.

Tampak bahwa tiap anggota A yang berbeda mempunyai peta yang berbeda di B

Fungsi f adalah fungsi injektif atau satu-satu.

2. Fungsi Surjektif

Suatu fungsi f : A Æ B disebut fungsi surjektif atau fungsi onto atau fungsi kepada jika dan hanya jika daerah hasil fungsi f sama dengan himpunan B atau Rf = B atau

.

B A f( )=

Contoh dalam diagram panah

A : {1,2,3,4} , B : {a,b,c} 1 • 2 • 3 • 4 • • a • b • c

Fungsi f : A Æ B dinyatakan dalam pasangan terurut : f = {(1,a), (2,c), (3,b), (4,c)}.

Tampak bahwa daerah hasil fungsi f adalah Rf :

{a,b,c} dan Rf = B maka fungsi f adalah fungsi surjektif atau fungsi onto atau fungsi kepada.

A f B

Fungsi f : A Æ B disebut fungsi into atau fungsi ke dalam jika dan hanya jika daerah hasil fungsi f merupakan himpunan bagian murni dari himpunan B atau Rf ⊂ B. Contoh :

A : {1,2,3,4} , B : {a,b,c}

fs f : A Æ B dinyatakan dalam pasangan terurut f : {(1,a), (2,b), (3,a), (4,b)}.

Tampak bahwa daerah hasil fs f : Rf : {a,b} dan Rf ⊂ B, maka fungsi f adalah fungsi into atau fungsi ke dalam. 1 • 2 • 3 • 4 • • a • b • c A f B

3. Fungsi Bijektif

Fungsi f : A Æ B disebut fungsi bijektif jika dan hanya jika fungsi f sekaligus merupakan fungsi surjektif dan fungsi injektif.

Contoh :

A : {1,2,3} , B : {a,b,c}

1 y _{fs f : A Æ B, dinyatakan dalam pasangan terurut f :}

{(1,a), (2,c), (3,b)}.

Tampak bahwa fungsi f adalah fungsi surjektif sekaligus fungsi injektif.

fungsi f adalah fungsi bijektif atau korespondensi satu-satu.

Contoh 1.1.4

a. Fungsi f :A→R dengan A:=

{

x∈R:x≠1

}

dan

1 ) ( − = x x x

f adalah fungsi injektif.

b. Fungsi f :R→ A dengan A:=

{

x∈R:x≥0

}

dan f(x)=x2 adalah fungsi surjektif. c. Fungsi f :[0,1]→[0,1] dengan f(x)=x adalah fungsi bijektif.

Definisi 1.1.7

Misalkan f :A→B fungsi injektif dengan domain A dan R(f) didalam B.

Jika maka g injeksi dengan domain . Fungsi

g disebut fungsi invers dari f dan dinotasikan .

{

b a BxA a b f

g:= ( , )∈ :( , )∈

}

D(g)=R(f)

1 −

f

Jadi jika dan hanya jika x= f −1(y) y= f(x).

Fungsi-Fungsi Komposisi

Untuk membuat komposisi dua fungsi, pertama dapatkan f(x) kemudian aplikasikan g untuk mendapatkan g(f(x)). Namun, ini mungkin terjadi hanya jika f(x) anggota domain g. Jadi haruslah range dari f termuat dalam domain g.

Definisi 1.1.8.

Misalkan dan , Fungsi komposisi adalah fungsi dari A ke C

didefinisikan oleh B A f : → g:B→C g_o f A x x f g x f g )( )= ( ( )),∀ ∈ ( _o . Contoh 1.1.5

Untuk x∈R, f(x)=2x dan g(x)= x3 2 −1. Fungsi komposisi 1 2 12 1 ) 4 ( 3 1 ) 2 ( 3 )) ( ( ) )( (g_o f x =g f x = x 2 − = x2 − = x2 − 6 ) 1 3 ( 2 )) ( ( ) )( (f _og x = f g x = x2 − = x2 − Terlihat bahwa (g_o f)≠(f _og). 2 y 3 y y a y b y c A B Fungsi f

Latihan 1.1

1. Buktikan Teorema 1.1.2!

2. Jika

{

A₁,A₂,_K,A_n

}

koleksi himpunan dan E sebarang himpunan, tunjukkan dan

(

)

U

_jn Aj

U

_jn E Aj E 1 1 = = ∩ = ∩

_U

n

_U

(

)

j n j j j E A A E 1 1 = = ∪ = ∪

3. Jika dan E, F adalah himpunan bagian dari A, tunjukkan

dan B A f : →

(

E F

)

f(E) f(F) f ∪ = ∪ f

(

E∩F

)

⊆ f(E)∩ f(F)?