Ringkasan Matematika SD-MI

(1)

Ringkasan Materi

Contoh Soal dan Pembahasan

Matematika

(2)

A. PENDAHULUAN

Bilangan merupakan suatu sebutan untuk menyatakan banyaknya sesuatu.

1. Lambang Bilangan

Lambang Dibaca Lambang Dibaca

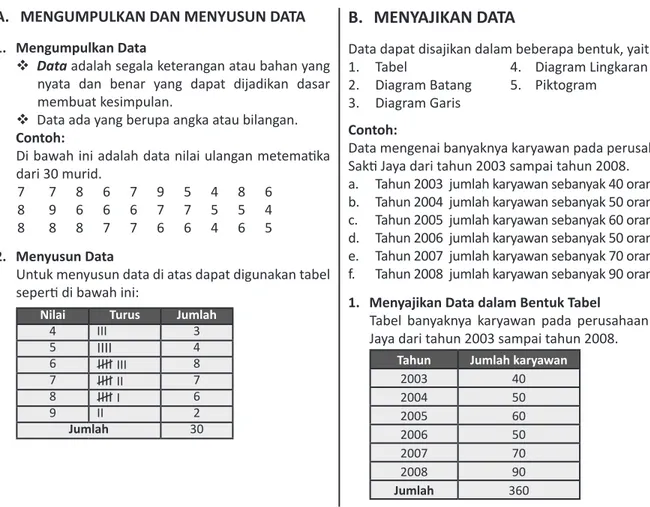
0 Nol 7 Tujuh 1 Satu 8 Delapan 2 Dua 9 Sembilan 3 Tiga 10 Sepuluh 4 Empat 11 Sebelas 5 Lima 12 Dua belas 6 Enam … dst

2. Membaca Lambang Bilangan

Lambang Cara Membaca

576 Lima ratus tujuh puluh enam

1.458 Seribu empat ratus lima puluh delapan 15.023 Lima belas ribu dua puluh tiga

541.236 Lima ratus empat puluh satu ribu dua ratus tiga puluh enam

Lambang bilangan 541.236 dapat diuraikan ber-dasarkan nilai tempatnya, yaitu:

541.236 = 500.000 + 40.000 + 1.000 + 200 + 30 + 6 3. Mengenal Nilai Tempat

Lambang bilangan 541.236 terdiri dari 6 angka, yaitu:

Angka Nilai

Angka 5 menempati ratusan ribu 500000 Angka 4 menempati puluhan ribu 40000 Angka 1 menempati ribuan 1000 Angka 2 menempati ratusan 200 Angka 3 menempati puluhan 30 Angka 6 menempati satuan 6

B. JENIS BILANGAN

1. Bilangan Asli

Bilangan asli adalah bilangan bulat positif yang

diawali dari angka 1 (satu) sampai dengan tak ter-hingga.

Contoh:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ... dan seterusnya.

(3)

[email protected]

2. Bilangan Bulat

Bilangan bulat adalah bilangan yang merupakan

gabungan dari bilangan bulat positif, nol (0), dan bi-langan bulat negatif.

Contoh:

..., –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, …. Bilangan bulat negatif Bilangan bulat positif

3. Bilangan Cacah

Bilangan cacah adalah bilangan bulat positif yang

diawali dari nol (0) sampai dengan tak terhingga.

Contoh:

0, 1, 2, 3, 4, 5, 6, 7, ... dan seterusnya.

4. Bilangan Genap

Bilangan genap adalah bilangan bulat yang habis

dibagi dua.

Contoh:

2, 4, 6, 8, 10, 12, 14, 16, 18, ... dan seterusnya.

5. Bilangan Ganjil

Bilangan ganjil adalah bilangan bulat yang tidak

habis dibagi dua.

Contoh:

1, 3, 5, 7, 9, 11, 13, 15, 17, ... dan seterusnya.

6. Bilangan Prima

Bilangan prima adalah bilangan yang tepat

memi-liki dua buah faktor yaitu 1 (satu) dan bilangan itu sendiri.

Contoh:

2, 3, 5, 7, 11, 13, 17, 19, 23, ....

Karena:

faktor dari 2 adalah 1 dan 2, faktor dari 3 adalah 1 dan 3,

faktor dari 5 adalah 1 dan 5, dan seterusnya.

7. Bilangan Komposit

Bilangan komposit adalah bilangan cacah yang

bu-kan 0 (nol), bubu-kan 1, dan bubu-kan bilangan prima.

Contoh:

4, 6, 8, 9, 10, 12, 14, 16, .... dan seterusnya.

8. Bilangan Rasional

Bilangan rasional adalah bilangan yang dapat

di-nyatakan sebagai suatu pembagian dari dua bilang-an bulat.

Contoh: 1 3 2, ,

2 5 77, dan sebagainya.

9. Bilangan Kuadrat

- Bilangan kuadrat adalah bilangan yang merupa-kan hasil perkalian suatu bilangan dengan bilang-an itu sendiri.

- Bilangan kuadrat disebut juga bilangan pangkat dua.

Contoh:

12_{(dibaca satu kuadrat) = 1 1 = 1}

22_{(dibaca dua kuadrat) = 2 2 = 4}

32_{(dibaca tiga kuadrat) = 3 3 = 9}

... dan seterusnya.

Jadi, bilangan 1, 4, 9, 16, 25, 36, 49 merupakan bilangan kuadrat.

(4)

[email protected]

10. Bilangan Kubik

Bilangan kubik adalah bilangan yang merupakan ha-sil perpangkatan tiga dari suatu bilangan.

Contoh:

13_{(dibaca satu pangkat tiga) = 1 1 1 = 1}

23_{(dibaca dua pangkat tiga) = 2 2 2 = 8}

33_{(dibaca tiga pangkat tiga) = 3 3 3 = 27}

... dan seterusnya.

Jadi, bilangan 1, 8, 27, 64, 125 merupakan bilangan kubik.

11. Bilangan Pecahan (disebut juga Bilangan Rasional)

a. Bilangan Pecahan Biasa

Contoh: 1₂

1 disebut pembilang dan 2 disebut penyebut. b. Bilangan Pecahan Campuran

Contoh: 2 , 4 ,1 1

2 5 dan sebagainya.

c. Bilangan Pecahan Desimal

Contoh:

1

2 ditulis 0,5 1

4 ditulis 0,25 dan sebagainya.

Jadi, bilangan pecahan desimal adalah

bilang-an ybilang-ang diberi tbilang-anda koma di belakbilang-ang bilbilang-angbilang-an satuan.

Contoh bilangan pecahan desimal: 0,1; 0,01; 2,5; 3,125; dan sebagainya.

12. Bilangan Irrasional

- Bilangan irrasional adalah bilangan-bilangan yang tidak dapat dinyatakan sebagai pecahan, atau

- Bilangan irrasional yaitu bilangan yang bukan bi-langan rasional.

Contoh:

2, 3, 5

Catatan:

9 = 3,maka 9 bukan bilangan irrasional.

13. Bilangan Riil

Bilangan riil adalah bilangan yang merupakan gabun-gan dari bilangabun-gan rasional dan bilangabun-gan irrasional.

Contoh:

0, 1, 2, 1 4_{2 7 7}, , 55, 2, 3, 5, .... dan seterusnya.

14. Bilangan Romawi

a. Lambang Dasar Bilangan Romawi

Lambang Bilangan Romawi Lambang Bilangan Desimal I 1 V 5 X 10 L 50 C 100 D 500 M 1.000 V 5.000 X 10.000 L 50.000

(5)

[email protected]

C 100.000

D 500.000 M 1.000.000

b. Aturan Penulisan Lambang Bilangan Romawi

1. Lambang yang sama hanya boleh dituliskan ber-urutan sebanyak 3 kali. Khusus untuk bilangan romawi I, X, C, dan M. Contoh: III = 3 XXX = 30 CCC = 300 MMM = 3.000

2. Lambang yang nilainya lebih kecil jika ditulis di sebelah kiri lambang yang lebih besar berarti pengurangan.

I untuk mengurangi V dan X. X untuk mengurangi L dan C. C untuk mengurangi D dan M.

Contoh: IV artinya 5 – 1 = 4 IX artinya 10 – 1 = 9 XL artinya 50 – 10 = 40 XC artinya 100 – 10 = 90 CD artinya 500 – 100 = 400 CM artinya 1.000 – 100 = 900

3. Lambang yang nilainya lebih kecil, jika dituliskan di sebelah kanan lambang yang nilainya lebih besar berarti penjumlahan.

Contoh: VIII artinya 5 + 3 = 8 XII artinya 10 + 2 = 12 LX artinya 50 + 10 = 60 CXX artinya 100 + 20 = 120 DCCC artinya 500 + 300 = 800 MC artinya 1.000 +100 =1.100 Kesimpulan:

1. Setiap pengurangan hanya boleh dilakukan satu kali terhadap bilangan yang sama.

2. V, L, dan D tidak dapat digunakan untuk mengurangi. 3. I hanya dapat digunakan untuk mengurangi V dan

X saja.

4. X hanya dapat digunakan untuk mengurangi L dan C saja.

5. C hanya dapat digunakan untuk mengurangi D dan M saja.

C. BILANGAN HABIS DIBAGI

1. Ciri Bilangan Dibagi 2 (Dua)

Jika angka terakhir dari bilangan itu adalah nol atau bilangan genap.

Contoh:

- 10 habis dibagi 2 karena angka terakhirnya nol. - 1.238 habis dibagi 2 karena angka terakhirnya

genap.

2. Ciri Bilangan Habis Dibagi 3 (Tiga)

Jika jumlah angka-angka dari bilangan itu habis dibagi 3.

(6)

[email protected]

Contoh:

- 228 habis dibagi 3, karena jumlah angka-angka-nya yaitu 2 +2 + 8 = 12 habis dibagi 3.

(228 : 3 =76)

- 6.294 habis dibagi 3, karena jumlah angka-ang-kanya yaitu 6 + 2 + 9 + 4 = 21 (21 habis dibagi 3) maka 6.294 habis dibagi 3.

(6294 : 3 = 2098)

3. Ciri Bilangan Habis Dibagi 4 (Empat)

- Jika dua (2) angka terakhirnya 00.

- Jika dua (2) angka terakhirnya habis dibagi 4.

Contoh:

- 3.100 habis dibagi 4, karena dua angka ter-akhirnya 00.

(3.100 : 4 = 775)

- 1.032 habis dibagi 4, karena dua angka ter-akhirnya (yaitu 32) habis dibagi 4.

(1.032 : 4 = 258)

4. Ciri Bilangan Habis Dibagi 5 (Lima)

Jika angka terakhirnya 0 atau 5.

Contoh:

- 20 habis dibagi 5, karena angka terakhirnya 0. (20 : 5 = 4).

- 6.995 habis dibagi 5, karena angka terakhirnya 5. (6.995 : 5 = 1.399).

5. Ciri Bilangan Habis Dibagi 6 (Enam)

Jika angka terakhirnya genap atau nol dan jumlah angka-angka yang membentuk bilangan itu habis dibagi 3.

Contoh:

- 228 habis dibagi 6, karena angka terakhirnya ge-nap dan jumlah angka-angkanya (2 + 2 + 8 = 12) habis dibagi 3.

(228 : 6 = 38)

- 720 habis dibagi 6, karena angka terakhirnya 0 dan jumlah angka-angkanya (yaitu 7 + 2 + 0 = 9) habis dibagi 3. Maka, 720 habis dibagi 6. (720 : 6 = 120)

6. Ciri Bilangan Habis Dibagi 7 (Tujuh)

Tidak ada ciri khusus.

7. Ciri Bilangan Habis Dibagi 8 (Delapan)

Jika tiga angka terakhirnya 000 atau tiga angka ter akhirnya habis dibagi 8.

Contoh:

- 3.000 habis dibagi 8, karena tiga angka terakhir-nya 000.

- 4.128 habis dibagi 8, karena tiga angka terakhir-nya (yaitu 128) habis dibagi 8. (128 : 8 = 16). Jadi, 4.128 : 8 = 516 .

8. Ciri Bilangan Habis Dibagi 9 (Sembilan)

Jika jumlah angka-angkanya habis dibagi 9.

Contoh:

- 117 habis dibagi 9, karena jumlah angka-angkanya (yaitu 1 + 1 + 7 = 9) habis dibagi 9.

Jadi, 117 : 9 = 13.

- 9.837 habis dibagi 9, karena (9 + 8 + 3 + 7 = 27). Jadi, 9.837 : 9 = 1.093.

9. Ciri Bilangan Habis Dibagi 10 (Sepuluh)

(7)

[email protected]

Contoh:

- 210 habis dibagi 10 (210 : 10 = 21). - 3.400 habis dibagi 10 (3.400 : 10 = 340).

10. Ciri Bilangan Habis Dibagi 11 (Sebelas)

Jika selisih dari jumlah angka-angka di tempat ganjil (gasal) dengan jumlah angka-angka di tempat ge-nap sama dengan nol (0) atau sebelas (11).

Contoh:

- 2.376 habis dibagi 11, karena (2 + 7) – (3 + 6) = 0.

Jadi, 2.376 : 11 = 216.

- 4.928 habis dibagi 11, karena (9 + 8) – (4 + 2) = 11.

Jadi, 4.928 : 11 = 448.

D. KELIPATAN SUATU BILANGAN

Kelipatan suatu bilangan adalah bilangan yang meru-pakan hasil perkalian suatu bilangan tertentu dengan bilangan-bilangan asli. Contoh: - Kelipatan 2 2 1 = 2 2 2= 4 2 3 = 6 ... dan seterusnya.

Jadi, 2, 4, 6, 8, .... adalah bilangan kelipatan 2. - Kelipatan 3 adalah: 3, 6, 9, 12, 15, ....

- Kelipatan 4 adalah: 4, 8, 12, 16, 20, 24, .... - Kelipatan 5 adalah: 5, 10, 15, 20, 25, 30, .... - Kelipatan 6 adalah: 6, 12, 18, 24, 30, 36, .... - ... dan seterusnya.

E. FAKTOR SUATU BILANGAN

Faktor suatu bilangan adalah bilangan-bilangan yang merupakan pembagi dari suatu bilangan.

Contoh:

- Faktor-faktor dari 2 adalah 1 dan 2. 2 : 1 = 2 dan 2 : 2 = 1

Maka faktor dari 2 adalah 1 dan 2.

- Faktor-faktor dari 16 adalah: 16 : 1 = 16; 16 : 2 = 8; 16 : 3 = tidak bisa; 16 : 4 = 4; 16 : 5 = tidak bisa; 16 : 6 =tidak bisa 16 : 7 = tidak bisa; 16 : 8 = 2; 16 : 16 = 1

Maka faktor-faktor dari 16 adalah 1, 2, 4, 8, dan 16.

F. FAKTOR PRIMA SUATU BILANGAN

- Faktor prima suatu bilangan adalah faktor-faktor dari suatu bilangan yang juga merupakan bilangan prima. - Perlu diingat himpunan bilangan prima adalah:

2, 3, 5, 7, 11, 13, 17, 19, ....

Contoh:

1. Faktor prima dari 6 adalah....

Jawab:

Cara I: dengan cara mengurutkan (mendaftar).

(8)

[email protected]

Karena 2 dan 3 adalah bilangan prima sedangkan 1 dan 6 bukan bilangan prima, maka yang merupakan faktor prima adalah 2 dan 3.

Jadi, faktor prima dari 6 adalah 2 dan 3.

Cara II: dengan pohon faktor.

6

3 2

Jadi, faktor primanya adalah 2 dan 3.

2. Faktor prima dari 70 adalah....

Jawab:

Dengan pohon faktor diperoleh: 70

35 2

7 5

Jadi, faktor prima dari 70 adalah 2, 5, dan 7.

SOAL DAN PEMBAHASAN

1. Bilangan 30 mempunyai faktor sebanyak .... a. 6

b. 7 c. 8 d. 9

Pembahasan:

Faktor dari 30 adalah: 30 : 1 = 30, 30 : 2 = 15, 30 : 3 = 10, 30 : 5 = 6, 30 : 6 = 5, 30 : 10 = 3, 30 : 15 = 2, 30 : 30 = 1,

Faktor dari 30 adalah 1, 2, 3, 5, 6, 10, 15, 30 ada sebanyak 8.

Jawaban: c

2. Di antara bilangan di bawah ini yang habis dibagi dengan 9 adalah …. a. 196 b. 254 c. 657 d. 773 Pembahasan:

Suatu bilangan habis dibagi dengan 9 apabila jumlah angka-angka penyusunya habis dibagi 9.

(9)

[email protected]

Di antara pilihan di atas yang jumlah angka-angka penyusunnya habis dibagi 9 adalah 657, karena jumlah angka-angka penyusunnya habis dibagi 9, yaitu:

6 + 5 + 7 = 18, sedangkan 18 : 9 = 2. 657 : 9 = 73.

Jawaban: c

3. Bilangan 49 apabila dituliskan dalam bilangan Ro-mawi adalah .... a. XLIX b. XLXI c. XLVIII d. XXXIX Pembahasan:

Ingat kembali aturan penulisan bilangan romawi. 49 = 40 + 9

= XL + IX = XLIX

Jawaban: a

4. Nilai angka 2 pada bilangan 325.147 adalah .... a. 200

b. 2.000 c. 20.000 d. 200.000

Pembahasan:

325.147 dapat dinyatakan dalam penjumlahan: 300.000 + 20.000 + 5.000 + 100 + 40 + 7

Jadi, angka 2 pada bilangan 325.147 nilainya adalah 20.000.

Jawaban: c

5. Nilai tempat 7 pada bilangan 1.759.246 adalah .... a. ribuan

b. puluhan ribu c. ratusan ribu d. satuan

Pembahasan:

Angka 7 pada bilangan 1.759.246 nilainya adalah 700.000. Jadi nilai tempat angka 7 adalah ratusan ribu.

(10)

OPERASI HITUNG BILANGAN BULAT

BAB 2

A. PENGERTIAN BILANGAN BULAT

Bilangan bulat adalah bilangan yang terdiri dari:

- Bilangan bulat positif, yaitu 1, 2, 3, 4, 5, … dan seterusnya.

- Bilangan bulat negatif, yaitu –1, –2, –3, –4, … dan seterusnya.

- Bilangan 0 (nol), disebut juga bilangan netral.

Lawan Suatu Bilangan Contoh:

–3 adalah lawan dari 3,

–5 adalah lawan dari 5, dan seterusnya.

Bilangan lawan dari bilangan asli disebut juga bilangan bulat negatif.

B. MEMBANDINGKAN BILANGAN BULAT

- Membandingkan dengan Garis Bilangan Bulat

Garis bilangan bulat adalah garis yang di dalam-nya

terdapat bilangan-bilangan bulat.

Contoh garis bilangan bulat:

Dari garis bilangan tersebut, semakin ke kanan nilai bilangan semakin besar, dan semakin ke kiri nilai bilangan semakin kecil.

- Untuk membandingkan dua bilangan bulat, digu-nakan tanda sebagai berikut.

> (dibaca lebih dari) < (dibaca kurang dari) = (dibaca sama dengan)

Contoh:

Dari garis bilangan sebelumnya diperoleh:

• 4 > 2 (Dibaca: 4 lebih besar dari 2), karena letak 4 di sebelah kanan 2.

• 1 < 3 (Dibaca: 1 lebih kecil dari 3), karena letak 1 di sebelah kiri 3.

• –2 < 0 • –3 > –4

C. OPERASI HITUNG BILANGAN BULAT

1. Penjumlahan dan Pengurangan Contoh:

(11)

[email protected]

2. 6 – 3 = 3 3. –3 + 4 = 1 4. –3 – (–2) = –1 Keterangan:

Untuk positif, panah ke arah kanan, sedangkan untuk negatif panah ke arah kiri.

2. Perkalian Bilangan Bulat

Rumus pada operasi perkalian bilangan bulat. + + = + + – = – – + = – – – = + Contoh: 3 4 = 12 3 (–2) = –6 –5 4 = –20 (–5) (–5) = 25

3. Pembagian Bilangan Bulat

Rumus pada operasi pembagian bilangan bulat. + : + = + + : – = – – : + = – – : – = + Contoh: 6 : 2 = 3 9 : (–3) = –3 –50 : 5 = –10 (–512) : (–8) = 64

Catatan: Suatu bilangan bulat tidak boleh dibagi

bilangan 0.

D. SIFAT OPERASI BILANGAN BULAT

1. Sifat-sifat Operasi Bilangan Bulat a. Sifat Komutatif (Pertukaran)

a + b = b + a a b = b a

Artinya: Pertukaran letak suku-suku dalam pen-jumlahan/perkalian bilangan bulat, tidak men-gubah hasil. Contoh: • 4 + 5 = 5 + 4 (4 + 5 = 9 dan 5 + 4 juga = 9). • 3 9 = 9 3 (3 9 = 27 dan 9 3 juga = 27). b. Sifat Asosiatif (Pengelompokan) (a + b) + c = a + ( b + c) (a b) c = a ( b c) Contoh: • (3 + 4) + 5 = 3 + (4 +5). • (7 8) 9 = 7 (8 9).

(12)

[email protected]

c. Sifat Distributif (Penyebaran) a (b + c) = (a b) + (a c) a (b – c) = (a b) – (a c) Contoh: • 2 (3 + 4) = (2 3) + (2 4). • 3 (5 - 2) = (3 5) - (3 2). d. Elemen Identitas a + 0 = a a 1 = a Contoh: • 7 + 0 = 7 • –5 1 = –5 e. Sifat Invers

Untuk setiap bilangan bulat a terdapat –a (invers/lawab bilangan dari a) sehingga berlaku.

a + (–a) = –a + a = 0 Contoh:

8 + (–8) = 0 hasilnya sama dengan –8 + 8 = 0

f. Sifat Urutan Bilangan Bulat

Pada 2 (dua) bilangan bulat a dan b terdapat tiga (3) kemungkinan hubungan, yaitu.

• Jika a > b maka a – b > 0

• Jika a < b maka a – b < 0 atau b – a > 0 • Jika a = b maka a – b = 0

Contoh:

• 6 > 4 maka 6 – 4 > 0 (karena 6 – 4 = 2 dan 2 > 0) • 3 < 5 maka 3 – 5 < 0 (karena 3 – 5 = –2 dan –2 < 0)

2. Mencari Harga n (Peubah) Contoh:

n + 7 = 15, berapakah n?

Aturan langkahnya:

- Tiap ruas jika dikurangi dengan bilangan yang sama, tidak akan mengubah persamaan. Maka: n + 7 = 15

n + 7 – 7 = 15 – 7 n + 0 = 8 n = 8.

- Perpindahan suku dari ruas kiri (sebelah kiri tanda =) ke ruas kanan (sebelah kanan tanda =) harus disertai dengan perubahan tanda. (Positif menjadi negatif dan sebaliknya). n + 7 = 15 (+7 dipindah ke ruas kanan menjadi –7)

Sehingga: n = 15 – 7 = 8. Jadi, nilai n = 8 Contoh: n – 5 = 12, berapakah n? Aturan langkahnya:

- Tiap ruas jika ditambah dengan bilangan yang sama, tidak akan mengubah persamaan. Maka:

n – 5 = 12 n – 5 + 5 = 12 + 5 n = 17

(13)

[email protected]

- Perpindahan suku dari ruas kiri (sebelah kiri tanda =) ke ruas kanan (sebelah kanan tanda +) harus disertai dengan perubahan tanda. Perhatikan contoh: n – 5 = 12

Maka: n – 5 = 12 (–5 dipindah ke ruas kanan, menjadi + 5)

Sehingga: n = 12 + 5 n = 17 Jadi, nilai n = 17

E. BILANGAN BULAT BERPANGKAT

32_{artinya = 3 3; 3}2_{dibaca tiga pangkat dua.}

33_{artinya = 3 3 3; 3}3_{dibaca tiga pangkat tiga.}

Bentuk-bentuk bilangan 32_{, 3}3_{disebut dengan bilangan}

berpangkat.

1. Menentukan Nilai Bilangan Berpangkat Contoh:

• 23_{= 2 2 2}

= 8

• (–2)3_{= (–2) (–2) (–2)}

= –8

2. Sifat-sifat pada Perpangkatan Bilangan Bulat

a. an_{= a a a ...} sebanyak n buah Contoh: 56_{= 5 5 5 5 5 5} b. n n 1 a a − ₌ _{, syaratnya a 0.} Contoh: 1 1 2 2 1 2 2 1_; 2 1 3 3 1 9 − − = = = = c. an_bn_{= (a b)}n Contoh: 32₅2_{= (3 5)}2 d. an_{: b}n_{= (a : b)}n Contoh: 42_{: 2}2_{= (4 : 2)}2 e. am_an_{= a}m + n Contoh: 32₃5_{= 3}2 + 5 = 37 f. am_{: a}n_{= a}m – n Contoh: 55_{: 5}2_{= 5}5 – 2 = 53

F. AKAR PANGKAT SUATU BILANGAN

1. Akar Pangkat Dua (Akar Kuadrat)

Akar pangkat dua atau disebut juga dengan akar

(14)

[email protected]

lis dengan (tanpa angka 2 di atasnya). Perhatikan contoh berikut!

32_{= 3 3}

= 9 maka 9 3=

42_{= 4 4}

=16 maka 16 4=

2. Akar Pangkat Tiga

Akar pangkat tiga dilambangkan dengan 3 _.

Perhatikan contoh berikut! 33_{= 3 3 3}

= 27 maka 3_{27 3}₌

44_{= 4 4 4}

= 64 maka 3_{64 4}₌

Tips mencari akar dari suatu bilangan. Contoh. Hitunglah nilai dari 144 !

144 1 1 = 2 2 2 = 1 44 44 0 – – 1 2 Hasil 12 Angka 2 diperoleh dari 1 + 1 2 ... ... = hasilnya mendekati 44. Untuk mengisi

titik-titik tersebut adalah 2.

Jadi hasil dari 144 adalah 12.

SOAL DAN PEMBAHASAN

1. 22_{+ 3}2_{+ 4}2_{= ...} a. 21 b. 24 c. 27 d. 29 Pembahasan: 22_{+ 3}2_{+ 4}2_{= (2 2) + (3 3) + (4 4)} = 4 + 9 + 16 = 29 Jawaban: d

2. Bilangan pangkat dua antara 50 dan 100 adalah .... a. 64, 81 b. 66, 77, 88, 99 c. 60, 70, 80, 90 d. tidak ada Pembahasan:

Bilangan pangkat dua:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, … Jadi, bilangan pangkat dua antara 50 dan 100 adalah 64 dan 81. Jawaban: a 3. (4 5) + (4 6) = 4 n. Maka n adalah.... a. 11 b. 12 c. 13 d. 14

(15)

[email protected]

Pembahasan:

Ingat! (a b) + (a c) = a (b + c)

Dengan menggunakan sifat distributif (penyebaran) maka ruas kiri menjadi:

(4 5) + (4 6) = 4 (5 + 6) = 4 11 Jadi, (4 5) + (4 6) = 4 n 4 11 = 4 n Nilai n adalah 11 Jawaban: a 4. Nilai dari (100 + 10) : 11 – 5 =.... a. 5 b. 6 c. 7 d. 8 Pembahasan:

Ingat! Kerjakan yang di dalam kurung terlebih

da-hulu kemudian perhatikan bahwa perkalian atau pembagian dikerjakan terlebih dahulu baru penjum-lahan atau pengurangan.

(100 + 10) : 11 – 5 = 110 : 11 – 5 = 10 – 5 = 5 Jawaban: a 5. 83₈2_{= ....} a. 8 b. 85 c. 86 d. 832 Pembahasan: Ingat! am_an_{= a}m + n 83₈2_{= 8}3 + 2 = 85 Jawaban: b 6. 252₂₆2_{= ....} a. (25 26)2 b. (25 + 26)2 c. (25 + 26)4 d. (25 26)4 Pembahasan: Ingat! an_bn_{= (a b)}n 252₂₆2_{= (25 26)}2 Jawaban: a 7. (–5) (–6) = .... a. 30 c. 11 b. –30 d. –11 Pembahasan:

Kedua bilangan mempunyai tanda –.

Ingat!

– – = + Jadi, (–5) (–6) = 30

(16)

[email protected]

Faktor Persekutuan

Contoh:

1. Tentukan faktor persekutuan dari 12 dan 18.

Jawab:

Faktor 12 = 1 , 2 , 3 , 4 , 6 , 12 Faktor 18 = 1 , 2 , 3 , 6 , 9 , 18

Jadi, faktor persekutuan dari 12 dan 18 adalah 1, 2, 3, dan 6.

2. Tentukan faktor persekutuan dari 24 dan 36.

Jawab:

Faktor 24 = 1 , 2 , 3 , 4 , 6 , 8 , 12 , 24 Faktor 36 = 1 , 2 , 3 , 4 , 6 , 9 , 12 , 18 , 36.

Jadi, faktor persekutuan dari 24 dan 36 adalah 1, 2, 3, 4, 6, dan 12.

Faktorisasi Prima

Faktorisasi prima yaitu bentuk perkalian bilangan prima suatu bilangan.

Contoh:

1. Tentukan faktorisasi prima dari 360. Jawab:

Caranya:

- Lakukan pembagian seperti bentuk di bawah. - Gunakan bilangan pembagi 2, 3, 5, 7 dan

seterus-nya yang merupakan bilangan prima.

- Hasil bagi harus sampai pada bilangan 1 (satu). - Lingkari pembagi-pembagi yang merupakan

bi-langan prima. Perhatikan! 90 2 45 3 15 3 5 1 5 90 2 45 3 15 3 5 Atau cukup ditulis: Diperoleh: 90 = 2 3 3 5 = 2 32_5.

Jadi, faktorisasi prima dari 90 = 2 32_5.

A. MENENTUKAN FPB

Untuk menentukan FPB (Faktor Persekutuan Terbesar) digunakan beberapa cara, antara lain:

- Dengan faktorisasi prima (pohon faktor). - Dengan tabel.

1. Menentukan FPB dengan Cara Faktorisasi Prima

Mencari FPB dari Dua Bilangan

Contoh:

Tentukan FPB dari 90 dan 120.

(17)

[email protected]

Jawab: 5 15 90 2 45 3 3 15 30 120 2 60 2 2 3 5

Faktorisasi prima dari 90 = 2 32_5.

Faktorisasi prima dari 120 = 23_{3 5.}

Cara menentukan FPB:

• Tulis bilangan-bilangan itu dalam bentuk perkalian faktor prima (faktorisasi prima). • Ambil faktor yang sama dari bilangan-bilangan itu. • Jika faktor yang sama itu pangkatnya berbeda,

ambil faktor yang pangkatnya terkecil. Maka:

FPB dari 90 dan 120 = 2 3 5 = 30. Jadi, FPB dari 90 dan 120 adalah 30.

2. Menentukan FPB dengan Cara Tabel Contoh:

Tentukan FPB dari 90 dan 120 dengan cara tabel.

Jawab: 120 60 20 4 3 15 45 90 2 3 5 Keterangan: • 90 : 2 = 45, dan 120 : 2 = 60. • 45 : 3 = 15 dan 60 : 3 = 20. • 15 : 5 = 3 dan 20 : 5 = 4.

• Bilangan 3 dan 4 tidak bisa dibagi dengan bilang-an prima ybilang-ang sama (berapapun bilbilang-angbilang-annya), maka selesai.

Jadi, FPB dari 90 dan 120 = 2 3 5 = 30.

B. MENENTUKAN KPK

Caranya:

1. Dengan faktorisasi prima (pohon faktor). 2. Dengan tabel.

Contoh:

Tentukan KPK dari 90 dan 120.

Jawab:

Cara I: dengan pohon faktor.

5 15 90 2 45 3 3 15 30 120 2 60 2 2 3 5

Faktorisasi prima dari 90 = 2 32_5.

Faktorisasi prima dari 120 = 23_{3 5.}

Cara menentukan KPK dengan pohon faktor:

• Tulis bilangan-bilangan itu dalam bentuk perkalian faktor prima.

• Ambil semua faktor, yang sama ataupun yang tidak sama dari bilangan-bilangan itu.

(18)

[email protected]

• Jika faktor yang sama itu mempunyai pangkat

yang berbeda, ambil faktor yang pangkatnya terbesar.

KPK dari 90 dan 120 = 23₃2_{5 = 360}

Jadi, KPK dari 90 dan 120 adalah 360.

Cara II: dengan tabel.

120 60 20 4 3 15 45 90 2 3 5

Cara menentukan KPK dengan tabel.

Kalikan bilangan pembagi dengan semua hasil bagi. Sehingga:

KPK dari 90 dan 120 = 2 32_{4 5 = 360}

Jadi, KPK dari 90 dan 120 adalah 360.

C. FPB DAN KPK DALAM KEHIDUPAN

SEHARI-HARI

Contoh:

1. Lonceng A berbunyi setiap 4 jam sekali. Lonceng B berbunyi setiap 6 jam sekali Lonceng C berbunyi setiap 8 jam sekali. Setiap berapa jam ketiga lonceng itu akan ber-bunyi bersama-sama?

Jawab:

Gunakan KPK dari 4, 6, dan 8.

Diperoleh: 4 = 22

6 = 2 3 8 = 23

KPK dari 4, 6, dan 8 = 23_{3 = 24.}

Jadi, ketiga lonceng itu akan berbunyi bersama-sama setiap 24 jam (setiap 1 hari).

2. Ada dua orang satpam yaitu satpam A dan satpam B yang bertugas menjaga sebuah gudang. Satpam A bertugas setiap 3 hari sekali dan satpam B setiap 4 hari sekali. Pada tanggal 1 Januari mereka bertugas bersama-sama. Pada tanggal berapa mereka bertugas bersama-sama lagi?

Jawab:

Dicari KPK dari 3 dan 4. KPK dari 3 dan 4 adalah 12.

Jadi, mereka bertugas bersama-sama lagi pada tanggal = 1 Januari + 12 hari = 13 Januari. 3. Ibu membeli tiga macam bunga, yaitu bunga A,

bunga B, dan bunga C. Bunga-bunga itu akan dirangkai di dalam vas bunga. Jika bunga A ada 6, bunga B ada 9, dan bunga C ada 12, berapa banyak vas bunga yang dibutuhkan supaya setiap vas masing-masing mendapat bunga yang sama banyak?

Jawab:

Dicari FPB dari 6, 9, dan 12. FPB dari 6, 9, dan 12 adalah 3.

Jadi, vas bunga yang dibutuhkan sebanyak 3 buah.

(19)

[email protected]

SOAL DAN PEMBAHASAN

1. FPB dari 24 dan 36 adalah.... a. 4 c. 8 b. 6 d. 12

Pembahasan:

Faktorisasi prima dari 24: 23₃

Faktorisasi prima dari 36: 22₃2

Maka:

FPB dari 24 dan 36 = 22_{3 = 12}

Jawaban: d

2. FPB dan 35, 40, dan 45 adalah.... a. 3 c. 7 b. 5 d. 8

Pembahasan:

Faktorisasi prima dari 35: 5 7 Faktorisasi prima dari 40: 23₅

Faktorisasi prima dari 45: 32₅

Maka:

FPB dari 35, 40, dan 45 adalah 5.

Jawaban: b

3. Kelipatan persekutuan terkecil (KPK) dari 6 dan 8 adalah....

a. 16 c. 24 b. 18 d. 36

Pembahasan:

Faktorisasi prima dari 6: 2 3 Faktorisasi prima dari 8: 23

KPK dari 6 dan 8 = 23_{3 = 24}

Jawaban: c

4. KPK dari bilangan 6, 8, dan 9 adalah.... a. 24 c. 36 b. 54 d. 72

Pembahasan:

Faktorisasi prima dari 6: 2 3 Faktorisasi prima dari 8: 23

Faktorisasi prima dari 9: 32

KPK dari 6, 8, dan 9 adalah 23₃2_{= 72}

Jawaban: d

5. Amir berenang setiap 3 hari, Bandi berenang setiap 4 hari, dan Cepi berenang setiap 6 hari. Pada tanggal 1 Agustus 2007 ketiga anak itu pergi berenang bers-ama untuk pertbers-ama kalinya. Pada tanggal berapakah mereka berenang bersama-sama untuk yang kedua kalinya?

a. 13 Agustus 2007 c. 24 Agustus 2007 b. 19 Agustus 2007 d. 25 Agustus 2007

Pembahasan:

Soal tersebut menggunakan konsep KPK. Dicari KPK dari 3, 4, dan 6.

Faktorisasi prima dari 3: 3 Faktorisasi prima dari 4: 22

Faktorisasi prima dari 6: 2 3 KPK dari 3, 4, dan 6 adalah 22_{3 = 12}

Jadi, mereka berenang bersama-sama lagi pada tanggal

= 1 Agustus 2007 + 12 hari = 13 Agustus 2007.

(20)

[email protected]

BILANGAN PECAHAN

BAB 4

A. PENGERTIAN PECAHAN

Perhatikan gambar di bawah!

Sebuah kue yang berbentuk lingkaran, dipotong menjadi 4 bagian yang sama besar.

Artinya: setiap potong adalah 1₄ bagian dari kue semula.

1. Arti Bilangan Pecahan

Bilangan pecahan adalah setiap bilangan yang

ber-bentuk p

q, dengan p dan q merupakan bilangan

bu-lat dan q 0.

Bentuk umum pecahan

pembilang p penyebut, q 0 q → → ≠ Contoh: 1 1 2 4 6, , , , 2 3 5 5 7 dan sebagainya. 2. Pecahan Senilai

Pecahan senilai adalah pecahan-pecahan yang

ber-nilai sama.

Contoh: 1 2 4 8 dan 3 6 18 2 4 8 16= = = 5 10 30= =

3. Garis Bilangan Pecahan

Berfungsi untuk membandingkan dua bilangan pecahan atau lebih.

Perhatikan gambar garis bilangan berikut!

Dari gambar di atas, maka:

1 2 4 1 3 9 ;

2 4 8 2 4 8= = < <

4. Cara Mencari Pecahan Senilai

a. Mengalikan pembilang dan penyebut dengan bilangan yang sama. Contoh: 3 3 2 6 5 5 2 10 3 3 3 9 3 6 9 12 Jadi, 5 5 3 15 5 10 15 20 3 3 4 12 5 5 4 20 ×  = = _ × _ ×  = _× =  = = =  ×  = = _ × 

(21)

[email protected]

b. Membagi pembilang dan penyebut dengan bi-langan yang sama.

Contoh: 18 18 : 2 9 24 24 : 2 12 18 18 : 3 6 18 9 6 3 Jadi, 24 24 : 3 8 24 12 8 4 18 18 : 6 3 24 24 : 6 4  = = _   = =  = = =   = = _

5. Cara Mengurutkan Pecahan

Mengurutkan pecahan dapat dilakukan dengan syarat:

- Penyebut suatu pecahan harus sama.

- Urutan pecahan dapat merupakan urutan naik ataupun urutan turun.

Contoh:

Manakah yang lebih besar 1

2 atau 3 5?

Jawab:

• Samakan dahulu penyebut-penyebutnya dengan mencari KPK dari 2 dan 5.

• Karena KPK dari 2 dan 5 adalah 10, maka: 1 5

2 10= dan

3 6

5 10=

Karena 5

10 lebih kecil dari 6 10. Jadi,

1 3 2 5< .

6. Cara Menentukan Pecahan-pecahan Lain di antara Dua Pecahan

Perhatikan contoh berikut!

Contoh:

Tentukan pecahan lain di antara 2

3 dan 4 5.

Jawab:

• Samakan penyebut dengan mencari KPK dari 3 dan 5.

• KPK dari 3 dan 5 adalah 15. Sehingga: 2 3 = 10 15 dan 4 5 = 12 15 Pecahan di antara 10 15 dan 12 15adalah 11 15.

Jadi, pecahan di antara 2

3 dan 4

5 adalah 11 15.

B. OPERASI HITUNG PECAHAN

1. Penjumlahan Pecahan a. Menjumlahkan Pecahan Biasa yang penyebutnya Sama Contoh: 1 3 1 3 4 5 5 5 5 + + = =

b. Menjumlahkan Pecahan Biasa yang Penyebut-nya Tidak Sama

Caranya:

Penyebut dari pecahan-pecahan itu harus disamakan.

(22)

[email protected]

Contoh: 2 3 2 4 3 5 _{(KPK dari 5 dan 4 = 20)} 5 4 20 20 8 15 20 20 8 15 20 23 20 × × + = + = + + = =

c. Menjumlahkan Pecahan Campuran dan Pecahan Biasa Contoh: 1 1 4 2 3+ = ….? Jawab: Cara I: Pecahan campuran 41 2 diubah dahulu ke

bentuk pecahan biasa, yaitu 41 (2 4) 1 9

2 2 2 × + = = 1 1 9 1 4 2 3 2 3 9 3 1 2 (KPK dari 2 dan 3 = 6) 6 6 27 2 6 6 29 6 5 4 6 + = + × × = + = + = = Cara II: • Pecahan campuran 41

2 tidak perlu diubah

menjadi pecahan biasa.

[email protected]

3 1 11 31 2 5 4 6 4 6 11 3 31 2 (KPK dari 4 dan 6 = 12) 12 12 33 62 12 12 95 12 11 7 12 + = + × × = + = + = = Cara II:

(

)

3 1 3 1 2 5 2 5 4 6 4 6 3 1 7 4 6 3 3 1 2 7 12 12 9 2 7 12 12 11 7 12 11 7 12   + = + +_ + _     = +_ + _   × ×   = +_ + _     = +_ + _     = +  _ _ = 2. Pengurangan Pecahan a. Mengurangkan Pecahan Biasa yang Penyebutnya Sama Contoh: 4 1 4 1 3_{5 5}− = ₅− =₅ b. Mengurangkan Pecahan Biasa yang Penyebutnya Tidak Sama Contoh: 3 2 3 5 2 4_{(KPK dari 4 dan 5 20)} 4 5 20 20 15 8 20 20 7 20 × × − = − = = − =

c. Mengurangkan Pecahan Campuran dan Pecahan Biasa Contoh:

(

4 7

) (

2 5

)

4 2 _{(KPK 5 dan 7 35)} 3 3 5 7 35 35 28 10 3 35 35 18 3 35 18 3 35 × ×   ₌ − = +_ − _     = +_ − _     = +  _ _ =

d. Mengurangkan Pecahan Campuran dan Pecahan Campuran. Contoh:

(

)

(

) (

)

4 1 4 1 3 2 3 2 5 3 5 3 4 3 1 5 _{(KPK 5 dan 3 15)} 1 15 15 12 5 1 15 15 7 1 15 7 1 15   − = − +_ − _   × ×   ₌ = +_ − _     = +_ − _     = +  _ _ =

(24)

[email protected]

(

)

(

) (

)

4 1 4 1 3 2 3 2 5 3 5 3 4 3 1 5 _{(KPK 5 dan 3 15)} 1 15 15 12 5 1 15 15 7 1 15 7 1 15   − = − +_ − _   × ×   ₌ = +_ − _     = +_ − _     = +  _ _ = 3. Perkalian Pecahan Rumus: a c a c b d b d × × = ×

a. Perkalian Pecahan Biasa dengan Bilangan Bulat

Caranya:

Kalikan bilangan bulatnya dengan pembilang pada pecahannya! Contoh: 2 4 ( 2) 4 15 15 8 15 × −   × −_ _=   − =

b. Perkalian Antarbilangan Pecahan Biasa

Caranya:

Pembilang dikalikan dengan pembilang, dan penyebut dikalikan dengan penyebut.

Contoh: 6 5 6 5 7 8 7 8 30 56 × × = × =

c. Perkalian Bilangan Pecahan Campuran dengan Pecahan Biasa

Caranya:

Pecahan campuran diubah dahulu menjadi pecahan biasa, kemudian dikalikan langsung.

Contoh:

(

2 3

)

1 1 4 4 2 3 5 3 5 7 4 3 5 28 15 13 1 15 × + × = × = × = =

d. Perkalian Antarbilangan Pecahan Campuran Contoh:

(

× +

)

(

× +

)

× = × = × = = = 5 3 1 2 4 3 1 3 5 2 3 4 3 4 16 11 3 4 176 12 8 14 12 2 14 3

(25)

[email protected]

4. Pembagian Pecahan Rumus: a c a d : b d b c= ×

a. Pembagian Bilangan Bulat dengan Pecahan Biasa

Caranya:

Kalikan bilangan bulatnya dengan kebalikan dari pecahan itu. Contoh: 3 5 8 : 8 5 3 8 5 3 40 3 1 13 3 = × × = = =

b. Pembagian Bilangan Bulat dengan Pecahan Campuran Contoh: 12 : 21 4= ....? Jawab: 1 2 4 diubah menjadi 94. = = × = = = 1 9 12 : 2 12 : 4 4 4 12 9 48 9 3 5 9 1 5 3 1 9 12 : 2 12 : 4 4 4 2 9 48 9 3 5 9 1 5 3 = = × = = =

c. Pembagian Pecahan Campuran Dengan Bilangan Bulat Contoh: 2 : 51 3 =....? Jawab: 1 2

3 diubah menjadi pecahan biasa, yaitu 7₃.

1 7 2 : 5 : 5 3 3 7 1 3 5 7 15 = = × =

d. Pembagian Pecahan Campuran dengan Pecahan Campuran Contoh: 1 1 5 4 2 : 1 : 2 3 2 3 5 3 2 4 15 8 7 1 8 = = × = =

(26)

[email protected]

C. BILANGAN DESIMAL

1. Pengertian Pecahan Desimal

Pecahan desimal atau bilangan desimal adalah suatu bilangan yang diperoleh dari hasil membagi suatu bilangan dengan angka 10, 100, 1.000, 10.000, dan seterusnya. Contoh: • 0,1 0,1 artinya 1 10. • 0,123 0,123 artinya 123 1.000.

2. Menentukan Nilai Tempat Bilangan Desimal

1.000 atau 0,003 =

2 = persepuluh ribu

(

=_10.0002 atau 0,0002

)

1 = perseratus ribu

(

1

)

100.000 atau 0,00001

=

Jadi,

6,54321 = 6 + 0,5 + 0,04 + 0,003 + 0,0002 + 0,00001

3. Operasi Pecahan Desimal

a. Operasi Penjumlahan Pecahan Desimal Contoh: 0,125 + 0,371 =....? Jawab: 0,125 0,371 0,496+ Jadi, 0,125 + 0,371 = 0,496.

b. Operasi Pengurangan Pecahan Desimal Contoh:

5,123 – 3,625 =....?

Jawab:

3 dikurangi 5 hasilnya negatif. Agar positif, pinjam 1 dari angka sebelah kirinya, sehingga menjadi 13. Jadi, 13 - 5 = 8

2 telah dipinjam, sekarang tinggal 1. 1 dikurangi 2 hasil negatif. Agar positif, pinjam dari angka di sebelah kirinya menjadi 11. Jadi, 11 - 2 = 9 1 telah dipinjam, sekarang tinggal 0. 0 dikurangi 6 hasil negatif. Agar positif, pinjam dari angka di sebelah kirinya menjadi 10. Jadi, 10 - 6 = 4

5 , 1 2 3 3 , 6 2 5 1 , 4 9 8

Tanda koma harus sejajar

5 telah dipinjam, sekarang tinggal 4. Jadi, 4 - 3 = 1

Keterangan: baca dari bawah.

(27)

[email protected]

c. Operasi Perkalian Pecahan Desimal Contoh: 1. 8 0,3 =....? Jawab: Cara 1: 3 24 8 0,3 8 2,4 10 10 × = × = =

Cara 2: (cara bersusun)

0,3 8 2,4×

8 3 = 24

Pada perkalian 8 0,3total ada 1 angka di belakang koma. Maka hasilnya, tanda koma 1 langkah ke kiri dari angka terakhir 2. 1,25 0,3 =....? Jawab: Cara 1: 125 3 375 1,25 0,3 0,375 100 10 1000 × = × = = Cara 2:

Pada perkalian 1,25 0,3total ada 3 angka di belakang koma. Maka hasilnya, tanda koma 3 langkah ke kiri dari angka terakhir

1,25 0,3 375 000 0,375 × +

1. 3 5 = 15. Tulis 5 yang satu diberikan ke kiri. 2. 3 2 = 6. Dari sebelumnya mendapat 1, menjadi 6 + 1 = 7. 3. 3 1 = 3. 4. 0 5 = 0. 4. 0 2 = 0. 5. 0 1 = 0. Jadi, 1,25 0,3 = 0,375. 3. 1,2 2,3 0,4 = ....? Jawab: 12 23 4 1,2 2,3 0,4 10 10 10 1.104 1,104 1.000 × × = × × = =

d. Operasi Pembagian Pecahan Desimal Contoh: 1. 0,75 : 15 = ...? Jawab: 75 0,75: 15 : 15 100 75: 15 100 5 100 0,05 = = = = 2. 0,48 : 0,6 = ...? Jawab: 48 6 0,48 : 0,6 : 100 10 48 10 100 6 48 0 = = × = 60 0 8 10 0,8 = =

(28)

[email protected]

D. MENGUBAH BILANGAN

1. Mengubah Pecahan Biasa Menjadi Desimal Contoh: × = = = × × = = = × 1 1 5 5 0,5 2 2 5 10 3 3 25 75 _0,75 4 4 25 100

2. Mengubah Desimal Menjadi Pecahan Biasa Contoh: 25 0,25 100 25: 25 100 : 25 1 4 = = = 275 2,75 100 275: 25 100 : 25 11 4 3 2 4 = = = =

3. Mengubah Pecahan Biasa Menjadi Persen Contoh: 1 1 _100% 2 2 50% 3 3 100% 4 4 75% = × = = × =

4. Mengubah Persen Menjadi Pecahan Biasa/ Campuran Contoh: 35 35% 100 35: 5 100 : 5 7 20 = = = 125 125% 100 125: 25 100 : 25 5 4 1 1 4 = = = =

5. Mengubah Desimal Menjadi Persen Contoh: 21 0,21 21% 100 316 3,16 316% 100 = = = =

6. Mengubah Persen Menjadi Desimal Contoh: 45 45% 0,45 100 105 105% 1,05 100 = = = =

(29)

[email protected]

SOAL DAN PEMBAHASAN

1. 324,01 + 56,3 – 2,097 = …. a. 378,213 b. 380,213 c. 379,213 d. 381,213 Pembahasan: Jumlahkan 324,01 + 56,3, yaitu: 324,01 56,3 380,31+

Hasilnya kurangkan dengan 2,097.

380,31 2,097 378,213− Jadi, 324,01 + 56,3 – 2,097 = 378,213 Jawaban: a 2. 5% dari 180 adalah …. a. 9 c. 15 b. 12 d. 18 Pembahasan: Ditanyakan 5% dari 180 . × = × = = 5 5% 180 180 100 900 100 9 Jawaban: a

3. Kebun Pak Ahmad luasnya 1.250 m2_{. Tiga per}

lima-nya digunakan untuk menanam pisang. Luas kebun untuk menanam pisang adalah ….

a. 500 m2

b. 750 m2

c. 1.000 m2

d. 1.100 m2

Pembahasan:

Diketahui luas kebun: 1.250 m2

Luas kebun untuk menanam pisang adalah

2 2 3 3.750 1.250 m 5 5 750 m × = = Jawaban: b

(30)

[email protected]

PERBANDINGAN DAN SKALA

BAB 5

A. MENULISKAN BENTUK PERBANDINGAN

A

A : B B =

Dibaca: A dibandingkan dengan B.

Contoh:

Umur Ayah = 50 tahun dan Umur Ibu = 40 tahun. a. Perbandingan umur Ayah dan umur Ibu. b. Jumlah umur Ayah dan umur Ibu. c. Selisih (beda) umur Ayah dan umur Ibu.

Jawab:

a. Perbandingan umur Ayah dan umur Ibu.

50 : 40 50 40 5 4 5: 4 = = = =

b. Jumlah umur Ayah dan umur Ibu = 50 + 40 = 90 c. Selisih umur Ayah dan umur Ibu = 50 – 40 =10

Catatan:

Selisih dinyatakan dengan bilangan positif.

B. BENTUK-BENTUK PERBANDINGAN

1. Perbandingan Senilai

Perbandingan senilai adalah suatu perbandingan antara nilai A dan nilai B, di mana jika nilai A ber-tambah besar, maka nilai B juga berber-tambah besar dan sebaliknya jika nilai A mengecil, maka nilai B juga mengecil.

Contoh perbandingan senilai:

Jumlah liter bensin dan jarak ditempuh.

Artinya: semakin banyak jumlah liter bensin yang dipakai semakin jauh jarak yang ditempuh.

Contoh:

Jika harga 3 buah buku adalah Rp 5.000,00. Berapakah harga 12 buah buku?

Jawab:

3 5.000 12 ....?

Dalam matematika, bentuk di atas dapat ditulis se-bagai berikut.

3 5.000 12 n

Maka nilai n dapat dicari dengan cara perbandingan senilai yaitu:

3 5.000 12= n

(31)

[email protected]

Jika dikalikan silang, bentuknya menjadi:

3 n 5.000 12 3n 60.000 60.000 n ₃ n 20.000 × = × = = =

Jadi, harga 12 buku adalah Rp 20.000,00.

2. Pebandingan Berbalik Nilai

Perbandingan berbalik nilai adalah suatu perban-dingan antara nilai A dan nilai B, di mana jika nilai A bertambah besar maka nilai B akan mengecil. Sebaliknya jika nilai A mengecil, maka nilai B mem-besar.

Contoh bentuk perbandingan berbalik nilai adalah:

Kecepatan kendaraan terhadap waktu tempuhnya. Artinya: Jika kecepatannya bertambah besar, maka waktu tempuhnya akan semakin kecil (sedikit).

Contoh:

Sebuah mobil menempuh jarak Jakarta–Bandung de-ngan kecepatan 50 km/jam dalam waktu 4 jam. Se-andainya kecepatan mobil itu 100 km/jam, berapa-kah waktu tempuhnya?

Jawab:

50 km/jam 4 jam 100 km/jam ....?

Dalam matematika, bentuk di atas ditulis: 50 4

100 n

Dengan perbandingan berbalik nilai, maka nilai n haruslah lebih kecil dari 4. Maka perbandingannya adalah:

50 n

100 4=

dengan perkalian silang didapat:

50 4 n 100 200 100n 200 n ₁₀₀ n 2 × = × = = =

Jadi, jika kecepatan mobil itu 100 km/jam maka waktu tempuhnya adalah 2 jam.

C. OPERASI HITUNG PERBANDINGAN

1. Untuk Perbandingan Dua Nilai Contoh 1:

Umur A dibanding umur B adalah 3 : 4. Jika umur B adalah 12 tahun, berapakah umur A?

Jawab: Diketahui: A : B = 3 : 4 atau A 3 B =4 B = 12 Ditanyakan: A = ....? A 3 B 4 3 A B 4 3 ₁₂ 4 36 4 9 = = × = × = =

(32)

[email protected]

A 3 B 4 3 A B 4 3 12 4 36 4 9 = = × = × = =

Jadi, umur A adalah 9 tahun.

Contoh 2:

Umur A dibanding umur B adalah 4 : 5. Jika umur A adalah 16 tahun, berapakah umur B?

Jawab: Diketahui: A : B = 4 : 5 atau A 4 B =5 A = 16 Ditanyakan: B = ....? A 4 B 5 5 A 4 B 4 B 5 A 5 A B 4 5 16 4 80 20 4 = × = × × = × × = × = = =

Jadi, umur B adalah 20 tahun.

2. Menentukan Suatu Nilai Jika Jumlah Perbandingan Diketahui

Contoh:

Umur A dibanding umur B adalah 3 : 5. Jika jumlah umur A dan umur B adalah 24 tahun, tentukanlah umur A dan umur B!

Jawab: Diketahui: A : B = 3 : 5 atau A 3 B =5 a b A + B = 24 Ditanyakan: Umur A = ....? Umur B = ....? - Umur A: Rumus a A (A B) a b = ´ + + Maka 3 A 24 3 5 3 ₂₄ 8 72 8 9 = × + = × = =

Jadi, umur A adalah 9 tahun.

- Umur B: Rumus b B (A B) a b = ´ + +

(33)

[email protected]

5 B 24 3 5 5 ₂₄ 8 120 8 15 = × + = × = =

3. Menentukan Suatu Nilai Jika Selisih Perbandingan Diketahui

Contoh:

Umur A dibanding umur B adalah 7 : 5.

Jika selisih antara umur A dan umur B adalah 10 tahun.

Tentukanlah umur A dan umur B.

Jawab: Diketahui: A : B = 7 : 5 atau A 7 B =5 a b A – B = 10 Ditanyakan: Umur A = ....? Umur B = ....? - Umur A: Rumus a A (A B) a b = × − − 7 A 10 7 5 7 10 2 70 2 35 = × − = × = =

Jadi, umur A adalah 35 tahun. - Umur B: Rumus b B (A B) a b = × − − 5 B 10 7 5 5 10 2 50 2 25 = × − = × = =

4. Untuk Perbandingan Tiga Nilai

Secara umum bentuk perbandingan tiga nilai dapat dituliskan dengan:

(34)

[email protected]

Contoh:

Perbandingan umur A, B, dan C adalah 2 : 3 : 4. Jika jumlah umur A, B, dan C adalah 36 tahun.

Tentukanlah: Umur A saja

Umur B saja Umur C saja. Jawab: Perbandingannya yaitu: A : B : C = 2 : 3 : 4 Jumlah umur (A + B + C) = 36. Maka: - Umur A: Rumus = × + + + + a A (A B C) a b c

(

2

)

(

)

A Jumlah umur A B C 2 3 4 2 36 9 72 9 8 = × + + + + = × = =

Jadi, umur A adalah 8 tahun. - Umur B: Rumus = × + + + + b B (A B C) a b c

(

3

)

(

)

B Jumlah umur A B C 2 3 4 3 36 9 108 9 12 = × + + + + = × = =

Jadi, umur B adalah 12 tahun. - Umur C: Rumus = × + + + + c C (A B C) a b c

(

)

(

)

4 C Jumlah umur A B C 2 3 4 4 ₃₆ 9 144 9 16 = × + + + + = × = =

Jadi, umur C adalah 16 tahun.

Contoh:

Tiga orang anak A, B, dan C mempunyai perban-dingan umur sebagai berikut.

A : B : C = 3 : 4 : 5 a b c

(35)

[email protected]

Jika jumlah umur A dan B adalah 14 tahun, tentu-kanlah: Umur A, B, C

Jawab:

)

5 C Jumlah umur A B 3 4 5 ₁₄ 7 70 7 10 = × + + = × = =

Jadi, umur C adalah 10 tahun.

Contoh:

Asmira, Bonia, dan Citra masing-masing mempunyai koleksi boneka. Perbandingan boneka milik Asmira, Bonia, dan Citra adalah 11 : 7 : 4. Jika selisih boneka Asmira dan Bonia adalah 16 buah, hitunglah banyaknya:

a. Boneka Asmira. b. Boneka Bonia. c. Boneka Citra.

(36)

[email protected]

Jawab:

Misalkan: Boneka Asmira =A

4 C selisih A B 11 7 4 16 4 16 = × − − = × =

Jadi, banyaknya boneka Citra = 16 buah.

D. SKALA

Skala pada peta menyatakan perbandingan antara ukuran pada gambar/peta dengan ukuran yang sebenarnya.

ukuran pada peta/gambar Skala

ukuran/jarak sebenarnya =

Contoh:

1. Jarak sebenarnya antara Jakarta–Bogor adalah 60 km. Jika jarak kedua kota itu pada peta 4 cm, berapa perbandingan skalanya?

Jawab:

Skala = Jarak pada peta : jarak sebenarnya = 4 cm : 60 km

= 4 cm : 6.000.000 cm = 4 : 6.000.000 (dibagi 4) = 1 : 1.500.000.

Jadi, perbandingan skala adalah 1 : 1.500.000. a b c

(37)

[email protected]

2. Skala pada peta tertulis 1 : 1.000.000. Jarak kota A dan B pada peta setelah diukur adalah 5 cm. Berapa kilometer jarak sebenarnya antara kota A dan kota B?

Jawab:

Skala 1 : 1.000.000 artinya:

1 cm pada skala mewakili 1.000.000 cm (10 km) pada jarak sebenarnya. Maka:

Jarak sebenarnya antara kota A dan kota B adalah: = 1.000.000 5 cm

= 5.000.000 cm = 50 km.

Jadi, jarak sebenarnya kota A dan B = 50 km.

Dengan menggunakan rumus:

= =

= ×

= =

Jarak pada peta Skala Jarak sebenarnya 1 5 cm 1.000.000 Jarak sebenarnya Jarak sebenarnya 5 cm 1.000.000 Jarak sebenarnya 5.000.000 cm Jarak sebenarnya 50 km

E. JARAK DAN KECEPATAN

Rumus menghitung jarak dan kecepatan

= ×

=

Jarak Kecepatan waktu Jarak Kecepatan

Waktu

Contoh:

1. Jarak kota A dan B adalah 200 km. Jika mobil menempuh kota A dan B dengan waktu 4 jam, berapakah kecepatan mobil tersebut!

Jawab: Jarak = 200 km Waktu = 4 jam jarak Kecepatan waktu 200 4 50 km/ jam = = =

2. Sebuah bus menempuh kota Cilacap-Yogyakarta dengan kepatan 60 km/jam dalam waktu 4 jam. Berapakah jarak kota Cilacap-Yogyakarta?

Jawab:

Kecepatan = 60 km/jam Waktu = 4 jam

Jarak kecepatan waktu 60 km/ jam 4 jam 240 km

= ×

(38)

[email protected]

SOAL DAN PEMBAHASAN

1. Perbandingan umur Ayah dan Anak adalah 6 : 2. Jika selisih umur keduanya adalah 24 tahun, maka umur anak adalah … tahun.

a. 10 b. 11 c. 12 d. 13

Pembahasan:

Perbandingan umur Ayah : Anak = 6 : 2 Selisih umur (Ayah–Anak) = 24

Rumus:

b

Umur Anak selisih umur (Ayah Anak) a b

= × −

− 2

Umur Anak selisih umur (Ayah Anak) 6 2 2 24 4 12 tahun = × − − = × = Jawaban: c

2. Jarak kota Semarang–Jakarta pada peta adalah 15 cm. Skala peta tersebut adalah 1 : 3.000.000, maka jarak sebenarnya adalah … km.

a. 45 b. 450 c. 20 d. 200 Pembahasan: Diketahui:

Jarak kota Semarang–Jakarta pada peta = 15 Skala peta tersebut = 1 : 3.000.000 = 1

3.000.000

Rumus:

Jarak pada peta Skala

Jarak sebenarnya =

jarak pada peta Jarak sebenarnya skala 15 1 3.000.000 15 3.000.000 1 45.000.000 cm 450 km = = × = = = Jawaban: b a b

(39)

[email protected]

A. PENGUKURAN PANJANG

km hm dam m dm cm mm turun 1 tingkat × 10 naik 1 tingkat : 10 Contoh: a. 5 km = 5 10 = 50 hm b. 3,75 hm = 3,75 100 m = 375 m c. 4,6 km = 4,6 100.000 cm = 460.000 cm d. 60 dm = 60 : 10 m = 6 m e. 5 km + 12 hm = (5 1000 m) + (12 100 m) = 5.000 m + 1.200 m = 6.200 m f. 120 cm + 10 dam = (120 : 100 m) + (10 10 m) = 1,2 m + 100 m = 101,2 m

B. PENGUKURAN LUAS

Pada pengukuran luas, satuan yang umum digunakan ada 2 macam yaitu:

1. Satuan dalam sistem metrik 2. Satuan dalam sistem are

1. Satuan dalam Sistem Metrik

km2 hm2 dam2 m2 dm2 cm2 mm2 turun 1 tingkat × 100 naik 1 tingkat : 100 Contoh: 1. 1 km2_{= 100 hm}2 = 10.000 dam2 = 1.000.000 m2 2. 4 dam2_{= 4 100 m}2 = 400 m2 3. 325 dam2_{= 325 : 100 hm}2 _{= 3,25 hm}2

PENGUKURAN

BAB 6

Keterangan: km = kilometer hm = hektometer dam = dekameter m = meter dm = desimeter cm = sentimeter mm = milimeter

(40)

[email protected]

4. 2,34 hm2_{+ 0,7 dam}2_{= .... m}2 Jawab: 2,34 hm2 _{= 2,34 10.000 m}2 _{= 23.400 m}2 0,7 dam2_{= 0,7 100 m}2 = 70 m2 Jadi, 2,34 hm2_{+ 0,7 dam}2_{= 23.400 m2 – 70 m}2 = 23.470 m2 5. 7 km2_{– 64 dam}2_{– 250 m}2_{= .... hm}2_. Jawab: 7 km2_{= 7 100 hm}2 = 700 hm2 64 dam2_{= 64 : 100 hm}2 = 0,64 hm2 250 m2_{= 250 : 10.000 hm}2 = 0,025 hm2 Jadi, 7 km2_{– 64 dam}2_{– 250 m}2 = 700 hm2_{– 0,64 hm}2_{– 0,025} = 699,335 hm2

2. Satuan dalam Sistem Are

ka ha daa a da ca ma turun 1 tingkat × 10 naik 1 tingkat : 10 Penting! 1 ha =1 hm2_{= 10.000 m}2 1 a = 1 dam2_{= 100 m}2 1 ca = 1 m2 Contoh: a. 825 ca = 825 : 10 da = 82,5 da. b. 4 are = 4 dam2 = 4 100 m2 = 400 m2_. c. 45 are + 25 ca = … m2 Jawab: 45 are + 25 ca = (45 100) m2 _{+ 25 m}2 = (4.500) m2 _{+ 25 m}2 = 4.525 m2 d. 5 ha – 200 dam2_{+ 6.500 m}2_{= ... are} Jawab: 5 ha = 5 100 are = 500 are 200 dam2_{= 200 1 are} = 200 are 6.500 m2_{= 6.500 : 100 are} = 65 are Jadi, 5 ha – 200 dam2_{+ 6.500 m}2

= 500 are – 200 are + 65 are = 365 are. Keterangan: ka = kiloare ha = hektoare daa = dekaare a = are da = desiare ca = sentiare ma = miliare

(41)

[email protected]

C. PENGUKURAN VOLUME (ISI)

1. Satuan Volume Sistem Kubik

km3 hm3 dam3 m3 dm3 cm3 mm3 turun 1 tingkat × 1000 naik 1 tingkat : 1000 Contoh: a. 2.500 mm3 _{= 2.500 : 1.000 cm}3 = 2,5 cm3_. b. 6,75 dam3 _{= 6,75 1.000 m}3 = 6.750 m3_.

2. Satuan Volume Sistem Liter

k h da d c m turun 1 tingkat × 10 naik 1 tingkat : 10 Penting! 1 k = 1 m3 1 = 1 dm3_{= 1.000 cm}3_{=1.000 cc} 1 m = 1 cm3 1 cm3_{= 1 cc} Contoh:

a. 2,5 k= 2,5 10 h (turun 1 tingkat dikali 10) = 25 h.

b. 736 c  = 736 : 100 (naik 2 tingkat dibagi 100) = 7,36 . c. 0,785 m3_{= ....}__. Jawab: 0,785 m3_{= 0,785 1000 dm}3 = 785 dm3 = 785. d. 89,5 d = .... cc . Jawab: 1 d = 0,1 liter = 0,1 1.000 cc = 100 cc. Sehingga: 89,5 d = 89,5 100 cc = 8.950 cc.

(42)

[email protected]

D. PENGUKURAN BERAT

kg hg dag g dg cg mg turun 1 tingkat × 10 naik 1 tingkat : 10 HAFALKAN!

1 ton = 1.000 kg 1 ton = 10 kwintal 1 kwintal = 100 kg 1 kg = 10 ons 1 kg = 2 pon 1 pon = 5 ons 1 ons = 1 hg Contoh: a. 3 kg = 3 10.000 dg = 30.000 dg. b. 465 g = 465 : 100 hg = 4,65 hg.

c. 2,5 ton + 4 kwintal + 200 pon = .... kg.

Jawab: 2,5 ton = 2,5 1.000 kg = 2.500 kg 4 kwintal = 4 100 kg = 400 kg 200 pon = 200 : 2 kg = 100 kg Jadi,

2,5 ton + 4 kwintal + 200 pon = 2.500 kg + 400 kg + 100 kg

= 3.000 kg.

d. 70 pon = .... ons.

Jawab:

70 pon = 70 5 ons (ingat, 1 pon = 5 ons) = 350 ons.

E. PENGUKURAN WAKTU

Satuan waktu yang sering digunakan adalah:

1 millenium = 1.000 tahun 1 abad = 100 tahun 1 windu = 8 tahun 1 dasawarsa = 10 tahun 1 dekade = 10 tahun 1 lustrum = 5 tahun 1 tahun = 12 bulan 1 tahun = 52 minggu 1 tahun = 365 hari 1 tahun = 2 semester 1 tahun = 4 triwulan 1 tahun = 3 caturwulan 1 bulan = 4 minggu 1 bulan = 30 hari 1 minggu = 7 hari 1 hari = 24 jam 1 jam = 60 menit 1 menit = 60 detik (sekon) 1 jam =3.600 detik Contoh: a. 1 2 3 abad = .... tahun. Jawab: 1 2 3 abad = 1 2 3 100 tahun = 350 tahun. Keterangan: kg = kilogram hg =hektogram dag = dekagram g = gram dg = desigram cg = sentigram mg = miligram

(43)

[email protected]

b. 2 tahun + 7 bulan = .... hari.

Jawab: 2 tahun = 2 365 hari = 730 hari 7 bulan = 7 30 hari = 210 hari Jadi,

2 tahun + 7 bulan = 730 hari + 210 hari = 940 hari.

c. 21₂Jam = .... menit = ....detik.

Jawab: • 1 2 2 Jam =21₂ _{60 menit} = 150 menit. • 1 2 2 jam = 1 2 2 3.600 detik = 9.000 detik. d. 25.200 detik = .... menit = .... jam

Jawab:

• 25.200 detik = 25.200 : 60 menit = 420 menit

• 25.200 detik = 25.200 : 3.600 jam = 7 jam

e. 1 jam 35 menit 50 detik 2 jam 30 menit 45 detik + .... jam ... menit ....detik. Jawab:

1 jam 35 menit 50 detik 2 jam 30 menit 45 detik +

3 jam 65 menit 95 detik tetap diubah diubah

Menjadi:

3 jam (60 + 5) menit (60 + 35) menit 3 jam 1 jam 5 menit 1 menit 35 detik. (3 + 1) jam (5 + 1) menit (35 detik)

4 jam 6 menit 35 detik

Jadi,

1 jam 35 menit 50 detik 2 jam 30 menit 45 detik +

4 jam 6 menit 35 detik

F. PENGUKURAN JUMLAH (KUANTITAS)

HAFALKAN! 1 rim = 500 lembar 1 gros = 144 buah 1 kodi = 20 buah 1 lusin = 12 buah 1 gros = 12 lusin Contoh: a. 1 4 3 kodi = .... buah. Jawab: 1 4 3 _{kodi =} 1 4 3 _{20 (1 kodi = 20 buah)} = 65 buah. b. 3 gros = .... lusin = .... buah

Jawab:

• 3 gros = 3 12 lusin (1 gros = 12 lusin) = 36 lusin

• 3 gros = 3 144 buah (1 gross = 144 buah) = 432 buah

(44)

[email protected]

G. PENGUKURAN SUHU

- Satuan ukuran suhu yang sering digunakan adalah: • CELCIUS (C)

• REAMUR (R) • FAHRENHEIT (F) • KELVIN (K)

- Satuan ukuran suhu adalah derajat (simbol:o₎

- Alat pengukur suhu dinamakan TERMOMETER.

1. Perbandingan Skala pada Termometer

- Celcius mempunyai skala 100 (dari 0o_sampai

100 o_).

- Reamur mempunyai skala 80 (dari 0o_{sampai 80}o_).

- Fahrenheit mempunyai skala 180 (dari 32o_sampai

212 o_).

- Kelvin mempunyai skala 100 (dari 273o_sampai

373 o_).

Karena skala pada termometer Kelvin sama dengan skala pada termometer Celcius, maka:

K = C + 273

Perbandingan skala ketiga termometer yang lain adalah:

C : R : (F – 32) = 100 : 80 : 180 Disederhanakan (dengan dibagi 20) menjadi, C : R : (F – 32) = 5 : 4 : 9

 Untuk mengubah derajat Celcius ke Reamur dan sebaliknya gunakan rumus:

5 C R 4 = × atau R 4 C 5 = ×

 Untuk mengubah derajat Celcius ke Fahrenheit dan sebaliknya gunakan rumus:

( ) 5 C F 32 9 = × − atau F 9 C 32 5   =_ × +_  

 Untuk mengubah derajat Reamur ke Fahrenheit dan sebaliknya gunakan rumus:

( ) 4 R F 32 9 = × − atau F 9 R 32 4   =_ × +_   Contoh: 1. 20 o_{C = ....}o_R Jawab: o o 4 R C 5 4 ₂₀ 5 16 = × = × = 2. 40 o_{C = ....}o_F Jawab:

(45)

[email protected]

  =_ × +_     =_ × _+     =_ _+   = + = o 9 F C 32 5 9 40 32 5 360 32 5 72 32 104 F 3. 176 o_{F = ....}o_R Jawab: ( ) ( ) o 4 R F 32 9 4 _{176 32} 9 4 ₁₄₄ 9 576 9 64 = × − = × − = × = =

H. PENGUKURAN KADAR EMAS

- Kadar yaitu bagian yang murni dari suatu benda. - Kadar emas yaitu bagian yang murni dari emas. - Satuan dari kadar emas adalah karat.

- Emas murni mempunyai kadar 24 karat.

Rumus Mencari Kadar Emas.

Berat emas murni

Kadar emas 24 karat

Berat seluruh benda

= ×

Rumus Mencari Persentase Emas Murni

Kadar emas

Persentase emas murni 100%

24 karat

= ×

Contoh:

1. Sebuah kalung beratnya 12 gram. Jika pada kalung tersebut terdapat 9 gram emas murni, tentukanlah kadar emas pada kalung itu.

Jawab:

Berat seluruh benda = 12 gram Berat emas murni = 9 gram

Berat emas murni

Kadar emas 24 karat

Berat seluruh benda 9 gram _{24 karat} 12 gram 9 24 karat 12 216 karat 12 18 karat = × = × = × = =

Jadi, kadar emas pada kalung itu adalah 18 karat. 2. Sebuah cincin mempunyai kadar emas 18 karat.

Berapakah persentase emas murninya?

Jawab:

(46)

[email protected]

kadar emas

Persentase emas murni 100%

24 karat 18 karat _100% 24 karat 18 _100% 24 3 _100% 4 75% = × = × = × = × =

Jadi, persentase emas murninya adalah 75%.

I. PENGUKURAN DEBIT AIR

Debit air adalah kecepatan aliran zat cair yang

dinya-takan dalam satuan liter perdetik (liter/detik) atau dalam satuan meter kubik perdetik (m3_/detik).

Rumus:

( )

Volume dalam liter Debit

Waktu dalam detik =

Contoh:

Sebuah sumber mata air setiap 2 jam mampu mengeluar-kan air sebanyak 72.000 liter. Hitunglah debit air pada sumber itu. Jawab: Waktu = 2 jam = 2 3.600 detik = 7.200 detik. Volume = 72.000 liter. ( ) ( )

Waktu dalam detik 72.000 liter 7.200 detik 10 liter/detik = = =

Jadi, debit airnya adalah 10 liter/detik.

SOAL DAN PEMBAHASAN

1. Sebuah koperasi mendapat kiriman kedelai seban-yak 60 karung yang masing-masing beratnya 45 kg. Maka berat seluruhnya adalah … kw.

a. 25 c. 27 b. 26 d. 28

Pembahasan:

Berat seluruhnya = 60 karung 45 kg/karung = 2700 kg

= 27 kw

Jawaban: c

2. 2 windu + 3 dasawarsa = … tahun. a. 46 c. 50 b. 48 d. 52

Pembahasan:

2 windu = 2 8 tahun = 16 tahun 3 dasawarsa = 3 10 = 30 tahun Jadi,

2 windu + 3 dasawarsa = 16 tahun + 30 tahun = 46 tahun

(47)

[email protected]

3. Keluarga pak Anton berangkat ke Bandung dari Jakarta menggunakan mobil pukul 08.45. Apabila Keluarga pak Anton tiba di Bandung pukul 11.30, maka lamanya perjalanan adalah ….

a. 3 jam 15 menit c. 2 jam 15 menit b. 3 jam 45 menit d. 2 jam 45 menit

Pembahasan:

Lamanya perjalanan adalah = 11.30 – 08.45

= 11 jam 30 menit – 8 jam 45 menit = 10 jam 90 menit – 8 jam 45 menit = (10 jam + 90 menit) – (8 jam + 45 menit) = (10 – 8)jam + (90 menit – 45 menit) = 2 jam + 45 menit

= 2 jam 45 menit

Jawaban: d

4. Sebuah pipa mengalirkan air selama 5 menit seba-nyak 300 liter. Debit air itu adalah … liter/jam. a. 60 c. 1.500

b. 900 d. 3.600

Pembahasan:

Waktu = 5 menit = 5 jam 1 jam

60 =12

Banyak air = volume = 300 liter

( ) ( )

1 12

Waktu dalam jam 300 liter jam 300 12 3.600 liter/jam = = = × = ( ) ( ) 1 12

Waktu dalam jam 300 liter jam 300 12 3.600 liter/jam = = = × = Jawaban: d 5. 50 o_{F = …}o_C. a. 10 c. 20 b. 15 d. 25 Pembahasan: ( ) ( ) o 5 C F 32 9 5 _{50 32} 9 5 ₁₈ 9 10 C = × − = × − = × = Jawaban: a 6. 18 km/jam = ... m/detik. a. 5 c. 15 b. 10 d. 20 Pembahasan: 18 1.000 m 18 km/ jam 3.600 detik 18.000 m 3.600 detik 5 m/detik × = = = Jawaban: a