Macam-macam Tegangan dan Lambangnya
Tegangan Normal
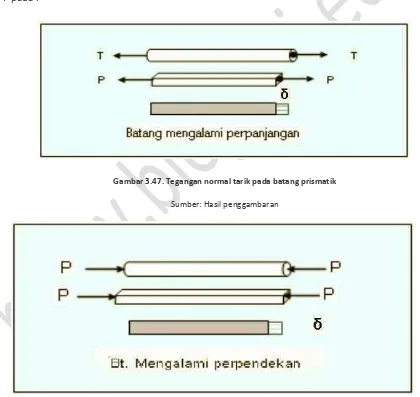
Pengetahuan dan pengertian tentang bahan dan perilakunya jika mendapat gaya atau beban sangat dibutuhkan di bidang teknik bangunan. Jika suatu batang prismatik, dengan luas tampang seragam di sepanjang batang, menerima beban atau gaya searah dengan panjang batang, maka gaya tersebut akan menimbukan tegangan atau tekanan pada tampang batang. Tegangan atau tekanan merupakan besaran gaya per satuan luas tampang. Sehingga besar tegangan yang dialami batang prismatik tersebut masing-masing sebesar T/A dan P/A. Pada gambar 3.47, A merupakan luas tampang melintang batang yang dikena T atau P pada .
Gambar 3.47. Tegangan normal tarik pada batang prismatik
Sumber: Hasil penggambaran
Gambar 3.48. Tegangan normal tekan pada batang prismatik
Jika batang tersebut menerima gaya tarikan (Gambar 3.47), maka akan timbul tegangan tarik. Sedang jika batang menerima gaya tekan, (Gambar 3.48) akan menyebabkan tegangan tekan pada tampang melintang batang. Tegangan dinyatakan dengan simbol σ. Secara umum besaran tegangan dapat ditulis dengan formula sebagai berikut.
σ = P / A (3.5)
Dimana: σ = Tegangan P = Besarnya gaya A = Luas tampang
Berdasarkan peristiwa tersebut maka tegangan normal dibagi menjadi : a. Tegangan Tarik (σ
t), yaitu tegangan yang timbul akibat gaya tarik. Rumus :
σ
t = tegangan tarik (kg/cm 2
atau kg/mm
2
)
P = gaya tarik (kg)
F = Luas penampang (cm
2
) 1. Contoh soal :
Diketahui : P = 9600 kg, b = 8 cm, h = 12 cm Ditanyakan : Tegangan tarik yang timbul (σ
t) ?
2. Contoh soal cerita:
Sebuah karet panjangnya 15 cm ditarik dengan gaya yang besar tetapi tidak sampai putus. Apabila gaya tarik dilepas, maka panjang karet bukan lagi 15 cm tetapi sudah menjadi 15.2 cm. Pertambahan panjang ini terjadi akibat regangan. Besarnya regangan adalah : 0.2 cm.
3. Contoh soal hitungan :
Diketahui :P = 2100 kg; b = 5 cm; h = 7 cm
L = 400 cm; E = 10
5
kg/cm
2
Ditanyakan : a. Tegangan tarik yang timbul (σ
t) ?
b. Perpanjangan yang timbul (ΔL) ? c. Regangan yang timbul (ε) ? jawab :
b. Tega ga teka atau desak σ
d), yaitu tegangan yang timbul akibat gaya tekan atau desak.
Rumus :
σ
d = tegangan tekan atau desak (kg/cm 2
atau kg/mm
2
)
P = gaya tekan (kg)
F = Luas penampang (cm
2
1. Contoh soal :
Diketahui : P = 785 kg; d = 10 mm Dita aka : Tega ga teka a g ti ul σ
d) ?
Jawab :
Tegangan geser
(S
hear
)
Jika gaya normal/tangensial merupakan gaya sejajar arah memanjang batang, gaya geser merupakan gaya yang berarah tegak lurus dengan panjang batang. Ilustrasi geseran ditunjukkan pada Gambar 3.49. Batang vertikal pada gambar tersebut menerima geseran di dua bagian potongan m dan potongan n. Besaran tega ga geser di ataka de ga si ol τ dala satua . Jika esara ga a geser S dikerjaka pada ata g aka e i ulka tega ga geser τ . Tegangan geser (τ), yaitu tegangan yang timbul akibat gaya geser atau gaya lintang. Ciri dari gaya geser atau gaya lintang adalah melintang batang atau tegak lurus
batang.
Rumus :
τ = tegangan geser (kg/mm2, kg/cm2, ton/m2)
Gambar 3.49. Geser pada sambungan baut
Sumber: Hasil penggambaran
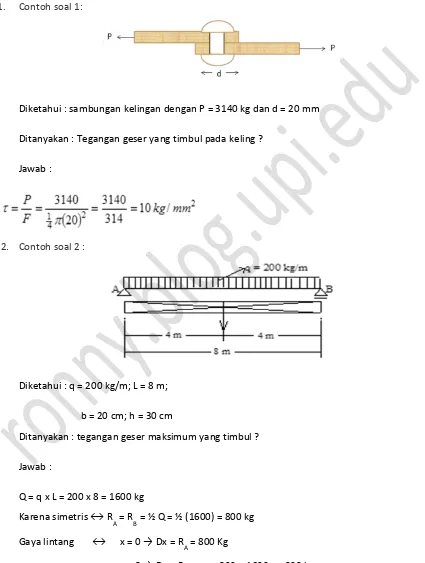
1. Contoh soal 1:
Diketahui : sambungan kelingan dengan P = 3140 kg dan d = 20 mm Ditanyakan : Tegangan geser yang timbul pada keling ?
Jawab :
2. Contoh soal 2 :
Diketahui : q = 200 kg/m; L = 8 m; b = 20 cm; h = 30 cm
Ditanyakan : tegangan geser maksimum yang timbul ? Jawab :
Q = q x L = 200 x 8 = 1600 kg Karena simetris ↔ R
A = RB = ½ Q = ½ (1600) = 800 kg
Gaya lintang ↔ x = 0 → Dx = R
A = 800 Kg
x = 8 → Dx = R
Tegangan Lentur/Lengkung
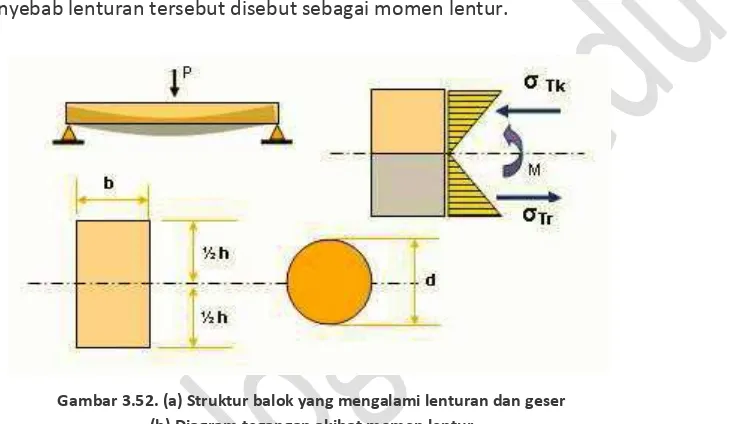
Balok merupakan struktur yang menerima beban tegak lurus terhadap arah panjang. Karenanya balok umumnya mengalami lenturan dan geseran pada bagian di dekat dudukan. Gaya geser, sering disebut gaya lintang akan menyebabkan tegangan geser. Gambar 3.52 menunjukkan diagram geser balok yang terjadi di sepanjang batang. Ditunjukkan pula diagram gaya momen yang menyebabkan lenturan pada balok. Momen penyebab lenturan tersebut disebut sebagai momen lentur.
Gambar 3.52. (a) Struktur balok yang mengalami lenturan dan geser (b) Diagram tegangan akibat momen lentur
Sumber: Hasil penggambaran
Tegangan lentur / lengkung (σ
L
), yaitu tegangan yang terjadi akibat momen lentur atau lengkung yang timbul. Momen yang diperhitungkan adalah momen maksimum.
Rumus : σ
L
= tegangan lentur atau lengkung (kg/cm
2
)
M
L
= momen lengkung maksimum (kg/cm)
W
L
= momen tahanan linier (cm
3
)
= 1/12 b h3 untuk tampang persegi panjang dengan lebar b dan tingg h
= πd4/64 untuk tampang lingkaran
1. Contoh Soal : Diketahui : balok jepit
P = 200 kg, L = 200 cm, b = 15 cm, h = 15 cm
Ditanyakan : tegangan lentur yang timbul pada balok ? Jawab :
Momen = P .L = 200 . 200 = 40000 kgcm
Tegangan Tumpu
Tegangan tumpu (σ
s), yaitu tegangan yang timbul akibat gaya yang menumpu pada dinding lubang. Hal
ini terlihat pada sambungan kelingan atau sambungan dengan mur baut. Apabila pada sambungan bekerja gaya, paku keling atau mur baut dengan lubangnya diadu kekuatannya. Jika paku keling atau mur baut menerima gaya maksimum akan terjadi tegangan geser. Jika lubang paku keling atau lubang mur baut yang menerima gaya maksimum, terjadi tegangan tumpu.
Rumus : σ
s = tegangan tumpu (kg/cm 2
) P = gaya tumpu
F = luas bidang tumpu.
Luas bidang tumpu ditentukan dengan lubang pelat atas yang tertumpu adalah ½ keliling dan lubang plat bawah yang tertumpu juga ½ keliling, sehingga jika digabungkan kedua-duanya menjadi satu keliling atau πd. Tinggi lubang seluruhnya adalah 2S (S = tebal plat) menjadi setebal pelat yaitu S. Lubang yang tertumpu juga tidak merata dimana dari tepi nol tak terhingga sampai ketengah membesar. Akibat dari tidak meratanya gaya-gaya tersebut dapat dibulatkan menjadi = d. Jadi luas bidang tumpu untuk lubang paku keling atau mur baut menjadi d.S.
Rumus :
Ada tiga hal kemungkinan yang terjadi jika sambungan menerima gaya :
I. Paku keling atau mur baut putus. Berarti pada saat itu
Menimbulkan tegangan geser yaitu
geser F
s
d
P
P paku keling atau mur baut
menerima gaya maksimum
s
d
P P
II. Paku keling atau mur baut kuat tapi lubangnya rusak (membesar). Berarti pada sat itu dinding lubang menerima gaya maksimum
Menimbulkan tegangan tumpu yaitu
III. Paku keling atau mur baut dan lubangnya kuat (sama-sama kuat). Berarti kedua-duanya menerima gay maksimum.
Menimbulkan tegangan geser dan tegangan tumpu
Rumus geser = Rumus tumpu
= ↔ P = τ.F (geser); P = d.S.σ
Jadi untuk sambungan tunggal :
• Jika d = 3.2 S dapat digunakan rumus geser atau tumpu
• Jika d > 3.2 S digunakan rumus tumpu
• Jika d < 3.2 S digunakan rumus geser Untuk sambungan kembar atau ganda :
• Jika d > 1.6 S digunakan rumus tumpu
• Jika d < 1.6 S digunakan rumus geser
1. Contoh soal :
Diketahui sambungan tunggal dengan mur baut dengan diameter 20 mm, tebal pelat (S) = 5 mm ditarik dengan gaya (P) sebesar 5000 kg. Hitung tegangan yang timbul ?
Diketahui : d = 20 mm; S = 5 mm; P = 5000 kg Ditanyakan : tegangan yang timbul ?
Jawab :
. X S= . = ↔ d > . S, aitu > , aka digu aka ru us tu pu.
Tegangan Torsi (Puntir)
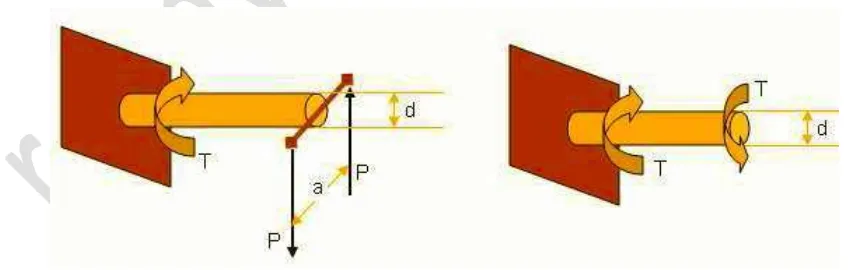
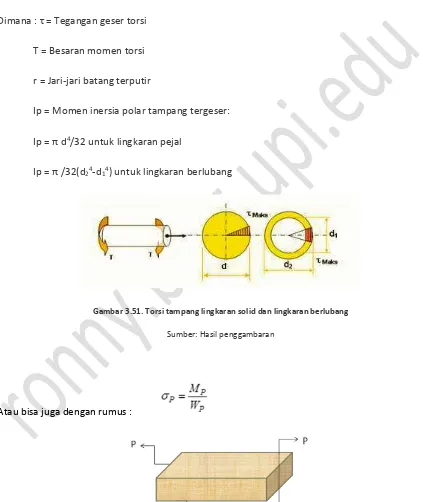
Terkadang suatu komponen struktur menerima puntiran, kopel puntir atau momen puntiran. Puntiran tersebut menimbulkan tegangan geseran yang disebut sebagai tegangan geser puntir. Ilustrasi batang yang mengalami torsi ditunjukkan pada Gambar 3.50.
Gambar 3.50. Batang yang mengalami puntiran (torsion)
Tega ga pu tir σ
P
), yaitu tegangan yang timbul akibat momen puntir. Besarnya tegangan yang diakibatkan oleh momen puntir/torsi pada tampang batang lingkaran dan lingkaran berlubang dituliskan dengan formula sebagai berikut. Rumus :
τ = T . r / Ip
Dimana : τ = Tegangan geser torsi
T = Besaran momen torsi
r = Jari-jari batang terputir
Ip = Momen inersia polar tampang tergeser:
Ip = π d4/32 untuk lingkaran pejal
Ip = π /32(d24-d14) untuk lingkaran berlubang
Gambar 3.51. Torsi tampang lingkaran solid dan lingkaran berlubang
Sumber: Hasil penggambaran
σ
P
= tegangan puntir (kg/cm
2
),
M
P
= momen puntir (kg.cm)
W
P
= momen tahanan polar (cm
3
)
1. Contoh soal :
Diketahui : d = 10 cm; P = 300 kg; L = 30 cm
Ditanyakan : tega ga pu tir a g ti ul σ
P) ?
Jawab : M
P
= P . L = 300 x 30 = 9000 kgcm
W
P
= 0.2 d
3
= 0.2 (10)
3
= 0.2 (1000) = 200 cm
3
Tegangan Tekuk
Tegangan tekuk, yaitu tegangan yang timbul akibat gaya tekan yang menekuk batang. Menurut Euler besarnya gaya tekuk adalah , dengan PK= ga a tekuk kg , π = . , E = odulus elastsitas kg/ 2), I =
momen Inersia (cm4), L
K = panjang tekuk. Panjang tekuk ini akan bergantung pada keadaan ujung-ujung
Bidang batang yang tertekuk akan mengalami kelangsingan dimana besarnya kelangsingan adalah:
λ = kelangsingan (dibaca lambda)
L
K
= panjang tekuk (cm)
i = jari-jari inersia (cm)
dimana :
i = jari-jari inersia (cm)
I = momen inersia linier (cm
4
)
F = luas penampang (cm
2
Rumus Euler menjadi
2
Rumus Euler menjadi
2
Rumus Euler menjadi
2
Rumus Euler menjadi
1. Contoh soal :
Tiang kayu tingginya 5 m, kedua ujungnya dianggap jepit akan menerima gaya tekan sentris. Jika E = 10
5
kg/cm
2
tentukanlah gaya tekan sentris maksimum pada tiang. Tentukan pula kelangsingan yang timbul pada tiang jika penampang kayu 12 x 12 cm !
Jawab : π
2
= 3.14
2
= 10 (dibulatkan)
Rumus Euleur hanya dapat digunakan apabila kelangsingan yang timbul sama atau lebih besar dari kelangsingan bahan. Kelangsingan bahan dihitung dengan rumus .
Misalnya:
1. Untuk baja E = 2.10
6
kg/cm
2
, σ
K= 2000 kg/cm 2
. Maka kelangsingan bahan :
2. Untuk kayu E = 10
5
kg/cm
2
, σ
K = 100 kg/cm 2.
Maka kelangsingan bahan :
• Mencari
• Mencari kelangsingan bahan σ
K
dan E diketahui
• Mencari kelangsingan yang timbul
• Terakhir dibandingkan kelangsingan yang timbul dengan kelangsingan bahan jika :
rumus Euler dapat dipakai tapi apabila maka rumus Euler tidak dapat digunakan.
Tegangan Kombinasi/Ideal
Tegangan kombinasi (σ
i
), dalam beberapa keadaan, sebuah batang tidak hanya dibebani oleh gaya-gaya atau momen saja, tetapi kombinasi dari keduanya. Misalnya tegangan lentur dan tegangan geser.
1. Contoh soal :
Diketahui : q = 200 kg/m; L = 8 m; b = 20 cm; h = 30 cm Ditanyakan : tegangan kombinasi (σi) yang timbul ?
Jawab :
Q = q x L = 200 x 8 = 1600 kg Karena simetris ↔ R
A = RB = ½ Q = ½ (1600) = 800 kg
x = 8 → Dx = R
A– qx = 800 – 1600 = - 800 kg
Momen ↔ =160000 kgcm
Tegangan kombinasi :
Tegangan Geser pada Balok
Balok yang menerima lentur dapat mengalami geseran ke arah memanjang. Ilustrasi perilaku balok yang mengalami geseran pada arah memanjang beserta diagram tegangan geser yang terjadi ditunjukkan seperti pada Gambar 3.53.
Gambar 3.53. Balok yang mengalami geseran arah memanjang
Sumber: Hasil penggambaran
τmaks = 3 V / 2A (3.10)
Dimana: V = Gaya geser / gaya lintang
A = Luas tampang melintang batang
= b.h untuk tampang persegi panjang
Sedangkan formula tegangan geser maksimum yang terjadi untuk tampang lingkaran adalah sebagai berikut.
τmaks = 4 V/ 3πr2 = 4 V / 3A (3.11)
Dimana: V = Gaya geser / gaya lintang
A = Luas tampang melintang batang