BAB IV PENGUMPULAN DAN PENGOLAHAN DATA

(1)

FORMAT LAPORAN MODUL III DISTRIBUSI VARIABEL

ACAK DISKRIT

ABSTRAK

ABSTRACT

KATA PENGANTAR

DAFTAR ISI

DAFTAR TABEL

DAFTAR GAMBAR

DAFTAR LAMPIRAN

BAB I PENDAHULUAN

(kalimat pengantar) 1.1 Latar Belakang

1.2 Tujuan Penulisan Laporan 1.3 Perumusan Masalah 1.4 Batasan masalah 1.5 Sistematika Penulisan

BAB II LANDASAN TEORI

(Minimal memuat teori tentang pembagian data, jenis-jenis distribusi variabel acak diskrit, dan aplikasi penggunaan distribusi variabel acak diskrit)

BAB III METODOLOGI PENELITIAN

BAB IV PENGUMPULAN DAN PENGOLAHAN DATA

(kalimat pengantar)

4.1 Pengumpulan Data

(2)

4.1.1 Hasil Pengumpulan Data Untuk Percobaan Distribusi Binomial

(kalimat pengantar) Jumlah sampel : Jumlah populasi : Jumlah produk cacat : Jumlah produk baik :

Tabel x.Rekapitulasi Jumlah Cacat Dan Baik dalam Sampel

4.1.2 Hasil Pengumpulan Data Untuk Percobaan Distribusi Hipergeometri

(kalimat pengantar) Jumlah sampel : Jumlah populasi : Jumlah produk cacat : Jumlah produk baik :

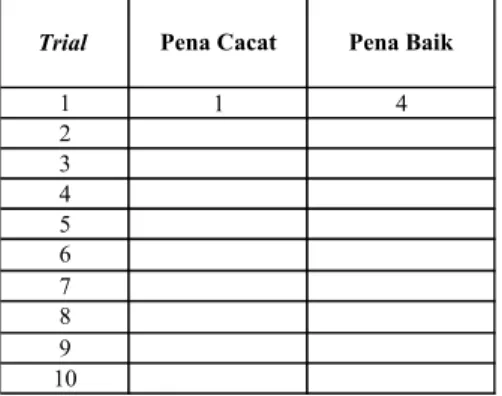
Tabel x.Rekapitulasi Jumlah Produk Cacat Dan Baik Dalam Sampel

1 1 4 2 3 4 5 6 7 8 9 10

Pena Cacat Pena Baik Trial 1 1 4 2 3 4 5 6 7 8 9 10

Pena Cacat Pena Baik Trial

(3)

4.1.3 Hasil Pengumpulan Data Untuk Percobaan Distribusi Poisson

(kalimat pengantar)

Tabel x.Rekapitulasi Waktu Kedatangan Kendaraan Di Jalan XX Pukul AA:BB – CC:DD

(Selanjutnya Terlampir pada Lampiran A)

4.2 Pengolahan Data

(kalimat pengantar)

4.2.1 Perhitungan Data Pengamatan Untuk Distribusi Binomial

(kalimat pengantar)

4.2.1.1Perhitungan Distribusi Frekuensi (kalimat pengantar)

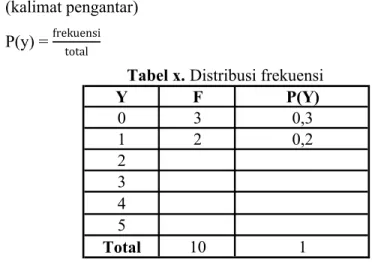
P(y) = frekuensi

total

Tabel x.Distribusi frekuensi

Contoh perhitungan (2 buah)

1 Motor 7:00:15 2 Mobil 7:00:17 3 Mobil 7:00:20 4 Motor 7:00:26 5 Motor 7:00:29 6 Motor 7:00:32 7 Mobil 7:00:35 8 Motor 7:00:39 9 Motor 7:00:41 10 Mobil 7:00:43

Kendaraan ke Jenis Kendaraan Waktu Kedatangan

Y F P(Y) 0 3 0,3 1 2 0,2 2 3 4 5 Total 10 1

(4)

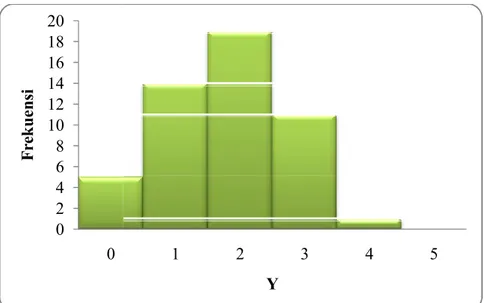
Gambar x.Grafik Frekuensi Terambilnya Produk Cacat Sebanyak Y

4.2.1.2 Perhitungan Ulang Percobaan Terhadap P(Y) (kalimat pengantar)

4.2.1.2.1Perhitungan Ulang Terhadap P(0)

Perhitungan ulang terhadap P(0) dilakukan setiap 10 menggunakan rumus P(Y).

P(Y) = f

Jumlah_Trial

Tabel

Contoh perhitungan (2 buah) 0 5 10 15 20 25 0 F re k u en si

Grafik Frekuensi Terambilnya Produk Cacat Sebanyak Y

Perhitungan Ulang Percobaan Terhadap P(Y) (kalimat pengantar)

Perhitungan Ulang Terhadap P(0)

Perhitungan ulang terhadap P(0) dilakukan setiap 10 trial

menggunakan rumus P(Y).

Trial

Tabel x.Ulangan Percobaan terhadap p(0)

1 2 3 4 Y Trial f(kum) P(0) 1 2 3 4 5 6 7 8 9 10

trial dengan 5

(5)

Perhitungan secara teoritis : P (Y) = _C_yn_.py_.qn-y

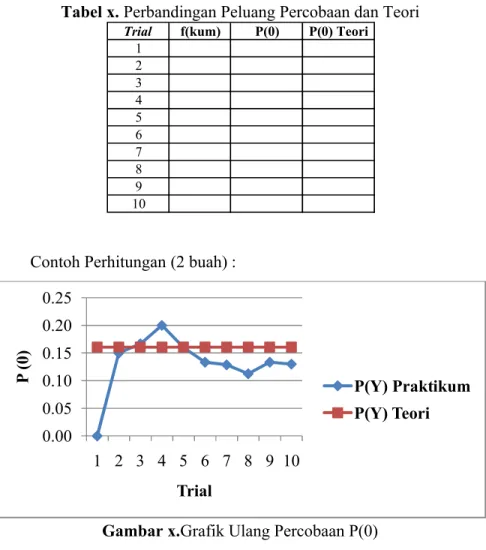
Tabel x. Perbandingan Peluang Percobaan dan Teori

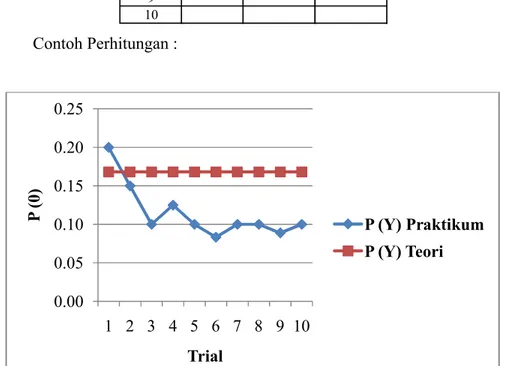
Contoh Perhitungan :

Gambar x.Grafik Ulang Percobaan P(0)

4.2.1.2.2 Perhitungan Ulang Terhadap P(1) 4.2.1.2.3 Perhitungan Ulang Terhadap P(2) 4,2,1,2,4 Perhitungan Ulang Terhadap P(3) 4.2.1.2.3 Perhitungan Ulang Terhadap P(4) 4.2.1.2.6 Perhitungan Ulang Terhadap P(5)

4.2.1.3Distribusi Probabilitas Kumulatif (kalimat pengantar)

Trial f(kum) P(0) P(0) Teori 1 2 3 4 5 6 7 8 9 10 0.00 0.05 0.10 0.15 0.20 0.25 1 2 3 4 5 6 7 8 9 10 P (0 ) Trial P (Y) Praktikum P (Y) Teori

(6)

Tabel

Contoh Perhitungan (2 buah)

Gambar

4.2.1.4 Perhitungan Probabilitas Terambilnya Produk Cacat secara Teoritis (kalimat pengantar)

p (y) = _Cyn_.py_.q

Keterangan :

n = jumlah sampel yang diambil Y = jumlah produk cacat yang diambil p = peluang terambilnya produk cacat q = 1 – p = peluang Y 0 1 2 3 4 5 Total 0 0.2 0.4 0.6 0.8 1 1.2 1 P (Y )

Tabel x.Distribusi Probabilitas Kumulatif

ar x. Grafik Distribusi Probabilitas Kumulatif

Perhitungan Probabilitas Terambilnya Produk Cacat secara Teoritis (kalimat pengantar)

qn-y

= jumlah sampel yang diambil Y = jumlah produk cacat yang diambil p = peluang terambilnya produk cacat

p = peluang terambilnya yang tidak cacat

F P(y) P(Y) kum

Total 10 1

2 3 4 5 6

Y

P (Y)

P (Y) Kumulatif

Perhitungan Probabilitas Terambilnya Produk Cacat secara Teoritis P (Y) Kumulatif

(7)

Perhitungan Probabilitas Secara Teoritis :

Tabel x.Perhitungan probabilitas terambilnya produk cacat secara teoritis

4.2.2 Perhitungan Data Pengamatan untuk Distribusi Hipergeometri

(kalimat pengantar)

4.2.2.1Perhitungan Distribusi Frekuensi (kalimat pengantar)

P(y) = frekuensi

total

Tabel x.Distribusi frekuensi

Y P(Y) 0 0,168 1 0,360 2 0,309 3 0,132 4 0,028 5 0,002 Total 1,000 Y F P(Y) 0 3 0,3 1 2 0,2 2 3 4 5 Total 10 1

(8)

Gambar x.Grafik Frekuensi Terambilnya Produk Cacat Sebanyak Y

4.2.2.2 Perhitungan Ulang Percobaan (kalimat pengantar)

4.2.2.2.1 Perhitungan Ulang Terhadap P(0) (kalimat pengantar)

P(Y) = f

Jumlah_Trial

Tabel

Contoh perhitungan (2 buah) Perhitungan secara teoritis :

P (Y) = 0 2 4 6 8 10 12 14 16 18 20 0 F re k ue ns i

Perhitungan Ulang Percobaan Terhadap P(Y) (kalimat pengantar)

Perhitungan Ulang Terhadap P(0) (kalimat pengantar)

Trial

Tabel x.Ulangan Percobaan terhadap p(0)

Contoh perhitungan (2 buah) Perhitungan secara teoritis :

= . 1 2 3 4 5 Y Trial f(kum) P(0) 1 2 3 4 5 6 7 8 9 10

(9)

Tabel x. Perbandingan Peluang Percobaan dan Teori

Contoh Perhitungan (2 buah) :

Gambar x.Grafik Ulang Percobaan P(0)

4.2.2.2.2 Perhitungan Ulang Terhadap P(1) 4.2.2.2.3 Perhitungan Ulang Terhadap P(2) 4,2,2,2,4 Perhitungan Ulang Terhadap P(3) 4.2.2.2.5 Perhitungan Ulang Terhadap P(4) 4.2.2.2.6 Perhitungan Ulang Terhadap P(5)

4.2.2.3 Distribusi Probabilitas Kumulatif (kalimat pengantar)

Trial f(kum) P(0) P(0) Teori 1 2 3 4 5 6 7 8 9 10 0.00 0.05 0.10 0.15 0.20 0.25 1 2 3 4 5 6 7 8 9 10 P (0 ) Trial P(Y) Praktikum P(Y) Teori

(10)

Tabel

Gambar

4.2.2.4. Perhitungan Probabilitas Terambilnya Produk Cacat secara Teoritis (kalimat pengantar) p (y) = Cy n_{. C} N-y N-r CnN Keterangan :

P (Y) = probabilitas terambilnya produk cacat dari sampel n = jumlah sampel yang diambil

r = jumlah produk cacat dalam populasi N = jumlah populasi

y =jumlah produk cacat yang ter

Perhitungan Probabilitas Secara Teoritis

Y 0 1 2 3 4 5 Total 0 0.2 0.4 0.6 0.8 1 1.2 1 P (Y )

Tabel x.Distribusi Probabilitas Kumulatif

ar x. Grafik Distribusi Probabilitas Kumulatif

.4. Perhitungan Probabilitas Terambilnya Produk Cacat secara Teoritis (kalimat pengantar)

y

= probabilitas terambilnya produk cacat dari sampel jumlah sampel yang diambil

lah produk cacat dalam populasi = jumlah populasi

umlah produk cacat yang terambil

Perhitungan Probabilitas Secara Teoritis

F P(y) P(Y) kum

Total 10 1

2 3 4 5 6

Y

P (Y)

P (Y) Kumulatif

.4. Perhitungan Probabilitas Terambilnya Produk Cacat secara Teoritis

(11)

Tabel x.Perhitungan Probabilitas Terambilnya Produk Cacat Secara Teoritis

4.2.3 Perhitungan Data Pengamatan Untuk Distribusi Poisson

(kalimat pengantar)

4.2.3.1 Perhitungan Data Pengamatan Untuk Kendaraan Sepeda Motor

(kalimat pengantar)

Tabel X.Data Jumlah Kedatangan Sepeda Motor Per 20 detik di Jalan XX Pukul AA:BB – CC:DD Y P(Y) 0 0,168 1 0,360 2 0,309 3 0,132 4 0,028 5 0,002 Total 1,000 3 1

(12)

Data maks : Data min :

Range :data maks-data min = Jumlah kelas :1 + 3,3 Log (N) = Lebar kelas : range

jumlah kelas=

Batas Bawah : data min – 0,5 =

Batas Atas : batas bawah + lebar kelas =

Tabel x.Perhitungan Standar Deviasi Waktu Kedatangan Kendaraan Sepeda Motor Per 20 Detik di Jalan XX Pukul AA:BB – CC:DD

Tabel x. Perhitungan Probabilitas Jumlah Kendaraan Sepeda Motor Per 20 Detik di Jalan XX Pukul AA:BB – CC:DD

Contoh perhitungan (2 buah) P (y) = λy . e-λ

y !

Kelas Batas Bawah Batas Atas fi Fkum xi fi.xi μ λ

1 -0,05 0,97 111 111 0,46 51,25 2 3 4 5 6 7 8 9 … n

Y F F relatif P(Y) P(Y)kum

0 111 0,123 0,686 0,686 1 2 3 4 5 6 7 8 9 … n

(13)

4.2.4 Pengolahan Data dengan Menggunakan Software

4.2.4.1 Perhitungan Menggunkan Software STATISTICA untuk Distribusi Binomial

4.2.4.2 Perhitungan Menggunkan Software STATISTICA untuk Distribusi Poisson

BAB V ANALISIS

5.1. Analisis Perbandingan Hasil Pengamatan Distribusi Binomial dan Hipergeometri

5.2. Analisis Hasil Pengamatan Distribusi Poisson pada Jalan XX Pukul AA:BB

5.3. Analisis Perbandingan Hasil Pengolahan Data Ms.Excel dengan Software STATISTICA

BAB VI PENUTUP

6.1 Kesimpulan 6.2 Saran

DAFTAR PUSTAKA

LAMPIRAN A REKAPITULASI WAKTU KEDATANGAN KENDARAAN

LAMPIRAN A1 Rekapitulasi Hasil Pengamatan Waktu Kedatangan Kendaraan Sepeda Motor dan Mobil di Jalan…..

LAMPIRAN A2 Rekapitulasi Hasil Pengamatan Waktu Kedatangan Kendaraan Sepeda Motor di Jalan…..

LAMPIRAN A3 Rekapitulasi Hasil Pengamatan Waktu Kedatangan Kendaraan Mobil di Jalan…..