Perhitungan Lattice QCD pada Energi Ikat
Hadronik ¯
Λ
Nowo Riveli
0300020499
Universitas Indonesia
Fakultas Matematika dan Ilmu Pengetahuan Alam
Jurusan Fisika
Perhitungan Lattice QCD pada Energi Ikat
Hadronik ¯
Λ
Skripsi
Diajukan sebagai salah satu syarat memperoleh gelar Sarjana Sains
Nowo Riveli
0300020499
Universitas Indonesia
Fakultas Matematika dan Ilmu Pengetahuan Alam
Jurusan Fisika
Halaman Persetujuan
Skripsi : Perhitungan Lattice QCD pada Energi Ikat B-Meson
Nama : Nowo Riveli
NPM : 0300020499
Skripsi ini telah diperiksa dan disetujui
Depok, 20 Oktober 2004
Mengesahkan
Pembimbing I Pembimbing II
Dr. LT Handoko Dr. Terry Mart
Penguji I Penguji II
Kata Pengantar
Lattice QCD adalah suatu teknik yang menjanjikan sebagai alternatif bagi teori
QCD kontinu ketika tidak dapat digunakan untuk mempelajari massa quark.
Meskipun sampai saat ini wilayah penelitiannya cukup sempit, yaitu seputar
B-meson, lattice QCD tetap menarik dan mungkin bisa diaplikasikan secara lebih
lu-as. Bidang ini menarik bagi penulis karena menyangkut dua bidang yang diminati
yaitu fisika partikel dan komputasi. Penulis pun memutuskan untuk mengambil
bidang ini sebagai topik tugas akhir.
Penulis mengucapkan terima kasih pada Pak L. T. Handoko selaku
pembimb-ing, yang telah memperkenalkan topik ini pada penulis, dan membimbing penulis
terutama pada pemahaman-pemahaman teori dasar fisika partikel dan lattice.
Ter-ima kasih juga pada Pak Terry Mart dan Pak Anto Sulaksono, yang banyak
men-dukung dan membantu penulis dalam menyelesaikan tugas akhir ini. Penulis
ju-ga mengucapkan terima kasih pada Pak Chairul Bachri dan Mas Suharyo, yang
bersedia menjadi teman diskusi via e-mail, dan sumber paper gratis bagi penulis.
Masih banyak pihak yang ingin kami ucapkan terima kasih, namun tidak dapat
disebutkan satu persatu.
Depok,
Abstract
We have used the simulation in Lattice QCD to calculate the binding energy of
hadron ¯Λ. Hadronic binding energy ¯Λ are defined non-perturbatively trough the
Lattice HQET lagrangian. The simulation works in small lattice volume, due to
limited performance of the author’s computer. The result are included in this final
assignment, and on the next step will be used to gain the heavy quark mass by
matching with MS renormalisation.
Abstrak
Kami telah menghitung energi ikat hadronik menggunakan simulasi Lattice QCD ¯
Λ. Energi ikat hadronik ¯Λ didefinisikan secara non-perturbatif dengan lagrangian
Lattice HQET. Simulasi dijalankan dengan volume lattice yang kecil, karena
keter-batasan performa komputer yang digunakan. Hasil perhitungan dicantumkan di
tugas akhir ini, dan akan digunakan untuk mendapatkan massa quark berat melalui
Daftar Isi
Halaman Persetujuan i
Kata Pengantar ii
Abstrak iii
Daftar Isi iv
Daftar Gambar v
Daftar Tabel vi
1 Pendahuluan 1
2 Lattice QCD 5
2.1 Path Integral Mekanika Kuantum . . . 5
2.2 Teori Medan Kuantum dengan Integral Fungsional . . . 8
2.3 Diskritisasi Lattice . . . 9
2.4 Medan Gauge dalam Lattice . . . 11
2.5 Landau gauge fixing . . . 13
2.6 Fermion pada Lattice . . . 14
2.6.1 Variabel Grassmann . . . 14
2.6.2 Aksi Fermionik pada Lattice . . . 15
3 Energi Ikat Hadronik dalam Lattice 18
3.1 Definisi ¯Λ . . . 19
3.2 Penentuan nilai residual mass δm . . . 21
4 Implementasi Perhitungan Numerik dan Hasil Peritungan Λ¯ 23 4.1 Metode Numerik : Integrasi Monte Carlo . . . 23
4.2 Parameter Simulasi . . . 24
4.3 Perhitungan δm . . . 25
4.4 Perhitungan ¯Λ . . . 27
4.5 Perbandingan hasil ¯Λ . . . 28
5 Penutup 30 A Pemrograman 31 A.1 Membaca data archive konfigurasi gauge, dan menghitung propagator 31 A.2 Menghitung massa residu . . . 43
Daftar Gambar
2.1 Interval waktu diskrit . . . 6
2.2 Lintasan suatu partikel . . . 7
2.3 Lattice 3 dimensi . . . 10
2.4 Link antara x dan y . . . 12
2.5 Sebuah plaquette . . . 12
Daftar Tabel
4.1 Parameter simulasi yang dilakukan . . . 25
Bab 1
Pendahuluan
QCD adalah teori yang menerangkan interaksi kuat, yaitu yang mempelajari
di-namika quark. Teori ini adalah teori gaugedengan representasi grup SU(3), yang memperkenalkan tiga macam coulor sebagai derajat kebabasan dari quark, dan delapan vektor boson (yaitu gluon) yang diekspansikan dalam suatu basis dari
delapan matriks Gell-Mann.
quark : qfi(x), i= 1,2,3, f = 1, . . . , Nf (1.1)
gluon : Aaµ(x), a= 1, . . . ,8. (1.2) idan aadalah indeks untukcoulor, f adalah indeksflavourdari quark, yaitu u, d, s,. . .,Nf, dan µadalah indeks Lorentz menggambarkan arah vektor ruang-waktu.
QCD mempunyai sifat yang disebut asymtotic freedom. Yaitu konstanta ko-pling dari interaksi bergantung pada skala energi yang digunakan dalam
eksperi-men. Hubungan konstanta koplingrunningdengan skala energi ditentukan dengan menggunakan persamaan grup renormalisasi, yang menghasilkan
gQCD2 (Q2) = 1 β0log(Q2/Λ2)
+. . . (1.3)
Penyelesaian analitis yang mungkin untuk menghitung suatu besaran berdasarkan
QCD adalah dengan metode perturbasi, dengan ekspansi terhadap koplingg. Dari
persamaan konstanta running di atas, tampak bahwa nilai konstanta running g akan berkurang menurut kenaikan energi. Pada skala energi tinggi, nilai g yang
kecil memungkinkan teori QCD dikerjakan dengan metode perturbasi. Akan tetapi
meskipun dapat diekspansi tidak semua bessaran dapat diselesaikan dengan
per-turbasi, contohnya adalah massa quark berat (dijelaskan di bab.3). Pada saat
teori perturbasi tidak dapat digunakan, maka dibutuhkan suatu teori yang dapat
menghitung suatu besaran melaluifirst principal, yaitu tanpa melakukan ekspansi teori, salah satu alternatif adalah dengan lattice QCD.
Ide dasar lattice QCD adalah menyusun teori QCD dalam suatu ruang waktu
yang diskrit, sehingga dimungkinkan perhitungan secara numerik. Penyusunan
formulasi lattice diawali dengan representasi path integral [1] dari suatu besaran fisis. Representasi path integral akan menghasilkan besaran tersebut dalam
ben-tuk integrasi fungsional. Lattice adalah suatu benben-tuk regularisasi dari integral
fungsional ini, dengan jarak kisi a sebagai regulator. Dalam teori QCD kontinu
faktor regulator adalah massa kopling µ. Salah satu tahap perhitungan lattice
adalah menyesuaikan hasil kalkulasi dengan data eksperimen, untuk hal ini perlu
dilakukan perbandingan antara a dan µ.
Integrasi multidimensi pada integrasi fungsional disimulasikan dalam komputer
dengan algoritma Monte Carlo. Ukuran kisi lattice biasanya terdiri dari 48 kisi temporal dan 24 kisi spasial. Karena itu dimensi integrasi adalah 48 × 323 =
663552, yang merupakan integral yang sangat besar. Pusat-pusat penelitian
sim-ulasi lattice di dunia menggunakan sarana komputasi pararel untuk mendapatkan
performa komputer yang sesuai dengan kebutuhan simulasi yang besar tersebut.
yang sederhana untuk melakukan simulasi lattice ini. Hal ini pernah digagas oleh
G. P. Lepage[2]. Simulasi dicoba dilakukan dalam PC (RAM 256 Mb, processor
1,7 GHz), juga dalam komputer alpha dengan Xeon dual prosessor (RAM 1 Gb)
yang terdapat dalam departemen tempat penulis mengambil studinya.
QCD adalah bagian dariStandard Modelyang mencakup semua interaksi dasar di dunia ini (kecuali gravitasi), penelitian untuk mencari massa quark sangatlah
penting dalam rangka melengkapi teori tersebut, terutama dalam melengkapi
el-emen matriks CKM. Berdasarkan massanya quark dibagi menjadi quark-ringan,
dengan massa yang lebih kecil dari ΛQCD (quarku, d, dans), dan quark-berat (b,
t).
Tujuan tugas akhir ini adalah untuk menghitung energi ikat hadronik, sebagai
langkah awal untuk mendapatkan massa quark. Dalam hadron yang mengandung
quark berat, didefinisikan suatu besaran energi ikat, yang merupakan selisih massa
hadron dengan massa quark berat. Massa hadron dapat diperoleh dalam
eksperi-men, akan tetapi tidak demikian dengan massa quark, karena quark tidak pernah
ditemukan dalam keadaan bebas. Tugas akhir ini menghitung nilai energi ikat ¯
Λ dengan lattice QCD. Untuk mendapatkan massa quark, energi ikat, harus
di-lakukan matchingdengan suatu skema renormalisai. Hal tersebut tidak dilakukan disini, jadi tugas akhir ini hanya terfokus pada perhitungan ¯Λ, karena kami hanya
menitikberatkan penggunaan teori lattice QCD dalam menghitung suatu besaran.
Penelitian untuk menghitung besaran yang sama pernah dilakukan sebelumnya
juga dengan lattice QCD[3,4]. Nantinya akan dibandingkan hasil yang didapat di
tugas akhir ini dengan hasil yang lain. Motivasi pengerjaan tugas akhir ini adalah
mencoba melakukan perhitungan lattice QCD, dengan tingkat akurasi yang
sebelumnya akan dijadikan acuan dalam menentukan apakah teori lattice QCD
benar-benar dapat digunakan untuk menghitung suatu besaran dalam QCD, dan
apakah simulasi yang dilakukan penulis dilakukan dengan benar dan dapat
diter-ima.
Berikut adalah sistematika penulisan dalam tugas akhir ini,
• penjelasan teori lattice QCD di bab 2,
• penjelasan tentang permasalahan massa quark berat, dan definisi energi ikat hadronik, di bab 3,
• prinsip perhitungan numerik dan hasil yang didapat di bab 4,
Bab 2
Lattice QCD
Sebelum masuk ke masalah utama yaitu defini energi ikat hadronik ¯Λ, di bab ini
akan dijabarkan terlebih dahulu teori lattice QCD. Isi sub-bab ini menggunakan
buku dari H. J. Rothe[5] dan beberapa lecture note[6,7] sebagai referensi.
Lattice QCD adalah suatu teknik non-perturbativ yang menempatkan
elemen-elemen QCD dalam ruang-waktu yang diskrit. Untuk itu dibuat representasi quark
dan gluon dalam dunia yang diskrit tersebut. Formulasi yang diskrit sangat mudah
didapatkan dari formulasi path integral untuk mekanika kuantum yang diusulkan
Feynman. Selanjutnya dalam bab ini akan dibahas formulasi path integral, dan
formulasi QCD dalam kisi ruang-waktu diskrit, yang pertama kali disusun oleh K.
Wilson di tahun 1974 [8].
2.1
Path Integral Mekanika Kuantum
Seperti pada kebanyakan referensi mengenai lattice QCD, path integral akan
Gambar 2.1: Interval waktu diskrit
Dengan hamiltonian yang berbentuk
H = p
2
2m +V(x)≡H0+V, (2.1)
amplitudo transisi adalah
hx′, t′
Membagi T menjadinbagian yang sama, T =n∆t, seperti pada gb.2.1, kita akan
dapatkan
hx′, t′|x, ti=
Z
dx1. . . dxn−1hx′|e−iH∆t|xn−1ihxn−1|e−iH∆t|xn−2i. . .hx1|e−iH∆t|xi. (2.5)
Untuk n yang besar, ∆t menjadi kecil. Selanjutnya dengan menggunakan
trans-formasi Fourier, untuk semua matrix elemen, amplitudo akan menjadi
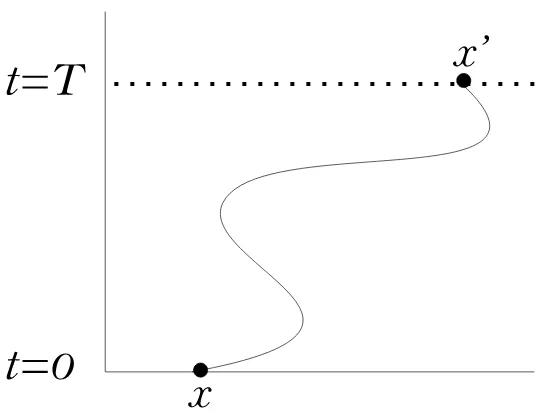
Gambar 2.2: Lintasan suatu partikel
Pada limitn → ∞kita akan mendapatkan eksponensial persamaan di atas menjadi
bentuk aksi klasik
n−1
untuk lintasan x(t) dari x ke x′ dengan x
k=x(k∆t), digambarkan di gb.2.2
Integrasi terhadapxk dinterprestasikan sebagai integrasi terhadap seluruh
ke-mungkinan lintasan x(t) yang dapat dibentuk. Untuk itu kita gunakan notasi
sehingga kita dapatkan formulasi path integral untuk amplitudo mekanika
kuan-tum satu dimensi
hx′
|e−iHT
|xi=
Z
2.2
Teori Medan Kuantum dengan Integral
Fung-sional
Formulasi path integral untuk mekanika kuantum di atas selanjutnya akan
digu-nakan untuk menentukan formulasi path integral untuk teori medan kuantum.
Pada teori medan besaran yang sangat penting adalah vacuum expectation value, yaitu fungsi Green
h0|φ(x1)φ(x2). . . φ(xn)|0i, t1 > t2 >· · ·> tn (2.10)
dari medan skalar φ(~x, t) dalam ruang-waktu4-vector.
Sebelum membahas fungsi Green lebih jauh, kita akan mentranslasikan
konsep-konsep di mekanika kuantum ke teori medan berdasarkan analogi. Dalam teori
medan, medan skalar menggambarkan partikel itu sendiri, sehinggaxi(t) di
mekani-ka kuantum menjadi φ(~x, t), translasi selanjutnya adalah
xi ←→ φ(~x, t)
L adalah densitas lagrangian yang digunakan dalam teori medan.
Dengan menganalogikan pada kasus mekanika kuantum, kita dapatkan formulasi
fungsi Green, dengan ekspresi yang sering dikenal sebagai integral fungsional:
Eksponensial imajiner pada intgrasi di atas menimbulkan masalah konvergensi
karena fungsi integral akan berosilasi. Hal ini diatasi dengan mentransformasikan
waktu real (ruang Wincowsky) ke waktu imajiner (ruang Euclid), dengan rotasi Wick, yaitu
t =−iτ. (2.13)
Fungsi Green setelah rotasi Wick akan memiliki eksponensial yang positif
GE(x1, . . . , xn) =
Besaran dalam ruang Euclid ini yang akan digunakan dalam setiap perhitungan
integal fungsional fungsi medan, yang dihasilkan dari formulasi path integral.
2.3
Diskritisasi Lattice
Setelah mendapatkan formulasi path integral untuk teori medan, yang berbentuk
integral fungsional, langkah selanjtnya dalam lattice QCD adalah
mendiskritkan-nya. Ruang-waktu 4 dimensi didiskritkan dengan membentuk lattice hiperkubik,
sehingga posisi ruang-waktu terlokalisasi hanya di titik-titik pada lattice,
xµ =anµ, (2.16)
lihat gb.2.3.
Derivatif diganti dengan selisih hingga, integral diganti dengan sumasi,
Gambar 2.3: Lattice 3 dimensi
Diskritisasi ruang-waktu menghasilkan konsekuensi adanya regularisasi dari
in-tegral fungsional, dengan jarak lattice a sebagai regulator. Hal ini dapat dilihat
dengan melakukan transformasi Fourier medan skalar ke ruang momentum
˜
φ(p) = X
x
a4e−ipxφ(x). (2.19)
Fungsi yang telah di transformasi Fourier-kan adalah fungsi yang periodik dalam
ruang momentum, sehingga kita bisa dapatkan
pµ ∼=pµ+
2π
a (2.20)
Transformsi Fourier invers akan menghasilkan
φ(x) =
Z π/a
−π/a
d4
(2π)4e
ipxφ(p)˜ (2.21)
dan kita dapatkan suatu nilai cutoff ultraviolet
|pµ| ≤
π
a. (2.22)
Jadi dapat terlihat bahwa teori medan dalam ruang-waktu yang diskrit, yaitu
Formulasi dalam dunia yang diskrit harus dapat kembali ke dunia kontinu
den-gan bentuk yang sama. Hal ini menjadi syarat yang harus selalu dipenuhi dalam
membuat formulasi diskrit, yang bisa non-trivial.
2.4
Medan Gauge dalam Lattice
Dalam teori medan, berlaku invariansi lagrangian terhadap transformasi gauge,
yaitu
φ(x)→Λ(x)φ(x), Λ(x)∈SU(N) (2.23)
dalam QCD transformasi dilakukan dengan grup SU(3). Derivatif dalam lagrangian
harus diubah menjadi derivatif kovarian, yaitu
Dµφ(x) = (δµ−ig0Aaµ(x)Ta)φ(x), (2.24)
dimana Taadalah generator grup, yang untuk grup SU(3) adalah delapan matriks
Gell-Mann, Aa
µ(x) adalah medan gauge. Derivatif kovarian ini invarian terhadap
transformasi gauge
Dµφ(x)→Λ(x)Dµφ(x). (2.25)
Besaran yang merupakan produk dari medan-medan di titik yang berbeda dalam
latice, tidak invarian. Untuk itu kita membutuhkan suatu matriks U(x, y) ∈
SU(N) yang bertransformasi menurut U(x, y) → Λ(x)U(x, y)Λ−1(y), sehingga
φ(x)U(x, y)φ(y) akan invarian. Matriks U tersebut dapat dibuat dari suatu
lin-tasan dari titikxhinggay, sehingga dia adalah integral lintasan dari medan gauge
Aa µ
U(x, y;C)≡P expig0
Z y x
Aaµ(z)Tadzµ, (2.26)
U pada definisi di atas bertransformasi sesuai yang dibutuhkan, sehingga produk
Gambar 2.4: Link antara xdan y
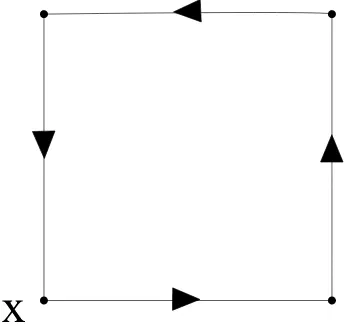
Gambar 2.5: Sebuah plaquette
dalam besaran ini.
Di dalam lattice parallel transporteradalah lintasan penghubung dua titik ter-dekat, disebut denganlink variablesLink ini menggantikan medan gaugeAa
µuntuk
setiap formulasi dalam lattice. Link bertransformasi sama seperti transformasi
parallel transporter di atas. Produk dari beberapa link, dalam lintasan tertutup, akan invarian, besaran yang paling mendasar adalah plaquetteyaitu loop terkecil yang dibentuk empat buah link, seperti di gambar
Pµν ≡Uµ(x)Uν(x+aµ)U−b µ(x+aµb+abν)U−ν(x+aν)b (2.27)
lattice,
Aksi yang diusulkan Wilson ini invarian dan real, dan pada limit kontinu akan
membentuk aksi Yang-Mills kontinu.
2.5
Landau gauge fixing
Medan gauge dalam lattice memiliki simetri dalam transformasi yang telah
dije-laskan di sub-bab sebelumnya. Sebuah medan yang merupakan hasil transformasi
tersebut dari medan lain, akan memiliki arti fisis yang sama. Sekumpulan medan
yang terhubung oleh transformasi tersebut, sehingga memiliki sifat fisis yang sama,
disebut orbit gauge. Identifikasi dari sebuah medan untuk setiap orbit gauge
dise-but dengan gauge fixing.
Salah satu metode gauge fixing yang sering digunakan adalah gauge Landau.
Dalam dunia kontinu, gauge Landau didefinisikan sebagai
∂−µAµ= 0. (2.29)
Kondisi ini menunjukkan suatu konfigurasi hyperplane
Γ≡ {A: ∂·A = 0}. (2.30)
Hyperplane di atas memiliki lebih dari satu gauge orbit. Selanjutnya ditentukan
suatu wilayah dalam hyperplane tersebut, yaitu Λ⊂Γ, yang merupakan
sekumpu-lan nilai minimum dari fungsional
FA[g] =
Z
d4xX
µ
Di dalam lattice gauge Landau didapatkan dengan memaksimalkan fungsional
FI[g] = CF
X
x,µ
Re{Tr[g(x)Uµ(x)g†(x+ ˆµ)]} (2.32)
dimana
CF =
1 NdimNcV
(2.33)
adalah konstanta renormalisasi, Ndim adalah dimensi ruang-waktu, Nc adalah
di-mensi grup gauge, dan V volume lattice. Seperti hanya pada dunia kontinu,
kon-figurasi yang memaksimalkan fungsional di pers() membentuk suatu wilayah Λ
yang memenuhi
Γ≡ {U : ∂·A(U) = 0}. (2.34)
Untuk mendapatkan nilai yang memiliki akurasi statistik yang baik, gauge
fix-ing harus digunakan dalam simulasi lattice.
2.6
Fermion pada Lattice
Setelah melihat bahwa medan gauge digambarkan sebagai link dalam lattice,
se-lanjutnya akan dibahas representasi fermion pada ruang-waktu diskrit.
2.6.1
Variabel Grassmann
Karena memenuhi statistik Dirac, fermion adalah variabel yang bersifat
Beberapa aturan dalam aljabar Grassmann yang berlaku pada adalah
{ηi, ηj} = 0 (2.35)
{ηi,η¯j} = 0 (2.36)
{η¯i,η¯j} = 0. (2.37)
Formulasi path integral dengan integrasi terhadap fermion dituliskan sebagai berikut,
h0|A|0i= 1 Z
Z
DψDψAe¯ −SF, (2.38)
denganSF adalah aksi fermionik. Untuk medan Dirac bebas aksi fermionik adalah
SF =
Z
d4xψ(x)(γ¯ µδµ+m)ψ(x). (2.39)
Dengan memanfaatkan integrasi Grassmann integral fungsional daiatas dapat
dis-elesaikan dengan sederhana, dan menghasilkan
Z
DψDψe¯ Rd4xΨ(¯ x)QΨ(x) = detQ (2.40) ini yang dikenal dengan determinan fermionik.
2.6.2
Aksi Fermionik pada Lattice
Aksi fermionik pada pers.(2.33) bila didiskritkan secara naif akan menjadi
SF =
Dengan aksi diskrit tersebut akan didapatkan propagator dengan bentuk
¯
∆(k) = −iσµγµsinkµ+m σµsinkµ2 +m2
(2.42)
yang memiliki 16 buah pole akibat sifat periodik pada penyebut. Hal ini tidak
sesuai dengan propagator pada limit kontinu yang mempunyai 1 buah pole,
modifikasi pada aksi fermionik, yang dapat menghilangkan efek fermion doubling
ini.
Modifikasi pertama dilakukan oleh Wilson yang menambahkan suku Wilson
pada aksi di atas,
−a5r 2
X
x,µ
¯ q(x)1
a2 [Uµ(x)q(x+abµ)−2q(x) +U−µ(x)q(x−abµ)] (2.43)
dengan 0 < r ≤ 1. Dengan penambahan suku ini, massa fermion akan
diver-gen bila a mendekati nol, dan fermion doubling tidak lagi ditemui. Akan tetapi,
aksi ini melanggar simetri chiral, sehingga tidak digunakan pada
permasalahan-permasalahan yang melibatkan simetri chiral. Alternatif lain meodifikasi aksi
un-tuk menghilangkan fermion doubling adalah aksi staggered. Dengan aksi ini,
setiap komponen fermion didistribusikan pada titik lattice yang berbeda, hal ini
akan menghasilkan 4 pole propagator dibanding dengan 16 yang ditemukan di
ak-si biasa. Pole tersebut dapat mewakili sebuah fermion, karena adalah komponen
yan tersebar dari sebuah fermion. Formulasi aksi staggered cukup rumit, sehinga
tidak dibahas lebih lanjut, selanjutnya dalam perhitungan tugas akhir ini, yang
digunakan adalah aksi Wilson.
2.7
QCD pada Lattice
QCD dirumuskan dalam lattice dengan menuliskan aksi total yang melibatkan aksi
fermionik SF dan aksi gaugeSG
S =SF +SG. (2.44)
Sifat antikomutatif dari fermion tidak dapat diperhitungkan dalam perhitungan
dan kita bekerja pada aksi efektif yang hanya melibatkan aksi bosonik e−Sef f(U) ≡e−SG(U)
detQ(U). (2.45)
Perhitungan detQ biasanya sangat besar, sehingga dalam lattice biasa dilakukan
pendekatan quenched, yang menjadikan Qsebagai konstanta.
Secara garis besar pada bab ini telah dijabarkan formulasi QCD pada lattice,
dengan titik awal formulasi path integral. Di bab ini dapat disimpulkan
perhitun-gan suatu observable pada lattice dilakukan denperhitun-gan integrasi fungsional, yaitu
hAi= 1 Z
Z Y
dUAe−SW (2.46)
dengan aksi yang telah didefinisikan. Permasalahan selanjutnya adalah metode
numerik yang digunakan dalam perhitungan integral fungsional tersebut. Hal ini
akan dijabarkan di bab 4, sebelumnya di bab 3 akan dijabarkan besaran yang
Bab 3
Energi Ikat Hadronik dalam
Lattice
Massa quark berat pada prinsipnya dapat diperoleh dari lagrangian QCD,
kare-na menurut sifat asymtotic freedom, massa quark berat memiliki konstanta
ko-pling yang kecil, sehingga dapat dilakukan teknik perturbasi. Akan tetapi, untuk
mengekstrak massa quark dari lagrangian QCD, terdapat suku-suku yang
meli-batkan propagator gluon, yang mengakimeli-batkan divergensi. Karena itu disusun
su-atu teori khusus untuk quark berat yaitu Heavy Quark Effective Theory (HQET).
Dalam teori ini, operator-operator dalam QCD diekspansikan dalam suku-suku
operator-operator HQET
OQCD =X
n,α
Cn,α(mQ/µ)
mn Q
OHQETn,α (µ), (3.1) mQ adalah massa quark berat dan µ adalah skala renormalisasi. Tampak bahwa
besaran fisis dalam HQET dipelajari sebagai ekspansi terhadap invers dari massa
quark mQ.
Untuk menghilangkan suku-suku divergen dalam ekspansi di pers.(3.1), atau
disebut sebagai singularitas renormalon, maka harus dibuat suatu definisi baru
suku-suku awal, dan koefisien fungsi Cn,α dapat dihitung dengan teori perturbasi.
Singularitas renormalon dalam ekspansi di atas dapat dihilangkan dengan
reno-malisasi berupa hard ultra-violet cut-offΛ. Namun dengan adanya hard cut-off Λ, besaran dalam HQET akan divergen menurut pangkat dari Λ, sehingga walaupun
singularitas renormalon pada walnya telah dihilangkan, muncul lagi divergensi
baru dari hard cut-off Λ.
Karena dua permasalahan quark berat di atas, yaitu singularitas renormalon
dan divergensi pangkat, diusulkan suatu definisi non-perturbativ dari
operator-operator OHQET
n,α , sehingga bebas dari dua permasalahan di atas[9]. Dengan
defin-isi yang bebas dari singularitas renormalon dan divergensi pangkat, akan
dap-at diekstrak sudap-atu besaran yang memiliki makna fisis, dalam arti sudap-atu besaran
yang independen terhadap skala renormalisasi, juga metode yang digunakan dalam
meregularisasi divergensi ultra-violet.
Dalam definisi non-pertrurbativ ini, parameter massa yang digunakan dalam
ekspansi dipilih berupa suatu ”massa pole yang disubtraksi”, ms
Q, dimana
ambi-guitas renormalon telah di subtraksi secara non-perturbativ. Untuk setiap hadron
yang mengandung quark berat didefinisikan parameter ¯Λ≡mH−msQ, dimanamH
adalah massa hadron.
3.1
Definisi
Λ
¯
Di sub-bab ini akan dibahas usulan definisi ¯Λ menurut paper dari G. Martinelli
dan C. T. Sachradja[9]. Untuk mendapatkan definisi yang non-perturbatif dari ¯Λ,
kita gunakan lagrangian HQET dalam formulasi lattice,
L= 1
1 +aδm ¯h(x)D4h(x) +δm¯h(x)h(x)
Pandang suatu fungsi korelasi
Untuk waktu t yang cukup besar,
C(t)→Z2exp(−Et) (3.4)
dimana Z adalah konstan.
Eksponen E sebanding dengan ¯Λ menurut definisi yang diusulkan di ref.[10],
yaitu
¯
Λ = −∂h0|HΓq¯ |Mi
h0|HΓq¯ |Mi (3.5)
E bukanlah suatu besaran fisis karena menghasilkan divergensi pada perhitungan perturbasi, karena itu ¯Λ juga tidak mempunyai makna fisis. Divergensi tersebut
kemudian disubtraksi dengan menambahkan suatu residual mass (massa residu) δm¯hh pada lagrangian pers.(3.2).
Massa residu pada lagrangian di atas dapat dipilih dalam beberapa cara. Salah
satu kemungkinan adalah dengan mempelajari sifat propagator quark pada waktu
yang besar, pada suatu fixed gauge,
−δm≡ ln(1 +aδm)
dengan asumsi rasio di atas memiliki nilai pada limit t yang besar. Persamaan di
atas bisa digambarkan sebagai kondisi dimana propagator quark pada waktu yang
besar tidak mempunyai perubahan yang eksponensial.
Maka untuk menghitung ¯Λ bisa disimpulkan langkah-langkah sebagai berikut,
i.) Hitung massa residuδm, menurut definisi pers.(3.6). Besaran ini yang
ii.) Dapatkan nilai E. Kami akan menggunakan hasil perhitungan yang telah
dilakukan oleh kolaborasi APE[11] di tahun 1995.
iii.) Definisi fisis ¯Λ adalah
¯
Λ≡ E −δm, (3.7)
dan massa pole quark yang tersubstraksi yang berkorespodensi dengan
per-samaan di atas adalah
mb ≡mb − E +δm. (3.8)
3.2
Penentuan nilai residual mass
δm
Seperti telah didefinisikan sebelumnya, untuk mendapatkan nilai δm harus
di-lakukan perhitungan terhadap propagator quark. Pada intinya, tugas akhir ini
berpusat pada perhitungan propagator quark. Bentuk propagator yang mungkin
adalah
S(x|0) =δ(x)θ(x4)P(x4|0), (3.9) dimana P(x4|y4) adalah path ordered lattice yang sring disebut ”P-line”,
P(x4|y4) =
tor yang diimproved yaitu dengan
PxI(x4|y4=
Untuk mengurangi kesalahan statistik, propagator dihitung dalam suatu fixed gauge, yaitu gauge Landau, dengan persamaan
dimana V adalah volume spasial dari lattice.
Untuk menentukan nilaiδmkita harus menghitung massa efektif yang
didefin-isikan dengan
aδm(t) =−ln
SH(t+a)
SH(t)
. (3.13)
Setelah mendapatkan massa efektif untuk beberapa nilai t, selanjutnya
digu-nakan hasil perhitungan perturbasi 1-loop[9] untuk difitkan terhadapδm, yaitu
aδm(t) =¯ aδm+γlnt+a
Bab 4
Implementasi Perhitungan
Numerik dan Hasil Peritungan
Λ
¯
4.1
Metode Numerik : Integrasi Monte Carlo
Untuk menghitung path integral dari besaranhΓ[x]i, kita akan menggunakan
prin-sip integrasi Monte Carlo. Representasi path integral dari hΓ[x]i adalah
hΓ[x]i=
R
DxΓ[x]e−S[x]
R
Dxe−S[x] , (4.1)
persamaan di atas adalah suatu rata-rata berbobot(weighted average)dari seluruh knfigurasi lintasanxyang mungkin, dengan berat exp(−S[x]). Dengan
membangk-itkan konfigurasi lintasan yang acak
xα ≡xα0xα1 . . . xαN−1 α= 1,2, . . . , Ncf (4.2)
dengan suatu cara sedemikian hingga tiap konfigurasi mempunyai probabilitas
P[xα]∝ e−S[xα]
(4.3)
maka nilai rata-rata Γ[x] tidak berbobot mendekati nilai rata-rata berbobot dari
lintasan ynag terdistribusi secara uniform
hΓ[x]i ≈Γ¯ ≡ 1 Ncf
Ncf
X
α=1
¯
Γ adalah estimasi Monte Carlo untuk besaran path integral hΓ[x]i yang dihitung
dalam lattice.
Nilai kesalahan dari estimasi Monte Carlo didapatkan dari nilai varian yaitu
σ2¯Γ =
Seperti yang telah dijelaskan, besaran pokok yang dihitung dalam lattice
pa-da tugas akhir ini apa-dalah nilai propagator sebagai fungsi waktu, yaitu papa-da
per-samaan,
S(x|0) =δ(x)θ(x4)P(x4|0), (4.6) Propagator pada fungsi di atas adalah fungsi dari konfigurasi link U dalam
lat-tice. Berdasarkan prinsip integrasi Monte Carlo, kita akan membentuk
konfigurasi-konfigurasi U, lalu menghitung besar propagator untuk setiap konfigurasi, lalu
mencari rata-ratanya.
4.2
Parameter Simulasi
Penyusunan tiap konfigurasi acak U harus memenuhi pers.(4.2), untuk itu tiap
konfigurasi dibangkitkan dengan algoritma tertentu yang dapat memenuhi kondisi
tersebut. Metode yang biasa digunakan adalah algoritma Metropolis dan
algo-ritma heat-bath. Pembentukan sebuah konfigurasi membutuhkan waktu
perhi-tungan komputer yang cukup lama, sedangkan untuk mendapatkan nilai estimasi
Monte Carlo dibutuhkan jumlah konfigurasi yang tidak sedikit. Penulis pernah
mencoba membentuk konfigurai dengan algoritma Metropolis, tetapi tidak dapat
diselesaikan karena masalah waktu, karena itu dalam tugas akhir ini digunakan
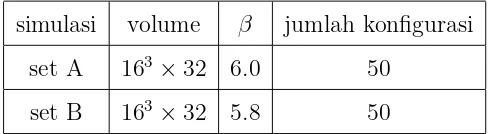
Tabel 4.1: Parameter simulasi yang dilakukan
simulasi volume β jumlah konfigurasi
set A 163×32 6.0 50
set B 163×32 5.8 50
Connection[12]. Konfigurasi yang diperoleh dari situs tersebut dibangun dengan menggunakan suatu algoritma tertentu yaitu algoritma heat-bath.
Dalam perhitungan yang dilakukan, penulis menggunakan dua macam susunan
konfigurasi, yaitu setA dan setB, masing-masing dengan parameter-parameter
sebagai berikut,
Nilai kesalahan statistik adalahσ dalam pers.(4.5).
4.3
Perhitungan
δm
Sebagai langkah awal dilakukan perhitungan propagator yang quark diimprove
seperti yang didefinisikan di pers.(3.9) hingga (3.11). Perhitungan dilakukan
den-gan dua macam parameter simulai pada tabel.4.1, setelah itu nilai residual mass
di-dapat dari hubungan di pers.(3.13). Berdasarkan perhitungan perturbasi 1-loop[9],
δm¯ di fit dengan fungsi
aδm(t) =¯ aδm¯ +γln
t+a t
, (4.7)
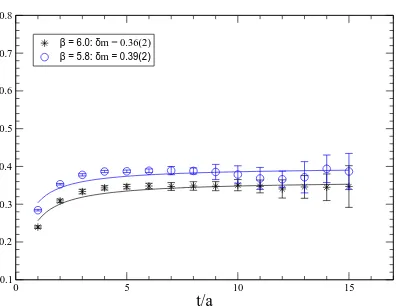
dimana γ dan δm¯ adalah parameter-parameter fitting yang bebas. gb.1
menun-jukkan hasil plot dan fitting fungsi pers.(4.7) untuk dua macam simulasi.
Nilaiδm¯ yang didapat adalah sebagai berikut
aδm= 0.36±0.02±0.01 pada β = 6.0 (4.8)
0 5 10 15
t/a
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
β = 6.0: δm = 0.36(2)
β = 5.8: δm = 0.39(2)
a
δ
m(t)
Gambar 4.1: Plot massa efektif yang berasal dari perhitungan propagator
Nilai kesalahan statistik yang digunakan adalah kesalahan dari estimasi Monte
Carlo yaitu akar dari pers.(4.5). Sedangkan untuk kesalahan sistematis di ambil
kesalahan dari pendekatan fitting fungsi yang digunakan.
Seperti yang dikatakan, kami akan menggunakan E dari hasil kolaborasi APE.
Akan tetapi masing-masing δmdi atas harus berkorespodensi dengan nilaiE yang
dihitung dengan konfigurasi yang sama. Kolaborasi APE tidak melakukan
perhi-tungan E pada konfigurasiβ = 5.8, karena itu kami hanya menggunakan nilaiδm
pada β = 6.0 (pers.(4.8)).
Dengan melihat kecenderungan plot δm¯ yang mirip, dan nilai δm yang cukup
dekat, kami berkesimpulan bahwa nilai δmindependen terhadap parameter
simu-lasi yang digunakan. Sehingga penggunaan nilaiδmhanya dari sebuah konfigurasi
dapat dilakukan.
4.4
Perhitungan
Λ
¯
Untuk mendapatkan nilai ¯Λ kita gunakan
• δm¯ dari pers.(4.8);
• nilai E dari kolaborasi APE[11], yaitu
aE = 0.52±0.01 (4.10)
• nilai a yang berkorespodensi dengan beta yaitu
a−1 = 1.8
±0.2 GeV untuk β = 6.0 (4.11)
Maka kami mendapatkan
¯
4.5
Perbandingan hasil
Λ
¯
Berikut adalah nilai ¯Λ yang telah didapatkan sebelumnya dengan metode yang
sama,
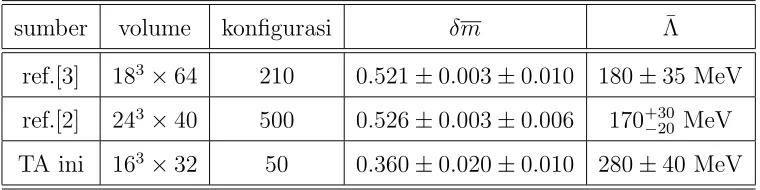
Tabel 4.2: ¯Λ yang didapat di perhitungan sebelumnya
sumber volume konfigurasi δm Λ¯
ref.[3] 183×64 210 0.521±0.003±0.010 180±35 MeV
ref.[2] 243×40 500 0.526±0.003±0.006 170+30
−20 MeV
TA ini 163×32 50 0.360±0.020±0.010 280±40 MeV
Hal-hal yang dapat disimpulkan dari tabel perbandingan di atas antara lain,
• δmyang didapat di tugas akhir ini memilili akurasi hanya sampai dua angka di belakang koma, sedangkan hasil-hasil yang lain mencapai akurasi tiga
angka di belakang koma. Kesalahan pada tugas akhir ini dihasilkan paling
banyak oleh kesalahan statistik. Hal ini berarti bahwa jumlah konfigurasi
dan ukuran volume yang digunakan penulis belum cukup untuk digunakan
dalam melakukan perhitungan. Jumlah konfigurasi jelas berpengaruh
kare-na kesalahan statistik berbanding mendekati 1/√N. Penulis tidak
meng-gunakan jumlah konfigurasi yang cukup banyak karena dibutuhkan waktu
yang cukup lama untuk men-downloadtiap konfigurasi dari situs The Gauge Connection, dengan ukuran tiap konfigurasi yang cukup besar yaitu 24 Mb
untuk sebuah konfigurasi. 50 buah konfigurasi berarti membutuhkan space
sebesar 1,2 Gb. Pemilihan jumlah konfigurasi sebanyak 50 selain karena
be-sarnya ukuran konfigurasi, penulis juga merujuk pada perhitungan di ref.[3]
yang awalnya hanya menggunakan konfigurasi hanya sebanyak 30. Besarnya
nilai yang didapat pada tugas akhir ini membutuhkan banyak koreksi untuk
dapat diterima.
• Λ yang didapat di tugas akhir menghasilkan nilai yang cukup berbeda den-¯ gan dua hasil sebelumnya, dan juga memiliki nilai kesalahan yang cukup
besar. Kesalahan pada besaran ini juga adalah pengaruh kesalahan
statis-tik yang besar. ¯Λ pada dua sumber sebelumnya didapat dari hasil
bebera-pa konfigurasi yang berbeda, sedangkan tugas akhir ini hanya menghitung
besaran pada satu macam konfigurasi yaitu pada β = 6.0. Sebelumnya
telah dijelaskan bahwa nilaiδmindependen dari konfigurasi yang digunakan,
meskipun memiliki perbedaan nilai. karena itu hasil yang menggabungkan
beberapa konfigurasi akan meningkatkan keakurasian.
• Dua hasil pertama dihitung dengan menggunakan konfigurasi yang sama, karena keduanya berasal dari satu grup penelitian. Penggunaan konfigurasi
berbeda oleh penulis mungkin mempengaruhi perbedaan nilai hasil
perhi-tungan. Perbedaan metode dan algoritma dalam membangkitkan konfigurasi
mungkin menghasilkan konfigurasi gauge dengan karakteristik yang berbeda,
walaupun dibuat pada parameter β yang berarti a (jarak spasi) yang sama.
Demikianlah hasil yang didapat di tugas akhir ini. Meskipun menghasilkan
nilai yang cukup jauh dari hasil sebelumnya, kami berkesimpulan bahwa
perhitun-gan yang telah kami lakukan masih cukup bisa diterima. Hal ini antara lain dilihat
dari grafik plot yang memiliki tren yang sama dengan plot di ref.[4](tidak
dita-mpilkan disini), juga adanya kesalahan yng mungkin ditimbulkan dari penggunaan
Bab 5
Penutup
Mengingat kembali tujuan pengerjaan tugas akhir ini, yaitu mencoba
menggu-nakan lattice QCD untuk menghitung sauatu besaran dalam QCD. Untuk itu kami
memilih suatu besaran yang telah dihitung sebelumnya, dan membandingkan
den-gan hasil perhitunden-gan yang kami lakukan. Hasil yang diperoleh memang cukup
jauh dari yang diharapkan, akan tetapi hal itu bisa dijelaskan dengan besarnya
sumber kesalahan seperti yang dijabarkan di bab sebelumnya. Sebagai sebuah
langkah awal, perhitungan yang dilakukan di tugas akhir bisa dilajutkan dengan
lebih menganalisa sumber-sumber kesalahan dan meminimalisasinya.
Karena kami terfokus pada penggunaan perhitungan lattice, maka kami hanya
memilih suatu besaran yang didefinisikan sebelumnya untuk dikerjakan di lattice.
Selain besaran yang dihitung di tugas akhir ini, lattice QCD bisa juga digunakan
untuk menghitung besaran-besaran lain seperti energi kinetik, walaupun sebagian
besar hanya berkisar di wilayah B-meson. Setelah diyakinkan perhitungan lattice
QCD telah dapat dilakukan, selanjutnya dapat dilakukan perhitungan untuk
Lampiran A
Pemrograman
A.1
Membaca data archive konfigurasi gauge, dan
menghitung propagator
/*===================================================================*/
/* Utility program to read and verify configs in QCD archive format */
/* dimodifikasi untuk menghitung propagator */
/* oleh Nowo Riveli (2004) */
/*===================================================================*/
/* Version: 1.0 */
#define TOL 0.0000001 /* tolerance for floating point checks */
#define BADPRINT 10 /* number of bad links to print out in full */
#undef FORTRANORDER /* define to use Fortran ordering for U[18] */
/* Return values for our parsers */
#define SUCCESS 0
#define FAILURE -1
#include <stdio.h> #include <math.h> #include <strings.h> #include <stdlib.h> #include <limits.h>
/*================================================================*/
/* We may do arithmetic on this machine in a precision different */
/* from the precision read in. Here is where we define the type. */
/*================================================================*/
typedef double REAL; /* type for doing internal arithmetic */
/*=============================================================*/
/* For checksums we want a 32 bit unsigned int, for which */
/* become a C semi-standard. Here we just check if INT_MAX */ /* is 2^31-1; if not, we assume we are on a T3E or equivalent, */
/* where unsigned short is 4 bytes. */
/*=============================================================*/ #if (INT_MAX==2147483647)
#define INTS_ARE_32BIT
typedef unsigned int uint32_t; #else
#undef INTS_ARE_32BIT
typedef unsigned short uint32_t; #endif
struct QCDheader { /* Structure to hold header tokens */
int ntoken; char **token; char **value; };
struct site { REAL U[4][18]; int neighbor[4]; };
/* Global variables */
int big_end_p; /* true if our machine is big-endian */
int n_badlink=0; /* number of non-unitary links we have found */
main(argc,argv)
struct site *lat, *p; REAL xx,yy,prop_tot; float xx_float;
int i,j,n,s,splus,t,tplus,mu,T; int dims[4];
int vol3, vol4;
uint32_t chksum,partial_chksum,uj; char *str;
struct QCDheader * get_header(), * hdr;
/* Check which end is up */ big_end_p = big_endian();
/* Check syntax */ if (argc!=2) {
printf("Usage: %s <U config>\n",argv[0]); exit(1);
}
/* Open file */
infile = fopen(argv[1],"r"); if (infile==NULL) {
printf("error opening: %s\n",argv[1]); exit(1);
}
hdr = get_header(infile);
/* Look for basic info, reporting if avalailable */
/* get_string("ENSEMBLE_LABEL",hdr,&str); if (str==NULL) str = "(not specified)"; printf("Ensemble label: %s\n",str);
get_string("ENSEMBLE_ID",hdr,&str); if (str==NULL) str = "(not specified)"; printf("Ensemble ID: %s\n",str);
printf("Sequence number: ");
i = get_int("SEQUENCE_NUMBER",hdr,&j); if (i==FAILURE) printf("(unknown)\n"); else printf("%9d\n",j);
*/
/* Get dimensions */
if (get_int("DIMENSION_1",hdr,dims+0)==FAILURE) error_exit("DIMENSION_1 not present"); if (get_int("DIMENSION_2",hdr,dims+1)==FAILURE) error_exit("DIMENSION_2 not present"); if (get_int("DIMENSION_3",hdr,dims+2)==FAILURE) error_exit("DIMENSION_3 not present"); if (get_int("DIMENSION_4",hdr,dims+3)==FAILURE) error_exit("DIMENSION_4 not present");
/* Make space for array in to which to read a timeslice ... */ vol3 = dims[0]*dims[1]*dims[2];
vol4 = dims[3]*vol3;
lat = (struct site *) malloc(2*vol4*sizeof(struct site));
/* fill in the navigation stuff */ init_navig(lat,dims);
/* Read in first lattice before main loop */ read_slice(infile,vol4,lat,&partial_chksum); chksum = partial_chksum;
check_unitarity(vol4,lat+vol4,0);
splus = 0; prop_tot = 0.0;
// membaca lattice for(s=0;s<vol4;s++){
splus = s + vol4; for(mu=0;mu<4;mu++){
for(i=0;i<18;i++){
(lat[s]).U[mu][i] = (lat[splus]).U[mu][i]; }
} }
for(T=2;T<18;T++){
compute_prop(dims,lat,&xx,T); prop_tot = xx/(3);
printf("% .9f ",prop_tot); }
printf("\n");
if (n_badlink>0) printf("Found %d bad links\n",n_badlink);
/*printf("Checksum = %x ... ",chksum); if (get_uint32_t("CHECKSUM",hdr,&uj) == FAILURE)
printf("(no CHECKSUM in header)\n");
else if (uj==chksum)
printf("(OK)\n"); else
printf("(mismatch with %12u)\n",uj);
xx = trace_tot;
printf("Avg trace = % .9f ... ",xx);
if (get_float("LINK_TRACE",hdr,&xx_float) == FAILURE) printf("(no LINK_TRACE in header)\n");
else if (fabs(xx-xx_float)<TOL) printf("(OK)\n");
else
printf("(mismatch with % .9f)\n",xx_float);*/
/*
if (get_float("PLAQUETTE",hdr,&xx_float) == FAILURE) printf("(no PLAQUETTE in header)\n");
else if (fabs(xx-xx_float)<TOL) printf("(OK)\n");
else
printf("(mismatch with % .9f)\n",xx_float);
printf("splus = %d\n ",splus);*/ exit(0);
}
error_exit(s) char *s; {printf("%s\n",s);exit(1);}
/*=========================================*/
/* read_slice: read one timeslice */
/*=========================================*/ read_slice(_in,_vol3,_lat,_chk)
FILE *_in; int _vol3;
struct site *_lat; uint32_t *_chk; {
struct site *p; float *uin,*q; int s,mu,i; uint32_t j=0;
uin = (float *) malloc(48*_vol3*sizeof(float)); fread(uin,48*_vol3*sizeof(float),1,_in);
if (!big_end_p) byte_swap(48*_vol3,uin); p = _lat+_vol3;
q = uin;
for (s=0;s<_vol3;s++) { for (mu=0;mu<4;mu++) {
}
*_chk = j; free(uin);
#ifdef FORTRANORDER
/* Tranpose if using fortran ordering for U[18] */ transpose(_vol3,_lat+_vol3);
#endif
}
/*============================================*/
/* check_unitarity(_n,_lat): Check out links */
/*============================================*/ check_unitarity(_n,_lat,_t)
int _n,_t;
struct site *_lat; {
int s,i,j,k,mu;
REAL xx,*p,tmpU[18],tmpZ[18];
for (s=0;s<_n;s++) { for (mu=0;mu<4;mu++) {
/* Point to U_mu(s) */ p = (_lat[s]).U[mu];
/* Compute (U.Udag - I) */
for (i=0;i<18;i++) xx += tmpZ[i]*tmpZ[i]; if (xx>TOL) {
n_badlink++;
/* print the first few errors */ if (n_badlink<BADPRINT)
printf("Bad link @ t=%d s=%d, mu=%d : %15.10f\n",_t,s,mu,xx); }
} } }
/*============================================*/
/* big_endian(): Check if we are big-endian */
/*============================================*/ big_endian() {
union {
long l;
char c[sizeof (long)]; } u;
u.l = 1;
return (u.c[sizeof (long) - 1] == 1); }
/*=============================================*/
/* byte_swap(_n,_u): Big/Little-Endian Filter */
byte_swap(_n,_u)
register char chr; int s;
for (s=0;s<_n;s++) { wrd.uint_wrd = _u[s]; chr = wrd.c[0]; wrd.c[0] = wrd.c[3]; wrd.c[3] = chr; chr = wrd.c[2]; wrd.c[2] = wrd.c[1]; wrd.c[1] = chr; _u[s] = wrd.uint_wrd; }
}
/*=======================================================*/
/* REAL compute_prop(_dims,_lat,_plaq,_T): */
/* menghitung propagator pada waktu T */
/*=======================================================*/
compute_prop(_dims,_lat,_plaq,_T) struct site *_lat;
int _dims[4], _T; REAL *_plaq;
s = site_addr(0,0,0,t,_dims); l = (_lat[s]).U[3];
transpose1(p,l); multAB(utmp,p,utmp); }
prop += utmp[0]+utmp[8]+utmp[16];
} struct site *_lat; int _dims[4]; {
int x,y,z,t; int s;
for (t=0; t<2; t++) {
for (z=0; z<_dims[2]; z++) { for (y=0; y<_dims[1]; y++) { for (x=0; x<_dims[0]; x++) {
s = site_addr(x,y,z,t,_dims);
(_lat[s]).neighbor[0] = site_addr((x+1)%_dims[0],y,z,t,_dims); (_lat[s]).neighbor[1] = site_addr(x,(y+1)%_dims[1],z,t,_dims); (_lat[s]).neighbor[2] = site_addr(x,y,(z+1)%_dims[2],t,_dims); (_lat[s]).neighbor[3] = site_addr(x,y,z,(t+1)%_dims[3],_dims); }}}}
}
/*====================================================*/
/* REAL one_plaquette(): ReTr(l1*l2*l3dag,l4dag) */
c[ 4] = a[ 4]*b[ 0]-a[ 5]*b[ 1]+a[10]*b[ 2]-a[11]*b[ 3]+a[16]*b[ 4]-a[17]*b[ 5];
c[ 6] = a[ 0]*b[ 6]-a[ 1]*b[ 7]+a[ 6]*b[ 8]-a[ 7]*b[ 9]+a[12]*b[10]-a[13]*b[11];
c[ 8] = a[ 2]*b[ 6]-a[ 3]*b[ 7]+a[ 8]*b[ 8]-a[ 9]*b[ 9]+a[14]*b[10]-a[15]*b[11];
c[10] = a[ 4]*b[ 6]-a[ 5]*b[ 7]+a[10]*b[ 8]-a[11]*b[ 9]+a[16]*b[10]-a[17]*b[11];
c[12] = a[ 0]*b[12]-a[ 1]*b[13]+a[ 6]*b[14]-a[ 7]*b[15]+a[12]*b[16]-a[13]*b[17];
c[14] = a[ 2]*b[12]-a[ 3]*b[13]+a[ 8]*b[14]-a[ 9]*b[15]+a[14]*b[16]-a[15]*b[17];
c[16] = a[ 4]*b[12]-a[ 5]*b[13]+a[10]*b[14]-a[11]*b[15]+a[16]*b[16]-a[17]*b[17];
c[ 1] = a[ 0]*b[ 1]+a[ 1]*b[ 0]+a[ 6]*b[ 3]+a[ 7]*b[ 2]+a[12]*b[ 5]+a[13]*b[ 4];
c[ 3] = a[ 2]*b[ 1]+a[ 3]*b[ 0]+a[ 8]*b[ 3]+a[ 9]*b[ 2]+a[14]*b[ 5]+a[15]*b[ 4];
c[ 5] = a[ 4]*b[ 1]+a[ 5]*b[ 0]+a[10]*b[ 3]+a[11]*b[ 2]+a[16]*b[ 5]+a[17]*b[ 4];
c[ 7] = a[ 0]*b[ 7]+a[ 1]*b[ 6]+a[ 6]*b[ 9]+a[ 7]*b[ 8]+a[12]*b[11]+a[13]*b[10];
c[ 9] = a[ 2]*b[ 7]+a[ 3]*b[ 6]+a[ 8]*b[ 9]+a[ 9]*b[ 8]+a[14]*b[11]+a[15]*b[10];
c[11] = a[ 4]*b[ 7]+a[ 5]*b[ 6]+a[10]*b[ 9]+a[11]*b[ 8]+a[16]*b[11]+a[17]*b[10];
c[13] = a[ 0]*b[13]+a[ 1]*b[12]+a[ 6]*b[15]+a[ 7]*b[14]+a[12]*b[17]+a[13]*b[16];
c[15] = a[ 2]*b[13]+a[ 3]*b[12]+a[ 8]*b[15]+a[ 9]*b[14]+a[14]*b[17]+a[15]*b[16];
c[17] = a[ 4]*b[13]+a[ 5]*b[12]+a[10]*b[15]+a[11]*b[14]+a[16]*b[17]+a[17]*b[16];
}
/*=========================================================================*/ /* multABdag(c,a,b): 3x3 matrix c=a*b-dagger, with arrays in Fortran order */ /*=========================================================================*/
c[ 4] = a[ 4]*b[ 0]+a[ 5]*b[ 1]+a[10]*b[ 6]+a[11]*b[ 7]+a[16]*b[12]+a[17]*b[13];
c[ 6] = a[ 0]*b[ 2]+a[ 1]*b[ 3]+a[ 6]*b[ 8]+a[ 7]*b[ 9]+a[12]*b[14]+a[13]*b[15];
c[ 8] = a[ 2]*b[ 2]+a[ 3]*b[ 3]+a[ 8]*b[ 8]+a[ 9]*b[ 9]+a[14]*b[14]+a[15]*b[15];
c[10] = a[ 4]*b[ 2]+a[ 5]*b[ 3]+a[10]*b[ 8]+a[11]*b[ 9]+a[16]*b[14]+a[17]*b[15];
c[12] = a[ 0]*b[ 4]+a[ 1]*b[ 5]+a[ 6]*b[10]+a[ 7]*b[11]+a[12]*b[16]+a[13]*b[17];
c[14] = a[ 2]*b[ 4]+a[ 3]*b[ 5]+a[ 8]*b[10]+a[ 9]*b[11]+a[14]*b[16]+a[15]*b[17];
c[16] = a[ 4]*b[ 4]+a[ 5]*b[ 5]+a[10]*b[10]+a[11]*b[11]+a[16]*b[16]+a[17]*b[17];
c[ 1] = -a[ 0]*b[ 1]+a[ 1]*b[ 0]-a[ 6]*b[ 7]+a[ 7]*b[ 6]-a[12]*b[13]+a[13]*b[12]; c[ 3] = -a[ 2]*b[ 1]+a[ 3]*b[ 0]-a[ 8]*b[ 7]+a[ 9]*b[ 6]-a[14]*b[13]+a[15]*b[12]; c[ 5] = -a[ 4]*b[ 1]+a[ 5]*b[ 0]-a[10]*b[ 7]+a[11]*b[ 6]-a[16]*b[13]+a[17]*b[12]; c[ 7] = -a[ 0]*b[ 3]+a[ 1]*b[ 2]-a[ 6]*b[ 9]+a[ 7]*b[ 8]-a[12]*b[15]+a[13]*b[14]; c[ 9] = -a[ 2]*b[ 3]+a[ 3]*b[ 2]-a[ 8]*b[ 9]+a[ 9]*b[ 8]-a[14]*b[15]+a[15]*b[14]; c[11] = -a[ 4]*b[ 3]+a[ 5]*b[ 2]-a[10]*b[ 9]+a[11]*b[ 8]-a[16]*b[15]+a[17]*b[14]; c[13] = -a[ 0]*b[ 5]+a[ 1]*b[ 4]-a[ 6]*b[11]+a[ 7]*b[10]-a[12]*b[17]+a[13]*b[16]; c[15] = -a[ 2]*b[ 5]+a[ 3]*b[ 4]-a[ 8]*b[11]+a[ 9]*b[10]-a[14]*b[17]+a[15]*b[16]; c[17] = -a[ 4]*b[ 5]+a[ 5]*b[ 4]-a[10]*b[11]+a[11]*b[10]-a[16]*b[17]+a[17]*b[16];
}
/*======================================================================*/ /* transpose(_n,_lat): filter to account for U/U-dag/U-star conventions */ /*======================================================================*/ transpose(_n,_lat)
int _n;
struct site *_lat; {
int s,mu,i,nsite; REAL *p,tmp[18]; for (s=0;s<_n;s++) {
for (mu=0;mu<4;mu++) { p = (_lat[s]).U[mu];
_p[15] = _p[ 0]*_p[11] - _p[ 4]*_p[ 7] + _p[ 1]*_p[10] - _p[ 5]*_p[ 6]; _p[16] = _p[ 0]*_p[ 8] - _p[ 2]*_p[ 6] - _p[ 1]*_p[ 9] + _p[ 3]*_p[ 7]; _p[17] = _p[ 2]*_p[ 7] - _p[ 0]*_p[ 9] + _p[ 3]*_p[ 6] - _p[ 1]*_p[ 8]; }
/*==============================================*/ /* get_header: read from stream, parsing tokens */ /*==============================================*/ struct QCDheader *
get_header(in) FILE *in;
{ #define MAX_LINE_LENGTH 1024 #define MAX_TOKENS 512 char line[MAX_LINE_LENGTH];
int i,n,len;
struct QCDheader *hdr; char **tokens, **values; char *p, *q;
/* Begin reading, and check for "BEGIN_HEADER" token */ fgets(line,MAX_LINE_LENGTH,in);
if (strcmp(line,"BEGIN_HEADER\n")!=0)
error_exit("Missing \"BEGIN_HEADER\"; punting \n");
/* Allocate space for QCDheader and its pointers */ tokens = (char **) malloc(MAX_TOKENS*sizeof(char *)); values = (char **) malloc(MAX_TOKENS*sizeof(char *));
hdr = (struct QCDheader *) malloc(sizeof(struct QCDheader)); (*hdr).token = tokens;
(*hdr).value = values;
/* Begin loop on tokens */ n = 0;
while (1) {
fgets(line,MAX_LINE_LENGTH,in);
if (strcmp(line,"END_HEADER\n")==0) break;
/* Tokens are terminated by a space */ q = index(line,’ ’);
/* Overwrite space with a terminating null */ *q = ’\0’;
len = (int) q - (int) line;
/* allocate space and copy the token in to it */ p = malloc(len+1);
(*hdr).token[n] = p; strcpy(p,line);
q = index(++q,’=’); q++; len = strlen(q);
q[len-1] = 0; p = malloc(len); (*hdr).value[n] = p; strcpy(p,q);
n++; }
(*hdr).ntoken = n; return (hdr); }
/* get_string: find a token and return its value as a string */ /*===========================================================*/ get_string(s,hdr,q)
char *s;
struct QCDheader *hdr; char **q;
{
/* find a token and return the value */ int i;
for (i=0; i<(*hdr).ntoken; i++) { if (strcmp(s,(*hdr).token[i])==0) {
*q = (*hdr).value[i]; return(SUCCESS);
/* get_uint32_t: return value as a uint32_t */
/*========================================*/ get_uint32_t(s,hdr,q)
char *s;
struct QCDheader *hdr; uint32_t *q;
{
char *p; int j;
get_string(s,hdr,&p);
if (p==NULL) return (FAILURE); #ifdef INTS_ARE_32BIT
/* get_int: return value as an int */
/*==================================*/ get_int(s,hdr,q)
char *s;
struct QCDheader *hdr; int *q;
{
char *p;
get_string(s,hdr,&p);
if (p==NULL) return (FAILURE); sscanf(p,"%d",q);
return (SUCCESS); }
/*=====================================*/
/* get_float: return value as a float */
/*=====================================*/ get_float(s,hdr,q)
char *s;
float *q; {
char *p;
get_string(s,hdr,&p);
if (p==NULL) return (FAILURE); sscanf(p,"%f",q);
return (SUCCESS); }
print_link(u) REAL *u; { int i;
printf("======\n"); for (i=0;i<18;i+=2)
A.2
Menghitung massa residu
/*===================================================================*/
/* Program menghitung residual mass rata-rata dan deviasinya */
/*===================================================================*/
#include <stdio.h> #include <math.h>
main(){ int i,j;
double tmp[100][100], array[100][100], dmarray[100][100]; double sum[100], avg[100], dev[100];
int bar, kol; int f;
double fi,div;
bar = 50; /* jumlah konfigurasi kol = 16; /* titik waktu yang diplot
/*================================================*/
/* membaca nilai propagator dan meng_improve_nya */
/*================================================*/ for(i=0;i<bar;i++){
for(j=0;j<kol;j++){
f = j + 1 + 1;
fi = (1 - pow((0.3333333),(double)f)); scanf("%lf", &tmp[i][j]);
array[i][j] = fi * tmp[i][j]; }
}
/*=====================*/ /* menghitung nilai dm */ /*=====================*/ for(i=0;i<bar;i++){
for(j=0;j<(kol-1);j++){
div = array[i][j+1]/array[i][j]; dmarray[i][j] = (-1.0) * log(div); }
}
/*=====================================*/ /* menghitung dm rata2 dan varians_nya */ /*=====================================*/
for(j=0;j<(kol-1);j++){ for(i=0;i<bar;i++){
avg[j] = sum[j]/bar;
sum[j] = 0;
for(i=0;i<bar;i++){
sum[j] += ((dmarray[i][j] - avg[j])*(dmarray[i][j] - avg[j])); }
dev[j] = sqrt(sum[j]/(double)(bar-1));
printf(" %d %lf %lf\n", j+1, avg[j], dev[j]/2); }
Daftar Acuan
[1] R. P. Feynman dan A. R. Hibbs (1965), Quantum Mechanics and Path
Integrals, McGraw-Hill.
[2] M. Alford et. al., Lattice QCD on Small Computers, Phys. Lett. B361
(1995) 87 (hep-lat/9507010).
[3] M. Crisafulli, V. Gimenez, G. Martinelli dan C. T. Sachradja, First Lattice
Calculation of The B-meson Binding and Kinetic Energy,
CERN-TH.7521/94 (hep-ph/9506210).
[4] V. Gimenez, G. Martinelli dan C. T. Sachradja, A High Statistics Lattice
Calculation of The B-meson Binding Energy, CERN-TH/96-163
(hep-ph/9607018).
[5] H. J. Rothe (1997), Lattice Gauge Theory, an Introduction, World
Sci-entific Publishing.
[6] G. M¨unster and M. Walzl, Lattice Gauge Theory A Short Primer,
(hep-lat/0012005).
[7] G. P. Lepage, Lattice QCD For Novices,
http://www.tech.plym.ac.uk/maths/bus.
[9] G. Martinelli dan C. T. Sachradja, Renormalons and the Heavy Quark
Effective Theory, CERN-TH.7517/94 (hep-ph/9502352).
[10] A. F. Falk, M. Neubert dan M. Luke, Nucl. Phys.B388 (1992) 363.
[11] The APE Collaboration, C. R. Alltonet al.,Result for the B-meson Decay Constan from the APE Collaboration, Nucl. Phys. B413 (1994);Phys. Lett. B326 (1994) 295.