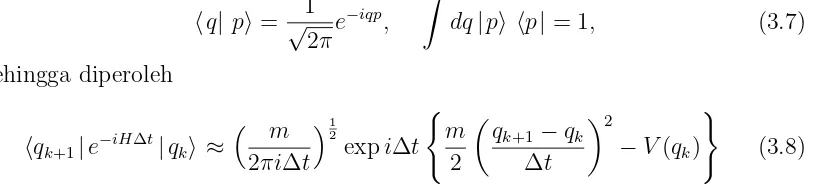Perhitungan Besaran Fisis Dinamika Fluida
Relativistik dengan Menggunakan
Lattice Gauge
Theory
Tugas Akhir
Diajukan sebagai salah satu syarat untuk meraih gelar Sarjana Sains
Andhika Oxalion
0303020139
Departemen Fisika
Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Indonesia
Lembar Persetujuan
Judul Skripsi : Perhitungan Besaran Fisis Dinamika Fluida Relativistik dengan Menggunakan Lattice Gauge Theory
Nama : Andhika Oxalion
NPM : 0303020139
Skripsi ini telah diperiksa dan disetujui
Depok, Mei 2007 Mengesahkan
Pembimbing I Pembimbing II
Dr. L. T. Handoko Dr. Terry Mart
Penguji I Penguji II
Kata Pengantar
Teori Medan Kuantum (Quantum Field Theory), alat kita untuk menjelaskan gaya fundamental, diformulasikan dalam ruang-waktu kontinu dengan memper-lakukan ruang dan waktu dalam dimensi yang setara. Di sisi lain, dinamika fluida klasik mengandung besaran yang bergantung ruang dan waktu. Hal ini menimbulkan ide mengenai kemungkinan dinamika fluida diformulasikan ulang menggunakan teori medan. Kemudian, jika dapat dilakukan, harus dapat dihi-tung besaran-besaran fisis yang ada dalam dinamika fluida tersebut.
Sebelumnya, penulis lain telah berhasil memformulasikan dinamika fluida meng-gunakan teori medan, yaitu mencari Lagrangian dinamika fluida yang bila dipro-ses lebih lanjut akan menghasilkan persamaan dinamika fluida relativistik. Pada tugas akhir ini, penulis menghitung besaran-besaran fisis dinamika fluida ber-dasarkan Lagrangian tersebut. Perhitungan besaran fisis ini dilakukan dengan menggunakan Lattice Gauge Theory di mana ruang dan waktu kontinu pada teori medan diganti dengan kumpulan titik diskrit pada kisi empat dimensi. Ke-untungan yang diperoleh adalah, perhitungan yang rumit secara analitik dapat diperoleh secara numerik. Penulis secara khusus mengucapkan terima kasih ke-pada semua pihak yang telah membantu penyelesaian tugas akhir ini baik secara langsung maupun tidak langsung, antara lain:
1. Dr. L.T. Handoko selaku pembimbing I yang telah membimbing penulis mulai dari awal diskusi hingga penyelesaian tugas akhir ini serta atas ide-ide, dukungan dan saran yang diberikan.
3. Dr. Anto Sulaksono dan Dr. Agus Salam selaku penguji I dan II atas diskusi dalam penyelesaian tugas akhir ini.
4. Orang tua dan kakak Alvin Stanza atas saran dan bantuan yang diberikan semasa kuliah.
5. Rekan-rekan di Lab Teori : Ryky, Victor, Juju, Beriya, Popo, Freddy, Han-dhika, Arum, Ardy, Nita, Harykin, Chandi, Pak Ayung, Pak Sulaiman, Mas Parada.
6. Teman-teman fisika angkatan 2003 dan teman-teman di KMK.
7. Special thanks, kepada Heribertus Bayu Hartanto serta Nowo Riveli yang sungguh membantu penulis mengejar materi dan juga dalam pemrograman. Kepada Arif Budi Mulyawan yang telah bersedia meminjamkan komputer-nya untuk menjalankan program.
8. Juga semua pihak yang tidak dapat disebutkan di sini atas dukungan dan doa kepada penulis selama penyelesaian tugas akhir ini.
Penulis menyadari bahwa karya tulis ini masih jauh dari sempurna, maka dari itu penulis mengharapkan kritik dan saran dari para pembaca demi perkembangan riset di Fisika UI.
Depok, Mei 2007
Abstrak
Dinamika fluida berbasis teori medan diformulasikan dalam kisi ruang waktu diskrit. Dengan formulasi tersebut dihitung besaran fisis dinamika fluida rela-tivistik dengan menggunakan simulasi Metropolis Monte Carlo. Formulasi ini memberikan pemahaman dasar untuk perhitungan bermacam-macam observable dari fenomena yang dimodelkan dengan Lagrangian dinamika fluida di mana ti-dak ada jaminan teori perturbasi berlaku.
Kata kunci: Lagrangian dinamika fluida, lattice gauge theory, interaksi sistem multi fluida
viii+30 hlm.; lamp.
Daftar Acuan: 13(1993-2006)
Abstract
Fluid dynamics based on the gauge field theory is formulated on a discrete space-time lattice. Using this formulation, physical observable of relativistic fluid dyna-mics is calculated using Metropolis Monte Carlo simulation. This formulation provides basic knowledge to calculate some observables for phenomenon modeled with the fluid dynamics Lagrangian where no guarantee that perturbation theory can be applied.
Keywords: Fluid dynamics Lagrangian, lattice gauge theory, multi-fluids intera-ction
Daftar Isi
Kata Pengantar iii
Abstrak v
Daftar Isi vi
Daftar Gambar viii
1 Pendahuluan 1
1.1 Latar Belakang . . . 1
1.2 Perumusan Masalah . . . 1
1.3 Metode Penelitian . . . 2
1.4 Tujuan Penelitian . . . 2
2 Dinamika Fluida Berbasis Teori Medan 4 2.1 Dinamika Fluida Klasik . . . 4
2.2 Teori MedanGauge untuk Dinamika Fluida . . . 6
2.3 Sistem Multi Fluida . . . 10
3 Teori Medan Gauge pada Lattice 12 3.1 Path Integral dalam Mekanika Kuantum . . . 13
3.2 Teori Medan Kuantum MenggunakanPath Integral . . . 15
3.3 Diskritisasi . . . 18
3.4 Transformasi Gauge pada Lattice . . . 19
3.5 Observable . . . 23
4 Hasil dan Pembahasan 26
5 Kesimpulan 30
A Evaluasi Path Integral dengan Metode Monte Carlo 31
B Pemrograman 35
B.1 Perhitungan Matriks Kompleks . . . 35
B.2 Generator Matriks SU(2) . . . 40
B.3 Program Simulasi pada Lattice . . . 41
B.4 Program Iterasi Z terhadap |v| . . . 44
Daftar Gambar
3.1 Diskritisasi interval waktu . . . 14
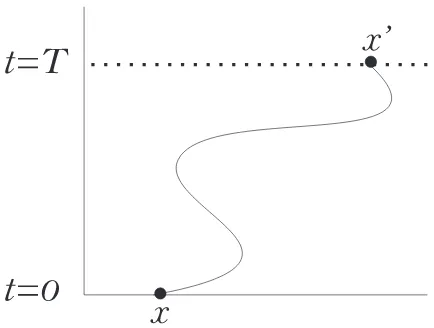
3.2 Lintasan partikel . . . 15
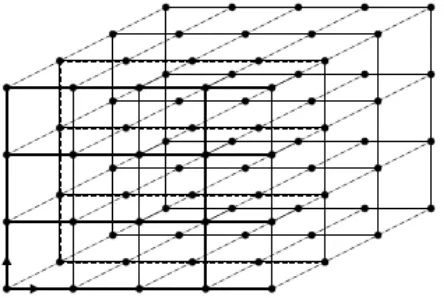
3.3 Lattice atau kisi 3 dimensi . . . 18
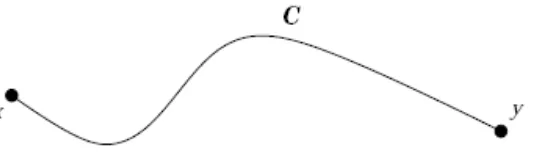
3.4 Lintasan C antara xdan y . . . 21
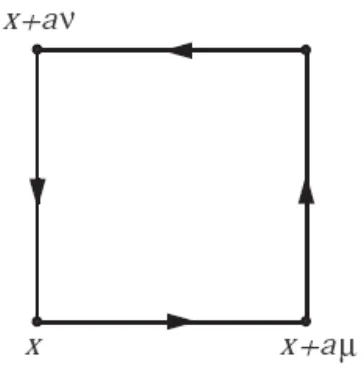
3.5 Uµνx pada sebuah Plaquette . . . 23
4.1 NilaiZ pada kisi 104 site |v|= 0,8c hingga 0.9c . . . . 27
4.2 NilaiZ pada kisi 304 site dengan |v|= 0.8 hingga 0.9c . . . . 28
4.3 NilaiZ pada kisi 304 site dengan |v|= 0 hingga 0.5c . . . . 28
Bab 1
Pendahuluan
1.1
Latar Belakang
Dinamika fluida klasik diturunkan dari Hukum II Newton dan hukum kekekal-an massa. Persamakekekal-an tersebut nonlinier sehingga mengakibatkkekekal-an solusi sulit dicari karena solusinya tidak dapat disuperposisikan[1]. Sementara itu, banyak sistem-sistem yang dapat dimodelkan dengan menggunakan dinamika fluida, mi-salnya kosmologi turbulen, quark-gluon plasma, dll yang memerlukan solusi ter-sebut untuk melakukan perhitungan-perhitungan berikutnya. Sebagai alternatif, dinamika fluida dimodelkan sebagai Lagrangian boson yang invarian terhadap transformasi gauge. Metode ini telah diaplikasikan pada sistem fluida yang ber-interaksi dengan soliton yaitu proteinαheliks yang berinteraksi dengan biofluida [2]. Lagrangian yang invarian terhadap transformasi gauge tersebut dapat difor-mulasikan untuk sistem relativistik yang invarian terhadap transformasi Lorentz sehingga dengan menggunakan persamaan Euler-Lagrange dapat diperoleh per-samaan dinamika fluida relativistik [3]. Dinamika fluida berbasis teori medan ini juga dapat mendeskripsikan sistem multi fluida dengan menggunakan Lagrangian yang invarian terhadap transformasi gauge non-Abelian.
1.2
Perumusan Masalah
terhadap transformasi gauge dengan menggunakan persamaan Euler-Lagrange. Interaksi pada sistem multifluida dimodelkan dengan menggunakan Lagrangian boson yang invarian terhadap transformasi gauge non-Abelian yang merepresen-tasikan fluida murni tanpa materi. Perhitungan fungsi partisi dan observable energi bebas interaksi fluida dilakukan dengan mengevaluasi path integral. Na-mun besarnya konstanta kopling g tidak diketahui, sehingga path integral secara umum harus dihitung secara non-perturbatif.
Perhitungan secara non-perturbatif dilakukan dengan menggunakan Lattice Ga-uge Theory. Formulasi Quantum Chromodynamics dalam ruang-waktu diskrit atau sering disebut dengan Lattice QCD digunakan untuk menghitung besaran-besaran QCD pada energi rendah di mana konstanta kopling QCD sangat be-sar. Pada Lattice Gauge Theory, aksi disusun pada kisi ruang dan waktu diskrit sehingga memungkinkan path integral dihitung secara numerik dengan menggu-nakan metode Monte Carlo. Dengan menghitung observable dari Lagrangian ini maka diharapkan kita bisa mempelajari perilaku atau sifat-sifatnya terutama dalam kaitannya dengan besar konstanta kopling g maupun kecepatan.
1.3
Metode Penelitian
Penelitian ini bersifat teoritik. Teori yang digunakan ialah dinamika fluida de-ngan pendekatan teori medan. Untuk memperoleh observable dari teori ini, aksi yang menggambarkan interaksi fluida murni terlebih dahulu diformulasikan da-lam ruang dan waktu diskrit. Setelah itu dapat dihitung fungsi partisi dengan mengevaluasi path integral menggunakan metode Metropolis Monte Carlo.
1.4
Tujuan Penelitian
Bab 2
Dinamika Fluida Berbasis Teori
Medan
Pada bab ini dibahas secara singkat teori dinamika fluida secara klasik maupun dengan pendekatan berbasis teori medan.
2.1
Dinamika Fluida Klasik
Fluida didefinisikan sebagai materi yang mengalami perubahan bentuk secara kontinu bila diberi tegangan geser. Dinamika fluida merupakan cabang dari ilmu fisika yang mempelajari aliran fluida (cairan dan gas). Persamaan dinamika fluida klasik, seperti mekanika klasik pada umumnya, diturunkan berdasarkan hukum II Newton dan hukum kekekalan massa
∂~v
∂t + (~v·∇~)~v =−
1
ρ∇~P +µ~∇
2~v (2.1)
dengan~v ialah kecepatan fluida, P ialah tekanan, ρ ialah kerapatan danµ ialah koefisien viskositas. Hukum kekekalan massa menyatakan bahwa fluida tidak dapat diciptakan maupun dimusnahkan. Bila kita memberi gangguan pada fluida, massa fluida sebelum dan sesudah gangguan haruslah tetap. Pandang suatu fluida dengan volume V dengan S merupakan permukaan tertutup dari volume
V. Massa fluida ialah R
V ρdV, sementara fluks massa fluida pada permukaan
tertutup S ialah H
(ρ~v)·dS sehingga hukum kekekalan massa dinyatakan sebagai berikut
I
(ρ~v)·dS =−∂
∂t
Z
V
dengan teorema Gauss diperoleh,
yang tidak lain merupakan persamaan kontinuitas. Hukum II Newton menyata-kan kekekalan momentum
~
F =md
2~x
dt2 (2.4)
Terdapat dua jenis gaya yang dapat bekerja pada fluida yang bergerak, yaitu
1. Gaya badan (body force), yang bekerja langsung pada elemen volume fluida. Contohnya adalah gaya gravitasi, listrik dan magnet.
2. Gaya permukaan, (surface force) yang bekerja langsung pada permukaan elemen fluida. Hanya ada 2 sumber gaya jenis ini: (a) distribusi tekanan pada permukaan dan (b) distribusi regangan dan tegangan normal pada permukaan elemen fluida.
Untuk aliran fluida bermassa m→ρV dan percepatan,
d2~x
Maka hukum II Newton untuk aliran fluida dapat ditulis menjadi
ρD~v Dt =
~ F
V (2.5)
Gaya yang fundamental pada aliran fluida ialah gradien tekanan yang dapat ditulis sebagai berikut,
dimana tensor tekanan, Πik diberikan oleh
denganP tekanan dan σik ialah tensor viskositas. Tensor viskositas secara umum
merupakan tensor asimetrik. Tensor viskositas dapat ditulis [4],
σij =η
dengan η dan ν masing-masing merupakan koefisien viskositas kinematis dan dinamis. Dengan melakukan substitusi persamaan (2.6), (2.7) dan (2.8) ke hukum II Newton untuk fluida pada persamaan (2.5) dapat diperoleh,
ρ Untuk fluida inkompresibel ∇ ·~ ~v = 0 dan µ≡η/ρ didapatkan persamaan gerak untuk fluida inkompresibel
seperti pada persamaan (2.1).
2.2
Teori Medan
Gauge
untuk Dinamika Fluida
Persamaan dinamika fluida merupakan persamaan nonlinier yang menggambark-an alirmenggambark-an fluida dengmenggambark-an kecepatmenggambark-an alirmenggambark-an~v ≡~v(t, xi), dimanaxi adalah koordinat
3 dimensi. Hal ini memungkinkan persamaan tersebut diperumum sebagai per-samaan nonlinier dalam koordinat 4 dimensi xµ≡(x0, xi) = (xt, ~r) = (ct, x, y, z)
dengan kecepatan ~v ≡~v(xµ) Dalam hal ini digunakan ruang Minkowski dengan
tensor metrik gµν = (1,−~1) = (1,−1,−1,−1) sehingga x2 = xµxµ = xµgµνxν =
x2
0 −x2 = x20 −x21 −x22 −x23. Karena diturunkan dari hukum II Newton maka,
secara prinsip, persamaan gerak fluida dapat diturunkan melalui mekanika ana-litik dengan prinsip aksi minimum. Penurunan telah dikerjakan dalam sejumlah
first principle mekanika analitik yaitu dengan Lagrangiandensity. Karena persa-maan gerak fluida secara umum bergantung pada ruang dan waktu, maka dapat digunakan metode pada teori medan relativistik yang memperlakukan ruang dan waktu dalam dimensi yang sama. Persamaan dinamika fluida diturunkan seba-gai persamaan gerak dari Lagrangian boson yang invarian terhadap transformasi
gauge dan transformasi Lorentz melalui persamaan Euler-Lagrange.
Lagrangian untuk medan boson yang invarian terhadap transformasi gauge lokal ialah
memenuhi kekekalan arus∂µJ
µ= 0. Suku-suku tambahan padaLAmuncul
seba-gai konsekuensi sifat invarian Lagrangian boson tersebut terhadap transformasi
gauge lokal U =exp[−iθ(x)] sehingga,
Seperti disebutkan dalam [1], kita dapat melihat kemiripan bentuk persamaan dinamika fluida dengan persamaan Maxwell dengan mengganti medan magnet dan medan listrik dengan vektor Lamb dan vortisitas
~
E → ~l=~ω×~v ~
B → ~ω=∇ ×~ ~v
sehingga persamaan ”Maxwell” untuk fluida ialah
dengan α= 1/~v2. Hasil ini memberi petunjuk bahwa kita dapat mengkonstruksi
Lagrangian yang bentuknya mirip dengan Lagrangian elektrodinamika kuantum yaitu LA pada persamaan (2.12). Hal ini dibuktikan dengan mengambil bentuk
spesifik dari medan gauge,
Aµ =
dengan ~v ialah kecepatan fluida. Bentuk medan gauge tersebut jelas tidak me-menuhi transformasi Lorentz. Namun, dengan pemilihan ini tampak jelas bahwa pada dinamika fluida, potensial skalar merupakan energi total per satuan massa berupa rapat energi kinetik, sementara potensial vektor menggambarkan dinami-ka dalam suku kecepatan. Dengan demikian, LA pada persamaan (2.12) tidak
lain ialah Lagrangian yang menghasilkan persamaan dinamika fluida dengan pe-milihan medan gauge di atas, LA=LDF.
Berdasarkan prinsip aksi minimumδS = 0 denganS =R
d4xL
Dengan melakukan substitusi persamaan (2.12) ke persamaan (2.17) maka diha-silkan persamaan gerak dalam Aµ,
∂ν(∂µAν)−∂2Aµ+gJµ= 0. (2.18)
dengan Aµ merepresentasikan medan fluida. Relasi nontrivial diperoleh untuk
µ6=ν sehingga dapat dihasilkan persamaan gerak fluida.
Untuk memperoleh persamaan gerak yang relativistik, kita dapat mendefinisikan medangauge Aa
µ=
dengan β = |~v|/c. Suku pertama pada persamaan (2.19) menunjukkan versi relativistik energi kinetik persatuan massa. Substitusi persamaan (2.19) dan (2.20) ke persamaan (2.18), diperoleh persamaan gerak yang relativistik,
1
dtJi. Kita dapat memperoleh bentuk nonrelativistik
dengan mengambil |~v| ≪cdan menggunakan relasi 1
Dengan demikian persamaan dinamika fluida untuk sembarang gaya konserva-tif telah dibentuk menggunakan teori medan gauge. Terlihat pada persamaan (2.22) terdapat gaya tambahan, yaitu pada suku g ~J˜dan suku ~v×(∇ ×~ ~v) yang relevan untuk fluida rotasional ∇ ×~ ~v. Untuk fluida irotasional ∇ ×~ ~v = 0 dan fluida inkompresibel ∇ ·~ ~v = 0. Persamaan (2.21) invarian terhadap transformasi Lorentz,
Dari model yang dibuat untuk dinamika fluida dengan menggunakan teori medan gauge, tampak adanya interaksi antara fluida (Aµ) dengan materi di dalamnya
(φ). Dari suku pure gauge 1/4FµνFµν tampak adanya interaksi fluida dengan
fluida itu sendiri. Sementara itu, potensial pada Lagrangian menggambarkan interaksi antar medan boson. Pada dinamika fluida klasik, arus vektor empat
Jµ = (ρ, ρ~v) menggambarkan distribusi makroskopik dari kerapatan dan vektor
rapat arus. Sementara dalam pendekatan ini,Jµmenggambarkan fungsi
medan fluida dengan mediumnya. Jadi kita dapat menginvestigasi dinamika flui-da walaupunJµ= 0. Dengan menggunakan Lagrangian tersebut, kita juga dapat
mempelajari interaksi antara fluida dengan medium lainnya.
2.3
Sistem Multi Fluida
Model yang telah dikembangkan pada sub-bab sebelumnya dapat digeneralisasi untuk sistem multi fluida. Pada sistem ini kita menggunakan simetri SU(N) un-tuk menggambarkan sistem multi fluida serta interaksinya dengan materi. Unun-tuk melakukannya, transformasigaugeyang digunakan ialah transformasigaugelokal yang bersifat non-Abelian
U = exp(−iTaθa(x)) (2.23) dimana Ta merupakan generator dari grup Lie dan memenuhi relasi komutasi
[Ta, Tb] = ifabcTc dengan fabc merupakan konstanta struktur antisimetrik.
La-grangian untuk sistem multi fluida dapat dituliskan
L = (∂µφ)†(∂µφ) +V(φ) +LA (2.24)
dimana
LA=−
1 4F
a
µνFaµν +gJµaAaµ+
i
2f
abcg2(φ†Taφ)Ab
µAcµ (2.25)
dengan tensor kuat medan Fa
µν ≡ ∂µAaν −∂νAaµ − gfabcAbµAcν, sementara arus
vektor empatnya,
Jµa=i
(∂µφ)†Taφ−φ†Ta(∂µφ)
(2.26)
dengan transformasi gauge untuk tiap-tiap medan ialah
φ → φ′ =e−iTaθa(x)
φ ≈(1−iTaθa(x))φ (2.27)
Aaµ → Aaµ′ =Aaµ+ 1
g(∂µθ
a) +fabcθbAc
µ (2.28)
Bila Aa
µ diperhatikan sebagai medan fluida yang mewakili sekumpulan fluida
Lagrangian dari persamaan dinamika fluida (LDF). Sebagai contoh, untuk
meng-gambarkan interaksi antara 2 fluida, dapat digunakan Lagrangian yang berbentuk [5]
Ltotal =LaDF +LbDF +Labint (2.29)
denganLab
int merupakan Lagrangian interaksi antara dua fluida. Dari model yang
dibuat untuk sistem multi fluida, kita dapat melihat interaksi antara fluida (Aa µ)
dengan materi di dalamnya (φ) berdasarkan grup simetri SU(N) untuk n ×1 medan φ dan n×n generator Ta secara umum. Pada Lagrangian juga terdapat
suku interaksi antar fluida yang digambarkan oleh suku pure gauge
LP G =−
1 4F
a
Bab 3
Teori Medan
Gauge
pada
Lattice
Pada bab ini dijelaskan secara singkat metode path integral dan formulasi lat-tice serta hubungan antara keduanya. Metode path integral diperkenalkan oleh Feynman pada tahun 1948. Metode ini merupakan formulasi alternatif dari meka-nika kuantum dan teori medan. Keuntungan menggunakan formulasi ini adalah dapat dilakukannya kuantisasi suatu teori hanya dengan menggunakan medan kompleks, tanpa mengubah medan menjadi operator [6]. Keuntungan lain yang didapat adalah
• Merupakan cara termudah dan langsung untuk mendapatkan aturan Feyn-man untuk teori medan apapun.
• Memungkinkan diperoleh solusi eksak ataupun numerik dari medan inte-raksi kuat, dimana ekspansi perturbasi tidak berlaku dengan lattice gauge theory.
• Memperlihatkan hubungan antara teori medan dengan mekanika statistik.
3.1
Path Integral
dalam Mekanika Kuantum
Perhitungan menggunakanpath integral dilakukan dengan menggunakan Lagrang-ian dan HamiltonLagrang-ian. Untuk lebih jelasnya, pandang suatu sistem mekanika kuan-tum satu dimensi dengan LagrangianL=L(q,q˙) dan Hamiltonian H =H(p, q), yang pada mekanika klasik dinyatakan dengan
L= 1 2mq˙
2
−V(q) (3.1)
H = p
2
2m +V q. (3.2)
Dalam persamaan tersebut, p dan q dihubungkan oleh persamaan kanonik p =
∂L/∂q˙=mq˙. Namun harus diperhatikan bahwa pada mekanika kuantum, p dan
q adalah operator dengan relasi komutasi [p, q] = i~.
Amplitudo transisi dalam mekanika kuantum dinyatakan dengan
hq′, t′| q, ti = hq′|e−iH(t′−t)|qi
= hq′|U(t′, t)|qi (3.3) dengan U(t′, t) = exp(−iH(t′ −t)) adalah operator evolusi waktu. Selanjutnya,
dengan melakukan diskritisasi waktu T = t′
−t = n∆t dan memasukkan relasi kelengkapan eigenstate koordinatqn
1 =
Z
dq|qi hq| (3.4)
sebanyak n−1 maka diperoleh
hq′, t′
| q, ti =
Z
dq1. . . dqn−1 hq′|e−iH∆t|qn−1i hqn−1|e−iH∆t|qn−2i ×. . .hq2|e−iH∆t|q1i hq1|e−iH∆t|qi. (3.5)
Matriks transfer ˆT didefinisikan sebagai amplitudo transisi suatu sistem pada interval waktu ∆t. Untuk n yang besar dan ∆t sangat kecil, eksponen pada elemen matriks ˆT dapat diaproksimasi menggunakan suku pertama dari formula Baker-Campbell-Hausdorff menjadi [7]
hqk+1|Tˆ|qki = hqk+1|e−iH∆t|qki
≈ hqk+1|e−i∆tp
2/2m
Gambar 3.1: Diskritisasi interval waktu
karena potensial V hanya bergantung pada koordinat spasial. Kemudian, elemen matriks hqk+1|e−i∆tp
2/2m
|qki dievaluasi dengan transformasi Fourier dan relasi
kelengkapan
Dengan mengevaluasi seluruh elemen matriks transfer, amplitudo transisi (3.3) dapat ditulis menjadi
Dengan S merupakan aksi fungsional dari suatu sistem,
S(q) =
Z t′
t
dtL(q(t),q˙(t)), (3.12) dan R
Dq merupakan integrasi dari seluruh fungsi q(t). Path integral merupakan penjumlahan terhadap semua lintasan partikel q(t).
Gambar 3.2: Lintasan partikel
seperti pada mekanika klasik. Lintasan klasik yang memenuhi persamaan gerak
δS(q) = 0 yang dinyatakan dengan persamaan Euler-Lagrange
∂L ∂q −
∂ ∂t
∂L
∂q˙ = 0 (3.13)
hanyalah satu dari seluruh lintasan tak berhingga yang mungkin sebab mekanika kuantum tidak memperbolehkan adanya hanya satu lintasan unik [8]. Akibat-nya, semua lintasan yang mungkin harus dilibatkan dalam perhitungan. Setiap lintasan memiliki bobot exp(iS) yang dinyatakan dalam persamaan (3.10) [9]. Munculnya faktor bobot (sebenarnya : eiS~) untuk setiap lintasan merupakan
konsekuensi bahwa lintasan klasik harus diperoleh pada limit klasik ~→0.
3.2
Teori Medan Kuantum Menggunakan
Path
Integral
antara lain [10]
dengan S adalah aksi klasik. Besaran yang penting di teori medan ialah nilai ekspektasi vakum dari produk time-ordered operator medan, yaitu fungsi Green:
h0|φ(x1)φ(x2). . . φ(xn))|0i, t1 > t2 > . . . > tn (3.14)
seperti contohnya ialah propagator
h0|φ(x1)φ(x2)|0i (3.15)
Dengan analogi path integral mekanika kuantum kita menuliskan representasi fungsi Green dalam integral fungsional [11],
h0|φ(x1)φ(x2). . . φ(xn)|0i =
Pada pembahasan sebelumnya, dapat dilihat bahwa perhitungan path integral melibatkan komponen eksponen imaginer, yang bila diekspansi merupakan kom-ponen yang berosilasi. Hal ini membuat integral tidak dapat dihitung secara numerik. Namun, hal ini dapat diatasi dengan menggunakan kontinuasi analitik ke waktu imaginer. Dengan cara ini, eksponen menjadi real dan dapat dihi-tung secara numerik. Sistem ruang waktu dengan komponen waktu imaginer ini disebut ruang waktu Euclidean. Karena sebelumnya diturunkan persamaan menggunakan ruang waktu Minkowski, maka harus dilakukan substitusi
t=x0 → −ix4 (3.18)
Sebagai contoh, kita lakukan kontinuasi pada medan skalar dengan aksi
Dengan melakukan integrasi parsial, aksi dapat ditulis sebagai
S = 1 2
Z
d4xφ(−∂2 −m2)φ. (3.20)
Kontinuasi ke waktu imaginer dilakukan dengan substitusi
d4x = dx0dx1dx2dx3
merupakan aksi medan skalar dalam ruang waktu Euclidean. Fungsi Green versi Euclidean adalah
3.3
Diskritisasi
Setelah membuat formulasi ruang-waktu secara Euclidean, kita membentuk kisi sebagai metode perhitungan. Kisi pada hal ini adalah susunan ruang waktu secara diskrit dengan geometri hiperkubik empat dimensi dengan jarak antar tiap titik kisi (sites) adalah a. Dengan demikian pada, medan hanya memiliki nilai pada titik-titik kisi
xµ =mµa, mµ = 0,1, . . . , N −1. (3.25)
sehingga panjang sisi dari kotak hiperkubik ialah L = Na dan volumenya L4.
Medan Aµ pada titik kisi xµ = mµa ditulis dengan notasi Aµx. Dengan
dilaku-Gambar 3.3: Lattice atau kisi 3 dimensi
kannya diskritisasi, maka integral dapat digantikan dengan sumasi
Z
d4x→a4
N−1
X
m1
N−1
X
m2
N−1
X
m3
N−1
X
m4
=a4X
m
=X
x
(3.26)
yang pada limit kontinu harus dipenuhi
X
x
f(x)→
Z L
0
d4xf(x), N → ∞, a→0, Ltetap (3.27) Sekarang akan dilakukan diskritisasi sukupure gauge pada persamaan 2.12. Ten-sor kuat medan yang diberikan oleh
Dengan turunan atau derivatif medan diganti dengan perbedaan atau selisih med-an med-antara dua titik kisi,
∂µAν =
dengan ˆµdan ˆν merupakan vektor satuan pada arahµdanν. Dengan diskritisasi yang telah dijelaskan maka kita dapat menulis aksi untuk medanpure gauge pada persamaan (2.12) dalam bentuk diskrit [7]
S = 1
3.4
Transformasi
Gauge
pada
Lattice
Perhatikan aksi dari medan skalar pada persamaan (3.19). Untuk medan skalar kompleks, setelah diskritisasi, aksi tersebut dapat ditulis menjadi
S=a4X
Aksi tersebut invarian terhadap transformasi gauge global
φx → φ′x = Ωφx
φ†x → φ†′x =φ†xΩ†
dengan Ω = e−iθ merupakan elemen dari grup U(1). Kemudian, aksi tersebut
harus invarian terhadap transformasi gauge lokal U(1), dengan elemen grup Ω bergantung pada titik kisi, Ω = Ωx. Sehingga medan φx bertransformasi sebagai
berikut,
φx → φ′x = Ωxφx (3.33)
φ†
x → φ†′x =φ†xΩ†x. (3.34)
Dari transformasi tersebut, perhatikan besaran φ†
xφx+aµˆ dan φ†xφx−aµˆ. Besaran
persamaan (3.32) dan (3.33)
φ†xφx+aµˆ → φ†xΩ †
xΩx+aµˆφx+aµˆ, (3.35)
φ†
xφx+aµˆ → φ†xΩ†xΩx−aµˆφx−aµˆ. (3.36)
Agar besaran tersebut invarian, maka kita membutuhkan suatu besaranUµx yang
bertransformasi sebagai berikut,
Uµx →ΩxUµxΩ†x+aµˆ (3.37)
Uµxmerupakan besaran yang menghubungkan titik kisi yang satu dengan titik kisi
lainnya pada lattice, dan disebut dengan variabel ”link”. Di dalam variabel link terdapat medangauge Aµagar besaran pada persamaan (3.31) invarian terhadap
transformasi gauge lokal. Variabel link didefinisikan sebagai
Uµx=Ux,x+aµˆ =eigaAµx (3.38)
Sehingga kita memiliki bentuk yang invarian terhadap transformasi gauge lokal pada lattice
φ†xφx+aµˆ → φ†xUx,x+aµˆφx+aµˆ (3.39)
φ†
xφx−aµˆ → φ†xU †
x−aµ,xˆ φx+aµˆ (3.40)
dimana
U−µx =Ux†−aµ,xˆ =Ux,x−aµˆ =e−igaAµx−aˆµ (3.41)
Pada teori kontinum Uµx tidak lain merupakan parallel transporter yang analog
dengan obyek yang sama pada geometri diferensial, yang memetakan vektor dari titik yang satu ke titik lainnya sepanjang kurva.
U(x, y;C) =eigRyxAµ(z)dzµ. (3.42)
Parallel transporter tidak hanya bergantung pada titik x dan y tetapi juga kurva
C yang dipilih.
Dengan diperkenalkannya variabel link Uµx yang didalamnya terdapat medan
Gambar 3.4: Lintasan C antara x dan y
invarian terhadap transformasi gauge lokal dalam Uµx. Untuk itu perhatikan
medan gauge yang didefinisikan sebagai berikut
FµνFµν = (∂µAν −∂νAµ) (∂µAν −∂νAµ) (3.43)
Pada Aµ telah dibuat ansatz bahwa Aµ dapat diseparasi menjadi ǫµ dan φ, di
mana φ merupakan suatu besaran medan berdimensi massa, [φ] = 1, atau suatu medan yang memiliki kecepatan ~v. Sehingga persamaan (3.42) dapat ditulis menjadi
FµνFµν = (∂µ(ǫνφν)−∂ν(ǫµφµ)) (∂µ(ǫνφν)−∂ν(ǫµφµ)) (3.46)
Kemudian dilakukan separasi komponen waktu dan ruang secara eksplisit untuk mempermudah perhitungan. Sebagai berikut
Dengan asumsi bahwa loop yang diamati sangat kecil maka dapat diasumsikan Dalam tugas akhir ini digunakan variabel link yang berbeda sebab digunakan separasi padaAµ. Variabellink, Uµx denganAµ yang kita gunakan dapat ditulis
sebagai
dengan ¯Ux =eigaφx. Dengan cara ini, kita dapat menuliskan medan gauge pada
persamaan (3.43) dalam variabel link U¯x sebagai
FµνFµν =ǫiǫj
Aksi pada kisi pada persamaan (3.31) yang kecil dapat dituliskan [7]
S = 1
yang dapat ditulis dalam bentuk singkat
Gambar 3.5: Uµνx pada sebuah Plaquette
3.5
Observable
Suatu besaran yang terukur (observable) dalam mekanika kuantum adalah hasil operasi suatu operator terhadap state tertentu. Didefinisikan hf| O |ii sebagai nilai observable dengan operatorO yang muncul akibat transisi dari keadaan|ii
ke keadaan |fi.
Observable suatu sistem tidak selalu bergantung pada transisi keadaan sistem. Kita definisikan operator observable yang tidak bergantung transisi dan yang bergantung transisi masing-masing sebagai O′ dan O′. Dengan demikian dapat
dituliskan
hf| O |ii = hf| O′+O′|ii
= hf| O′|ii +hf| O′|ii
= hi| O′|ii+ hf| O′|ii (3.57)
Pada suku pertama r.h.s, keadaan akhir tetap |fi sebab interaksi tidak me-nyebabkan transisi, maka dari itu hanya suku kedua r.h.s yang diperhitungkan. Dalam kaitannya dengan path integral didapatkan
hi| O′|ii =
Z
D[medan]e−S0
(3.58)
hf| O′
|ii =
Z
D[medan]e−(S0+S′)
di mana pada persamaan tersebut, interaksi yang mengakibatkan munculnya ob-servable O′ dan O′ adalah aksi S0 dan S′, sementara D[medan] menandakan
integrasi terhadap seluruh medan yang terdapat dalam integran. Langkah selan-jutnya ialah normalisasi besaran hf| O |ii terhadap hi| O′|ii, dinotasikan sebagai
hingga orde pertama, didapatkan
Z =
R
D[medan](1−S′)e−S0
R
D[medan]e−S0
Pada persamaan (2.11) dan (2.12) tampak bahwa medan pada Lagrangian fluida terdiri atas φ dan Aµ. Dengan menyatakan bahwa S′ adalah aksi yang
mengan-dung Aµ saja danS0 sebagai aksi yang hanya mengandung φ, dapat dituliskan
Z =
DA pada r.h.s tidak diperhitungkan karena tidak bergantung transisi. Karena aksi merupakan integrasi Lagrangian terhadap ruang-waktu tak berhing-ga dan tidak dapat dipastikan memiliki suatu harberhing-ga tertentu, maka integrasi ini tidak dilakukan sehingga kita hanya dapat menghitung densitas Z yang dinota-sikan sebagai Z
Persamaan di atas masih dapat disederhanakan mengingat S0 hanya bergantung
pada φ dan L′ hanya bergantung pada A
µ sehingga didapatkan
3.6
Path Integral
dan Mekanika Statistik
fungsional memiliki bentuk serupa dengan fungsi partisi pada mekanika statis-tik. Berikut ini adalah beberapa analogi antara formulasi teori medan kuantum Euclidean dengan mekanika statistik [10].
Z
Dφe−SE → Σe−βH
SE → βH
Dengan dasar analogi formal tersebut dapat digunakan metode yang berlaku pada mekanika statistik dalam teori medan, dan sebaliknya. Bahkan terminologi yang digunakan pada keduanya seringkali identik. Dalam tugas akhir ini, fungsi partisi yang digunakan adalah densitas fungsi partisi yang telah dinormalisasi (3.66), sehingga besaran fisis yang didapat juga dalam bentuk densitas.
Dengan persamaan (3.63) dan (3.52) dapat dihitung Z sebagai berikut
Z = 1
Bab 4
Hasil dan Pembahasan
Fluida murni dapat dimodelkan dengan Lagrangian pada persamaan (2.11 - 2.12) untuk kasus non-Abelian. Dalam persamaan tersebut terdapat suku pure gauge yang merepresentasikan fluida murni, yaitu
LP G =−
1 4F
a
µνFaµν (4.1)
Dari persamaan tersebut dapat dilihat adanya interaksi antar fluida yang berbeda (ditunjukkan oleh indeks a), maka Lagrangian untuk kasus non-Abelian meng-gambarkan sistem multi fluida. Melalui definisi Fa
µν ≡∂µAaν−∂νAaµ−gfabcAbµAcν
kita dapat mengetahui bahwa Lagrangian tersebut hanya mengandung suku ki-netik (derivatif). Oleh karena itu, Lagrangian ini menggambarkan pergerakan (aliran) fluida saja, sehingga diinterpretasikan sebagai Lagrangian fluida murni. Besaran fisis dapat dihitung menggunakan fungsi partisi, sementara itu dari sub-bab (3.6) sudah diketahui bahwa terdapat hubungan antarapath integral dengan mekanika statistik. Dengan demikian dapat dicari besaran-besaran fisis sistem dengan menghitung path integral. Masalahnya adalah tidak diketahuinya besar konstanta kopling, g, untuk kasus fluida. Solusinya adalah perhitungan harus dilakukan secara nonperturbatif dengan metode Lattice Gauge Theory. Perhi-tungan path integral secara nonperturbatif dilakukan dengan menyusun aksi pa-da persamaan (3.56) pa-dalam kerangka ruang-waktu diskrit berpa-dasarkan teori papa-da bab 3, kemudian dilakukan perhitungan dengan metode Monte Carlo menggu-nakan algoritma Metropolis.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
0.79 0.8 0.81 0.82 0.83 0.84 0.85 0.86 0.87 0.88 0.89 0.9 0.91
Z density
v(c) simulasi 1
simulasi 2 simulasi 3
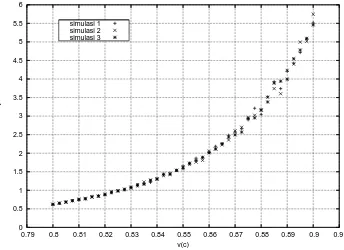
Gambar 4.1: NilaiZ pada kisi 104 site |v|= 0,8c hingga 0.9c
0,54f m4. Nilai konstanta kopling yang digunakan pada keduanya sama, yakni
g = 1. Alasan pemilihan volume kisi yang kecil tersebut adalah karena kita mengharapkan fungsi yang dintegrasi tidak banyak berfluktuasi, sementara itu perhitungan secara nonperturbatif diwakili dengan nilai g = 1.
Gambar 4.1 menunjukkan hasil perhitunganZ terhadapv pada kisi dengan jum-lah titik kisi 84. Pada gambar tersebut, diplot dua set data dengan parameter
yang sama. Tampak bahwa hasil ketiga perhitungan tidak berhimpit, terutama pada daerah kecepatan mendekati c. Hasil ini menunjukkan bahwa perhitung-an harus diulperhitung-ang dengperhitung-an jumlah titik kisi lebih bperhitung-anyak. Maka dari itu dilakukperhitung-an perhitungan pada kisi dengan jumlah titik 304titik dengan parameter yang sama,
hasilnya adalah gambar 4.2. Secara umum, fluktuasi nilai Z dapat terjadi karena metode Monte Carlo yang digunakan dalam perhitungan. Namun, fluktuasi ini dapat diperkecil dengan memperbanyak konfigurasi dalam perhitungan.
0 50 100 150 200 250 300 350 400 450 500 550 600 650
0.79 0.8 0.81 0.82 0.83 0.84 0.85 0.86 0.87 0.88 0.89 0.9 0.91
Z density
v(c) simulasi 1
simulasi 2
Gambar 4.2: NilaiZ pada kisi 304 site dengan |v|= 0.8 hingga 0.9c
-0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1
-0.05 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55
Z density
v(c)
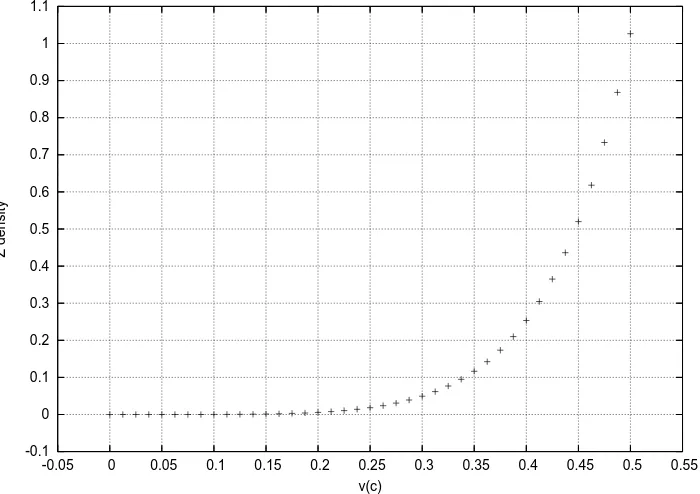
Gambar 4.3: NilaiZ pada kisi 304 site dengan |v|= 0 hingga 0.5c
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
F density
v(c)
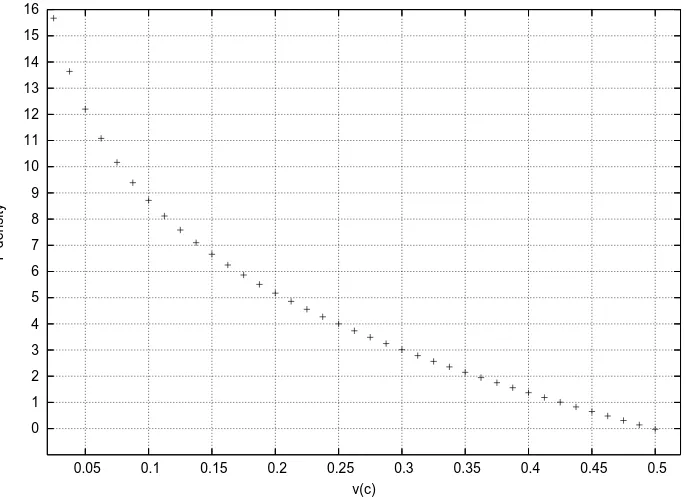
Gambar 4.4: NilaiF pada kisi 304 site dengan |v|= 0 hingga 0.5c
Pada gambar 4.4 diplot nilaiF terhadap |v|. Dalam konteks sistem multi fluida,
F adalah nilai densitas energi bebas yang dapat digunakan dalam interaksi antar fluida. Dengan demikian, nilaiF yang asimtotik pada|v|= 0 menandakan bahwa fluida berinteraksi sangat kuat dengan fluida lainnya. Namun kuat interaksi ini menurun bila fluida bergerak dan akhirnya interaksi tidak terjadi lagi bila energi kinetik sudah lebih besar daripada energi interaksi.
Sekilas bila kita perhatikan persamaan (3.63), tampak bahwa nilai konstanta lebar kisi aberada di luar tanda integral. Hal ini tentu menimbulkan pertanyaan mengenai pengaruh pemilihan a terhadap nilai Z. Untuk menjawabnya, perlu ditekankan bahwa nilaiZ yang dihitung adalah nilai densitas pada satu titik kisi, belum nilaiZ sebenarnya. Untuk menghitung nilaiZ perlu dilakukan integrasiZ terhadap ruang-waktu 4 dimensi, yang tentu saja akan menghilangkan pengaruh nilai a4 pada penyebut. Perhitungan tersebut melibatkan teori finite temperature
Bab 5
Kesimpulan
Dari perhitungan dan analisis yang dilakukan pada pemodelan fluida murni de-ngan dinamika fluida berbasis teori medan, dapat disimpulkan bahwa besarnya densitas fungsi partisi Z berubah secara asimtotik terhadap kecepatan |v| Perbe-daan nilai Z dengan jarak antar titik kisi yang berbeda bukanlah suatu masalah sebab nilai Z adalah nilai densitas, bukan nilai Z sebenarnya. Fisika seharusnya tidak berubah terhadap pemilihan jarak antar titik kisi. Fluktuasi memang dapat terjadi, tetapi hanya dapat disebabkan oleh kesalahan statistik pada perhitung-an dengperhitung-an menggunakperhitung-an simulasi Monte Carlo. Perhitungperhitung-an yperhitung-ang stabil pada jumlah titik kisi yang besar (jarak antar titik kisi yang kecil, bila volume kisi konstan) menunjukkan bahwa metode lattice memberi hasil yang baik pada dae-rah perhitungan sangat kecil. Nilai energi yang diskontinu pada kecepatan|v|= 0 menunjukkan bahwa interaksi antar fluida pada|v|= 0 sangatlah kuat. Kuat in-teraksi ini menurun secara asimtotik pula dengan bertambahnya kecepatan, hal ini disebabkan partikel yang bergerak, secara logis, akan berinteraksi sangat kecil satu sama lain hingga pada kecepatan tertentu di mana energi interaksi sudah sangat kecil akibat besarnya energi kinetik.
Lampiran A
Evaluasi
Path Integral
dengan
Metode Monte Carlo
Berikut ini akan dijelaskan metode yang digunakan untuk mengevaluasi path in-tegral secara numerik. Integrasi yang harus dilakukan untuk mengevaluasi path integral sangat banyak, sehingga metode Monte Carlo merupakan metode yang paling efisien. Sebagai ilustrasi, simulasi pada lattice dengan 40 titik kisi pada setiap arah, maka terdapat variabellink sebanyak 4·404. Bila simulasi dilakukan
untuk grup gauge SU(3) maka terdapat variabel real sebanyak 81.920.000.
Secara prinsip, rata-rata path integral hhΓ[x]ii dari sembarang fungsional Γ[x] dapat digunakan untuk menghitung berbagai sifat fisis di teori kuantum. Besaran
hhΓ[x]ii=
R
Dx(t)Γ[x]e−S[x]
R
Dx(t)e−S[x] (A.1)
merupakan rata-rata terhadap konfigurasi dengan bobote−S[x]. Konfigurasi acak
dibuat dalam jumlah yang banyak, Ncf,
xα ≡
xα0xα1 . . . xαN−1 , α= 1,2, . . . , Ncf (A.2)
sehingga probabilitas untuk memperoleh konfigurasi tertentu x(α) ialah
P[xα]∝e−S[x] (A.3)
Kemudian himpunan konfigurasi ini dirata-ratakan untuk mengaproksimasi nilai harapan hhΓ[x]ii
hhΓ[x]ii ≈Γ≡ 1
Ncf
Ncf
X
α=1
Γ merupakan ”Monte Carlo estimator” untuk hhΓ[x]ii dilattice. Namun, seperti statistik pada umumnya, akurasi dipengaruhi oleh banyaknya data yang diguna-kan, dalam hal ini : besar Ncf. KarenaNcf tidak mungkin dibuat tak berhingga,
ketidakpastian Monte CarloσΓ pada estimasi merupakan sumber kesalahan yang potensial. Kesalahan atau deviasi dihitung seperti pada umumnya,
σΓ2 ≈ 1 Ncf
(
1
Ncf
Ncf
X
α=1
Γ2[x(α)]−Γ2
)
(A.5)
Persamaan di atas menjadi
σ2Γ= hhΓ
2ii − hhΓii2
Ncf
(A.6)
untuk Ncf yang besar. Dari persamaan (A-6) tampak bahwa ketidakpastian
sta-tistik sebanding dengan 1/√Ncf.
Untuk mendapatkan konfigurasi acak dengan probabilitas (A.1), diperlukan al-goritma tertentu. Berikut adalah beberapa metode yang umum digunakan untuk membuat konfigurasi :
• Metode Metropolis
• Algoritma Langevin
• Algoritma Heatbath
• Algoritma Hybrid dan Hybrid Monte Carlo
• Metode Molecular Dynamics
Simulasi untuk tugas akhir ini dilakukan dengan algoritma Metropolis. Prose-dur adalah yang paling sederhana walaupun bukan yang terbaik. ProseProse-dur ini dimulai dengan konfigurasi sembarang x(0) (inisialisasi) dan memodifikasinya
de-ngan mengunjungi setiap titik kisi pada lattice, dan membangkitkan bilangan acak untuk xj pada titik kisi tersebut, dengan cara yang akan dijelaskan
beri-kutnya. Di sini dibuat konfigurasi acak yang baru dari konfigurasi sebelumnya:
x(0) →x(1). Cara ini disebut dengan update konfigurasi. Dengan menerapkan
Ncf konfigurasi. Himpunan konfigurasi ini akan terdistribusi secara tepat bila Ncf
cukup besar.
Algoritma untuk membangkitkan bilangan acak untuk xj pada titik kisi j ialah
sebagai berikut [13]:
• Bangkitkan bilangan acak ζ, dengan probabilitas terdistribusi seragam an-tara −ǫ dan ǫ dengan ǫ suatu konstanta.
• Ganti xj →xj +ζ dan hitung perubahan aksi ∆S.
• Bila aksi berkurang, ∆S < 0, ambil nilai baru untuk xj dan lanjutkan
proses ke titik kisi berikutnya.
• Bila ∆S >0, bangkitkan bilangan acakη yang terdistribusi secara uniform antara 0 dan 1; ambil nilai yang baru untuk xj bila exp(−∆S)> η,
selain-nya ambil nilai yang lama dan lanjutkan proses ke titik kisi berikutselain-nya.
Terdapat dua hal penting terkait dengan algoritma ini. Pertama, secara umum, akan terdapat beberapa bahkan banyak nilai xj yang sama pada dua konfigurasi.
Jumlah overlap ini ditentukan oleh parameter ǫ: bila ǫ sangat besar, perubahan pada xj biasanya besar dan sebagian besar akan ditolak; sementara bilaǫ sangat
kecil, perubahannya akan kecil dan kebanyakan akan diterima, tetapi nilai xj
yang baru akan mendekati atau sama dengan nilai yang lama. Parameter ǫharus disesuaikan sehingga 40%-60% xj akan berubah untuk tiap update pada titik
ki-si. Berapapun ǫ, konfigurasi yang berurutan akan mirip (berkorelasi tinggi) dan mengandung informasi yang mirip pula. Solusinya, konfigurasi x(α) diakumulasi
untuk estimasi Monte Carlo, kemudian hanya diambil tiap Ncor konfigurasi
se-hingga memberikan kita konfigurasi yang tidak bergantung secara statistik. Nilai optimal dari Ncor bergantung dari teori dan dapat diperoleh dengan mencoba.
Ncor juga bergantung pada jarak antar titik kisi a,
Ncor ∝
1
a2 (A.7)
sebelum memulai mengumpulkan nilaix(α). Pengabaian 5N
corhingga 10Ncor
kon-figurasi biasanya cukup. Proses ini disebut dengan ”termalisasi lattice”.
Sebagai ringkasan, langkah-langkah perhitunganhhΓ[x]iisecara Monte Carlo un-tuk suatu Γ[x] dengan konfigurasi x adalah
1. Inisialisasi konfigurasi, misalnya semua xdiset menjadi nol. 2. Update konfigurasi 5Ncor sampai 10Ncor kali untuk termalisasi.
3. Update konfigurasi Ncor kali, lalu hitung Γ[x] kemudian simpan dan ulangi
sebanyak Ncf kali.
4. Rata-ratakan Ncf nilai dari Γ[x] yang disimpan pada langkah sebelumnya
Lampiran B
Pemrograman
B.1
Perhitungan Matriks Kompleks
#include <iostream> #include <iomanip.h> #include <stdlib.h>
const int N = 2;
class Matriks {
public:
double re[N][N]; double im[N][N]; Matriks(); void identity(); void nol(); void printm(); void conjugate(); void dagger(); void kali(float a); float retrace();
Matriks operator + (Matriks m2); Matriks operator - (Matriks m2); Matriks operator * (Matriks m2); //Matriks Matriks::dagr(Matriks m2); };
class Kompleks {
public:
double re; double im; Kompleks();
void isi(float a, float b); void print();
Kompleks operator * (Kompleks k2);
void Kompleks::isi(float a, float b) {
cout << re << " " << im << "i" << endl; }
else{
cout << re << " + " << im << "i" << endl; }
}
Kompleks Kompleks::operator + (Kompleks k2) {
Kompleks Kompleks::operator * (Kompleks k2) {
Kompleks tmp;
}
cout << setw(8) << re[i][j] << im[i][j] << "i"; }
else {
cout << setw(8) << re[i][j] << "+" << im[i][j] << "i"; }
}
}
}
Matriks Matriks::operator + (Matriks m2) {
tmp.re[i][j] = re[i][j] + m2.re[i][j]; tmp.im[i][j] = im[i][j] + m2.im[i][j]; }
}
return(tmp); }
Matriks Matriks::operator - (Matriks m2) {
tmp.re[i][j] = re[i][j] - m2.re[i][j]; tmp.im[i][j] = im[i][j] - m2.im[i][j]; }
}
return(tmp); }
Matriks tmp2; for (i=0;i<N;i++){
for (j=0;j<N;j++){ for (k=0;k<N;k++){
tmp1.re[i][j]+=re[i][k]*m2.re[k][j]; tmp2.re[i][j]+=im[i][k]*m2.im[k][j]; tmp1.im[i][j]+=re[i][k]*m2.im[k][j];
tmp2.im[i][j]+=im[i][k]*m2.re[k][j]; }
tmp.re[i][j]=tmp1.re[i][j] - tmp2.re[i][j]; tmp.im[i][j]=tmp1.im[i][j] + tmp2.im[i][j]; }
}
return(tmp); }
B.2
Generator Matriks SU(2)
#include <iostream.h> #include <iomanip.h> #include <stdlib.h>
double a[4], phi, sin_alpha, sin_theta, cos_theta;
using namespace std;
void GenSU2() {
M_SU2.nol();
a[0]=2.0*(rand()/(RAND_MAX+1.0))-1.0; cos_theta=2.0*(rand()/(RAND_MAX+1.0))-1.0; sin_theta=sqrt(1.0-cos_theta*cos_theta); sin_alpha=sqrt(1-a[0]*a[0]);
phi=2.0*Pi*(rand()/(RAND_MAX+1.0)); a[1]=sin_alpha*sin_theta*cos(phi); a[2]=sin_alpha*sin_theta*sin(phi); a[3]=sin_alpha*cos_theta;
B.3
Program Simulasi pada Lattice
#include <iostream.h> #include <iomanip.h> #include <stdlib.h>
Matriks plaqsum, plaq, U0, U1, U2, U3, Uprod; Matriks staplesum, staple, dS;
int getsite(int x[]){
int s = x[0]+nsite*(x[1]+nsite*(x[2]+nsite*x[3])); return s;
float KONST(int i, int j){ float result2 = 0; if (i==0)
x[d]+=1;
if (x[d]>=nsite) x[d]-=nsite; }
void movedown(int x[],int d){ x[d]-=1;
if (x[d]<0) x[d]+=nsite; }
movedown(x,nu);
plaqsum = plaqsum + plaq; }}} staplesum = staplesum + staple;
old_U = U[s][mu];
float dS_tr = dS.retrace(); float u = rand()/(RAND_MAX+1.0); if (dS_tr >0 && exp(-dS_tr)< u){
U[s][mu]=old_U;
//cout << "terima" << endl; }
//cout << "tolak" << endl; }}}}
} }
B.4
Program Iterasi
Z
terhadap
|
v
|
#include <iostream.h>
float v, beta, dS_tr, lorentz, jac, spc;
#include "matriks_kompleks.h"
Matriks U[nsite*nsite*nsite*nsite][ndim], M_SU2, old_U;
#include "matriks_su2.h" //cout << "GOOOO" << endl;
srand(time(0)); v = 0.025*vi;
lorentz = eps(0)*eps(1)*eps(2)*eps(3); //cout << "Inisialisasi link" << endl; inisialisasi();
//cout << "Metropolis Update" << endl; for(iter=0; iter<n_iter; iter++){
Metropolis_Update();
//cout << iter << " " << plaquette(1,1) << endl; }
cout << v << " " << jac*lorentz*plaquette(1,1) << endl; }
//cout << "done" << endl; return 0;
Daftar Acuan
[1] Sulaiman, A. Constructing Navier Stokes Equation using Gauge
Fi-eld Theory Approach. Tesis S2. (2005).
[2] Sulaiman, A. Large Amplitude of The Internal Motion of DNA
Im-mersed in Bio-fluid. arXiv:physics/0512206.
[3] Handoko, L.T. dan Sulaiman, A. Relativistic Navier Stokes Equation
from a Gauge-invariant Lagrangian. arXiv:physics/0508219.
[4] http://scienceworld.wolfram.com/physics/Navier-StokesEquation.html
[5] Handoko, L.T. dan Sulaiman, A. Gauge Field Theory Approach to
Construct The Navier Stokes Equation. arXiv:physics/0508086.
[6] Gross, Franz. Relativistic Quantum Mechanics and Field Theory. Wiley-Interscience. (1993).
[7] Rothe, H.J. Lattice Gauge Theories: An Introduction. World Scienti-fic. (1997).
[8] Aitchison, I.J.R. and Hey, A.J.G. Gauge Theories in Particle Physics. Institute of Physics Publishing. (2001).
[9] Smit, J. Introduction to Quantum Fields on A Lattice. Cambridge University Press. (2002).
[10] Munster, G. dan Walzl, M. Lattice Gauge Theory A Short Primer. arXiv:hep-lat/0012005.
[12] Laine, M. Finite Temperature Field Theory : with Applications to
Cosmology. Lectures given at the Summer School on Astroparticle Physics
and Cosmology. Trieste. (2002).