Matematika SMK/MAK Kelas X Semester 1

(1)

SMK/MAK Kelas X Semester 1

Matematika

Disusun oleh:

Anna Yuni Astuti

Disklaimer

Disklaimer Daftar isiDaftar isi

(2)

• Powerpoint pembelajaran ini dibuat sebagai Powerpoint pembelajaran ini dibuat sebagai alternatif guna membantu Bapak/Ibu Guru alternatif guna membantu Bapak/Ibu Guru melaksanakan pembelajaran.

melaksanakan pembelajaran.

• Materi Materi powerpoint powerpoint ini mengacu pada Kompetensi ini mengacu pada Kompetensi Inti (KI) dan Kompetensi Dasar (KD) Kurikulum 2013.

Inti (KI) dan Kompetensi Dasar (KD) Kurikulum 2013.

• Dengan berbagai alasan, materi dalam Dengan berbagai alasan, materi dalam powerpoint powerpoint ini disajikan secara ringkas, hanya memuat poin- ini disajikan secara ringkas, hanya memuat poin- poin besar saja.

poin besar saja.

• Dalam penggunaannya nanti, Bapak/Ibu Guru dapat Dalam penggunaannya nanti, Bapak/Ibu Guru dapat mengembangkannya sesuai kebutuhan.

mengembangkannya sesuai kebutuhan.

• Harapan kami, dengan Harapan kami, dengan powerpoint powerpoint ini Bapak/Ibu ini Bapak/Ibu Guru dapat mengembangkan pembelajaran secara Guru dapat mengembangkan pembelajaran secara kreatif dan interaktif.

kreatif dan interaktif.

Disklaimer

(3)

DAFTAR ISI

Bab 1. Pangkat, Akar, dan Logaritma

Bab 2. Persamaan dan Pertidaksamaan Nilai Mutlak Bab 3. Sistem Persamaan Linear Dua Variabel

Bab 4. Program Linear Bab 5. Barisan dan Deret

(4)

BAB

Pangkat Akar dan Logaritma

I

A. Pangkat Bulat

B. Bentuk Akar

C. Merasionalkan Penyebut

D. Pangkat Pecahan

E. Logaritma

Kembali ke daftar isi

(5)

A. Pangkat Bulat

1. Pangkat Bulat Positif

2. Pangkat Nol

3. Pangkat Bulat Negatif

4. Sifat-Sifat pada Pangkat Bulat

Kembali ke daftar isi Kembali ke awal bab

(6)

1. Pangkat Bulat Positif

Jika a bilangan real dan n bulat positif maka ∈ ∈ aⁿ (dibaca a pangkat n) didefinisikan sebagai perkalian berulang a sebanyak n kali (n faktor).

(7)

2. Pangkat Nol

(8)

3. Pangkat Bulat Negatif

Jika a bilangan real, a ≠ 0 dan n bilangan bulat ∈ ∈ positif, berlaku:

(9)

4. Sifat-Sifat pada Pangkat Bulat

Jika a, b bilangan real dan p, q bilangan bulat, ∈ ∈ berlaku sifat-sifat berikut.

(10)

Contoh soal

(11)

B. Bentuk Akar

1. Akar Pangkat n suatu Bilangan

2. Bentuk Akar

3. Sifat-Sifat Bentuk Akar

4. Operasi Hitung pada Bentuk Akar

(12)

1. Akar Pangkat n Suatu Bilangan

Misalkan n bilangan bulat positif, a dan b bilangan real.

Jika berlaku bⁿ = a maka b disebut sebagai akar pangkat n dari a.

Contoh:

4 4 4

3 3 3

16 2 2

8 ( 2) 2

 

    

(13)

2. Bentuk Akar

Bentuk akar adalah akar-akar bilangan rasional yang hasilnya bukan bilangan rasional (irasional).

Contoh:

merupakan bilangan bentuk akar bukan bilangan bentuk akar

3, 5, 6

4, 9, 16

(14)

3. Sifat-Sifat Bentuk Akar

(15)

4. Operasi Hitung pada Bentuk Akar

a. Penjumlahan dan Pengurangan Bentuk Akar Bentuk-bentuk akar yang dapat dijumlahkan atau

dikurangkan yaitu bentuk akar yang sejenis.

(16)

b. Perkalian Bentuk Akar

1). Bentuk-bentuk akar yang langsung dapat dikalikan

adalah bentuk akar yang senama (akar pangkat sama).

(17)

2) Jika bentuk-bentuk akar belum senama, pangkat akar disamakan terlebih dahulu, lalu dikalikan.

(18)

Contoh soal

(19)

C. Merasionalkan Penyebut

1. Merasionalkan Penyebut

2. Menyederhanakan Bentuk

(20)

1. Merasionalkan Penyebut

Pecahan dengan penyebut irasional dapat diubah menjadi pecahan dengan penyebut rasional. Caranya dengan

mengalikan pecahan dengan bentuk sekawan dari penyebut.

Contoh:

(21)

2. Menyederhanakan Bentuk .

Bentuk dapat disederhanakan menjadi bentuk berikut.

Contoh:

(a b) 2 ab  

(a b) 2 ab 

7 2 10 (5 2) 2 5 2 5 2 3 2 10 (5 2) 2 5 2 5 2

      

      

(a b) 2 ab a b (a b) 2 ab a b

   

   

(22)

Contoh soal

1. Rasionalkan penyebut pecahan-pecahan berikut.

a. 36

11 5 10 3 13 b. 2 13 7





2. Nyatakan bentuk berikut ke dalam bentuk p  q

a. 7 2 12 b. 9 4 5





(23)

D. Pangkat Pecahan

1. Pangkat Pecahan

2. Sifat-Sifat Operasi Bilangan Pangkat Pecahan

(24)

1. Pangkat Pecahan

Untuk a bilangan real dan n bilangan bulat positif ∈ ∈ berlaku :

(25)

2. Sifat-Sifat Operasi Bilangan Pangkat Pecahan

(26)

Contoh soal

(27)

E. Logaritma

1. Pengertian Logaritma

2. Nilai Logaritma

3. Sifat-Sifat Logaritma

(28)

1. Pengertian Logaritma

Logaritma merupakan kebalikan (invers) dari pemangkatan.

(29)

2. Nilai Logaritma

(30)

3. Sifat-Sifat Logaritma

(31)

Contoh soal

(32)

BAB

Persamaan dan

Pertidaksamaan Nilai Mutlak

II

A. Konsep Nilai Mutlak

C. Pertidaksamaan Nilai Mutlak B. Persamaan Nilai Mutlak

(33)

A. Konsep Nilai Mutlak

1. Konsep Nilai Mutlak Suatu Bilangan 2. Sifat-Sifat Nilai Mutlak

3. Fungsi Nilai Mutlak

4. Menggambar Grafik Fungsi Mutlak dari Fungsi Linearnya

(34)

1. Konsep Nilai Mutlak Suatu Bilangan

Nilai mutlak bilangan x, dinotasikan dengan |x|, didefinisikan sebagai berikut.

|x| = jarak x dari titik nol pada garis bilangan

Contoh:

|5| = 5

|–9| = 9

(35)

2. Sifat-Sifat Nilai Mutlak

(36)

3. Fungsi Nilai Mutlak

Fungsi nilai mutlak adalah fungsi yang variabelnya di dalam tanda mutlak^.

(37)

4. Menggambar Grafik Fungsi Nilai Mutlak dari Fungsi Linearnya

Grafik fungsi mutlak linear y = |f(x)| dapat digambar dengan cara menggambar grafik fungsi linear f(x), lalu mencerminkan terhadap sumbu X grafik fungsi f(x) yang berada di bawah sumbu X.

(38)

Contoh soal

(39)

B. Persamaan Nilai Mutlak

1. Persamaan Nilai Mutlak

2. Cara Menyelesaikan Persamaan Nilai Mutlak a. Menggunakan Definisi Nilai Mutlak

b. Menggunakan Grafik

c. Menggunakan Definisi Nilai Mutlak

d. Menggunakan Cara Menguadratkan Kedua Ruas

(40)

1. Persamaan Nilai Mutlak

Bentuk umum persamaan nilai mutlak sebagai berikut.

|f(x)| = c dengan syarat c ≥ 0

|f(x)| = |g(x)|

|f(x)| = g(x) dengan syarat g(x) ≥ 0

Penyelesaian persamaan yang memuat nilai mutlak adalah bilangan-bilangan pengganti dari variabel yang membuat persamaan menjadi pernyataan bernilai benar.

Contoh:

Untuk x = 5 maka |x – 2| = |5 – 2| = 3

Untuk x = –1 maka |x – 2| = |(–1) – 2| = 3

Penyelesaian persamaan |x – 2| = 3 adalah 5 atau –1.

(41)

2. Cara Menyelesaikan Persamaan Nilai Mutlak

a. Menggunakan Definisi Nilai Mutlak Sebagai Jarak b. Menggunakan Grafik

(42)

a. Menggunakan Definisi Nilai Mutlak sebagai Jarak

Menurut definisi, nilai mutlak suatu bilangan dapat diartikan sebagai jarak bilangan dari nol.

Sebagai contoh |3| = jarak 3 dari 0 dan |–3| = jarak –3 dari 0.

Bentuk |x – 2| = 3 dapat dibaca jarak x dari 2 sama dengan 3.

Penyelesaian |x – 2| = 3 adalah x = –1 atau x = 5.

(43)

b. Menggunakan Grafik

Kedua ruas persamaan dimisalkan sebagai fungsi dan digambar grafiknya dan ditentukan titik potong kedua grafik tersebut.

Persamaan |x – 2| = 3.

Misalkan y₁ = |x – 2| dan y₂

= 3.

Kedua grafik berpotongan di x = 5 atau x = –1.

Penyelesaian |x – 2| = 3 adalah x = 5 atau x = –1.

(44)

c. Menggunakan Definisi Nilai Mutlak

Dari definisi nilai mutlak dapat diperoleh hubungan sebagai berikut.

|ax + b| = c ax + b = c atau –(ax + b) = c⇔ ax + b = c atau ax + b = –c ⇔

Persamaan|ax + b| = c dapat diselesaikan dengan menyelesaikan ax + b = c atau ax + b = –c.

Contoh:

|x – 2| = 3

⇔ x – 2 = 3 atau x – 2 = –3

⇔ x = 5 atau x = –1

(45)

d. Menggunakan Cara Menguadratkan Kedua Ruas

Menyelesaikan persamaan nilai mutlak dengan cara menguadratkan kedua ruas hanya boleh dilakukan jika kedua ruas bernilai positif

|x – 2| = 3

Oleh karena kedua ruas bernilai positif, kedua ruas boleh dikuadratkan.

|x – 2|

⇔ ² = 3² (x – 2)

⇔ ² – 3² = 0

(x – 2 + 3)(x – 2 – 3) = 0

⇔

(x + 1)(x – 5) = 0

⇔

x = –1 atau x = 5

⇔

(46)

Contoh soal

Tentukan penyelesaian persamaan berikut menggunakan cara grafik, cara analisis nilai x, dan cara menguadratkan kedua ruas.

1. |2x – 6| = |x|

2. |x + 3| – |x – 2| = 4

(47)

C. Pertidaksamaan Nilai Mutlak

1. Pertidaksamaan Nilai Mutlak

2. Cara Menyelesaikan Pertidaksamaan Nilai Mutlak a. Menggunakan Definisi Nilai Mutlak

b. Menggunakan Grafik

(48)

1. Pertidaksamaan Nilai Mutlak

Misalkan f(x) suatu fungsi dalam variabel x maka berlaku fungsi nilai mutlak |f(x)| sebagai berikut.

a. Jika |f(x)| ≤ a maka –a ≤ f(x) ≤ a.

b. Jika |f(x)| ≥ a maka f(x) ≤ –a atau f(x) ≥ a.

Contoh:

| x 2 | 3

3 x 2 3

3 2 x 2 2 3 2 1 x 5

 

    

       

   

(49)

2. Cara Menyelesaikan Pertidaksamaan Nilai Mutlak

a. Menggunakan Definisi Nilai Mutlak Sebagai Jarak b. Menggunakan Grafik

(50)

a. Menggunakan Definisi Nilai Mutlak sebagai Jarak

Pertidaksamaan |x – 2| ≤ 3 dapat diterjemahkan menjadi jarak bilangan x dari 2 kurang dari atau sama dengan3.

Penyelesaian |x – 2| ≤ 3 adalah –1 ≤ x ≤ 5.

Menggunakan cara yang sama, coba tentukan penyelesaian

|x – 2| ≥ 3.

(51)

b. Menggunakan Grafik

Persamaan |x – 2|  3.

Misalkan y₁ = |x – 2| dan y₂ = 3.

Penyelesaian y₁  y₂ adalah nilai-nilai x yang membuat grafik fungsi y₁ berada di bawah grafik y₂.

Grafik fungsi y₁ berada di bawah grafik y₂ untuk

–1  x  5.

Penyelesaian |x – 2|  3 adalah –1  x  5.

(52)

c. Menggunakan Definisi Nilai Mutlak

Ingat definisi nilai mutlak.

Jika |f(x)| < a maka –a < f(x) < a.

Jika |f(x)| ≥ a maka f(x) ≤ –a atau f(x) ≥ a.

Pertidaksamaan nilai mutlak:

|ax + b| < c –c < ax + b < c ⇔

|ax + b| ≥ c ax + b ≥ –c atau ax + b ≥ c⇔ Pertidaksamaan |x – 2| ≤ 3.

–3 ≤ x – 2 ≤ 3

⇔

–3 + 2 ≤ x – 2 + 2 ≤ 3 + 2

⇔

–1 ≤ x ≤ 5

⇔

Penyelesaian |x – 2| ≤ 3 adalah –1 ≤ x ≤ 5

(53)

d. Menggunakan Cara Menguadratkan Kedua Ruas

Menyelesaikan pertidaksamaan nilai mutlak dengan cara menguadratkan kedua ruas hanya boleh dilakukan jika

kedua ruas bernilai positif.

Pertidaksamaan|x – 2|  3

Oleh karena kedua ruas pertidaksamaan bernilai positif, kedua ruas boleh dikuadratkan.

|x – 2|

⇔ ²  3² (x – 2)

⇔ ² – 3²  0

(x – 2 + 3)(x – 2 – 3)

⇔  0

(x + 1)(x – 5)

⇔  0

⇔ –1  x  5

Penyelesaian |x – 2|  3 adalah –1  x  5.

(54)

Contoh soal

Tentukan penyelesaian pertidaksamaan berikut.

a. |3x – 1| < 8 b. |9 – 2x| > 11

c. |2x – 1| < |x + 2|

d. |2 – x²| ≥ 3

(55)

BAB

Sistem Persamaan Linear Dua Variabel

III

A. Sistem Persamaan Linear Dua Variabel

B. Menyelesaikan Sistem Persamaan Linear Dua Variabel C.

Menyelesaikan Masalah Sistem Persamaan Linear Dua V ariabel

(56)

A. Sistem Persamaan Linear Dua Variabel

1. Persamaan Linear Dua Variabel

2. Sistem Persamaan Linear Dua Variabel

(57)

1. Persamaan Linear Dua Variabel

Persamaan linear dua variabel merupakan persamaan linear yang hanya memiliki dua variabel.

Bentuk umum persamaan linear dua variabel dalam x dan y:

ax + by = c Contoh:

1) 2x – y = 4

2) 4x – 5y = 1 + 3y

Penyelesaian persamaan linear dua variabel adalah pasangan-pasangan nilai (x, y) yang menyebabkan

persamaan ax + by = c bernilai benar. Penyelesaian

persamaan ax + by = c jika digambarkan berupa garis lurus ax + by = c.

(58)

2. Sistem Persamaan Linear Dua Variabel

Sistem persamaan linear dua variabel (SPLDV)

merupakan kumpulan beberapa persamaan linear dua variabel yang saling terkait.

Bentuk umum sistem persamaan linear dua variabel dalam x dan y:

ax + by = c dx + ey = f

Penyelesaian sistem persamaan linear dua variabel adalah pasangan-pasangan nilai (x, y) yang menyebabkan semua persamaan dalam sistem bernilai benar.

(59)

Kemungkinan penyelesaian sistem persamaan linear dua variabel (SPLDV):

1.mempunyai 1 penyelesaian,

2.tidak mempunyai penyelesaian, atau 3.mempunyai banyak penyelesaian Contoh:

•SPLDV x + 2y = 5 dan 3x – y = 1 mempunyai penyelesaian (1, 2) saja.

•SPLDV x + 2y = 5 dan x + 2y = 1 tidak mempunyai penyelesaian.

•SPLDV x + 2y = 5 dan 2x + 4y = 10 mempunyai banyak penyelesaian.

(60)

Contoh soal

(61)

B. Menyelesaikan Sistem Persamaan Linear Dua Variabel

1. Metode Grafik 2. Metode Eliminasi

3. Metode Substitusi

4. Metode Eliminasi-Substitusi

(62)

1. Metode Grafik

Menyelesaikan SPLDV menggunakan metode grafik

dilakukan dengan menggambar grafik dari kedua persamaan pada satu bidang kartesius. Koordinat titik potong kedua

grafik merupakan penyelesaian dari sistem persamaan tersebut.

Tentukan penyelesaian SPLDV berikut menggunakan metode grafik.

2x – 3y = –10 . . . (1) x + 2y = 2 . . . (2)

(63)

Contoh soal

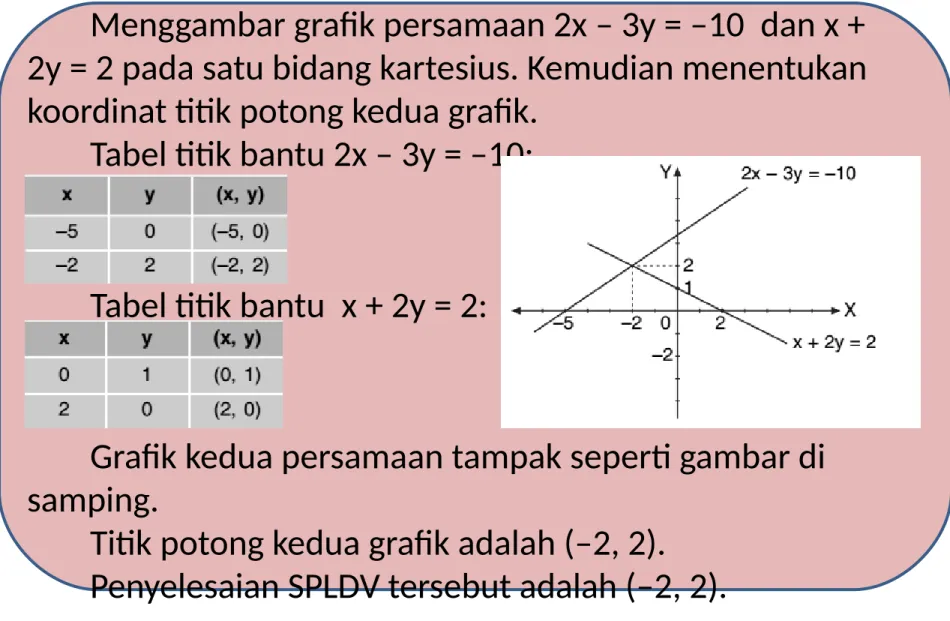
Menggambar grafik persamaan 2x – 3y = –10 dan x + 2y = 2 pada satu bidang kartesius. Kemudian menentukan koordinat titik potong kedua grafik.

Tabel titik bantu 2x – 3y = –10:

Tabel titik bantu x + 2y = 2:

Grafik kedua persamaan tampak seperti gambar di samping.

Titik potong kedua grafik adalah (–2, 2).

Penyelesaian SPLDV tersebut adalah (–2, 2).

(64)

2. Metode Eliminasi

Menyelesaikan SPLDV dengan metode eliminasi dilakukan dengan cara menghilangkan salah satu variabelnya.

Contoh:

Tentukan penyelesaian SPLDV berikut menggunakan metode eliminasi.

2x – 3y = –10 . . . (1) x + 2y = 2 . . . (2)

(65)

(66)

3. Metode Substitusi

Menyelesaikan SPLDV menggunakan metode substitusi dilakukan dengan cara berikut.

a. Ambil satu variabel pada salah satu persamaan.

Selanjutnya, nyatakan variabel tersebut dalam variabel lain.

Dengan begitu akan diperoleh persamaan dalam bentuk baru.

b.Substitusikan persamaan baru tersebut ke persamaan yang lain. Kemudian, selesaikan persamaan tersebut.

Contoh:

Tentukan penyelesaian SPLDV berikut menggunakan metode substitusi.

2x – 3y = –10 . . . (1) x + 2y = 2 . . . (2)

(67)

(68)

(69)

Contoh soal

(70)

4. Metode Eliminasi Substitusi

Untuk menentukan penyelesaian suatu SPLDV dapat pula menggunakan kombinasi atau campuran antara metode

substitusi dan eliminasi. Penggunaan metode ini dapat mempermudah/mempercepat pengerjaan penyelesaian SPLDV.

(71)

(72)

(73)

Contoh soal

(74)

C. Menyelesaikan Masalah Sistem Persamaan Linear Dua Variabel

Langkah-langkah mengubah permasalahan sehari-hari menjadi SPLDV dilakukan sebagai berikut.

1.Tentukan variabel-variabelnya, lalu lakukan pemisalan.

2.Terjemahkan permasalahan tersebut menjadi model matematika berbentuk SPLDV.

3.Selesaikan model matematika yang diperoleh pada langkah 2.

4.Selanjutnya, nilai-nilai variabel yang telah diperoleh dicocokkan dengan pemisalan awal sehingga

permasalahan dapat diselesaikan.

(75)

Contoh soal

Tiket masuk sebuah tempat wisata terdiri atas tiket dewasa dan tiket anak-anak. Pada hari Minggu terjual 100 tiket

dewasa dan 250 tiket anak-anak. Hasil penjualan tiket

tersebut sebesar Rp4.500.000,00. Pada hari Senin terjual 60 tiket dewasa dan 180 tiket anak. Hasil penjualan tiket

pada hari Senin sebesar Rp3.000.000,00.

Tentukan:

a. harga 1 tiket anak-anak;

b. hasil penjualan tiket pada hari Selasa jika terjual 50 tiket dewasa dan 100 tiket anak

(76)

BAB

Program Linear

IV

A. Sistem Pertidaksamaan Linear Dua Variabel B. Program Linear

(77)

A. Sistem Pertidaksamaan Linear Dua Variabel

1. Pertidaksamaan Linear Dua Variabel 2.

Penyelesaian Pertidaksamaan Linear Dua Variabel

3. Sistem Pertidaksamaan Linear Dua Variabel

(78)

1. Pertidaksamaan Linear Dua Variabel

Pertidaksamaan linear dua variabel merupakan pertidaksamaan yangmemiliki dua variabel dan setiap variabel memiliki pangkat satu.

Bentuk umum pertidaksamaan linear dua variabel dalam variabel x dan y:

ax + by ≤ c ax + by ≥ c

ax + by < c ax + by > c

(79)

2. Penyelesaian Pertidaksamaan Linear Dua Variabel

Penyelesaian pertidaksamaan dua variabel merupakan himpunan pasangan bilangan (x, y) yang memenuhi

pertidaksamaan linear tersebut.

Jika digambarkan pada bidang koordinat kartesius, himpunan pasangan bilangan (x, y) tersebut berada dalam suatu daerah yang disebut daerah penyelesaian (DP).

(80)

Langkah-langkah menentukan daerah penyelesaian (DP) pertidaksamaan linear dua variabel.

Langkah 1: Menggambar garis pembatas

a.Jika PtLDV memiliki tanda ketidaksamaan ≤ atau ≥, garis pembatas digambarkan utuh.

b.Jika PtLDV memiliki tanda ketidaksamaan < atau >, garis pembatas digambarkan putus-putus.

Langkah 2: Melakukan uji titik untuk menentukan DP

(81)

Menentukan daerah penyelesaian (DP) pertidaksamaan x + 3y > 6.

Langkah 1: Menggambar garis pembatas

PtLDV x + 3y > 6 memiliki tanda ketidaksamaan >, garis pembatas digambarkan putus-putus.

Langkah 2: Melakukan uji titik untuk menentukan DP Mensubstitusikan titik (0, 0) ke dalam pertidaksamaan x + 3y > 6.

x + 3y > 6 0 – 3 ⇔  0 > 6 0 > 6 (salah)⇔

Oleh karena pernyataan 0 > 6 bernilai salah maka DP dibatasi garis x + 3y = 6 dan tidak memuat

titik (0, 0).

(82)

Daerah penyelesaian x + 3y > 6 (DP) dibatasi garis x + 3y = 6 dan tidak memuat titik (0, 0).

(83)

3. Sistem Pertidaksamaan Linear Dua Variabel

Sistem pertidaksamaan linear dua variabel (SPLDV)

merupakan kumpulan beberapa pertidaksamaan linear dua variabel yang saling terkait.

Salah satu bentuk umum sistem pertidaksamaan linear dua variabel dalam x dan y:

ax + by > c dx + ey  f

Penyelesaian sistem pertidaksamaan linear dua variabel adalah himpunan nilai (x, y) yang menyebabkan semua

pertidaksamaan dalam sistem bernilai benar. Daerah

penyelesaian SPtLDV berupa daerah irisan dari penyelesaian setiap pertidaksamaan di dalam sistem.

(84)

Contoh Soal

Tentukan daerah penyelesaian SPtLDV:

Daerah penyelesaian SPtLDV ditentukan dengan

menentukan penyelesaian setiap pertidaksamaan dalam sistem lalu menentukan daerah irisannya.

(85)

Daerah irisannya:

Daerah penyelesaian sistem x + y < 2 dan x – 2y  4 ditunjukkan oleh daerah yang diarsir.

(86)

Contoh Soal

(87)

B. Program Linear

1. Model Matematika

2. Nilai Optimum Fungsi Tujuan

(88)

1. Model Matematika

Model matematika pada permasalahan program linear berupa SPtdLDV. SPtdLDV tersebut dinamakan pembatas atau kendala.

Contoh:

Seorang pengusaha mebel akan memproduksi meja dan kursi menggunakan bahan dari kayu dengan ukuran tertentu.

Satu meja memerlukan bahan 10 potong kayu dan satu kursi memerlukan bahan 5 potong kayu. Pengusaha memiliki

persediaan kayu 500 potong. Banyak meja yang akan

diproduksi paling sedikit 10 unit dan banyak kursi yang akan diproduksi paling sedikit 20 unit. Biaya produksi meja 210.000 rupiah per unit dan biaya produksi kursi 100.000 rupiah per unit. Berapa biaya produksi minimum meja dan kursi tersebut?

(89)

Jawaban:

Langkah 1: Membuat model matematika permasalahan Misalkan:

x adalah banyak meja yang akan diproduksi.

y adalah banyak kursi yang akan diproduksi.

Banyak meja yang akan diproduksi paling sedikit 10 unit sehingga diperoleh pertidaksamaa:

x ≥ 10 . . . (1)

Banyak kursi yang akan diproduksi paling sedikit 20 unit sehingga diperoleh pertidaksamaan

y ≥ 20 . . . (2)

(90)

1 unit meja memerlukan kayu10 potong.

x unit meja memerlukan kayu 10x potong.

1 unit kursi memerlukan kayu 5 potong.

y unit kursi memerlukan kayu 5y potong.

x unit meja dan y unit kursi memerlukan kayu (10 x + 5y) potong.

Persediaan kayu 500 potong berarti (10 x + 5y) kurang dari atau sama dengan 500 sehingga diperoleh pertidaksamaan 10x + 5y

≤ 500 . . . (3)

Biaya produksi meja 210.000 rupiah per unit dan biaya produksi kursi 100.000 rupiah per unit

sehingga diperoleh fungsi tujuan:

f(x, y) = 210.000x + 100.000y . . . (4)

(91)

Dari pertidaksamaan (1) sampai dengan (3) dan persamaan (4) diperoleh model matematika sebagai berikut.

Meminimumkan fungsi tujuan

f(x, y) = (210x + 100y) ribu dengan kendala:

x ≥ 10 y ≥ 20

10x + 5y ≤ 500

(92)

Contoh Soal

(93)

2. Nilai Optimum Fungsi Tujuan

Fungsi tujuan disebut juga fungsi sasaran atau fungsi objektif.

Nilai fungsi tujuan f(x, y) = ax + by tergantung dari nilai- nilai x dan y yang memenuhi kendala. Nilai fungsi tujuan bisa minimum atau maksimum. Nilai minimum atau nilai

maksimum disebut juga nilai optimum atau nilai ekstrim.

Nilai optimum fungsi tujuan dapat ditentukan

menggunakan metode uji titik pojok dan metode garis selidik.

a. Menggunakan Metode Garis Selidik b. Menggunakan Metode Uji Titik Pojok

(94)

Tentukan penyelesaian memaksimumkan fungsi tujuan f(x, y) = 17.000x + 20.000y dengan kendala:

Persamaan fungsi tujuan:

f(x, y) = 17.000x + 20.000y = (17x + 20y) ribu sehingga persamaan garis selidik adalah 17x + 20y = k dengan

k bilangan real. ∈

Misalkan dipilih k = 17 × 20 maka diperoleh persamaan garis selidik awal f₀: 17x + 20y = 340.

a. Menggunakan Metode Garis Selidik

(95)

Menggambar daerah penyelesaian sistem pertidaksamaan dan garis-garis yang sejajar dengan f₀: 17x + 20y = 340 dan

melalui setiap titik pojok daerah penyelesaian.

(96)

Menentukan persamaan garis selidik yang sejajar dengan f₀ yaitu f(x, y) = ax + by.

Jika memaksimumkan fungsi tujuan, dipilih nilai k terbesar.

Jika meminimumkan fungsi tujuan, dipilih nilai k terkecil.

Dengan mensubstitusikan titik A(25, 30), B(115,30), dan

C(25, 120) ke dalam persamaan fungsi tujuan f(x, y) = 17x + 20y diperoleh persamaan

f1: 17x + 20y = 1.025,

f2: 17x + 20y = 2.555, dan f3: 17x + 20y = 2.825

Nilai k terbesar adalah k₃ = 2.825 sehingga nilai maksimum fungsi tujuan f(x, y) = (17x + 20y) ribu adalah 2.825 ribu atau 2.825.000.

(97)

b. Menggunakan Metode Uji Titik Pojok

Nilai optimum fungsi tujuan dapat ditentukan menggunakan metode uji titik pojok yaitu dengan menguji titik pojok daerah penyelesaian.

Perhatikan kembali titik pojok daerah penyelesaian pada pembahasan metode garis selidik di muka.

(98)

Dari Gambar 4.9 diperoleh titik pojok daerah penyelesaian yaitu titik A(25, 30), B(115, 30), dan C(25, 120).

Uji titik pojok ke fungsi tujuan f(x, y) = 17.000x + 20.000y

Dari diperoleh nilai maksimum fungsi tujuan f(x, y) = 17.000x + 20.000y adalah 2.825.000 .

(99)

Contoh Soal

(100)

Contoh Soal

(101)

BAB

Barisan dan Deret

V

A. Barisan dan Deret Aritmetika B. Barisan dan Deret Geometri

C. Aplikasi Barisan dan Deret Bilangan

(102)

A. Barisan dan Deret Aritmetika

1. Barisan Aritmetika 2. Deret Aritmetika

(103)

1. Barisan Aritmetika

Barisan aritmetika disebut juga barisan hitung.

Perhatikan contoh barisan aritmetika berikut.

Barisan aritmetika mempunyai selisih yang sama di antara dua suku berurutan. Selisih tersebut disebut dengan beda.

Beda pada barisan aritmetika:

(104)

Rumus suku ke-n (U_n) barisan aritmetika:

Dengan a = U₁ = suku pertama, n = nomor suku,

b = beda barisan Contoh:

Suku ke-50 barisan aritmetika 17, 10, 3, –4, . . . adalah . . . .

Jawaban:

Suku ke-50:

U₅₀ = 17 + (50 – 1) × (–7)

= 17 + 49 × (–7)

= 17 + (–343)

= –326

(105)

Contoh Soal

1. Tentukan tiga suku pertama dari barisan aritmetika jika diketahui Un dan b berikut.

a. U₉ = 20; b = 5 b. U₂₃ = –3; b = – 3

2. Suku ketiga suatu barisan aritmetika sama dengan 11, sedangkan suku kesepuluh sama dengan 39.

a. Carilah suku pertama dan beda barisan itu.

b. Carilah rumus suku ke-n.

(106)

2. Deret Aritmetika

Jika suku-suku suatu barisan aritmetika dijumlahkan maka akan diperoleh deret aritmetika. Deret aritmetika disebut juga deret hitung.

Contoh:

4 + 11 + 18 + 25 ^Deret aritmetika dengan 4 suku

26 + 20 + 14 + 8 + 2 Deret aritmetika dengan 5 suku

Hasil penjumlahan suku-suku deret aritmetika disebut dengan jumlah n suku pertama.

Deret aritmetika 4 + 11 + 18 + 25.

Jumlah 1 suku pertama = 4

Jumlah 2 suku pertama = 4 + 11 = 15

Jumlah 3 suku pertama = 4 + 11 + 18 = 33

(107)

Rumus jumlah n suku pertama (S_n) barisan aritmetika:

Dengan a = U₁ = suku pertama, n = nomor suku

b = beda barisan

(108)

Contoh Soal

1. Diketahui barisan aritmetika 25, 19, 13, 7, . . . .

Tentukan jumlah 12 suku pertama barisan tersebut.

2. Feri menabung di sebuah bank setiap bulan. Pada bulan pertama ia menabung Rp50.000,00. Pada bulan-bulan berikutnya uang yang ia tabung selalu lebih besar

Rp5.000,00 daripada bulan sebelumnya.

a. Berapa jumlah tabungan Feri setelah setahun?

b. Setelah berapa tahun jumlah tabungan Feri menjadi Rp1.665.000,00?

(109)

B. Barisan dan Deret Geometri

1. Barisan Geometri 2. Deret Geometri

(110)

1. Barisan Geometri

Dari kedua contoh barisan geometri tersebut terlihat setiap dua suku yang berurutan pada barisan geometri memiliki rasio yang sama.

(111)

Misalkan U₁, U₂, U₃, U₄, U₅, . . . , U_n merupakan suku-suku barisan geometri. Rumus suku ke-n barisan tersebut

dinyatakan dengan:

Rasio dua suku yang berurutan pada barisan geometri dirumuskan dengan

(112)

Contoh Soal

(113)

2. Deret Geometri

Jika suku-suku suatu barisan geometri dijumlahkan maka akan diperoleh deret geometri. Deret geometri disebut juga deret ukur.

Contoh deret geometri sebagai berikut.

Deret 1:

1 + 2 + 4 + 8 +16 Deret 2:

162 + 54 + 8 + 6 + 2

(114)

Rumus jumlah n suku pertama deret geometri:

dengan: a merupakan suku pertama n merupakan banyak suku

r merupakan rasio

S_n adalah jumlah n suku pertama

S_{n – 1}adalah jumlah (n – 1) suku pertama

(115)

Contoh Soal

(116)

3. Deret Geometri Tak Hingga

Barisan geometri yang mempunyai banyak suku tak hingga disebut barisan geometri tak hingga.

Contoh barisan geometri tak hingga:

Rumus jumlah deret geometri tak hingga:

(117)

Contoh Soal

(118)

C. Aplikasi Barisan dan Deret Bilangan

1. Pertumbuhan 2. Peluruhan

3. Bunga Majemuk

4. Anuitas

(119)

1. Pertumbuhan

Pada bahasan ini, pertumbuhan yang dimaksud adalah pertumbuhan eksponensial, yaitu pertumbuhan menurut deret ukur (geometri). Pertumbuhan selalu bertambah dengan suatu persentase yang tetap dalam jangka waktu tertentu.

Misalkan pertumbuhan nilai suatu benda setiap tahun adalah r. Jika nilai awal benda adalah H

maka pertambahan nilai benda adalah H  r.

Rumus umum nilai benda setelah t tahun:

(120)

Contoh Soal

Pada tahun 2000 penduduk suatu negara tercatat 25 juta jiwa. Jika tingkat pertumbuhannya mencapai 3% per tahun, tentukan perkiraan jumlah penduduk di negara tersebut pada tahun 2020.

(121)

2. Peluruhan

Peluruhan yang dimaksud adalah peluruhan eksponensial, yaitu peluruhan menurut deret ukur (geometri). Peluruhan selalu berkurang dengan suatu persentase yang tetap dalam jangka waktu tertentu.

Misalkan peluruhan nilai suatu benda setiap tahun adalah r.

Jika nilai awal benda adalah H maka penyusutan nilai benda adalah H × r.

Rumus umum nilai benda setelah t tahun:

(122)

Contoh Soal

Diketahui harga beli sebuah sepeda motor Rp15.000.000,00 dan harga jualnya menurun sebesar 10% setiap tahun.

Tentukan harga jual sepeda motor setelah pemakaian selama lima tahun.

(123)

3. Bunga Majemuk

Bunga majemuk adalah bunga yang dihitung atas jumlah pinjaman pokok ditambah bunga yang diperoleh sebelumnya.

Uang yang dibungakan dengan bunga majemuk akan bertambah sebagaimana pertumbuhan.

Misalkan nilai awal uang (modal) adalah M dan

pertambahannya dalam periode waktu tertentu adalah suku bunga yang berlaku, yaitu i.

Nilai uang setelah t periode dirumuskan:

(124)

Contoh Soal

1. Modal sebesar Rp4.000.000,00 ditabung dengan suku bunga majemuk 5% per tahun. Tentukan besar modal setelah 4 tahun.

2. Pak Junaidi menginvestasikan modal sebesar

Rp20.000.000,00 di bank dengan suku bunga majemuk 4%

per semester. Jika modal tersebut menjadi Rp27.372.000,00, berapa tahun Pak Junaidi menginvestasikan modalnya?

(125)

4. Anuitas

Anuitas adalah suatu pembayaran atau penerimaan uang setiap jangka waktu tertentu dalam jumlah sama atau tetap.

Jangka waktu tertentu tersebut dinamakan periode.

Pembayaran secara anuitas dilakukan setiap akhir periode.

Periode pembayaran bisa setiap bulan, triwulan, kuartal, semester, atau setiap tahun. Jumlah pembayaran anuitas terdiri atas angsuran dan bunga.

Nilai anuitas A dari suatu pinjaman M dengan suku bunga i

% dirumuskan dengan:

(126)

Hubungan Antara Anuitas, Angsuran, Bunga, dan Sisa Pinjaman

Nilai anuitas sama pada setiap akhir periode pembayaran.

Anuitas terdiri atas angsuran dan bunga. Nilai anuitas merupakan jumlahan antara angsuran dan bunga.

(127)

Contoh Soal

Suatu pinjaman akan dilunasi dengan anuitas dan diangsur setiap tiga bulan selama dua tahun. Suku bunga yang

diberikan sebesar 2% per tiga bulan.

Jika besar angsuran pertama Rp600.000, hitunglah:

a. besar anuitas;

b. besar bunga tiga bulan pertama;

c. besar pinjaman;

d. sisa pinjaman setelah diangsur selama setahun.

(128)