07350015%2E2012%2E669668
Teks penuh
Gambar
Garis besar
Dokumen terkait
Remark 2. It is important to note that in model I , the limit distribution does not depend on c , and in this case we can expect the tests to be unaffected by size distortions
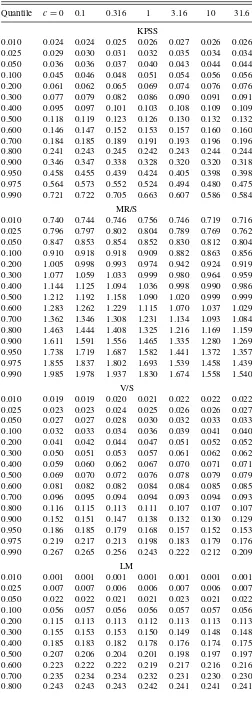
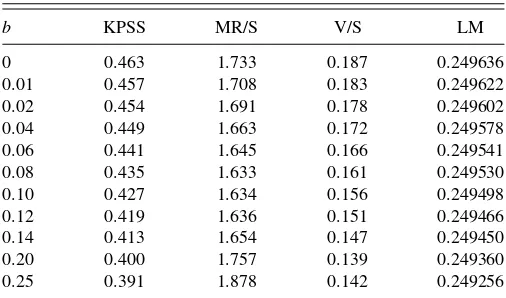
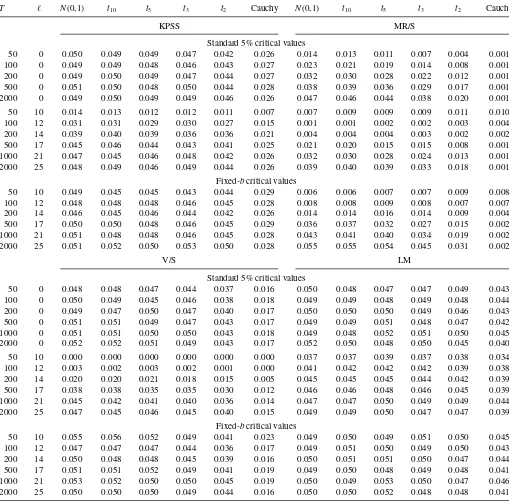
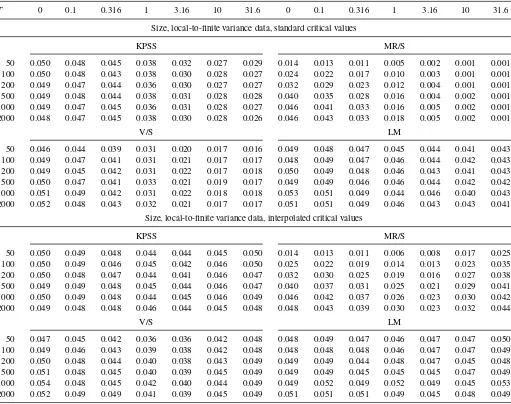
Table 1 reports the null rejection probabilities for various two- sided 5% tests. It is clear that the tests based on the near-unity fixed-smoothing approximation are in general
c , it is fairly straightforward to adjust the numerical derivation of the tests in Section 4.2 to obtain nearly weighted average power maximizing tests that controls size only under
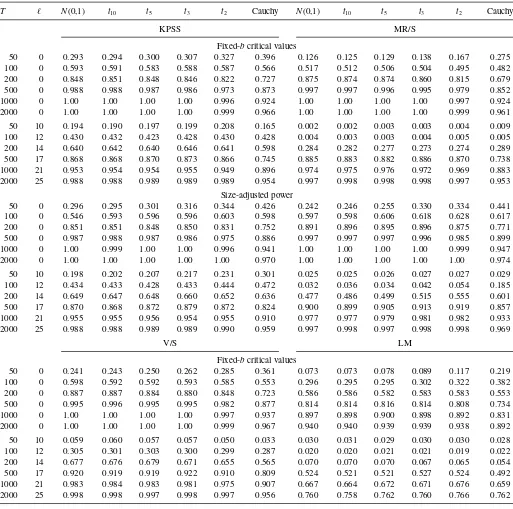
We see in Table 4 that, using the asymptotic critical values given in Table 1 , GKSn and GCVMn have large size distortions in most cases, confirming asymptotic theory, whereas GKS ∗
A set of simulation experiments was designed to uncover the size and power properties of bootstrap tests based on our proposed family of statistics, and to compare these properties
(erf) of the tests LR1, LR2, and LR3 and of the overall “LR1 → LR2 → LR3” testing strategy; the column “Asymptotic” reports the erf computed using the asymptotic critical
This article therefore studies the asymptotic behavior of panel unit root tests based on the Cauchy estimator in panels with unconditionally heteroscedastic innovations as
Both the local asymptotic power and the size-adjusted Þnite sample power of the long-run variance ratio tests based on the pair of inconsistent estimators II are found to be