HIRASAWA
G54103030
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRACT
HIRASAWA. Modelling The Exchange Rate of Rupiah to US Dollar Used The Hidden Markov Time Series Hamilton Model. Under the direction of BERLIAN SETIAWATY and N. K. KUTHA ARDANA.
The exchange rate of Rupiah to US Dollar can be fluctuated every time. It is effected by war, financial and economic crisis, or the government policy. The fluctuated of exchange rate might generate unconvinced motion for foreign investors to invest their funds in Indonesia. This matter cause at height of exchange rate Rupiah to US Dollar. But this occurrence is not observed directly (hidden).
To describe the exchange rate of the Rupiah, this research used the hidden Markov time series Hamilton (1994) as a model. This model assumes that the exchange rate of Rupiah to US Dollar is based on Markov chain which is explained by the cause of occurence and the previous exchange rate of Rupiah.
The parameter of the hidden Markov time series is estimated by using the Maximum Likelihood method. The estimation of the parameter is calculated using the Expectation Maximization algorithm which is implemented in Mathematica 5.2 for Student.
The forecast of the exchange rate can also be calculated by using the model. For example: the forecast of the exchage rate at February 2007 is Rp. 9088,98 with maximum and minimum error are Rp. 2328,48786 and Rp. 1,63577 respectively. (The exact exchange rate is Rp. 9073,11)
ABSTRAK
HIRASAWA. Pemodelan Nilai Tukar Rupiah Terhadap US Dolar Menggunakan Deret Waktu
Hidden Markov Model Hamilton. Dibimbing oleh BERLIAN SETIAWATY dan N. K. KUTHA
ARDANA.
Nilai tukar Rupiah terhadap US Dollar mengalami perubahan setiap waktunya. Perubahan nilai tukar Rupiah dapat diakibatkan karena perang, krisis keuangan dan ekonomi, atau perubahan yang cukup signifikan pada kebijakan pemerintah, sehingga menimbulkan mosi tidak percaya bagi investor asing yang akan menginvestasikan dananya di Indonesia. Hal ini berakibat pada tingginya nilai tukar Rupiah terhadap US Dollar. Namun kejadian ini, tidak diamati secara langsung
(hidden).
Untuk menggambarkan perilaku nilai tukar Rupiah tersebut, dalam karya ilmiah digunakan model deret waktu hidden Markov model Hamilton (1994). Model ini mengasumsikan bahwa nilai tukar Rupiah terhadap US Dollar bergantung pada rantai Markov yang merupakan penyebab kejadian yang tidak diamati dan nilai tukar Rupiah suatu waktu sebelumnya.
Dalam model ini akan dicari penduga parameter. Salah satu metode untuk pendugaan parameter tersebut adalah dengan menggunakan Maximum Likelihood Estimators yang perhitungannya mengunakanalgoritma Expectation Maximization. Untuk mempermudah mencari penduga parameter dalam model deret waktu Hidden Markov, dibuat suatu program komputasi dengan menggunakan Mathematica 5.2 for Student, agar hasil perhitungannya maksimal.
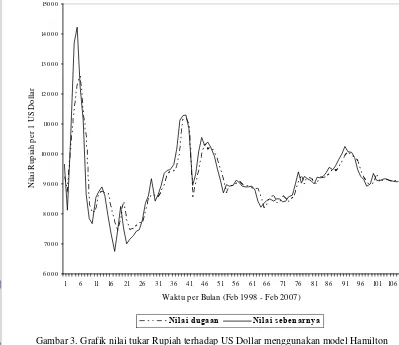
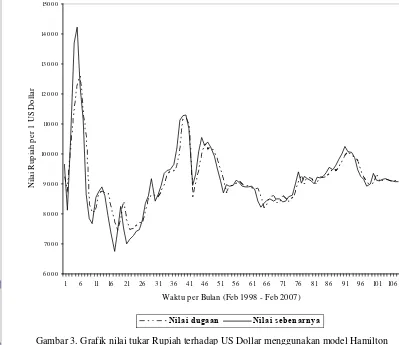
Dengan diperolehnya parameter, maka dapat dihitung nilai tukar Rupiah terhadap US Dollar yang akan datang. Sebagai contoh, nilai dugaan pada bulan Februari 2007 adalah 9088.98, mendekati nilai sebenarnya yaitu 9073.11. Nilai galat maksimum adalah 2328.48786 dan nilai galat minimum adalah 1.63577.
PEMODELAN NILAI TUKAR RUPIAH TERHADAP US DOLAR
MENGGUNAKAN DERET WAKTU
HIDDEN
MARKOV
MODEL HAMILTON
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Oleh :
HIRASAWA
G54103030
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul
: Pemodelan Nilai Tukar Rupiah Terhadap US Dolar
Menggunakan Deret Waktu
Hidden
Markov Model Hamilton
Nama :
Hirasawa
NRP :
G54103030
Menyetujui:
Pembimbing I,
Dr. Berlian Setiawaty, MS
NIP. 131 835 248
Pembimbing II,
Ir. N. K. Kutha Ardana, M.Sc
NIP. 131 842 412
Mengetahui:
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Prof. Dr. Ir. Yonny Koesmaryono, MS
NIP. 131 473 999
PRAKATA
Puji syukur penulis panjatkan kepada Allah SWT atas segala karunianya sehingga penulis dapat menyelesaikan tugas akhir yang berjudul Pemodelan Nilai Tukar Rupiah Terhadap US Dolar Menggunakan Deret Waktu Hidden Markov Model Hamilton. Shalawat dan salam semoga senantiasa tercurah kepada Rasulullah Muhammad SAW beserta keluarga, sahabat dan pengikutnya hingga akhir zaman.
Tugas akhir ini saya persembahkan untuk kedua orang tua, nenek dan ketiga adik saya yang telah banyak memberikan dukungan yang luar biasa (terutama nasehat dan doa-doanya) sehingga karya ilmiah ini dapat terselesaikan.
Keterbatasan dan ketidaksempurnaan membuat penulis membutuhkan bantuan, dukungan dan semangat dari orang-orang secara langsung ataupun tidak langsung berkontribusi besar dalam pembuatan tugas akhir ini. Oleh karena itu penulis ingin mengucapkan rasa terima kasih yang sebesar-besarnya kepada Ibu Berlian Setiawaty dan Bapak Kutha Ardana yang dengan sabar telah membimbing dan mengarahkan selama penulisan karya ilmiah ini. Bapak I Wayan Mangku atas kesediaannya menjadi penguji luar dalam sidang tugas akhir penulis. Yudi, Dimas, dan Lia atas kesediaannya menjadi pembahas dalam seminar penulis.
Tak lupa penulis ingin mengucapkan terima kasih kepada Muhammad Mukafi, Astrie Lestari, Mufti Alban, Ifni Husnul Khatimah dan tim PKM (Nurmaulidah dan Ari Septian) atas dukungan dan doanya. Kepada Bapak Ridwan Hasan Saputra dan tim KPM (Teh Desi, Bu Anis, Bu Astri dkk). Seluruh Dosen Departemen Matematika atas segala ilmu yang telah diberikan. Staf dan karyawan TU Matematika IPB. Matematika angkatan 40 atas persahabatannya selama ini semoga tidak akan berakhir. Serta seluruh pihak yang tidak dapat penulis sebutkan satu per satu.
Penulis mengetahui bahwa tugas akhir ini masih jauh dari kesempurnaan. Semoga tugas akhir ini dapat bermanfaat bagi penulis khususnya dan bagi pihak lain yang membutuhkan.
Bogor, Mei 2007
RIWAYAT HIDUP
Penulis dilahirkan di Bogor pada tanggal 11 Juli 1985 sebagai anak pertama dari empat bersaudara. Ayah penulis bernama Aang Suhata dan Ibu bernama Sri Mulyanti.
Pada tahun 1997 penulis menyelesaikan pendidikan SD Negeri Pajeleran 01 Cibinong. Penulis melanjutkan pendidikan di SLTP Negeri 2 Cibinong pada tahun yang sama. Pada tahun 2000 penulis melanjutkan pendidikan di SMU Negeri 2 Bogor. Pada tahun 2003, penulis diterima di Institut Pertanian Bogot (IPB) melalui jalur Ujian Seleksi Masuk Institut Pertanian Bogor (USMI) di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam IPB.
Selama mengikuti kegiatan perkuliahan, penulis aktif di berbagai kegiatan mahasiswa yaitu sebagai sekretaris Gugus Mahasiswa Matematika IPB periode 2004/2005 dan sebagai ketua Gugus Mahasiswa Matematika IPB periode 2005/2006. Penulis juga aktif sebagai panitia pada beberapa acara antara lain “Seminar Ekonomi Islam” tahun 2004, Matematika RIA tahun 2005, “MIPA sport tournament” tahun 2005. Selain itu, penulis juga aktif menjadi asisten mata kuliah “Algoritma dan pemrograman” pada tahun ajaran 2005/2006 dan pernah mengikuti lomba kreatifitas mahasiswa yang diselenggarakan oleh DIKTI tahun 2006/2007.
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... viii
DAFTAR LAMPIRAN ... viii
I. PENDAHULUAN ... 1
1.1 Latar Belakang ...1
1.2 Tujuan ...1
II. LANDASAN TEORI ... 1
2.1 Ruang Contoh, Kejadian dan Peluang...1
Definisi 2.1.1 (Percobaan Acak) ...1
Definisi 2.1.2 (Ruang Contoh dan Kejadian)...1
Definisi 2.1.3 (Medan-σ ) ...2
Definisi 2.1.4 (Ukuran Peluang) ...2
Definisi 2.1.5 (Peluang Bersyarat)...2
Definisi 2.1.6 (Kejadian Saling Bebas)...2
Definisi 2.1.7 (Kontinu Absolut) ...2
Teorema 2.1.8 (Radon Nikodym) ...2
2.2 Peubah Acak dan Fungsi Sebaran ...2
Definisi 2.2.1 (Peubah Acak)...2
Definisi 2.2.2 (Fungsi Sebaran) ...2
Definisi 2.2.3 (Peubah Acak Diskret) ...2
Definisi 2.2.4 (Fungsi Kerapatan Peluang) ...2
Definisi 2.2.5 (Peubah Acak Kontinu)...2
Definisi 2.2.6 (Fungsi Sebaran Bersama Dua Peubah Acak)...3
Definisi 2.2.7 (Fungsi Kepekatan Peluang Bersama) ...3
Definisi 2.2.8 (Fungsi Kepekatan Peluang Bersyarat) ...3
Definisi 2.2.9 (Nilai Harapan Peubah Acak Diskret)...3
Definisi 2.2.10 (Nilai Harapan Peubah Acak Kontinu) ...3
Definisi 2.2.11 (Nilai Harapan Bersyarat) ...3
Definisi 2.2.12 (Himpunan Konveks dan Fungsi Konveks)...3
Teorema 2.2.13 (Ketaksamaan Jensen)...3
2.3 Rantai Markov...3
Definisi 2.3.1 (Ruang State) ...3
Definisi 2.3.2 (Proses Stokastik)...3
Definisi 2.3.3 (Rantai Markov) ...4
Definisi 2.3.4 (Rantai Markov dengan Waktu Diskret) ...4
2.4 Algoritma EM (Expectation Maximization)...4
III. MODEL HIDDEN MARKOV ... 5
3.1 Model Hidden Markov dan Karakteristiknya ...5
3.2 Reestimasi Parameter Menggunakan Algoritma EM ...6
IV. DERET WAKTU HIDDEN MARKOV HAMILTON ... 8
4.1 Model Deret Waktu Hidden Markov Hamilton...8
4.2 Pendugaan Parameter θ ...9
4.3 Reestimasi Parameter Menggunakan Algoritma EM ...11
V. PEMODELAN NILAI TUKAR RUPIAH TERHADAP US DOLLAR... 12
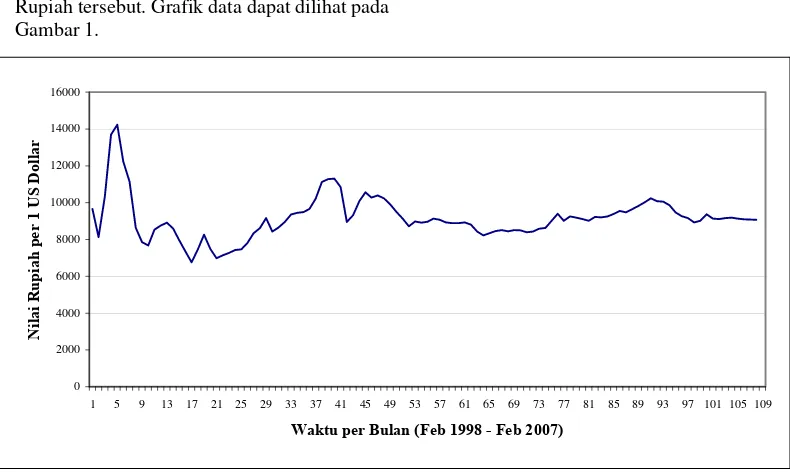
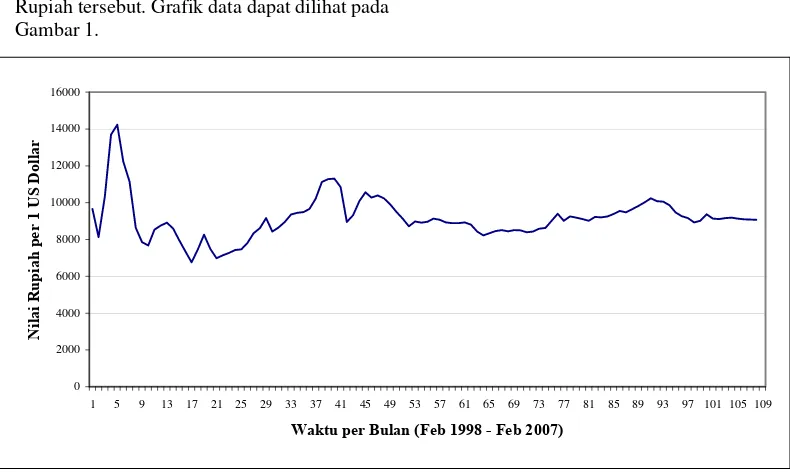
5.1 Data Input Nilai Tukar Rupiah ...13
5.2 Pemodelan Kasus Nilai Tukar Rupiah Untuk Banyaknya Penyebab Kejadian N=2 ...13
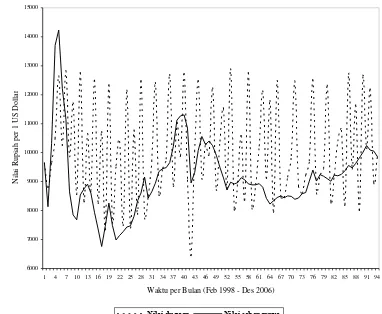
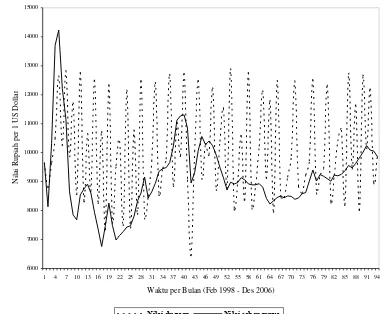
5.2.1 Model Elliot ...13
5.2.2 Model Hamilton...14
SIMPULAN ... 16
DAFTAR GAMBAR
Halaman Gambar 1. Grafik perubahan nilai tukar Rupiah terhadap US Dollar per bulan ... 13 Gambar 2. Grafik nilai tukar Rupiah terhadap US Dollar menggunakan model Elliot ... 14 Gambar 3. Grafik nilai tukar Rupiah terhadap US Dollar menggunakan model Hamilton ... 15
DAFTAR LAMPIRAN
I. PENDAHULUAN
1.1 Latar BelakangPerkembangan perekonomian di Indonesia, kian hari semakin membaik. Terlihat pada angka nilai tukar Rupiah terhadap US Dollar yang mulai stabil pada tingkat sembilan ribu Rupiah per US Dollar. Setiap perubahan suatu kejadian berkaitan erat dengan penyebab kejadiannya. Perubahan kejadian ekonomi di masa lalu memiliki kemungkinan akan terulang kembali di masa yang akan datang. Sehingga dapat dimodelkan dengan suatu proses stokastik. Jika penyebab kejadiannya tidak diamati secara langsung dan membentuk rantai Markov, maka pasangan kejadian dan penyebabnya dapat dimodelkan dengan model Hidden Markov (Hidden
Markov Model, HMM).
Dalam karya ilmiah ini, dibahas aplikasi dari model deret waktu hidden Markov untuk menggambarkan perilaku nilai tukar Rupiah terhadap US Dollar dan menduga nilai tukar Rupiah yang akan datang.
Perubahan pada nilai tukar Rupiah terhadap US Dollar dapat diakibatkan karena perang, krisis keuangan dan ekonomi, atau perubahan yang cukup signifikan pada kebijakan pemerintah, sehingga menimbulkan mosi tidak percaya bagi investor asing yang akan menginvestasikan dananya di Indonesia. Hal ini berakibat pada tingginya nilai tukar Rupiah terhadap US Dollar. Namun kejadian ini, tidak diamati secara langsung (hidden).
Terdapat beberapa faktor yang menyebabkan terjadinya perubahan suatu kejadian. Faktor penyebab (state) tersebut dapat berkembang menurut model rantai Markov di mana state yang akan datang hanya dipengaruhi oleh state sekarang dan bebas terhadap state yang lalu.
Untuk model hidden Markov, kejadian yang diamati dipengaruhi oleh faktor penyebab terjadinya suatu kejadian dan beberapa paramater. Sedangkan untuk model deret waktu hidden Markov, kejadian yang diamati selain dipengaruhi oleh faktor penyebab terjadinya suatu kejadian dan beberapa paramater, juga dipengaruhi oleh kejadian sebelumnya.
Dalam model ini akan dicari penduga parameter. Salah satu metode untuk pendugaan parameter tersebut adalah dengan menggunakan MLE (Maximum Likelihood
Estimators) yang perhitungannya
meng-gunakan algoritma EM (Expectation
Maximization).
Dengan diketahuinya penduga parameter yang memaksimumkan peluang terjadinya suatu kejadian, maka dapat dilakukan penarikan kesimpulan yang optimal dan peramalan pada state.
Dalam perkembangan lebih lanjut, dibuat suatu program komputasi untuk mencari parameter yang akan digunakan dalam model deret waktu hidden Markov, agar hasil perhitungannya maksimal. Software yang digunakan adalah Mathematica 5.2 for Student.
Kelebihan program ini adalah waktu kerja yang lebih efesien serta mempermudah dalam analisis data karena sudah dilengkapi dengan fungsi-fungsi yang mudah digunakan.
1.2 Tujuan
Tujuan dari karya ilmiah ini adalah
1.Mempelajari model hidden Markov dan deret waktu hidden Markov Hamilton beserta penduga parameternya.
2.Mengimplementasikan model deret waktu
hidden Markov Hamilton untuk masalah
nilai tukar Rupiah terhadap US Dollar
II. LANDASAN TEORI
Pada bab ini dijelaskan beberapa definisi yang digunakan dalam pembahasan selanjutnya.
2.1 Ruang Contoh, Kejadian dan Peluang Definisi 2.1.1 (Percobaan Acak)
Dalam suatu percobaan seringkali dilakukan pengulangan dengan kondisi yang sama. Semua kemungkinan hasil yang akan muncul dapat diketahui, akan tetapi hasil pada percobaan berikutnya tidak dapat diduga
dengan tepat. Percobaan semacam ini, yang dapat diulang dalam kondisi yang sama, disebut percobaan acak.
[Hogg dan Craig, 1995] Definisi 2.1.2 (Ruang Contoh dan Kejadian)
Himpunan semua kemungkinan hasil dari suatu percobaan acak disebut ruang contoh, dinotasikan dengan Ω. Suatu kejadian A
adalah himpunan bagian dari Ω.
Definisi 2.1.3 (Medan-σ )
Koleksi F dari himpunan bagian Ω disebut sebagai medan-σ jika memenuhi syarat: a. φ ∈F
b. jika A A1, 2,...∈F maka 1 i i
A ∞
= ∈
∪ F
c. Jika A∈Fmaka Ac∈F.
[Grimmet dan Stirzaker, 1992] Definisi 2.1.4 (Ukuran Peluang)
Misalkan F adalah Medan-σ dari ruang contoh Ω. Ukuran peluang adalah suatu fungsi P:F →
[ ]
0,1 pada(
Ω,F)
yang memenuhi:1. P
( )
φ =0,P( )
Ω =1,2.Jika A A1, 2, ∈F adalah himpunan yang
saling lepas yaitu Ai∩Aj =φuntuk setiap pasangan i≠ j, maka
( )
1 1
i i
i i
P A P A
∞ ∞
= =
⎛ ⎞=
⎜ ⎟
⎝
∪
⎠∑
.Pasangan
(
Ω,F,P)
disebut ruang peluang.[Grimmet dan Stirzaker, 1992] Definisi 2.1.5 (Peluang Bersyarat)
Jika P B
( )
>0 maka peluang bersyarat dari kejadian A setelah diketahui kejadian B ialah(
|)
P A(
( )
B)
P A B
P B
∩
= .
[Grimmet dan Stirzaker, 1992] Definisi 2.1.6 (Kejadian Saling Bebas) Kejadian A dan B dikatakan saling bebas jika
(
)
( ) ( )
P A∩B =P A P B .
Misal I adalah himpunan indeks. Himpunan kejadian
{
A ii: ∈I}
disebut saling bebas jika( )
i( )
ii J i J
P A P A
∈ ∈ = ∏
∩
untuk setiap himpunan bagian berhingga J
dari I.
[Grimmet dan Stirzaker, 1992] Definisi 2.1.7 (Kontinu Absolut)
Jika vdan µmerupakan ukuran peluang pada
(
Ω,F)
. Ukuran peluang v dikatakan kontinu absolute terhadap ukuran peluang µ jika0
A
µ = maka vA= 0, untuk setiap A∈F. Dinotasikan v<<µ.
[Royden, 1963]
Teorema 2.1.8 (Radon Nikodym)
Jika P dan Pmerupakan dua ukuran peluang pada
(
Ω,F)
sehingga untuk setiap B∈F,( )
0P B = menyebabkan P B
( )
=0, maka terdapat peubah acak tak negative ∆ sehingga( )
C
P C = ∆
∫
dP untuk semua C∈F . DinotasikandP dPF = ∆.
[bukti lihat Wong dan Hajek, 1985]
2.2 Peubah Acak dan Fungsi Sebaran Definisi 2.2.1 (Peubah Acak)
Misalkan F adalah medan-σ dari Ω. Peubah acak X merupakan fungsi X:Ω → di mana
{
ω∈ Ω:X( )
ω ≤x}
∈F untuk setiapx∈ .
[Grimmet dan Stirzaker, 1992] Peubah acak dinotasikan dengan huruf besar, sedangkan nilai dari peubah acak tersebut dinotasikan dengan huruf kecil.
Definisi 2.2.2 (Fungsi Sebaran)
Fungsi sebaran dari peubah acak X adalah suatu fungsiF: →
[ ]
0,1 di mana( )
(
)
X
F x =P X ≤x .
[Grimmet dan Stirzaker, 1992] Definisi 2.2.3 (Peubah Acak Diskret) Peubah acak X disebut sebagai peubah acak diskret jika nilainya hanya berada pada himpunan bagian yang terhitung dari .
[Grimmet dan Stirzaker, 1992] Definisi 2.2.4 (Fungsi Kerapatan Peluang) Fungsi kerapatan peluang dari peubah acak diskret X adalah fungsi p: →
[ ]
0,1 di mana( )
(
)
X
p x =P X =x .
[Grimmet dan Stirzaker, 1992] Definisi 2.2.5 (Peubah Acak Kontinu) Peubah acak X disebut kontinu jika fungsi sebarannya dapat dinyatakan sebagai
( )
( )
;x X
F x f u du x
−∞
= ∫ ∈
di mana f : →
[
0,∞)
adalah fungsi yang terintegralkan. f merupakan fungsi kepekatan peluang dari peubah acak X.Definisi 2.2.6 (Fungsi Sebaran Bersama Dua Peubah Acak)
Fungsi sebaran bersama dua peubah acak X
dan Y merupakan suatu fungsi 2
[ ]
: 0,1
F →
yang didefinisikan oleh
(
,)
(
,)
F x y =P X ≤x Y≤ y .
[Grimmet dan Stirzaker, 1992] Definisi 2.2.7 (Fungsi Kepekatan Peluang Bersama)
Misalkan X dan Y peubah acak kontinu, maka fungsi kepekatan peluang bersama dari X dan
Y adalah
(
)
(
)
2 , ,
XY
F x y f x y
x y
∂ =
∂ ∂
dan fungsi kepekatan peluang marginal dari peubah acak Y adalah
( )
( )
,Y XY
f y f x y dx
∞
−∞
= ∫ .
[Grimmet dan Stirzaker, 1992] Definisi 2.2.8 (Fungsi Kepekatan Peluang Bersyarat)
Misalkan X dan Y peubah acak kontinu dengan fungsi kepekatan peluang marginal
( )
0Y
f y > , maka fungsi kepekatan peluang bersyarat dari X dengan syarat Y = y adalah
(
)
( )
( )
|
,
| XY
X Y
Y
f x y
f x y
f y
= .
[Grimmet dan Stirzaker, 1992] Definisi 2.2.9 (Nilai Harapan Peubah Acak Diskret)
Misalkan X adalah peubah acak diskret dengan fungsi kerapatan peluang
( )
(
)
X
p x =P X =x maka nilai harapan dari X
adalah
[ ]
X( )x
E X = ∑xp x asalkan jumlah di atas konvergen.
[Hogg dan Craig, 1995] Definisi 2.2.10 (Nilai Harapan Peubah Acak Kontinu)
Misalkan X adalah peubah acak kontinu dengan fungsi kepekatan peluang fX
( )
xmaka nilai harapan dari X adalah
[ ]
X( )
E X xf x dx
∞ −∞ = ∫ asalkan integralnya ada.
[Hogg dan Craig, 1995] Definisi 2.2.11 (Nilai Harapan Bersyarat) Misalkan X dan Y adalah peubah acak kontinu dan fX Y|
(
x y|)
adalah fungsi kepekatanpeluang bersyarat dari X dengan syarat Y = y,
maka nilai harapan dari X dengan syarat Y = y
adalah
[
|]
X Y|(
|)
E X Y y xf x y dx
∞
−∞
= =
∫
.[Hogg dan Craig, 1995] Definisi 2.2.12 (Himpunan Konveks dan Fungsi Konveks)
Misalkan N
S∈ adalah himpunan vektor. Maka S disebut sebagai himpunan konveks
jika untuk semua , 'x x ∈Sterdapat λ∈
[ ]
0,1 maka(
1−λ)
x+λx'∈S.Misalkan f merupakan fungsi dengan peubah x
yang terdefinisi pada himpunan konveks S. Maka f disebut sebagai fungsi konveks jika f
memenuhi persamaan
(
)
(
1 ')
(
1) ( )
( )
'f −λ x+λx ≤ −λ f x +λf x .
Jika f memiliki turunan kedua, maka f disebut sebagai fungsi konveks jika dan hanya jika
( )
2
0,
f x x S
∇ ≥ ∀ ∈
dan merupakan strictly convex jika
( )
2
0,
f x x S
∇ > ∀ ∈ .
[Osborne, 1997] Teorema 2.2.13 (Ketaksamaan Jensen) Misalkan X∈ adalah peubah acak dengan
X
⎡ ⎤ ⎣ ⎦
berhingga dan g(x) adalah fungsi konveks. Maka ⎡⎣g X
( )
⎤⎦≥g(
[ ]
X)
.[bukti lihat Weisstein, 1999] 2.3 Rantai Markov
Definisi 2.3.1 (Ruang State)
Misalkan S⊂ merupakan himpunan nilai dari barisan peubah acak, maka S disebut ruang state.
[Grimmet dan Stirzaker,1992] Definisi 2.3.2 (Proses Stokastik)
Proses stokastik S={ ,S t Tt ∈ } adalah suatu koleksi dari peubah acak yang memetakan suatu ruang contoh Ω ke suatu ruang state K. Jadi, untuk setiap t pada himpunan indeks T,
St adalah suatu peubah acak.
[Ross,1996] Dalam hal ini anggap t sebagai waktu dan nilai dari peubah acak St sebagai state
Definisi 2.3.3 (Rantai Markov)
Proses S adalah rantai Markov jika memenuhi syarat Markov, yaitu:
0 0 1 1 1 1
1 1
( | , ,..., )
( | ).
t t t
t t t
P S s S s S s S s
P S s S s
− −
− −
= = = =
= = =
[Grimmet dan Stirzaker,1992] Definisi 2.3.4 (Rantai Markov dengan Waktu Diskret)
Misalkan St suatu peubah acak. Proses
stokastik { ,S tt =0,1, 2,...}, dengan ruang state {0,1,2,…,N} disebut rantai Markov dengan waktu diskret jika untuk setiap t={0,1,2,..} berlaku
1 2 1
1
{ | , ,...}
{ | }
t t t t t t
ij
P S j S i S i
P S j S i
p
− − −
−
= = =
= = =
=
untuk semua kemungkinan nilai dari
io,i1,i2,…,in-1,i,j∈{1,2,3,…,N}
[Ross,1996] Jadi untuk suatu rantai Markov, sebaran bersyarat dari sebarang state saat ini St dengan
syarat state yang lalu S0,S1,S2,…,St-2 dan state
kemarin St-1adalah bebas terhadap semua state
yang lalu, dan hanya bergantung pada state
kemarin.
Proses di atas dapat digambarkan sebagai
N-state rantai Markov dengan peluang transisi
{pij} i,j = 1,2,…,N. Nilai dari peluang transisi
pij menyatakan peluang bahwa jika proses
tersebut berada pada state i maka berikutnya akan beralih ke state j. Karena nilai peluang adalah tak negatif dan karena proses tersebut harus mengalami transisi ke suatu state maka
a. pij
≥
0, untuk semua i,j∈ {1,2,…,N}b.
1 1
N ij j
p
= =
∑ untuk semua i∈{1,2,…,N} Peluang transisi (N x N) dapat dituliskan dalam bentuk matriks P yang disebut juga sebagai matriks transisi, yaitu
11 1
1
N N NN
p p
p p
⎛ ⎞
⎜ ⎟
= ⎜ ⎟
⎜ ⎟
⎝ ⎠
P
…
di mana i menandakan kolom dan j
menandakan baris dari matriks P. 2.4 Algoritma EM (Expectation Maximization)
Misalkan
{
Pθ,θ∈ Θ}
adalah himpunan ukuran peluang yang terdefinisi pada(
Ω,F)
dan kontinu absolut terhadap P0. Misalkan⊂
Y F. Fungsi Likelihood yang digunakan untuk menghitung penduga parameter θ berdasarkan informasi Y adalah
( )
0 0|
dP L
dP θ
θ = Ε ⎢⎡ ⎤⎥ ⎣ Y⎦.
Penduga Maximum Likelihood (MLE) didefinisikan oleh
( )
ˆ arg maxL
θ
θ θ
∈Θ
∈ .
Umumnya MLE sulit dihitung secara langsung, oleh karena itu diperlukan suatu metode aproksimasi berulang, yakni algoritma Expectation Maximization (EM). Langkah-langkah dalam metode tersebut adalah:
1. Set nilai awal parameter θˆkdengan
0
k= .
2. Set θ* =θˆk dan hitung
(
)
*
, θ θ
Q
dengan
(
)
**
*
, logdP |
dP
θ θ
θ
θ θ = Ε ⎢⎡ ⎤⎥
⎣ ⎦
Q Y .
3. Cari
(
*)
1
ˆ arg max ,
k
θ + ∈ Q θ θ .
4. Ganti k dengan k+1 dan ulangi langkah 2 sampai 4 hingga kriteria hentinya tercapai, yaitu ketika selisih
1
ˆ
k
θ + dan θˆkkurang dari suatu
bilangan yang sangat kecil. Bilangan tersebut dapat ditentukan sesuai dengan seberapa besar ketelitian yang diinginkan.
Misalkan g x
( )
log 1x
⎛ ⎞
= ⎜ ⎟
⎝ ⎠, karena turunan
kedua dari g x
( )
selalu positif( )
2 2
2 1 log 1
0, 0
g x
x x x
⎛ ⎞
∇ = ∇ ⎜ ⎟
⎝ ⎠ = > ∀ >
maka g x
( )
merupakan fungsi konveks. Karena log 1x
⎛ ⎞ ⎜ ⎟
⎝ ⎠ merupakan fungsi konveks,
maka berdasarkan ketaksamaan Jensen dapat dihasilkan barisan
{
θˆ ,k k≥0}
, yang merupakan fungsi likelihood yang tak turun yaitu( )
ˆ 1( ) (
ˆ ˆ 1 ˆ)
log log L θk+ − L θk ≥Q θk+,θk (2.4.1)
Definisikan 1 , 1 k k i i k λ = Λ =
∏
≥ dengan 1 i i i dP dP θ θ λ − = maka 1 20 1 1
0 1 1 2
, 1
. ...
. ... k
k k P k i i k k dP dP dP
dP dP dP
dP dP θ θ θ θ θ θ θ θ λ λ λ λ − = Λ = ≥ = = =
∏
atau 0 k k k dP dP θ θ ∆ = G . Dengan cara serupa maka1 0 1 1 k k k dP dP θ θ + + + ∆ = G serta 1 1 k k k dP dP θ θ λ + + = Akibatnya
( )
( )
1 1 ˆ ˆ 0 0 0 0 ˆ ˆ log loglog k | log k |
k k L L dP dP dP dP θ θ θ θ + + − = ⎡ ⎤ ⎡ ⎤ = ⎢ ⎥− ⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎣ Y⎦ ⎣ Y⎦
[
]
[
]
[
]
0 1 0
1
log | log |
log | log
k k
k k λk k
+ + = ∆ − ∆ = ∆ − ∆ Y Y Y
(
θˆk+1,θˆk)
=log∆k k[
λk+1|]
−log∆kQ Y
[
]
1 1 ˆ ˆ ˆ log |log k | .
k k k k k k dP dP θ θ θ λ + + ∆ = ∆ ⎡ ⎤ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ Y Y
Berdasarkan Teorema ketaksamaan Jensen maka
1 1
ˆ ˆ
ˆ ˆ
ˆ ˆ
log k | log k |
k k k k dP dP dP dP θ θ θ θ θ θ + + ⎡ ⎤ ⎡ ⎤ − ⎢ ⎥≤ − ⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎣ Y⎦ ⎣ Y⎦
atau
( )
( )
ˆ 1ˆ 1
ˆ
ˆ ˆ
log log log k |
k k k k dP L L dP θ θ θ θ θ + + ⎡ ⎤ − ≥ ⎢ ⎥ ⎢ ⎥
⎣ Y⎦
.
Hasil kedua ruas pada persamaan (2.4.1) akan bernilai sama jika dan hanya jika θˆk+1=θˆk.
Bentuk Q
(
θ θ, *)
disebut Pseudo Likelihoodbersyarat.
III. MODEL
HIDDEN
MARKOV
3.1 Model Hidden Markov danKarakteristiknya
Pada bab ini dibahas model Hidden Markov beserta karakteristiknya. Model ini terdiri atas pasangan state (St) penyebab kejadian yang tidak diamati dan proses observasinya (Yt).
Misalkan St adalah proses yang tidak diamati
dengan ruang state
{
1, 2, 3,...N}
. Jika Stberadapada state j, maka proses yang diamati Yt
mempunyai sebaran normal
(
2)
,j j
N µ σ . Pasangan {St,Yt} disebut model Hidden
Markov. Oleh karena itu, fungsi kerapatan peluang dari Yt dengan syarat peubah acak St
bernilai j adalah
(
)
(
)
2
2 1
| ; exp
2 2 t j t t j j y
f y S jθ µ
σ πσ ⎧− − ⎫ ⎪ ⎪ = = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ (3.1.1)
untuk j = 1,2,…N . Dalam hal ini θ adalah vektor dari parameter populasi yang memuat
1, 2, 3,..., N
µ µ µ µ dan 2 2 2 2 1, 2, 3,..., N
σ σ σ σ . Peubah yang tidak diamati {St} diduga telah
dibangkitkan oleh beberapa sebaran peluang, di mana peluang tak bersyarat St = j
dinotasikan dengan πj:
P S
{
t = j;θ}
=πj (3.1.2) untuk j = 1,2,…,N .Peluang π π π1, 2, 3,...,πN juga termasuk
dalamθ, sehingga θ didefinisikan sebagai
(
2 2)
1,..., N, 1,..., N, 1,..., N
θ = µ µ σ σ π π .
Peluang dari kejadian bersama St = j dan Yt
(
t, t ;)
(
t| t ;) {
t ;}
P y S = jθ = f y S = jθ ⋅P S = jθ
(3.1.3) Sehingga persamaan (3.1.1), (3.1.2) dan (3.1.3) diperoleh
(
)
(
)
2
2
, ; exp
2 2 t j j t t j j y
P y S jθ π µ
σ πσ ⎧− − ⎫ ⎪ ⎪ = = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ . (3.1.4) Fungsi kerapatan tak bersyarat dari Yt
diperoleh dengan menjumlahkan persamaan (3.1.4) untuk semua kemungkinan nilai j:
(
)
(
)
1
; , ;
N
t t t
j
f y θ P y S jθ
=
=
∑
= (3.1.5) Karena St merupakan peubah yang tidakdiamati, persamaan (3.1.5) merupakan fungsi kerapatan yang relevan untuk meng-gambarkan data yang diamati sebenarnya Yt .
Jika St bersifat bebas stokastik identik maka
log-likelihood untuk data yang diamati dapat
dihitung dari
( )
(
(
) (
)
(
)
)
(
)
1 2 1 .log ; ; ;
log ; (3.1.6)
T T
t t
f y f y f y
f y θ θ θ θ θ = = ⋅⋅⋅ = ∑ L
Penduga kemungkinan maksimum dari θ diperoleh dengan memaksimumkan persamaan (3.1.6) dengan kendala
1 2 3 N 1
π π+ +π + ⋅⋅⋅ +π = dan π ≥j 0 untuk 1, 2, ,
j= ⋅⋅⋅ N . Hal tersebut dapat diperoleh dengan menggunakan algoritma EM.
Setelah diperoleh penduga bagi θ, dapat diketahui peluang terjadinya suatu kejadian Yt
serta dapat disimpulkan state mana yang paling memungkinkan menjadi penyebab terjadinya suatu kejadian. Dari definisi peluang bersyarat diperoleh
{
}
{
(
)
}
(
)
(
)
. , ; | ; ; | ; ; t t t t t j t tt
P y S j
P S j y
f y
f y S j
f y θ θ θ π θ θ = = = ⋅ = = (3.1.7) Dengan diperolehnya parameter populasi θ , memungkinkan digunakan persamaan (3.1.1) dan (3.1.5) untuk menghitung persamaan (3.1.7) pada setiap pengamatan Yt.
3.2 Reestimasi Parameter Menggunakan Algoritma EM
Penduga maksimum likelihood θˆ dapat diperoleh dengan memaksimumkan
( )
(
)
1 log ; T t t f y θ θ = =∑
L dengan kendala1 2 3 N 1.
π π+ +π + +π =
Untuk menyelesaikan masalah tersebut maka digunakan metode Lagrange, misalkan
( )
( )
(
)
(
)
1 2 1 2 1 J 1log ; .
N T t N t f y θ θ λ π π π θ λ λπ λπ λπ = = + − − − − =
∑
+ − − − L (3.2.1) Berdasarkan persamaan (3.2.1) diperoleh(
)
(
)
(
)
2 2 ; 1 exp 2 2 | ; . t j tj j j
t t
y f y
f y S j
µ θ π πσ σ θ ⎧− − ⎫ ∂ ⎪ ⎪ = ⎨ ⎬ ∂ ⎪ ⎪ ⎩ ⎭ = = (3.2.2)
(
)
(
) (
)
(
)
2 2 2 2 ; exp 2 2 , ;t j t j j
t
j j j j
t j t t j y y f y y
P y S j
µ µ π θ µ πσ σ σ µ θ σ ⎧− − ⎫ − ∂ ⎪ ⎪ = ⎨ ⎬⋅ ∂ ⎪ ⎪ ⎩ ⎭ − = ⋅ = (3.2.3)
(
)
(
)
(
)
(
) (
)
22 2 2 2
2 3 2 2 2 4 ; exp 2 2 exp 2 2 2 exp 2 2 2 t j j t
j j j j
t j j
j j
t j t j j j j j y f y y y y 2 µ π θ σ σ πσ σ µ π σ πσ µ µ π σ σ πσ ⎛ ⎧− − ⎫⎞ ∂ = ∂ ⎜ ⎪ ⎪⎟ ⎨ ⎬ ⎜ ⎟ ∂ ∂ ⎜ ⎪⎩ ⎪⎭⎟ ⎝ ⎠ ⎧− − ⎫ ⎪ ⎪ = − ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ ⎧− − ⎫ − ⎪ ⎪ + ⎨ ⎬⋅ ⎪ ⎪ ⎩ ⎭
(
)
(
)
(
)
(
)
2 22 4 2
2 2
4 1
exp
2 2 2 2
1
, ; .
2
t j j t j
j j j j
t j
j t t
j
y y
y
P y S j
µ π µ σ σ πσ σ µ σ θ σ − ⎧ − ⎫ ⎧− − ⎫ ⎪ ⎪ ⎪ ⎪ = −⎨ + ⎬ ⎨ ⎬ ⎪ ⎪ ⎪ ⎪ ⎩ ⎭ ⎩ ⎭ ⎧ − ⎫ ⎪ ⎪ = −⎨ + ⎬⋅ = ⎪ ⎪ ⎩ ⎭ (3.2.4)
( )
(
) (
)
1 1 | ; ; T t t t j tf y S j
( )
(
)
2(
)
1 1 , ; ; T t j t t t
j t j
y
P y S j
f y µ θ θ µ = θ σ − ∂ = ⋅ ⋅ = ∂
∑
L (3.2.6)( )
( )
(
)
(
)
2 2 2 4 1 1 1 , ; .; 2 2
T
t j
j t t
t t
j j
y
P y S j f y µ θ σ θ θ σ = − σ ⎧ − ⎫ ∂ ⎪ ⎪ = ⎨− + ⎬ = ∂ ⎪ ⎪ ⎩ ⎭
∑
L (3.2.7) Kemudian, berdasarkan (3.1.7), persamaan (3.2.5) hingga (3.2.7) dapat dituliskan sebagai:( )
(
) (
) (
)
(
)
1 1 1 1 1 , | ; ; | ; . Tt t t j t
j t
T
j t t t
f y P S j y
f y
P S j y
θ θ θ π π θ π θ − = − = ∂ = = ∂ = =
∑
∑
L (3.2.8)( )
(
)
(
) (
)
(
)
2 1 2 1 1 ; | ; ; | ; . T t jt t t t
j t j
T t j
t t t j
y
f y P S j y f y
y
P S j y
µ θ θ θ µ θ σ µ θ σ = = − ∂ = ⋅ = ∂ − = =
∑
∑
L (3.2.9)( )
(
)
(
)
(
) (
)
(
)
(
)
2 2 2 4 1 2 2 4 1 1 1; 2 2
; | ; 1 | ; . 2 2 T t j j t t j j
t t t T
t j
j t t
t j
y
f y
f y P S j y
y
P S j y
µ θ σ θ σ σ θ θ µ σ θ σ − = − = ⎧ − ⎫ ∂ = ⎪− + ⎪ ⎨ ⎬ ∂ ⎪ ⎪ ⎩ ⎭ ⋅ = ⎧ − ⎫ ⎪ ⎪ = ⎨− + ⎬ = ⎪ ⎪ ⎩ ⎭
∑
∑
L (3.2.10) Untuk mencari nilai µ σˆj, ˆ2jdan ˆπj yangmemaksimumkan fungsi log-likelihood maka turunan pertama dari persamaan (4.2.1) harus sama dengan nol, yaitu
( )
(
)
2 1
J
| ; 0
T t j t t t j j y
P S j y
µ θ θ µ = σ − ∂ = = = ∂
∑
(
)
(
)
1 1 | ; | ; T Tt t t j t t
t t
y P S j y θ µ P S j y θ
= = = = =
∑
∑
. Sehingga diperoleh:(
)
(
)
1 1 ˆ | ; ˆ ˆ | ; Tt t t t
j T
t t t
y P S j y
P S j y
θ µ θ = = = = =
∑
∑
. (3.2.11)Selanjutnya
( )
(
)
(
)
2 2 2 4 1 J 1 2 2| ; 0
T t j j t j j t t y
P S j y
µ θ σ σ σ θ − = ⎧ − ⎫ ∂ = ⎪− + ⎪ ⎨ ⎬ ∂ ⎪ ⎪ ⎩ ⎭ ⋅ = =
∑
(
)
2(
)
2
4 4
1
| ; 0
2 2
T
t j j
t t
t j j
y
P S j y
µ σ θ σ σ = ⎧ − ⎫ ⎪− + ⎪ = = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭
∑
(
)
{
2 2}
(
)
1
| ; 0
T
j t j t t t
y P S j y
σ µ θ = − + − = =
∑
(
)
(
)
(
)
2 1 2 1 | ; | ; , Tt j t t t
T
j t t t
y P S j y
P S j y
µ θ σ θ = = − = = =
∑
∑
akan menghasilkan(
)
(
)
(
)
2 2 1 1 ˆ ˆ | ; ˆ ˆ | ; Tt j t t t
j T
t t t
y P S j y
P S j y
µ θ σ θ = = − = = =
∑
∑
. (3.2.12)( )
1(
)
1 J
| ; 0
T
j t t t
j
P S j y
θ π θ λ π − = ∂ = = − = ∂
∑
(
)
1 1| ; 0
T
j t t
t
j j
P S j y θ λπ
π = π = − =
∑
(
)
1 | ; Tt t j
t
P S j y θ λπ
=
= =
∑
.(3.2.13)
Dari persamaan di atas, untuk j=1, 2, ,N
diperoleh
(
)
(
)
(
)
{ }
{ }
1 1 2 11 | ; | ;
1 1
T
t t t t
t
N T
t
P S y θ P S N y θ
λ π π π λ = = = + + = = + + + = ⋅
∑
∑
yang mengakibatkan T =λ. Jika T =λ
dimasukan dalam persamaan (3.2.13) maka
(
)
1
| ;
T
t t j
t
P S j y θ Tπ
= = =
∑
, sehingga diperoleh(
)
1 ˆ | ; ˆ T t t t jP S j y
T
θ
π =
=
=
∑
. (3.2.14) Karena persamaan (3.2.11), (3.2.12), dan (3.2.14) tak-linear, maka digunakan Algoritma EM untuk mencari penduga maksimumIV. DERET WAKTU
HIDDEN
MARKOV HAMILTON
4.1 Model Deret Waktu Hidden MarkovHamilton
Pada karya ilmiah ini dibahas model deret waktu hidden markov Hamilton (1994) yaitu: 1
t t
t S S t t
Y =c +φ Y− +E (4.1.1)
di mana:
(
2)
0,
t ∼N σ
E bebas stokastik identik
{ }
Yt proses yang diamati dan bernilai skalar{ }St rantai Markov dengan ruang state
{ }
1, 2S =
1, 2, ,1
c c φ dan φ2adalah konstanta real
(
2)
1, 2, ,1 2,
c c
θ = φ φ σ
11 21 12 22
P = p p
p p
⎡ ⎤
⎢ ⎥
⎣ ⎦merupakan matriks peluang transisi.
Karena
(
2)
0,
t ∼N σ
E bebas stokastik identik
maka dapat diperoleh fungsi sebaran bagiEt:
( )
(
)
(
)
( )
2 2 0 2 2 0 0 1 exp 2 2 1 exp . 2 2 t t tt t t y t t y t t
F y P y
d d ε ε σ πσ ε ε σ πσ = ≤ ⎧− − ⎫ ⎪ ⎪ = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ ⎧− ⎫ ⎪ ⎪ = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭
∫
∫
E E (4.1.2) Berdasarkan persamaan 4.1.2 diperoleh fungsi sebaran bagi Yt:( )
(
)
(
)
(
)
( )
1 1 1 2 2 0 1 exp . 2 2 t t t t tt St Stt
Y t t t
S S t t t t t S S t y c Y
t t
Y
F y P Y y
P c y
P y c Y
d φ φ φ ε ε σ πσ − − − − − + + ≤ ≤ − − = ≤ = = ⎧− ⎫ ⎪ ⎪ = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭
∫
E EMisalkan v=yt−cSt −φStYt−1, maka
( )
( )
22 0 1 exp 2 2 t v tY t t
F y ε dε
σ πσ ⎧− ⎫ ⎪ ⎪ = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭
∫
dan( )
( )
( )
2 2 1 1 exp 2 2 t tY t Y t t
t
f y F y
y v v y σ πσ ∂ = ∂ ⎧ ⎫ ∂ ⎪ ⎪ = ⎨ ⎬⋅ ∂ ⎪ ⎪ ⎩ ⎭
(
)
(
)
2 1 2 2 1 2 1 exp 1 2 2 1 exp . 2 2 t t t tt S S t
t S S t
Y Y y c y c φ σ πσ φ σ πσ − − − − − − ⎧− ⎫ ⎪ ⎪ = ⎨ ⎬⋅ ⎪ ⎪ ⎩ ⎭ ⎧− ⎫ ⎪ ⎪ = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ (4.1.3) Misalkan ϒtadalah medan-σ yang lengkap
dan dibangun oleh Y Y Y1, 2, 3, ,Yt. Karena
t
Smerupakan rantai Markov 2 state maka terdapat 2 fungsi kerapatan peluang bagi Yt. Kumpulan fungsi kerapatan peluang tersebut dalam vektor
(
2 1×)
dilambangkan dengant
η , sehingga diperoleh:
(
)
(
)
(
)
(
)
1 1 21 1 1
2
2
2 2 1
2
| 1, ;
| 2, ;
1 exp 2 2 . 1 exp 2 2
η t t t t
t t t
t t t t
f y S
f y S
y c y
y c y
ϒ θ ϒ θ φ σ πσ φ σ πσ − − − − − − − − = ⎡ ⎤ = ⎢ ⎥ = ⎢ ⎥ ⎣ ⎦ ⎡ ⎧⎪− ⎫⎪⎤ ⎢ ⎨ ⎬⎥ ⎢ ⎪⎩ ⎪⎭⎥ ⎢ ⎥ = ⎧ ⎫ ⎢ ⎪− ⎪⎥ ⎢ ⎨ ⎬⎥ ⎢ ⎪⎩ ⎪⎭⎥ ⎣ ⎦ (4.1.4) Misalkan ( ) ( ) 1 | 1
| 1 2
| 1 ˆ ˆ ˆ t t t t t t ξ ξ − − − ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎝ ⎠
ξ melambangkan vektor
(
2 1×)
di mana ξˆ( )t t|j−1 pada vektor mere-presentasikan P S{
t = j|ϒt−1;θ}
dan ⊗me-lambangkan perkalian elemen per elemen, maka
| 1
ˆ
t t− ⊗ t
ξ η
(
)
(
)
(
)
(
)
(
) (
)
(
) (
)
1 1 1 1 1 1 1 11| ; | 1, ;
2 | ; | 2, ;
1| ; | 1, ;
.
2 | ; | 2, ;
t t t t t
t t t t t
t t t t t t t t t t
P S f y S
P S f y S
P S f y S
P S f y S
ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ − − − − − − − − = = ⎡ ⎤ ⎡ ⎤ =⎢ ⎥ ⎢⊗ ⎥ = = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ = ⋅ = ⎡ ⎤ = ⎢ ⎥ = ⋅ = ⎢ ⎥ ⎣ ⎦ (4.1.5) Berdasarkan persamaan (4.1.5) maka dapat dituliskan:
(
)
(
) (
)
1 1 1 , | ; | ; | , ;t t t
t t t t t
P y S j
P S j f y S j
(
)
(
)
(
) (
)
(
) (
)
(
) (
)
(
)
1 2 1 1 2 1 1 1 1 1 1 1 | 1 | ; , | ; | ; | , ;1| ; | 1, ;
2 | ; | 2, ;
ˆ (4.1.7)
t t
t t t j
t t t t t j
t t t t t t t t t t t t t
f y
P y S j
P S j f y S j
P S f y S
P S f y S
ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ − − = − − = − − − − − = = = = ⋅ = = = = + = = ′ = ⊗
∑
∑
1 ξ η
di mana 1′ =
[ ]
1 1 .Berdasarkan persamaan (4.1.6) dan (4.1.7), maka diperoleh
(
)
(
)
(
)
(
)
(
(
)
)
(
)
(
)
(
)
(
)
(
)
(
)
1 1 1 1 1 1 1 1 1 1 1 , | ; | ; , , ; ; ; , ; , , ; , ; , , ; , ; | , ;| ; . (4.1.8)
t t t t t
t t t t
t t t
t t t t t t t t
t t t t t t t
P y S j
f y
P y S j P
P P y
P y S j
P y P S j y
P y
P S j y
P S j
ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ − − − − − − − − − − − = = = ⋅ = = = = = = = =
Sehingga berdasarkan persamaan (4.1.6), (4.1.7) dan (4.1.8) diperoleh
(
)
(
(
)
)
(
)
(
)
1 1 | 1 | | 1 , | ; | ; | ; ˆˆ . (4.1.9)
ˆ
t t t t t
t t t t t t t
t t t
P y S j
P S j
f y ϒ θ ϒ θ ϒ θ − − − − = = = ⊗ = ′ ⊗ ξ η ξ
1 ξ η
(
)
(
)
(
) (
)
1| 1 2 1 1 2 1 1ˆ 1| ;
1, | ;
1| , ; | ;
t t t t
t t t j
t t t t t
j
P S
P S S j
P S S j P S j
ϒ θ ϒ θ ϒ θ ϒ θ + + + = + = = = = = = = = = ⋅ =
∑
∑
ξ(
)
( ) ( ) 2 1 | 1 2 1 | 1 ˆ 1| ; ˆ j t t t t jj j t t j
P S S j
p θ ξ ξ + = = = = = ⋅ =
∑
∑
(1) ( 2)
11 | 12 |
1|
(1) (2)
21 | 22 |
(1) | 11 12
( 2)
21 22 |
| ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ .
t t t t t t
t t t t t t t t t t p p p p p p p p ξ ξ ξ ξ ξ ξ + ⎡ ⋅ + ⋅ ⎤ ⎢ ⎥ = ⎢ ⋅ + ⋅ ⎥ ⎣ ⎦ ⎡ ⎤ ⎡ ⎤ =⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ = ⋅ ξ P ξ | |
ˆ m ˆ
t m t+ = ⋅ t t
ξ P ξ . (4.1.10) Fungsi log-likelihood L
( )
θ untuk data yang diamati Yt dapat dihitung dengan cara( )
(
(
) (
) (
)
)
(
)
1 0 2 1 1
1 1
log | ; | ; | ;
log | ; .
t t T
t t t
f y f y f y
f y θ ϒ θ ϒ θ ϒ θ ϒ θ − − = = =
∑
L (4.1.11) Salah satu pendekatan yang digunakan untuk memilih nilai awal bagi ξˆt t|−1adalah denganmembuat ξˆ1|0sama dengan vektor peluang tak
bersyarat π=
[
π1 π2]
yang memenuhi sifatergodic, yaitu
1 2 1.
π π
=
+ =
π Pπ
Berdasarkan persamaan (4.1.7) diperoleh
(
)
(
) (
)
(
) (
)
1 1 1 1 1 | ;1 | ; | 1, ;
2 | ; | 2, ;
t t
t t t t t t t t t t
f y
P S f y S
P S f y S
ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ − − − − − = = ⋅ = + = ⋅ =
(
)
(
)
(
)
(
)
2 1 1 11 2
2 2 2 1
1 2
1
1| ; exp
2 2
1
2| ; exp .
2 2 t t t t t t t t
y c y
P S
y c y
P S φ ϒ θ σ πσ φ ϒ θ σ πσ − − − − − − − − ⎧− ⎫ ⎪ ⎪ = = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ ⎧− ⎫ ⎪ ⎪ + = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ (4.1.12) 4.2 Pendugaan Parameter θ
Penduga kemungkinan maksimum bagi θ diperoleh dengan memaksimumkan:
( )
(
1)
1
log | ;
T t t t f y θ ϒ − θ = =
∑
L .Untuk memperoleh nilai c cˆ ˆ1, 2, ,φ φˆ ˆ1 2 dan 2 ˆ σ yang memaksimumkan fungsi log-likelihood
Untuk memperoleh nilai cˆ1 dan cˆ2 , berdasar-kan persamaan (4.1.12) diperoleh
(
)
(
)
(
)
(
)
(
) (
)(
)
1 1 2 1 1 11 2
1 1 1 2
1 1 1
1 1 2
| ;
1
1| ; exp
2 2
1| ; | 1, ;
t t
t t t t
t t
t t t t t t t
c y
f y c
y c y
P S y
y c y
P S f y S
φ ϒ θ φ ϒ θ σ πσ σ φ ϒ θ ϒ θ σ − − − − − − − − − − − − − ∂ ∂ ⎧− ⎫ ⎪ ⎪ = = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ ⋅ = = =
( )
1 0 c θ ∂ = ∂ L(
)
(
1)
1 1 1
| ; 1 0 | ; T t t t t t
f y
f y c
ϒ θ ϒ θ − = − ∂ ⋅ = ∂
∑
(
) (
)
(
)
(
)
1 1 1 11 1 1
2
1| ; | 1, ;
| ;
0
T
t t t t t
t t t
t t
P S f y S
f y
y c y
ϒ θ ϒ θ ϒ θ φ σ − − = − − − − ⎡ = ⋅ = ⎢ ⎢⎣ ⎤ ⋅ ⎥= ⎦
∑
(
) (
)
(
)
(
)
(
) (
)
(
)
1 1 1 1 1 1 1 1 1 1 11| ; | 1, ;
| ;
1| ; | 1, ;
| ;
T
t t t t t
t t
t t t
T
t t t t t
t t t
P S f y S
y y
f y
P S f y S
c f y ϒ θ ϒ θ φ ϒ θ ϒ θ ϒ θ ϒ θ − − − = − − − = − = ⋅ = ⋅ − = ⋅ = =
∑
∑
(
) (
)
(
)
(
)
(
) (
)
(
)
1 1 1 1 1 1 1 1 1 1 1 ˆ ˆ1| ; | 1, ;
ˆ | ;
ˆ .
ˆ ˆ
1| ; | 1, ;
ˆ | ;
T t t t t t
t t
t t t
T
t t t t t
t t t
P S f y S
y y
f y c
P S f y S
f y ϒ θ ϒ θ φ ϒ θ ϒ θ ϒ θ ϒ θ − − − = − − − = − = ⋅ = ⋅ − = = ⋅ =
∑
∑
(4.2.1) Dengan cara yang sama diperoleh:(
) (
)
(
)
(
)
(
) (
)
(
)
1 1 2 1 1 1 2 1 1 1 1 ˆ ˆ2| ; | 2, ;
ˆ | ;
ˆ .
ˆ ˆ
2| ; | 2, ;
ˆ | ;
T
t t t t t
t t
t t t
T t t t t t
t t t
P S f y S
y y
f y c
P S f y S
f y ϒ θ ϒ θ φ ϒ θ ϒ θ ϒ θ ϒ θ − − − = − − − = − = ⋅ = ⋅ − = = ⋅ =
∑
∑
(4.2.2)Untuk memperoleh nilai φˆ1 dan φˆ2 , berdasar-kan persamaan (4.1.12) diperoleh
(
)
(
)
(
)
(
)( )
1 1 2 1 1 11 2
1 1 1 1
2
| ;
1
1| ; exp
2 2
t t
t t t t
t t t
f y
y c y
P S
y c y y
ϒ θ φ φ ϒ θ σ πσ φ σ − − − − − − − − − ∂ ∂ ⎧− ⎫ ⎪ ⎪ = = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ ⋅
(
) (
)
(
)( )
1 11 1 1 1
2
1| ; | 1, ;
t t t t t t t t
P S f y S
y c y y
ϒ θ ϒ θ φ σ − − − − − − = = = ⋅
( )
1 0 θ φ ∂ = ∂ L(
)
(
1)
1 1 1
| ; 1 0 | ; T t t t t t
f y f y ϒ θ ϒ θ φ − = − ∂ ⋅ = ∂
∑
(
) (
)
(
)
(
)( )
1 1 1 11 1 1 1
2
1| ; | 1, ;
| ;
0
T
t t t t t
t t t
t t t
P S f y S
f y
y c y y
ϒ θ ϒ θ ϒ θ φ σ − − = − − − − − ⎡ = ⋅ = ⎢ ⎢⎣ ⎤ ⋅ ⎥= ⎦
∑
(
) (
)
(
)
(
)( )
(
) (
)( )
(
)
1 1 1 1 1 1 21 1 1
1
1 1
1| ; | 1, ;
| ;
1| ; | 1, ;
| ;
T
t t t t t
t t
t t t
T
t t t t t t
t t t
P S f y S
y c y
f y
P S f y S y
f y ϒ θ ϒ θ ϒ θ ϒ θ ϒ θ φ ϒ θ − − − = − − − − = − = ⋅ = ⋅ − = ⋅ = =
∑
∑
(
) (
)
(
)
(
)( )
(
) (
)
( )
(
)
1 1 1 1 1 1 1 21 1 1
1 1
ˆ ˆ
1| ; | 1, ;
ˆ ˆ
| ;
ˆ .
ˆ ˆ
1| ; | 1, ;
ˆ | ;
T
t t t t t
t t
t t t
T t t t t t t
t t t
P S f y S
y c y f y
P S f y S y
f y ϒ θ ϒ θ ϒ θ φ ϒ θ ϒ θ ϒ θ − − − = − − − − = − = ⋅ = ⋅ − = = ⋅ =
∑
∑
(4.2.3) Dengan cara yang sama diperoleh(
) (
)
(
)
(
)( )
(
) (
)
( )
(
)
1 1 2 1 1 1 2 21 1 1
1 1
ˆ ˆ
2| ; | 2, ;
ˆ ˆ
| ;
ˆ .
ˆ ˆ
2| ; | 2, ;
ˆ | ;
T
t t t t t
t t
t t t
T
t t t t t t
t t t
P S f y S
y c y f y
P S f y S y
Untuk memperoleh nilai σˆ2, berdasarkan persamaan (4.1.12) diperoleh
(
)
(
)
(
)
(
)
(
)
(
)
1 2 2 2 11 3 2
1 2 1 1 2 2 1 4 | ; 1
| ; exp
2 2 2
1
| ; exp
2 2
2
t t
t j j t t t
j
t j j t t t
t j j t
f y
y c y
P S j
y c y
P S j
y c y
ϒ θ σ φ ϒ θ σ σ π φ ϒ θ σ σ π φ σ − − − = − − − − − − − − − ∂ ∂ ⎡ ⎧⎪− ⎫⎪ ⎢ = − = ⎨ ⎬ ⎢ ⎪ ⎪ ⎢ ⎩ ⎭ ⎣ ⎛ ⎧⎪− ⎫⎪ ⎜ + = ⎨ ⎬ ⎜⎜ ⎪⎩ ⎪⎭ ⎝ ⎤ ⎞ ⎥ ⎟ ⋅ ⎥ ⎟ ⎥ ⎠⎦
∑
(
)
(
)
(
)
2 2 1 1 2 1 2 1 2 4 1| ; exp
2 2
1
2 2
t j j t t t
j
t j j t
y c y
P S j
y c y
φ ϒ θ σ σ π φ σ σ − − = − − − − − ⎡ ⎧⎪− ⎫⎪ ⎢ = ⎢ = ⎨ ⎬ ⎪ ⎪ ⎢ ⎩ ⎭ ⎣ ⎤ ⎛− ⎞ ⎥ ⎜ ⎟ ⋅ + ⎥ ⎜ ⎟ ⎥ ⎝ ⎠ ⎦
∑
(
) (
)
(
)
2 1 1 1 2 1 2 4 | ; | , ; 1 2 2t t t t t j
t j j t
P S j f y S j
y c y
ϒ θ ϒ θ φ σ σ − − = − − − = ⎡⎣ = = ⎤ ⎛ − ⎞ ⎥ ⎜ ⎟ ⋅ + ⎥ ⎜ ⎟ ⎥ ⎝ ⎠ ⎦
∑
(
) (
)
(
)
2 1 1 1 2 2 1 4 4 | ; | , ; 2 2t t t t t j
t j j t
P S j f y S j
y c y
ϒ θ ϒ θ φ σ σ σ − − = − − − = ⎡⎣ = = ⎤ ⎛− ⎞ ⎥ ⎜ ⎟ ⋅ + ⎥ ⎜ ⎟ ⎥ ⎝ ⎠ ⎦
∑
( )
2 0 θ σ ∂ = ∂ L(
)
(
2 1)
1 1 | ; 1 0 | ; T t t t t t
f y f y ϒ θ ϒ θ σ − = − ∂ ⋅ = ∂
∑
(
) (
)
(
)
(
)
(
)
2 1 11 1 1
2 2 1 | ; | , ; | ; 0 t t T
t t t t t
t j t t
t S S t
P S j f y S j
f y
y c y
ϒ θ ϒ θ ϒ θ σ φ − − = = − − − − ⎡ = = ⎢ ⎢⎣ ⎤ ⋅ − + = ⎥⎦
∑∑
(
) (
)
(
)
(
) (
)
(
)
(
)
2 1 1 21 1 1
2
2 1 1 1
1 1 1
| ; | , ; | ; | ; | , ; | ; t t T
t t t t t t j t t
T t t t t t t S t S
t j t t
P S j f y S j
f y
P S j f y S j y c y
f y ϒ θ ϒ θ σ ϒ θ ϒ θ ϒ θ φ ϒ θ − − = = − − − − = = − − − = = = = =
∑∑
∑∑
(
) (
)(
)
(
)
(
) (
)
(
)
2 21 1 1
1 1 1
2
2
1 1
1 1 1
ˆ ˆ ˆ ˆ | ; | , ; | ; ˆ . ˆ ˆ | ; | , ; ˆ | ; t t T
t t t t t t S S t
t j t t
T
t t t t t t j t t
P S j f y S j y c y
f y
P S j f y S j f y ϒ θ ϒ θ φ ϒ θ σ ϒ θ ϒ θ ϒ θ − − − = = − − − = = − − − = = = = =
∑∑
∑∑
(4.2.5) 4.3 Reestimasi Parameter MenggunakanAlgoritma EM
Karena persamaan (4.2.1) sampai (4.2.5) merupakan persamaan tak-linear, maka untuk mempermudah mencari solusi bagi ˆθ digunakan algoritma EM. Langkah-langkahnya sebagai berikut:
Langkah 1:
Tentukan banyaknya data (T) yang akan digu-nakan untuk perhitungan, tentukan juga nilai
(
y y y0, 1, 2, ,yT−1)
dan matriks transisi11 21 0 12 22 p p p p ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ P
Beri nilai awal bagi ˆθ yang dilambangkan
dengan
(
2)
0 1 2 1 2
ˆ c cˆ ˆ, , ,ˆ ˆ,ˆ
θ = φ φ σ .
Langkah 2:
Cari fungsi kerapatan bersyarat bagi yTuntuk
setiap t=1, 2, ,T dengan cara
(
)
(
)
(
)
(
)
1 1 21 1 1
2
2
2 2 1
2
| 1, ;
| 2, ;
1 exp 2 2 1 exp 2 2
η t t t t
t t t
t t t t
f y S
f y S
y c y
y c y
ϒ θ ϒ θ φ σ πσ φ σ πσ − − − − − − − − = ⎡ ⎤ = ⎢ ⎥ = ⎢ ⎥ ⎣ ⎦ ⎡ ⎧⎪− ⎫⎪⎤ ⎢ ⎨ ⎬⎥ ⎢ ⎪⎩ ⎪⎭⎥ ⎢ ⎥ = ⎧ ⎫ ⎢ ⎪− ⎪⎥ ⎢ ⎨ ⎬⎥ ⎢ ⎪⎩ ⎪⎭⎥ ⎣ ⎦ . Langkah 3:
Penarikan kesimpulan optimal dan peralaman untuk setiap waktu t pada contoh dapat diperoleh melalui iterasi:
3.1.Tentukan nilai awal bagi ξˆt t|−1yang dilambangkan dengan ξˆ1|0
(
)
(
)
(
)
(
)
(
)
(
)
1 | 1 2 1 1 11 2 2 2 1 2 1 2 | ; ˆ 1
1| ; exp
2 2
1
2| ; exp
2 2
1 ξ
t t t t t
t t t t
t t t t
f y
y c y
P S
y c y
P S ϒ θ η φ ϒ θ σ πσ φ ϒ θ σ πσ − − − − − − − − − − ′ = ⊗ ⎧− ⎫ ⎪ ⎪ = = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ ⎧− ⎫ ⎪ ⎪ + = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭
{
}
{
}
(
(
)
)
1 | 1
| | 1 1 ˆ ˆ 1 ; ˆ ˆ ˆ 2 ;
t t k t t t t t
t t t t t k
P S P S ϒ θ ϒ θ − − − − ⎡ = ⎤ ⊗ ⎢ ⎥ =⎢ ⎥= ′ ⊗ = ⎢ ⎥ ⎣ ⎦ ξ η ξ
1 ξ η