Pemodelan Nilai Tukar Rupiah terhadap $Us Menggunakan Hidden Markov*

(1)

JMA, VOL. 4, NO.2, DESEMBER, 2005, 13-19 13

PEMODELAN NILAI TUKAR RUPIAH TERHADAP $US MENGGUNAKAN HIDDEN MARKOV*

BERLIAN SETIAWATY dan DEWI NOVIYANTI SARI

Departemen Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor

Jl Meranti, Kampus IPB Darmaga, Bogor 16680 Indonesia

ABSTRAK. Perilaku nilai tukar Rupiah terhadap $US dari tahun 1998 sampai dengan 2005 dicoba dimodelkan dengan menggunakan Hidden Markov (Elliott, et. al. 1995) Pendugaan parameter model dilakukan mengunakan Metode

Maximum Likelihood dan pendugaan ulang menggunakan metode Expectation Maximization yang melibatkan perubahan ukuran. Hasil yang diperoleh kurang baik karena galat antara nilai harapan dengan nilai sebenarnya cukup besar.

Kata kunci: Rantai Markov, model Hidden Markov, metode

Expectation Maximization, perubahan ukuran.

1. PENDAHULUAN

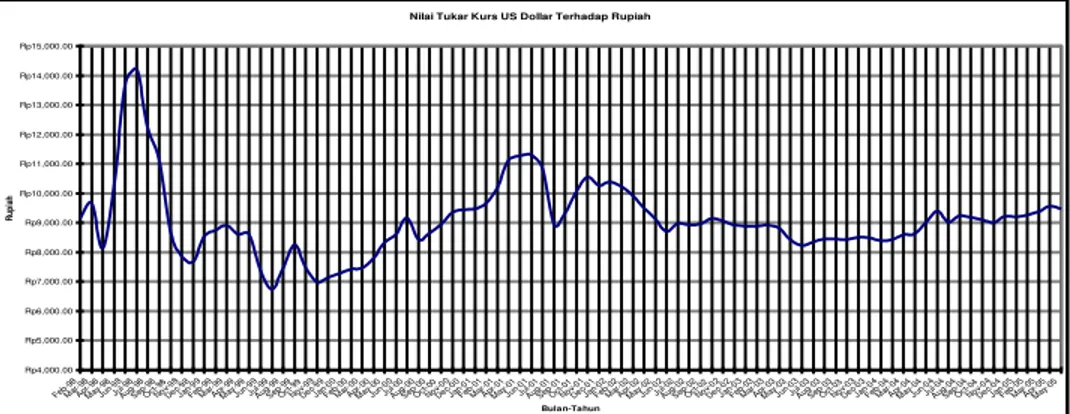
Nilai tukar Rupiah telah mengalami perubahan yang berfluktuasi. Bahkan pada saat krisis ekonomi pada tahun 1998 fluktuasi tersebut sangat besar dan tidak beraturan (Gambar 1.1). Hal ini tidak saja dipengaruhi oleh faktor ekonomi, tetapi juga oleh situasi politik dalam negeri yang tidak stabil, pergantian pemerintahan yang tidak berjalan dengan semestinya dan situasi keamanan yang kurang terjamin.

Nilai Tukar Kurs US Dollar Terhadap Rupiah

Rp4,000.00 Rp5,000.00 Rp6,000.00 Rp7,000.00 Rp8,000.00 Rp9,000.00 Rp10,000.00 Rp11,000.00 Rp12,000.00 Rp13,000.00 Rp14,000.00 Rp15,000.00 Fe b-98 Mar -98 Apr-9 8 May-9 8 Ju n-98 Jul-98 Au g-98 Se p-98 Oct-9 8 Nov-9 8 Dec-9 8 Ja n-99 Fe b-99 Mar -99 Apr-9 9 May-9 9 Ju n-99 Jul-99 Au g-99 Se p-99 Oct-9 9 Nov-9 9 Dec-9 9 Ja n-00 Fe b-00 Mar -00 Apr-0 0 May-0 0 Ju n-00 Jul-00 Au g-00 Se p-00 Oct-0 0 Nov-0 0 Dec-0 0 Ja n-01 Fe b-01 Mar -01 Apr-0 1 May-0 1 Ju n-01 Jul-01 Au g-01 Se p-01 Oct-0 1 Nov-0 1 Dec-0 1 Ja n-02 Fe b-02 Mar -02 Apr-0 2 May-0 2 Ju n-02 Jul-02 Au g-02 Se p-02 Oct-0 2 Nov-0 2 Dec-0 2 Ja n-03 Fe b-03 Mar -03 Apr-0 3 May-0 3 Ju n-03 Jul-03 Au g-03 Se p-03 Oct-0 3 Nov-0 3 Dec-0 3 Ja n-04 Fe b-04 Mar -04 Apr-0 4 May-0 4 Ju n-04 Jul-04 Au g-04 Se p-04 Oct-0 4 Nov-0 4 Dec-0 4 Ja n-05 Fe b-05 Mar -05 Apr-0 5 May-0 5 Bulan-Tahun R up ia h

Gambar 1.1 Nilai tukar Rupiah terhadap $US dari tahun 1998 s/ d 2005

(Sumber: Bank of Canada 21 Agustus 2005)

(2)

14 BERLIAN SETIAWATY DAN DEWI NOVIYANTI SARI

Untuk menjelaskan perilaku nilai tukar Rupiah tersebut dibangun suatu model matematis. Pada penelitian ini model Hidden Markov Elliott, et. al. (1995)dipilih karena model ini memperkenankan terjadinya perubahan parameter pada setiap state, sehingga diharapkan lebih fleksibel dalam menggambarkan perubahan-perubahan yang dramatis seperti yang terjadi pada nilai tukar Rupiah terhadap $US.

Pendugaan parameter model dilakukan menggunakan metode Maximum likelihood

dan metode expectation maximization serta data histories nilai tukar Rupiah. Dengan diketahuinya seluruh parameter, model Hidden Markov kemudian dipakai untuk menjelaskan perilaku nilai tukar Rupiah selama ini

Tulisan ini dimulai dengan pemodelan nilai tukar Rupiah menggunakan Hidden

Markov. Pada bagian 3 dibahas Pendugaan Parameter model. Pada bagian 4 dibahas interpretasi model nilai tukar Rupiah. Sebagai penutup disertakan pula kesimpulan dan saran.

2. MODEL HIDDEN MARKOV

Pada bagian ini kita memodelkan perilaku nilai tukar Rupiah terhadap $US dalam kurun waktu dari Februari 1998 sampai dengan Mei 2005, menggunakan model

Hidden Markov Elliott, et. al. (1995).

Faktor-faktor yang menyebabkan terjadinya perubahan nilai tukar Rupiah terhadap $US diasumsikan sebagai state dari suatu rantai Markov

{

X

k

}

. Misalkan banyaknya

faktor tersebut adalah N. Pada setiap state,data nilai tukar Rupiah dibangkitkan oleh peubah acak

Y

_k yang menyebar dengan sebaran tertentu pada ruang peluang

( ,

:

F

, )

P

.

Misalkan bahwa hubungan antara

{

X

k

}

dan

{ }

Y

k ditentukan oleh persamaan:

1 1 1

,

1

k k k k k k k

X

AX

V

Y

c X

V

X

Z

k

••

di mana

ƒ

^ `

X

k adalah rantai Markov dengan matriks transisi

A

(

a

ji

)

N Nu , di mana aji = P(Xk = ejGXk-1 = ei) , i, j = 1, 2, ..., N.

ƒ

V

k ₁ adalah martingale increments.

ƒ

Z

k adalah peubah acak yang bebas stokastik identik menyebar N(0,1).

ƒ 1

, ,...,

2

N N

c

c c

c

•ƒ

.

ƒ

V

i

!

0,

i

1, 2,..., .

N

Asumsikan bahwa penyebab perubahan nilai tukar Rupiah tidak diketahui atau tidak diamati. Sehingga proses

{

X

k

}

tersembunyi (hidden) di balik data pengamatan nilai

tukar Rupiah

{ }

Y

k . Jadi pasangan

^

X Y

k

,

k

`

merupakan model Hidden Markov Elliott et. al. (1995).

Parameter model di atas berbentuk

^

(

a

ji

), 1

i j

,

N c

; , 1

i

N

; , 1

i

N

`

T

d

d d

V

d d

.

Menggunakan data pengamatan nilai tukar Rupiah

Y

_k pada kurun waktu dari Februari 1998 sampai dengan Mei 2005 parameter model akan diduga. Proses pendugaan parameter menggunakan metode maximum likelihood dan metode expectation

(3)

JMA, VOL. 4, NO.2, DESEMBER, 2005, 13-19 13

maximization yang algoritmanya diambil dari Setiawaty dan Kristina (2005). Dalam proses pendugaan parameter model, diambil N = 2.

Data nilai tukar Rupiah yang diperoleh dari Bank of Canada (21 Agustus 2005) adalah rataan nilai tukar Rupiah harian. Untuk diskretisasi waktu dan untuk mengurangi banyaknya data, diambil rataan perbulan dari data harian tersebut. Sehingga

Y

_k

menyatakan rataan nilai tukar Rupiah terhadap $US pada bulan ke

k k

,

••

, dengan

1 k

adalah bulan Februari 1998. Sehingga dalam kurun waktu Februari 1998 sampai dengan Mei 2005 diperoleh 88 buah data.

3. PENDUGAAN PARAMETER MODEL 3.1 Metode Expectation Maximization (Metode EM)

Metode EM dikembangkan oleh Baum and Petrie (1966) dengan ide dasar sebagai berikut.

Misalkan

^

P

_T

:

T

•4

`

adalah koleksi ukuran peluang yang terdefinisi pada ruang

( , )

:

G

dan kontinu absolut terhadap

P

₀. Misalkan

Y

• G

. Definisikan fungsi

likelihood untuk menentukan penduga parameter

T

berdasarkan informasi

Y

sebagai 0 0

( )

dP

L

E

dP

T

ª

_«

º

_»

¬

Y

¼

dan penduga maksimum likelihood didefinisikan sebagai

Ö

_{arg max ( )}

L

T

•4

•

.

Secara umum penduga maksimum likelihood

T

Ö

sulit dihitung secara langsung. Algoritma EM memberikan suatu metode iteratif untuk mengaproksimasi

T

Ö

, dengan prosedur sebagai berikut.

Langkah 1: Set

p

0

dan pilih

T

Ö

₀. Langkah 2: [Langkah-E]

Set

T

Ö

p dan hitung

,

log

dP

Q

E

dP

T T T

T T

ª

«

º

»

«

»

¬

¼

Y

. Langkah 3: [Langkah-M]

Tentukan

Ö

p ₁

arg max

Q

,

T

T T

•4

•

.

Langkah 4:

p

m

p

1

Ulangi langkah 2 sampai kriteria berhenti dipenuhi. Catatan 3.3.1

1. Barisan

^

T

Ö

p

:

p

t

0 `

memberikan barisan

^

L

T

Ö

p

:

p

t

0

`

yang tak turun. 2. Menurut ketaksamaan Jensen,

1 1

Ö

_,

Ö

_{log (}

Ö

_{) log (}

Ö

₎

p p p p

Q

T

d

L

T

L

T

.

(4)

16 BERLIAN SETIAWATY DAN DEWI NOVIYANTI SARI 3.2 Algoritma untuk menduga parameter

Diketahui parameter model berbentuk

^

(

a

ji

), 1

i j

,

N c

; , 1

i

N

; ,1

i

N

`

T

d

d d

V

d d

.

Akan ditentukan parameter

^

`

Ö

_{( )}

_k

₍

_a

_Ö

_ji

_{( )), 1}

_k

_{i j}

_,

_{N c k}

_{; ( ), 1}

_Ö

_i

_N

_{; ( ),1}

_Ö

_i

_k

_i

_N

T

d

d d

V

d d

yang memaksimumkan pseudo-loglikelihood bersyarat seperti pada bagian 3.1. Algoritma untuk memperoleh parameter tersebut yang diperoleh dari Setiawaty dan Kristina (2005) adalah sebagai berikut.

Algoritma untuk menentukan parameter

T

Ö

( )

k

Langkah 1: Tetapkan N = 2 (banyaknya state), M = 88 (banyaknya data) Input data

{ }

y

k .

Langkah 2: Tetapkan Nilai awal

1 1 1

( )

(

)

( )

.

i N ji N N i N i N

A

a

c

S

V

u u u u

Catatan:

S

E X

> @

₀ dan memenuhi

A

S S

. Langkah 3: Lakukan untuk

l

0 sampai dengan

M

1. Tetapkan 0 0 0 0 0 0 0 0 2 0 0

, di mana

vektor unit di

0

0 ( )

0 (

)

0.

N i i i rs r

a

Ae

e

X

O

y

J

S

J

J W

ƒ

s r

J

(5)

JMA, VOL. 4, NO.2, DESEMBER, 2005, 13-19 13 a. Hitung penduga rekursif

1 1 1 1 1, 1 1 , 1 1 1 1 1 1, 1 1 1, 1 1 , 1 1 1 1 1 ( ) ( ), ( ) ( ) ( ), ( ) ( ), ( ) ( ) ( ), 1 ( ) ( ), ( ) ( ), ( ) ( N i k k k k k i i N rs rs i r k k k k k k k i k k k sr s i rs rs k k k k k N r r i r k k k k k k k i k k k r i r k k X X y a y a X y a e O O y a X y a O

J

* * * * *

¦

J J J J 1, 1 1 1, 1 1 , 1 1 1 1 1 1 1, 1 1 2 2 2 1, 1 1 , 1 1 1 1 ) ( ), 1 ( ( )) ( ( )), ( ) ( ), ( ) ( ( )) ( ( )), 1 ( ( )) ( ( )), ( ) ( ), ( ) r k k k N r r i r k k k k k k k i k k k k r i r r k k k k k N r r i r k k k k k k k i k k k k r i k O y y y a X y y a y y y y y a X y y a

J

W

J

W

J

W

J

W

J

W

J

W

J

* * * *

¦

2 2 1( 1( )) 1, 1( 1( )), 1 r r k y k k k y

W

J

W

di mana:

:

k k k y c

y

e

y

V

I

V I

˜ ˜ ˜ ˜ ˜

§

· ¨

¸

©

¹

*

( )

I

˜

adalah fungsi kepadatan peluang N(0,1).

1 1 1

:

1, 1 1

k

H

k

X

k k k

H

k

J

1 (1,...,1,1,1,...,1)

_•ƒ

N . a. Hitung penduga parameter

1 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 1 1

Ö

(

1)

( )

Ö

(

1)

(

)

2 ( )

Ö

(

1)

.

rs k k sr r k k r k k r r k k i i i k k i k k i k k i _i k k

a

k

O

y

c k

O

y

c

y

c

O

k

O

J

W

J

W

J

W

J

V

J

b. Tuliskan

Ö

₍

₁₎

_Ö

₍

₁₎

Ö

(

1)

Ö

(

1)

Ö

(

1)

Ö

(

1) .

sr r i

A k

a

k

c k

k

V

d. Tentukan

S

Ö

(

k

1) dari persamaan (

A k

Ö

1) (

S

Ö

k

1)

S

Ö

(

k

1)

. e. Ulangi langkah a sampai dengan d untuk k berikutnya. 3. Beri nilai

(6)

18 BERLIAN SETIAWATY DAN DEWI NOVIYANTI SARI

Ö

_{( )}

Ö

( )

Ö

( ).

A

A k

c

c k

k

V

m

4. Ulangi langkah 1 sampai dengan 3 untuk l berikutnya. Langkah 4: Untuk

k

1 sampai dengan

M

, cetak

A k

Ö

( ), (k), ( ), ( ), (

S

Ö

c k

Ö

V

Ö

k

J

k

X

k

)

4. INTERPRETASI MODEL

Dari algoritma di atas dibuat programnya menggunakan Mathematica 5.2.

Dari hasil run program pada bagian 3 untuk

N

2

diperoleh parameter model sebagai berikut.

0.071 0.152

Ö

_,

_Ö

_{9094.365 9094.613 ,}

_Ö

_{2277.793 1659.249}

0.929 0.848

A

§

_¨

· _¸

c

V

©

¹

. (4.1) Pada state-1, nilai tukar Rupiah terhadap $US mempunyai rataan

c

Ö

₁

9094.365

dan simpangan

V

_Ö

₁

2277.794

. Pada state-2, nilai tukar Rupiah terhadap $US mempunyai rataan

c

Ö

₁

9094.613

dan simpangan

V

Ö

₁

1659.249

.

Gambar 4.1. Grafik Peluang

P X

k

2 |

y y

₁

,

₂

,...,

y

k

Dari Grafik 4.1. terlihat bahwa jika

P X

k

2 |

y y

₁

,

₂

,...,

y

k mendekati 1 maka nilai Rupiah mengalami lonjakan yang cukup berarti. Hal ini menunjukkan bahwa nilai

1 2

2 |

,

,...,

k k

P X

y y

y

dapat dijadikan indikator untuk melihat terjadi lonjakan drastis pada nilai tukar Rupiah.

k = 1 k = 20 k = 40 k = 60 k = 80

Feb-98 Sep-99 Mei-01 Jan-03 Sep-04

Bulan-Tahun

P

eluang

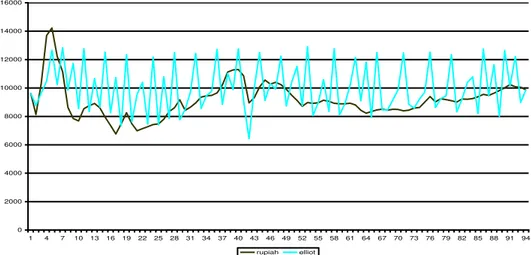
0,84 0,80 0,76 0,72

(7)

JMA, VOL. 4, NO.2, DESEMBER, 2005, 13-19 13 Perbandingan nilai tukar Rupiah dengan nilai harapannya yang ditunjukkan oleh Grafik

4.2 berikut. Karena galat antara nilai tukar Rupiah dengan nilai harapannya cukup besar, maka nilai harapan dari model Elliott ini tidak dapat dipakai sebagai alat untuk memodelkan perilaku nilai tukar Rupiah terhadap US Dollar.

Gambar 4.2. Grafik nilai tukar Rupiah terhadap US Dollar menggunakan model Elliot

6. KESIMPULAN DAN SARAN

Dari uraian di atas terlihat bahwa menggunakan model Elliott et.al. (1995), pemodelan nilai tukar Rupiah tingkat akurasinya tidak terlalu baik, oleh sebab itu perlu penelitian lanjutan menggunaan model lain, misalnya dengan memperhitungkan nilai tukar sebelumnya sehingga merupakan suatu deret waktu seperti model Hamilton (1994).

DAFTAR PUSTAKA

[1]. Baum,L.E. and Petrie, T. 1966. Statistical inference for probabilistic functions of finite state Markov chains. Annals of the Institute of Statistical Mathematics, 37:1554-1563.

[2]. Elliot, R. J., Aggoun, L. dan Moore, J. B. 1995. Hidden Markov models, Springer Verlag, New York.

[3]. Hamilton, J. D. 1994. Time Series Analysis. Princeton University Press, New Jersey.

[4]. Setiawaty, B. dan Kristina, L. 2005. Pendugaan parameter model Hidden Markov.

Jurnal Matematika dan Aplikasinya, Vol: 4, No.1.

0 2000 4000 6000 8000 10000 12000 14000 16000 1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 61 64 67 70 73 76 79 82 85 88 91 94 rupiah elliot