Kajian numerik model hidden markov satu waktu sebelumnya untuk nilai tukar Rupiah terhadap Dolar Amerika

KAJIAN NUMERIK MODEL

HIDDEN

MARKOV SATU

WAKTU SEBELUMNYA UNTUK NILAI TUKAR RUPIAH

TERHADAP DOLAR AMERIKA

AULIA RETNONINGTYAS

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa skripsi berjudul Kajian Numerik Model Hidden Markov Satu Waktu Sebelumnya untuk Nilai Tukar Rupiah terhadap Dolar Amerika adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

ABSTRAK

AULIA RETNONINGTYAS. Kajian Numerik Model Hidden Markov Satu Waktu Sebelumnya untuk Nilai Tukar Rupiah terhadap Dolar Amerika. Dibimbing oleh BERLIAN SETIAWATY dan RUHIYAT.

Model hidden Markov adalah model yang terdiri atas pasangan proses stokastik yaitu proses observasi dan faktor penyebab proses observasinya, di mana faktor penyebab observasinya tidak diamati secara langsung dan diasumsikan membentuk rantai Markov. Model hidden Markov satu waktu sebelumnya merupakan model hidden Markov yang proses observasinya dipengaruhi oleh faktor penyebab kejadian saat ini dan satu waktu sebelumnya. Model hidden Markov satu waktu sebelumnya dapat diaplikasikan untuk nilai tukar rupiah terhadap dolar Amerika di mana nilai tukar rupiah sebagai proses observasinya dan faktor penyebabnya sebagai rantai Markov. Parameter model diduga dengan menggunakan metode Maximum Likelihood dan perhitungannya menggunakan metode iteratif Expectation Maximization (EM). Dengan menggunakan nilai awal yang diperoleh secara trial and error Santoso (2008) dapat memodelkan nilai tukar rupiah terhadap dolar Amerika dengan MAPE 14.58%. Pada tugas akhir ini nilai awal dibangkitkan secara terstruktur pada selang tertentu sehingga keakuratan model meningkat. MAPE yang diperoleh 4.13% dengan hanya satu kali iterasi.

Kata kunci: algoritme EM, MAPE, model hidden Markov, nilai tukar Rupiah

ABSTRACT

AULIA RETNONINGTYAS. Numerical Study if the Previous Time Hidden Markov Model for the Exchange Rate of Rupiah to US Dollar. Supervised by

BERLIAN SETIAWATY and RUHIYAT.

Hidden Markov model is a model that consists of a pair stochastic processes, ie: the process of observation and the cause factors of the observation, where the cause factors of the observation are not observed directly and assumed to be a Markov chain. The previous time hidden Markov model is a hidden markov model that the observation process is influenced by current events and one previous time cause factors. The previous time hidden Markov model can be applied to the exchange rate of rupiah to US dollar, where the exchange rate of rupiah to US dollar is the observation and the contributing factor is a Markov chain. Parameters of the model are estimated using the maximum likelihood method and calculated using expectation maximization (EM) iterative algorithm. Using the initial value obtained by trial and error, Santoso (2008) was able to model the exchange rate of rupiah to US dollar with MAPE 14.58%. In this paper, the initial value is structuredly generated on a specific interval so that the accuracy of model increases. Retrieved MAPE is 4.13% with only one iteration.

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

KAJIAN NUMERIK MODEL

HIDDEN

MARKOV SATU

WAKTU SEBELUMNYA UNTUK NILAI TUKAR RUPIAH

TERHADAP DOLAR AMERIKA

AULIA RETNONINGTYAS

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya, sehingga karya ilmiah berjudul Kajian Numerik Model Hidden Markov Satu Waktu Sebelumnya untuk Nilai Tukar Rupiah terhadap Dollar Amerika ini dapat diselesaikan. Terima kasih sebesar-besarnya penulis ucapkan kepada:

1. Dr Berlian Setiawaty, MS selaku dosen pembimbing I dan Ruhiyat, MSi selaku dosen pembimbing II atas semua ilmu, bimbingan, kesabaran serta motivasi yang telah diberikan selama penulisan karya ilmiah ini.

2. Ir Ngakan Komang Kutha Ardana, MSc selaku dosen penguji yang telah banyak memberikan saran.

3. Dosen-dosen di Departemen Matematika atas semua ilmu yang diberikan, serta staf dan pegawai di Departemen Matematika atas semua bantuan dan layanannya selama ini.

4. Mama, Papa, Tika dan Widy atas doa, dukungan, semangat, kesabaran dan kasih sayang yang selalu diberikan kepada penulis. Serta seluruh keluarga besar yang ada di Jakarta, Depok, Bogor dan Malang atas doa, dukungan dan kasih sayangnya.

5. Atih, Asti, Benz, Uci, Anggi, Je, Devi dan sahabat-sahabat tersayang yang ada di Malang, Surabaya dan Depok lainnya atas perhatian, semangat, dukungan dan doa yang selalu diberikan.

6. Deva, Sari, Della, Devi, Pandi, Dian, Rofi, Denda, Rizky, Mutia, Rachma, Sri, Ayung, Fajar, Imam, Lukman, Yogie dan semua teman-teman Matematika 44 lainnya, serta kakak-kakak dan adik-adik Matematika 42, 43, 45, 46, dan 47 atas dukungan dan doanya.

7. Teman-teman IPB dari departemen lainnya.

8. Semua pihak yang telah membantu dalam proses penyusunan karya ilmiah ini. Semoga karya ilmiah ini bermanfaat.

DAFTAR ISI

DAFTAR GAMBAR vi

DAFTAR LAMPIRAN vi

PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 1

TINJAUAN PUSTAKA 2

Ruang Contoh, Kejadian, dan Peluang 2

Peubah Acak dan Sebaran 3

Nilai Harapan 5

Rantai Markov 6

Algoritme Expectation Maximization (EM) 8

Mean Absolute Percentage Error (MAPE) 9

MODEL DERET WAKTU HIDDEN MARKOV SATU WAKTU

SEBELUMNYA 9

Model Hidden Markov 9

Model Hidden Markov Satu Waktu Sebelumnya 10

PEMODELAN NILAI TUKAR RUPIAH TERHADAP DLLAR AMERIKA

DAN KAJIAN NUMERIKNYA 18

Data Input Nilai Tukar Rupiah 18

Model Hidden Markov Satu Waktu Sebelumnya 19

Penentuan Nilai Awal untuk Penduga Parameter Model Hidden Markov Satu

Waktu Sebelumnya 19

Hasil Progam 20

SIMPULAN 21

DAFTAR PUSTAKA 21

LAMPIRAN 23

DAFTAR GAMBAR

1 Perubahan nilai tukar rupiah terhadap dolar Amerika per bulan 19 2 Plot persamaan baru dari data yang ada dikurangi rataannya 20 3 Perubahan nilai tukar rupiah terhadap dolar Amerika per bulan dan nilai

dugaan yang didapatkan 21

DAFTAR LAMPIRAN

1 Bukti Lema 1 23

2 Bukti persamaan (13) sampai dengan (16) 24

3 Progam untuk mencari nilai dugaan dan MAPE minimum

menggunakan software Mathematica 9.0 37

PENDAHULUAN

Latar Belakang

Nilai tukar mata uang sering digunakan untuk mengukur level perekonomian suatu negara. Nilai tukar mata uang memegang peranan penting dalam perdagangan antar negara, di mana hampir sebagian besar negara-negara di dunia saat ini terlibat dalam aktivitas ekonomi pasar bebas. Bagi perusahaan investasi dan investor mancanegara, nilai tukar mata uang akan berdampak pada return dan portofolio investasinya. Salah satu nilai tukar mata uang yang berpengaruh di negara ini adalah nilai tukar rupiah terhadap dolar Amerika. Faktor-faktor yang mempengaruhi nilai tukar rupiah terhadap dolar Amerika antara lain perbedaan tingkat suku bunga, rasio ekspor dan impor, perbedaan tingkat inflasi serta kestabilan politik negara. Penting bagi pemerintah untuk mengetahui lebih dini perubahan nilai tukar rupiah terhadap dolar Amerika agar dapat mengantisipasi serta menentukan kebijakan ekonomi yang akan diambil selanjutnya.

Model hidden Markov terdiri atas sepasang proses stokastik yaitu proses observasi dan proses yang mempengaruhi terjadinya proses observasi yang diasumsikan membentuk rantai Markov dan diasumsikan tidak diamati. Model hidden Markov dicirikan oleh beberapa parameter yaitu peluang awal, peluang transisi, dan peluang observasinya.

Nilai tukar rupiah terhadap dolar Amerika dapat dimodelkan dengan model hidden Markov jika proses yang memengaruhi proses observasinya diasumsikan tidak diamati secara langsung dan membentuk rantai Markov. Dalam hal ini nilai tukar rupiah terhadap dolar Amerika sebagai proses observasinya dan faktor-faktor yang memengaruhi perubahannya sebagai proses yang memengaruhi proses observasinya.

Pada karya ilmiah ini akan dibahas model deret waktu hidden Markov satu waktu sebelumnya seperti yang dibahas pada karya ilmiah Santoso (2008). Pada model ini nilai tukar rupiah bergantung pada nilai tukar rupiah sebelumnya dan juga faktor penyebab perubahan nilai tukar pada saat ini dan satu waktu sebelumnya.

Perhitungan numerik yang dilakukan oleh Santoso (2008) menggunakan nilai awal yang ditentukan secara trial and error yang menghasilkan galat minimum 0.2934 (0.0032%) dan galat maksimum 807.6963 (5.6773%). Pada tugas akhir ini akan dicari cara menentukan nilai awal yang lebih efisien sehingga diharapkan diperoleh galat yang lebih kecil. Perhitungan numerik yang dilakukan dalam karya ilmiah ini menggunakan software Mathematica 9.0. Kelebihan progam tersebut adalah waktu kerja yang lebih efisien serta mempermudah dalam analisis data karena sudah dilengkapi dengan fungsi-fungsi yang mudah untuk digunakan.

Tujuan Penelitian

2

awal yang lebih tepat sehingga modelnya lebih akurat jika dibandingkan dengan Santoso (2008).

TINJAUAN PUSTAKA

Pada bagian ini akan diuraikan beberapa definisi dan penjelasan istilah-istilah yang digunakan dalam karya ilmiah ini.

Ruang Contoh, Kejadian, dan Peluang

Percobaan Acak

Dalam suatu percobaan seringkali dilakukan pengulangan yang biasanya dilakukan dalam kondisi yang sama. Semua kemungkinan hasil yang akan muncul dapat diketahui, namun hasil pada percobaan berikutnya tidak dapat diketahui dengan tepat. Percobaan semacam ini, yang dapat diulang dalam kondisi yang sama, disebut percobaan acak. (Ross 1996)

Ruang Contoh dan Kejadian

Himpunan dari semua kemungkinan hasil dari suatu percobaan acak disebut ruang contoh, dinotasikan dengan Ω. Suatu kejadian A adalah himpunan bagian dari Ω. (Grimmet dan Stirzaker 2001)

Medan-�

Medan-� adalah suatu himpunan yang anggotanya terdiri atas himpunan bagian dari Ω yang memenuhi kondisi berikut:

3 himpunan berhingga. Suatu fungsi � ∶Ω→S disebut peubah acak diskret jika memenuhi sifat ∀� ⊆ �berlaku {� ∈Ω∶ �(�) ∈ �}∈ ℱ. (Ross 1996) massa peluang bersama dari peubah acak diskret X dan Y adalah suatu fungsi �:�×� →[0,1] yang didefinisikan oleh

���(�,�) =�(�= �,� =�),∀�,� ∈ �.

4

Jika � dan � merupakan peubah acak diskret, maka fungsi massa peluang bersyarat dari � jika diberikan � = �, terdefinisi untuk setiap �sedemikian sehingga�(�=�) > 0adalah �_�|�(�|�) =�(�_�=�,�=�)

(�=�) .(Ross 1996) Peubah Acak Kontinu

Peubah acak � disebut peubah acak kontinu jika fungsi sebarannya dapat dinyatakan sebagai �_�(�) = ∫ �_−∞� (�)�� untuk suatu fungsi �:ℝ →(0,∞) yang terintegralkan. Selanjutnya fungsi � =�_� disebut fungsi kepekatan peluang (probability density function) bagi X. (Ross 1996)

Fungsi Kepekatan Peluang Bersama

Misalkan X dan Y peubah acak kontinu, maka fungsi kepekatan peluang bersama dari X dan Y adalah �_��(�,�) =�2_�����(�,�).(Grimmet dan Stirzaker 2001)

Fungsi Kepekatan Peluang Marjinal

Misalkan X dan Y peubah acak kontinu yang menyebar bersama dengan fungsi sebaran �(�,�) dan fungsi kepekatan peluang bersama �(�,�). Fungsi kepekatan peluang marjinal dari peubah acak X dan Y adalah berturut-turut

��(�) = � �(�,�)��

Misalkan X dan Y peubah acak kontinu dengan fungsi kepekatan peluang marginal ��(�) > 0, maka fungsi kepekatan peluang bersyarat dari X dengan syarat �=�

adalah �_�|�(�|�) =���(�,�)

5 Nilai Harapan

Nilai Harapan Peubah Acak Diskret

Misalkan X adalah peubah acak diskret dengan fungsi massa peluang �_�(�) = �(�= �) maka nilai harapan dari X adalah �[�] =∑ ��_{� �}(�) asalkan jumlah tersebut konvergen mutlak. (Hogg and Craig 2014)

Nilai Harapan Peubah Acak Kontinu

Misalkan X adalah peubah acak kontinu dengan fungsi kepekatan peluang �_�(�) maka nilai harapan dari X adalah �[�] =∫ ��_−∞∞ _�(�)�� asalkan integralnya ada. (Hogg and Craig 2014)

Nilai Harapan Bersyarat

Misalkan X dan Y adalah peubah acak kontinu dan �_�|�(�|�) adalah fungsi kepekatan peluang bersyarat dari X dengan syarat � =�, maka nilai harapan dari X dengan syarat �=� adalah �[�|�= �] =_{∫ ��−∞}∞ _�|�(�|�)��. (Hogg dan Craig 2014)

Teorema Dasar Kalkulus Bagian 1

Jika f kontinu pada [�,�], maka fungsi g didefinisikan oleh g(�) = ∫ �_�� (�)�� , � ≤ � ≤ � adalah kontinu pada [�,�] dan terdiferensialkan pada (�,�) dan g′(�) =�(�). (Stewart 1998)

Himpunan dan Fungsi Konveks

Misalkan � ⊂ ℝ� adalah himpunan vektor. Maka S disebut sebagai himpunan konveks jika untuk semua �,�′ ∈ � dan � ∈[0,1] maka (1− �)�+��′ ∈ �. Misalkan f merupakan fungsi dengan peubah x yang terdefinisi pada himpunan konveks S. Maka f disebut sebagai fungsi konveks jika f memenuhi persamaan

��(1− �)�+��′� ≤(1− �)�(�) +��(�′). (Osborne 1997)

Fungsi Konveks

Misalkan f memiliki turunan kedua. f adalah fungsi konveks jika dan hanya jika ∇2_{�(�)≥ 0,∀� ∈ � dan merupakan strictly convex jika ∇}2_{�(�) > 0,∀� ∈ �.} (Osborne 1997)

Ketaksamaan Jensen

6

Rantai Markov

Ruang State

Misalkan � ⊂ ℝ merupakan himpunan nilai dari barisan peubah acak, maka � disebut ruang state. (Grimmet dan Stirzaker 2001)

Proses Stokastik

Proses stokastik �= {�_�,���} adalah suatu koleksi dari peubah acak yang memetakan suatu ruang contoh ٠ke suatu ruang state K. Jadi, untuk setiap t pada himpunan indeks T, St adalah suatu peubah acak. (Ross 1996)

Dalam hal ini anggap t sebagai waktu dan nilai dari peubah acak St sebagai state (keadaan) dari proses pada waktu t.

Rantai Markov dengan Waktu Diskret

Proses stokastik {�_�,�= 0,1,2, … }, dengan ruang state {1,2,3, … ,�}, disebut

Jadi untuk suatu rantai Markov, sebaran bersyarat dari sebarang state saat ini �_� dengan syarat state yang lalu �₀,�₁,�₂, … ,�_�−2 dan state sebelumnya �_�−1 adalah bebas terhadap semua state yang lalu, dan hanya bergantung pada state sebelumnya. Hal ini disebut sebagai sifat Markov (Markovian Property).

Proses di atas dapat digambarkan sebagai N-state rantai Markov dengan peluang transisi ��_����,� = 1,2,3, … ,�. Nilai dari �_�� menyatakan peluang bahwa, jika proses tersebut berada pada state i, maka berikutnya akan beralih ke state j. Karena �_�� adalah nilai peluang dan proses tersebut harus bertransisi, maka

1. 0≤ �_�� ≤ 1, untuk �,� ∈{1,2,3, … ,�}, dan 2. ∑�_�=1�_�� = 1, untuk � ∈ {1,2,3, … ,�}.

Peluang transisi ini dapat ditulis dalam bentuk matriks P yang disebut sebagai matriks transisi.

dengan j menyatakan baris dan i menyatakan kolom dari matriks P. Terakses

7

Kelas State

Kelas state dari suatu rantai Markov, adalah suatu himpunan takkosong � sehingga semua pasangan state yang merupakan anggota dari � berkomunikasi satu dengan yang lainnya, serta tidak ada state yang merupakan anggota � yang berkomunikasi dengan suatu state yang bukan anggota dari �. (Ross 1996)

Rantai Markov Tak Tereduksi

Rantai Markov disebut tak tereduksi jika hanya terdapat satu kelas state (satu gugus tertutup state), yaitu jika semua state berkomunikasi satu dengan yang lainnya. (Ross 1996)

First-Passage Time Probability �_��(�)

menyatakan peluang bahwa mulai dari state i, proses bertransisi untuk pertama kali ke state j terjadi pada waktu n. Peluang ini disebut first-passage time probability. Jadi untuk setiap � = 1,2,3, …

�_��(�) tidak habis dibagi d, dan d adalah bilangan bulat terbesar yang memenuhi sifat ini. Dengan kata lain, suatu state i disebut memiliki periode d jika d adalah persekutuan pembagi terbesar (the greatest common divisior) bagi n sehingga �_��(_�)

> 0.

2. Suatu state dengan periode = 1 disebut aperiodik, sedangkan state dengan periode ≥ 2 disebut periodik. (Ross 1996)

Positive Recurrent dan Null Recurrent

Suatu state disebut berulang positif (positive recurrent) jika state tersebut adalah berulang (recurrent) serta berlaku jika proses dimulai dari state i maka nilai harapan dari waktu sampai proses tersebut kembali ke state i adalah bilangan terhingga (finite). State recurrent yang tidak positive recurrent disebut null recurrent. (Ross 1996)

Ergodic

8

Rantai Markov Ergodic Tak Tereduksi

Untuk rantai Markov ergodic tak tereduksi lim_�→∞�_��(�) ada dan nilainya tak

disebut vektor peluang steady state atau sebaran steady state. Karena π adalah vektor peluang, maka harus memenuhi syarat bahwa semua unsurnya adalah bilangan tak negatif serta jumlah semua unsurnya adalah sama dengan satu. Sebaran steady state sering juga disebut sebaran stationer, atau sebaran setimbang (equilibrium distribution) dari rantai Markov yang bersangkutan. (Ross 1996)

Algoritme Expectation Maximization (EM)

Misalkan {�_�,� ∈ Θ} adalah himpunan ukuran peluang yang terdefinisi pada (Ω,ℱ) dan kontinu absolut terhadap �₀. Misalkan � ⊂ ℱ. Fungsi Likelihood yang digunakan untuk menghitung penduga parameter θ berdasarkan informasi � adalah

�(�) =�0���_���

0|��

. Penduga Maximum Likelihood (MLE) didefinisikan oleh

�� ∈arg max

�∈� �(�).

Umumnya MLE sulit dihitung secara langsung, oleh karena itu diperlukan suatu metode aproksimasi berulang, yakni algoritme Expectation Maximization (EM). Langkah-langkah dalam metode tersebut adalah:

1. Tentukan nilai awal parameter ��_� dengan �= 0,

2. Tentukan �∗ =��_� dan hitung �(�,�∗) dengan �(�,�∗) =�_�∗�������

9 3. Cari ��_�+1 ∈arg max�(�,�∗),

4. Ganti � dengan �+ 1 dan ulangi langkah 2 sampai 4 hingga kriteria hentinya tercapai, yaitu ketika selisih ��_�+1 dan ��_� kurang dari suatu bilangan yang sangat kecil. Bilangan tersebut dapat ditentukan sesuai dengan seberapa besar ketelitian yang diinginkan.

konveks, maka berdasarkan ketaksamaan Jensen dapat dihasilkan barisan ����,� ≥0�, yang merupakan fungsi Likelihood yang takturun yaitu

log����_�+1� −log���_� ≥ ����_�+1,��_�+1�.

Bentuk �(�,�∗) disebut Pseudo Likelihood bersyarat. (Elliot et al. 1995)

Mean Absolute Percentage Error (MAPE)

Mean Absolute Percentage Error (MAPE) adalah rataan persentase kesalahan absolut pada tiap periode dibagi dengan nilai observasi yang nyata untuk periode tersebut. Rumus MAPE adalah sebagai berikut

����= 100%

dengan n menyatakan banyaknya data yang digunakan, �_� menyatakan nilai yang sebenarnya, dan �_� menyatakan nilai dugaan. (Mynsbrugge 2010)

MODEL DERET WAKTU

HIDDEN

MARKOV SATU WAKTU

SEBELUMNYA

Model Hidden Markov

Model hidden Markov terdiri atas sepasang proses stokastik {�_�,�_�}. {�_�} dengan state {1,2, … ,�} adalah proses penyebab terjadinya {�_�} yang tidak diamati secara langsung dan membentuk rantai Markov. {�_�}adalah proses observasinya. Karakteristik {�_�} hanya bisa diamati melalui proses observasinya.

10

Peluang tak bersyarat proses yang tidak diamati �_� berada pada state j adalah

Dari persamaan (1) dan (2) serta definisi fungsi kerapatan peluang bersyarat, maka didapatkan fungsi kerapatan peluang bersama �_� dan �_� =�, yaitu

Fungsi kerapatan peluang marjinal tak bersyarat dari �_� diperoleh dengan menjumlahkan �(�_�,�_� = �) untuk semua kemungkinan nilai dari j, yaitu

�(�_�)=� �(�_�,�_� =�)

�

�=1

. (5)

Dari persamaan (1), (2), (3), (4) dan (5) diperoleh

�(�₁, … ,�_�) =∑�_�1=1…∑_��_�=1�_�1�_�1�2…�_{��−1��}�(�₁,�₁ = �₁) …�(�_�,�_� = �_�).

Model Hidden Markov Satu Waktu Sebelumnya

Pada bab ini akan dibahas model deret waktu hidden Markov satu waktu sebelumnya (Hamilton 1996) sebagai berikut

11

{�_�} adalah rantai Markov dengan ruang state {1,2,3,4} dan matriks transisi � =�

Bukti dapat dilihat pada Lampiran 1.

Selanjutnya, karena �_�~ �(0,�2_{) bebas stokastik identik maka dapat}

12 merupakan rantai Markov 4 state maka terdapat 4 fungsi kerapatan peluang bagi �� . Kumpulan fungsi kerapatan peluang tersebut dalam vektor (4 × 1)

dilambangkan dengan �_�, sehingga diperoleh

�_� = melambangkan perkalian elemen per elemen, maka

��|�−1⨂�� =

Berdasarkan persamaan (12) maka dapat ditulis

�(�_�,�_�=�|�_�−1) =�(�_� =�|�_�−1)�(�_�|�_�=�,�_�−1) (13)

13

Berdasarkan persamaan (14) dan (15) maka dapat diperoleh ����,�_� =�|�_�−1�

14

Salah satu pendekatan yang dapat digunakan untuk memilih nilai awal bagi �̂_�|�−1 adalah dengan membuat �̂_1|0 sama dengan vektor dari peluang tak bersyarat �= [�1�2�3�4] yang memenuhi sifat ergodic, yaitu

�=��

�1+�2+�3+�4 = 1.

Penduga kemungkinan maksimum bagi � diperoleh dengan memaksimumkan

ℒ(�) =�log�(�_�|�_�−1;�)

�

�=1

15 Bukti dapat dilihat pada lampiran 2.

Karena persamaan (19) sampai (22) taklinear, maka untuk mencari penduga kemungkinan maksimum bagi θ digunakan algoritma iteratif yang merupakan kasus khusus dari prinsip EM.

Langkah-langkah yang harus dilakukan adalah:

1. Tentukan banyaknya data (T) yang akan diamati serta input data (�₁,�₂,�₃, … ,�_�).

17

18

E��_�|S_� = �,�_�−1;��(�)�= E�����−1− ��_�−∗ ₁�+�� +��_�∗|S� =�,��−1;��(�)�

=���_�−1− ��_�−∗ ₁�+��_�∗

��� = E���|��−1;��(�)�

= � �_����_�|�_�−1;��(�)����

= � �_�� ��S_� =�|�_�−1;��(�)�����|S� =�,��−1;��(�)����

�

�=1

= � �_�(_|�_�−) ₁⋅E��_�|S_� = �,�_�−1;��(�)�

�

�=1

.

PEMODELAN NILAI TUKAR RUPIAH TERHADAP DOLLAR

AMERIKA DAN KAJIAN NUMERIKNYA

Pada bab ini akan dibahas pemodelan nilai tukar rupiah terhadap dolar Amerika beserta kajian numeriknya. Namun terlebih dahulu akan dibahas mengenai data input yang digunakan sebagai data observasi pada model. Kemudian dilanjutkan dengan pemodelan nilai tukar rupiah dan yang terakhir kajian numeriknya.

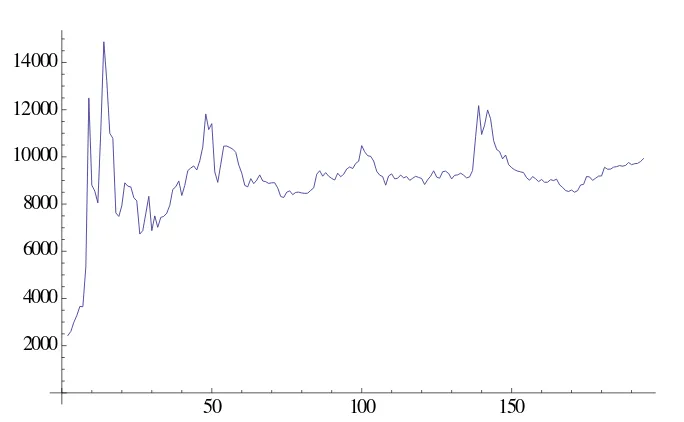
Data Input Nilai Tukar Rupiah

19

Gambar 1 Perubahan nilai tukar rupiah terhadap dolar Amerika per bulan

Model Hidden Markov Satu Waktu Sebelumnya

Model yang digunakan adalah model hidden Markov satu waktu sebelumnya seperti pada hal 10 yaitu:

��− ���∗ =����−1− ��_�−∗ 1�+��.

Berdasarkan model di atas nilai tukar rupiah saat ini diasumsikan tidak hanya bergantung pada faktor penyebab saat ini dan satu waktu sebelumnya, tetapi juga bergantung pada nilai tukar rupiah satu waktu sebelumnya. Pada karya ilmiah Santoso (2008) nilai awal yang digunakan �= �9182.96

9126.66�, � = 0.840756 dan �= 356984. MAPE yang dihasilkan dari nilai awal secara trial and error yang digunakan sebesar 14.58%. Pada tugas akhir ini akan dibangkitkan nilai awal yang tepat agar keakuratan pada model meningkat. Keakuratan dianggap baik bila MAPE < 5%.

Penentuan Nilai Awal untuk Penduga Parameter Model Hidden Markov Satu Waktu Sebelumnya

Penentuan Nilai Awal �_�, �_� dan �

20

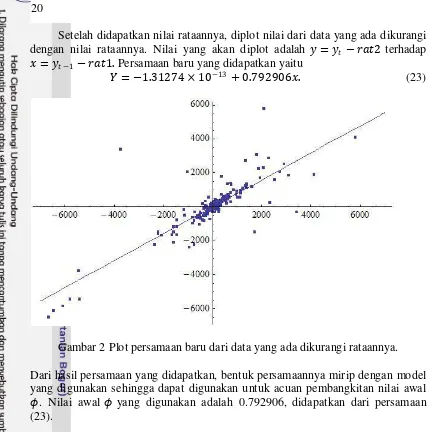
Setelah didapatkan nilai rataannya, diplot nilai dari data yang ada dikurangi dengan nilai rataannya. Nilai yang akan diplot adalah �= �_� − ���2 terhadap � =�_�−1− ���1. Persamaan baru yang didapatkan yaitu

�=−1.31274 × 10−13 + 0.792906�. (23)

Gambar 2 Plot persamaan baru dari data yang ada dikurangi rataannya. Dari hasil persamaan yang didapatkan, bentuk persamaannya mirip dengan model yang digunakan sehingga dapat digunakan untuk acuan pembangkitan nilai awal �. Nilai awal � yang digunakan adalah 0.792906, didapatkan dari persamaan (23).

Penentuan Nilai Awal P

Sedangkan untuk nilai awal P, dibangkitkan secara acak dari interval peluangnya [0,1] karena 0≤ �_�� ≤1. Hasil dari satu kali iterasi nilai awal yang digunakan untuk P adalah �

0.87 0 0.87 0 0.13 0 0.13 0 0 0.74 0 0.74 0 0.26 0 0.26

�.

Penentuan Nilai Awal �

Nilai awal untuk � yang digunakan dibangkitkan dari interval nilai [100,2000] yang merupakan selang nilai dari standar deviasinya. Standar deviasi dari data yang digunakan sebesar 1440.26. Hasil dari satu kali iterasi nilai awal untuk �yang dibangkitkan dan digunakan adalah 1454.

Hasil Progam

21

�= �

0.87 0 0.87 0 0.13 0 0.13 0 0 0.74 0 0.74 0 0.26 0 0.26

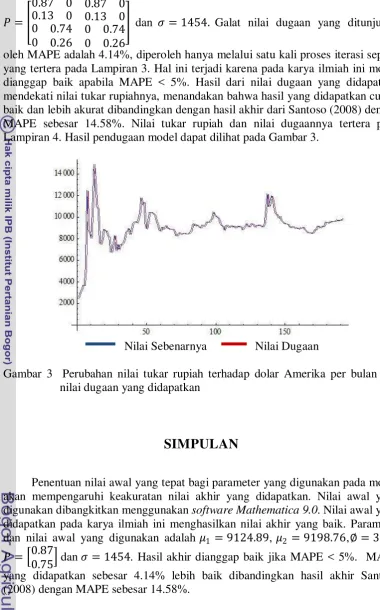
� dan �= 1454. Galat nilai dugaan yang ditunjukan oleh MAPE adalah 4.14%, diperoleh hanya melalui satu kali proses iterasi seperti yang tertera pada Lampiran 3. Hal ini terjadi karena pada karya ilmiah ini model dianggap baik apabila MAPE < 5%. Hasil dari nilai dugaan yang didapatkan mendekati nilai tukar rupiahnya, menandakan bahwa hasil yang didapatkan cukup baik dan lebih akurat dibandingkan dengan hasil akhir dari Santoso (2008) dengan MAPE sebesar 14.58%. Nilai tukar rupiah dan nilai dugaannya tertera pada Lampiran 4. Hasil pendugaan model dapat dilihat pada Gambar 3.

Nilai Sebenarnya Nilai Dugaan

Gambar 3 Perubahan nilai tukar rupiah terhadap dolar Amerika per bulan dan nilai dugaan yang didapatkan

SIMPULAN

Penentuan nilai awal yang tepat bagi parameter yang digunakan pada model akan mempengaruhi keakuratan nilai akhir yang didapatkan. Nilai awal yang digunakan dibangkitkan menggunakan software Mathematica 9.0. Nilai awal yang didapatkan pada karya ilmiah ini menghasilkan nilai akhir yang baik. Parameter dan nilai awal yang digunakan adalah �₁ = 9124.89, �₂ = 9198.76,∅= 3.94, �= �0.87

22

DAFTAR PUSTAKA

Elliot RJ, Aggoun L, Moore JB. 1995. Hidden Markov Models Estimation and Control. New York (US): Springer-Verlag.

Grimmet GR, Stirzaker DR. 2001. Probability and Random Processes. Ed ke-3. Oxford (GB): Oxford Univ Pr.

Hamilton J D. 1996. Time Series Analysis. New Jersey (US): Princenton Univ Pr. Hogg RV, Craig AT. 2014. Introduction to Mathematical Statistics. Ed ke-7. New

Jersey (US): Prentice Hall, Englewood Cliffs.

Krantz SG. 1999. Kim CJ. 1994. Dynamic linear models with Markov-switching. Journal of

Econometrics 60:1-22.

Mynsbrugge JV. 2010. Bidding strategies using price based unit commitment in a deregulated power market [tesis]. Belgium (BE): K.U.Leuven.

Ross SM. 1996. Stochastic Process. Ed ke-2. New York (US): John Wiley & Sons. Royden HL. 1963. Real Analysis. New York (US): The Macmilan Company. Santoso DH. 2008. Pemodelan nilai tukar Rupiah terhadap Dollar Amerika

menggunakan deret waktu hidden markov satu waktu sebelumnya [skripsi]. Bogor (ID): Institut Pertanian Bogor.

Stewart J. 1998. Kalkulus Jilid I. Ed ke-4. Jakarta (ID): Erlangga.

Osborne MJ. 1997. Concave and Convex Function of Many Variables. Canada (CA): University of Toronto.

37 Lampiran 3 Progam untuk mencari nilai dugaan dan MAPE minimum

38

�� − ��_�∗ = ����−1 − ��_�−∗ ₁�+��

40

k

41

43 Lampiran 4 Nilai tukar Rupiah terhadap Dollar Amerika dan nilai dugaannya

45 t Nilai Rupiah Nilai Dugaan

167 8535.81 8560.93

168 8594.84 8523.41

169 8504.66 8582.35

170 8567.95 8492.30

171 8809.94 8555.50

172 8835.28 8797.13

173 9169.74 8822.44

174 9150.26 9156.41

175 9005.36 9136.96

176 9094.86 8992.27

177 9184.77 9081.64

178 9191.62 9171.42

179 9563.07 9178.26

180 9477.97 9549.16

181 9484.13 9464.19

182 9565.09 9470.34

183 9587.16 9551.18

184 9631.91 9573.22

185 9605.02 9617.90

186 9637.90 9591.05

187 9760.44 9623.88

188 9668.13 9746.24

189 9710.34 9654.07

190 9723.19 9696.22

191 9803.09 9709.05

192 9927.76 9788.83

46

RIWAYAT HIDUP