BAB II FUNGSI, PERSAMAAN DAN PERTIDAKSAMAAN KUADRAT

(1)

FUNGSI, PERSAMAAN DAN PERTIDAKSAMAAN

KUADRAT

Standar kompetensi:

2. Memecahkan masalah yang berkaitan dengan fungsi, persamaan dan pertidaksamaan kuadrat

Kompetensi Dasar:

2.1Memahami konsep fungsi

2.2Menggambar grafik fungsi aljabar sederhana dan fungsi kuadrat

2.3Menggunakan sifat dan aturan tentang persamaan dan pertidaksamaan kuadrat 2.4Melakukan manipulasi aljabar dalam perhitungan yang berkaitan dengan

persamaan dan pertidaksamaan kuadrat

2.5Merancang model matematika dari masalah yang berkaitan dengan persamaan dan/atau fungsi kuadrat

2.6 Menyelesaikan model matematika dari masalah yang berkaitan dengan persamaan dan/atau fungsi kuadrat dan penafsirannya

3.1 Menyelesaikan pertidaksamaan satu variabel yang melibatkan bentuk pecahan aljabar

3.2 Merancang model matematika dari masalah yang berkaitan dengan pertidaksamaan satu variabel

3.3 Menyelesaikan model matematika dari masalah yang berkaitan dengan pertidaksamaan satu variabel dan penafsirannya.

Jembatan: Verrazano-Narrowsbridge

Sumber: http://selebsexy.com/10-jembatan-tertinggi-di-dunia/ Bentuk parabola merupakan salah satu bentuk kurva yang sering Anda jumpai dalam kehidupan. Salah satunya tampak pada tali menggantung menghubungkan tiang jembatan pada gambar di atas.

(2)

Fungsi, Persamaan dan Pertidaksamaan Kuadrat Page | 2

A.

Fungsi Kuadrat

1. Relasi dan Fungsi

p q r s

1 2 3 4 f

A B

a b c d

C

1 2 3

f D

(ii) (i)

Fungsi merupakan relasi khusus. Suatu relasi dari himpunan A ke himpunan B disebut fungsi jika setiap unsur (anggota) himpunan A dipasangkan tepat satu dengan unsur himpunan B gambar (i). Sedangkan gambar (ii) yang menunjukan relasi dari C ke D bukan fungsi karena ada anggota himpunan A (yaitu b) tidak memiliki pasangan dengan satu unsur himpunan B.

Jika fungsi itu diberi nama f maka fungsi tersebut dapat ditulis dengan lambang:

f: A  B

dibaca f memetakan A ke B atau B adalah peta dari A.

Peta dari x sering ditulis f(x) dan bentuk f(x) disebut rumus untuk f. Contoh:

1) f : x  x – 5, rumusnya ditulis f(x) = x - 5

2) f : x  x2 – 2x + 3, rumusnya ditulis f(x) = x2 – 2x + 3 2. Domain, Kodomain dan Range

Misalkan f sebuah fungsi yang memetakan tiap anggota A ke B (f : A  B) maka:

 Himpunan A disebut domain  Hinpunan B disebut kodomain

 Himpunan semua anggota B yang dipasangkan dengan tiap anggota himpunan A atau semua anggota yang merupakan peta dari himpunan A disebut range

(3)

Contoh 1:

Diketahui fungsi f : x  2x + 1 dengan daerah asal {x|1 ≤ x ≤ 3, xR} a. Carilah nilai fungsi f untuk x = 1, x = 2 dan x = 3

b. Gambarlah grafik f pada bidang cartesius c. Tentukan wilayah hasilnya (range). Penyelesaian

f : x  2x + 1, rumusnya f(x) = 2x + 1 a. Nilai fungsi f(x) = 2x + 1

Untuk x = 1 f(1) = 2(1) + 1 = 3 Untuk x = 2 f(2) = 2(2) + 1 = 5 Untuk x = 3 f(3) = 2(3) + 1 = 7 b. Grafik f(x) = 2x + 1

Y

X

1 2 3 4 5 6 7

O ₁ ₂ ₃

y = f(x) = 2x + 1

domain

(4)

Uji Kompetensi 1

Kerjakan soal-soal berikut!

1. Dari relasi-relasi pada gambar berikut ini manakah yang merupakan fungsi

2. Daerah asal fungsi f : x  x – 3 adalah Df = {x|0 ≤ x ≤ 4, xR}

a. Tentukan nilai fungsi f untuk x = 0, x = 1, x = 2, x = 3 dan x = 4 b. Gambarlah grafik fungsi pada bidang cartesius

c. Tentukan wilayah hasil fungsi f (Rf)

3. Diketahui fungsi f : x  (ax + b) dengan a, bB. Jika f(1) = 1 dan f(2) = -1 a. Carilah nilai a dan b

b. Hitunglah nilai f(-2), f(-1), f(0), f(3) dan f(4)

c. Gambarlah grafik tersebut pada bidang cartesius.

4. Diketahui fungsi f : x  2x + 1 dengan daerah asal Df = {-2, -1, 0, 1, 2}. Tentukan wilayah hasilnya.

3. Beberapa Macam Fungsi Khusus

(5)

1) Fungsi konstan

Suatu fungsi y = f(x) dengan f(x) sama dengan sebuah konstanta (tetapan) untuk semua nilai x dala daerah asalnya. Artinya untuk semua nilai x dalam Df hanya berpasagan dengan sebuah nilai dalam Rf atau dengan kata lain fungsi f memasangkan setiap bilangan real k.

Fungsi konstan ditulis sebagai: f : x  k, dengan rumus f(x) = k, dengan k konstanta dan xR.

Contoh 2:

Y

1 1 2 3

O ₁ ₂ ₃

3

X

2

f(x) = 3 f(x) = 2

2) Fungsi Identitas

Fungsi y = f(x) dengan f(x) = x untuk semua nilai dalam daerah asalnya. Artinya untuk sebuah nilai x dalam Df berpasangan dengan nilai x itu sendiri dalam Rf.

Fungsi identitas ditulis sebagai:

(6)

3) Fungsi Modulus (Fungsi Nilai Mutlak)

Fungsi y = f(x) dengan f(x) = |x| untuk semua nilai x dalam daerah asalnya atau fungsi yang memasangkan bilangan eal dengan nilai mutlaknya.

Bentuk |x| dibaca nilai mutlak x didefinisikan:

Untuk xR, maka nilai mutlak x dientukan oleh aturan

  

 



0 ,

| |

x jika x

x

Oleh karena nilai mutlak suatu bilangan real x tidak pernah negatif, maka grafik y = f(x) = |x| tidak pernah berada di bawah sumbu x.

Contoh 3:

f : x  |x| atau f(x) = |x|

4) Fungsi Linear

Fungsi y = f)x) dengan f(x) = ax + b, a, b R dan a ≠ 0 untuk semua x dala daera asalnya

Fungsi linear dikenal dengan fungsi polinom (suku banyak) berderajat satu dengan variabel x.

Contoh 4:

(7)

5) Fungsi Kuadrat

Fungsi y = f(x) dengan f(x) = ax2_{+ bx + c. a, b dan c}_{R dan a ≠ 0} untuk semua nilai x dalam daerah aalnya.

Fungsi kuadrat dikenal dengan fungsi polinom berderajat dua dengan variabel x.

Grafik fungsi kuadrat berbenytuk parabola dan pada kesempatan ini grafik fungsi kuadrat kita akan bahas lebih lanjut.

4. Sifat-sifat Fungsi

Telah dikenal beberapa fungsi khusus, fungsi tersebut mempunyai sifat-sifat khas sebagi berikut:

1) Fungsi Into

Fungsi f : A  B dikatakan fungsi Into jika ada b  B yang bukan peta dari a  A.

Contoh 5:

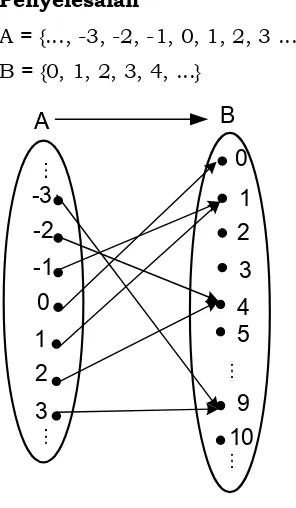
Misalkan A himpunan bilangan bulat dan B himpunan bilanga cacah. f suatu fungsi dri A ke B yang disajikan denga rumus f : x  x2_. Apakah f suatu ungsi into?

Penyelesaian

A = {..., -3, -2, -1, 0, 1, 2, 3 ...} B = {0, 1, 2, 3, 4, ...}

3 2 1 0

A B

1 2 3

5

9 0

10 4

1. Range: Rf B 2. Ada b  B bukan

peta dari a  A yaitu b2

Dari diagram di samping ternyata ada anggota B yang tidak

(8)

2) Fungsi Onto/Pada/Surjektif

Fungsi f : A  B dikatakan surjektif (onto) jika setiap anggota b  B mempunyai prapeta di A atau Rf = B.

Contoh 6:

Misalkan A = {-4, -3, -2, -1, 0, 1, 2, 3, 4} dan B = {-2, -1, 0, 1, 2}. f suatu fungsi A ke B yang disajikan dengan aturan

   

genap n jika n

ganjil n jika o n f

, 2

, ) (

Apakah fungsi f surjektif/onto? Penyelesaian

3) Fungsi Satu-satu/Injektif/one to one

Fungsi f : A  B dikatakan fungsi satu-satu jika setiap anggota A yang berbeda mempunya peta berbeda di B.

a1 a2 a3 a4

b2 b3 b4

A B

b1 f

Rf = B

1. Terlihat setiap anggota B memunyai prapeta di A 2. Rf = B

(9)

Contoh 7:

Misalkan A himpunan bilangan cacah, B himpunan bilangan bulat, f suatu fungsi yang disajikan dengan rumus f : x  x + 1. Apakah f suatu fungsi injektif.

Penyelesaian A = {0, 1, 2, 3, ...}

B = {..., -3, -2, -1, 0, 1, 2, 3, ...}

...

4) Fungsi Bijektif (Korespondensi Satu-satu)

Fungsi f : A  B disebut fungsi bijektif apabila fungsi tersebut injektif sekaligus surjektif (satu-satu dan pada).

Contoh 8:

Diketahui A = {1, 2, 3, 4, 5, ...} dan B = {2, 4, 6, 8, 10, ...}. suatu fungsi disajikan f : x  2x. Apakah fungsi f suatu fungsi bijektif?

Penyelesaian f

1 2 3 4

4 6 8

A B

2

5... 10...

Pada diagram di samping terlihat setiap anggota A yang berbeda mempunyai peta di B yang berbeda juga. Sehingga f : A  B adalah fungsi injektif

1. Terlihat Rf = B berarti f fungsi pada

2. Setiap anggota A yang berbeda mempunyai peta yang berbeda dengan anggota B, berarti f fungsi satu-satu.

(10)

 Note :

 Fungsi kepada B disebut pula fungsi surjektif (onto)

 Fungsi kedalam B disebut pula fungsi into

Uji Kompetensi 2

Kerjakan soal-soal berikut!

1. Diantara fungsi berikut, manakah yang merupakan fungsi into, fungsi pada, fungsi satu dan fungsi yang merupakn korespondensi satu-satu!

2. Manakah yang merupakan fungsi into, fungsi pada, fungsi satu-satu dan fungsi bijektif dari fungsi dengan D = {1, 2, 3, 4} yang didefinisikan sebagai berikut:

a. R = {(1, 1), (2, 3), (3, 5), (4, 7)}; jika K = {1, 2, 3, 4, 5, 6, 7} b. R = {(1, 1), (2, 2), (3, 3), (4, 1)}; jika K = {1, 2, 3}

c. R = {(1, 4), (2, 3), (3, 2), (4, 1)}; jika K = {1, 2, 3, 4} 3. Misalkan A = [-1, 1] = {x|-1 ≤ x ≤ 1, x  R}.

Apakah fungsi-fungsi berikut surjektif untuk a. f : A  A didefinisikan f(x) = x

(11)

5. Grafik Fungsi Kuadrat

Fungsi kuadrat adalah fungsi dimana pangkat tertinggi dari varaibel x pada tiap fungsi sama dengan dua.

Bentuk baku: f(x) = ax2_{+ bx + c, a ≠ 0} dengan a, b, c  R

a = koefisien x2 b = koefisien x c = konstanta

Grafik fungsi kuadrat berupa parabola.

a. Menggambar grafik fungsi kuadrat yang sederhana

Sebelum kita membahas cara-cara menggambar sketsa grafik fungsi kuadrat, marilah kita ingat at kembali mengenai bentuk umum fungsi kuadrat yaitu: f(x) = ax2_{+ bx + c (a 0), a, b, c R.}

Fungsi kuadrat tersebut merupakan fungsi kuadrat dalam peubah x. Grafik fungsi kuadrat ditulis dengan notasi y = f(x) = ax2_{+ bx + c,} dan grafik fungsi kuadrat disebut parabola.

Langkah-langkah menggambar sketsa grafik fungsi kuadrat yang sederhana:

Langkah 1:

Tentukan beberapa anggota fungsi f, yaitu koordinat titik-titik yang terletak pada grafik fungsi f. Titik-titik ini dapat kita tentukan dengan memilih beberapa nilai x bilangan bulat yang terletak dalam daerah asalnya kemudian kita hitung nilai fungsi f. Titik-titik pada fungsi f itu biasanya akan lebih mudah jika kita sajikan dengan menggunakan tabel atau daftar.

Langkah 2:

Gambarkan koordinat titik-titik yang telah kita peroleh pada Langkah 1 pada sebuah bidang Cartecius.

Langkah 3:

Hubungkan titik-titik yang telah digambarkan pada bidang Cartecius pada Langkah 2 dengan menggunakan kurva mulus. Agar Anda lebih memahami dan terampil menggambar sketsa grafik fungsi kuadrat yang sederhana dengan menggunakan langkah-langkah di atas, perhatikanlah beberapa contoh di bawah ini. Contoh 9:

1. Gambarkan grafik fungsi kuadrat yang ditentukan dengan

persamaan f(x) = x2_{+ 2x, jika daerah asalnya adalah} D = {x | -4 x 2, x R}

Penyelesaian:

(12)

Langkah 1:

Kita buat tabel atau daftar untuk menentukan titik-titik yang terletak pada fungsi f.

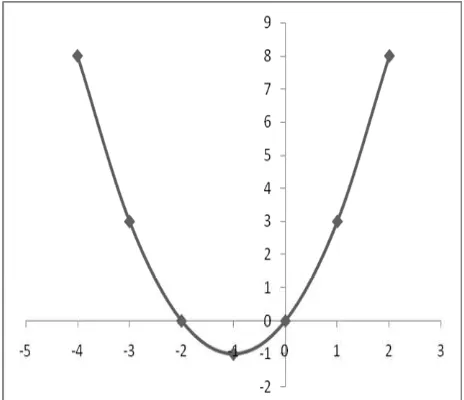
x -4 -3 -2 -1 0 1 2 y = x2_{+ 2x 8} ₃ ₀ _-1 ₀ ₃ ₈ Langkah 2:

Gambarkan titik-titik (-4,8), (-3,3), (-2,0), (-1,-1), (0,0), (1,3), dan (2,8) pada bidang Cartecius seperti Gambar 3-4.

Langkah 3:

Hubungkan titik-titik pada Langkah 2 tersebut dengan kurva mulus, sehingga diperoleh grafik fungsi kuadrat f(x) = x2_{+ 2x. seperti} ditunjukkan pada Gambar di bawah ini. Grafik fungsi kuadrat ini berbentuk parabola.

Dari grafik fungsi, dapat kita ketahui beberapa istilah sebagai berikut:

1) Daerah Asal

Daerah asal fungsi f adalah {x | -4 x 2, x R} 2) Daerah Hasil

Daerah hasil fungsi f adalah {y | -1 y 8. y R} 3) Pembuat Nol

(13)

4) Persamaan Sumbu Simetri

Parabola dengan persamaan y = x2_{+ 2x mempunyai sumbu} simetri yang persamaannya adalah x = -1.

5) Koordinat Titik Balik atau Titik Puncak

Dari Gambar 3-4b, koordinat titik balik atau titik pusat parabola adalah

P(-1, -1). Pada titik P(-1, -1), nilai ordinat y = -1 merupakan nilai terkecil (minimum) dari fungsi f, maka titik P (-1, -1) disebut titik balik minimum.

6) Nilai Maksimum atau Minimum Fungsi

Untuk x = -1 diperoleh f(-1) = -1. Nilai f(-1) = -1 ini disebut nilai minimum fungsi karena nilai itu adalah nilai yang terkecil dari fungsi f.

2. Gambarkan grafik fungsi kuadrat yang ditentukan dengan

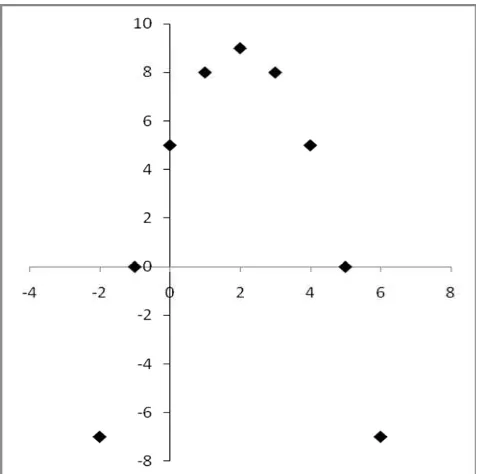
persamaan f(x) = -x2_{+ 4x + 5, jika aderah asalnya adalah} D = {x | -2 x 6, x R}

Penyelesaian

Grafik fungsi kuadrat f(x) = -x2 + 4x + 5 adalah sebuah parabola dengan persamaan: y = -x2_{+ 4x + 5.}

Langkah 1:

Kita buat tabel atau daftar untuk menentukan titik-titik yang terletak pada fungsi f.

x ... ... ... ... ... ... ... ... ... y = -x2_{+ 4x + 5 ... ... ... ... ... ... ... ... ...} Langkah 2:

Gambarkan titik-titik (..., ...), (..., ...), (..., ...), (..., ...), (..., ...), (..., ...), (..., ...), (..., ...), dan (..., ...).

Langkah 3:

(14)

Dari grafik fungsi pada Gambar 3-5, dapat kita tentukan hal-hal sebagai berikut:

1) Daerah asal fungsi f adalah {x | -2 x 6, x R} 2) Daerah hasil fungsi f adalah {y | -7 y 9. y R}

3) Pembuat nol fungsi f adalah x = -1 dan x = 5, karena f(-1) = 0 dan f(5) = 0 Persamaan sumbu simetri adalah garis x = 2. Koordinat titik-titik maksimum adalah (2, 9)

4) Nilai maksimum fungsi f adalah 9, karena nilai itu adalah nilai yang terbesar dari fungsi f.

b. Menggambar Sketsa Grafik Fungsi Kuadrat Secara Umum Pada bagian a, Anda telah mempelajari cara menggambar sketsa grafik fungsi kuadrat yang sederhana. Kali ini Anda akan mempelajari materi tentang menggambar sketsa grafik fungsi kuadrat secara umum. Untuk lebih jelasnya, marilah kita perhatikan penjelasan berikut.

Misalkan suatu fungsi kuadrat ditentukan dengan persamaan f(x)= ax + bx + c (a ≠ 0), a, b, c, R. Grafik fungsi kuadrat itu adalah sebuah parabola dengan persamaan y = ax2_{+ bx + c.}

Untuk menggambar sketsa grafik fungsi kuadrat secara umum, dapat Anda gunakan langkah-langkah sebagai berikut:

i. titik potong grafik dengan sumbu x dan sumbu y. ii. titik balik atau titik puncak parabola.

(15)

Untuk lebih jelasnya, marilah kita pelajari materi di bawah ini. 1. Titik Potong Grafik dengan Sumbu X dan Sumbu Y

a. Titik Potong Grafik dengan Sumbu X

Titik potong grafik dengan sumbu X diperoleh jika y = 0, sehingga

ax2_{+ bx + c = 0 merupakan kuadrat dalam x. Akar-akar} persamaan kuadrat itu merupakan absis titik-titik potongnya dengan sumbu x. Nilai diskriminan persamaan kuadrat ax2_{+ bx + c = 0, yaitu D = b}2_{- 4ac menentukan banyak titik} potong grafik dengan sumbu x.

1. 2.

3.

Jika D > 0, maka grafik fungsi f memotong sumbu x di dua titik yang berlainan.

Jika D = 0, maka grafik fungsi f memotong sumbu x di dua titik yang berimpit. Dalam hal ini, grafik fungsi f dikatakan menyinggung sumbu x.

Jika D < 0, maka grafik fungsi f tidak memotong maupun menyinggung sumbu x.

b. Titik Potong Grafik dengan Sumbu Y

Titik potong grafik dengan sumbu y diperoleh jika x = 0, sehingga

y = a(0)2_{+ b(0) + c = c. Jadi, titik potong grafik dengan sumbu} y adalah (0,c)

2. Titik Balik atau Titik Puncak dan Persamaan Sumbu Simetri Titik balik atau titik puncak suatu parabola dapat ditentukan

dengan mengubah bentuk kuadrat pada ruas kanan persamaan parabola menjadi bentuk kuadrat sempurna. Dari bentuk kuadrat itu selanjutnya dapat pula ditentukan sumbu simetrinya. Sebagai contoh, perhatikan kembali parabola-parabola pada contoh 9.

Untuk parabola pada contoh 9 nomor 1 y

y y

= x2_{+ 2x}

= x2_{+ 2x + 1 - 1} = (x + 1)2_{- 1}

Oleh karena itu bentuk (x+1)2_{selalu bernilai positif atau sama} dengan nol untuk x R, maka nilai terkecil (minimum) dari (x+1) adalah 0. Dengan demikian, y = (x+1)2_{- 1 mempunyai nilai} minimum -1, dan nilai itu dicapai jika (x+1) = 0 atau x = -1. Jadi, titik balik atau titik puncak minimum parabola y = (x+1)2_{- 1} adalah (-1,-1) dan persamaan sumbu simetrinya adalah x = -1. Untuk parabola pada contoh 9 nomor 2 :

y y y y

= -x2_{+ 4x + 5} = -(x2_{- 4x) + 5}

= -(x2_{- 4x + 4) + 4 + 5} = -(x - 2) 2_{+ 9}

(16)

Jadi, titik balik atau titik puncak maksimum parabola y = -(x-2) 2_{+ 9 adalah (2, 9) dan persamaan sumbu simetrinya}

adalah x = 2.

Selanjutnya, marilah kita tinjau persamaan parabola dalam bentuk umum: y = ax2_{+ bx +c sebagai berikut:}

y = ax2 + bx +c y = a(x2₊

a

b_{x) + c}

y = a(x2₊

a b_{x +}

2 2

4a b _{) -}

a b

4 2

+ c

y = a(x +

a b

2 )2 - a b 4 2 + a ac 4 4

y = a(x +

a b

2 )2 - a ac b

4 4

2_

Untuk a > 0: Maka bentuk a(x +

a b

2 )2 selalu bernilai positif atau sama dengan nol untuk semua x  R, sehingga nilai terkecil (minimum) dari a(x +

a b

2 )2 adalah 0. Dengan demikian, y = a(x +

a b

2 )2 - a ac b

4 4

2_

mempunyai nilai minimum - a ac b 4 4 2_

, dan nilai itu dicapai jika a(x +

a b

2 )2 = 0 atau x + a b

2 = 0 atau x = -

a b

2 .

Jadi titik balik minimum parabola y = a(x+

a b

2 )2 - a ac b 4 4 2_ adalah (-a b

2 , - a ac b 4 4 2_ ).

Untuk a < 0: Maka bentuk a(x +

a b

2 )2 selalu bernilai negatif atau sama dengan nol untuk semua x R, sehingga nilai terbesar (maksimum) dari a(x +

a b

2 )2 adalah 0. Dengan demikian, y = a(x+

a b

2 )2 - a ac b

4 4

2_

mempunyai nilai maksimum - a ac b 4 4 2_

, dan nilai itu dicapai jika a(x +

a b

2 )2 = 0 atau x + a b

2 = 0 atau x = -

a b

(17)

Jadi titik balik maksimum parabola y = a(x+

a b

2 )2- a ac b

4 4

2_

adalah

(-a b

2 ,- a ac b

4 4

2_

).

Dari penjelasan di atas, maka dapat kita ambil kesimpulan sebagai berikut: 1. Parabola y = ax2_{+ bx +c (a ≠ 0), a, b, c,}_{R mempunyai titik balik}

(-a b

2 , - a ac b

4 4

2_

) (i).

(ii).

Jika a > 0, maka titik baliknya adalah titik balik minimum atau parabola terbuka ke atas.

Jika a < 0, maka titik baliknya adalah titik balik maksimum atau parabola terbuka ke bawah.

2. Persamaan sumbu simetri parabola y = ax2 + bx + c adalah garis x = -

a b

2 Selanjutnya, berdasarkan penjelasan di atas ada beberapa kemungkinan sketsa grafik fungsi kuadrat f(x) = ax2 + bx + c jika ditinjau dari nilai a dan nilai diskriminan D = b2_{- 4ac yaitu:}

 jika a > 0 maka parabola terbuka ke atas atau mempunyai titik balik minimum

 jika a < 0 maka parabola terbuka ke bawah atau mempunyai titik balik maksimum

 jika D > 0 maka parabola memotong sumbu x di dua titik yang berlainan

 jika D = 0 maka parabola memotong sumbu x di dua titik yang berimpit atau parabola menyinggung sumbu x

 jika D < 0 maka parabola tidak memotong dan tidak menyinggung sumbu x

Secara geometris seperti diperlihatkan pada gambar bawah ini.

(18)

Contoh 10:

1. Gambarkan sketsa grafik fungsi kuadrat f(x) = x2_{- 4x - 5.} Penyelesaian:

Grafik fungsi kuadrat f(x) = x2_{- 4x - 5 adalah sebuah parabola dengan} persamaan y = x2 - 4x - 5, berarti a = 1, b = -4, dan c = -5.

(i) Titik potong grafik dengan sumbu x, dan sumbu y.

a). Titik potong grafik dengan sumbu x, diperoleh jika y = 0. Ini berarti: x2_{- 4x - 5 = 0}

(x + 1)(x - 5) = 0

x + 1 = 0 atau x - 5 = 0 x = 0 - 1 atau x = 0 + 5 x = -1 atau x = 5

Jadi, titik potongnya dengan sumbu x adalah (-1,0) dan (5,0).

b). Titik potong grafik dengan sumbu y, diperoleh jika x = 0. Ini berarti: y = (0) 2_{– 4(0) - 5}

y = 0-0-5 y = -5

Jadi, titik potongnya dengan sumbu y adalah (0,-5) (ii) Koordinat titik balik

p(-a b

2 , - a ac b

4 4

2_

)

p( ) 1 ( 2

) 4 (

 , -

) 1 ( 4

) 5 )( 1 ( 4 ) 4

(_ 2_ _ )

p( 2 4

, - 4

20 16

)

p(2,-9)

Oleh karena a = 1 > 0, maka p merupakan titik balik minimum sehingga parabolanya terbuka ke atas

(iii) Persamaan sumbu simetri adalah x = -

a b

2

x = - ) 1 ( 2

) 4 ( 

x = 2 4

x = 2

(19)

Setelah mempelajari contoh 1 di atas, apakah Anda sudah paham? Baiklah, agar Anda lebih paham simaklah contoh 2 di bawah ini.

2. Gambarkan sketsa grafik fungsi kuadrat f(x) = -x2_{+ 2x – 1} Penyelesaian:

Grafik fungsi kuadrat f(x) = -x2 + 2x - 1 adalah sebuah parabola dengan persamaan y = -x2_{+ 2x - 1, berarti a = -1, b = 2, dan c = -1.}

(i) Titik potong grafik dengan sumbu x, dan sumbu y.

a). Titik potong grafik dengan sumbu x, diperoleh jika y = 0. Ini berarti: -x2_{+ 2x - 1 = 0 (kedua ruas dikalikan -1)}

x2_{- 2x + 1 = 0} (x - ....)(x - ....) = 0

x - .... = 0 atau x - .... = 0 x = 0 + .... atau x = 0 + .... x = .... atau x = ....

Jadi, titik potongnya dengan sumbu x adalah (...., ....) atau grafik menyinggung sumbu x di titik (...., ....).

b). Titik potong grafik dengan sumbu y, diperoleh jika x = 0. Ini berarti: y = -(....)2_{+ 2(....) - 1}

y = .... + .... - 1 y = ....

Jadi, titik potongnya dengan sumbu y adalah (...., ....) (ii) Koordinat titik balik

p(-a b

2 , - a ac b

4 4

2_

)

p(-) .... ( 2

.... _{, -}

) .... ( 4

) .... )( .... ( 4 ....2_

(20)

p(-2 ....

 ,- 4

.... ....

 

)

p(...., ....)

Oleh karena a = -1 < 0, maka p merupakan titik balik ... sehingga parabolanya terbuka ke ...

(iii) Persamaan sumbu simetri adalah x = -

a b

2

x = - ) .... ( 2

....

x = - 2 ....



x = ....

(21)

Diskusi dengan teman sebangku! Gambarlah grafik fungsi kuadrat berikut! a. f(x) = x2 _{– x – 2}

b. f(x) = 2x – x2

c. apakah syarat parabola terbuka ke atas dan parabola terbuka ke bawah?

3. Menggambar Sketsa Grafik Fungsi Dengan Translasi Selain dengan cara di atas untuk menggambar grafik fungsi kuadrat dapat pula memanfaatkan sifat pergeseran (translasi). Fungsi f(x) = ax2 + bx + c dapat dibentuk f(x) = a(x – p)2 + q, dengan p =

-a b

2 , dan q = - a ac b

4 4

2_

.

Peranan p dan q pada fungsi f(x) = a(x – p)2_{+ q:}

 p adalah arah pergeseran horizontal, untuk p < 0 parabola geser kekanan sumbu x sejauh p satuan dan p > 0 parabola geser kekiri sumbu x sejauh p satuan.

 q adalah arah pergeseran vertikal, untuk q > 0 parabola geser ke atas sumbu y sejauh q satuandan q < 0 parabola geser ke bawah sumbu y sejauh q satuan.

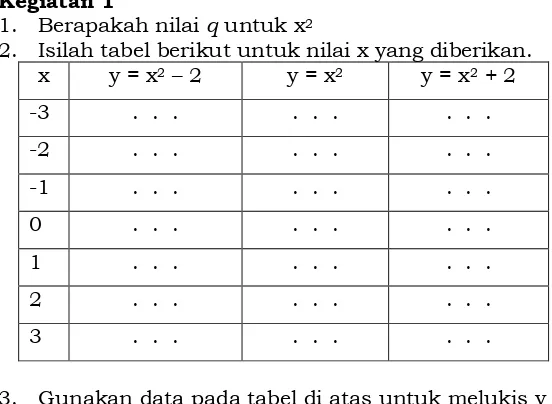
Agar lebih jelas, lakukan kegiatan berikut! Kegiatan 1

1. Berapakah nilai q untuk x2

2. Isilah tabel berikut untuk nilai x yang diberikan. x y = x2 – 2 y = x2 y = x2 + 2 -3 . . . . . . . -2 . . . . . . . . . -1 . . . . . . . . . 0 . . . . . . . . . 1 . . . . . . . . . 2 . . . . . . . . . 3 . . . . . . . . .

(22)

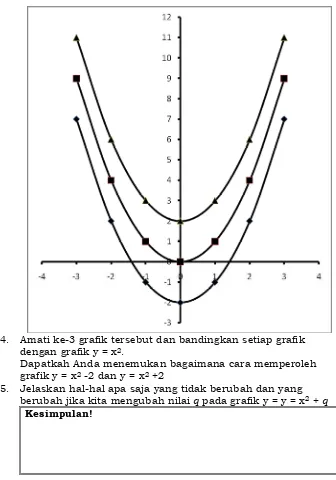
4. Amati ke-3 grafik tersebut dan bandingkan setiap grafik dengan grafik y = x2_.

Dapatkah Anda menemukan bagaimana cara memperoleh grafik y = x2_{-2 dan y = x}2₊₂

5. Jelaskan hal-hal apa saja yang tidak berubah dan yang berubah jika kita mengubah nilai q pada grafik y = y = x2₊_q

Kesimpulan!

Kegiatan 2

(23)

2. Gunakan data pada tabel di atas untuk melukis y = (x – 1)2_, y = x2_{dan y = (x + 2)}2

3. Amati ketiga gambar denganm saksama. Dapatkah anda menemukan cara memperoleh grafik y = (x – 1)2_{, y = x}2_dan y = (x + 2)2_?

Kesimpulan!

Kegiatan 3 “Menggambar grafik y = a(x – p)2₊_q”

Gambarlah grafik y = -2(x + 4)2_{– 2, kemudian tentukan daerah} asal dan daerah hasilnya!

Penyelesaian

1. Isilah tabel di bawah ini

x y = -2x2 x y = -2(x + 4)2 - 2

-2 . . . -6 . . .

-1 . . . -5 . . .

0 . . . -4 . . .

1 . . . -3 . . .

(24)

2. Gunakan data di atas untuk melukis grafik y = -2x2 dan y = -2(x + 4)2_{– 2}

3. Amati kedua grfik di atas, dapatkahAnda menenmukan cara memperoleh grafik y = -2(x + 4)2 – 2 dan grafik y = -2x2 dengan translasi?

Kesimpulan:

6. Syarat Fungsi Kuadrat Definit Positif dan definit Negatif

Untuk memahami definit positif dan definit negatif suatu fungsi kuadrat. Lakukan kegiatan berikut!

1. Gambarlah grafik fungsi kuadrat berikut:

(25)

2. Tentukan nilai diskriminan yaitu D = b2_{– 4ac dari masing-masing} fungsi kuadrat pada nomor 1.

3. Lakukan lagi kegiatan seperti nomor 1 dan 2 untuk fungsi kuadrat berikut!

(26)

4. Amatilah hubungan antara nilai diskriminan (D) dan perpotongan grafik fungsi kuadrat dengan sumbu x.

Kesimpulan apa yang Anda peroleh?

Grafik memotong sumbu x di dua titik berbeda bila .... Grafik memotong (menyinggung) sumbu x di satu titik bila ... Grafik tidak memotong/menyinggung sumbu x bila .... Dari hasil kesimpulan di atas. Isilah tabel dibawah ini!

Tanda

a dan D Bentuk grafik Titik potong dengan sumbu x Jenis titik balik

a > 0

D > 0

D = 0

D < 0

a < 0

D > 0

D = 0

D < 0

Perhatikan tabel di atas, tampak bahwa untuk x bilangan real maka.

 Khusus D < 0, grafik seluruhnya berada di atas sumbu x (terbuka ke atas) atau grafik seluruhnya di bawah sumbu x (terbka ke bawah).

 a > 0 dan D < 0, fungsi kuadrat selalu bernilai positif disebut definit positif (seluruh grafiknya berada di atas sumbu x).

 a < 0 dan D < 0, fungsi kuadrat selalu bernilai negatif disebut definit negatif (seluruh grafiknya berada di bawah sumbu x)

x

(27)

Contoh 27:

1. Tentukan apakah fungsi kuadrat berikut ini definit positif, definit negatif atau tidak keduanya!

a. f(x) = x2_{– 4x + 5} b. f(x) = -x2_{+ 10x – 30} c. f(x) = x2_{– 4x – 5} Penyelesaian

a. f(x)

D

= x2_{– 4x + 5}

a =1 > 0; b = -4 dan c = 5 = b2_{– 4ac}

= (-4)2_{– 4(1)(5)} = 16 – 20 = - 4 < 0

Karena a > 0 dan D < 0 maka fungsi kuadrat f(x) = x2_{– 4x + 5} definit positif

Untuk b dan c silakan dicoba sebagai latihan!

2. Tentukan batas-batas nilai p agar fungsi f(x) = px2_{+ 4x + 1 definit} positif:

Penyelesaian

f(x) = px2_{+ 4x + 1}

a = p; b = 4 dan c = 1 Syarat definit positif:

(i) a > 0 p > 0

(28)

Batas nilai p adalah irisan dari kedua garis bilangan

Jadi agar f(x) = px2_{+ 4x + 1 definit positif maka batas nilai p adalah} p > 4

3. Tentukan batas nilai k, agar fungsi f(x) = (k-1)x2 - 2kx + (k-2) definit negatif!

Penyelesaian:

Fungsi kuadrat f(x) = (k-1)x2_{- 2kx + (k-2), berarti a = (k-1), b= -2k,} dan c = (k-2).

Syarat agar fungsi kuadrat f definit negatif adalah a < 0 dan D < 0. (i) _{a < 0, maka (k-1)}

k-1 k k

< 0 < 0 < 0 + 1 < 1 (ii) _{D < 0, maka: b - 4ac}

(-2k) - 4(k-1)(k-2) 4k - 4(k -2k-k+2) 4k - 4(k - 3k + 2) 4k - 4k + 12k - 8 12k – 8 12k 12k

< 0 < 0 < 0 < 0 < 0 < 0 < 0 + 8 < 8 k <

12 8

k < 3 2 (i)

(29)

Dengan menyatukan syarat (i) dan (ii) atau mencari irisannya, maka batas nilai k seperti diperlihatkan pada di bawah ini.

1 (i)

3 2 (ii)

3 2

hasilnya

Berdasarkan Gambar di atas batas nilai k yang memenuhi adalah k <

3

2_{. Jadi, agar fungsi kuadrat f(x) = (k-1)x}₂_{- 2kx + (k-2) definit}

negatif adalah k < 3 2_.

Diskusikan!

1. Selidiki masing-masing fungsi kuadrat di bawah ini, apakah definit positif, definit negatif atau tidak kedua-duanya.

a). f(x) = 2x2_{+ 3x + 4.} b). f(x) = -x2 + 2x – 5. c). f(x) = x2_{- x – 2.}

2. Tentukan batas-batas nilai m, agar fungsi kuadrat f(x) = -x2_{- 8x +} m definit negatif!

3. Tentukan batas-batas nilai k, agar fungsi kuadrat: f(x) = (k + 1)x2_{+ (2k+1)x + (k+2) definit positif.}

7. Pengaruh Koefisien-koefisien a, b dan c pada Grafik Fungsi Kuadrat Pada pembahasan sebelumnya telah kita bahas pengaruh koefisien a terhadap bentuk grafik fungsi kuadrat, yaitu.

a. a > 0 maka grafik terbuka ke atas b. a < 0 maka grafik terbuka ke bawah

sekarang bagaimana pengaruh b dan c? Untuk lebih jelasnya lakukan kegiatan berikut!

(30)

2. Dengan memperhatikan grafik di atas isilah tabel berikut! _Note!

 Parabola disebut berat kekiri jika titik puncaknya berada disebelah kiri sumbu y

 Parabola disebut berat kekanan jika titik puncaknya berada disebelah kanan sumbu y

No Fungsi Kuadrat Koefisien Tanda a x b kekiri/kekanan Parabola berat a b

(31)

4. Simpulkan pengaruh koefisien a x b pada grafik fungsi kuadrat



Titik potong grafik dengan sumbu y diperoleh jika x = 0 sehingga y = a(0)2_{+ b(0) + c}

y = c

titik potong grafik dengan sumbu y adalah (0, c) sedang untuk letak titik (0, c) tergantung nilaic . pengaruh nilai c terhadap grafik fungsi kuadrat sebagai berikut:

Pengaruh koefisien-koefisien a, b dan pada grsgik y = ax2_{+ bx + c} 1.  Tanda a > 0 menyatakan parabola terbuka ke atas

 Tanda a < 0 menyatakan parabola terbuka ke bawah

2.  Tanda a x b > 0 menyatakan parabola berat kekiri (puncak berada di sebelah kiri sumbu y)

 Tanda a x b < 0 menyatakan parabola berat kekanan (puncak berada di sebelah kanan sumbu y)

3.  Tanda c > 0 menyatakan parabola memotong sumbu y di atas titik (0, 0)

 Tanda c = 0 menyatakan parabola melalui titik (0, 0)

(32)

4.  Tanda D > 0 menyatakan parabola memotong sumbu x di dua titik

 Tanda D = 0 menyatakan parabola memotong sumbu x di satu titik (menyinggung sumbu x)

 Tanda D < 0 menyatakan parabola tidak memotong sumbu x Contoh 12:

1. Jika parabola y = ax2_{+ bx + c, grafiknya seperti pada gambar berikut} ini maka

Penyelesaian

 Parabola terbuka ke bawah berarti a < 0

 Parabola memotong sumbu x di dua titik berarti D > 0

 Parabola berat kekanan berarti a x b < 0, karena sudah diketahui a < 0, maka b > 0

 Parabola memotong sumbu y di atas titik O(0, 0) berarti c > 0 Jadi semua Penyelesaianan benar

2. Perhatikan gambar berikut!

(33)

Penyelesaian y = 4 + 3x – x2

a = -1; b = 3 dan c = 4

a = -1 < 0 berarti parabola terbuka kebawah a x b = -3 < 0 parabola berat kekanan jadi yang tepat gambar b.

Uji Kompetensi 3

Kerjakan soal-soal berikut.

1. Gambarlah grafik fungsi kuadrat berikut! a. f(x) = x2_{– 2x – 8 dengan Df = {x|-2 ≤ x ≤ 4}} b. f(x) = x2_{+ 4 – 9 dengan Df = {x|-1 ≤ x ≤ 5}}

2. dengan menentukan titik potong denga sumbu koordinat, titik puncak dan titik bantu lainnya, gambarlah grafik fungsi kuadrat berikut! a. f(x) = x2_{– x – 2} _{c. f(x) = -x}2_{+ 3}

b. f(x) = x2_{– 6x – 9} _{d. f(x) = -2x}2_{+ 4x - 5}

3. dengan memAnfaatkan translasi gambarlah sketsa grafik fungsi kuadrat berikut!

a. y = (x + 4)2 c. y = (x – 1)2 + 2 b. y = x2_{– 3} _{d. y = -2(x – 3)}2_{+ 7}

4. Grafik fungsi kuadrat f(x) = (a + 3)x2_{+ (a + 1)x + a melalui titik (1, -2)} a. Carilah nilai a

b. Gambarlah grafik fungsi kuadrat

c. Gambar grafik fungsi kuadrat tersebut dalam daerah asala (Df) {x|-3 ≤ x ≤ 3}, x  R}

5. Diketahui fungsi kuadrat f(x) = ax2 + bx + 5. Nilai maksimum fungsi f dicapai untuk x = 4

a. Tentukan nilai a dan b

b. Gambarlah sketsa frafik fungsi kuadrat tersebut.

6. Fungsi kuadrat f(x) = (p + 3)x2_{– 2(p – 1)x + (p – 5). Absis titik balik grafik} adalah p

a. Tentukan niLai p dan koordinat titik balik fungsi kuadrat tersebut. b. Gambarlah sketas grafik fungsi kuadrat tersebut.

7. Tentukan apakah bentuk berikut ini definit positif, definit negatif atau tidak keduanya.

a. f(x) = x2_{+ 6x + 12} _{d. f(x) = -3x}2_{+ x - 4} b. f(x) = 3x2_{+ 5} _{e. f(x) = -2x}2_{- 2x + 1} c. f(x) = 2(x – 3)2_-4 _{f. f(x) = -3(x + 1)}2

8. Tentukan nilai m agar grafik f(x) = -2x2_{+ 4x + m definit negatif} 9. Tentukan nilai k agar f(x) = x2_{+ 6x + k definit positif}

10. Tentukan nilai p agar grafik f(x) = (p - 1)x2_{+ 2px + (p – 3) seluruhnya} berada di bawah sumbu x

(34)

8. Menyusun Fungsi Kuadrat

Telah Anda pelajari cara-cara menggambar sketsa grafik fungsi kuadrat atau parabola apabila persamaan atau rumus fungsi kuadrat tersebut diketahui. Kali ini Anda akan mempelajari cara menentukan persamaan fungsi kuadrat apabila sketsa grafik fungsi kuadrat tersebut diketahui atau apabila fungsi kuadrat tersebut melalui tiga titik yang tidak segaris. Untuk lebih jelasnya, pelajarilah materi berikut.

a. Grafik Fungsi Kuadrat Memotong Sumbu X di A (x1,0) dan B (x2,0),

serta Melalui Sebuah Titik Tertentu.

Persamaan fungsi kuadrat tersebut dapat dinyatakan sebagai: y = f(x) = a( x – x1 ) ( x – x2 )

dengan nilai a ditentukan kemudian.

Agar Anda memahami dan terampil menggunakan rumus di atas, perhatikan contoh-contoh di bawah ini.

Contoh 13:

1. Suatu fungsi kuadrat memotong sumbu x di A(1, 0) dan B(5, 0). Jika fungsi kuadrat itu melalui titik (0, 10), tentukanlah persamaan fungsi kuadrat tersebut!

Penyelesaian:

Gunakan rumus y = f (x) = a ( x – x1 ) ( x – x2 ) , sehingga _{persamaan fungsi kuadrat itu dapat dinyatakan sebagai:} y = a ( x – 1 ) ( x – 5 ) ...……….(1)

karena fungsi kuadrat melalui titik ( 0,10 ) berarti jika x = 0 , maka diperoleh y = 10. Selanjutnya Anda tentukan nilai a sebagai berikut:

10 = a ( 0 – 1 ) ( 0 – 5 ) _{10 = a (-1) (-5)}

 10 = 5a

 a =

5 10

 _{a = 2}

Subsitusikan a = 2 ke persamaan (1), diperoleh: y = f (x) = 2 ( x – 1 ) ( x – 5 )

 y = f (x) = 2 ( x2_{– 5x – x + 5 )}  y = f (x) = 2 ( x2 _{– 6x + 5 )}  y = f (x) = 2x2_{– 12x + 10}

Jadi persamaan fungsi kuadratnya adalah _{y = f (x) = 2x}₂_{– 12x + 10}

2. Suatu fungsi kuadrat memotong sumbu x di A (-1,0 ) dan B (3,0). Jika fungsi kuadrat itu melalui titik (4,-5), tentukanlah

persamaan fungsi kuadrat itu! Penyelesaian:

Anda gunakan rumus y = f (x) = a ( x - x_{persamaan fungsi kuadrat itu dapat dinyatakan sebagai:}1 ) ( x - x2 ) , sehingga y = a ( x – (-1) ) ( x – 3 )

(35)

karena fungsi kuadrat melalui titik ( 4,-5 ) berarti jika x = 4 , maka diperoleh y = -5. Selanjutnya Anda tentukan nilai a sebagai berikut:

 -5 = a ( 4 + 1 ) ( 4 – 3 )  -5 = a (5) (1)

 -5 = 5a

 a =

5 5



 _{a = -1}

Subsitusikan a = -1 ke persamaan (1), diperoleh: y = (-1) ( x + 1 ) ( x – 3 )

 y = -( x2_{– 3x + x – 3 )}  y = -( x2– 2x – 3 )  _{y = -x}2_{+ 2x + 3}

Jadi persamaan fungsi kuadratnya adalah y = f (x) = -x2_{+ 2x + 3} b.Grafik Fungsi Kuadrat Menyinggung Sumbu X di A(x1, 0) dan

Melalui Sebuah Titik Tertentu.

Persamaan fungsi kuadrat tersebut dapat dinyatakan sebagai berikut: y = f (x) = a (x – x1) 2

Contoh 14:

1. Perhatikan gambar di bawah, diperlihatkan sketsa grafik dari suatu fungsi kuadrat. Tentukan persamaan grafik fungsi kuadrat tersebut!

Penyelesaian:

Berdasarkan grafik fungsi dapat ditentukan bahwa fungsi kuadrat itu menyinggung sumbu x di titik (2,0) dan melalui titik (0,3). Gunakan rumus y = f (x) = a ( x – x1 )2 , sehingga persamaan fungsi kuadrat itu dapat dinyatakan sebagai:

y = a (x – 2) 2_{...……….(1)}

(36)

3 = a ( 0 – 2 ) 2  3 = a (-2) 2  3 = 4a  a =

4 3

Subsitusikan a = 4

3_{ke persamaan (1), diperoleh:}

y = 4

3_{(x – 2)}₂

 y = 4 3_(x₂

– 4x + 4)

 y = 4

3_x₂_{– 3x + 3}

Jadi persamaan fungsi kuadratnya adalah y = f (x) = 4

3_x₂_{– 3x + 3}

2. Tentukan persamaan fungsi kuadrat yang menyinggung sumbu x di titik (1,0) dan melalui titik (-1, -4)

Penyelesaian:

Gunakan rumus y = f (x) = a (x – x1)_{kuadrat itu dapat dinyatakan sebagai:}2 , sehingga persamaan fungsi y = a (x – 1)2_{...……….(1)} Karena fungsi kuadrat melalui titik ( -1,-4 ) berarti jika x = -1 , maka _{diperoleh y = -4. Selanjutnya Anda tentukan nilai a sebagai berikut:} -4 = a (-1 – 1) 2

 -4 = a (-2) 2  -4 = 4a

 a =

4 4



 a = -1

Subsitusikan a = -1 ke persamaan (1), diperoleh: y = (-1) ( x – 1 ) 2

 y = (-1)( x2_{– 2x + 1 )} _{y = -x}2_{+ 2x – 1}

(37)

c. Grafik Fungsi Kuadrat Melalui Titik Puncak atau Titik Balik P(xp, yp), dan Melalui Sebuah Titik Tertentu.

Persamaan fungsi kuadrat tersebut dapat dinyatakan sebagai: y = f(x) = a(x – xp)2 + yp

Contoh 15:

Tentukan persamaan fungsi kuadrat yang mempunyai titik puncak atau titik balik di P (3, -1) dan melalui titik (0, 8) !

Penyelesaian:

Gunakan rumus y = f (x) = a ( x – xp )_{kuadrat itu dapat dinyatakan sebagai:} 2 + yp, sehingga persamaan fungsi y = a (x – 3) 2_{+ (-1)}

_{y = a (x – 3)} 2_{- 1 ...……….(1)}

Karena fungsi kuadrat melalui titik ( 0,8 ) berarti jika x = 0 , maka _{diperoleh y = 8. Selanjutnya Anda tentukan nilai a sebagai berikut:} 8 = a ( 0 – 3 ) 2_{– 1}

 _{8 = a (-3)} 2_{– 1}  8 = 9a – 1  _{8 + 1 = 9a}

 9 = 9a

 a =

9 9

 a = 1

Subsitusikan a = 1 ke persamaan (1), diperoleh: y = 1 . (x – 3) 2_{– 1}

 _{y = 1 .(x}2_{– 6x + 9) – 1}  y = x2_{– 6x + 9 – 1}  y = x2– 6x + 8

Jadi persamaan fungsi kuadratnya adalah y = f(x) = x2_{– 6x + 8}

Contoh 16:

Tentukan persamaan fungsi kuadrat yang mempunyai titik puncak atau titik balik di P (-1, -2) dan melalui titik (-2, -4)!

Penyelesaian:

Gunakan rumus y = f (x) = a ( x – xp )_{kuadrat itu dapat dinyatakan sebagai:}2 + yp, sehingga persamaan fungsi y = a(x – (-1)) 2_{+ (-2)}

 y = a(x + 1)2 _{- 2 ...……….(1)}

(38)

-4 = a(-2 + 1) 2 _{– 2}  -4 = a(-1) 2 _{– 2}  _{-4 = a – 2}

-4 + 2 = A  - 2 = A  _{a = -2}

Subsitusikan a = -2 ke persamaan (I), diperoleh: y = -2 ( x + 1 ) 2_{– 2}

 y = -2 ( x2_{+ 2x + 1 ) – 2}  _{y = -2x}2_{– 4x – 2 – 2}  y = -2x2_{– 4x – 4}

Jadi persamaan fungsi kuadratnya adalah y = f (x) = -2x2– 4x -4

d.Grafik Fungsi Kuadrat Melalui Titik-titik A(x1, y1), B(x2, y2), dan

C(x3,y3)

Persamaan fungsi kuadratnya dapat dinyatakan sebagai: y = f(x) = ax2_{+ bx + c}

dengan nilai a, b, dan c ditentukan kemudian.

Contoh 17:

Tentukan persamaan fungsi kuadrat yang melalui titik A(0, -10), B(1, -6), dan C(3, 8)!

Penyelesaian:

Misalkan persamaan fungsi kuadrat itu adalah : y = f (x) = ax2 + bx + c _{Melalui titik A ( 0,-10 ) , berarti:}

-10 = a(0) 2_{+ b (0) + c} _{-10 = 0 + 0 + c}

_{-10 = c}

 c = -10

_{Melalui titik B ( 1,-6 ) , berarti:} -6 = a (1) + b (1) + c  -6 = a + b + c

karena c = -10, maka:  -6 = a + b + (-10) _{-6 = a + b – 10}

 -6 +10 = a + b  4 = a + b

_{a + b = 4 ...………(1)}

[image:38.612.156.449.70.241.2]

(39)

 8 = 9a + 3b + c karena c = -10, maka: 8 = 9a + 3b + (-10) 8 = 9a + 3b – 10 8 + 10 = 9a + 3b 18 = 9a + 3b

9a + 3b = 18 (kedua ruas dibagi 3)

_{3a + b =6 ...………(2)}

_{Eliminasi b dari persamaan (1) dan (2) , berarti:}

a + b = 4

3a + b = 6

––––––––––

-2a = -2

a =

2 2

 

a = 1

Subsitusikan a = 1 ke persamaan (1) atau (2) (pilih salah satu) _{Misalkan kita pilih ke persamaan (1), maka:}

a + b = 4

_{a + b = 4}

b = 4 – 1

_{b = 3}

Subsitusikan a = 1, b = 3, dan c = -10 ke persamaan _{y = f (x) = ax}₂_{+ bx + c , diperoleh:} y = f(x) = (1) x2_{+ (3) x + (-10)} y = f(x) = x2_{+ 3x – 10} Jadi persamaan fungsi kuadratnya adalah: y = f (x) = x2 + 3x – 10

Uji Kompetensi 4

Kerjakan soal-soal berikut.

Kerjakan soal-soal di bawah ini dengan singkat, jelas, dan benar! 1. Susunlah sebuah fungsi kuadrat yang grafiknya:

a. Melalui titik (0, 3), (2, -5), dan (-4, 13) b. Melalui titik (-3, 0), (1, 0), dan (-2, 6)

c. Menyinggung sumbu x di (-2, 0) dan titik (2, -8) d. Menyinggung sumbu x di (1, 0) dan titik (0, 3)

e. Melalui titik (-2, 0), (4, 0), dan (0, -16)

f. Memiliki titik puncak (-1, 1) dan melalui (-2, 4)

(40)

2. Tentukan persamaan fungsi kuadrat yang mempunytai grafik seperti gambar di bawah ini!

9. Penerapan Fungsi Kuadrat pada Masalah maksimum dan Minimum Grafik fungsi kuadrat y = ax2_{+ bx + c berbentuk parabola dengan} koordinat titik puncak (x, y) = 

  



_ _

a D a b

4 ,

2 . Puncak parabola merupakan titik terendah (minimum) atau titik tertinggi (maksimum).

 Untuk a < 0:

Terdapat nilai maksimum

a D

4

 yang dicapai untuk x =

a b

2



 Untuk a > 0:

Terdapat nilai minimum

a D

4

 yang dicapai untuk x =

a b

2



Dalam kehidupan sehari-hari tentunya Anda sering menjumpai suatu permasalahan yang berkaitan dengan fungsi kuadrat. Oleh karena itu nilai ekstrim (maksimum atau minimum) berperan penting dalam memecahkan masalah yang berkaitan dengan fungsi kuadrat.

Nilai maksimum atau minimum diungkapkan dengan menggunakan kata-kata yang berbeda, misalnya:

a) terbesar, terjauh, tertinggi, terpanjang, terluas, atau yang sama artinya dengan kata-kata itu, dapat dikaitkan dengan konsep nilai maksimum fungsi kuadrat.

b) terkecil, terdekat, terendah, terpendek, tersempit, atau yang sama artinya dengan kata-kata itu, dapat dikaitkan dengan konsep nilai minimum fungsi kuadrat.

[image:40.612.158.391.110.262.2]

(41)

1) Nyatakan besaran yang ada dalam masalah sebagai variabel (dilambangkan dengan huruf-huruf) untuk mendapatkan hubungan atau ekspresi matematikanya.

2) Rumuskan fungsi kuadrat yang merupakan model matematika dari masalah.

3) Tentukan penyelesaian dari model matematika fungsi kuadrat yang diperoleh pada langkah 2.

4) Tafsirkan hasil-hasil yang diperoleh pada langkah 3 terhadap masalah semula.

Contoh 18:

1. Ekonomi. Biaya untuk membuat x satuan barang adalah 25

35 4

1_x2_ _x_ _{(dalam jutaan rupiah). Sedangkan harga jual untuk x}

satuan barang (50 – 2

1_{x)x (dalam jutaan rupiah). Berapa banyak} satuan barang yang harus diproduksi agar diperoleh keuntungan maksimum? Berapakah keuntungan maksimum tersebut?

Penyelesaian:

Biaya total = 35 25 4

1_x2_ _x_ _{(dalam jutaan rupiah)}

Harga jual = (50 – 2

1_{x)x (dalam jutaan rupiah)}

= 50x - 2 1_x₂

Keuntungan diperoleh dari selisih harga jual dan biaya total untuk x satuan barang, sehingga

Keuntungan (K(x)) = harga jual – biaya total = (50x -

2

1_x₂_{) – (} ₃₅ ₂₅ 4

1_x2_ _x_ ₎

= 50 35 25

4 1 2

1 2_ 2_ _ _

 x x x x

= 50 35 25

4 1 2

1 2_ 2_ _ _

 x x x x

= 15 25

4

3 2_ _

 x x

a = 4 3

 < 0  nilai maksimum b = 15

(42)

x = 10

2 3 15

4 3 2

15

2 __ 

       

a b

Jadi keuntungan masimum (K) =

a 4

ac 4 b a 4

D 2_

  

=

 

     

        

4 3 4

) 25 ( 4 3 4 15 2

=

3 150 3

75

225 _

  

= 50 atau

Subtitusi x = 10 pada K = 15 25 4

3 2_ _

 x x

= (10) 15(10) 25 4

3 2_ _



= 7515025= 50

Jadi, agar diperoleh keuntungan maksimum harus diproduksi 10 satuan barang dan keuntungan maksimumnya adalah Rp 50.000.000,00

2. Geometri.Kawat ram yang panjangnya 100 m akan digunakan untuk memagari kandang ayam seperti gambar di bawah ini.

Kandang ayam tersebut berbentuk persegi panjang yang salah satu sisinya adalah tembok.

Tentukan ukuran kandang tersebut agar luas kandang maksimum dan berikan penjelasan tafsiran dari solusi masalahnya!

Penyelesaian:

•) Anda buat sketsa kandang ayam seperti gambar berikut:

•) Misalkan x = panjang dan y = lebar _{Berdasarkan gambar di atas, keliling pagar ayam = panjang kawat} ram

 y + x + y = 100

(43)

Fungsi, Persamaan dan Pertidaksamaan Kuadrat Page | 43  2y = 100 – x  y = 50 - 1₂x

•) _{Luas kandang ayam = panjang x lebar}

 L = x . y

 L = x . (50 - ₂1x)

 L = 50x – ₂1x2

•)

L merupakan fungsi kuadrat dalam x yaitu: L(x) = 50x – 2 1_x₂

berarti a =

-2

1_{, b = 50, dan c = 0.}

Agar L maksimum maka x =

a b

2



 x =

      

2 1 2

50

 x =50 Untuk x = 50 maka:  y = 50 –

2 1₅₀

 y = 50 – 25

 y = 25 •) Penafsiran solusi masalahnya:

Agar diperoleh luas kandang maksimum maka kawat ram tersebut harus digunakan untuk memagari kandang ayam yang berbentuk persegi panjang dengan salah satu sisinya tembok dengan ukuran panjang = 50 meter dan lebar = 25 meter.

Uji Kompetensi 5

Kerjakan soal-soal berikut.

1. Jumlah dua buah bilangan adalah 30.

Jika hasil kali kedua bilangan itu maksimum maka tentukan bilangan-bilangan tersebut dan jelaskan penafsiran solusi masalahnya!

2. Selisih dua buah bilangan adalah 10

Tentukan hasil kali minimum kedua bilangan itu dan jelaskan penafsiran solusi masalahnya!

(44)

3. Sebuah peluru ditembakkan vertikal ke atas.

Tinggi peluru h (dalam meter) sebagai fungsi waktu t (dalam detik) Dirumuskan dengan h (t) = 100t – 5t2_.

Tentukan tinggi maksimum yang dapat dicapai peluru dan waktu yang diperlukan serta jelaskan penafsiran solusi masalahnya!

4. Perhatikan gambar di samping. Persegi ABCD memiliki panjang sisi 8 cm, sedangkan AK = x cm, dan DL = 2x cm. Jika L menyatakan luas CKL, tunjukkan bahwa : L (x) = x – 8x + 32, kemudian tentukan luas minimum segitiga CKL dan jelaskan penafsiran masalahnya !

5. Pada gambar berikut merupakan persegi panjang yang panjangnya 8 cm dan lebarnya 4 cm. Titik-titik E, F, G dan H terletak pada AB, BC, CD dan AD sehingga BE = CF = DG = AH = x cm

a. Jika L (cm2_{) menyatakan luas} daerah segi empat EFGH. Nyatakan L dalam x

b. Tentukan luas minimum segi empat EFGH itu

B.

Persamaan Kuadrat

1. Pengertian Persamaan Kuadrat

Misalkan a,b,c Є R dan a ≠ 0 maka persamaan yang berbentuk 0

2 __bx__c_

ax dinamakan persamaan kuadrat dalam peubah x.

Dalam persamaan kuadrat _ax2__bx__c_0_{, a adalah koefisien dari}_x₂_{, b} adalah koefisien dari x dan c adalah suku tetapan.

Contoh:

1. x2_{– 4, nilai a = 1, b= 0, c = -4} 2. x2_{+ 2x = 0 nilai a = 1, b =2, c = 0} 3. x2 – 5x + 2 = 0 nilai a = 2, b = -5, c = 2 4. x2 + x – 2 = 0 nilai a = 1, b =2, c = -2

Berkaitan dengan nilai-nilai a, b, dan c, dikenal beberapa persamaan kuadrat, diantaranya adalah:

(i) Jika a = 1, maka persamaan menjadi x + bx + c = 0 dan persamaan seperti ini disebut persamaan kuadrat biasa.

(ii) Jika b = 0, maka persaman menjadi x + c = 0 dan persaman seperti ini disebut persamaan kuadrat sempurna.

(iii) Jika c = 0, maka persamaan menjadi ax + bx = 0 dan persamaan seperti ini disebut peramaan kuadrat tak lengkap.

Jika a, b, dan c bilangan-bilangan rasional maka ax + bx + c = 0 disebut persamaan kuadrat rasional.

A D

B C

E F G

H

4 c

m

8 cm x

x

(45)

seringkali persamaan kuadrat tidak langsung berupa bentuk umum tetapi dengan operasi aljabar kita dapat mengubahnya kebentuk umum. Contoh 19:

Tuliskan persamaan kuadrat berikut ke dalam bentuk umum dan tentukan nilai a, b dan c?

1. 3x2_{+ x = 3x – 5} 2. 2(x2 _{– x) = 5x(x – 2)} 3. (2x + 5) (4x – 1) = 4

4. 2

2 3

4 _

 

x

x dengan x ≠ 0 dan x ≠ 2

Penyelesaian

1. 3x2_{+ x = 3x – 5} _{3. (2x + 5) (4x – 1) = 4}

 3x2_{+ x - 3x + 5 = 0} __{2x(4x – 1) + 5(4x – 1) = 4}

 3x2_{-2x + 5 = 0} __{.... - 2x + 20x - ... – 4 = 0} a = 3; b = -2 dan c = 5  .... + 18x - .... = 0 2. 2(x2 _{– x) = 5x(x – 2)} _{a = ....; b = 18; c = ....}

 2x2 _{- .... = 5x}2_{- ....} _4. 2 2 3

4 _

 

x

x ; x ≠ 0 dan x ≠ 2

 2x2 - .... - 5x2 + .... = 0 4(x -2) + 3x = 2x(x – 2) a = ...; b = .... dan c = .... 4x – 8 + 3x = 2x2_{- 4}

 7x .... – 8 .... – 2x2_{+ .... = 0}  -2x2_{+ ... - ... = 0}

 a = ....; b = ....; c = .... 2. Menyelesaikan Persamaan Kuadrat

Setelah Anda memahami beberapa bentuk persamaan kuadrat, selanjutnya marilah kita pelajari cara-cara menentukan akar-akar persamaan kuadrat. Kita masih ingat bahwa untuk menetukan akar-akar persamaan kuadrat dapat dilakukan dengan beberapa cara yaitu: a. Memfaktorkan (pemfaktoran)

b. Menggunakan rumus kuadrat.

c. Melengkapkan bentuk kuadrat sempurna.

Kali ini, kita akan mempelajari cara menentukan akar-akar persamaan kuadrat dengan cara memfaktorkan dan menggunakan rumus kuadrat. Untuk itu, Anda pelajari baik-baik materi berikut ini.

a. Menentukan Akar-Akar Persamaan Kuadrat dengan Memfaktorkan Jika suatu persamaan kuadrat ax2_{+ bx + c = 0 dapat difaktorkan} menjadi berbentuk P x Q = 0, maka akar-akar persamaan kuadrat tersebut dapat ditentukan dengan cara memfaktorkan (pemfaktoran). Contoh persamaan kuadrat yang dapat difaktorkan antara lain:

x2 + 3x + 2 (x+2) (x+1) = 0 = 0

2x2 - x - 1 (2x+1) (x-1) = 0 = 0

P Q

(46)

Lalu bagaimana menentukan akar-akar persamaan kuadrat dengan cara pemfaktoran?

Baiklah, untuk lebih jelasnya Anda pelajari beberapa contoh soal di bawah ini.

Untuk lebih mudah dalam melakukan faktorisasi kita bagi persamaan ax2_{+ bx + c = 0 menjadi dua kasus}

 _{Kasus a = 1}

x2_{+ bx + c = 0 dapat difaktokan menjadi (x + m)(x + n) = 0 dengan} m + n = b dan m . n = c

lebih mudah jika Anda menggunakan bagan seperti pada gambar di samping!

Contoh 20:

1. Tentukan akar-akar persamaan kuadrat x2_{+ 5x + 6 = 0 dengan} cara pemfaktoran!

Penyelesaian:

x2 + 5x + 6 = 0 (cari pasangan bilangan hasil kalinya 6 dan berjumlah 4)

Sehingga x2_{+ 5x + 6 = 0} (x + 3)(x + 2) = 0

x + 3 = 0 atau x + 2 = 0 x = - 3 atau x = -2

Jadi, akar-akar x2_{+ 5x + 6 = 0 adalah 2 atau 3}

Hp = {2, 3}

2. Tentukan akar-akar persamaan kuadrat: x2_{– x – 12 = 0 dengan} cara pemfaktoran!

Penyelesaian:

x2_{– x – 12 = 0} _{(cari pasangan bilangan hasil kalinya -12 dan} berjumlah -1)

Sehingga x2 - x - 12 = 0 (x - ...)(x + 3) = 0

x - ... = 0 atau x + 3 = 0 x = ... atau x = ...

Jadi, akar-akar x2_{- x - 12 = 0 adalah ... atau ...}

Hp = {..., ...}

m n

c x _ b

3 2

6 x + 5

... 3

(47)

3. Tentukan akar-akar persamaan kuadrat: x2 – 4 = 0 dengan cara pemfaktoran!

Penyelesaian:

x2_{– 4 = 0} _{(cari pasangan bilangan hasil kalinya -4 dan} berjumlah 0)

Sehingga x2_{– 4 = 0}

(x + ...)(x - ...) = 0

x + ... = 0 atau x - ... = 0 x = ... atau x = ...

Jadi, akar-akar x2 - 4 = 0 adalah ... atau ...

Hp = {..., ...}

 Kasus a ≠ 1

ax2_{+ bx + c =}



ax bx c



a  

2 1

=



ax m



ax n



a  

1

ax2_{+ bx + c = 0 dapat difaktorkan menjadi}

a

1_{(ax + m)(ax + n) = 0} dengan m + n = b dan m . n = ac

lebih mudah jika Anda menggunakan bagan seperti pada gambar di samping!

Contoh 21:

1. Tentukan akar-akar persamaan kuadrat: 2x2_{+ 3x + 1 = 0 dengan} cara pemfaktoran!

Penyelesaian:

2x2_{+ 3x + 1 = 0 (cari pasangan bilangan hasil kalinya 2 dan} berjumlah 3)

Sehingga 2x2 + 3x + 1 = 0

2

1_{(2x + 2)(2x + 1) = 0}

2

1_{. 2(x + 1)(2x + 1) = 0} (x + 1)(2x + 1) = 0

x + 1 = 0 atau 2x + 1 = 0 x = -1 atau x = -

2 1

Jadi, akar-akar x2_{x 12 = 0 adalah 1 atau}

-2 1

Hp = {1, -2 1_} ...

...

-4 x + 0

m n

ac x _ b

2 1

(48)

atau

2x2_{+ 3x + 1} 2x2 + 2x + x + 1

= 0

= 0 Penjelasan:

disini 3x kita ubah menjadi 2x + x karena: 2x . x = 2x2_{. 1}

2x2_{= 2x}2

secara skema dapat dijelaskan sbb:

2x2 + 2x difaktorkan menjadi 2x(x+1) x + 1 difaktorkan menjadi 1(x+1) 2x(x+1) + x + 1 = 0

2x(x+1) + 1(x + 1) = 0 (x + 1) (2x + 1) = 0 x+1=0 atau 2x+1=0 _{x = 0–1 atau 2x = 0-1} x = -1 atau 2x = -1

x = -2 1

Jadi akar-akar persamaan kuadrat 2x2 + 3x + 1 = 0 adalah x1 = -1 atau x2 = -

2 1_.

Hp = {1, -2 1_}.

2. Tentukan akar-akar persamaan kuadrat: 7 + 19x – 6x2_{= 0 dengan} cara pemfaktoran!

Penyelesaian: 7 + 19x – 6x2 = 0 -6x2_{+ 19x + 7 = 0}

6x2_{- 19x - 7 = 0} _{x (-1)} Sehingga 6x2_{- 19x - 7 = 0}

...

1 _{(6x ...)(6x ...) = 0}

...

1 _{. 3(2x ...)2(3x ...) = 0} (2x ...)(3x ...)

2x ... = 0 atau 3x ... = 0 x = ... atau x = ...

Jadi, akar-akar 6x2 - 19x - 7 = 0 adalah ... atau ...

Hp = {..., ...}

b.Menentukan Akar-Akar Persamaan Kuadrat dengan Melengkapkan Kuadrat Sempurna

Cobalah Anda ingat kembali beberapa contoh bentuk kuadrat sempurna, antara lain: 4 = 22_{, 9 = 3}2_{, 4x}2_{= (2x)} 2_{, x}2_{+ 2x + 1 = (x + 1)}2_, x2 _{– 4x + 4 = (x–2)}2_{, dan sebagainya.}

Pada prinsipnya, tiap bentuk kuadrat dapat dimanipulasi secara aljabar menjadi bentuk kuadrat sempurna. Untuk lebih jelasnya marilah kita perhatikan beberapa contoh pengubahan bentuk kuadrat menjadi bentuk kuadrat sempurna di bawah ini.

... ...

(49)

a. Bentuk x2_{+ 2x + 5 dapat dimanipulasi secara aljabar sebagai} berikut :

x2_{+ 2x + 5}

_(x2_{+ 2x + 4) + (-4) + 5}



 (x + 2)2 ₊ ₁

Bentuk ini memuat bentuk kuadrat sempurna, yaitu : (x + 2)2 b. Bentuk -x2_{- 6x + 10 dapat dimanipulasi secara aljabar sebagai}

berikut : -x2_{- 6x + 10}

 -(x2_{+ 6x + 9) + (9) + 10}



 - (x + 3)2 ₊ ₁₉

Bentuk ini memuat bentuk kuadrat sempurna, yaitu : -(x + 3)2 c. Bentuk x2_{- 8x - 1 dapat dimanipulasi secara aljabar sebagai}

berikut : x2_{- 8x - 1}

 _(x2_{- 8x + 16) + (-16) – 1}



 (x - 4)2 _{+ (-17)}  (x - 4)2 - 17

Bentuk ini memuat bentuk kuadrat sempurna, yaitu : (x - 4) 2 Dari ketiga contoh tersebut di atas, proses pengubahan bentuk kuadrat menjadi bentuk kuadrat sempurna semacam itu disebut melengkapkan kuadrat sempurna.

Selanjutnya, kita akan menggunakan proses melengkapkan bentuk kuadrat untuk menentukan akar-akar persamaan kuadrat. Apabila suatu persamaan kuadrat dapat difaktorkan, maka dengan mudah kita dapat menentukan akar-akarnya dengan pemfaktoran. Tetapi apabila suatu persamaan kuadrat tidak dapat difaktorkan, maka salah satu cara untuk menentukan akar-akarnya adalah dengan melengkapkan kuadrat sempurna.

Contoh 22:

1. Tentukan akar-akar persamaan kuadrat x2_{+ 4x - 1 = 0} Penyelesaian:

x2_{+ 4x - 1} _{= 0}

 x2_{+ 4x - 1 + 1 = 0 + 1} _{kedua ruas ditambah 1)}

 x2_{+ 4x} _{= 1}

 x2 + 4x + (( 2

1_.4)2) = 1+(( 2

1_.4)2) Kedua ruas ditambah 4 yang merupakan kuadrat dari

2 1_kali koefisien x, yaitu ((

2

(50)

Fungsi, Persamaan dan Pertidaksamaan Kuadrat Page | 50 



= =

1 + 4 1 + 4

 (x + 2)2 _{= 5}

 x + 2 = ±√5

 x = - 2 ± √5

x = -2 + √5 atau x = -2 - √5

Jadi akar-akar persamaan kuadrat x2_{+ 4x - 1 = 0 adalah} x1 = -2 + √5 atau x2 = -2 - √5

Hp = {-2 +√5 , -2 - √5}

2. Tentukan akar-akar persamaan kuadrat x2_{- 6x + 4 = 0} Penyelesaian:

x2_{- 6x + 4} _{= 0}

_x2_{- 6x + 4 + (-4)} _{= 0 + ...} _{(kedua ruas ditambah -4)}

_x2_{- 6x} _{= ....}

_x2_{- 6x + (} 2

1_(...))2 _{= ... + (} 2

1_(...))2_{(Kedua ruas ditambah ...} yang merupakan kuadrat dari setengah kali koefisien x, yaitu (

2

1_(...))2

 x2_{- 6x + 3}2_{= ...+ ...}...

 ( x - 3 ) 2 _{= ...+ ...}

_{x - 3 = ± ...} _x = ... ± ...

x = ... - ... Atau x = ... + ... Jadi akar-akar persamaan kuadrat x2_{- 6x + 4 = 0} adalah

x1 = ... - ... Atau x2 = ... + ...

Hp = ... - ..., ... + ...}

3. Tentukan akar-akar persamaan kuadrat 2x2_{- 4x + 1 = 0} Penyelesaian :

2x2_{- 4x + 1} _{= 0}

_x2_{- 2x +} 2 1

= 0 (kedua ruas dibagi 2)

_x2_{- 2x +} 2

1_{+ (...) = 0 + (...)} _{(kedua ruas ditambah (...))}

_x2_{- 2x}

= 2 1 

_x₂_{- 2x +}

 

... 2

2

1 _

   

 ₌ 2 1

 +

 

... 2

2

1 _

   

 (Kedua ruas ditambah ... yang merupakan kuadrat dari

setengah kali koefisien x, yaitu

_x2 - 2x + (