BAB 2 Persamaan dan Fungsi Kuadrat fixs

(1)

BAB 2

PERSAMAAN , PERTIDAKSAMAAN, DAN FUNGSI KUADRAT A. PERSAMAAN KUADRAT

1. Bentuk umum persamaan kuadrat

Bentuk umum persamaan kuadrat adalah ax2 bx c 0 ; a 0  � 2. Menyelesaikan persamaan kuadrat

Basic concept :

Ada beberapa cara untuk menyelesaikan persamaan kuadrat, antara lain :

 Memfaktorkan 2

ax bx c 0  _{diuraikan menjadi}1a



ax p ax q

 





_{dengan p +} q = b dan pq = ac atau bentuk



x x 1

 

x x 2



0

Maka diperoleh :

1 2

 Melengkapkan kuadrat sempurna

Bentuk seperti 16 = 42_{; 4x}2_{= (2x)}2_{; (x + 1)}2_{; (2x – 3)}2 _merupakan beberapa contoh bentuk kuadrat sempurna.

Bentuk x2 2x 7 dapat dimanipulasi aljabar sebagai berikut :

(2)

memuat bentuk kuadrat sempurna (x 1) 2. Proses mengubah bentuk kuadrat menjadi bentuk kuadrat sempurna semacam itu dinamakan melengkapkan kuadrat sempurna.

Contoh:

Selesaikan persamaan kuadrat x2  3x 2 0 dengan cara melengkapkan kuadrat sempurna !

Jawab :

x 2 cari separonya

(3)

c bilangan real dan a 0� maka akar-akar persamaan kuadrat

3. Menentukan jenis akar-akar persamaan kuadrat

Penyelesaian persamaan kuadrat ax2bx c 0 dengan (a 0)  �

. Tampak bahwa akar-akarnya ditentukan oleh nilai dari b2_{– 4ac yang disebut dengan diskriminan disingkat D.} Jenis akar-akar persamaan kuadrat ax2  bx c 0, ditentukan oleh nilai Diskriminannya (D) yaitu D =b24ac

 D > 0 : mempunyai dua akar real yang berbeda  D = 0 : mempunyai dua akar real yang sama  D < 0 : akar-akarnya imajiner (khayal) Metode supertrik :

Jika menemui tanda < atau � maka pilih di jawaban : …< x <…

Jika menemui tanda > atau � maka pilih di jawaban : x <… ATAU x >….

4. Jumlah dan hasil kali akar – akar persamaan kuadrat Basic concept :

(4)

 

5. Menyusun persamaan kuadrat yang diketahui akar-akarnya

Jika akar-akar persamaan kuadrat ax2  bx c 0 telah diketahui, maka persamaaan kuadrat baru dengan akar – akar x1 dan x2 dapat dinyatakan dalam bentuk: x2(x1x )x x x2  1 20

2. PERTIDAKSAMAAN KUADRAT

a. Bentuk baku

pertidaksamaan kuadrat

Bentuk baku dari pertidaksamaan kuadrat dalam variabel ada 4 jenis, yaitu:

Himpunan penyelesaiannya dari pertidaksamaan kuadrat 2

x   3x 4 0_adalah… Jawab :

Cari pembuat nol :



 



(5)

Sehingga himpunan penyelesaiannya : HP {x| 1 x 4,x R}    � (selang terbuka/bolong karena tidak memuat tanda sama dengan)

Contoh 2 :

Himpunan penyelesaiannya dari x2 3x 4 0� adalah… Jawab :

Dengan cara mencari pembuat nol pada contoh 1, diperoleh garis bilangan :

Sehingga himpunan penyelesaiannya : HP {x| 1 x 4,x R}  � � � (selang tertutup karena memuat tanda sama dengan)

Contoh 3 :

Himpunan penyelesaian dari pertidaksamaanx2  3x 4 0adalah… Jawab :

Dengan cara mencari pembuat nol pada contoh 1, diperoleh garis bilangan :

Sehingga himpunan penyelesaiannya : HP {x|x  1 atau x 4,x R} � (selang terbuka/bolong karena tidak memuat tanda sama dengan).

Contoh 4 :

Himpunan penyelesaiannya dari x2 3x 4 0� adalah… Jawab:

Dengan langkah awal mencari pembuat nol pada contoh 1, diperoleh garis bilangan :

(6)

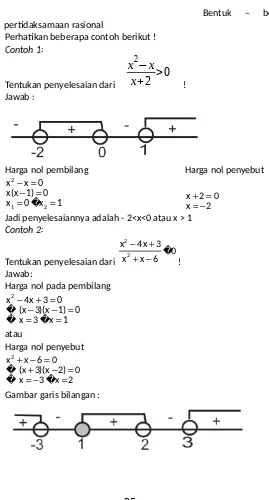
c. Bentuk – bentuk pertidaksamaan rasional

Perhatikan beberapa contoh berikut ! Contoh 1:

Tentukan penyelesaian dari

x

2

−

x

+

2 >

0

_! Jawab :

Harga nol pembilang Harga nol penyebut 2

1 2

x x 0 x(x 1) 0

x 0 x 1

   

 �  x 2 0_x _{ }₂

Jadi penyelesaiannya adalah - 2<x<0 atau x > 1 Contoh 2:

Tentukan penyelesaian dari 2

2 x 4x 3

0 x x 6

  _�

  _!

Jawab:

Harga nol pada pembilang 2

x 4x 3 0 (x 3)(x 1) 0 x 3 x 1   

  

�

 

� �

atau

Harga nol penyebut 2

x x 6 0 (x 3)(x 2) 0

x 3 x 2

     

�

  

� �

(7)

Jadi himpunan penyelesaian dari 2

2 x 4x 3

0 x x 6

  _�

  _adalah





HP x|x 3 atau 1 x 2 atau x 3� 

3. FUNGSI KUADRAT

a. Bentuk Umum

Bentuk umum fungsi kuadrat adalah f(x) = y = ax2_{+ bx + c , dengan} a 0, dan a,b,c R� �

b. Menggambar grafik

fungsi kuadrat Basic concept :

Langkah – langkah dalam menggambar grafik fungsi kuadrat adalah : (1) Menentukan titik potong dengan sumbu x (syarat : y = 0)

(2) Menentukan titik potong dengan sumbu y (syarat : x = 0) (3) Menentukan titik puncak / ekstrim (Xp, Yp) :

Dengan :

p p

b D

x dan y

a 4a

  

 Keterangan :

Xp = persamaan sumbu simetri Yp = nilai maksimum/minimum D = diskriminan = b2_{– 4ac}

(4) Bantuan titik – titik lain dengan tabel PAKET SOAL DAN PEMBAHASAN 1. UN 2010

Grafik fungsi kuadrat f(x) x  2 bx 4 menyinggung garis y = 3x + 4. Nilai b yang memenuhi adalah . . .

A. – 4 D. 3

B. – 3 E. 4

C. 0

Pembahasan :

Karena garis dan grafik bersinggungan, maka berlaku:





2 2

x bx 4 3x 4 x b 3 x 0 *)

(8)

Menggunakan sifat garis singgung grafik fungsi kuadrat, maka berlaku nilai diskriminan (D) pada persamaan *) adalah 0, sehingga:





2





2

b 3 4 1 0 0�� � b 3 0�b 3

Jawaban:D 2. UN 2011

Grafik y = px2_{+ (p + 2)x – p + 4 memotong sumbu x di dua titik. Batas –} batas nilai p yang memenuhi adalah…

A.

Syarat memotong : D > 0









real. Batas – batas nilai m yang memenuhi adalah…

(9)

Tidak mempunyai akar – akar real : D < 0, artinya pilih KECIL < x < BESAR (jadi pilihan A,B,C jelas salah)









berbeda. Batas – batas nilai p yang memenuhi adalah…

A. p 2 atau p 8� � Metode supertrik :

Akar – akar real berbeda : D > 0 artinya pilih KECIL ATAU BESAR (pilihan D dan E jelas salah)





dua titik yang berlainan. Batas – batas nilai t adalah… A. 1 t 3  

(10)

E. t�1 atau t 3� Pembahasan : Memotong : D > 0 y = y sehingga diperoleh :





PAKET SOAL LATIHAN

(11)

A.

7. Persamaan kuadrat x2_{– 8x + k = 0 mempunyai perbandingan akar – akar} 3 : 1. Nilai k adalah…

A. 16 D. 8

B. 12 E. – 8

C. 10

8. Agar persamaan 2mx2_{+ 4x + m – 1 = 0, mempunyai akar – akar real (nyata)} dan berbeda, maka nilai m yang memenuhi adalah…

A. m < – 1 atau m > 2 – 3. Jumlah akar – akar persamaan kuadrat tersebut adalah…

A. 4 D. – 2

B. 2 E. – 4

C. – 1

(12)

B. x 2_{+ 9x + 8 = 0} _{E. x}2 _{+ 9x – 8 = 0} C. x2_{– 9x – 8 = 0}

11. Himpunan penyelesaian dari pertidaksamaan kuadrat x2_{– 3x – 4 > 0} adalah…

A. x < - 1 atau x > 4 D. – 4 < x < - 1 B. x < - 1 atau x > - 4 E. x > - 1 atau x < - 4 C. – 1 < x < 4

12. Nilai x yang memenuhi

x 5 ₀ x 8

 _�

 _adalah…

A. x < -8 atau x ≥ 5 D. – 5 ≤ x < 8 B. - 8 < x ≤ 5 E. x ≤ - 8 atau x ≥ 5 C. x < - 12

13. Nilai x yang memenuhi pertidaksamaan 2 2

x 5x 6

x 2x 3

 

  _{≤ 0 adalah…} A. x ≤ - 3 atau 1 < x ≤ 2

B. – 3 < x < 1 atau 2 ≤ x ≤ 3 C. 1 < x ≤ 2 atau x > 3 D. 1 < x ≤ 2 atau x ≥ 3

E. x < - 3 atau 1 < x ≤ 2 atau x ≥ 3

14. Penyelesaian dari : x x 22   x 6 adalah…

A. – 6 < x ≤ 2 D. – 2 < x ≤ - 1 atau 2 ≤x < 4 B. – 4 < x < 2 E. – 4 < x ≤ - 2 atau – 1 ≤ x < 2 C. – 6 < x < - 1

15. Nilai yang memenuhi : |2x – 3| ≥ 5 adalah…

A. 1 ≤ x ≤ 4 D. x ≤ 1 atau x ≥ 4 B. 1 < x < 4 E. 3 ≤ x ≤ 5 C. x ≤ - 1 atau x ≥ 4

16. Pertidaksamaan x 2

2 x 3

 _�

 _{akan bernilai benar jika…} A. – 4 ≤ x < - 3 D. – 8 ≤ x < -3

B. x ≤ - 8 atau x ≥ 4 3 

E. – 8 ≤ x ≤ - 1 C. x ≤ - 4 atau x ≥ 3

17. Titik potong dengan sumbu Y dan titik puncak fungsi f(x) = –3x2_{+ 6x – 5,} berturut – turut adalah…

(13)

B. (0,5) dan (2,1) E. (0,5) dan (1,2) C. (0, - 5) dan (2, - 1)

18. Fungsi kuadrat y = 2x2_{– 4x + 10 mempunyai titik…} A. Minimum yaitu (2,10)

B. Maksimum yaitu (2,10) C. Minimum yaitu (1,8) D. Maksimum yaitu (1,8) E. Minimum yaitu ( - 1, 16)

19. Diketahui parabola y = (x – 3)2_{– 25. Pernyataan di bawah ini benar,} kecuali…

A. Persamaan sumbu simetri x = 3 B. Nilai minimumnya y = – 25 C. Titik baliknya ( –25, 3)

D. Koordinat titik potong sumbu x adalah (8,0) dan (- 2,0) E. Koordinat titik potong sumbu y adalah (0, - 16)

20. Fungsi kuadrat yang grafiknya berpuncak di titik (3,2) dan melalui titik (2,4) adalah…