Analisis Heteroskedastisitas Pada Regresi Linier Berganda Dan Cara Mengatasinya

ANALISIS HETEROSKEDASTISITAS PADA REGRESI LINIER

BERGANDA DAN CARA MENGATASINYA

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar sarjana sains

UCI SUPRIANA 100823009

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : ANALISIS HETEROSKEDASTISITAS PADA

REGRESI LINIER BERGANDAN DAN CARA MENGATASINYA

Kategori : SKRIPSI

Nama : UCI SUPRIANA

Nomor Induk Mahasiswa : 100823009

Program Studi : SARJANA (S1) MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PERNGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di

Medan, Juli 2012 Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Liling Peranginangin M.Si Drs. Pengarapen Bangun, M.Si NIP 194707141984031001 NIP 195608151985031005

Diketahui / Disetujui Oleh

Departemen Matematika FMIPA USU Ketua,

PERNYATAAN

ANALISIS HETEROSKEDASTISITAS PADA REGRESI LINIER BERGANDA DAN CARA MENGATASINYA

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juni 2012

PENGHARGAAN

Bismillahirrahmanirrahim,

Puji dan syukur Penulis panjatkan kepada Allah SWT Yang Maha pemurah dan Maha Penyayang, dengan limpahan karunia – Nya skripsi ini berhasil diselesaikan dalam waktu yang telah ditetapkan .

Selama dalam penyusunan skripsi ini penulis telah banyak memperoleh bantuan dan bimbingan, untuk itu pada kesempatan ini penulis ingin mengucapkan terimakasih yang sebesar- besarnya kepada Bapak Drs. Pengarapen Bangun, M.Si selaku pembimbing 1 dan Bapak Drs. Liling Peranginangin, M.Si selaku pembimbing 2 pada penulisan skripsi ini, yang telah bersedia memberikan arahan, bimbingan dan petunjuk kepada penulis dalam menyelesaikan skripsi ini. Penulis juga mengucapkan terimakasih kepada Bapak Drs. Henry Rani Sitepu, M.Si dan Drs. Pasukat Sembiring, M.Si , sebagai dosen penguji, atas setiap saran dan masukannya selama pengerjaan skripsi ini. Ucapan terimaksih juga penulis tujukan kepada Ketua dan Sekretaris Departemen Prof. Dr. Tulus, M.Si dan Dra. Mardiningsih, M.Si dan kepada Bapak/ Ibu dosen pada Departemen Matematika FMIPA USU beserta semua Staf Administrasi di FMIPA USU.

Sepenuhnya penulis menyadari bahwa dalam penulisan skripsi ini masih terdapat banyak kekurangan dan kelemahan dengan demikian penulis harapkan saran dan kritik yang sifatnya membangun demi kemajuan ilmu pengetahuan pada saai ini dan yang akan datang.

Akhirnya penulis berharap semoga penulisan skripsi ini dapat memberikan manfaat kepada semua pihak yang memerlukannya.

Medan, Juni 2012 Penulis

ABSTRAK

ABSTRACT

Multiple linear regression is heteroscedasticity, if the regression have different variance errors. In contrast, a regression is called homoskedasticity if it has constant variance errors. Regression analysis using heteroscedasticity data will still provide an unbiased estimate for the relationship between the predictor variable and the outcome, but it is inefficient. Biased variance errors lead to biased inference, so results of hypothesis tests are possibly wrong. Grafik test, and Golfeld Quant test is some methods to test for the presence of heteroscedasticity. Heteroscedasticity can be removed by a transformation, such as dividing regression be the standard deviation of error term and applying the usual least squares procedures to transformed regression. The covariance matrix for error of regression is E

 

T V

 

 ˆ2V, where V is symetric matrix. So we can using inverse of matrix pto transform regression, where

 



V p p

pT  2  , so we have transformed regression _p1_Y _p1_X _p1 _or *

* * _X  

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak vi

Abstract vii

Daftar Isi viii

Daftar Tabel x

Daftar Gambar xi

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 2

1.3 Batasan Masalah 2

1.4 Tinjauan Pustaka 2

1.5 Tujuan Penelitian 4

1.6 Kontribusi Penelitian 5

1.7 Metode Penelitian 5

BAB 2 LANDASAN TEORI 6

2.1 Aljabar Matriks 6

2.1.1 Definisi 6

2.2 Regresi Linier Berganda 8

2.3 Heteroskedastisitas 14

2.3.1 Teknik Mendeteksi Heteroskedastisitas 14

2.4 Metode Weight least Square (WLS) 17

BAB 3 PEMBAHASAN 19

3.1 Model Regresi linier Berganda dengan Heteroskedastisitas 19

3.2 Variansi Error dengan Unsur Heteroskedastisitas 20

3.4 Estimasi Regresi Linier berganda dengan Heteroskedastisitas 24

3.5 Contoh Penerapan 26

3.5.1 Analisis Regresi Berganda 26

3.5.2 Uji Grafik 29

3.5.3 Uji Golfeld Quandt 30

3.5.4 Estimasi Parameter Menggunkana metode WLS 34

3.5.5 Uji Grafik pada Metode WLS 37

BAB 4 KESIMPULAN DAN SARAN 38

4.1 Kesimpulan 38

4.2 Saran 38

Daftar Pustaka 39

DAFTAR TABEL

Halaman Tabel 3.1 Data Pengaruh Biaya Produksi, Distribusi, dan Promosi terhadap

Tingkat Penjualan 27

Tabel 3.2 Hasil Perhitungan Koefisien Determinasi 27

Tabel 3.3 ANOVAb 28

Tabel 3.4 Koefisien Regresi 28

Tabel 3.5 Data Nilai X dan Y pada Uji Grafik 29

Tabel 3.6 Kelompok 1 (Data X1,X2, dan X3 yang Bernilai Rendah) 31 Tabel 3.7 Kelompok 2 (Data X1,X2, dan X3 yang Bernilai Tinggi) 31 Tabel 3.8 ANOVA b Untuk Data yang Bernilai Rendah (Kelompok 1) 32

Tabel 3.9 Koefisien Regresi pada Kelompok 1 32

Tabel 3.10 ANOVA b Untuk Data yang Bernilai Tinggi (Kelompok 2) 32

Tabel 3.11 Koefisien Regresi pada Kelompok 2 33

Tabel 3.12 Data Transformasi untuk Pendugaan Model Regresi Menggunakan

Metode Weight Least Square 34

Tabel 3.13 Perhitungan Koefisien Determinasi pada WLS 36

DAFTAR GAMBAR

Halaman

Diagram 3.1 Uji Grafik Scatterplot 30

ABSTRAK

ABSTRACT

Multiple linear regression is heteroscedasticity, if the regression have different variance errors. In contrast, a regression is called homoskedasticity if it has constant variance errors. Regression analysis using heteroscedasticity data will still provide an unbiased estimate for the relationship between the predictor variable and the outcome, but it is inefficient. Biased variance errors lead to biased inference, so results of hypothesis tests are possibly wrong. Grafik test, and Golfeld Quant test is some methods to test for the presence of heteroscedasticity. Heteroscedasticity can be removed by a transformation, such as dividing regression be the standard deviation of error term and applying the usual least squares procedures to transformed regression. The covariance matrix for error of regression is E

 

T V

 

 ˆ2V, where V is symetric matrix. So we can using inverse of matrix pto transform regression, where

 



V p p

pT  2  , so we have transformed regression _p1_Y _p1_X _p1 _or *

* * _X  

BAB 1

PENDAHULUAN

1.1 Latar Belakang Masalah

Analisis regresi merupakan ilmu peramalan dalam statistik. Analisis regresi dapat dikatakan sebagai usaha memprediksi atau meramalkan perubahan. Regresi mengemukakan tentang keingintahuan apa yang terjadi dimasa depan untuk memberi sumbangan dalam menentukan keputusan yang terbaik. Regresi biasanya dinyatakan dalam rumus:

i ki k i

i

i X X X

X

Y 01 1 2 2 3 3 ... 

dimana Y adalah variabel terikat, X adalah variabel bebas, adalah parameter koefisien regresi variabel bebas dan _iadalah kesalahan residual (error).

Dalam regresi linier berganda, ada beberapa asumsi yang harus dipenuhi agar estimasi yang diperoleh benar dan efektif. Salah satu asumsi yang harus dipenuhi adalah Homoskedastisitas, bila asumsi itu tidak terpenuhi maka yang terjadi adalah sebaliknya, yakni heteroskedastisitas yang artinya variansi error tidak konstan. Variansi error tidak konstan menyebabkan kesimpulan yang dicapai tidak valid atau bias. Jadi unsur heteroskedastisitas yang termuat dalam suatu regresi harus diatasi agar tercapai kesimpulan yang valid.

Berdasarkan latar belakang yang telah diuraikan diatas maka penulis

mengambil judul “Analisis Heteroskedastisitas Pada Regresi Linier Berganda dan Cara Mengatasinya”

1.2 Perumusan Masalah

Berdasarkan latar belakang yang telah diuraikan diatas, maka rumusan masalahnya adalah sebagai berikut :

1. Bagaimana mendeteksi unsur heteroskedastisitas pada regresi linier berganda?

2. Bagaimana mengatasi unsur heteroskedastisitas pada regresi linier berganda?

1.3 Batasan Masalah

Dalam penelitian ini memiliki batasan-batasan masalah sebagai berikut:

1. Dalam mendeteksi adanya heteroskedastisitas, uji yang akan digunakan adalah Uji Grafik dan Uji Golfeld Quant .

2. Metode yang digunakan dalam mengatasi unsur heteroskedastisitas adalah Weighted Least Square (WLS).

1.4 Tinjauan Pustaka

 Regresi Linier Berganda

i ki k i

i

i X X X

X

Y ₀_{1 1} _{2 2} _{3 3} ...  dimana:

Y = variabel tidak bebas

ki i

i X X

X1 , 2 ,..., = variabel bebas

k

 

1, 2,..., = parameter koefisien regresi variabel bebas

0= intersep yaitu titik potong antara regresi dengan sumbu tegak y bila

x= 0

k = Jumlah variabel bebas pada observasi ke-i i = Banyak pengamatan

i

 = Variabel kesalahan ke-i

(Supranto, 2009:239).

 Uji Golfeld Quant

Adapun langkah –langkah pada metode ini adalah sebagai berikut: a. Urutkan data X berdasarkan nilainya

b. Bagi data menjadi 2, satu bagian memiliki nilai yang tinggi, bagian lainnya memiliki nilai yang rendah, sisihkan data pada nilai tengah

c. Lakukan regresi pada masing –masing data

d. Buatlah rasio RSS(Residual Sum Square =error sum if square) dari regresi kedua terhadap regresi pertama (

1 2

RSS RSS

), sehingga didapat Fhitung =

1 2

RSS RSS

. e. Lakukan uji Ftabel dengan menggunakan derajat kebebasan (degree of

freedom) sebesar (n-d-2k)/2, dengan: n = banyaknya observasi

Dan bila Fhitung ≥ Ftabel, maka ada heteroskedastisitas dalam hal lain tidak ada heteroskedastisitas.

 Estimasi Unsur Heteroskedastisitas dengan Weighted Least Square (WLS)

Apabila variansi error (_2) diketahui atau dapat diperkirakan, cara yang paling mudah untuk mengatasi adanya heteroskedastisitas adalah dengan metode kuadrat terkecil terboboti (Weighted Least Square) yang memberikan hasil bersifat BLUE.

(Gujarati, 2010: 493).

Untuk menggambarkan metode ini, akan diberikan model sebagai berikut:

i ki k i

i i

i X X X X

Y 01 1 2 2 3 3 ... 

untuk mendapatkan taksiran variansi parameter regresi, diasumsikan untuk sementara bahwa variansi error sebenarnya (_2) untuk setiap observasi diketahui, sehingga transformasi persamaan yang dihasilkan dari model regresi linier berganda adalah:

 

 

 

 

    

i i i i

X X

Y _{    }

...

1 ₂

2 1 1 0

1.5 Tujuan Penelitian

Berdasarkan rumusan masalah yang telah ditetapkan, maka didapat tujuan sebagai berikut:

1. Mengetahui cara mendeteksi unsur heteroskedastisitas pada regresi linier berganda.

1.6 Kontribusi Penelitian

1. Dapat diketahui bahwa dalam penggunaan regresi terdapat beberapa asumsi dasar yang harus dipenuhi agar taksiran parameter dalam regresi linier berganda memenuhi sifat BLUE (Best Linier Unbiased Estimator) salah satunya adalah homoskedastisitas.

2. Menambah wawasan dan memperkaya literatur dalam bidang statistika tentang heteroskedastisitas pada regresi linier berganda dan cara mengatasinya.

1.7 Metode Penelitian

Penelitian ini merupakan sebuah penelitian kepustakaan (Library Research), yakni mengumpulkan data secara literatur yang akan dipergunakan sebagai acuan dalam menganalisis masalah. Penelitian ini mengikuti langkah –langkah sebagai berikut:

1. Mengumpulkan dan mempelajari pustaka – pustaka yang berkenaan dengan materi penelitian seperti regresi linier berganda, heteroskedastisitas, Uji Grafik, Uji Golfeld Quant, dan Weighted Least Squares (WLS).

2. Menganalisis dan menyusun hasil langkah pertama yang mencakup tentang:

a. Konsep dasar heteroskedastisitas pada regresi linier berganda b. Mendeteksi adanya heteroskedastisitas pada regresi linier berganda c. Akibat adanya heteroskedastisitas pada regresi linier berganda d. Mengatasi unsur heteroskedastisitas pada regresi linier berganda

e. Mengestimasi parameter model regresi linier berganda dengan unsur heteroskedastisitas

BAB II

LANDASAN TEORI

2.1 Aljabar Matriks

2.1.1 Definisi

Matriks

Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga berbentuk persegi panjang, dimana panjang dan lebarnya ditunjukkan oleh banyaknya kolom dan baris

serta dibatasi tanda “[ ]” atau “( )”. Sebuah matriks dinotasikan dengan simbol huruf

besar seperti A, X, atau Z dan sebagainya. Sebuah matriks A yang berukuran m baris dan n kolom dapat ditulis sebagai berikut :

Atau juga dapat ditulis :

Determinan Matriks

Determinan adalah semua hasil perkalian elementer yang bertanda dari suatu matriks A dan dinyatakan dengan det (A). Misalkan A = [ ] adalah matriks nxn. Fungsi determinan dari A ditulis dengan det (A) atau |A|. Secara matematiknya ditulis :

Dengan merupakan himpunan S = {1, 2, …, n}. Teorema

Jika A = [ ] adalah matriks nxn yang mengandung sebaris bilangan nol, maka det(A) = 0.

Teorema

Jika A adalah matriks segitiga nxn, maka det(A) adalah hasil kali elemen – elemen pada diagonal utama, yaitu

Teorema

Jika A adalah sebarang matriks kuadrat, maka .

Invers Matriks

Misalkan A matriks nxn disebut non singular (invertible) jika terdapat matriks B maka AB = BA = I

Matriks B disebut invers dari A jika tidak terdapat matriks B maka matriks A disebut singular (non-invertible).

Adjoint matriks A adalah suatu matriks yang elemen-elemennya terdiri dari semua elemen-elemen kofaktor matriks A, dengan adalah kofaktor elemen-elemen

Sehingga dapat ditulis dalam bentuk matriks sebagai berikut :

dengan :

Sifat – sifat invers :

a. Jika A adalah matriks non singular, maka adalah non singular dan

b. Jika A dan B adalah matriks non singular, maka AB adalah non singular dan

2.2 Regresi Linier Berganda

Dalam menentukan nilai variabel tidak bebas (Y), perlu diperhatikan variabel – variabel bebas (X) yang mempengaruhinya terlebih dahulu, dengan demikian harus diketahui hubungan antara satu variabel tidak bebas (Dependent Variable) dengan beberapa variabel lain yang bebas (Independent Variable). Untuk meramalkan Y, apabila semua variabel bebas diketahui, maka dapat dipergunakan model persamaan regresi linier berganda sebagai berikut:

i ki k i

i

i X X X

X

Y 01 1 2 2 3 3 ...  (2.1) dimana:

Y = variabel tidak bebas

ki i

i X X

k

 

₁, ₂,..., = parameter koefisien regresi variabel bebas

0= intersep yaitu titik potong antara regresi dengan sumbu tegak y bila

x= 0

k = Jumlah variabel bebas pada observasi ke-i i = Banyak pengamatan

i

 = Variabel kesalahan ke-i

Apabila dinyatakan dalam bentuk matriks

                                                                  n k kn n n n k k k

n X X X X

X X X X X X X X X X X X Y Y Y Y         ... ... ... 1 ... ... ... ... 1 ... 1 ... 1 ... 3 2 1 2 1 0 3 2 1 3 33 23 13 2 32 22 12 1 31 21 11 3 2 1

Dengan k < n yang berarti banyak observasi harus lebih banyak dari pada banyak variabel bebas, akan diperoleh:

(2.2) atau

Salah satu metode estimasi parameter untuk regresi linier berganda adalah Ordinary Least Square (OLS). Konsep dari metode OLS adalah menaksir parameter regresi dengan meminimumkan jumlah kuadrat dari error. Tujuan OLS adalah meminimumkan jumlah kuadrat error yaitu:

S =



 n i i 1 2 

=





    

 

    

 

2 2 2 2 1 2 2 2 2 1

... ...

n n

  

  

=



T



=



y X 

 

T y X



=



yT (X )T

 

y X 



=



yT TXT

 

y X



= yTyyTX TXTy TXTX

Karena yTX  adalah scalar, maka matriks transpose –nya adalah



yTX 



T TXTy (2.3)

Jadi

S = yTy2TXTyTXTX (2.4) Untuk mengestimasi parameter regresi (



) maka jumlah kuadrat error harus diminimumkan (Supranto, 2009: 241 -242), hal tersebut bisa diperoleh dengan melakukan turunan pertama terhadap(



), dengan aturan penurunan skalar berikut: Misalkan z dan w adalah vektor vektor berordo mx1, sehingga y =zTw adalah skalar,

maka, w

dz dy _

, _T wT dz

dy _

, z dw dy _

,dan _T zT dw

dy _

Sehingga didapatkan hasil turunan jumlah kuadrat error sebagai berikut:



 S

= 02XTy XTX (TXTX)T = 2XTyXTXXTX

=2XTy2XTX (2.5)

dan hasil estimasi parameter  didapatkan dengan menyamakan hasil turunan jumlah kuadrat error dengan nol, sehingga pada saat hasil turunan jumlah kuadrat error disamakan dengan nol parameter  menjadi ˆ, dan diperoleh:

0

ˆ

2

2  

 XTy XTX

y X X

XT ˆ 2 T

ˆ = X X X y

T

T 1

)

(  _(2.6)

Akan ditunjukan bahwa ˆadalah estimasi linier tak bias dari 

 

E





X X



X y



Eˆ  T 1 T



XTX



1XTE

 

y





XTX



1XTX







dari sini terbukti bahwa ˆ adalah estimasi linier tak bias dari  .

Dengan mensubtitusi persamaan (2.2) ke dalam persamaan (2.5) didapat:

ˆ =(XTX)1XTy







 

X X X XT 1 T

) (



 T T

T T X X X X X X

X 1 1

) ( ) (     

 T T

X X X ) 1

( 



 (2.7)

Untuk dapat menunjukkan bahwa ˆ adalah penaksir OLS yang paling baik (Best Estimator) dalam arti taksiran variansi parameter (Var(ˆ)) adalah yang terendah, maka bisa diperlihatkan sebagai berikut:

 



 





 



_ 

 _{ }

E E E T

Cov ˆ ˆ ˆ ˆ ˆ

                              2 2 2 1 1 2 2 2 2 2 2 2 1 1 1 1 2 2 1 1 2 1 1 ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( ) ˆ ( k k k k k k k k k k E E E E E E E E E E E E E E E                                                     ) ˆ ( ) ˆ , ˆ ( ) ˆ , ˆ ( ) ˆ , ˆ ( ) ˆ ( ) ˆ , ˆ ( ) ˆ , ˆ ( ) ˆ , ˆ ( ) ˆ ( 2 1 2 2 2 1 1 2 1 1 k k k k k Var Cov Cov Cov Var Cov Cov Cov Var                      

Jelas terlihat bahwa variansi adalah anggota dari diagonal utama, sedangkan kovarian adalah unsur –unsur diluar diagonal utama. Kovariansi tersebut bisa dituliskan dalam notasi matriks sebagai berikut:

 



 





 



_ 

 _{ }

 E E E T

Covˆ ˆ ˆ ˆ ˆ



 



_ 

 _{ }

E ˆ  ˆ  T

















_



 _{   }

 T  T T  T T

X X X X X X

E  1    1  

















_

 

 T  T T  T T

X X X X X X

E 1  1 



















1 1



E XTX XT TX XTX





1

  



1  XTX XTET X XTX





1

 





1  XTX XTV  X XTX

(2.8)

Dengan V

 

 adalah matriks diagonal. Pada saat variansi error bersifat homoskedastisitas, maka bisa ditulis V

 







2I dengan asumsi tersebut persamaan menjadi:

 

ˆ





1 ₂





1

 X X X IX X X



XTX



1XTX



XTX



1I

2  





XTX



1I

2  





1

2 

 XTX _(2.9)

Apabila variansi error tidak diketahui, maka harus didapat taksirannya, dan untuk taksiran variansi error dilakukan dengan menaksir konstanta variansi error

) ˆ

(2 sebagai berikut:

k n

n

i i

 



1

2 2

ˆ

 

(2.10)

dengan variansi taksiran ini diperoleh variansi parameter regresi sebagai berikut:

 

₂





1

ˆ

ˆ 

 X X

Var  T

(2.11)

Dalam regresi linier berganda, ada beberapa asumsi yang harus dipenuhi agar tahap estimasi yang diperoleh benar dan efektif, bila memenuhi teorema Gauss Markov sebagai berikut (Nachrowi, 2002:123):

1. Rata –rata (harapan) variabel  bernilai nol atau E()=0

2. Tidak terdapat korelasi serial atau autokorelasi antar variabel error untuk setiap observasi atau Cov(_i,_j)=0 ; ij.

3. Memiliki error yang bersifat homoskedastisitas atau Var (_i X_i)2.

4. Nilai variabel (X) tetap atau nilainya independen terhadap factor error () atau Cov(X,)=0

5. Model regresi dispesifikasi secara benar, dan

6. Tidak ada hubungan linier (kolinieritas) antar variabel –variabel bebas.

Istilah ini diciptakan oleh Ragner Frish, yang berarti ada hubungan linier yang sempurna atau eksak diantara variabel-variabel bebas dalam model regresi 2. Heteroskedastisitas

Salah satu asumsi dasar yang harus dipenuhi adalah varians error harus konstan (Var (_i X_i)2), jika tidak konstan, maka terdapat unsur heteroskedastisitas. Data cross-section cenderung memuat unsur heteroskedastisitas karena pengamatan dilakukan pada individu yang berbeda pada saat yang sama.

3. Autokorelasi

Autokorelasi merupakan gangguan pada fungsi yang berupa korelasi diantara variabel error, ini berarti tidak terpenuhinya asumsi yang menyatakan bahwa nila-nilai variabel tidak berkorelasi.

2.3 Heteroskedastisitas

Salah satu asumsi yang harus dipenuhi agar model bersifat BLUE (Best Linear Unbiased Estimator) adalah harus terdapat variansi yang sama dari setiap error-nya atau homoskedastisitas, secara simbolis E(_i2)2, i=1,2,…,n apabila asumsi ini tidak terpenuhi maka yang terjadi adalah sebaliknya, yakni heteroskedastisitas. Heteroskedastisitas berarti variansi error berbeda dari suatu observasi ke observasi lainnya. Sehingga setiap observasi mempunyai reliabilitas yang berbeda.

Unsur heteroskedastisitas menyebabkan hasil dari t-test dan F-test menyesatkan, karena kedua uji tersebut menggunakan besaran variansi taksiran, lebih besarnya variansi taksiran dibanding variansi sebenarnya akan menyebabkan standar taksiran error juga lebih besar, sehingga interval kepercayaan sangat besar pula. (Nachrowi, 2002:133).

2.3.1 Teknik Mendeteksi Heteroskedastisitas

1. Melihat scatter plot (nilai prediksi dependen ZPRED dengan residual SRESID) Metode ini yaitu dengan cara melihat grafik scatterplot antara standardized predicted value (ZPRED) dengan studentized residual (SRESID). Ada tidaknya pola tertentu pada grafik scatterplot antara SRESID dan ZPRED dimana sumbu Y adalah Y yang telah diprediksi dan sumbu X adalah residual (Y prediksi – Y sesungguhnya).

Dasar pengambilan keputusan yaitu:

 Jika ada pola tertentu, seperti titik –titik yang ada membentuk suatu pola tertentu yang teratur (bergelombang, melebar kemudian menyempit), maka terjadi heteroskedastisitas.

 Jika tidak ada pola yang jelas, seperti titik –titik menyebar diatas dan dibawah angka 0 pada sumbu Y, maka tidak terjadi heteroskedastisitas.

2. Uji Goldfeld – Quandt

Adapun langkah –langkah pada metode ini adalah sebagai berikut: a. Urutkan data X berdasarkan nilainya

b. Bagi data menjadi 2, satu bagian memiliki nilai yang tinggi, bagian lainnya memiliki nilai yang rendah, sisihkan data pada nilai tengah c. Lakukan regresi pada masing –masing data

d. Buatlah rasio RSS(Residual Sum Square =error sum if square) dari regresi kedua terhadap regresi pertama (

1 2

RSS RSS

), sehingga didapat

Fhitung =

1 2

RSS RSS

.

e. Lakukan uji Ftabel dengan menggunakan derajat kebebasan (degree of freedom) sebesar (n-d-2k)/2, dengan:

n = banyaknya observasi

d = banyaknya data atau nilai observasi yang hilang k =banyaknya parameter yang diperkirakan.

Pada Uji Goldfeld –Quant seandainya tidak ada data yang dibuang (d=0) tes masih berlaku tetapi kemampuan untuk mendeteksi adanya heteroskedastisitas agak berkurang.

3. Uji Park

Untuk pengujian heteroskedastisitas melalui pengujian hipotesis dapat dilakukan dengan uji park.R.E. Park pada tahun 1966 mengemukakan keyakinan bahwa terdapat suatu hubungan fungsional antara ragam galat, yang bersifat heteroskedastisitas dan variabel penjelas, X. Park merumuskan bentuk fungsional itu sebagai berikut:

Atau: ln

di mana adalah bentuk gangguan yang bersifat stokastik.

Karena pada umumnya tidak diketahui, park mengunakan sebagai variabel proxy, kemudian merumuskan model regesi sebagai berikut:

=

Berdasarkan uji park, kita melakukan pengujian hipotesis tentang parameter dalam model regresinya, apabila koefisien besifat nyata dalam statistik, maka menujukkan hetersokedastisitas dalam data, sebaliknya apabila uji terhadap koefisien bersifat tidak nyata secara statistik, maka menujukan bahwa asumsi homoskedastisitas dari model regresi dapat dipenuhi.

a. Terapkan ordinary least square estimation (0LSE) untuk menaksir model:

b. Menerapakan OLSE untuk menaksir ln dengan menggunakan ln .

4. Uji White

Dalam implementasinya, model ini relative lebih mudah dibandingkan dengan uji –uji lainnya. Perhatikan persamaan berikut:

i i

i x

x

Y ₀_{1 1} _{2 2} 

Berdasarkan regresi yang mempunyai tiga variabel bebas diatas, dapat dilakukan uji white dengan beberapa tahapan prosedur, yaitu:

a. Hasil estimasi dari model diatas akan menghasilkan nilai error, yaitu : ˆ_i2 b. Buat persamaan regresi:

i i i i

i i

i

i   x  x  x  x  5x1 x2 v

2 2 4 2 1 3 2 2 1 1 0 2

ˆ      



Perhatikan model diatas, uji ini mengasumsikan bahwa varian error merupakan fungsi yang mempunyai hubungan dengan variabel bebas, kuadrat masing – masing variabel bebas, dan interaksi antar variabel bebas.

c. Dengan hipotesis:

H0 : Homoskedastisitas / tidak heteroskedastisitas H1 : Heteroskedastisitas.

Sampel berukuran n dan koefisien determinasi R2 yang didapat dari regresi akan mengikuti distribusi Chi- Square dengan derajat bebas jumlah variabel bebas atau jumlah koefisien regresi diluar intercept. Dengan demikian, formulasi Uji White adalah sebagai berikut :

2

nR _~ 2

2.4 Metode Weight Least Square (WLS)

Apabila variansi error (_2) diketahui atau dapat diperkirakan, cara yang paling mudah untuk mengatasi adanya heteroskedastisitas adalah dengan metode kuadrat terkecil terboboti (Weighted Least Square) yang memberikan hasil bersifat BLUE. (Gujarati, 2010: 493).

Untuk menggambarkan metode ini, akan diberikan model sebagai berikut:

i ki k i

i i

i X X X X

Y ₀_{1 1} _{2 2} _{3 3} ... 

Untuk mendapatkan taksiran variansi parameter regresi, diasumsikan untuk sementara bahwa variansi error sebenarnya (_2) untuk setiap observasi diketahui, sehingga transformasi persamaan yang dihasilkan dari model regresi linier berganda adalah:

 

 

 

 

    

i i i i

X X

Y

  



 1 2 ...

2 1 1 0

Transformasi ini dilakukan dengan membagi baik sisi kiri maupun sisi kanan regresi dengan akar variansi error (_ ). Sekarang anggaplah



 i i

v  dan vi bisa disebut

faktor error yang ditransformasikan, apabila faktor error tersebut bersifat homoskedastisitas, maka bisa diketahui bahwa estimator OLS dari parameter-parameter pada persamaan tersebut bersifat BLUE. Untuk melihat bahwa faktor error (vi) homoskedastisitas bisa dengan cara berikut:

2 2 2



 _i

i

v 

Sehingga

E( _

    

 2₂

2

)



 _i

i E

v

 

v_i2 1₂ E( _i2)

E 

_ _

Karena E(v_i2)_i2, maka

 

2 1_{2 } 2 1

          i v E

Yang jelas merupakan konstanta, maka bisa diketahui bahwa error pada persamaan hasil transformasi (vi) bersifat homoskedastisitas. (Gujarati, 2006:475).

BAB III

PEMBAHASAN

3.1 Model Regresi Linier Berganda dengan Heteroskedastisitas Model regresi linier berganda secara umum ditulis sebagai berikut:

   X Y (3.1) dimana :                                                                     n k kn n n n k k k n dan X X X X X X X X X X X X X X X X X Y Y Y Y Y           ... , ... , ... 1 ... ... ... ... 1 ... 1 ... 1 , ... 3 2 1 2 1 0 3 2 1 3 33 23 13 2 32 22 12 1 31 21 11 3 2 1

Karena persamaan (3.1) diatas memuat unsur heteroskedastisitas, maka variansi error pada regresi tersebut tidak konstan karena nilai – nilainya tergantung pada nilai variabel bebas (X). Jika variansi error (V

 

 )diketahui, maka bisa dipergunakan untuk mengatasi heteroskedastisitas. Akan tetapi, jarang sekali variansi error pada kasus heteroskedastisitas diketahui, sehingga harus didapatkan estimasi variansi error tersebut terlebih dahulu agar bisa dilakukan estimasi parameter regresi yang memuat unsur heteroskedastisitas.

 

ˆ





1 ₂





1

 X X X VX X X

Var  T T T _(3.2)

sehingga bisa diketahui bahwa V merupakan unsur heteroskedastisitas. Dari sini bisa diketahui bahwa untuk mendapatkan variansi error



V

 





harus didapatkan V yang bisa didapatkan dari data yang diketahui (telah diuji) memuat unsur heteroskedastisitas.

3.2 Variansi Error dengan Unsur Heteroskedastisitas

Dalam analisis regresi secara umum seperti persamaan (3.1) bila k parameter yang ditaksir dari n observasi, maka error–nya yang sebanyak n tersebut memiliki n-k derajat bebas, jadi jelas error tersebut tidak mungkin bebas, hal ini bisa dijadikan dasar dalam menentukan unsur heteroskedastisitas(V). Error dalam regresi linier berganda ditulis dalam notasi sebagai berikut:

 YYˆ

ˆ

X Y 





X X



X Y X

Y  T 1 T









I X XTX 1XT



Y



apabila H =



T



T

X X X

X 1 , maka

 



IH



Y _(3.3)

Karena E(Y) X, akibatnya

  

I H



Y E





I H



Y



E    

 





IH

 

Y I H



E(Y)





I H

 

Y I H



X





I H



YX







IH





 (3.4)

Dari sini bisa didapat variansi error sebagai berikut:

 





 





 



T



E E

E







 









T



H I H I

E    

























T



H I H I

E    







 

T





T

H I E H

I  

 



 



T

H I I H

I 

 2







T

H I H

I 

2

(3.5) Di lain pihak





T



T T



H I H

I   









T

T T X X X X

I  1





T



T

X X X X

I  1



H I



Dan HH HT H

, dengan kata lain H bersifat idempotent, sehingga persamaan (3.5) menjadi

 



I H



I H



Cov 2  



I H HHH



2



I H



2

(3.6)

Sehingga dapat diketahui bahwa

V IH



T



T

X X X X

I  1

 _(3.7)



   n i i k n ₁ 2 2 1 ˆ    T k n  1



Y X

 

Y X



k n T     1

 



Y X





Y X



k n

T

T _{ }



 1



Y  X





Y X



k n

T T

T _{ }



 1



Y Y Y X  X Y  X X



k n T T T T T

T   



 1



Y Y  X Y  X X



k n T T T T

T  



 1 2

(3.8)

Dari persamaan (3.7) dan persamaan (3.8) didapatkan hasil estimasi dari variansi error

V

 

 ˆ2V



T T T T T







T



T



X X X X I X X Y X Y Y k n 1 2 1          (3.9)

3.3 Mengatasi Heteroskedastisitas pada Regresi Linier Berganda

Seandainya metode OLS tetap digunakan dalam model regresi linier berganda dengan heteroskedastisitas tanpa mengatasi heteroskedastisitas tersebut terlebih dahulu, maka nilai estimasi parameter tetap tidak bias akan tetapi memiliki variansi yang bias, hasil taksiran tersebut bisa lebih kecil atau lebih besar dari variansi parameter yang sebenarnya.





₂





1 hom

ˆ 

 X X

Var  o  T

Dan untuk regresi yang bersifat heteroskedastisitas adalah:

 

ˆ





1 ₂





1

 X X X VX X X

Var heter T T T

Dan secara umum



 

1



1





1

 X X X VX X X

X

XT T T T

Karena matriks bukanlah matriks identitas, maka besar kecilnya nilai unsur – unsur matriks mempengaruhi besar kecilnya taksiran variansi parameter. Sehingga bisa diketahui bahwa hasil taksiran variansi parameter yang bersifat heteroskedastisitas tidak sesuai dengan nilai variansi parameter yang sebenarnya. Dan untuk mengatasi sifat heteroskedastisitas pada suatu regresi bisa digunakan metode Weight Least Square (WLS).

Error pada persamaan regresi linier berganda yang memuat heteroskedastisitas memiliki variansi yang tidak konstan, variansi error pada kasus heteroskedastisitas bisa ditulis:

 

V

 

V

ET   ˆ2

Maka aka ada matriks p yang bersifat simetri,

 



V p pp p

pT   2 

Sesuai dengan metode WLS, mengatasi heteroskedastisitas dilakukan dengan mentransformasikan persamaan (3.1) dengan cara mengalikan persamaan tersebut dengan inverse dari standar deviasi error ( p ), dan hasil transformasi yang diperoleh adalah:



 1

1

1  

_{Y  p X  p} p

bisa juga ditulis dengan *

dimana Y*  p1Y, X*  p1X dan



*  p1



3.4 Estimasi Regresi Linier Berganda dengan Heteroskedastisitas

Untuk mengestimasi model regresi linier berganda yang memuat unsur heteroskedastisitas digunakan metode Weighted least Square (WLS), yakni metode OLS yang diterapkan pada hasil trasformasi regresi.

Untuk mendapatkan hasil estimasi parameter regresi ( ˆ*) digunakan metode least square dengan meminimumkan jumlah kuadrat error (S*), yaitu:

*

S =



 n i i 1 2 * 

=₁*2 ₂*2..._n*2

=





              2 * 2 * 2 2 * 1 2 * 2 * 2 2 * 1 ... ... n n      

=



*T



*

=



* *

 

* *



X Y X

Y  T 

=



* *

 

* *



)

(X Y X

Y T  T 

=



*  *

 

* *



X Y X

Y T  T T 

= Y*TY*Y*TX* TX*TY*TX*TX*

Karena Y*TX* adalah scalar maka matriks transpose –nya adalah



* *



* *

Y X X

Y T  T T T (3.10)

Sehingga diperoleh

*

S = Y*TY*2TX*TY*TX*TX* (3.11)

Misalkan z dan w adalah vector- vektor berordo mx1, sehingga y =zTw adalah skalar,

maka, w

dz dy _

, _T wT dz

dy _

, z

dw dy _

, dan _T zT dw

dy _

. Sehingga didapatkan hasil turunan jumlah kuadrat error berikut:



  *

S

= 02X*TY* X*TX* (*TX*TX*)T = 2X*TY*X*TX*X*TX*

=2X*TY*2X*TX* (3.12)

Dan hasil estimasi parameter  didapatkan dengan menyamakan hasil turunan jumlah kuadrat error dengan nol, sehingga pada saat hasil turunan jumlah kuadrat error disamakan dengan nol parameter  menjadi ˆ*_{, dan diperoleh:}

*

ˆ

 = * * 1 * *

)

(X TX  X Ty







p1X T p1X



1



p1X



T p1Y



 



XT p1 T p1X



1XT

 

p1 T p1Y





XTp1p1X



1XTp1p1Y



 



XT pp 1X



1XT

 

pp 1Y



 







XT V 1X



1XT



V

 



1Y

  

Karena V

 

 ˆ2V, maka

 



XT 2V 1X



1XT

 

2V 1Y

* ˆ ˆ

ˆ   

  



Y V X

X V

XT T ₂ 1

1 1

2 ˆ

1

ˆ

1 _  _

   

  

 



XTV 1X



1 ₂ XTV 1Y

2

ˆ

1

ˆ   



 



XTV1X



1XTV1Y

3.5 Contoh Penerapan

Untuk memperoleh gambaran yang lebih jelas tentang kegunaan teori yang telah diuraikan, maka didalam bab ini penulis sajikan sebuah contoh pemakaiannya.

3.5.1 Analisis Regresi Berganda

Setiap data merupakan alat bagi pengambil keputusan untuk dasar pembuatan keputusan-keputusan atau untuk memecahkan suatu persoalan. Keputusan yang baik dapat dihasilkan jika pengambilan keputusan tersebut didasarkan atas data yang baik. Demikian juga halnya dalam meramal dengan menggunakan multipel regresi. Dengan meramal menggunakan regresi dapat membuat keputusan dan memperoleh gambaran tentang suatu keadaan permasalahan.

Dalam analisis regresi ada beberapa syarat yang harus dipenuhi agar hasil estimasi yang diperoleh benar dan efektif. Salah satu asumsi yang penting dan harus terpenuhi adalah homoskedastisitas. Tetapi jika model regresi estimasi diperoleh tidak efisien, baik dan efektif maka terjadi kasus heteroskedastisitas. Berikut ini contoh kasus heteroskedastisitas pada estimasi regresi berganda.

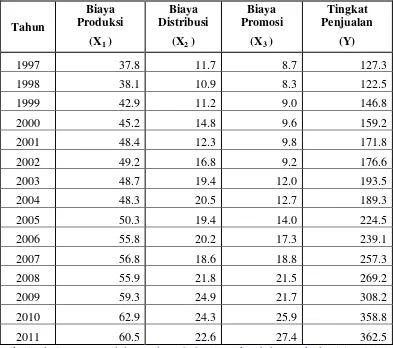
Data yang dipakai dalam penelitian ini adalah data tentang pengaruh biaya produksi, distribusi, dan promosi terhadap tingkat penjualan. Dengan memisalkan variabel-variabel sebagai berikut:

[image:40.595.107.500.260.608.2]

Tabel 3.1

Data Pengaruh Biaya Produksi, Distribusi, dan Promosi terhadap Tingkat Penjualan (Dalam Jutaan Rupiah)

Tahun

Biaya Produksi

Biaya Distribusi

Biaya Promosi

Tingkat Penjualan (X1 ) (X2 ) (X3 ) (Y)

1997 37.8 11.7 8.7 127.3

1998 38.1 10.9 8.3 122.5

1999 42.9 11.2 9.0 146.8

2000 45.2 14.8 9.6 159.2

2001 48.4 12.3 9.8 171.8

2002 49.2 16.8 9.2 176.6

2003 48.7 19.4 12.0 193.5

2004 48.3 20.5 12.7 189.3

2005 50.3 19.4 14.0 224.5

2006 55.8 20.2 17.3 239.1

2007 56.8 18.6 18.8 257.3

2008 55.9 21.8 21.5 269.2

2009 59.3 24.9 21.7 308.2

2010 62.9 24.3 25.9 358.8

2011 60.5 22.6 27.4 362.5

Dikutip dari : www.scribd.com/doc/76462042/makalah-heteroskedastisitas

Dari tabel diatas dapat diperoleh persamaan regresi berganda menggunakan SPSS adalah sebagai berikut:

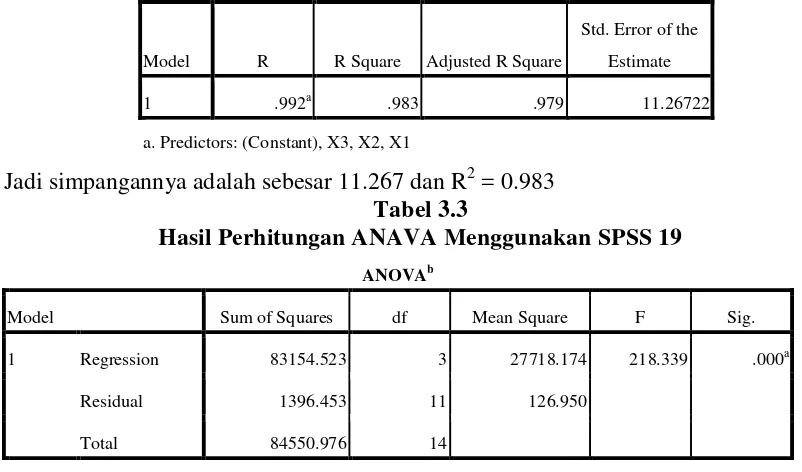
Tabel 3.2

Hasil Perhitungan Koefisien determinasi (R2) Menggunakan SPSS 19

Model R R Square Adjusted R Square

Std. Error of the

Estimate

1 .992a .983 .979 11.26722

a. Predictors: (Constant), X3, X2, X1

[image:41.595.106.507.85.321.2]

Jadi simpangannya adalah sebesar 11.267 dan R2 = 0.983 Tabel 3.3

Hasil Perhitungan ANAVA Menggunakan SPSS 19

ANOVAb

Model Sum of Squares df Mean Square F Sig.

1 Regression 83154.523 3 27718.174 218.339 .000a

Residual 1396.453 11 126.950

Total 84550.976 14

a. Predictors: (Constant), X3, X2, X1

b. Dependent Variable: Y

[image:41.595.107.508.432.594.2]

nilai variansnya adalah 126.950

Tabel 3.4

Hasil perhitungan Koefisien Regresi Linier Berganda Menggunakan SPSS 19

Coefficientsa

Model

Unstandardized Coefficients

Standardized

Coefficients

T Sig.

B Std. Error Beta

1 (Constant) -66.233 35.553 -1.863 .089

X1 3.109 1.155 .310 2.691 .021

X2 .572 1.427 .035 .401 .696

X3 7.894 1.176 .668 6.712 .000

a. Dependent Variable: Y

Dapat dilihat dari tabel diatas persamaan regresi linier berganda pada data tersebut adalah:

3 2

1 0.572 7.894

109 . 3 233 . 66

ˆ _{X X X}

Y    

tidak ada biaya produksi, biaya distribusi dan biaya promosi, maka tingkat penjualan sebesar -66.233 (nilai ini adalah mustahil karena tingkat penjualan tidak akan pernah negatif), maka jika tidak ada ketiga variabel tersebut tingkat penjualan juga tidak ada atau bernilai 0.

Sedangkan jika besarnya biaya produksi meningkat sebesar 1 juta rupiah, maka tingkat penjualan meningkat sebesar 3.109 juta rupiah. Dan jika besarnya biaya distribusi meningkat sebesar 1 juta rupiah maka tingkat penjualan meningkat sebesar 0.572 juta rupiah. Kemudian jika biaya promosi meningkat sebesar 1 juta rupiah, maka tingkat penjualan meningkat sebesar 7.894 juta rupiah. Dari ketiga variabel diatas dapat dilihat bahwa yang paling berpengaruh terhadap tingkat penjualan adalah biaya promosi.

3.5.2 Uji Grafik

Metode ini yaitu dengan cara melihat grafik scatterplot antara standardized predicted value (ZPRED) dengan studentized residual (SRESID). Ada tidaknya pola tertentu pada grafik scatterplot antara SRESID dan ZPRED dimana sumbu Y adalah Y yang telah diprediksi dan sumbu X adalah residual (Y prediksi – Y sesungguhnya). Tabel 3.5

Data Nilai X dan Y pada Uji Grafik )

ˆ (Y Y

X   _Y _Yˆ

-0.643 1.475 -2.205 -0.658 -3.161 -7.636 -2.500 6.611 -12.738 16.270 12.105 20.551 -4.527

-11.123 -11.416

347.677 351.084

Diagram 3.1 Uji Grafik Scatterplot

Dari grafik diatas dapat dilihat bahwa ada pola tertentu, seperti titik –titik yang ada membentuk suatu pola tertentu yang teratur (bergelombang, melebar kemudian menyempit), maka dapat disimpulkan bahwa data tersebut mengandung heteroskedastisitas.

3.5.3 Uji Goldfeld – Quandt

1. Hipotesis yang diuji adalah: H0 : tidak ada heteroskedastisitas H1 : ada heteroskedastisitas 2. Statistik penguji

F hitung = RSS =

1 2

RSS RSS

3. Kriteria Pengujian

Jika F hitung < F tabel, maka terima H0

Sebaliknya jika F hitung ≥ F tabel, maka tolak H0 4. Perhitungan

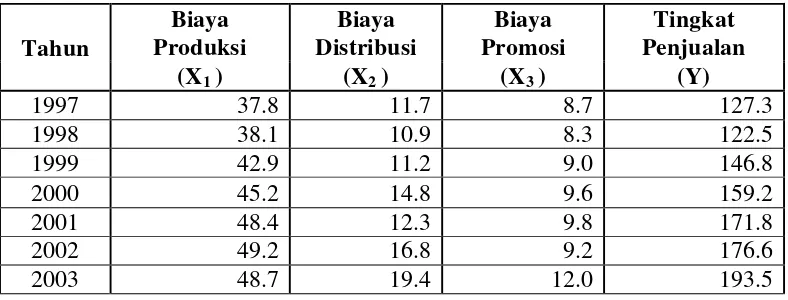
[image:44.595.119.513.329.479.2]

Dari data pada tabel 3.1, urutkan data X1, X2, dan X3 berdasarkan nilainya. Sehingga menjadi:

Tabel 3.6

Kelompok 1 (Data X1, X2, dan X3 yang Bernilai Rendah)

Tahun

Biaya Produksi

Biaya Distribusi

Biaya Promosi

Tingkat Penjualan (X1 ) (X2 ) (X3 ) (Y)

1997 37.8 11.7 8.7 127.3

1998 38.1 10.9 8.3 122.5

1999 42.9 11.2 9.0 146.8

2000 45.2 14.8 9.6 159.2

2001 48.4 12.3 9.8 171.8

2002 49.2 16.8 9.2 176.6

[image:44.595.120.513.593.747.2]

2003 48.7 19.4 12.0 193.5

Tabel 3.7

Kelompok 2 (Data X1, X2, dan X3 yang Bernilai Tinggi)

Tahun

Biaya Produksi

(X1 )

Biaya Distribusi

(X2 )

Biaya Promosi

(X3 )

Tingkat Penjualan

(Y)

2005 50.3 19.4 14.0 224.5

2006 55.8 20.2 17.3 239.1

2007 56.8 18.6 18.8 257.3

2008 55.9 21.8 21.5 269.2

2009 59.3 24.9 21.7 308.2

2010 62.9 24.3 25.9 358.8

[image:45.595.106.511.245.324.2]

Dengan menghilangkan data tahun 2004 sebagai nilai tengah, maka diperoleh hasil:

Tabel 3.8

ANAVA untuk Data yang Bernilai Rendah (Kelompok 1)

ANOVAb

Model Sum of Squares Df Mean Square F Sig.

1 Regression 4105.889 3 1368.630 389.557 .000a

Residual 10.540 3 3.513

Total 4116.429 6

a. Predictors: (Constant), X3, X1, X2

[image:45.595.107.514.428.556.2]

b. Dependent Variable: Y

Tabel 3.9

Hasil perhitungan Koefisien Regresi pada Kelompok 1 Menggunakan SPSS 19

Coefficientsa

Model

Unstandardized Coefficients

Standardized

Coefficients

T Sig.

B Std. Error Beta

1 (Constant) -76.453 8.663 -8.826 .003

X1 3.666 .234 .685 15.672 .001

X2 1.001 .447 .124 2.242 .111

X3 5.977 1.123 .276 5.324 .013

a. Dependent Variable: Y

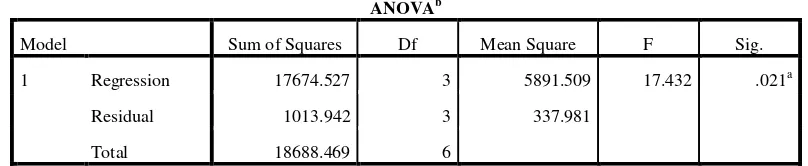
Tabel 3.10

ANAVA untuk Data yang Bernilai Tinggi (Kelompok 2)

ANOVAb

Model Sum of Squares Df Mean Square F Sig.

1 Regression 17674.527 3 5891.509 17.432 .021a

Residual 1013.942 3 337.981

[image:45.595.108.506.666.744.2]

ANOVAb

Model Sum of Squares Df Mean Square F Sig.

1 Regression 17674.527 3 5891.509 17.432 .021a

Residual 1013.942 3 337.981

Total 18688.469 6

a. Predictors: (Constant), X3, X2, X1

[image:46.595.102.506.92.175.2]

b. Dependent Variable: Y

Tabel 3.11

Hasil perhitungan Koefisien Regresi pada Kelompok 2 Menggunakan SPSS 19

Coefficientsa

Model

Unstandardized Coefficients

Standardized

Coefficients

t Sig.

B Std. Error Beta

1 (Constant) -59.964 184.029 -.326 .766

X1 1.480 4.615 .108 .321 .769

X2 3.488 4.701 .151 .742 .512

X3 8.974 3.860 .758 2.325 .103

a. Dependent Variable: Y

Hasil regresi kelompok 1(yang bernilai rendah) adalah 1013.942 dan hasil regresi kelompok 2 (yang bernilai tinggi) adalah 10.540, maka diperoleh F hitung :

F hitung = RSS =

1 2

RSS RSS

RSS =

540 . 10

942 . 1013 = 96.1994

Dari tabel F((n-d-2k)/2) diperoleh F((15-1-8)/2) = F(3,3) pada p=0.05 adalah 9.28

5. Kesimpulan:

Karena H0 ditolak, maka dapat disimpulkan bahwa adanya gejala heteroskedastisitas dalam data tersebut.

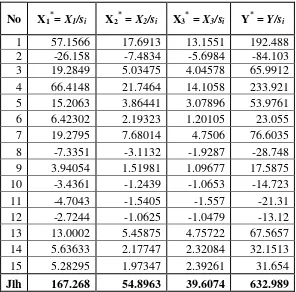
[image:47.595.175.471.404.696.2]

3.5.4 Estimasi Parameter Menggunakan Metode Weight Least Square

Tabel 3.12

Data transformasi Untuk Pendugaan Model Regresi Menggunakan Metode Weight Least Square ( Dalam Jutaan Rupiah)

No X1*= X1/si X2* = X2/si X3* = X3/si Y* = Y/si

1 57.1566 17.6913 13.1551 192.488 2 -26.158 -7.4834 -5.6984 -84.103 3 19.2849 5.03475 4.04578 65.9912 4 66.4148 21.7464 14.1058 233.921 5 15.2063 3.86441 3.07896 53.9761

6 6.42302 2.19323 1.20105 23.055

7 19.2795 7.68014 4.7506 76.6035

8 -7.3351 -3.1132 -1.9287 -28.748 9 3.94054 1.51981 1.09677 17.5875 10 -3.4361 -1.2439 -1.0653 -14.723

11 -4.7043 -1.5405 -1.557 -21.31

12 -2.7244 -1.0625 -1.0479 -13.12 13 13.0002 5.45875 4.75722 67.5657 14 5.63633 2.17747 2.32084 32.1513 15 5.28295 1.97347 2.39261 31.654 Jlh 167.268 54.8963 39.6074 632.989

*

ˆ

                                          







































 * * 3 * * 2 * * 1 * 1 2 * 3 * 3 * 2 * 3 * 1 * 3 * 3 * 2 2 * 2 * 2 * 1 * 2 * 3 * 1 * 2 * 1 2 * 1 * 1 * 3 * 2 * 1 * 3 * 2 * 1 * 0 ˆ ˆ ˆ ˆ Y X Y X Y X Y X X X X X X X X X X X X X X X X X X X X X n                                             99 . 7744 10984 6 . 34149 989 . 632 683 . 497 765 . 701 81 . 2181 6074 . 39 765 . 701 45 . 1001 13 . 3106 8963 . 54 81 . 2181 13 . 3106 49 . 9717 268 . 167 6074 . 39 8963 . 54 268 . 167 15 ˆ ˆ ˆ ˆ 1 * 3 * 2 * 1 * 0                             1834 . 0 0897 . 0 0122 . 0 0205 . 0 0897 . 0 1624 . 0 0317 . 0 004 . 0 0122 . 0 0317 . 0 0129 . 0 0044 . 0 0205 . 0 004 . 0 0.0044 0.08644 )

(X*TX* 1

                                                 99 . 7744 10984 6 . 34149 989 . 632 1834 . 0 0897 . 0 0122 . 0 0205 . 0 0897 . 0 1624 . 0 0317 . 0 004 . 0 0122 . 0 0317 . 0 0129 . 0 0044 . 0 0205 . 0 004 . 0 0.0044 0.08644 ˆ ˆ ˆ ˆ * 3 * 2 * 1 * 0                                179 . 7 962 . 3 601 . 0 044 . 2 ˆ ˆ ˆ ˆ * 3 * 2 * 1 * 0    

Sehingga didapat Yˆ* 2.0440.601X₁*3.962X₂*7.179X₃*

Ini berarti bahwa besarnya nilai ˆ*

Sedangkan jika besarnya biaya produksi meningkat sebesar 1 juta rupiah, maka tingkat penjualan meningkat sebesar 0.601 juta rupiah. Dan jika besarnya biaya distribusi meningkat sebesar 1 juta rupiah maka tingkat penjualan meningkat sebesar 03.962 juta rupiah. Kemudian jika biaya promosi meningkat sebesar 1 juta rupiah, maka tingkat penjualan meningkat sebesar 7.179 juta rupiah. Dari ketiga variabel diatas dapat dilihat bahwa yang paling berpengaruh terhadap tingkat penjualan adalah biaya promosi.

[image:49.595.111.500.372.723.2]

.

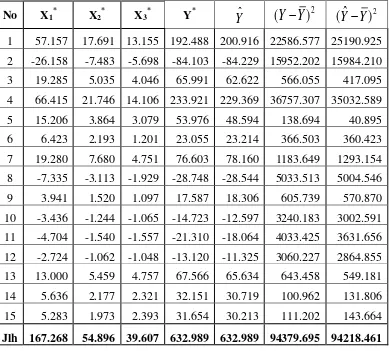
Tabel 3.13

Perhitungan Koefisien Determinasi pada WLS Menggunakan Excel No X1* X2* X3* Y*

Y

ˆ

(

Y



Y

)

2

(

Y

ˆ



Y

)

2





 





 

 ₂

2 2

ˆ Y

Y Y Y R

695 . 94379

461 . 94218

2 

R

R2 = 0.998

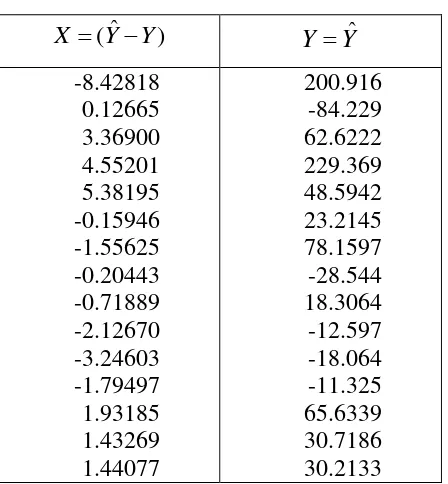
[image:50.595.202.426.450.692.2]

3.5.5 Uji Grafik pada Metode Weight Least Square

Tabel 3.14

Data Nilai X dan Y WLS pada Uji Grafik )

ˆ

(Y Y

X   _Y _Yˆ

-8.42818 0.12665 3.36900 4.55201 5.38195 -0.15946 -1.55625 -0.20443 -0.71889 -2.12670 -3.24603 -1.79497 1.93185 1.43269 1.44077

Dari Grafik diatas dapat dilihat bahwa tidak ada pola yang jelas pada grafik tersebut, dan titik –titik juga menyebar diatas dan dibawah angka 0 pada sumbu Y, maka tidak terjadi heteroskedastisitas.

BAB 4

PENUTUP 4.1 Kesimpulan

Dari hasil pembahasan diatas dapat disimpulkan bahwa:

1. Regresi linier berganda yang memuat unsur heteroskedastisitas memiliki variansi error yang tidak konstan, estimasi variansi error tersebut adalah

 

V

V  ˆ2 dengan



  



 Y Y X Y X X

k n

T T T T

T  



 1 2

ˆ2

dan



T



T

X X X X I

Untuk mengatasi unsur heteroskedastisitas pada regresi linier berganda bisa dilakukan dengan metode WLS. Pada metode ini, didapat matriks p yang memilki sifat pTp pp p2 V

 



sehingga transformasi persamaan untuk mengatasi heteroskedastisitas dilakukan dengan mengalikan persamaan yang memuat unsur heteroskedastisitas dengan 1

p _.

2. Estimasi dilakukan dengan metode WLS, yakni penerapan metode OLS pada hasil trsansformasi persamaan, sehingga menghasilkan taksiran parameter regresi (ˆ*) sebagai berikut:



XTV 1X



1XTV 1Y

*

ˆ _   



4.2 Saran

Didalam penelitian ini penulis menggunakan model regresi linier berganda. Bagi pembaca yang ingin melakukan penelitian yang serupa, peneliti menyarankan menggunakan model nonlinier atau model –model lain yang lebih rumit.

DAFTAR PUSTAKA

Algifari.2000. Analisis Regresi Teori Kasus dan Solusi. Edisi Kedua. Yogyakarta: BPPE

Drapper N, dan Smith H. 1992. Analisis Regresi Terapan. Edisi Kedua. Jakarta: Gramedia Pustaka Utama.

Gasperz, Vincent. 1991. Ekonometrik Terapan. Edisi Kedua. Bandung : Tarsito. Greene WH. 1997. Econometrik Analisis. Third Edition. New York: Prantice Hall

International.

Gujarati, N. Damodar dan Dawn C. Porter, DKK.1999.Ekonometrika Dasar. Jakarta: Erlangga.

Sudjana. Metoda Statistika. 1996. Bandung: Tarsito

Sudjana.1996. Teknik Analisis Regresi dan Korelasi. Bandung : Tarsito. Supranto. 2009. Statistik Teori dan Aplikasi. Jilid II . Jakarta: Erlangga Supranto. 2004. Ekonometri. Jilid I. Bogor : Ghalia Indonesia.