Garis dan Bidang Dalam Ruang Euclid Berdimensi N

SKRIPSI

Diajukan dalam rangka menyelesaikan Studi Strata Satu untuk mencapai gelar Sarjana Sains

Oleh

Nama : M SOLIKIN ADRIANSAH NIM : 4150402019

Program Studi : Matematika S1 Jurusan : Matematika

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI SEMARANG

ii

Semarang, Skripsi, Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Negeri Semarang 2006

Sistem geometri yang dipelajari dari sekolah dasar hingga sekolah menengah merupakan suatu sistem geometri yang dikembangkan oleh Euclides, sehingga dinamakan Geometri Euclid atau dapat disebut dengan Geometri seperti yang kita kenal sekarang. Meskipun pada tingkatan universitas diperkenalkan sistem lain dari geometri yaitu geometri non-euclid.

Gagasan digunakannya pasangan bilangan terurut lebih dari tiga atau dalam ruang dimensi-3, karena para ahli matematika dan fisika menyadari bahwa tidak harus berhenti pada ganda tiga. Diakui bahwa bahwa bilangan – bilangan ganda empat

(

a₁ ,a₂ ,a₃ ,a₄

)

dapat dikorespondensikan sebagai titik – titik dalam ruang dimensi-4 dan seterusnya.

Garis dan bidang merupakan obyek yang cukup penting untuk dibahas dan menjadi pijakan awal dari geometri, sehingga konsep garis dan bidang sering digunakan dalam geometri. Perluasan garis dan bidang pada ruang yang melebihi dimensi-3 dapat dilakukan yaitu dengan bekerja melalui sifat – sifat analitisnya dan bukan melalui sifat – sifat geometris.

iv

ª Ilmu itu lebih cantik dari mangkuk yang cantik,

orang yang menuntut ilmu itu lebih manis dari

madu, dan ber’amal dengan ilmu yang dimiliki itu

lebih sulit dari meniti sehelai rambut. (Usman bin

Affan)

ª Sebaik – baik isteri adalah jika kamu memandangnya

membuat hatimu senang, jika kamu perintah dia

mentaatimu, dan jika kamu tinggal maka dia akan

menjaga untukmu harta dan dirinya. ( Ibnu Jahir)

PERSEMBAHAN

ª Bapak dan Mamah yang memberikan

doa dan kasih sayangnya.

ª M’Lel, Bekti, Drajat dan Ayu .

ª Someone in Somewhere, Wait me.

ª Adit, Pirlo, Bira, dan Pilar

“capek”.

ª Fina, Asih, Isti, Diana, Cahya

dan Dewi.

ª M’ Tamie dan Ida.

ª Raras thanks for everything.

v

Segala puji hanya bagi ALLAH SWT atas segala limpahan rahmat dan hidayah-Nya, sehinggga dapat menyelesaikan skripsi ini dengan judul “ GARIS DAN BIDANG DALAM RUANG EUCLID BERDIMENSI N “.

Terselesaikannya skripsi ini tidak lepas dari bantuan berbagai pihak, oleh karena itu disampaikan ucapan terima kasih kepada:

1. Prof. Dr. A. T. Soegito, SH, MM, Rektor Universitas Negeri Semarang. 2. Drs. Kasmadi Imam S, M. S, Dekan FMIPA UNNES.

3. Drs. Supriyono, M. Si, Ketua Jurusan Matematika FMIPA UNNES.

4. Drs. Suhito, M. Pd, Dosen pembimbing utama yang telah membimbing dan memberikan masukan dalam penulisan skripsi.

5. Drs. Amin Suyitno, M. Pd, Dosen pembimbing pendamping yang telah membimbing dan memberikan masukan dalam penulisan skripsi ini.

6. Bapak dan Mamah yang selalu mendoakan.

7. Kakakku terima kasih atas bantuannya semoga aku dapat melakukan hal yang sama.

8. Teman – teman angkatan 2002 yang memberikan semangat untuk terus berjuang dalam menyelesaikan skripsi ini.

vi pembaca.

Semarang, September 2006

vii

ABSTRAK ...ii

HALAMAN PENGESAHAN ...iii

MOTTO dan PERSEMBAHAN ...iv

KATA PENGANTAR ...v

DAFTAR ISI ...vii

BAB I PENDAHULUAN ...1

A. Latar Belakang Masalah ...1

B. Permasalahan ...4

C. Tujuan Penulisan ...3

D. Manfaat Penulisan ...5

E. Penegasan Istilah ...6

F. Sistematika Skripsi ...7

BAB II LANDASAN TEORI ...10

A. Ruang Linear ...11

1. Ruang Linear ...11

2. Ruang Bagian dari Ruang Linear ...23

3. Ruang Linear Bernorma ...23

4. Ruang Inner Product ...25

B. Ruang Vektor ...12

viii

A. Kajian Pustaka ...11

B. Perumusan Masalah ...12

C. Pemecahan Masalah ...23

D. Penarikan Simpulan ...56

BAB IV PEMBAHASAN ...40

A. Titik ...11

B. Garis Lurus Real ...12

1. Persamaan Garis lurus-n ...22

2. Sudut Antara Dua Garis Lurus-n ...33

3. Jarak Titik terhadap Garis Lurus-n ...36

4. Jarak Antara Dua garis Lurus-n ...36

C. Bidang Datar-n ...13

1. Persamaan Bidang Datar-n ...22

2. Persamaan Hesse Bidang Datar-n ...33

3. Jarak Titik terhadap Bidang Datar-n ...23

4. Kedudukan Dua Bidang Datar-n ...23

BAB V PENUTUP ...45

A. Simpulan ...11

B. Saran ...22

A. Latar Belakang Masalah

Kata “ geometri ” berasal dari bahasa Yunani yang berarti “ ukuran bumi “. Maksudnya mencakup segala sesuatu yang ada di bumi. Geometri kuno sebagian dimulai dari pengukuran praktis yang diperlukan untuk pertanian orang-orang Babylonia dan Mesir. Kemudian hal tersebut diperluas untuk perhitungan panjang ruas garis, luas dan volum. Hasil-hasil ini sering dinyatakan sebagai deret arimetika yang secara empiris tidak benar (Wallace dalam Mulyati, 1).

Menurut tradisi, mempelajari geometri penting karena geometri telah menjadi alat utama untuk mengajar seni berpikir. Dengan berjalannya waktu, geometri telah berkembang menjadi pengetahuan yang disusun secara menarik dan logis. Geometri terutama terdiri dari serangkaian pernyataan tentang titik-titik, garis-garis, dan bidang-bidang, dan juga planar (proyeksi bidang) dan benda-benda padat. Geometri dimulai dari istilah-istilah yang tidak terdefinisikan, definisi-definisi, aksioma-aksioma, postulat-postulat dan selanjutnya teorema-teorema.

Geometri adalah sistem pertama untuk memahami ide. Dalam geometri beberapa pernyataan sederhana diasumsikan, dan kemudian ditarik menjadi pernyataan-pernyataan yang lebih kompleks. Sistem seperti ini disebut sistem deduktif. Geometri mengenalkan tentang ide konsekuensi deduktif dan logika yang dapat digunakan sepanjang hidup.

Dalam mendefinisikan sebuah kata, pertama digunakan kata yang lebih sederhana kemudian kata yang lebih sederhana ini pada gilirannya didefinisikan menjadi kata yang lebih sederhana lagi, sehingga pada akhirnya, proses tersebut akan berakhir. Pada beberapa tingkatan, definisi harus menggunakan sebuah kata yang artinya sudah sangat jelas, ini dikarenakan agar artinya diterima tanpa memerlukan definisi lagi, dengan kata lain dapat disebut dengan istilah tak terdefinisikan (undefined term).

Sistem dari geometri yang dipelajari dari sekolah dasar hingga menengah merupakan geometri yang didasarkan atas postulat ataupun aksioma yang dikemukakan oleh Euclides yang biasa disebut geometri euclid, meskipun pada tingkat universitas diperkenalkan sistem lain dari geometri yaitu geometri non-euclid. Gagasan digunakannya pasangan bilangan terurut lebih dari tiga, karena para ahli matematika dan fisika menyadari bahwa tidak harus berhenti pada ganda tiga. Diakui bahwa bilangan ganda empat

(

a₁ ,a₂ ,a₃ ,a₄

)

dapat dianggap sebagai titik pada ruang dimensi-4, ganda lima

(

a₁ ,a₂ ,a₃ ,a₄ ,a₅

)

sebagai titik pada ruang dimensi-5 dan seterusnya. Walaupun visualisasi geometrik tidak melebihi ruang dimensi tiga.

Perluasan garis dan bidang pada ruang yang melebihi dimensi-3 dapat dilakukan yaitu dengan bekerja melalui sifat – sifat analitisnya dan bukan melalui sifat – sifat geometris. Dari latar belakang di atas maka judul dari skripisi ini adalah GARIS DAN BIDANG DALAM RUANG EUCLID BERDIMENSI N

B. Permasalahan

Permasalahan yang dikaji dalam penulisan ini adalah

1. Bagaimana bentuk dari persamaan garis lurus-n dan bidang datar-n? 2. Bagaimana persamaan kedudukan dua garis lurus-n dan dua bidang

3. Bagaimana persamaan sudut dua garis lurus-n dan dua bidang datar-n?

4. Bagaimana persamaan jarak antara sebuah titik dengan garis lurus-n dan jarak antara dua garis lurus-n?

5. Bagaimana persamaan jarak antara sebuah titik dengan bidang datar-n?

C. Tujuan Penulisan

Tujuan penulisan ini adalah untuk mengetahui persamaan dari garis n dan didang datar-n serta relasi yang terkait dengan gair lurus-n dalurus-n bidalurus-ng datar-lurus-n

D. Manfaat Penulisan

Dari hasil penulisan ini diharapkan dapat digunakan sebagai sumbangan pemikiran bagi mahasiswa Universitas Negeri Semarang, khususnya Jurusan Matematika yang ingin mengembangkan penulisan ini.

E. Penegasan Istilah 1. Garis

Sebuah garis (garis lurus) dapat dibayangkan sebagai kumpulan dari titik – titik yang memanjang secara tak terhingga ke kedua arah.

2. Bidang

Sebuah bidang dapat dianggap sebagai kumpulan titik yang jumlahnya tak terhingga yang membentuk permukaan rata yang melebar ke segala arah sampai tak terhingga.

( Kohn, 2003 : 4 )

3. Ruang Euclid Dimensi N

Jika n bilangan bulat positif maka himpunan dari n bilangan real (x₁,x₂,...,x_n) adalah sebuah titik atau vektor pada dimensi n yang dinotasikan dengan Rn =

{

(

x₁, x₂ ,..., x_n

)

x₁, x₂,...,x_n∈R

}

. Ruang linear _{R dan ruang vektor} n _{R yang dilengkapi oleh suatu inner} n product dan dinotasikan dengan

{

Rn , x ,y

}

disebut ruang Euclid dimensi n (Euclidean n-space).

( Ruckle, 1961 : 31 )

F. Sistematika Skripsi Bab I Pendahuluan

Bab ini berisi tentang latar belakang masalah, penegasan istilah, permasalahan, tujuan, manfaat dan sistematika dari penulisan skripsi.

Bab II Landasan Teori

Bab III Metode Penelitian

Bab ini berisi langkah-langkah yang digunakan dalam penyusunan skripsi ini.

Bab IV Pembahasan

Bab ini berisi garis dan bidang yang terdiri dari persamaan garis dan bidang, kedudukan dua garis dan dua bidang serta jarak garis dan bidang dalam ruang Euclid berdimensi n

Bab V Penutup

A. Ruang Linear 1. Ruang Linear

Definisi A.1

Sebuah ruang linear atas lapangan F adalah sebuah himpunan

E yang dilengkapi dengan operasi penjumlahan E×E→E dan

operasi perkalian F×E→E dimana kedua operasi tersebut harus memenuhi aksioma-aksioma berikut.

a. Untuk semua x, y, z di E berlakux+

(

y+z

) (

= x+y

)

+z. b. Untuk semua x,y di E berlakux+y=y+x.

c. Ada elemen identitas 0 di E sehinggax+0=xuntuk setiap x di E. d. Untuk semua x di E, ada elemen –x di E sehingga x+

( )

-x =0. e. Untuk semua a, b di F dan x di E berlaku a

( ) ( )x.

bx = ab

f. Untuk semua a, b di F dan x di E berlaku

(

a+b

)

x=ax+bx. g. Untuk semua a di F dan x, y di E berlaku a

(

x+y

)

=ax+ay. h. Untuk semua x di E berlaku 1x = x.

Contoh A.1.1

Selidiki apakah Rn dengan operasi penjumlahan dan perkalian merupakan

ruang linear atas lapangan R.

Penyelesaian :

Rn = R×R×R×...×R =

{

(

x₁,x₂,...,x_n

)

x₁,x₂,...,x_n∈R

}

.

Ambil sembarang x = (x₁, x₂,..., x_n), y = (y₁, y₂,..., y_n) dan z = ( z₁,

z₂,..., zn) n R

∈

a). Jelas x + (y + z) = (x₁, x₂,..., x_n) + (y₁, y₂,..., y_n+ z₁, z₂,..., z_n)

= (x₁+ y₁+ z₁, x₂+ y₂+ z₂, ... , x_n+ y_n+ z_n)

= (x₁+ y₁, x₂+ y₂, ... , x_n+ y_n) + (z₁, z₂,..., zn)

= (x + y) + z .

b). Jelas x×y = (x₁, x₂,..., x_n)×(y₁, y₂,..., y_n) = (x₁× y₁, x₂× y₂,..., x_n× y_n)

= (y₁× x₁, y₂× x₂,..., yn× xn) =y×x.

c). Pilih 0 = (0₁, 0₂,..., 0_n) ∈Rn

Jelas x + 0 = (x₁, x₂,..., x_n) + (0₁, 0₂,..., 0_n)

= 0 + (x₁, x₂,..., x_n) = x. d). Pilih (-x₁, -x₂,..., -x_n)∈_Rn

Ambil sembarang a, b ∈R

e).a

( )

bx = a×

(

bx₁,bx₂,...,bx_n

)

= a×

(

b

(

x₁, x₂,..., x_n

)

)

=

( )x

ab .

f).

(

a+b

)

x=

(

a+b

)

×(x₁, x₂,..., xn)

= a×(x₁, x₂,..., x_n) + b×(x₁, x₂,..., x_n) = ax + bx.

g). a(x+y) = a

{

(

x₁,x₂,...,x_n

) (

+ y₁,y₂,...,y_n

)

}

=a × (x₁, x₂,..., x_n) + a × (y₁, y₂,..., y_n) = ax + ay.

h). 1x = 1(x₁, x₂,..., x_n)

= (x₁, x₂,..., x_n)

= x

Jadi∀(x₁, x₂,..., xn), (y1, y2,..., yn) dan ( z1, z2,..., zn) n R

∈ dan a, b ∈ R maka Rn merupakan ruang linear atas R.

2. Ruang Bagian dari Ruang Linear

Jika V ruang linear atas F. Jika B≠φ dan B⊂V. B dengan sifat, untuk setiap vektor x , y di V dan skalar α, β di F berlaku αx + βy di B maka B disebut ruang bagian dari ruang linear.

Contoh A.1.2

Tunjukan untuk setiap bilangan asli m, n dengan m≤ n maka Rm

merupakan ruang bagian dari ruang linear terhadap Rn.

Penyelesaian :

Dipunyai Rm = R×R×R×...×R =

{

(

x₁,x₂,...,x_m

)

x₁,x₂,...,x_m∈R

}

. Ambil sembarang x = (x₁, x₂,..., x_m), y = (y₁, y₂,..., y_m)∈_Rm _{dan ambil} sembarang skalar α, β di R

Jelas Rm merupakan ruang vektor atas Rn sendiri dan untuk setiap x, y di

Rm dan a, b di R sehingga berlaku

α(x₁, x₂,..., x_m) + β(y₁, y₂,..., y_m)

= (α x₁+ β y₁, α x₂+ β y₂, ... , α x_m+ β y_m)

∈

Rn. Jadi Rm merupakan subruang dari Rn.

3. Ruang Linear Bernorma

Dipunyai V ruang Linear atas R. Jika terdapat fungsi . :V→R

yang memenuhi :

a. αx =α x

b. x ≥0 dan x =0⇔x = θ dengan θ vektor nol di V

c. x+y ≤ x + y

maka fungsi . disebut norma pada V.

Contoh A.1.3

Di punyai fungsi Rn→R yang didefinisikan

2 1 n 1 i 2 i x x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

= untuk setiap

vektor x = (x₁, x₂,..., x_n)∈ Rn adalah suatu norm pada ruang euclid Rn. Tunjukkan fungsi tersebut merupakan suatu norm pada ruang euclid Rn?

Penyelesaian :

Ambil sembarang vektor x = (x₁, x₂,..., x_n), y = (y₁, y₂,..., y_n),

z = (z₁,z₂,..., z_n) ∈Rndan skalar α∈R memenuhi: a. Jelas αx =α x

Karena 2 1 n 1 i 2 i 2 2 1 n 1 i 2 i x x x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

∑

= = α α α x x 2 1 n 1 i 2 i α α ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

=

b. x ≥0 dan x 0 x 0sebab, x x 0

2 1 n 1 i 2

i ⎟ ≥

⎠ ⎞ ⎜ ⎝ ⎛ = = ⇔ =

∑

= .

( )

⇐ jika x = 0 maka x_i= 0 untuk setiap i (i = 1, 2,...,n), yang berakibat

2 1 n 1 i 2 i x x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

= = 0.

( )

⇒ jika

2 1 n 1 i 2 i x x 0 dipunyai maka 0 x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = = =

∑

=

, sehingga untuk

c. x+y ≤ x + y .

Ditunjukan sebagai berikut

Karena untuk setiap i (i = 1, 2,...,n) berlaku

(

) (

i i

)(

i i

) (

i i

) ( ) ( )

(

i i

) (

i i

) (

i i i

)

i

2 i

i y x y x y x y x y x y x x y y

x + = + + ≤ + + = + + +

maka dengan memanfaatkan teorema Cauchy-Shcwarstz didapat

(

)

∑

(

)

∑

(

)

∑

= = = + + + ≤ + n 1 i n 1 i i i i i i i n 1 i 2 i

i y x y x x y y

x

(

)

(

)

n 12

1 i 2 i 2 1 n 1 i 2 i i 2 1 n 1 i 2 i 2 1 n 1 i 2 i

i y x x y y

x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ ≤

∑

∑

∑

∑

= = = =

dalam hal x_i+y_i≠0 maka diperoleh

(

)

(

)

2 1 n 1 i 2 i 2 1 n 1 i 2 i 2 1 n 1 i 2 i i n 1 i 2 i i y x y x y x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≤ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊

∑

∑

∑

∑

= = = =

(

)

n 12

1 i 2 i 2 1 n 1 i 2 i 2 1 n 1 i 2 i

i y x y

x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≤ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ ⇔

∑

∑

∑

= = =

Dengan kata lain diperoleh x+y ≤ x + y .

Berdasarkan ketiga point a, b dan c maka fungsi Rn→R yang

didefinisikan 2 1 n 1 i 2 i x x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

=

untuk setiap vektor x = (x₁, x₂,..., xn)∈ R

n

4. Ruang Hasil Kali Dalam (Inner Product Space)

Dipunyai V ruang linear atas lapangan real R. Jika terdapat

fungsi , :V×V→R sehingga untuk setiap vektor x,y,z ∈ V dan

skalar α∈R memenuhi:

a. x,y = y,x

b. αx,y =α x,y

c. x,y+z = x,y + x,z

d. x,x ≥0dan x,x =0⇔x = θ (θ vektor nol di V) Sehingga , merupakan ruang inner product.

( Wuryanto, 2003 : 36 )

Contoh A.1.4

n

R terhadap perkalian titik yang didefinisikan

∑

=

= n

1 i

i iy x y

x, merupakan

ruang inner product. Ditunjukan bahwa perkalian titik tersebut adalah

suatu inner product. Dibentuk fungsi , dari Rn×Rn→Ryang

didefinisikan

∑

=

= n

1 i

i iy x y

x, untuk setiap vektor x = (x₁,x₂,...,x_n), y =

(y₁, y₂,..., yn) di n

R . Fungsi tersebut merupakan suatu inner product

pada R sebab, untuk setiap vektor x = (xn ₁,x₂,...,xn), y = (y1, y2,..., yn)

di R dan skalar real n α memenuhi:

a. Jelas x,y = y,x oleh sebab,

∑

=

= n

1 i

i iy x y

x, = y x y,x

n

1 i

i

i =

∑

=

b. Jelas αx,y =α x,y oleh sebab,

∑

= = n 1 i i iy x y x, α α

∑

= = = n 1 i i

iy x,y

x α

α .

c. Jelas x,y+z = x,y + x,z

karena

∑

(

)

∑

(

)

∑

∑

= = = = + = + = + = + n 1 i n 1 i i i i i n 1 i n 1 i i i i i i

i y z x y x z x y x z

x , i z y x

= x,y + x,z .

d. x,x ≥0oleh sebab x,x x 0.

n 1 i 2 i > =

∑

=

Jadi berdasarkan a, b dan c maka R terhadap perkalian titik yang n

didefinisikan

∑

= = n 1 i i iy x y

x, untuk i = 1, 2, ... , n.

B. Ruang Vektor 1. Ruang Vektor

Definisi B.1

Sebuah ruang vektor V adalah sebuah himpunan dari objek x, y,

z, .... yang disebut vektor. Satu vektor yang dikenal dinamakan vektor

nol yang dinotasikan dengan θ. Untuk setiap vektor x dimana dikenal sebuah vektor –x, dinamakan invers dari x. Aksioma – aksioma yang

mengikuti agar asumsi dari ruang vektor terpenuhi adalah

a. Untuk setiap sepasang vektor x, y dimana penjumlahan vektor dari

x, y dinotasikan x + y. Penjumlahan dari vektor harus memenuhi:

i).

_ _

y

x+ =

_ _

ii). ( _ _

y x+ ) +

_ z =

_ x +(

_ _

z y+ ).

iii). _ x + 0 =

_ x

iv). _ x

+(-_ x ) = 0.

b. Untuk setiap skalar k dan setiap vektor x dimana perkalian vektor

dari x oleh k dinotasikan kx. Perkalian vektor oleh skalar harus

memenuhi:

i). k( _ _

y

x+ )= kx_ + k _ y

ii). (k + j) _ x = k

_ x + j

_ x

iii).(kj) _ x = k(j

_ x )

iv).1 _ x =

_ x

Pada b.i) simbol + memiliki dua arti yaitu untuk penjumlahan

skalar dan vektor. Pada b.iii) memiliki dua arti yaitu perkalian dua

skalar atau perkalian sebuah skalar dan sebuah vektor.

( Berberian, 1961 : 1 )

Contoh B.1.1

Tunjukan Rn_{merupakan ruang vektor.}

Penyelesaian :

Ambil sembarang x= (x₁, x₂,..., x_n), y = (y₁, y₂,..., y_n) dan z = (z₁, z₂,..., z_n)∈_Rn

(a)Jelas _ _

y

= (x₁y₁ + x₂y₂ + ... + x_ny_n)

= (y₁x₁ + y₂x₂ + ... + y_nx_n)

= (y₁, y₂,...,y_n) + (x₁, x₂,...,x_n)

= _ _

x y+ .

(b)( _ _

y x+ ) +

_

z =

(

(

x₁, x₂,..., x_n

) (

+ y₁ ,y₂,...,y_n

)

) (

+ z₁ ,z₂,...,z_n

)

=

(

(

x₁, x₂,..., x_n

) (

+ y₁ ,y₂,...,y_n

) (

+ z₁ ,z₂,...,z_n

)

)

=

(

x₁, x₂,..., x_n

) (

+

(

y₁ ,y₂,...,y_n

) (

+ z₁ ,z₂,...,z_n

)

)

= _ x +(

_ _

z y+ ). (c)Pilih 0 = (0₁, 0₂,..., 0_n) ∈Rn

Jelas x 0

_

+ = _

x

0+ = (0₁, 0₂,..., 0_n) + (x₁, x₂,..., x_n) = _ x .

(d)Pilih −x = (-x₁, -x₂,..., -xn) n R

∈

Jelas x

( )

-x _

+ = (x₁, x₂,..., x_n) + (-x₁, -x₂,..., -x_n) = (x₁- x₁, x₂- x₂,..., xn- xn) = 0.

Ambil sembarang k, j R∈ (e)k(

_ _

y

x+ ) = k

{

(

x₁,x₂,...,x_n

) (

+ y₁,y₂,...,y_n

)

}

= k×(x₁, x₂,...,x_n) + k×(x₁, x₂,...,x_n) = kx_ + k _ y .

(f) (k + j) _

x = (k + j) ×(x₁, x₂,...,x_n)

= k×(x₁, x₂,...,x_n) + j×(x₁, x₂,...,x_n)

= k _ x + j

(g)(kj) _

x = (kj) ×(x₁, x₂,...,x_n) = k

(

j×

(

x₁, x₂ ,..., x_n

)

)

= k(j _ x ).

(h)1× _

x = 1×(x₁, x₂,...,x_n) = (x₁, x₂,...,x_n) = _ x .

Karena aksioma ruang vektor Rndipenuhi, maka Rnmerupakan ruang

vektor. Teorema B.1 Jika _ x , _ y , _

z adalah vektor-vektor dalam Rn dan k adalah

sebarang skalar, maka:

a. _ x .

_ y =

_ y .

_ x b. ( _ _ y x+ ) .

_ z =

_ x .

_ y +

_ y .

_ z

c. (k

_ x ) .

_ y = k(

_ x .

_ y )

d. _ x .

_

x ≥ 0. Selanjutnya _ x .

_

x = 0, jika dan hanya jika _ x = 0

Bukti :

Ambil sembarang _

x= (x₁,x₂,...,x_n), _

y = (y₁, y₂,..., y_n) dan _

w = (w₁,

w₂,..., w_n)

(a).Jelas _ x .

_

y = x₁y₁ + x₂y₂ + ... + x_ny_n= y₁x₁ + y₂x₂ + ... + y_nx_n

= _ y .

_ x

(b).Jelas ( _ _

y x+ ) .

_

z = (x₁+ y₁, x₂+ y₂, ... , x_n+ y_n) . (z₁, z₂,..., z_n)

=(x₁z₁+x₂z₂+...+x_nz_n)+(y₁z₁+y₂z₂+...+y_nz_n)

= _ x .

_ z +

_ y .

_ z

(c).Jelas (k _ x ) .

_

y = (kx₁, kx₂, ... , kxn) . (y1, y2, ... , yn)

= k(x₁, x₂, ... , xn) . (y1, y2, ... , yn)

= k(x₁y₁ + x₂y₂ + ... + x_ny_n)

= k( _ x .

_ y )

(d).Kita mempunyai

_ x .

_

x = x₁2+x₂2+...+x_nn ≥0. Selanjutnya kesamaan tersebut benar jika dan hanya jika x₁=x₂=...=x_n =0,

yaitu jika dan hanya jika _ x = 0.

2. Hasil Kali Dalam (Inner Product) dan Norm Definisi B.2

Jika V suatu ruang vektor, maka inner product adalah fungsi dari

V×V ke R, didefinisikan dengan (x_,y_)→ x,y ,∀

_

x,y_ ∈V

memenuhi aksioma berikut.

a. x,y ≥0,∀x∈V.

b. x,x =0 jika dan hanya jika x =0.

c. x,y = y .x ∀x,y∈V.

d. x+y,z = x,z + y,z ∀x,y,z∈V.

Ruang vektor yang dilengkapi dengan hasil kali dalam (inner

product) dinamakan ruang hasil kali dalam.

( Rochmad, 2000 : 24 )

Contoh B.1.2

Rn _{terhadap perkalian titik yang didefinisikan}

∑

= = k 1 i i i _ _ y x y . x merupakan

ruang hasil kali dalam. Ditunjukkan perkalian titik tersebut adalah suatu

inner product. Dibentuk suatu fungsi Rn×Rn →R yang didefinisikan y

. x y ,

x = untuk setiap vektor

_

x= (x₁,x₂,...,x_n), _

y = (y₁, y₂,..., y_n) dan

skalar a di Rn maka fungsi tersebut merupakan suatu inner product sebab

memenuhi aksioma dari ruang inner product.

Bukti

a. x,y = y .x sebab x,y x .y x y y x y .x y,x

k 1 i i i k 1 i i

i = = =

=

=

∑

∑

= =

.

b. ax,y =a x ,y sebab,

( )

ax.y a xy a x y a

( )

x.y a x,y y , x a k 1 i i i k 1 i i

i = = =

=

=

∑

∑

= =

.

c. x+ y,z = x,z + y,z sebab

d. Jelas x,x =

( )

x.x =0 jika dan hanya jika x =0.

e. x,y >0,andaikan xbukanvektor nol karena x,x x.x x 0 k

1 i

2 i >

=

=

∑

=

Jadi Rnperkalian titik yang didefinisikan

∑

=

= k

1 i

i i _ _

y x y .

x merupakan ruang

hasil kali dalam.

Definisi B.3

Jika V suatu ruang vektor, maka norm pada V adalah fungsi dari

V ke R dinyatakan dengan x_ → x yang memenuhi

a. x ≥0 dan x = 0⇔ x_ = θ dengan θ vektor nol di V.

b. αx =α x

c. x+y ≤ x + y

Ruang vektor yang dilengkapi dengan norm dinamakan ruang

bernorm. Panjang suatu vektor x sering disebut sebagai norm x dan

dinyatakan dengan x = x,x 2 x ,x 1

=

( Rochmad, 2000 : 24 )

Teorema B.2 ( Ketaksamaan Cauchy – Schwartz )

Misalkan V suatu ruang inner product dalam R. Untuk setiap

vektor x_ dan y_ di V berlaku x,y ≤ x y . Bukti:

b. Untuk y_ ≠0

Ambil vektor y_ dengan y = 1 dan vektor z=x− x,y y

Sehingga didapat 0≤ z2= z ,z

= x− x,y y,x− x,y y

= x,x − x,y 2

Diperoleh x,y 2 ≤ x 2⇔ x,y ≤ x

Untuk vektor y_ dengan y > 0, sehingga diperoleh

. x atau x,y x y

y y ,

x ≤ ≤

Jadi teorema diatas terbukti.

Dengan menggunakan ketaksamaan Cauchy – Schwartz diatas

dapat didefinisikan cosinus sudut antara dua vektor. Misalkan x_, y_ di

Rn maka bilangan cos θ = y . x

y , x

disebut cosinus sudut antara vektor

_

x dan vektor y_ dan θ disebut sudut antara vektor

_

x dan vektor y_

Dari pengertian cosinus sudut diatas dapat didefinisikan, jika dua

Telah diketahui jika dua vektor di Rn _{tetap dapat dilihat sebagai}

dua vektor yang terletak dalam sebuah bidang di Rn. Maka dari itu

dipunyai teorema sebagai berikut.

Teorema B.3 (Ketaksamaan Segitiga)

Misalkan

_

x dan y_ dua vektor yang terletak di Rn. Maka berlaku

≤ +y

x x + y

Bukti:

Dengan menggunakan teorema B.2 diperoleh

y x . y x y

x+ 2 = + +

_ _ _ _ _ _

y . y y . x 2 x .

x + +

=

y . y y . x 2 x .

x + +

≤

2 2

y y . x 2

x + +

=

Atau x+y 2≤

(

x + y

)

2

Dengan mengambil akarnya diperoleh ketaksamaan segitiga.

Definisi B.4

Dua titik (vektor) x,y∈Rndikatakan searah (sejajar) jika ada bilangan k∈R, k≠0 sehingga y = kx. Dengan kata lain x dan y tak bebas linear. Pasangan n bilangan real

{

α₁,α₂,...,α_n

}

disebut bilangan arah vektor x ≠0 jika

. x : : x : x : :

: _{2 n 1 2 n}

1 α Λ α = Λ

Dengan kata lain, ada bilangan

(

2

)

12

n 2 2 2 1 ... x α α α + + + ± = l

Sehingga, terdapat vektor α =

(

α₁,α₂,...,α_n

)

yang komponennya terdiri dari bilangan arah vektor x yang disebut vektor arah bagi vektor

x. Secara khusus, pasangan n bilangan real

{

λ₁,λ₂,...,λ_n

}

disebut

cosinus arah vektor x jika

x e x, e x e x,

cos k k k k

k

= =

=

θ

λ

untuk setiap k

= 1, 2, ... , n dan

(

θ₁,θ₂,...,θ_n

)

disebut sudut arah vektor x.

Teorema B.4

Jika

(

λ₁,λ₂,...,λ_n

)

cosinus arah vektor x ≠0 maka

∑

= = + + + = n 1 k 2 n 2 2 2 1 2

k λ λ ... λ l.

λ

Bukti :

Diketahui _k

n 1 k k e e x, x

∑

=

= dengan

(

e₁,e₂,...,e_n

)

dengan basis

orthonormal standart pada R , didapat n

x x, x 2 =

∑

∑

= = = n 1 k n 1 k k k k

k e , x,e e e x,

∑

= = n 1 k 2 k e x,

Karena x ≠0

(

x ≠0

)

diperoleh

∑

∑

( )

Atau

∑

=

= + + + =

n

1 k

2 n 2

2 2 1 2

k λ λ ... λ l.

λ

Selanjutnya vektorλ={λ₁,λ₂,...,λ_n

}

disebut vektor cosinus arah bagi vektor x.

Jika vektorλ={λ₁,λ₂,...,λ_n

}

merupakan vektor cosinus arah, maka

.

l

=

λ

Jadi untuk setiap x∈Rn, x ≠0 berlaku x₁: x₂: . ..: x_n =λ₁:λ₂: ...:λ_n.

Selanjutnya ada bilangan h sehingga x x ... x h

n n

2 2

1

1 = = = =

λ λ

λ , dengan

x

h=± .

Dari pemahaman tersebut diatas, disimpulkan sebagai berikut:

(a). Dua titik (vektor) x, y ∈_Rn_{searah (sejajar) jika dan hanya jika x} dan y mempunyai sudut arah yang sama jika dan hanya jika

bilangan arah x sebanding dengan bilangan arah y.

(b). Terlihat bahwa (vektor) x∈Rnmempunyai banyak sekali

bilangan arah, tetapi setiap dua bilangan arah sebanding. Oleh

karena itu, jika vektor x = (x₁, x₂,...,x_n) dengan salah satu

bilangan arahnya adalah

(

α₁,α₂,...,α_n

)

dan cosinus arah vektor x

adalah

{

λ₁,λ₂,...,λ_n

}

dengan

α

λ

α

α

θ

λ

k k

k k

k e e , cos = =

= berarti

. : : : :

:

: _{2 n 1 2 n}

1 α α λ λ λ

Definisi B.5

Himpunan x =

{

}

n

k 2

1,x ,...,x R

x ⊂ dari ruang inner product

disebut himpunan orthonormal jika himpunan tersebut adalah

himpunan orthogonal dan x_i =1,∀idi x.

( Arifin, 2001 : 106 )

Definisi B.6

Himpunan x =

{

x₁,x₂,...,x_k

}

⊂Rn denganx_i ≠0 dari ruang inner product disebut himpunan orthogonal jika xi ≠ yj ,untuk setiapi≠ j.

( Arifin, 2001 : 106 )

Teorema B.5

Setiap himpunan orthogonal, bebas linear

Bukti:

Bentuk α₁x₁+α₂x₂+...+α_nx_n =0 ,dengan α₁,α₂,...,α_n∈R. Ambil sembarang Li, dengan

(

1≤i≤n

)

, diperoleh:

( )_{, x}( ) _x( ) _{... x}( ) _{x,0 0}

xi α₁ 1 +α₂ 2 + +α_n n = =

Karena

( )_{,x 0,untuk i j}

x i j = ≠ dan x( )i,x( )j = x( )i 2 =0 ,untuk i= j.

Diperoleh α_i x( )i 2 =0dan berakibat α_i=0untuk L diatas. Karena i sembarang, diperoleh α₁,α₂,...,α_n =0

Akibat dari teorema B. 5

Setiap himpunan orthonormal bebas linear.

Bukti:

Bentuk himpunan orthonormal

(

e₁,e₂,...,e_n

)

terdiri dari n vektor

dengan e_k =

(

0,0,...,1,0,...,0

)

∈Rn. Komponen ke-k sama dengan L.

Diperoleh pengertian bahwa untuk setiap vektor x = (x₁,

x₂,...,x_n)∈Rn.

Sehingga x = (x₁, 0,...,0) + (0, x₂,...,0) + ...+ (0, 0,...,x_n)

⇔ x = x₁(1, 0,...,0) + x₂(0, 1,...,0) + ...+ x₂(0, 0,...,1)

⇔ x =

∑

=

= n

1 i

i i n

n 2 2 1

1e,x e ,...,x e xe x

Jadi himpunan orthonormal

(

e₁,e₂,...,e_n

)

membangun Rn. Oleh karena

(

e1,e2,...,en

)

bebas linear, maka dia merupakan basis bagi R

n

. Karena

himpunan orthonormal ini mempunyai elemen sebanyak n maka

diperoleh bahwa ruang vektor Rn berdimensi n.

Selanjutnya himpunan orthonormal

(

e₁,e₂,...,e_n

)

disebut basis

orthonormal standart bagi ruang vektor Rn.

Akibat

Setiap (n+1) vektor di dalam Rn tak bebas linear.

Teorema B.6

Bukti:

Diambil sebarang ek

(

1≤k≤n

)

Dengan inner product x∈Rn, diperoleh

k k k k k k k k n n 2 2 1 1 k x e , e x 0 ... 0 e , e x ... 0 0 e , e x ... e x e x e x, = = + + + + + + = + + + = Teorema B.7

Setiap x∈_Rn_{dapat dituliskan menjadi}

k n

1 k

k k,e e x

x

∑

=

=

Bukti:

Diket

(

e₁,e₂,...,e_n

)

basis orthonormal standart Rn, maka untuk setiap x

= (x₁, x₂,...,x_n)∈Rn dengan x₁, x₂,...,x_n∈Rberlaku

x =

∑

= = + + + n 1 i i i n n 2 2 1

1e x e ... x e xe

x

Karena x_k = x,e_k untuk setiap k

(

1≤k≤n

)

. Diperoleh

k n

1 k

k k,e x x

x

∑

=

=

Telah diketahui bahwa di dalam ruang berdimensi n, sebarang

vektor (titik) dapat dihadirkan sebagai kombinasi linear dari n vektor

(titik) yang termasuk di dalam basis ruang Rn. Berikut ini akan

dihadirkan mengenai vektor (titik) yang dihadirkan sebagai kombinasi

Teorema B.8

Jika diberikan dua vektor (titik) x,y∈Rntidak sama dengan nol maka

ada vektor-vektor n

2 1,y R

y ∈ sehingga y₁=kyuntuk suatu skalar k,

2

1 y

y ⊥ dan x=y₁+y₂ lebih lanjut dengan y

y y , x

y₁= ₂ dan

y y

y , x -x

y₂= ₂ .

Gambar 2.1

Bukti :

Diasumsikan teorema diatas berlaku

Jadi akan ditentukan bilangan k∈Rdengan y1=ky dan vektor-vektor

n 2 1,y R

y ∈ yang saling orthogonal sehingga x dapat ditulis

sebagaix=y₁+y₂, berarti didapat y₂ =x−y₁. Selanjutnya dilakukan inner product antara vektor x vektor y, didapat

y , y y y ,

x = ₁+ ₂

= ky+y₂,y

=k y 2+ y₂,y 2

y

1 y

x

[image:36.612.179.509.131.434.2]

Karena y₂⊥y maka y₂,y =0, sehingga persamaan ini menghasilkan

2 y

y , x k=

Karena y₁=kydiperoleh y

y y , x

y₁= ₂

Dengan demikian diperoleh juga y

y y , x -x

y₂ = ₂ .

C. Ruang Metrik

Definisi C.1.

Misalkan X≠φ. Fungsi d : X×X disebut metrik pada X jika memenuhi aksioma - aksioma sebagai berikut.

(M1) d(x,y) ≥0, untuk setiap x, y∈X, d(x,y) = 0 ⇔x = y.

(M2) d(x,y) = d(y,x), untuk setiap x, y∈X.

(M3) d(x,y)≤d(x,z) + d(z,y), untuk setiap x, y,z∈X.

( Ruckle, 1961 : 47 )

Contoh C.1.1

Buktikan bahwa fungsi d:Rn×Rn →R _{yang didefinisikan}

d(x,y)=

(

)

2 1 n

1 i

2 i

i y

x ⎟

⎠ ⎞ ⎜

⎝

⎛

∑

₋

=

memenuhi semua sifat metrik.

Penyelesaian :

d(x,y) =

(

x y

)

0 2 1 n 1 i 2 i

i ⎟ ≥

⎠ ⎞ ⎜ ⎝ ⎛

∑

₋ =

, jelas karena

(

x_i −y_i

)

2 ≥0

( )

⇒ dipunyai d(x,y) = 0, ditunjukkan x = y.

karena d(x,y) =

(

)

2 1 n 1 i 2 i i y x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∑

₋ =

berakibat

∑

(

)

= = − n 1 i 2 i

i y 0

x

berakibat

(

x_i−y_i

)

2 =0 ∀i=1,2,... ,n sebab andaikan ∃i ∋

(

x_i −y_i

)

2 >0

berakibat 0

(

x -y

)

0

n 1 i 2 i i > =

∑

=

diperoleh fakta 0 > 0, kontradiksi.

jadi x_i −y_i =0 ∀i=1,2,...,n Jadi x = y.

( )

⇐ dipunyai x = y, ditunjukkan d(x,y) = 0

karena x = y maka x_i =y_i ∀i=1,2,...,n

berakibat x_i−y_i =0 ∀i=1,2,...,n

berakibat

(

x_i−y_i

)

2 =0 ∀i=1,2,...,n

berakibat

∑

(

)

= = − n 1 i 2 i

i y 0

x

berakibat

(

)

2 1 n 1 i 2 i i y x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∑

₋ = = 0

Jadi d memenuhi M1.

2. Ditunjukkan d memenuhi M2

d(x,y) = d(y,x) untuk setiap x,y di R

dipunyai d(x,y) =

(

)

2 1 n 1 i 2 i i y x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∑

₋ =

maka d(x,y) =

(

)

2 1 n 1 i 2 i i y x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∑

₋ = =

(

(

)

)

2 1 n 1 i 2 i i y x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∑

_{− −} = =

(

)

2 1 n 1 i 2 i i x y ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∑

₋ =

= d(y,x).

3. Ditunjukkan d memenuhi M3

d(x,y)≤d(x,z) + d(z,y), untuk setiap x, y,z∈R

dipunyai d(x,y) =

(

)

2 1 n 1 i 2 i i y x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∑

₋ =

= x_i −y_i = x_i−z+z−y_i

(

)

(

)

y). d(z, z) d(x, y -z z x y -z z -x 2 1 n 1 i 2 i i 2 1 n 1 i 2 i i + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ = + ≤

∑

∑

= =

Jadi d memenuhi M3.

Jadi d(x,y) =

(

)

2 1 n 1 i 2 i i y x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∑

₋ =

A. Kajian Pustaka

Terdapat materi yang menarik terkait dengan bidang geometri yang mungkin pernah disinggung dalam perkuliahan tapi tidak diangkat dalam bentuk tulisan yaitu mengenai garis dan bidang dalam ruang berdimensi n.

Dengan melakukan telaah pustaka dari berbagai referensi yang ada dan melakukan konfirmasi dan konsultasi dengan dosen yang membidangi masalah tersebut membuahkan gagasan untuk menuliskannya dalam bentuk skripsi.

B. Perumusan Masalah

Dengan menemukan tema yang cocok, langkah selanjutnya adalah merumuskan masalah dari tema yang diangkat tersebut sesuai dengan bahasan yang akan digunakan dengan bantuan dosen pembimbing. Perumusan masalah dinyatakan dalam bentuk pernyataan yang singkat dan jelas sehingga mudah untuk dipahami.

C. Pemecahan Masalah

masalah ini meliputi penjelasan tema yang telah ditetapkan dan pembahasan mengenai masalah yang telah diungkapkan sebelumnya secara lengkap dengan landasan teori yang ada, tentunya dengan menggunakan referensi yang ada di samping hasil olahan kajian penulis sendiri disertai konsultasi dengan dosen pembimbing.

Dalam proses pemecahan masalah ini, diterangkan berbagai cara menyelesaikan masalah dengan pendekatan yang ditetapkan sebelumnya berdasarkan landasan teori yang sudah ada.

D. Penarikan Kesimpulan

A. Titik

Titik adalah bentuk yang paling sederhana dari geometri, ini

dikarenakan titik hanya digunakan untuk menunjukkan posisi. Dalam

ruang euclid dimensi n titik disimbolkan sebagai pasangan terurut bilangan

real yang biasa dinotasikan dengan, misalkan titik A pada Rn yaitu

A

(

x₁,x₂,...,x_n

)

.

Telah ditunjukkan bahwa d:Rn×Rn →R yang didefinisikan

d(x,y) =

(

)

2 1 n

1 i

2 i

i y

x ⎟

⎠ ⎞ ⎜

⎝

⎛

∑

₋

=

memenuhi semua sifat metrik. Jadi jarak antara

dua titik x_i∈Rndan y_i∈Rnadalah d(x,y) =

(

)

2 1 n

1 i

2 i

i y

x ⎟

⎠ ⎞ ⎜

⎝

⎛

∑

₋

=

=

(

x₁−y₁

) (

2+ x₂−y₂

)

2+...+

(

x_n−y_n

)

2 . Contoh A.4.1

1. Misal A(2, 5, 8) dan B(4, 5, 6) hitung jarak antara titik A dan B.

Penyelesaian :

d(x,y) =

(

)

2 1 n

1 i

2 i i y

x ⎟

⎠ ⎞ ⎜

⎝

⎛

∑

₋

=

=

(

x₁−y₁

) (

2+ x₂−y₂

) (

2+ x₃−y₃

)

2

=

(

2−4

) (

2+ 5−5

) (

2+ 8−6

)

2 = 5.

2. Misal A(4, 6, 8, 10) dan B(3, 2, 5, 4) hitung jarak antara dua titik

Penyelesaian :

d(x,y) =

(

)

2 1 n 1 i 2 i i y x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∑

₋ =

=

(

x₁−y₁

) (

2+ x₂−y₂

) (

2+ x₃−y₃

) (

2+ x₄−y₄

)

2

=

(

4−3

) (

2+ 6−2

) (

2+ 8−5

) (

2+ 10−4

)

2 = 62 .

B. Garis Lurus Real (Real Line) 1. Persamaan Garis Lurus-n

Diberikan X adalah ruang Euclid dan x₁, x₂ ∈X atas lapangan R.

Himpunan G =

{

x∈X:x-x₁=t

(

x₂−x₁

)

dan t∈R

}

disebut garis lurus (real line), dengan syarat keanggotaannya adalah

x-x₁=t

(

x₂−x₁

)

dan t∈R Jadi x=x₁+t

(

x₂−x₁

)

dan t∈R.

Jika X = Rn,

( )

(

)

( )

(

)

n

n 2 1 2 n n 2 1

1 _{a ,a ,...,a R dan x b ,b ,...,b R}

x = ∈ = ∈ maka persamaan

garis real yang melalui x( )1_{dan x}( )2 _adalah

( ) _t

(

_x( ) _x( )

)

(

_{x ,...,x}

) (

_{a ,...,a}

)

_t

{

(

_{b ,...,b}

) (

_a,...,a

)

}

x

-x 1 = 2 − 1 ⇔ _{1 n} − _{1 n} = _{1 n} − _{1 n}

⇔

(

x₁-a₁,...,x_n −a_n

)

=t

{

(

b₁−a₁,...,b_n −a_n

)

}

⇔

(

)

(

1 1 n n

)

n n 1 1 a b ,..., a b a x ,..., a x t − − − − =

(

(

)

)

(

(

)

)

(

(

)

)

n n n n 2 2 2 2 1 1 1 1 a -b a x ... a -b a x a -b a x

t= − = − = = −

Dari persamaan di atas dapat dipahami bahwa garis lurus-n yang

melalui atau memuat titik x( )1 _{dan mempunyai bilangan}

arah

{

α₁,α₂,...,α_n

}

mempunyai persamaan dalam bentuk parametrik adalah

t a x₁= ₁+α₁

t a x₂ = ₂+α₂ ...

t a

X_n = _n+α_n .

Jadi persamaan parametrik garis lurus di R adalah n X_n =a_n+α_nt. Contoh B.4.1

a. Tulis persamaan parametrik untuk garis h yang melalui titik A(3, 0, -1,

2) dan titik B(2, -1, 4, 6).

Penyelesaian :

Karena bilangan arah α= AB = (-1, -1, 5, 4) sejajar g dan A(3, 0, -1, 2) terletak pada g, maka persamaan parametriknya garis g adalah

x = 3 – t, y = – t, z = –1 – 5t dan w = 2 + 4t

b. Tulis persamaan parametrik untuk garis g yang melalui titik A(2, 4, -1)

dan titik B(5, 0, 7).

Penyelesaian :

Karena bilangan arah α= AB = (3, -4, 8) sejajar garis g dan A(2, 4, -1) terletak pada garis g, maka persamaan parametriknya

2. Sudut Antara Dua Garis Lurus-n

Diberikan dua garis lurus-n g dan h dengan bilangan arahnya

berturut-turut adalah

(

α₁,α₂,...,α_n

)

dan

(

β₁,β₂,...,β_n

)

. Selanjutnya, jika x, y ∈g dan u, v ∈h maka vektor x-y dan vektor u-v berturut-turut sejajar dengan bilangan arah

(

α₁,α₂,...,α_n

)

dan

(

β₁,β₂,...,β_n

)

. Oleh karena itu, sudut antara g dan h sama dengan sudut antara vektor x-y

dan vektor u-v. Jadi, jika θ sudut antara g dan h diperoleh rumus

β α β α β α β α β α β α θ , ...

cos = = 1 1+ 2 2+ + n n _.

Dengan 2 1 n 1 i 2 i 2 1 n 1 i 2

i dan ⎟

⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

∑

= = β β α α

Dengan demikian diperoleh hubungan sebagai berikut

a. Garis lurus-n g dan garis lurus-n h sejajar (g // h) jika dan hanya

jika mempunyai bilangan arah yang sebanding.

. ... n n 2 2 1 1 β α β α β α _{= = =}

b. Garis lurus-n g dan garis lurus-n h saling tegak lurus (g⊥h) jika dan hanya jika

0 ...

atau 0

,β = α₁β₁+α₂β₂+ +α_nβ_n =

α .

Contoh B.4.2

1). Tentukan besar sudut dua garis lurus-n, jika diketahui

g: x = 2 + 3t, y = 4 – 4t, z = –1 + 8t, w = 3 + 6t

Penyelesaian:

Karena bilangan arah g: (3, –4, 8, 6) dan garis h: (4, 5, –7, 2)

maka β α β α β α β α β α β α θ , ...

cos = = 1 1+ 2 2 + + n n

(

) ( )

(

)

(

( )

) (

)

( )

( )

. 69 , 118 48 , 0 69 , 9 18 , 11 52 2 7 5 4 6 8 4 3 2 6 7 8 5 4 4 3 0 2 2 2 2 2 2 2 2 = − = × − = + − + + + + + − + × + − × + × − + × =

2). Diberikan persamaan parameter garis g: x = 3 – t, y = – t, z = –1 –

5t, w = 2 + 4t dan garis h: x = 2 – 5t, y = – 1 – 2t, z = 4 + 3t, w = 6

+ t. Tentukan besar sudut antara kedua garis tersebut?

Penyelesaian:

Bilangan arah g: (-1, -1, 5, 4) dan garis h: (-5, -2, 3, 1) sehingga

β α β α θ , cos = β α β α β α β

α_{1 1}+ _{2 2}+...+ _{n n}

=

( ) ( )

(

) ( ) ( )

(

) (

) ( )

( ) ( )

( ) ( )

. 66 , 48 66 , 0 6 56 , 6 26 1 3 1 5 4 5 1 1 1 4 3 5 2 1 5 1 0 2 2 2 2 2 2 2 2 = = × = + + − + − + + + − + − × + × + − × − + − × − =

3). Tunjukan garis g dan h sejajar jika x = 6 + 3t, y = 4 – 2t, z = –2 +

4t, w = 4 – 6t adalah persamaan parametrik garis h dan persamaan

parametrik garis g adalah x = 2 – 6t, y = 4 + 4t, z = –2 – 8t, w = 6 +

Penyelesaian:

Bilangan arah dari g adalah (3, –2, 4, –6) dan h adalah (–6, 4, –8,

12).

Maka

12 6 8 4 4

2 6

3 −

= − = − =

− . Jadi kedua bilangan arah tersebut

sebanding sehingga garis g dan h sejajar.

4). Tunjukan garis g dan h tegak lurus jika x = 1 + t, y = 4 + 8t, z = 3 –

9t adalah persamaan parametrik garis h dan x = 2 – 6t, y = 4 +

3t, z = –2 + 2t persamaan parametrik garis g.

Jawab:

Bilangan arah dari g adalah (1, 8, –9) dan h adalah (–6, 3, 2).

Kedua garis tersebut tegak lurus jika α,β =0. Diperoleh α,β =

(

1×

( )

−6

) (

+ 8×3

) ( )

+

(

−9 ×2

)

=0 Jadi kedua garis tersebut saling tegak lurus.

3. Jarak Titik terhadap Garis Lurus-n

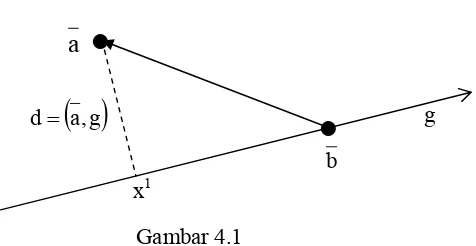
Jarak antara sebuah titik a ∈ Rn dengan sebuah garis lurus-n g adalah jarak terdekat antara titik a dengan setiap titik x ∈g, yang dinotasikan d

( )

a,g =inf

{

d

( )

a,x :x∈g

}

.

Gambar 4.1

Teorema 3.1

Jika diberikan sebuah titik a ∈ Rn dengan sebuah garis lurus-n g dengan bilangan arah

(

α₁,α₂,...,α_n

)

dan suatu titik b ∈g, maka jarak [image:48.612.234.472.99.222.2]

antara titik a dan g adalah

( ) ( )

a-b, b

-a g , a

d ₂ α

α α

−

=

Bukti

Akan ditentukan jarak antara titik a dan garis lurus-n g (ditulis:

d(a ,g)). Diketahui titik b∈g. Dibentuk vektor a−b≠0, maka d(a,g) adalah besar (norm) dari komponen orthogonal vektor a−b terhadap

vektor arah α dengan a−b= α₁+α₂ ,α₁=kα,k≠0. Dengan kata lain diperoleh

( ) ( )

a-b, b

-a g , a

d ₂ α

α α

−

= .

Terbukti.

.

b

g

( )

a,g

d=

x1

.

4. Jarak Antara Dua Garis Lurus-n

Definisi

Jarak antara dua garis lurus-n adalah jarak terpendek antara titik – titik

pada salah satu garis lurus-n dengan titik – titik pada garis lurus-n

lainya. Dari definisi diatas jika diketahui dua garis lurus-n g dan h,

maka jarak antara g dan h dapat ditulis

d(g,h) = inf

{

d

( )

x ,y :x∈g,y∈h

}

a. Jarak antara dua garis lurus-n yang sejajar

Ambil dua garis lurus-n yang sejajar g dan h.

Misal g : x = a + tα, t∈R h : y = b + tα, t∈R.

Ambil satu titik di g dan h, misal a∈g dan b∈h. Dibentuk vektor b – a dengan vektor arah α diperoleh

( ) ( )

b-a, a

-b h , a

d ₂ α

α α

−

= .

Dengan kata lain, didapat jarak antara garis lurus-n g dan h adalah

d(g,h) = d( a ,h).

b. Jarak antara dua garis lurus-n yang bersilangan

Ambil dua garis lurus-n yang bersilangan g dan h.

Misal g : x = a + tα, t∈R dan h : y = b + t

β

, t∈R.

Karena pada setiap titik di garis lurus-n h dapat dibuat garis lurus-n

yang sejajar g dan melalui titik b_i sehingga dapat dibentuk

himpunan sebagai berikut

{

y R :y b t , t R

}

h_i = ∈ n = i+ α ∈

Dimana h_i untuk setiap i =

(

i=1 ,2,3,...

)

adalah garis lurus-n yang memotong h dan sejajar g. Sehingga jarak garis lurus-n g dan garis

lurus-n h adalah

d

(

g ,h_i

)

= d

( )

a ,h_i

( )

, b -a b

-a ₂

i

i α

α α

− =

Dengan kata lain d

(

g ,h_i

)

= inf

{

d

( )

a ,h_i

}

.

Contoh B.4.3

Gambar 4.2

1). Pada sebuah balok pada gambar 4.1 hitung

(a).Jarak titik A terhadap garis BC.

(b).Jarak garis BC terhadap garis AD. x

y z

A B

C D

E F

G H

A(4, 0, 0) E(4, 0, 8)

B(4, 6, 0) F(4, 6, 8)

C(0, 6, 0) G(0, 6, 8)

Penyelesaian:

(a).Misal garis BC ≡ g

Maka bilangan arah g = (0, 6, 0) - (4, 6, 0) = (–4, 0, 0) = α. Karena

( )

a−b ≡AC⇒

( )

a−b =

(

0,6,0

) (

− 4 ,0,0

) (

= −4,6,0

)

Jadi d(A, BC) = d

( )

a ,g

( )

α

α α 2 , b -a b -a − =

(

)

(

) (

)

( )

(

)

(

)

(

)

(

4,6,0

) (

4,0,0

) (

0,6,0

)

0 , 0 , 4 16 0 0 16 0 , 6 , 4 0 , 0 , 4 0 0 4 0 , 0 , 4 , 0 , 6 , 4 0 , 6 , 4 ₂ 2 2 2 = − − − = − × + + − − = − × ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{− + +} − − − − = 2 6 = = 6.

(b).Misal BC ≡ g dan AD ≡h

Sehingga bilangan arah g = (0, 6, 0) - (4, 6, 0) = (–4, 0, 0)

=α( )1 dan bilangan arah h = (0, 0, 0) - (4, 0, 0) = (–4, 0, 0) =

( )2

α .

Ambil satu titik di g dan h, misal a∈g dan b∈h

Karena

( )

b−a ≡AB⇒

( )

b−a =

(

4,6,0

) (

− 4 ,0,0

) (

= 0,6,0

)

Jadi

( ) ( )

α

α α 2 , a -b a -b h , a

=

(

)

(

) (

)

( )

4 0 0

(

4,0,0

)

0 0, 4, -, 0,6,0

0,6,0 ₂

2 2 2

− × ⎟ ⎠ ⎞ ⎜

⎝

⎛ _{− + +}

−

(

)

6 0 6 0 0,6,0

2 2

2+ + =

= =

C. Bidang Datar-n

1. Persamaan Bidang Datar-n

Diberikan x∈Rn, dan

( )

x-a , dengan a adalah vektor tetap di Rn. Himpunan V =

{

x∈Rn,

( )

x-a ⊥a

}

=

{

x∈Rn:

( )

x-a,a =0

}

Disebut hyperplane di Rn Karena x-a,a =0

0 a , a a ,

x − =

⇔

a , a a ,

x =

⇔

... a

a ,

x = 2

⇔ disebut persamaan bidang datar-n

(hyperplane).

Jika x =

(

x₁, x₂,...,x_n

)

dan a =

(

a₁ ,a₂,...,a_n

)

maka persaman bidang datar-n berbentuk

a₁x₁+a₂x₂+...+a_nx_n =a₁2+a₂2+...+a_n2 ⇔

∑

=γ

=

n

1 i

i ix

Contoh C.4.1

(a) Tulis persamaaan bidang datar di 3

R , R , 4 R 5

Penyelesaian:

Persamaan bidang datar di R , artinya n = 3 diperoleh 3

D Cz By Ax x

a x a x

a_{1 1}+ _{2 2}+ _{3 3}=γ ⇔ + + = .

Persamaan bidang datar di _{R , artinya n = 4 diperoleh} 4

E Dw Cz By Ax x

a x a x a x

a_{1 1}+ _{2 2}+ _{3 3}+ _{4 4}=γ ⇔ + + + = .

Persamaan bidang datar di R , artinya n = 5 diperoleh 5

F Eu Dw Cz By Ax x

a x a x a x a x

a_{1 1}+ _{2 2}+ _{3 3}+ _{4 4}+ _{5 5}=γ ⇔ + + + + =

.

2. Persamaaan Hesse Bidang Datar-n

Persamaan Hessee bidang datar-n adalah persamaan bidang datar-n

dengan norm vektor arah sama dengan satu. Jika bidang datar-n V

dengan persamaan a ,x =c

a 1 c x , a a 1

= ⇔

a c x , a

a ₌

⇔

p x , =

⇔ λ

Jadi persamaan Hesse : λ ,x =p dengan

a e , a

cos _k k

k= θ =

λ

3. Jarak Titik terhadap Bidang Datar-n

Jika a adalah vektor arah dan sekaligus titik yang termuat di V, maka

0 a x , a :

V − = atau V: a ,x = a a

Jadi persamaan Hesse dari V adalah ,x a

a a

=

Hal ini menunjukkan bidang jarak titik O terhadap bidang datar-n

d

(

O,V

)

= a .

a. Jarak titik O terhadap bidang datar-n V

Jika bidang datar-n V mempunyai persamaan umum a ,x =c, maka jarak V terhadap titik O adalah

d

(

)

a c V

O, =

b. Jarak titik a ∈ Rn terhadap bidang datar-n V

Diberikan sebarang titik a ∈ Rn dan bidang datar-n V: α,γ =c Maka jarak antara titik a dengan V adalah

( )

α γ α,a v

a,

d = −

Bukti:

Bidang datar-n V : α,γ =c⇔ λ,γ −p=0

dengan

α α

λ = dan p c

α

=

gambar 4.3 x

a

a – x d(a,V) = d

α _V

Ditentukan d(a,V)

Melalui a dibuat bidang datar-n V1 // dengan V

Jarak V dan V1 terhadap O sebut d

Jadi persamaan bidang datar-n V1 adalah

V1 = λ,x −p±d=0

Bidang datar-n melalui a, diperoleh

V1 = λ,a −p±d=0

Karena d(a,V) = d, diperoleh

d =

( )

a c a , V

a, d p x

, − ⇔ = α −

λ . Terbukti

di R3 : V≡Ax +By + Cz + D = 0 dan P(x1, y1, z1)

maka jarak P terhadap V

d(P,V) =

2 2 2

1 1 1

C B A

D Cz By Ax

+ +

+ + +

di R4 : V ≡Ax1 +Bx2 + Cx3 + Dx4 + E = 0 dan P(v1, x1, y1, z1)

maka jarak P terhadap V

d(P,V) =

2 2 2 2

1 1 1 1

D C B A

E Dz Cy Bx Av

+ + +

Contoh C.4.3

[image:56.612.187.524.109.311.2]

Gambar Kubus 4.4

(a) Tentukan jarak titik E terhadap bidang BDG pada kubus 4 satuan ?

Penyelesaian:

Persamaan Bidang BDG

a = CE = ( 4, -4, 4 ) = ( 1, -1, 1 ) dan a⊥ BDG Sehingga a ,

( )

x−b =0

⇔

( ) ( )

a ,x − a ,b =0

⇔ a ,x = a ,b

⇔

(

1,-1,1

)

,x =

(

1,-1,1

) (

, 4,4,0

)

⇔

(

1,-1,1

)

, x =0

Jarak titik E terhadap bidang BDG :

d( E, BDG ) =

(

) (

)

( )

2 2

2

1 1 1

0 4 0, 4, , 1 1, -1,

+ − +

−

= .

3 3 8 x

y z

A B

C D

E _F

G H

A(4, 0, 0) E(4, 0, 4)

B(4, 4, 0) F(4, 4, 4)

C(0, 4, 0) G(0, 4, 4)

(b) Tentukan jarak titik A terhadap bidang BDG pada kubus 4 satuan ?

Jawab:

Persamaan Bidang BDG

BD= (-4, -4, 0), BG = (4, 0, 4) dan DG = (0, 4, 4)

Misalkan a =

(

a₁ ,a₂,a₃

)

dan a⊥ BDG Sehingga berlaku a ,BD =0

a ,BG =0

a ,DG =0 Maka

(

-4,-4,0

) (

, a ,a ,a

)

4a 4a 0 BD

,

a = _{1 2 3} =− ₁− ₂ = ….……..(1)

(

4,0,4

) (

,a ,a ,a

)

4a 4a 0 BG

,

a = _{1 2 3} = ₁+ ₃ = ……….(2)

(

0,4,4

) (

,a ,a ,a

)

4a 4a 0 DG

,

a = _{1 2 3} = ₂+ ₃ = ……...….…(3)

Dari (1), (2) dan (3) diperoleh a =

(

a₁ ,a₂,a₃

)

= (1, -1, 1)

Sehingga a ,

( )

x−d =0

⇔

( ) ( )

a ,x − a ,d =0

⇔

(

1,-1,1

)

,x =

(

1,-1,1

) (

, 0,0,0

)

⇔

(

1,-1,1

)

, x =0

Jarak titik A terhadap bidang BDG :

d( A, BDG ) =

(

) (

)

( )

2 2

2

1 1 1

0 0 0, 4, , 1 1, -1,

+ − +

−

= .

3 3 4

(c) Tentukan jarak A(2, 4, -3, 0) terhadap bidang yang melalui empat

titik yaitu B(1, 3, -5, 2), C(3, 4, -1, 4), D(4, -2, 1, 0) dan E(2, 4, -3,

0)?

Penyelesaian:

Persamaan bidang datar-n di R4

BC= (2, 1, 4, 2), BD = (3, -1, 6, 2)

CD = (1, -2, 2, -4), BE = (1, 1, 2, 2)

Misalkan a =

(

dan a₁ ,a₂ ,a₃ ,a₄

)

a⊥ BCDG Sehingga berlaku a ,BC =0 a ,DE =0

a ,BE =0 a ,BD =0 Maka

1. a ,BC =

(

2,1,4,2

) (

, a₁ ,a₂,a₃ ,a₄

)

=2a₁+a₂ +4a₃+2a₄ =0

2. a ,BD =

(

3,-1, 6,2

) (

,a₁ ,a₂ ,a₃ ,a₄

)

=3a₁−1a₂+6a₃+2a₄ =0

3. a ,BE =

(

1,1,2,2

) (

,a₁ ,a₂ ,a₃,a₄

)

=a₁+a₂ +2a₃+2a₄ =0

Dari (1), (2), (3) dan (4) diperoleh a = (a1 ,a2 ,a3 ,a4

)

= (2, -2, -1, 1)

Bidang BCDG:

(

2,-2,-1,1

)

, x

(

2,-2,-1,1

) (

, 2,4,-3,0

)

C

x ,

a = ⇔ =

⇔

(

2,-2,-1,1

)

,x =-1

Jarak titik A terhadap bidang BCDG di R4 :

d(A, BCD) =

(

) (

) ( )

10

1 1 1, -2, -2, , 0 3, -4,

2, − −

0

= .

4. Kedudukan dua bidang datar-n

Misal diberikan dua bidang datar-n

α

=

a x, : V

β

=

b x, : U

θ adalah sudut antara U dan V sehingga

(

)

b . a

b a,

-cos

cosθ = π θ =

a. Dua bidang tegak lurus

2 V

U⊥ ⇒θ =π

(

)

b . a

b a, 2 -cos 2

cos = =

⇒ π π π

b a 0 b

a, = ⇔ ⊥

b. Dua bidang sejajar

0 V

/ /

U ⇒θ =

( )

b . a

b a, cos

0

cos = =

⇒ π

b . a b

a, =

⇒

Ambil sebarang αa=bsehingga a

. a a

a,α = α

⇒

2 a . a

a, α

α =

⇒ 2 2

a .

a α

α =

A. Simpulan

Dari hasil pembahasan dapat ditarik simpulan sebagai berikut. 1. Persamaan garis lurus-n dan bidang datar-n (hyperplane)

a. Garis lurus-n adalah X_n =a_n+α_nt. b. Bidang datar-n adalah x,a = a 2.

2. Kedudukan antara dua garis lurus-n dan dua bidang datar-n (hyperplane) a. Kedudukan antara dua garis lurus-n

i). Dua garis lurus-n g dan h dikatakan sejajar jika dan hanya jika mempunyai bilangan arah yang sebanding.

. ...

n n 2

2 1 1

β α β

α β

α _{= = =}

ii). Gais lurus-n g dan h dikatakan saling tegak lurus jika dan hanya jika α,β =0atau α₁β₁+α₂β₂+...+α_nβ_n =0.

b. Kedudukan antara dua bidang datar-n i). Dua bidang datar-n tegak lurus

2 V

U⊥ ⇒θ =π

(

)

b . a

b a, 2 -cos 2

cos = =

⇒ π π π

b a 0 b

a, = ⇔ ⊥

ii). Dua bidang sejajar 0 V

/ /

U ⇒θ =

( )

b . a b a, cos 0

cos = =

⇒ π b . a b a, = ⇒

Ambil sebarang αa=bsehingga a

. a a

a,α = α

⇒ 2 a . a a, α α =

⇒ 2 2

a .

a α

α =

⇔ .

3. Persamaan sudut antara dua garis lurus-n dan bidang datar-n a. Sudut antara dua garis lurus-n

β α β α β α β α β α β α θ , ...

cos = = 1 1+ 2 2 + + n n _.

b. Sudut antara dua bidang datar-n

(

)

b . a b a, -cos

cosθ = π θ = .

4. Persamaan jarak antara sebuah titik dengan garis lurus-n dan jarak antara dua garis lurus-n

i). Jarak antara sebuah titik dengan garis lurus-n adalah

( ) ( )

a-b,

b -a g , a

d ₂ α

α α

−

= .

ii). Jarak antara dua garis lurus-n adalah

( ) ( )

, b -a b -a g , a

d ₂ α

α α

−

5. Persamaan jarak sebuah titik terhadap bidang datar-n

adalah

( )

α γ α,a v

a,

d = − .

B. Saran

1. Diharapkan penulisan ini dapat digunakan untuk membantu dalam pemecahan soal – soal geometri pada ruang dimensi 3 khususnya garis dan bidang.

56

BERBERIAN, Sterling. K. 1961. Introduction to Hilbert Space. New York : Oxford University Press

CARICO, Charles. C. 2005. Analytic Geometry. New York : John Wiley & Sons CHOW, Wung Yung. 1997. Linear Geometry in Euclidean 4-Space. Singapore :

SEAMS

CLEMENTS, Stanley. R. 1984. Geometry With Application and Problem Solving. USA : Addison-Wesley Publishing Company

GANS, David. 1973. An Introduction to non-Euclidean Geometry. New York : Academic Press Inc

KOHN, Ed. 2003. Cliffs Quick Review Geometry. Bandung : Pakar Karya

MARSDEN, Jerrold. E. 1993. Basic Multivariabel Calculus. New York : Springer-Verlag

MULYATI, Sri. . Geomeri Euclid. Malang : JICA

SUHITO. 2004. Geometri Analit Rangkuman Hasil Penelitian / Magang. Yogyakarta. UGM

ROCHMAD. 2001. Analisis Real II. Semarang : UNNES

RUCKLE, William. H. 1960. Modern Analysis. Boston : PWS – KENT Publishing Company