PENGGUNAAN METODE NUMERIK DAN METODE MATRIKS
DALAM PERHITUNGAN PARAMETER PADA REGRESI
LINIER BERGANDA
SKRIPSI
ZULIVA EVASARI SILALAHI
090823004
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
MEDAN
PENGGUNAAN METODE NUMERIK DAN METODE MATRIKS
DALAM PERHITUNGAN PARAMETER PADA REGRESI
LINIER BERGANDA
SKRIPSI
Diajukan untuk melengkapi tugas akhir dan memenuhi syarat mencapai gelar Sarjana Sains
ZULIVA EVASARI SILALAHI
090823004
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
MEDAN
PERSETUJUAN
Judul : PENGGUNAAN METODE NUMERIK DAN
METODE MATRIKS DALAM PERHITUNGAN PARAMETER PADA REGRESI LINIER
BERGANDA
Kategori : SKRIPSI
Nama : ZULIVA EVASARI SILALAHI
Nomor Induk Mahasiswa : 090823004
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA
UTARA
Diluluskan di
Medan, Juni 2011
Komisi pembimbing:
Pembimbing 2 Pembimbing 1
Drs. Djakaria Sebayang, M.Si Drs. Suwarno Ariswoyo, M.Si
NIP.1951 1227 1985 03 1002 NIP. 1950 2103 1980 03 1001
Diketahui /Disetujui oleh
Departemen Matematika FMIPA USU
Ketua,
PERNYATAAN
PENGGUNAAN METODE NUMERIK DAN METODE MATRIKS DALAM PERHITUNGAN PARAMETER PADA REGRESI LINIER BERGANDA
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing–masing disebutkan sumbernya.
Medan, Juni 2011
ZULIVA EVASARI SILALAHI
PENGHARGAAN
Puji dan Syukur penulis panjatkan kepada Tuhan Yang Maha Esa yang telah memberikan Rahmat, Karunia dan Petunjuk-Nya, sehingga penulis dapat menyelesaikan Skripsi ini dalam waktu yang telah ditetapkan.
Dengan kerendahan hati penulis menyadari bahwa skripsi ini masih jauh dari sempurna, tetapi penulis berharap kiranya skripsi ini dapat menambah bahan bacaan yang bermanfaat bagi siapa saja yang membacanya. Selama proses penulisan skripsi ini penulis banyak mendapat bantuan moril maupun materil dari berbagai pihak, karena itu penulis mengucapkan terimakasih yang sebesar-besarnya kepada:
1. Bapak Drs. Suwarno Ariswoyo, M.Si, selaku pembimbing I dan Bapak Drs. Djakaria Sebayang, M.Si, selaku pembimbing II, atas segala
bimbingan dan arahan serta kebaikannya untuk meluangkan waktu, tenaga, pikiran dan bantuannya.
2. Bapak Prof. Dr. Tulus, M.Si selaku Ketua Departemen Matematika dan Bapak Drs. Pangarapen Bangun, M.Si selaku Koordinator Ekstensi Matematika FMIPA USU.
3. Bapak Drs. Faigiziduhu Bu’ulölö, M.Si dan Bapak Drs. H. Haludin Panjaitan, selaku dosen pengujian saya, yang telah memberikan saran terhadap penulis untuk menyempurnakan tulisan ini.
4. Staf Pengajar Matematika serta Staf Pegawai Administrasi di Fakultas Matematika dan Ilmu pengetahuan Alam.
5. Kedua Orang Tua Bapak dan Mamak yang sangat saya sayang dan cintai, yang selalu berusaha dan berdoa agar perkuliahan saya dapat berjalan dengan lancar.
7. SimSon yang telah banyak memberi dorongan, waktu, pengertian, semangat dan selalu ada untuk membantu penulis dalam kelancaran perkuliahan sampai selesainya skripsi ini.
8. Semua teman-teman mahasiswa Eks-Mat 09, yang telah membantu dalam kelancaran skripsi ini.
9. Semua pihak yang turut membantu dalam proses penyelesaian skripsi ini baik secara langsung maupun tidak langsung.
Semoga Allah membalas kebaikan dari semua pihak dan memberikan berkatnya kepada kita semua. Saya berharap agar skripsi ini bermanfaat, terutama kepada penulis maupun para pembaca yang berhubungan dengan skripsi ini.
Medan, Juni 2011
Penulis
ABSTRAK
Banyak masalah peramalan dapat diselesaikan dengan cepat dalam model matematika, seperti di dalam persamaan regresi linier berganda. Bentuk persamaan regresi linier berganda yang menunjukkan hubungan antara variabel terikat Y dengan dua atau lebih
variabel bebas X, dalam bentuk model .
ABSTRACT
Many prediction problems can be expressed into mathematical model such as Multiple Linier Regression Equation. General shape of Multiple Linier Regression Equation that show the correlation between dependent variable Y with two independent variable
X is User can approximately predict the
DAFTAR ISI
Persetujuan ii
Pernyataan iii
Penghargaan iv
Abstrak vi
Abstract vii
Daftar Isi viii
Daftar Tabel x
Daftar Gambar xi
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 2
1.3 Tinjauan Pustaka 3
1.4 Tujuan Penelitian 4
1.5 Kontribusi Penelitian 4
BAB 2 LANDASAN TEORI 6
2.3.1 Perhitungan Parameter dengan Menggunakan
Metode Numerik (Gauss-Seidel) 15
2.4 Metode Matriks 17
2.4.1 Tranpose Matriks 18
2.4.2 Determinan 19
2.4.3 Invers Matriks 19
2.4.4 Perhitungan Parameter dengan Menggunakan
Metode Matriks (Invers Matriks) 20
2.5 Perhitungan Simpangan Baku dari Model Persamaan 24
2.6 Interval Kepercayaan Sehubungan dengan Regresi
Linier Berganda 25
2.7 Hipotesis 25
BAB 3 PEMBAHASAN 28
3.1 Perhitungan Penurunan Persamaan Linier dengan
Pendekatan Model Kuadrat Terkecil 28
3.2 Perhitungan Nilai Parameter dengan Menggunakan
3.3 Perhitungan Nilai Parameter dengan Menggunakan
Metode Matriks (Invers Matriks) 35
3.4 Perhitungan dan Perbandingan Simpangan Baku yang
Dihasilkan dari Setiap Model Persamaan 39
3.5 Perhitungan Interval Kepercayaan Sehubungan dengan
Regresi Linier Berganda 40
3.6 Uji Hipotesis 41
BAB 4 KESIMPULAN DAN SARAN 43
4.1 Kesimpulan 43
4.2 Saran 44
Daftar Pustaka
DAFTAR TABEL
Halaman
Tabel 3.1 Penyajian Data 28
Tabel 3.2 Hasil Iterasi Gauss-Seidel 33
Tabel 3.3 Perbandingan Simpangan Baku dari Setiap Model Persamaan 39
DAFTAR GAMBAR
Halaman
Gambar 2.1 Diagram Pencar 9
ABSTRAK
Banyak masalah peramalan dapat diselesaikan dengan cepat dalam model matematika, seperti di dalam persamaan regresi linier berganda. Bentuk persamaan regresi linier berganda yang menunjukkan hubungan antara variabel terikat Y dengan dua atau lebih
variabel bebas X, dalam bentuk model .
ABSTRACT
Many prediction problems can be expressed into mathematical model such as Multiple Linier Regression Equation. General shape of Multiple Linier Regression Equation that show the correlation between dependent variable Y with two independent variable
X is User can approximately predict the
BAB 1
PENDAHULUAN
1.1Latar Belakang
Metode analisis yang dibicarakan hingga saat ini adalah analisis terhadap data mengenai sebuah variabel. Tetapi, sebagaimana disadari bahwa banyak persoalan yang meliputi lebih dari sebuah variabel. Misalnya: berat badan dalam taraf tertentu tergantung pada tinggi badannya, produktivitas kerja pada taraf tertentu tergantung pada efisiensi dan efektivitas kerjanya, produksi padi dalam taraf tertentu tergantung pada kesuburan tanah, teknologi yang dipakai, banyak curah hujan dan sebagainya. Sehingga, terasa perlu untuk mempelajari analisis data yang terdiri atas banyak variabel.
Secara umum, dalam analisis regresi akan dibedakan dua jenis variabel, yaitu variabel bebas (independent variable) dan variabel terikat (dependent variable). Variabel bebas biasanya disimbolkan dengan X, sedangkan variabel terikat disimbolkan dengan Y.
diatas, hubungan fungsional ini akan ditulis dalam bentuk persamaan matematik, yang disebut persamaan regresi dan bergantung pada parameter-parameter.
Regresi merupakan suatu metode analisis statistika yang mempelajari pola hubungan antara dua atau lebih variabel. karena pada kenyataannya sering dijumpai sebuah kejadian yang dipengaruhi oleh lebih dari satu variabel. Oleh karena itu, dikembangkanlah regresi berganda. Regresi berganda adalah perluasan dari regresi sederhana, yang mempunyai lebih dari satu variabel bebas X. Regresi linier berganda digunakan untuk memodelkan hubungan antara variabel terikat dan variabel bebas
dalam bentuk model + Nilai ,
dikenal sebagai parameter/koefisien dari model. Nilai-nilainya hanya dapat ditentukan jika keseluruhan nilai populasi dari (X, Y) diketahui. Banyak metode yang dapat digunakan untuk memecahkan perhitungan dalam menentukan nilai parameter
, dalam persamaan regresi linier berganda seperti Metode Kuadrat Terkecil, Metode Numerik dan Metode Matriks.
Berdasarkan uraian di atas, maka judul dalam penulisan ini adalah “PENGGUNAAN METODE NUMERIK DAN METODE MATRIKS DALAM PERHITUNGAN PARAMETER PADA REGRESI LINIER BERGANDA”.
1.2Perumusan Masalah
Berdasarkan latar belakang yang telah diuraikan, permasalahan yang dibahas dalam penulisan ini adalah sebagai berikut:
1. Bagaimana cara menentukan nilai parameter pada persamaan regresi linier berganda dengan cara pendekatan metode numerik dan metode matriks.
3. Bagaimana hasil standard deviasi dan output model yang diperoleh dari metode numerik dan metode matriks.
1.3Tinjauan Pustaka
Dalam penulisan ini, penulis menggunakan buku-buku sebagai sumber utama. Diantaranya adalah sebagai berikut:
1. SUDJANA (2002), jika melibatkan hubungan antara atas , maka model regresi bergandanya adalah sebagai berikut:
Keterangan
= Variabel terikat
= Variabel bebas
= Parameter yang harus ditentukan
2. SPYROS MAKRIDAKIS (1999), bila bentuk fungsi yang menghubungkan dengan beberapa variabel , maka bentuk regresinya adalah sebagai berikut:
Keterangan
= Variabel terikat
= Variabel bebas
3. MONTGOMERY (2007), variabel terikat dapat dihubungkan pada variabel-variabel bebas, maka modelnya sebagai berikut:
Keterangan
Adapun tujuan dari penulisan ini adalah sebagai berikut:
1. Untuk menguraikan dan menentukan nilai parameter pada regresi linier berganda dengan menggunakan metode numerik dan metode matriks.
2. Membandingkan hasil perhitungan nilai parameter antara metode numerik dan metode matriks.
3. Membandingkan hasil standard deviasi dari output yang telah diperoleh dari metode numerik dan metode matriks.
1.5Kontribusi Penelitian
1.6Metode Penelitian
Adapun metode penelitian dalam penulisan ini adalah sebagai berikut:
1. Penurunan persamaan linier dengan pendekatan model kuadrat terkecil.
2. Perhitungan nilai parameter persamaan regresi dengan menggunakan metode numerik dan metode matriks.
3. Perhitungan dan perbandingan simpangan baku yang dihasilkan tiap model persamaan regresi dari setiap model yang digunakan.
4. Menentukan selang kepercayaan dan pengujian hipotesa pada nilai parameter yang telah diperoleh.
BAB 2
LANDASAN TEORI
2.1 Analisis Regresi
Perubahan nilai suatu variabel tidak selalu terjadi dengan sendirinya, namun perubahan nilai variabel itu dapat disebabkan oleh berubahnya variabel lain yang berhubungan dengan variabel tersebut. Untuk mengetahui pola perubahan nilai suatu variabel yang disebabkan oleh variabel lain diperlukan alat analisis yang memungkinkan untuk membuat perkiraan (prediction) nilai variabel tersebut pada nilai tertentu variabel yang mempengaruhinya.
Teknik yang umum digunakan untuk menganalisis hubungan antara dua atau lebih variabel adalah analisis regresi. “Analisis regresi (regression analisis) merupakan suatu teknik untuk membangun persamaan garis lurus dan menggunakan persamaan tersebut untuk membuat perkiraan”. (Mason, 1996. Hal: 489).
Persamaan regresi yang digunakan untuk membuat taksiran mengenai nilai variabel terikat (dependent) disebut persamaan regresi estimasi. “ Persamaan regresi estimasi adalah suatu formula matematis yang menunjukkan hubungan keterkaitan antara satu atau beberapa variabel yang nilainya sudah diketahui (known variable) dengan satu variabel yang nilainya belum diketahui (unknown variable)”.
Regresi pertama kali diperkenalkan pada tahun 1877 oleh Sir Francis Galton, pada penelitiannya terhadap manusia. Penelitian tersebut membandingkan antara tinggi anak laki-laki dan tinggi badan orang tuanya. Istilah regresi pada mulanya bertujuan untuk membuat perkiraan nilai suatu variabel (tinggi badan anak) terhadap suatu variabel yang lain (tinggi orangtua). Pada perkembangan selanjutnya, analisa regresi digunakan sebagai alat untuk membuat perkiraan nilai suatu variabel dengan menggunakan beberapa variabel lain yang berhubungan dengan variabel tersebut.
2.1.1 Regresi Sederhana
Regresi sederhana (simple regression) merupakan bagian regresi yang mencakup hubungan linier antara satu variabel terikat dengan satu variabel bebas. Variabel bebas biasanya disimbolkan dengan X, sedangkan variabel terikat disimbolkan dengan Y. Variabel bebas adalah variabel yang nilai-nilainya tidak bergantung pada variabel lainnya, variabel bebas digunakan untuk meramalkan atau menerangkan nilai variabel yang lain. Variabel terikat adalah variabel yang nilainya bergantung pada variabel lainnya, variabel terikat merupakan variabel yang diramalkan atau diterangkan nilainnya.
Bentuk umum persamaan regresi linier sederhana yang menunjukkan hubungan antara dua variabel, yaitu variabel X sebagai variabel bebas dan variabel Y sebagai variabel terikat dari suatu populasi adalah sebagai berikut:
Keterangan:
= Variabel terikat
= Variabel bebas
= Jarak titik pangkal dengan titik potong garis regresi dengan sumbu Y (intercept)
= Kemiringan (slope) garis regresi
= Nilai kesalahan
Parameter dan diduga dengan menggunakan garis regresi. Bentuk persamaan garis regresi adalah sebagai berikut :
(2.2)
Keterangan:
= Intersept, jarak titik pangkal dan titik potong garis regresi dengan sumbu Y
= Kemiringan garis regresi
Dalam hal ini:
merupakan penduga titik bagi
merupakan penduga titik bagi
Pendugaan dilakukan dengan mengambil contoh acak berukuran n dari suatu populasi. Hasil pengamatan berupa pasangan X dan Y sebagai berikut :
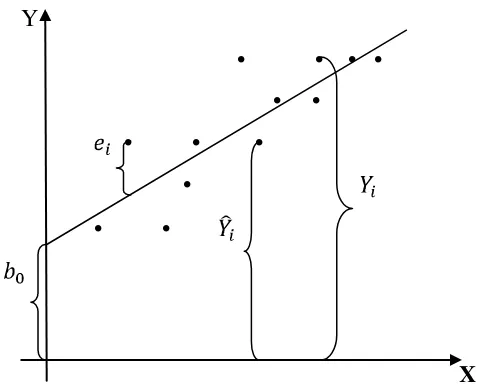
Jika data berpasangan tersebut digambarkan pada sumbu koordinat siku-siku, maka diperoleh gambar sebagai berikut :
Y
Gambar 2.1 Diagram Pencar
Dengan demikian diperoleh model regresi linier sederhana sebagai berikut:
Pada umumnya tidak sama dengan , perbedaan antara dan dinyatakan dengan yang disebut dengan sisa (residual). Dalam hal ini:
(2.4)
Nilai dan diperoleh dengan menggunakan metode kuadrat terkecil (least squares method). Metode kuadrat terkecil merupakan satu cara untuk memperoleh
dan sebagai perkiraan dan , dengan meminimumkan jumlah kuadrat sisa sebagai berikut:
(2.5)
Syarat minimum adalah sebagai berikut:
(2.6)
(2.7)
2.1.2 Regresi Berganda
Regresi Berganda (multiple regression) merupakan bagian regresi yang mencakup hubungan linier antara dua atau lebih variabel bebas dengan satu variabel terikat. Variabel bebas disimbolkan dengan X, sedangkan variabel terikat disimbolkan dengan Y. variabel bebas adalah variabel yang nilai-nilainya tidak bergantung pada variabel lainnya, variabel bebas digunakan untuk meramalkan atau menerangkan nilai variabel yang lain. Sedangkan variabel terikat adalah variabel yang nilainnya bergantung pada variabel lainnya, variabel terikat merupakan variabel yang diramalkan atau diterangkan nilainnya.
Bentuk umum persamaan regresi linier berganda yang melibatkan lebih dari satu variabel bebas yang mempengaruhi variabel terikat Y dari suatu populasi adalah sebagai berikut:
(2.8)
Jika = 0, maka diperoleh persamaan regresi linier ganda dari suatu populasi adalah sebagai berikut:
Pendugaan garis regresi populasi diatas dapat dilakukan dengan mengambil contoh acak berukuran dari populasi tersebut. Model populasi diatas dinyatakan dalam bentuk sebagai berikut :
(2.10)
Keterangan:
merupakan penduga titik bagi
merupakan penduga titik bagi
2.2 Metode Kuadrat Terkecil
Metode kuadrat terkecil (least squares method) adalah salah satu metode yang terbaik untuk memperoleh persamaan linier. Persamaan ini merupakan petunjuk yang terbaik untuk menerangkan diagram pencaran data. Karena setiap garis yang ditarik belum tentu melalui semua titik dalam diagram pencaran. Apabila garis lurus tidak tepat pada titik-titik diagram pencaran, akan terdapat deviasi antara setiap nilai Y dan nilai yang ditunjukkan oleh garis . Garis yang berdasarkan metode kuadrat terkecil menunjukkan penyimpangan tiap nilai dengan garis regresi. Metode ini ditemukan oleh Adrien Legendre seorang ahli matematika Perancis pada awal abad ke 19.
Dengan meminimumkan jumlah kuadrat sisa yang dikuadratkan, sehingga diperoleh S sebagai berikut:
Dengan syarat minimum adalah sebagai berikut:
(2.12)
(2.13)
(2.14)
(2.15)
Dari persyaratan minimum diatas, menghasilkan suatu kumpulan persamaan normal sebagai berikut:
. . .
(2.16)
2.3 Metode Numerik
Metode numerik adalah suatu teknik penyelesaian yang diformulasikan secara matematis dengan cara operasi perhitungan dan dilakukan secara berulang-ulang dengan cara manual atau bantuan komputer.
2.3.1 Perhitungan Parameter dengan Menggunakan Metode Numerik (Gauss Seidel)
Dalam melakukan perhitungan parameter dengan menggunakan metode Gauss Seidel, proses penyelesaiannya dapat dimulai dengan nilai awal untuk sama dengan nol. Nilai-nilai awal nol ini dapat dimanfaatkan untuk menghitung variabel berikutnya. Menentukan nilai parameter pada regresi linier berganda dengan menggunakan metode Gauss-Seidel adalah sebagai berikut:
. . .
Sehingga berlaku prosedur iterasi sebagai berikut:
Iterasi 0
. . .
Iterasi 2
. .
. (2.17)
2.4 Metode Matriks
Matriks didefinisikan sebagai suatu himpunan angka, variabel atau parameter dalam bentuk suatu persegi panjang, yang tersusun di dalam baris dan kolom dan diantarai oleh dua buah kurung siku atau kurung biasa. Pada umumnya, matriks di notasikan dalam huruf besar sedangkan elemen-elemennya dalam hurup kecil, sebagai berikut:
atau
dimana:
A = Matriks A
[ ] atau ( ) = Notasi matriks
adalah elemen dari matriks A, dimana menyatakan baris dan menyatakan
kolom. Misalnya: adalah elemen dari matriks A yang terletak pada baris ke-1 dan kolom ke-1. (PUDJIASTUTI,2006)
Jenis-jenis matriks adalah sebagai berikut:
1. Matriks diagonal
Adalah suatu matriks bujur sangkar yang semua elemen di luar elemen diagonal utama sama dengan nol, dan paling tidak satu elemen pada diagonal utamanya tidak sama dengan nol.
2. Matriks identitas
3. Matriks segitiga atas
Adalah matriks bujur sangkar yang elemen-elemen di bawah diagonal utama bernilai nol. Jadi yang tidak sama dengan nol adalah elemen-elemen pada segitiga atasnya dan paling tidak satu elemen pada diagonal utama tidak sama dengan nol.
4. Matriks segitiga bawah
Adalah matriks bujur sangkar yang elemen-elemen di atas diagonal utama bernilai nol. Jadi yang tidak sama dengan nol adalah elemen-elemen pada segitiga bawahnya dan paling tidak satu elemen pada diagonal utama tidak sama dengan nol.
5. Matriks nol
Adalah suatu matriks yang semua elemenya bernilai nol. Matriks ini biasanya diberi simbol O dan bentuknya tidak selalu bujur sangkar.
6. Matriks baris
Adalah matriks yang hanya terdiri dari satu baris. Matriks ini sering disebut dengan vektor baris.
7. Matriks kolom
Adalah matriks yang hanya terdiri dari satu kolom. Matriks ini sering disebut dengan vektor kolom.
8. Matriks simetris
Adalah suatu matriks bujur sangkar yang memiliki , sehingga
transposenya sama dengan matriks semula.
2.4.1 Tranpose suatu matrik
2.4.2 Determinan
Determinan adalah suatu skalar (angka) yang diperoleh dari suatu matriks bujur sangkar selalui operasi khusus. Disebut operasi khusus karena dalam proses penurunan determinan dilakukan perkalian-perkalian. Determinan dinotasikan dengan tanda | |.
Salah satu cara dalam perhitungan determinan, adalah dengan cara singkat. Cara singkat yang lazim dikenal untuk menghitung determinan dari matriks adalah dengan menggunakan metode sarrus. Caranya dengan menempatkan elemen-elemen pada dua kolom pertama disebelah kanan notasi determinan sebagai berikut:
2.4.3 Invers Matriks
Invers matriks sering disebut dengan matriks kebalikan. Biasanya dituliskan sebagai
berikut: jika A adalah suatu matriks bujur sangkar maka merupakan
2.4.4 Perhitungan Parameter dengan Menggunakan Metode Matriks (Invers Matriks)
Nilai parameter pada regresi linier berganda dapat ditentukan dengan menggunakan metode matriks. Jika banyaknya peubah bebas adalah , maka model regresi populasi dinyatakan dengan:
(2.18)
Keterangan:
= Variabel terikat
= Variabel bebas
= Parameter regresi yang belum diketahui nilainya
= Nilai kesalahan
Pendugaan garis regresi populasi diatas dapat dilakukan dengan mengambil contoh acak berukuran n dari populasi tersebut. Model regresi diatas dinyatakan dengan bentuk sebagai berikut:
(2.19)
Keterangan:
= Variabel terikat
= Variabel bebas
Dalam hal ini:
merupakan penduga titik bagi
merupakan penduga titik bagi
Dengan menggunakan persamaan matriks
(2.20)
Dengan
(2.21)
Metode kuadrat terkecil merupakan suatu metode untuk mendapatkan nilai-nilai vektor dengan meminimumkan adalah sebagai berikut:
Langkah-langkah untuk menentukan nilai koefisien dari parameter pada regresi linier berganda adalah sebagai berikut:
Langkah 1
Menghitung nilai matriks dengan cara sebagai berikut:
(2.25)
Langkah 2
Menghitung nilai determinan matrik dengan cara sebagai berikut:
(2.26)
Langkah 3
Mencari Adjoint matriks , dimana:
Langkah 4
Mencari invers matriks dengan cara sebagai berikut:
(2.28)
Langkah 5
Mencari nilai matriks dengan cara sebagai berikut:
(2.29)
Sehingga untuk memperoleh nilai koefisien dari adalah dengan cara sebagai berikut:
2.5Perhitungan Simpangan Baku dari Model Persamaan
(SUDJANA,2002 hal 93) Ukuran simpangan yang paling banyak digunakan adalah simpangan baku atau deviasi standar. Pangkat dua dari simpangan baku disebut
varians. Untuk sampel, simpangan baku disimbolkan dengan , sedangkan untuk
populasi disimbolkan dengan . Varians untuk sampel dan populasi .
Pada umumnya, nilai-nilai koefisien regresi bervarias dan variansnya dari dalam bentuk vektor matriks adalah sebagai berikut:
(2.31)
Karena umumnya tidak diketahui, maka diduga dengan , sehingga perkiraan varians adalah:
Keterangan:
= Varians dari kesalahan pengganggu
= Banyaknya observasi
= Banyak variabel bebas
dapat dihitung langsung dari yaitu selisih antara nilai
2.6Interval Kepercayaan Sehubungan dengan Regresi Linier Berganda
Jika simpangan baku populasi tidak diketahui dan ukuran sampel kurang dari 30, maka dugaan selang bagi rataan populasi ditentukan dengan menggunakan sebaran t dan jika ukuran sampel cukup besar, rataan populasi ditentukan dengan menggunakan sebaran data z. untuk menghitung estimasi interval yang telah ditaksir oleh titik . Selang kepercayaan (1-α) 100% bagi adalah sebagai
Hipotesis berasal dari kata hipo dan tesis yang berasal dari bahasa Yunani. Hipo berarti di bawah, kurang atau lemah dan tesis berarti teori atau proposisi. Jadi, secara umum hiportesis dapat didefinisikan sebagai asumsi atau dugaan atau pernyataan sementara yang masih lemah kebenarannya tentang karateristik populasi. Oleh karena itu hipotesis perlu di uji kebenarannya. Pengujian hipotesis dilakukan berdasarkan hasil sampel yang diambil dari populasi.
Adapun jenis hipotesis adalah sebagai berikut:
1. Hipotesis penelitian
2. Hipotesis statistik
Hipotesis statistik merupakan pernyataan atau dugaan mengenai satu atau lebih populasi. Ada dua jenis hipotesis statistik, yaitu:
a. Hipotesis nol atau nihil ( )
Istilah nol atau nihil menunjuk tidak adanya perbedaan pada populasi. akan selalu dituliskan dengan tanda kesamaan, sehingga spesifik pada nilai tunggal.
b. Hipotesis alternatif atau tandingan ( )
Merupakan hipotesis tandingan atau isinya berlawanan dengan hipotesis .
Hipotesis yang mengandung pengertian sama pada pasangan dan adalah:
1. ,
2.
3.
4.
Hipotesis yang mengandung pengertian maksimum pada pasangan dan adalah:
Hipotesis yang mengandung pengertian minimum pada pasangan dan adalah:
Langkah-langkah uji hipotesis adalah sebagai berikut:
1. Tentukan hipotesis dan
, melawan salah satu alternatif
2. Tentukan taraf signifikan/taraf nyata α
3. Tentukan uji statistik yang sesuai dan lakukan perhitungan uji statistik berdasarkan data sampel
4. Tentukan wilayah kritis atau wilayah penolakan berdasarkan nilai α Tolak jika Fhitung Ftabel
Terima jika Fhitung Ftabel
BAB 3
PEMBAHASAN
3.1 Perhitungan Penurunan Persamaan Linier dengan Pendekatan Model Kuadrat Terkecil
Andaikan suatu persoalan penentuan model regresi berganda, diberikan data sebagai berikut:
Tabel 3.1 Penyajian Data
Observasi Y X1 X2
1 9,95 2 50
2 24,45 8 110
3 31,75 11 120
4 35,00 10 550
5 25,02 8 295
6 16,86 4 200
7 1.438 2 375
8 9,60 2 52
Sumber: buku Douglas Montgomery (probability and statistics)
Dari daftar tabel di atas diperoleh harga-harga sebagai berikut:
77.177
2.396
3.531.848
Bentuk persamaan yang diperoleh dari data di atas adalah sebagai berikut:
Persamaan normal yang diperoleh dari data di atas dengan pendekataan model kuadrat terkecil, menggunakan rumus (2.16), maka diperoleh persamaan normal sebagai berikut:
3.2 Perhitungan Nilai Parameter dengan Menggunakan Metode Numerik (Iterasi Gauss Seidel)
Untuk menentukan nilai parameter pada persamaan regresi linier berganda yang telah diperoleh, maka dengan menggunakan rumus (2.17) sebagai berikut:
Iterasi 1
Iterasi 2
Iterasi 4
Demikian seterusnya sampai pada iterasi ke 42, diperoleh hasil sebagai berikut:
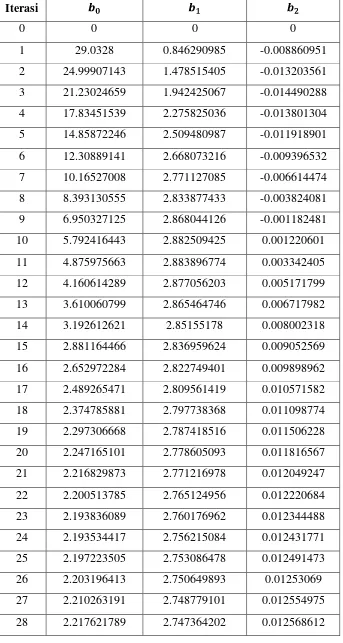
Tabel 3.2 Hasil Iterasi Gauss-Seidel Iterasi
0 0 0 0
1 29.0328 0.846290985 -0.008860951
Iterasi
3.3 Perhitungan Nilai Parameter dengan Menggunakan Metode Matriks (Invers Matriks)
Bentuk matriks dari variabel Y dan X adalah sebagai berikut:
,
Langkah 1
Membentuk persamaan normal dari data dengan rumus (2.16) diperoleh hasil sebagai berikut:
Langkah 2
Menentukan nilai matrik dengan meggunakan rumus (2.25), maka diperoleh hasil sebagai berikut:
Langkah 3
Kemudian dicari nilai determinan dari matriks , dengan rumus (2.26) sehingga di peroleh hasil sebagai berikut:
D
Langkah 4
Tahapan 5
Invers matriks dari dengan menggunakan rumus (2.28) adalah sebagai berikut :
Langkah 6
Sehingga nilai koefisien dan dapat diperoleh dengan menggunakan rumus (2.31) yang hasilnya diperoleh sebagai berikut:
Nilai koefisien , dan
Dengan demikian, maka diperoleh persamaan regresi dengan menggunakan metode Invers Matriks, sebagai berikut:
3.4 Perhitungan dan Perbandingan Simpangan Baku yang Dihasilkan dari Setiap Model
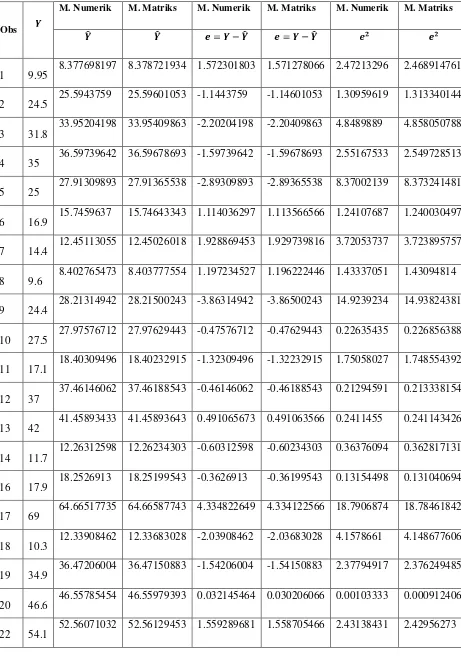
Tabel 3.3 Perbandingan Simpangan Baku dari Setiap Model Persamaan
Obs
M. Numerik M. Matriks M. Numerik M. Matriks M. Numerik M. Matriks
1 9.95 8.377698197 8.378721934 1.572301803 1.571278066 2.47213296 2.468914761
2 24.5
25.5943759 25.59601053 -1.1443759 -1.14601053 1.30959619 1.313340144
3 31.8 33.95204198 33.95409863 -2.20204198 -2.20409863 4.8489889 4.858050788
4 35
36.59739642 36.59678693 -1.59739642 -1.59678693 2.55167533 2.549728513
5 25 27.91309893 27.91365538 -2.89309893 -2.89365538 8.37002139 8.373241481
6 16.9 15.7459637 15.74643343 1.114036297 1.113566566 1.24107687 1.240030497
7 14.4 12.45113055 12.45026018 1.928869453 1.929739816 3.72053737 3.723895757
8 9.6 8.402765473 8.403777554 1.197234527 1.196222446 1.43337051 1.43094814
9 24.4
28.21314942 28.21500243 -3.86314942 -3.86500243 14.9239234 14.93824381
10 27.5 27.97576712 27.97629443 -0.47576712 -0.47629443 0.22635435 0.226856388
11 17.1 18.40309496 18.40232915 -1.32309496 -1.32232915 1.75058027 1.748554392
12 37 37.46146062 37.46188543 -0.46146062 -0.46188543 0.21294591 0.213338154
13 42 41.45893433 41.45893643 0.491065673 0.491063566 0.2411455 0.241143426
14 11.7
12.26312598 12.26234303 -0.60312598 -0.60234303 0.36376094 0.362817131
16 17.9
18.2526913 18.25199543 -0.3626913 -0.36199543 0.13154498 0.131040694
17 69 64.66517735 64.66587743 4.334822649 4.334122566 18.7906874 18.78461842
18 10.3 12.33908462 12.33683028 -2.03908462 -2.03683028 4.1578661 4.148677606
19 34.9 36.47206004 36.47150883 -1.54206004 -1.54150883 2.37794917 2.376249485
20 46.6
46.55785454 46.55979393 0.032145464 0.030206066 0.00103333 0.000912406
22 54.1
Obs
M. Numerik M. Matriks M. Numerik M. Matriks M. Numerik M. Matriks
24 22.1
19.98081971 19.98219243 2.149180291 2.147807566 4.61897592 4.613077341
25 21.2
20.99680121 20.99626543 0.153198794 0.153734566 0.02346987 0.023634317
726 115.173514 115.1734828
STD 5,23515973 5,235158309
3.5 Perhitungan Interval Kepercayaan Sehubungan dengan Regresi Linier Berganda
Perkiraan , , dimana adalah matriks dari baris
ke-i dan kolom ke-j terletak pada dke-iagonal pokok, maka:
= 5,235158309 (
= 1,123742437
=
= 5,235158309 (
Untuk menghitung estimasi interval untuk dan yang telah ditaksir oleh dan dengan interval kepercayaan 95%, diperoleh α = 0,05.
Dengan menggunakan persamaan rumus (2.33), maka estimasi interval pada parameter adalah sebagai berikut:
3.6 Uji Hipotesis
Untuk menguji kepastian dari persamaan regresi yang telah di peroleh, dengan langkah-langkah sebagai berikut:
5. Keputusan Uji Statistik
di tolak. karena nilai Fhitung < Ftabel
6. Kesimpulan
Hal ini berarti bahwa ada hubungan antara variabel Y terhadap variabel dan Sumber Regresi 5990,64721 2 2995.323605
580,3158245
Galat 113,55389 22 5,161540455
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Pada bab 1, bab 2 dan bab 3, telah diuraikan beberapa konsep tentang penggunaan metode numerik dan metode matriks dalam melakukan perhitungan nilai parameter pada regresi linier berganda, sehingga dapat disimpulkan bahwa:
1. Metode numerik dan metode matriks dapat digunakan untuk meelakukan perhitungan nilai parameter pada regresi linier berganda.
2. Penggunaan pendekatan metode kuadrat terkecil dalam tulisan ini adalah untuk mendapatkan persamaan normal, sehingga persamaan yang telah diperoleh dapat digunakan untuk melakukan perhitungan nilai parameter dengan metode numerik dan metode matriks.
4.2 Saran
DAFTAR PUSTAKA
Clark, Virginia A. 1986. Analysis Of Variance and Regression. Canada: Jhon Wiley & Sons.
Dixon, Wilfrid J. 1997. Pengantar Analisis Statistik. Yogyakarta: Gadjah Mada University Press.
Iswardono. 1998. Analisis Regresi dan Korelasi. Edisi ke-4. Yogyakarta: BPFE
Lungan, Richard. 2006. Aplikasi Statistika dan Hitung Peluang. Edisi ke-1. Yogyakarta: Graha Ilmu.
Makridakis, Spyros. 1999. Metode dan Aplikasi Peramalan. Edisi ke-2. Jakarta: Erlangga.
Montgomery, Douglas C. 2007. Probability and Statistics In Engineering and Management Science. Edisi ke-3. Canada: John Wiley & Sons.
Pudjiastuti. 2006. Matriks Teori dan Aplikasi. Yogyakarta: Graha Ilmu
Sangadji. 2008. Metode Numerik. Yogyakara: Graha Ilmu
Sudjana. 2002. Metoda Statistika. Edisi ke-6. Bandung: Tarsito.
Supranto, J. 2001. Statistik Teori dan Aplikasi. Edisi ke-7. Jakarta: Erlangga.
Usman, Husaini. 2006. Pengantar Statistika. Edisi ke-2. Yogyakarta: Bumi Aksara.
Walpole, Ronald E. 1986. Ilmu Peluang dan Statistika untuk Insinyur dan Ilmuwan.