Sifat Nilai Eigen Kompleks Matriks SCCM (Strongly Connected Closed Models) dari Model Kompartemental

(1)

SIFAT NILAI EIGEN KOMPLEKS

MATRIKS SCCM (Strongly Coizizected Closed Models)

DARI MODEL KOMPARTEMENTAL

KUSNANDAR

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

(2)

KUSNANDAR. Sifat Nilai Eigen Kompleks Matriks SCCM (Strongly Connected Closed hforlels) dari Model Kompartemental (Characteristics of Complex Eigenvohres of SCCM (Strongly Connected

Closed Models) Matrix of Comnparh~ental Model). Dibimbing ole11 BEERLIAN SETIAWATY

dan

PAIAN

SIANTURI.

Model koinparteniental adalall suatu turnusan matematika dari suatu sistem, dengm memisalkan sistem menjadi sejumlall kompa~teinen, yang dapat dianggap sebagai wadah penyimpanan material. Kolnpartelnen tersebut dihubungkan dengan aliran yang inenunjukkan dinaiNka inaterial dalam sistem.

Pemballan material pada kompartemen diinodelkan dalaiu bentuk persaliiaan diferensial yang &pat ditulis sebagai :

dengan x dan b adalah vektor kolom nxl clan A adalah nzcrtriks konzp~~rtenzerttcrl n m . Matriks kolnparte~nental A ini memiliki elemen diagonal utama nonpositif, elemen lainnya nomegatif dan jumlah eleinen tiap kolomnya nonpositif. Semua nilai eigen A lneiiipunyai bagian real nonpositif dan A tidak me~lipunyai nilai eigen inlajiner mnmni.

Tujuan dari penulisan ini adalall :

1. mempelajari sifat dari nilai eigen inatriks kompartemental yang inempunyai bagian ilnajiner tak nol. 2. memperoleh selang yang membatasi nilai dari jumlah kuadrat nilai eigenA yang imajiner,

dan

3. mempelajari sifat nilai eigen A yang imajiner. dengan A merepresentasikan kombimasi .cycle.

Diastunsikan bahwa matriks A bersifat SCCM (Strongly Connected Closed A4odels). Jika A merepresentasikan digraf dengan cycle terpanjang kurang dari atau sama dengan dua, maka seinua nilai eigen A bernilai real. Jika cycle terpanjang lebii~ dari dua, maka ada nilai eigen A=-p+iv dari A yang

K (tril)'

~ne~nennhi lvl tan- 2 p . dimana nz adalah panjang cycle tetpanjang dari digmf Jika h,?

- -

< O .

nt 1 7 - 1

inaka ada bagian imajiner Nlai eigen A yang tak nol.

(3)

SIFAT NILAI EIGEN KOMPLEKS

MATRIICS SCCM

(Strongly Connected Closed Models)

KUSNANDAR

Skripsi

sebagai salah satu syarat untuk memnperoleh gela Sa jana Sains

pada

Jurusan Matematika

JURUSAN MATEMATIKA

BOGOR

(4)

Judul

:

Sifat Nilai Eigen Kompleks Matriks SCCM

(Sfi'ongly Conszected Closed

Models)

dari Model Kompartemental

Nama

:

Kusnandar

N I M

: GO5496001

Dr. Berlian Setiawaty.

M.

S.

Pe~nbimbing I

(5)

RIWAYAT HJDUP

Penulis dildurkan di Cirebon pada tanggal 29 September 1978 sebagai anak kedua dari empat

bersaudara, anak dari pasangan Tjarba dan Rumsiti.

Ta11un 1996 penulis lulus dari SMU Negeri Sindanglaut dan pada tahun yang sama lulus seleksi

masuk IF'B melalui jalur Undangan Seleksi Masuk IF'B (USMI) di J w s a n Matematika, Fakultas

Matelnatika dan nmu Pengetahuan Alam.

Selama mengikuti perkuliahan penulis pemah aktii di Senat Mahasiswa FMIPA IF'B di bidang minat

dan bakat pada periode 199711998. Penulis juga pemah menjadi asisten Praktikum Fisika Dasar I pada

tahun ajaran 199711998. asisten mata kuliah Kalkulus I1 pada tahun ajaran 199811999, mata kulid~ _- Kalkulus I pada tal~un ajaran 199811999 dan 199912000, lnata kuliah Pengantar Matelnatika pada tallun

(6)

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala ralunat clan karnnia-Nya seliingga

karya ilmiah ini berliasil diselesaikan. Judul yang dipilili dala~n penelitian studi pustaka yang dilaksanakan

sejak bulan Februari 2000 ini adalali Sifat Nilai Eigen Ko~npleks Matriks SCCM (Strong!v Connecled

Closedh1odels) dari Model Komparte~llental.

Teri~na kasih penulis s m p h kepada berbagai p i l d yang telah ~nembantu penyelesaian karya

ilmiah ini, antara lain Ibu Dr. Berlian Setiawaty, M.S. yang telah ~nembimbing dengan penul~ ketekunan

dan kesabam hingga selesainya penulisan kaya ilmiali ini, Bapak Dr. Paian Siantnri selaku pe~nbilnbing

11, Ibu Dra. Nur Aliatiningtyas, M.S. selaku penguji. Bapak Ir. Toni Baklrtiar.M.Sc. dan Bapak Ir. I Wayan

Mangku, M.Sc. yang telah nle~nbantu dalam ha1 pengadaan referensi. serta staf pegawai jurusan

Matematika IPB atas segala bantuannya.

PenghargaaA yang tinggi penulis berikan kepada ayah, ibu, kak& adik-adikku dan saudara-

saudaraku tercinta atas segala do'a

&an

dorongannya. serta tak lupa ucapai terilna kasih kepada teuian-

te~itanku Engkus, Budi. Jaka, Ismail. Kiki. Didi. Minar, Joko, Dalfi. Frengky. Reza. Wicak. Beni. Yuce.

Heny, Cycil, tell Ati, tell Ade, warga kost Bafak 20. warga kost DC7

,

rvarga Mat'33, warga Mat'i4 d a i

lainnya yang tak tersebutkan, atas segala bantuan dan dorongan semangatnya.

Semoga karya ilmial~ ini dapat bennanfaat.

Bogor* September 2000

(7)

DAFTAR IS1

Halaman

DAETAR GAMBAR vi

I . PENDAHClLUAN

...

1.1 Latar Belakang

.

1

I I

...

1 I1

.

LANDASAN TEORI

2.1 Definisi dan Lema Dasar dalam Aljabar Linear

...

1

...

2.2 Ruang VeMor Kompleks 3

2.3 Teori Directed Graph

...

6

111 . DESKRIPSI MODEL KOMPARTEMENTAL

...

7

IV . NILAI EIGEN KOMPLEKS MATRIKS KOMPARTEMENTAL

4.1 Nilai Eigen Matriks Kompartemental

...

9

...

4.2 Sifat Nilai Eigen Kompleks Matriks SCCM

...

: 10

...

V

.

CYCLE

.

13

.

KOMBINASI CYCLE _{. .}

...

6.1 Ilustrasi Koinbinasi Cycle 15

6.2 Nilai Eigen dari Clustered Rosette ... 16 VII . KESIMPULAN

...

I 9

(8)

DAFTAR GAMBAR

Halaman

...

1 . Sistem kompartemental 7

...

2

.

Diagram model aliran timbal dalam tubuh manusia S

3 . Diagram daur hidrologi ... S

... ...

I . Lingkaran Gerschgorin

.

9

5 . Digrafyang bersesnaian dengan matriks SCCM ... 10

6 . Cycle dengan panjang n ... 13

(9)

I.

PENDAHULUAN

1.1 Latar Belakang

Pemodelan kompartemental mempunyai aplikasi pada berbagai bidang, seperti pergerakan obat pada fannakologi, analisis ekosistem, studi sistem ~iletabolisrne dan gerak pada reaksi kimia.

Sistenl pada model ini dianalisis ~nelalui pelisahan sistem menjadi sejumlali komponen, yang disebut kompartemen, yang berhubungan langsung dengan pembalm material. Twri ~nate~ilatika untuk perilaku sistem ini disebut antrlisis konipartenientnl.

Sistem koinpartemental terdiri dari dua atau lebih ko~i~partemen. Sistem tersebut dilnodelkan dalain bentuk persanaan diferensial, d i i a setiap persamaan menggarnbarkan laju pembahan jumlah material terladap waktu pada konipartemen tertentu.

Salall satu model kompartemental addah persamaan diferensial berbentuk

dengan x dan b adalah vektor kolom n s l dan A adalah rnatriks konipartenientrrl nsn. Matriks ko~upartemental A ini memiliki elemen dia~onal utana nonpositif, elemen Iaiunya nomegatif dan jumlal~ elemen tiap kolomnya nonpositif. Menurut Anderson (1983) semua nilai eigen dari A mempunyai bagian real nonpositif dan A tidak memnpunyai nilai eigen ilnajiner murni. Jadi, nilai eigen '4 dapat mneiniliki bagian imajiner tak no1 pada saat bagian realnya negatif, selkgga dari aspek dinanik: osilasi teredam mungkin tejadi pada solusi persamaan (1). Tetapi tulisan ini tidak ~uembahas aspek kedinamikan dari model ko~l~partemental, melainkan mempelajari aspek aljabarnya.

Masdall yang dibahas pada tulisan ini adalah rnerupelajari kondisi pada saat nilai eigen A

memiliki bagian imajiner tak no1 dan memperoleh pertidaksamaan dari jumlah kuadrat bagian imajiner nilai eigen A. Masalah lain adalab lnempelajari sifat-sifat bagian imajiner nilai eigen A, dengan A lnerepresentasikan kornbinasi dua atau lebih cycle.

1.2 Tujuan

Tujuan dari pennlisan ini adalah :

1. melnpelajd sifat dari nilai eigen matriks komparten~ental yang mempunyai bagian irnajiner tak nol.

2. memnperolel~ selang yang lnembatasi nilai dari jumlali kuadrat nilai eigen A yang imajiner, dan

3. me~npelajari sifat nilai eigen A yang imajiner, dengan A rnerepresentasikan ko~nbinasi cycle.

1.3 Metode

Metode yang digunakan dalam tulisan dengan topik sifat nilai eigen kolnpleks lnatriks SCCM (Stongly Connected Closed Models) dari model kompartemental ini adalah metode studi pustaka. yang lneliputi penelusuran dan pennlisan kembali suatu jumal dalam bentuk yang lebih utuh.

1.4 Sistematika

Sistenlatika penulisan pada tulisan ini adalah sebagai berikut. Pada bab dua diberikan landasan teori sebagai dasar analisis masalall.

Pada bab tiga diberikan deskripsi mengenai model kompartemental. Bab empat akan membahas sifat-sifat dari nilai eigen ko~npleks matriks SCCM.

Bab lima nienlbahas nilai eigen suatu matriks SCCM yang rnerepresentasikan cycle dan bab enan lnernbahas nilai eigen suatu litatriks SCCM yang lnerepresentasikan kombinasi cycle. Kesimpulan dari tulisan ini ada pada bab teraklur.

II.

LANDASAN. TEORI

2.1 Definisi dan L e n ~ a Dasar dalam AIjabar Definisi 2 fNoble. 19691

Linear Deterniinan dari ru~atriks A=(o,),,, didefinisikan

oleh ekspresi Definisi 1 [Noble. 19691

Misalkan matriks A =(ai,),. Minor dari n, adalah \A\ =

d e t ~

= i a , , ~ , ,

deter~~inan dari matriks vane dioeroleh i=l

~. . . ,. .,. . . , ,

- .

dengan mengl~ilangkan basis ke-i dan kolom ke-j

dari ~llatriks A,,, dan dinotasikan dengan n/fv Definisi 3 [Noble. 19691

Bilangan

B,=(-l)'iJhJ/,

disebut kofaktor dari a, Misalkan A adalal~ ~natriks 17m. Polinori~

(10)

pers;unaanl(A)=O disebut persumuun kurakterisfik dari A. Nilai eigen dari A adalah skalar A> dimana A x = k atau (A - W ) x =O mnenipunyai solusi tak nol.

Solusi tak no1 x disebut vektor eigerz dari A.

Definisi 4 [Anton, 19951

Jika matriks A={aij},, maka trunspose dari A adalah ~ ' = { b ~ } " ~ , dengan bo= a,;.

Lema 1

Nilai eigen lnatriksA d a n ~ ' adalah sama.

Bulti :

Misalkan A adalah ~ l a i eigen dari matriks A, maka polinom karakteristik dari A adalah

fA(A)=IA

-

21. Karena

(A

-

ailT

= ( A ~

-

a ) , maka dari sifat detemkan

J;,(A)=H

-

21= IAT- AII=

f,,

(A)

Karena polinom karakteristik dari A dan

A*

sama. maka A dan A' mnempunyai nilai eigen yang

sama. 0

Terus dari matriks A={aii},, ditulis trA, adalall jnmlah dari elemen-elemen diagonal utamanya.

Matriks A,, disebut segitiga atus jika semua elenlen di bawah diagonal utama adalah nol.

Lema 2 [Marcus & Minc, 19691

1. Jika matriks A={av)m,dan B={bv}-, maka

Lema 3 pIoble, 19691

Polinom karakteristik dari matriks A={av)na adalah polinom berderajat-11 ,XA) dengan

XA)=ao An+al A"-'+.

.

. + a,.~ A+ a,

dengan a; adalah jumlah prinsif minor orde-i berganti tanda (~YSJ?) dan

untuk

00, al dan a, memenulli

0 0 = (-1):11 al = (-1) t r A 3

an=

IAl.

Jika lulai eigen

-4

adalah Al,. . . ,Iln Inaka

Bukti:

Jika W-AII diperluas &lam bentnk elemen pada baris pertama, maka diperoleh

Bv adalah kofaktor dari elemen (iJ) pada A-A1 dengan ,

Ell polinom A berderajat n-1

Bljpolinom Aberderajat 17-2 untuk j=2,3,. ..,n

,

sellingga ,

X.2) =(all- A) Bll -1-{Polinom berderajat (17-2)). Argumen yang sana diterapkan pa& Bll dan dengan pengulangan diperoleh.

j(A) = (all- A)(ar

-

A). .

.

(a,,

-

A) +{Polinom berderajat (17-2) atau knrang)

n

= (-l)"An

+

(-I)"-' x u i i An-'

+

{Polinom

;=I

berderajat (n-2) atau kurang) (2) sellingga polinom karakteristik dari matriks A,. adalah polimom berderajat-n dengan koefisien An adalah (-1)" dan koefisien

,T1

adalah

I / I? I ,

"

i=l

(ii) trAAT = C C a , a v = ~ C a i .

;=I j = l j=li=I Misalkan

,&>

2,=1,2 ,..., n adalah nilai eigen A.

, m&i

2. Jika Tmn adaldl m a a s segitiga atas, maka

XA) ==lil.aI=(A121- I,)(h. A) t) , , A)

2 I' "

t r n T = C t i j

+ C

XI,;

;=I ;=I j = ~ =(-1)"X +(-I)"-'

C

Ai 2.'

+

. . .

i=l (3)

ic i

Untuk lnenentukan konstanta a,

,

pilih A=O Definisi 7 [Noble, 19691 padaj(A) sellingga dari persamaan (3) diperoleh Matriks A,,, disebut nonsingulur atau mempunyai !Al=AlA2. .

A

invers, jika ada matriks B sehungga AB=BA=I, Jadi, dari persamaan (2) dan (3) terbukti dengan I matriks identitas. Matriks B disebut v

irzvers dari A dan dinotasikm dengan A-I.

CA; =Ca,,

=trA 0

(11)

Aliibat 1 [Noble, 19691

Jika nilai eigen matriks A,, adalah At ,...,

A,,,

maka

f r ~ ' =:A; .

i=l

Bukti :

Misalkan

A

i=1.2, ..., n adalall nilai eigen yang bersesuaian dengan matriks A artinya Ax=+, Inaka dari Lema 3

dan

~AX=A@X)=A(G)=.~(AX)=A{.ZSC)=&~X.

Berarti nilai eigen yang bersesuaian dengan matriksA.4 adalall

Definisi 8. [Marcus & Minc, 19691

Matriks nomegatif K,, disebut tak terurai jika matriks tersebut tidak dapat diuraikan (melalui pertukaran baris, kemudian pertukaran yang sama terhadap kolomnya) ke dalam bentuk

1 ~ 2~ 3 1 '

dengan K2 matriks sembamng, Kl dan K3 adalah sub mahiks segi, sedangkan 0 adalah ma* nol.

Lema 4 warcus & Minc, 19691

Misalkan K,, adalah matriks tak terurai yang nomegatif dan A+=maks{ A

I

Kx >Ax. x 2 01, maka ada suatu nilai eigen real nomegatif A' dan vektor eigen x+ nomegatif yang bersesuaian dengan A' ,

sehingga fi'=A+xi dan jika A adalah nilai eigen lain dari K ,maka

14

21 A'.

Selanjutnya A' disebut nilai eigezz Perron.

Buliti: Liliat Oksaviri (1997)

2.2 Ruaug Vektor Kompleks Definisi 9 [Paliouras, 19871

Bilazrgan konrpleks adalah suatu pasangan t e m t bilangan real yang dinyatakan oleh (p, v) atau p+iv, dengan i2= -1.

Untuk sen~barang bilangan kompleks z =p+iv, nrgrinren z , ditulis arg z, didefinisikan sebagai salal~ satu sudut yang dibentuk ole11 vektor z dengan surnbu real positif. Dengan kata lain

arg(p+iv) adalall suatu sudut sedemikian Npa sehingga tan 0 = v / p .

Lema 5 [Hall & Knight, 19641

Pada polinom dengan koefisien real. jika mempmyai akar kompleks, maka selalu dengan sekawannya.

Bukti :

Misalkan JA) =O adalah polinom dengan koefisien real dan ~nelnpunyai

akar

konipleks p+i v. akan dibuktikan bal~wa p -i v juga akar dari XA). Faktor dari XA) yyag bersesuaian untuk dua

akar adalal1

(A-p

-

iv)(A-p +iv) atau (A-p)2+?. MisalkanXA) dibagi ole11 (A-p)'+

2,

maka

~ d ) = f i ( A ) { ( A - p ) 2 + $ ) + aA+b,

dengan a,b~'iR danfi(A) adalah polinom berde~ajal '17-2.

Karena A=p+iv, maka dari hipotesis .flA)=O dan (A-p)'+?=0, sellingga a(p+iv)+b=O. Bagian real dan imajiner di atas sama dengan nol, sehingga ap+b=O

clan

U F O . Karena MfO. maka a=O; mengakibatkan b=0. Sehingga XA) lhabis dibagi ole11 ( ~ - p ) ~ +

?,

jadi p -iv juga

akar

dari polinom tersebut.

0

Akibat 2

Misalkan

4

, j=l, ..., n adalali nilai eigen dari matriks A, maka rata-ntanya,

A ,

bemilai real.

Buliti :

Misalkan nilai eigen dari mahiks A real atau kompleks, untuk nilai eigen real , maki

2

real dan untuk nilai eigen kompleks, berdasarkan Lema 5 maka penjumlahan bagian imajiner dari nilai eigen akan saling menglulangkan, yang berakibat

2

real. 0

Lema 6 [Paliouras. 19871 Misalkan

z = p+iv= r(cos0

+

i si170) = rd8, dengan $ =

@+

3)

dan 0 = arctan@ /v). Jika 17

bilangan bulat positif, maka

I"= ~ " ( C O S n0+isi1? n 0 ) =

me"'.

Buliti :

Proses pembuktian dilakukan dengan induksi malemalika.

(12)

r'=

zz = rfcos B+isin 0 ) r(cos B+isin 8 ) Lema 9 IPaliouras, 19871

.

-

Asumsikan benar untuk n=k, sehingga

9

= ~ ( C O S k8+isin k 8 ) = peika. Untuk 17=k+ l

?I=

22

= ~ ( C O S k@+isin k 8 ) r(cos0+isin 8 )

= T1(cos( kB+B)+isin( k@+@))

= ?'(cos( k+1)8+isi17(k+1)8)

= ++lei(il+l)8 13

Lema 7 [Paliouras. 19871 Misalkan

z" = ~"(COS n 8 + isin 170) = i-"e'"'. dan z, = r, (cos@, + i sin@,).

Jika z" = z,. ~naka akar ke-n dari z diberikan oleh 17 bilangan kolnpleks

zk= r,'"(cos (B,ln+2d/n)+ i sin (8&+2d/n)), k=O. 1, ... ,n-1.

Buliti :

Misalkan

z" = z ,

r"(cosn8+ i sin 178) = r,(cosO,+ i sin8,), sehingga

r"= r, , n0=BO+2&

untuk beberapa bilangan bulat k. Karena r dan r, bilangan real positif, berarti r adalal~ akar pangkat ke-n dari r, yaitu

r = (rJ1'"

dan

8 = ($+2nk)h7 ,

selingga akar pangkat n dari z adalah

zk= r,""(cos (Bo/,7+2nk/n)+ i sin (8Jn+2xk A?)), k=0,1 .... ,n-1.

0

Lema S

Buliti :

Dati persalnaan trigonometri .

sin (x+n) =sin x cos a

+

sin n cos x. sin (x

-

n) =sin x cos n

-

sin n cos x, sehingga

sin (x+n)

-

sin (x - a) = 2sin a cos x. Misalkan ~ 2 n W n dan n=dn. rnaka

sin(k+1/2)2rdn -sin(k-1/2)2dn =2sind17 cos2nk/r? . Julnlalkan untuk k0.1. ... , n-1. maka

sinfn-l+112~2rd1~

-

sin(-112)2dn

. .

=

k=I

sinfn-ll2)2dn + sin rdn =

I

sin(2n-dn )+ sin d n =2sind7

sin 2n cos d n -sin d n cos 271 + sin d n =

I

Suatu vektor p disebut konrbinrrsi lilterlr dari vektor-vektor kompleks xl,...,xn jika vektor tersebut dapat dinyatakan dala~n bentuk

Buliti : dengan c,,

lr

i S n adalali skalar kolupleks.

Bukti dari lelna tersebut menggunakan deret

geornetri. Definisi 11 [Anton, 19951

e2dlt,[(e2dl,?r Misalkan xi, ..., x, adalah vektor-vektor pada ruang

I,-I vektor kompleks I/. Jika masing-masing vektor

-

Ce'"'" - e3ni~,r pada I/ dapat dinyatakan sebagai ko~ilbinasi linear

k=1 -1 _{dari xl.}_...,_{x,, inaka vektor-vektor ini dikat<&an}

e2mi!!ead(+~-~)~,? - e 2 m i r i

-

nrererttfntg I/.

-

e?mlrr _-1

e?" 1 - e 2 m ~ n Definisi 12 [Anton 19953

-

- = - I . 0 Jika S={x l,...,xn) adalah himpunari vektor

2m 1 ,r e'm'#t

(13)

n vektor yang berbeda dalau lumpunan tersebut

C c i x i = 0 , _ortogonnl.Suatu himpunan ortogonal yang setiap i=l

vektomya lnempunyai nonna satu disebut melnpunyai paling sedikit satu solusi, yakni c,=O, _ortonor,llaL

untuk setiap i. Jika ini adalah satu-satunya solusi,

Inaka S hinlprrnan bebas linear. Jika ads _L~~~₁₀_{(proses ~ r a l , l . ~ c ~ 7 n l i ~ ~ )}_{[ h t o n , 19951} solusi lain, maka S disebut Irinpunarr tcrk bebas _Misalkan_{{ x l , , , , , x n )} _{basis untuk}_ruang

lirtear. _I/, _lnisalkan

Jika V se~nbarang ruang vektor kolnpleks dan S={xl,.

.

..xm) merupakan lumpunan berlungga dari vektor-vektor pada V, maka S disebut basis untuk J'jika

1. S bebas limear 2. S merentang V.

Jika u=(ul, ...: zt?)

dan

v=(vl, . . ., v,) adalah vektor- vektor di

C",

maka basil kali dalam (u,v) didefinisikan ole11

"

( u , v ) =

crc;v,

,

i=l

dengan ii, adalah sekawan dari v; , i = l , . .

., n

Definisi 15 [Anton 19951

Suatu hasil knli dalanr pada ruang vektor kompleks V adalah fungsi yang menghubungkan bilangan kompleks (u,v) dengan masing-masing pasangan vektor u dan I ) pada V sedemikian

sel~ingga aksioma-aksioma berikut terpenuhi untuk semua vektor

-

u, v dan w di V dan semua skalar k.

1. (u,1+=(v,u)

.. ..

dan definisikan tr2, ..., rr, secara rekursif ole11

untuk h=1,2,

. .

.,

17-1, dengan

PL= ( ~ k + l , t ~ l ) I I I + . . .

+

(xl+l,l~k) Ilk

adalah proyeksi ortogonal xk+~ pada ruang yang d i b a n p ole11 vl, ..., uk, ~uaka lumpunan ( 1 1 ~ ,.... zr,)

adalali basis ortononnal untuk I,!

Bulti: Lihat Anton (1995)

Definisi 19 [Anderson, 19831

Matriks -4, disebut definit positif, jika A bersifat ( x . 4 ~ ) > 0. untuk setiap vektor tak no1 x.

Definisi 20 [Marcus & Minc, 19691

Misalkan U,, adalali matriks dengan unsur kompleks: maka trunspos sekmvan U, dinyatakan oleh

U'

dan didefinisikan ole11 U * =

uT

,

dengan adalah matriks yang unsur-unsurnya sekawan dengan unsur-unsur yang bersesuaian dalam U. 2. (11+v, w)=(tl,>v)+(v. w )

3 . (ku,v) = k(u,v) Definisi 21 [Marcus & M i x C 19691

M a a s U,, disebut nratriks u~riter, jika u'=u'. 4 . (v,v) 2 0 dan ( I ~ v ) = 0 o v = 0

Suatu ruang vektor kompleks dengan suatu lusil

Lema 11 [Marcus Mint, 19691

kali dalaln disebut run~rg hasil kali dalam

konrpleks/ruairg uniter. Misalkan

U={hu),,,

adalah lnatriks dengan unsur

.kompleks, m&i ,.

Ruang uniter dua vektor u dan 11 disebut ortogo~tal

jika ( L I , ~ ) =O.

Jika If. adalall sebuall mang miter. lnaka nornzu vektor 11 dinyatakan ole11 llull

dan

didefinisikan oleh

1 1 ~ 1 1

i =(u,

zt)In.

Suatu liili~punan vektor pada ruang uniter disebut hirirprinan ortogoncrl jika selnua pasangan vektor-

Lema 12 [Marcus & Minc, 19691

Untuk setiap matriks real A ,

.

ada lnatriks uniter U,, . sehingga UmAU=T

.

dengan

T,,

adalali matriks segitiga atas .

Bulcti :

Proses pe~nbuktian lema ini n~enggunakan induksi matematika. Untuk selnbarang nilai n,

(14)

IV, adalab vektor eigen yang bersesuaian dengan

A . Menggunakan proses Gram-Sclunidt, konstruksi vektor ~2

.

... .\ir,, sehingga {w,, ... .w.}

adalal~ basis ortonormal unruk C'. Misalkan Q adalah lnatriks yang vektor kolom ke-i adalal~ IV;

untuki=l ,...: n.

Q=[ > V I , ~ V ~ . ... , lvn]=[ 7l',, prq,

dengan ~V=[IV~, ...

.

w"].

Dari konstdsi, Q adalab matriks uniter, lne~nberikan

s e l u n ~ ~ a W-wl =O. Karena Aivl =Al wl, maka

Lemna ini benar untuk n=2 karena C inatriks 1x1 dan B ~natriks 1x1, sehingga Q-AQ adalah matriks segitiga atas.

Asumsikan benar untuk n=k, maka ada matriks ortogonal kxkk lfl: seldngga 1,jil Pj =TI: dengan TI ~natriks segitiga atas.

Untuk n=k+l, maka C inatriks kxk dan B mnatriks lxk, dengan hipotesis induksi, Inaka ada lnatriks ortogonal kxk, Ifl, selkgga l/,*Cl/,=~~, dengan TI mahiks segitiga atas.

Misalkan

Misalkan U=Qli, U nlatriks muter, karena U-U=(Ql.)'Ql/.=

r;

Q'Ql/=I. seldngga C'A U=T, dengan T ~natriks segitiga atas.

0

Lema 13 (Pertidaksaniaan Schrrr) Narcus& Minc, 19691

Jika.4={ov), mempunyai nilai eigen

4,

i=l,

...,

n ,

maka

BuMi :

Berdasarkan Lema 12, untuk setiap ~natriks .4.,, ada matriks uniter U,,: seldngga U> U =T. dengan T lnatriks segitiga atas, maka

(u-AAU)'=T' U'A'U=T. TU*A'U=TT. (u.AU)U>.U=TT'

U.M'U=TT'. Dari Lema 2, diperoleh

tr U'AA'U= PM'

,

sehingga

trAAm = t r l T

2 . 3 Teori Directed Graph

Definisi 22 [Thulasiraman & Swamy, 19921 Directed graph (Digran, D=(V,E) adalah pasangan t e m t V dan

E,

dengan V adalah himpunan tak kosong dan terbatas dari verteks (simpul) dan E adalah himpunan pasangan tenuut elemen-elemen tak identik lf , yang disebut arc (busur/sisi berarah).

Definisi 23 [Thulasiramnan & Swamy, 19921 Suatu walk pa& digraf D=(V,E) adalal~ suatu barisan verteks dan arc pada digraf D dengan bentuk 1~l,(l~l,f~2). V2,(1;2,1/3) ,..., Vn.l,(l/;.l,Vn)J*',v Walk yang semua verteksnya berbeda disebut path. Pat17 dengan verteks awal dan akhirnya sana (i,;=I/,) disebut cycle.

(15)

IIt.

DESKRIPSI MODEL KOMPARTEMENTAL

Misalkan suatu sistem terdiri dari n- kompartemen. Gambaran mum untuk kedinainikan pembahan lnaterial berkenaan dengan komparteinen ke-i adalah persamaan,

xi = laju aliran masuk

-

laju aliran keluar ,

i=l, ..., 17 (4)

dengan xi@)

r

0 adalah jumlah material pada koiparteinen-i pada waktu I. Laju aliran material dari koinpartemen-j ke kompartemen-i (i*) diinodelkan ole11 aGj, dengan ay adalah koefisien aliran, bernilai nomegatif dan konstan, sellingga dari persanaan (4) model komparteinental linear adalah

n

x i ( t ) = b , ( t ) + C a i j x j - C a j j x j , V i = L ..., n (5)

j = l j = O

i t i i i i

dimana fungsi hi(/) adalah laju input material ke koinpartemen-i dari luar sistem. Material yang dialirkan keluar sistem disebut ekskresi. Laju ekskresi material keluar sistein dari komparteine11-i adalal~ aojxj. dengan aoi adalal~ koefisien ekskresi.

bll input bi

I

input

Gainbar 1. Siste~n koinpartemental

Gainbar 1 mejelaskan bahwa pembahan material pada kompartemen ke-i, yaitu 11; adalah laju aliran nlasuk = bj+ ai,., xi.]

laju aliran keluar = noixi + ai+l,;x; sehingga

x, = ( b;+ a,,, X,I )- ( noixj + ai+,,;x;)

Definisikan

maka dari (5) dan (6) , jumlah aliran keluar dari kompartemen-i ke kompartemen lain dan keluar sistem adalah ai&.

Persanwan (6) mempakan eleinen dari matriks konstanA={a,],,,

.

yang lne~niliki sifat .

a. Setiap elemen di luar diagonal nomegatif b. Setiap elemen diagonal nonpositif

c. Jumlah setiap kolom ke-i adalal~ bilangan nonpositif -00;. i=1,2

,...,

n.

Matriks dengan elemen memenuhi sifat a,b.c disebut ntatriks kontparte~tte~ttal.

Eleinen ay ( i d ) adalal~ nomegatif karena berhubungan dengan aliran masuk. sedangkan a:; adalah nonpositif karena IIIe~pZkan ukuran dari aliran keluar. Bentuk matriks-vektor dari model kompartemental (5) dapat ditulis kembali sebagai sistem persamaan diferensial biasa

x = Ax+b (7)

dengan A={a,}, adatah matriks dari koefisien aliran dan b=[bl, ... .b

J'.

Sifat dari persamaan (7) ini bergmtung pada penyusunan eleinen no1 dan tak no1 dari matriks kompartemental A. Jika ay=O (id): maka tidak ada aliran material dari komnparte~nen-j ke kompartetnen-i. Jika a@ (i;g'): maka material langsung nlengalir dari komparteinen-j ke komparteinen-i.

Sistem kon~partemental ini direpresentasikan oleh diagram keterl~ubungan yang il~enunjukkan alimn material tak no1 pada suatu digraf.

Misalkan A={ay).,. adalall inahiks kompartemental, digmf yang bersesuaian dengan matriks tersebut adalah D=(l<E) dengan V={VI, ... ,i~,] adalah kompartet~~en dan E={(i$i~j)}

adalah aliran tak no1 dari nwterial untuk a i i t 0,

iq.,

i=l, ..., n d m j=l, ..., 17.

Di bawah ini diberikan contoh inodel komnpartemental untuk pergerakan zat tii~lbal pada tubuh inanusia.

Contoll 1

(16)

Input bl Makanqair,udara

[image:16.544.284.490.380.533.2]

,L

Gambar 2. Diagram model a l i i timbal &lam tubub manusia (digambar kembali dari Anderson, 1983).

Aliran timnbal pada tubuh mnanusia ini di~nodelkan dengan, sistein koinparte~llental dengan 3-konlpartemnen, yang ditunjukkan pada gambar 2.

Sejumlah timbal mas& ke tnbuh melal~ii makanan, minuman dan udara, dari saluran pencemaan dan saluran pemapasan. Sebagian besar timbal diterima oleh sel darah merah dan sebagian kecil ole11 plasma darah. Dari daral~ timbal disebarkan dengan cepat ke jaringan lain (pertama ke hati dan ginjal, selanjutnya dengan waktu berbeda ke bagian lain dari tnbuh). Secara perlalm tirnbal diteri~na ole11 tulang. Pertukaran timbal pada jaringan dan tulang dengan daral~ melalui proses

difnsi.

Misalkan t2O adalah waktu, xj(t), i=1,2,3 adalah jumlall timbal pada kompartemen-i dan hi([) adalah laju input ke kompartemnen-i, maka persamaan kesetirnbangan nntuk aliran timbal antar konlpartenlen seperti pada garnbar 2 adalall:

XI =(bl +ar2x2 +aljx3)-(aOlxl +a21xl + a j l x I )

xz =a2,xI -(amx2 +a12x2) (8)

x j = a j l x l -a13xj

dengan a, adalah konstanta positif.

Laju input bl memerlukan penjelasan lebih lanjut. Laju input ini terdiri dari dua komnponen, satu d a i uiluran pemapasan dan satu dari saluran pencemaan. Misalkan a adalah laju konstan dari seju~nlall timnbal yang mas& ke salwm pemapasan dari lingkungan. Sebagian dari input a ini yakni p (O<p<l) benar-benar diserap ole11 darah. Laju konstan input timbal yang rnasuk ke darah (la1) dari salunn pernapawl adalah p a . Misalkan ,8 adalal~ lajir konstan dari sejumlah limubal yang mnasuk ke saluran pencemaan nlelalui ruakanan dan ~ninumarl (iuga ada beberapa timbal yang ~nasuk ke makanan

ini dari air liur, sekresi lambung, empedu, tetapi tidak ditentukan). Dari input P i @ hanya sebagian

(rp

) yang diserap melalui saluran pencemaan ke danh, dengan 0-1.

Akllimya laju input bl(t) adalah konstanta bl =pa+$,

dan persarnaan (8) dapat dibentuk menjadi :

r - i

- -

dengan

a l l = -(aol +a2, +a,, ) ,

=-(a, + a l 2 ) , a3j = -arj .

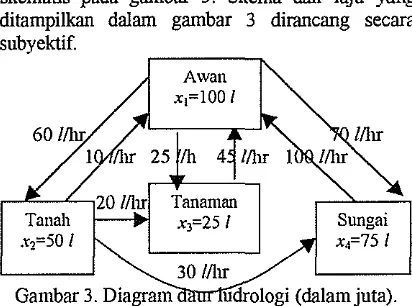
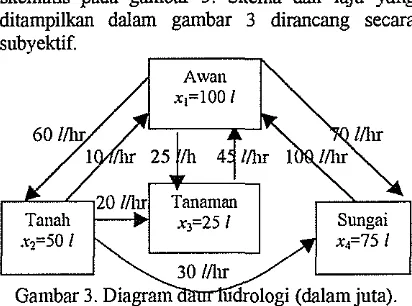
Selanjutnya di bawah ini diberikan contoh untuk inodel konlpattemental yang tertutup dan strongly connected dari daur hidrologi.

Contoh 2

Daur hidrologi dapat ditunjukkan secara ske~natis pada gambar 3. Skema dan laju yang ditampilkan dalam gambar 3 dimcang secara subyektif.

Dalam daur hidrologi, air hujan akan turun ke tanall. tana~nan dan sungai. Dari tanall sebagian air akan diserap ole11 tanaman dan sebagian mengalir ke sungai. Energi panas matahari mnenyebabkan terjadinya proses evaporasi di sungai, tanah dan tanaman. Uap air tersebut akan dibawa angin melintas daratan yang bergunnng maupun datar dan apabila keadaan atrnosfer menlungkinkan, sebagian dari uap air tersebut akan mnenjadi 11ujan. Kejadian tersebut terns berlangsung, selungga terjadi siklus.

(17)

Dengan cam yang sama dapat diperoleh koefisien lainnya. sebingga

r.

i x4 = (n41x1 +n42x2)-n14x4,

dengan a;< adalah koefisien aliran dari _{- -} kompartem&-j ke kompartemen-i.

Sebagai ilushasi nil. o12 diperoleh dengan cara

I

/'

1

O 7 berikut. ~erdasarkan gambar 3 diperoleh a,g2=l0 1x41

liter/hari, dengan x ~ 5 0 liter, maka a,,=O.Z/hari.

N.

NILAI EIGEN KOMPLEKS MATRTKS KOMPARTEMENTAL

4.1 Nilai Eigen Matrilis Kompartemental seldngga nilai eigen h terletak pada lingkar~m Ri. O Menurut Anderson (1983) selnua nilai eigen

dari niatriks komparteinental A mempunyai bagian Teoremn 2 [Anderson, 19831

real nonpositif dan A tidak meinpunyai nilai eigen Bagian real dari nilai eigen mahiks imajiner inumi. Namun sebelwnnya akan diberikan konlpartemental A adalah nonpositif dan A tidak Teoreina Lingkaran Gerscl~gorin. ~nempunyai nilai eigen iinajiner inwni.

Teorema 1 (Teorerna Lingknrnn Gerscl~gnrin). plarcus & Minc. 19691

Misalkan A={av}, ,

dan

I 1

dengan Ri adalah lingkaran pada bidang kornpleks

dengan pusat nii dan jari-jari i l a j i l , maka setiap

i=l

i= j

Nlai eigen A terletak pada sedikitnya satu dari n lingkaran Rj.

Bukti :

Dari Teorema Lingkaran Gerschgorin,

Khususnya jika A adalal~ matriks kompartemental, maka nji 2 0, V iz j dan karena jumlah seluruh kolom ke-i adalal~ -aoi, maka

$lajii=-aoi -a, <-a, =laijl,t/ i=1,2 ,..., n ,

]=I

is j

sehingga nntvk setiap

--

i. linnkamn Ri terletak pada -

daemh lingkaran z a 5 a , sebagaimana Buliti :

terlihat pada gambar 4. Karena setiap nilai eigen A Berdasarkan Lelna 1, jika A adalah ~ l a i eigen

terletak pads sedikitnya satu daerah inaka

matriks A dan x v e k eigennya, nl*a 1 jugs _{bagian real dari}_nilai_{eigen A terletak} _bidang

lne~pakan nilai eigen nlatriks A'. sehingga _{sebelall kiri} _{(nonpositif),} _{Selanjutnya karena} .ATx=k, yang berimplikasi dengan _{daerahnva berbentuk lingkam maka tid<ak ada}

-

Nlai eigen yang terletak pada axis imajiner (kecuali nol).

"

D

C a . . x . + a . . x . J Z J rx 2

= h .

c . j=1

i i j

Misakai Ix,l = maks xJ , niaka

2

_< 1 dan lijr9r

I

/:I

IA-niillxii=

Galnbar 4. Lingkaran Gerschgorin, dengan

- njj

1

5 ln

<

jj

ll:l

inij

1

. a = ?In,

I

dan b = ln,,~

]=I ]=I ,=I

ir, 'iJ 1x1

i a j i x j

j = l i i ,

_< ilnsx,l

<

(18)

4.2 Sifat Nilai Eigen Kompleks Matriks SCCM Misalkan model kompartemental berdasarkan persanaan diierensial

x = A x + b , (9)

dengan A ={aw), adalah matriks kompartemental. Asumsi yang digunakan adalah :

1. Digraf yang bersesuaian dengan mahiks. A adalall slrorlgly connected, dengan kata lain A adalah matriks tak tenuai

2. Modelnya adalah tertutup, yaitu tidak ada aliran material yang masuk dan keluar sistem, dengan kata lain b=O pada persamaan (9) dan ciri pada matriks A adalah

C a , =O. i=1,2 ,... n .

j = l

Model yang berdasarkan dua asumsi diatas dimotasikan oleh SCCM (Strongly Connected, Closed Models)

dan

matriks kompartemental dari niodel SCCM disebut nzafriks SCCM.

Teorema 3 [Hearon, 19631

Misalkan A ~natriks SCCM. nlaka A menlpnnyai tepat satu nilai eigen no1 dan bagian real negatif untuk nilai eigen lainnya.

Bukti: L i a t Hearon (1963)

Di bawall ini diberikan contoh suatu digraf yang bersesuaian dengan mahiks SCCM

Contoh 3

Misalkan suatu inodel komparte~nental berdasarkan persaniaan diferensial

r = A x d e n e l

niaka digraf yang bersesuaian dengan inatriks A adalal~,

Ga~nbar 5. Digraf yang bersesuaian dengan inatriks SCCM

dengan polinom karakteristik f(A) = (-2-A)(-1-A)(-2-A)+2 - (-2-2)

= -( A ~ + ~ A ~ + ~ A )

= -4A+SA+7),

sehingga nilai eigen dari A adalah

In

Al=O , ,Izt,,= -2.5

*

i ( 3 ) 12.

Definisi 25 [Walter, 19841

Misalkan A adaiah mahiks SCCM

&,

As,. . .

A

adalah nilai eigen tak no1 dari A dan

i

adalah rata- ratanya, maka JIlrnlah Kuadraf Deviasi (JKD) dari nilai eigen tersebut didefinisikan oleh

Teorema 4 [Walter, 19841

MisalkanA adalal~ matriks SCCM ~naka

2 (trAl2

trA

--

r

JKD

< t r m T

--

(tr~)'

n-1 n - l

Bukti :

Misalkan A={av), adalah ~iiatriks SCCM. Dari Lema 3 clan Akibat 1 telall dibuktikan bahwa

=:aii =trA dan =A;=irA2,

i=l i=l i=l

sehingga

= ;A; -67-l)i2

i=2

=

:a;

-

z(i7-i),?

+G7-1)2

i=2

= :A; -2;2?ni +(1~-1),?

i=? i=2

= =(A; -2;iai +;i2) i=2

= =(A; - i ) 2 i=2

5

i / a j

-i12

i=2

(19)

dan i l ~ ~ / ~ < $ 5 l a ~ l ~ = t r i t i l ~ .

,=I ,.=I 2

i=l

iIa,

-21'

=

5bJ.

-fi)

+v,

,

Jika

1;

adalah sekawan d a i A, dan karena

i

i=2 j = 2

sehingga Teorema 4 dapat ditulis kembali dalain

real, lnaka _bentuk

=lai

-i12

=

=(ai -ix& -i)

i=2 i=2

PA)'

t e 2

L

=

ibi

-by-15

n

-

1 i=z

=

i n i &

- & i - a j i + i 2

i=2 _i _- ₎ ₂ ₊ ₁ _i 2 _<trmT--(h.A)Z

17-1

.

(10)

A n - i=2

=51ai12

-i?ai

-azai

+ ~ 7 - 1 1 2

i=2 i=2 i=2

I

Pada Teorema 5 di bawall ini diberikan

=ta12-i(ts+&

+(~~-l).i' pertidaksarnaan

dari

j u i l a l ~ kuadrat bagian

i=2 ,=2 imajiner nilai eigen A.

= A

1

- (

-

1

-

1 ) Teorerna 5 [Walter. 19851

i=2 _{Misalkan.4 adalah matriks SCCM}

dan

_v;_,i=2,._..,₁₇

=

i1,ail2

- 6 7 - l ) i 2 adalah bagian imajiner dari nilai eigen A, maka

i=2 ( t r ~ ) ~ n

(i)

-

tc4

<

El>,-

<

tid"i T

--

(hi)'

1 7 - 1 i=2 17-1

=5/,$12-

i=2 _{( i i}_I

'I

₂ _{< i k r ~ J A - t r ~ ~}

.

i=2 17-1 i=2 2

U Bulti :

(i) Dari persanaan (10) diperoleh

t r ~ ' =

tll;

-hi

-by

Misalkan nilai eigen dari matriks A real

dan

--

kompleks, yaitu n - 1 i=2

2?= -,q , j=2,

...,

nz

<

Elli

" 2

4=

-pj

+Iv,

j=111+l, ...p i=2

A,=

- ' L - I v , j=p+l, ..., 17

dengan

<

i J L i - p p + l ~ :

i=2 p,,,+1=pp+l ,... ,pp =/I" d m V,+I = V ~ + I < . . . , vP =vn

1

"

-

C - p .

=-i

T (tr~)"

S t r A --,

J 0

17-1 j = 2 n - 1

maka, (ii) Kurangkan tiap sisi pada persalnaan (10)

P dengan

i(~,~-,i)'=

g(-pj+bp+

2(-pj++it;+;)2

(20)

(21)

V.

CYCLE

[image:21.541.18.474.36.713.2]

v n 1'5

Gambar 6. Cycle dengan panjang n.

Misalkan .4={aij), adalal~ matriks SCCM

yang merepresentasikan suatu cycle dengan panjang n, Inaka secara umum lnatriks tersebut

berbentuk.

-

sehingga batas atas dan batas bawah dari

JKD

adalah

A =

Misalkan didefinisikan rata-nta koefisien aliian

- a , 0 0 ... a,,

a, -a2 0 ... 0

0 a 2 -a,

...

0

.

o

0 0 ... - a ,

-

Ekspresi

i

(a,

-

h)2 dapat dikatakan sebagai i=l

julnlali kuadrat deviasi dari koefisien aliran, yang bernilai lninilnnm jika semua a, bemilai sama (misalkan a).

Pada kasns semua ai bemilai salna yaitu a, nilai eigen A dapat dillitung secara eksplisit karena polinom karakteristihya adalah

f ( d ) = ( d + a ) " - a n ,

sellingga berdasarkan Lema 7, nilai eigennya adalal~

Zldk1,r

A, =-a+ae . k=0:1:2

,...

n - 1 , dengan ai

>

0, i=l,

...,

n dan a, adalah koefisien

aliran atau dalaln bentuk digraf sesuai dengan galnbar 6 di bawah ini

dan karena

1

"

ole11 h =

-

C

a , , maka maka

(22)

Selanjufnya akan dibahas hubungan antan bagian real dan imajiner nilai eigen matriks SCCM.

Definisi 26 pisenfeld, Beltz & Gmdy, 19841 Suatu matriks A, yang dikategorikan ma&iks SCCM dikatakan mempunyai nilai eigen utarna p, jika

(i) p adalah nilai eigen real dari A

(ii)p adalah nilai terbesar dari bagian real Nlai eigen A yang laimya.

Lema 15 [Kellog & Stephens, 19781

Misalkm KnXF adalab matriks nonnegatif dengh nilai eigen Perron i'

dan

D adalali digraf yang bersesuaian dengan K. Misalkan nr adalah panjang dari cycle terpanjang D. Jika mS2 , maka seluua nilai eigen K adalall real. Jika 17722, maka nilai eigen A=p+i vdari A memenuhi

72

p + / v I t a n - < A + . 111

ICr=

A*x

(A + q I ) ~ = a + ~ AX=@+

-

q)x Ax= px,

Inaka p =A+-q adatall nilai eigen utzna dari A. Misalkan n~ adalali panjang dari cycle terpanjang pada digraf matriks K. Karena A dan K mempunyai elemen selain diagonal yang identik, maka keduanya ~ne~npunyai digraf yang sana.

Menurut Lema 15 , jika 17152. maka selnua nilai eigen A adalah real. Jika rn >2, maka nilai eigen A= (-p+q)+ i v dari K, memenuhi

KarenaA adalah SCCM, Inaka PO, sehingga

7c

Ivl tan-

s

p

Ill

U Bukti: L i a t Kellog & Stephens (1978).

Berdasarkan lasil Kellog dan Stephens &pat _{~ i ~ ~ l k a n}_{A=-p+ivadal& bilangan kompleks yang} diperoleh Iiubungan antam bagian real

dan

imajiner _{memenuhi persamaan (13), maka ada suatu matriks} nilai eigen mah'iks SCCM, sebagaimana Yang _{yang merepresentasikan cycle}_{dengan panjang}_m, terdapat pada teorema berikut ini. _{dimana Aadalah salah satu Nlai eigennya.}

Teorema 7 [Eisenfeld, Beltz & G m d y , 19841 Misalkan A adalah matriks SCCM dan D adalah digraf yang bersesuaian dengan A. Misalkan m adalal~ panjang dari cycle terpanjang D. Jika m<2,

maka serum nilai eigen A adalah real. Jiia m>2, xnaka ~ l a i eigen A=-p+ivdariA memenuhi

IT

Ivl tan-

r

p nr

Buliti :

Misalkan A={aij},,, adalah matriks SCCM, untuk setiap konstanta q yang memenuhi

q 2 maslail

I

,

15iin

maka K=A +qI adalah matriks nomegatif.

Misalkan x adalah vektor eigen yang bersesuaian dengan A, nnlaka

A F ~

Bukti :

Misalkan A adalah matriks SCCM dengan panjang cycle m

dan

koefisien d i m ,

dengan O < a 51 dan P O , maka polin0111 karakteristik dari A adalah

. . - a(a+lXa+2)...(a+nr-l)

p"'

.

111!

Untuk PO, ~naka koefisien aliran lnenjadi

yang berakibat digraf yang bersesuai dengan A bukan cycle

dan

sehingga A adalah nilai eigen A jika dan hanya jika _yang_{berakibat matriks .4 lllempunyai nilai eigen} A+q adalah nilai eigen dari K. _{real berbeda.}

Misalkan A+ adalah nilai eigeii Perron dari

K

_{Untuk a=l, selnua koefisien alinn sanla}

(23)

f,.p(n) =

-P",

yang nlenurut Lenla 7 nilai eigennya adalah

, 2 d / m

A = - P + P e , ,

:

k=0,1. ... , m-1. Untuk O<a<l, mla elgen tak no1 Al(a

.p

)

dengan modulus terkecil dan bagian imajiner positif, bervariasi dari

A, (1,

p)=-p

+,Benn""

ke

n1

( ~ , , ~ ) = - p n .

Lintasan yang dilalui oleh &(a

,P

) adalah k w a kontinu yang dil~ubungkan oleh titik-titik tersebut. Karena

p

hanya faktor skala, kurva Al(a

, p

) adalah tiruan skala dari kurva lainnya untuk nilai ,B yang berbeda. Karena 0C.D <m , kurva 21 ( a

, p

) berada pada daeral~ antara sinar z=arg/tl(l,l) dan axis real negatif. Untuk melilmt hi, kunra Rl(a.l) beraral~ dari -l+cos(2n:/m)+ i sin(2nIi11) ke -112.

Tiap sinar

'

dari asal z=O untuk argAl(l,l)=n12+rcln~ $ 0 5 n berpotongan dengan kuna Al(a,l) sedikitnya sekali, sellingga tiap titik pada suatu sinar berpotongan sedikitnya sekali dengan M a 21 ( a , p ).

~ ~

.p

+ p e"" t ~

'

" ~= -,u+iv i inemnenuhi persamaan (13). yaitu dari penurunan di bawah ini.

-p

+pe'2"'rn= -,u+iv

-p

+pcos2n /ni+ipsin 2n: /ni = -,u+iv, yang berarti

-p+pco~Zn:/m=-p

dan

psinZn/rn=v.

Untuk - p +pcos2n /m = -,u

.

maka P

P = ~ - c o s ~ n / r n :

substitusikan ke persatnaan psin 2n/n1 = v , diperoleli

iT

vtan-=,u.

m

selingga s e m b m g nilai eigen dengan bagian iinajiner positif memenulu persamaan (13) terletak pada daerah ini dan merupakan nilai eigen dari suatu cycle dengan panjang In. 0

VI. KO&@~INASI

CYCLE

6.1 IIustrasi Kombinasi Cycle

Bab ini akan membahas tentang nilai eigen koinpleks dari inatriks SCCM A yang ~nerepreseritasikan gabungan dari dua atau lebili q x l e .

Contoh 5

Misalkan A adalah mahiks SCCM yang terdiri dari dua cycle, yang ~nasing-masing panjangnya tiga, yaitu

f , ( ~ ) = - & I 2 +(CI + c>+ c3) A+ CI c2+ cz c3+ c3 C I ) Perbatikan beberapa kasus di bawah ini. (i) Jika ai= ci = l , i=1,2,3, maka

A(,?) =&A) =

-xn2

+3 n+3),

sehingga

A =

yang berarti junlah kuadrat bagian imajiner dari tiap cycle adalali sama, yaitu

- .

-al 0 0 3 0 0

a , - a 2 0 0 0

0 n2 - a j - c 3 0 cI

0 0 c3 - c 2 0

0 0 0 c2 - C 1

-

Polinoin karakteristik untuk mahiks.4 adalah

~ ( 2 ) = ( & I ) (-aa2+3a+3))

+

( a + i ) (131) (-a(n2+3 n+3))+ a(n+i) ( h i ) ( n + i ) ('+I)

=

n

(n+i)' { ( n + i ) 2

-

2(a2+3A+3))

=

n

(A+ i)2

(-n2

-

4 n

-

51, sellingga

Al=O,

A=&=

-1, A , , = - 2 i i , dengan ai > 0, i=1,2,3 adalal~ koefisien aliran pada

cycle pertamna dan ci

>

0, i=1,2,3 adalal~ koefisien aliran pada cycle kedua .

Polinom karakteristik dari mnatriks A adalah . ~ n ) = ( n + a , ) ( n + a , m ~ ) + (n+c1)(n+c2mn)

+ x a + a l ) (n+a2) (n+cl) (n+cz),

dengan,fi(L) d m &(,I) adalali polinoin karakleristik dari tiap cvcle, dimana

.I;(A)=-A(.1' +(al + n2+ a,) A+ a1 a2+ a2 a,-!- a? n l )

(24)

(ii) Jika a, = cl =l, a2 = c2 =2, a; = c; =8,maka

J(A) =

- 4 A 2

+11d+26).

sehingga

yang berarti jumlah kuadrat bagian ilnajiner d a i tiap cycle adalall nol.

Polinom kamkteristik untuk mattiks A adalah f(A) = (R+1) (A+2) (-A(A2 + l lL+26))

+

@+I)

(A+2) (-&,I2 +11A+26))+ ?dA+l) (A+2) (a+ 1) (A+2)

= L(A+l)(A+g{(A+l) (d+2)- 2(?,'+11d+26)}

= 1 (L+l) (A+2)

(-a2-

19'- 50), sehingga

-19

Ji-81

al=o, &=-I,

A=

-2

a,,,

=-+-- ._I 3

L L

yang berarti jumlah kuadrat bagian irnajiner dari gabungan tiap cycle adalah nol.

0

Pada pembahasan ini dias~unsikan bahwa digraf yang bersesuaian dengan matriks .4 adalah clustered rosette.

Suatu digraf disebut rosette jika ada suatu verteks yang terletak pada semua cycle, dimana cycle satu dengan lainnya terpisal~.

Suatu digraf D dari sekumpulan rosette yang strongly connected dan tiap arc terletak pada tepat satu cycle disebut clustered rosette.

Misalkan A adalah matriks SCCM dengan digrafkya adalah clustered rosette. Digraf D

dari

matriks A

akan

terurai menjadi digraf-digraf yang memuat tepat satu cycle tetapi dengan llimpunan verteks yang sama dengan digaf D. Notasikan digraf ke-i dengan D; dan panjang cycle dari tiap

D,

oleh Ini , maka

D=DluD2u.. . u D,

sela~na D dan D; keduanya nlen~pnnj~ai himpunan verteks yang sarna dan tiap arc dari D terlnuat pada satu Di.

Matriks A;

.

i=l, ..., n bersesuaian dengan koefisien alimn tak no1 pada posisi yang bersesuaian dengan sisi bermdl pada Dj . sehingga A juga terurai menjadi

A=Al+A2+ ... +.4,.

Contoh 6

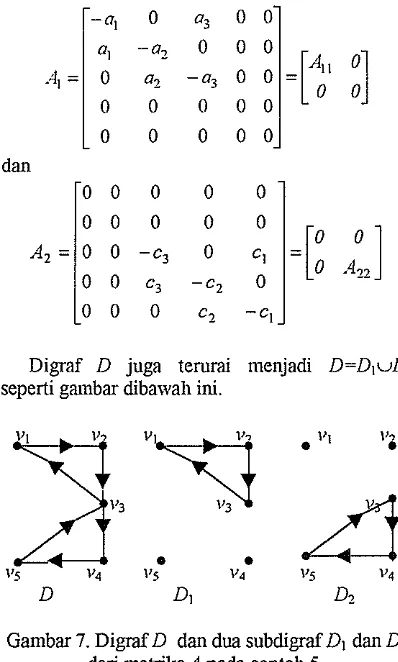
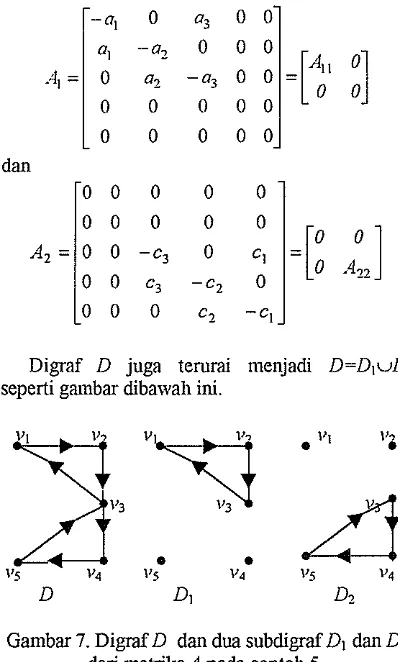
Misalkan diberikan nlattiks SCCM A , seperti pada contoh 5, maka A t e m i n~enjadi A=AI +A2 ,

dengan

1 0

0 0 0 0 1 dan

y o 0 0 0 0 1

[image:24.541.259.458.29.360.2]

Digraf D juga terurai ~nenjadi D=DluD2 seperti garnbar dibawah ini.

Gambar 7. Digraf D dan dua subdigraf Dl dan D2 dari matriksA pada contoh 5.

6.2 Nilai Eigen dari Clustered Rosette

Sekarang

akan

ditwunkan l~ubungan antara nilai eigen matriks A dan matriks Ai , i=1,2 ,.... p. yang terdapat pada teorema berikut ini.

Misalkan A adalah lnatriks SCCM dari suatu

P

clustered rosette D, dengan uraian A =

C

A, , ,=I

P

D =

U

D, . Misalkan

R,

,,,..

An.,

adalah nilai eigen ;=I

tak no1 dari A. q),...;~f;-, adalah nilai eigen tak

no1 dari Ai dan

i :

i(')

adalah rata-ratanya, maka

,,-I p "I, -1

(i)

C

a,

=

C

c

k=l ,=I j=,

(25)

i r j

JKDt =

C

:I

[

trAiA,?

:!

--

(:

;=I

JKDs

= C

[

frAz

:I

--

?!

i=l

Bukti : _{Perhatikan bal~wa}

(i) Dari k e l i n e m teras, diperoleh

n-l i P p ">,-I

X I ,

=frA=CfrAj

= C C

A ? ) . 114) i=1 k=1 ;=I ;=I j=l

(ii) Dapat diamati ballwa jumlah nilai eigen tak no1 (16)

adalah sama pada kedua sisi persamaan di atas, _lnenyatakan

judah kuadrat deviasi dari nilai eigen dengan menghitung jumlah verteks yang terpisah _tiap

cycle,

pada D = ~ J D ;

,

yaitu P P

?=I JKDh = c!~A~A;

;=I j=1 (17)

P i t j

n - l = ~ ( t ? l i - l ) ,

;=I menyatakan hnbungan beberapa cycle. yaitu

maka pers-an (14) &pat diMis kembali jumlah perkalian semua pasangan dari koefisien

meniadi aliran yang meninggalkan verteks yang sama.

,z-I P "$,-I

~ 2 ,

= C

c

A?) Bentuk berikut

I.=] i=l j = l

(n

-

1) n-1 P - 1

(s

(mi

-

1)

-Cn,

= C

4

- ;=I (n -1) 3 (18)

( 7 - 1) k 1 ;=I j=l (,?I; - 1)

.

P nit -1 i(j) . dapat disederlmakan dengan lnelnisalkan

n = ~ -

mi -1 P

n-1 a . =- , sehingga

Ca,

= 1 dan persalnaan

n - 1 i=l

Selanjutnya dapat diperoleh bal~wa (18) menjadi

P P P P P

.uT

=CA,CA;=CA,A:+CCA,A;,

i=1 ,=I i=l ;=I j = l

is j

,'I

sehingga

,,-I

clnl.

-i12

= ? l ~ , 1 ~ - ~ ; - i ) i ~ =

(n-a[-&i[i(;)]'

i=l

- [ b a j ~ c ) ' ]

k=l k=I

2

(26)

Jadi d a i p e r s m a n (15)-(19) diperoleh JKD

r

JKDt +JKDa+JKDh.

Selanjutnya karena

dan berdasarkan Teorema 4,

=JKDs + M a +JKDh

.

selungga

K D s 5 JKD - JKDa

-

K D h

<

JKDt. ₍₂₀₎ 0

Dengan

cam

yang sama, ~naka dapat diperoleh

(21) Kelnudian dengan ~nengurangi kedua sisi pada persa~naan (20) dengall persanlaan (2 1)diperoleh

sehingga dalam bentuk kompleks diperoleh

Misalkan bagian imajiner nilai eigen tiap cycle dinotasikan oleh

v , j = ~ , , . . . , I .i=1.2 ,..., p , maka persamaan pada Teorema 5 berlaku juga untuk bagian imajiner nilai eigen tiap cycle, yaitu

Misalkan suatu cycle dengan panjang 11

~ne~npunyai koefisien aliran yang salna yaitu a. ~naka

t r ~ y 2 n2a2 2 i2 -2n

l r & ~

-L

= 2na -- = a

-

JKD

.

11-1 11-1 11-1

Dengan cam p e n m a n yang sruna seperti pada Teorema 5(ii), maka diperoleh

n-1

2 x 4 = I ~ A A ~ -PA',

k=I

selungga berlaku juga untuk bagian ilnajiner nilai eigen tiap cycle dengan panjang tiap cycle adalah mi , i=1,2, ..., p , yaitu

dimana

2

trili.4T -IYA: = 2 ~ 1 ~ n ~ -nt,n,? = m,o'

Teorema 10 [Walter. 19851

Misalkan A adalah ~nat~iks SCCM yang bersesuaian dengan clustered rosette dan Ai adalah lnatriks yang bersesuaian dengan cycle ke-i, i=1,2, ...,p, rnaka bagian ilnajiner vi dari nilai eigen A memenuhi

(27)

,?-I P ",,-I 1 P 1 p m , - l bagian real dan iniajiner nilai eigen

dari

cycle ke-i

~ v i 5

c c

(@)Z

=-Cmia;"

<-c

c

(,$))Z

*=I ;=I j = l 2 i,l 2 ; s ,=I engan panjang lebili besar 2, maka dari fakta

balwa dengan 17ii adalah panjang, a; koefisien aliran , _"-1

v?)dan

,up)

bagian real dan imajiner nilai eigen, u;,(c -v;)= i a j = t r ~ '

*=I k=l

dari qxle ke-i dengan r7zi > 2.

dan

Bulcti:

(i) Berdasarkan persamaan (22), maka

sehingga

(ii) Jika tiap cycle ke-i, i=l,

...,

p menlpunyai koefisien alinn yang salna dan misalkan nt; adalal)

li)

panjangnya, a; koefisien a l i v(j)dan pi

n-l

CV;

<@A2,

k=I

sehingga

n-l p P

2 ~ v i

r

C(wAi4~

-PA;)= x m p ; = 2C

C

(v:)

k=I i=I i=l i=l pms-l ,.=I

(7

P

21.; =

$y[&)Y

-(,.fl]

i=l i=l ;=I

p 4-1 P m,-t

r

2 1

C

Lp)p

r

1

&))Z.

;=I (=I i=l ;=I

Jadi

"-1 p "5-1 P 1 P mt-l

~ 1 , ; 5

1

(+))?

= LCmia:

r

-C

c

b!j)Y.

r=l i=l ;=I 2 i=I 2 ;=I ;=I

Suatu model kompartemental &pat ditulis panjang cycle terpanjang dari digraf. Jika dalain bentuk persamaan diferensial

(*A)2 < 0

,

maka ada bagian imajiner nilai

t7A-

--

x = A x + b 17-1

dengan A adalah ~natriks kompartemental.

Diasu~nsikan bahwa ~natriks A bersifat SCCM (Strorzgly Connected Closed Models). Jika A ~nerepresentasikan digmf dengan cycle terpanjang kurang dari atau sama dengan dua, maka semua nilai eigen A bemilai real. Jika cycle terpanjang lebih dari dua. inaka a& nilai eigen A=-p+iv dari

eigen A yang tak nol.

Pada niatriks A yang bersesuaian dengan ko~ubinasi cvcle, jika tiap cycle mempunyai .koefisien aliran yang salna, maka jumlah kuadrat nilai eigen yang imajiner dari matriks kombinasi cycle akan kurang dari atau sama dengan juinlali kuadrat iiilai eigen yang i~najiner dari matriks tiap cvcle.

iT

A yang memenuhi lvl tan- S p , di~nana m adalall

(28)

DAPTAR PUSTAKA

Anderson, D. H. 1983. Compartmei~tnl Modeling and Tracer Kinetics. Springer-Verlag, Berlin.

Anton, H. 1995. Aljabar Linear Elementer. Ed. ke- 5. Terjemahan PaoN Silaban & I Nyoman Susila Erlangga, Jakarta.

Eisenfeld, J., W. F. Belb & S. M. Grundy. 1984. The Role of Nomeal Eigenvalues in Tbe Identification of Cycle in a Colnparhnental System. A4ntheinatical Biosciences. 71:41-55.

Hall, H.S. & S.R Knight. 1964. Higher Algebra. Maclllillan & Co.. Ltd. London.

Hearon, J.2. 1963. Tl~eorenls on Lmear System.

Annals New York Academy of Sciences. 108:36-

68.

Kellogg,

R

B., & A. B. Stephens. 1978. Conlplex Eigenvalues of a Non-Negative Matrix with a Specified Graph. Linear Algebra and. Its Applications. 20:179-187.

Noble, B. 1969. Applied Linear Algebra. Prentice Hall, Inc., New Jersey.

Oltsaviri, Y. 1997. Peran Sifat-sifat Matriks Tak Negatif dalam Model Dinamik Leontief. Skripsi. Jurusan Matematika FMlPA IPB, Bogor (tidak dipublikasikan).

Patiouras, J. D ,1987. Peubah Kompleks untuk Ilr~izi~vnn h 7 Insinyur. Terjemalm Wibisono

Gunawan. Erlangga, Jakarta.

Thulasirarnan, K. & M. M. S. Swamy. 1992. Graphs: T h e o y and -4 lgoritl~ins. Jolm Wiley &

Sons, Inc, New York.

Walter G. G. 1984. Eigenvalues and Structure of Conlpartmental Models. Motl?ematicnl Bioscier~ces. 71: 181-199.

Waltel; G. G. 1985. On Complex Eigenvalues of Comparhnental Models. Mathematical Biosciences. 75:143-157.

(29)

SIFAT NILAI EIGEN KOMPLEKS

MATRIKS SCCM (Strongly Coizizected Closed Models)

KUSNANDAR

JURUSAN MATEMATIKA

BOGOR

(30)

(31)

I.

PENDAHULUAN

1.2 Tujuan

1.3 Metode

1.4 Sistematika

II.

LANDASAN. TEORI

d e t ~

= i a , , ~ , ,

~. . . ,. .,. . . , ,

- .

Bilangan

B,=(-l)'iJhJ/,

(32)

I.

PENDAHULUAN

1.2 Tujuan

1.3 Metode

1.4 Sistematika

II.

LANDASAN. TEORI

d e t ~

= i a , , ~ , ,

~. . . ,. .,. . . , ,

- .

Bilangan

B,=(-l)'iJhJ/,

(33)

pers;unaanl(A)=O disebut persumuun kurakterisfik dari A. Nilai eigen dari A adalah skalar A> dimana A x = k atau (A - W ) x =O mnenipunyai solusi tak nol.

Solusi tak no1 x disebut vektor eigerz dari A.

Jika matriks A={aij},, maka trunspose dari A adalah ~ ' = { b ~ } " ~ , dengan bo= a,;.

Lema 1

Nilai eigen lnatriksA d a n ~ ' adalah sama.

Bulti :

Misalkan A adalah ~ l a i eigen dari matriks A, maka polinom karakteristik dari A adalah

fA(A)=IA

-

21. Karena

(A

-

ailT