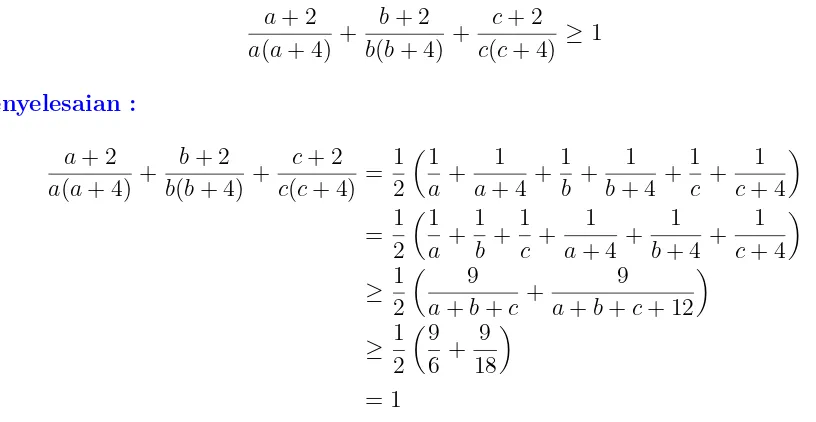Pembahasan OSN Matematika SMA Tahun 2013

Pembahasan OSN Matematika SMA Tahun 2013

Seleksi Tingkat Provinsi

Tutur Widodo

Bagian Pertama : Soal Isian Singkat

1. Diberikan tiga lingkaran dengan radiusr = 2, yang saling bersinggungan. Total luas dari ketiga lingkaran tersebut berikut daerah yang dibatasinya sama dengan ...

Penyelesaian :

A B

C

ABC adalah segitiga samasisi dengan panjang sisi 2r = 4. Sehingga Luas _△ABC = 1

2 ×4

2 _{×sin 60}◦ _{= 4}√_{3. Sedangkan luas ketiga daerah lingkaran diluar segitiga ABC}

yaitu

900◦

360◦ ×π×2

2 _{= 10π}

Jadi, luas daerah yang diminta soal adalah 4√3 + 10π satuan luas.

2. 2013 lampu dikontrol oleh 2013 tombol saklar yang diberi nomor 1,2,3,_{· · ·} ,2013. Menekan tombolsaklar satu kali akan merubah nyala lampu (hidup atau mati). Pada awalnya se-mua lampu dalam keadaan mati. Pada hari pertama, sese-mua tombol saklar ditekan satu kali. Pada hari kedua, semua tombol saklar bernomor 2 atau kelipatan 2 ditekan sekali. Dengan melakukan hal yang sama pada hari ke-n, semua tombol saklar lampu bernomor n atau kelipatan n ditekan sekali. Demikian seterusnya. Berapa banyak lampu dalam kondisi hidup setelah operasi pada hari ke 2013 dilakukan ?

Perhatikan bahwa jika saklar lampu ditekan sebanyak k kali dengan k bilangan ganjil maka lampu tersebut akan menyala. Itu artinya cukup dicari bilangan yang memiliki banyak faktor ganjil. Dan tentu saja bilangan yang memiliki sifat demikian adalah bi-langan kuadrat sempurna. Padhal bibi-langan kuadrat sempurna kurang dari 2013 ada sebanyak 44. Oleh karena itu, banyak lampu dalam kondisi hidup setelah operasi pada hari ke 2013 adalah 44 lampu.

3. Diberikan fungsi real f dengan f(x) = cx

2x₋3, x 6=

Dari keterangan bahwa f

f(x)

= x dapat disimpulkan bahwa f adalah invers dari

dirinya sendiri. Padahal f−1_{(x) =} 3x

2x₋c. Oleh karena itu, karena f(x) = f

−1_(x)

diperoleh c= 3. Sehingga diperoleh f(x) = 3x

2x₋3 dan karenanya f(2013) = 6039 4023. 4. Pasangan bilangan bulat positif (x, y) yang memenuhi

xy2 x+y

bilangan prima adalah ...

Penyelesaian :

p+1 prima, ada dua kasus yang

mungkin

Jadi, ada dua pasangan bilangan (x, y) yang memenuhi yaitu (2,2) dan (6,2).

5. Jika _|x_|+x+y= 10 dan x+_|y_{| −}y= 12, maka nilai dari x+y adalah ...

Penyelesaian :

Bagi menjadi 4 kasus,

b. x _≥ 0 dan y _≥ 0, diperoleh x+_|y_{| −}y = 12 _⇔ x = 12. Tetapi _|x_|+x+y = 10, tidak memenuhi.

c. x < 0 dan y _≥ 0, diperoleh _|x_|+x+y = 10 _⇔ y = 10 sehingga x+_|y_{| −}y = 12 _⇔ x= 12, tidak memenuhi karena x <0.

d. x _≥ 0 dan y < 0, diperoleh _|x_|+x+y = 10 _⇔ 2x+y = 10 dan x+_|y_{| −}y = 12 _⇔ x₋2y= 12. Dengan eliminasi sederhana kita peroleh x= 32

5 dan y=− 14

5 sehingga x+y= 18

5 .

Jadi, x+y= 18 5 .

6. Banyaknya bilangan bulat positif n yang memenuhi

n2₋660

merupakan bilangan kuadrat sempurna adalah ...

Penyelesaian :

Misalkan n2 _{−660 = k}2 _{untuk suatu bilangan bulat positif k. Selanjutnya kita peroleh}

n2_−k2 _{= 660 ⇔ (n+k)(n−k) = 2}2_{·3·5·11. Karena (n+k)>(n−k) dan keduanya}

memiliki paritas yang sama, akibatnya ada empat kasus yang mungkin,

• n+k= 330 dan n₋k= 2 sehingga diperoleh n= 166 dan k = 164.

• n+k= 110 dan n₋k= 6 sehingga diperoleh n= 58 dan k = 52.

• n+k= 66 dan n₋k = 10 sehingga diperoleh n= 38 dan k = 28.

• n+k= 30 dan n₋k = 22 sehingga diperoleh n= 26 dan k = 4.

Jadi, ada 4 bilangan aslin yang memenuhi.

7. Ada berapa barisan sembilan sukua₁, a₂, a₃,_{· · ·} , a₉, yang masing - masing sukunya adalah 0,1,2,3,_{· · ·},8 atau 9 dan memuat tepat satu urutanai, aj dimanaai genap danaj ganjil?

Penyelesaian :

Misalkan bola biru mewakili kemungkinan tempat untuk bilangan genap dan bola merah mewakili kemungkinan tempat untuk bilangan ganjil. Dua bola biru dan merah yang berada di dalam kotak merupakan dua bilangan dengan urutan genap ganjil seperti yang diharapkan pada soal.

• Terdapat 5 bilangan ganjil dan 4 bilangan genap dalam barisan.

Untuk memilih 4 bilangan genap dari 5 bilangan genap yang tersedia ada 5 cara. Perhatikan juga bahwa cara memilih dua bilangan yang diletakkan didalam kotak ada 4_×5 = 20 cara. Sedangkan untuk menempatkan 4 bilangan ganjil sisanya ada 4! + 3!1! + 2!2! + 1!3! + 4! = 64 cara. Dan untuk menempatkan 3 bilangan genap sisanya ada 3! + 2!1! + 1!2! + 3! = 16 cara. Jadi barisan berbeda yang dapat dibentuk pada kasus ini adalah

5_×20_×64_×16 = 102400

• Terdapat 4 bilangan ganjil dan 5 bilangan genap dalam barisan.

Untuk kasus ini sama persis dengan kasus pertama hanya mengganti jumlah genap dan ganjilnya saja. Jadi untuk kasus ini juga diperoleh 102400 barisan.

Jadi, total ada 204800 barisan sembilan digit yang bisa dibentuk.

8. Bilangan aslin dikatakan cantik jika n terdiri dari 3 digit berbeda atau lebih dan digit-digit penyusunnya tersebut membentuk barisan aritmetika atau barisan geometri. Se-bagai contoh 123 adalah bilangan cantik karena 1, 2, 3 membentuk barisan aritmetika. Banyak bilangancantik adalah ...

Penyelesaian :

Kemungkinan barisan geometri yang bisa disusun yaitu

a. 1,2,4,8.

Banyak bilangan cantik yang dapat disusun dari barisan ini adalah 3_×2 = 6.

b. 1,3,9.

Banyak bilangan cantik yang dapat disusun dari barisan ini adalah 1_×2 = 2.

Kemungkinan barisan aritmetika yang bisa disusun yaitu

a. 0,1,2,3,4,5,6,7,8,9

Banyak bilangan cantik yang dapat disusun dari barisan ini adalah 7 + 6 + 5 + 4 + 3 + 2 + 1 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 64.

b. 0,2,4,6,8

Banyak bilangancantik yang dapat disusun dari barisan ini adalah 2+1+3+2+1 = 9.

c. 1,3,5,7,9

Banyak bilangancantik yang dapat disusun dari barisan ini adalah 3+2+1+3+2+1 = 12.

d. 0,3,6,9

Banyak bilangan cantik yang dapat disusun dari barisan ini adalah 1 + 2 + 1 = 4.

e. 1,4,7

f. 2,5,8

Banyak bilangan cantik yang dapat disusun dari barisan ini adalah 2_×2 = 1.

g. 0,4,8

Banyak bilangan cantik yang dapat disusun dari barisan ini adalah 1.

h. 1,5,9

Banyak bilangan cantik yang dapat disusun dari barisan ini adalah 2_×1 = 2.

Jadi, total bilangancantik yang dapat disusun adalah

6 + 2 + 64 + 9 + 12 + 4 + 2 + 2 + 1 + 2 = 104

9. Misalkan M adalah titik tengah sisi BC pada _△ABC dan ∠CAB = 45◦_{,∠ABC = 30}◦

maka tan∠AM C adalah ...

Penyelesaian :

A 45◦

C

105◦

B M

30◦

Berdasarkan aturan sinus pada _△ABC diperoleh

AC sinB =

BC sinA ⇔

AC sin 30◦ =

BC sin 45◦

⇔ AC1 2

= ₁BC

2 √

2

⇔ AC2 = 1 2BC

2

⇔ AC_BC =

1 2BC

AC

⇔ AC_BC = M C AC

Jadi, _△ABC sebangun dengan _△AM C sehingga ∠AM C = ∠CAB = 45◦_{. Akibatnya}

tan∠AM C = 1.

10. Diberikan bilangan prima p > 2013. Misalkan a dan b adalah bilangan - bilangan asli sehingga a+b habis dibagi p tetapi tidak habis dibagi p2_{. Jika diketahui a}2013 _+b2013

pn _{adalah ...}

Penyelesaian :

Karenaa+b _≡0 mod p=_⇒a_{≡ −}b modp. Selain itu, kita juga punya

a2013+b2013 = (a+b)a2012₋a2011b+a2010b2_{− · · ·}+a2b2010₋ab2011+b2012

karena p membagi (a+b) tetapi p2 tidak membagi (a+b) maka pmembagi

(a2012_−a2011_b+a2010_b2_{− · · ·+a}2_b2010_−ab2011 _+b2012_{). Dengan demikian diperoleh}

a2012₋a2011b+a2010b2_{− · · ·}+a2b2010₋ab2011+b2012 _≡0 mod p

b2012+b2012+b2012+_{· · ·}+b2012 +b2012+b2012 _≡0 mod p

2013b2013 _≡0 mod p

b_≡0 mod p

Jadi, p_|b =_⇒ p_|a. Sehingga p2013 (

a2013+b2013). Sehingga diperoleh pn (

a2013+b2013) untuk setiap bilangan asli n_≤2013.

Jadi, banyak bilangan asli n _≤2013 sehingga a2013_+b2013 _{habis dibagi p}n _{adalah 2013.}

11. Ada enam anak TK masing-masing membawa suatu makanan. Mereka akan mengadakan kado silang, yaitu makanannya dikumpulkan dan kemudian dibagi lagi sehingga masing-masing anak menerima makanan yang bukan makanan yang dibawa semula. Banyaknya cara untuk melakukan hal tersebut adalah ...

Penyelesaian :

Jika hanya ada satu anak jelas tidak ada proses pertukaran kado. Jika terdapat dua anak maka banyak cara pertukaran kado ada tepat 1 cara. Jika anak ketiga masuk dalam kelompok maka dia punya kesempatan untuk bertukar kado dengan 2 orang yang telah ada dalam kelompok sebelumnya. Jadi, jika terdapat tiga anak maka banyak cara pertukaran kado ada 2_×1 = 2 cara. Seterusnya jika anak keempat masuk maka anak keempat memiliki kesempatan untuk bertukar kado dengan 3 teman yang lain, anak ke-lima memiliki 4 kesempatan dan anak keenam memiliki 5 kesempatan. Jadi jika terdapat enam anak maka banyak cara pertukaran kado ada 5_×4_×3_×2_×1 = 120 cara.

Lebih umum, jika terdapat nanak maka banyak cara pertukaran kado ada (n₋1)! cara.

12. Grafik parabolay=x2₋adan x=y2₋bdengana >0 danb > 0 berpotongan di empat titik (x1, y1),(x2, y2),(x3, y3) dan (x4, y4). Nilai (x1+x2)(x1+x3)(x1+x4) adalah ...

Penyelesaian :

Dari y=x2₋a=_⇒y2 =x4₋2ax2_+a2 _{sehingga x=y}2_−b=⇒x=x4_−2ax2_+a2_−b

yang equivalen dengan persamaan derajat empat x4 ₋2ax2 _−x+a2 _{−b = 0. Karena}

-akar darix4₋2ax2_−x+a2_{−b= 0. Berdasarkan teorema Vieta untuk polinom derajat}

empat diperoleh

x1+x2+x3+x4 = 0

x₁x₂x₃ +x₁x₂x₄+x₁x₃x₄+x₂x₃x₄ = 1

Oleh karena itu diperoleh,

(x₁+x₂)(x₁+x₃)(x₁+x₄) = x3₁+x2₁x₂+x2₁x₃+x2₁x₄+x₁x₂x₃+x₁x₂x₄+x₁x₃x₄+x₂x₃x₄

=x2₁(x1+x2 +x3+x4) + 1

=x2_1·0 + 1

= 1

13. Sebuah dadu dilempar 2 (dua) kali. Misalkana dan b berturut-turut adalah angka yang muncul pada pelemparan pertama dan kedua. Besarnya peluang terdapat bilangan real x, y, dan z yang memenuhi persamaan

x+y+x=a dan x2+y2+z2 =b

sebesar ...

Penyelesaian :

x+y+x=a=_⇒x2+y2+z2+ 2(xy+yz+zx) =a2 =_⇒b+ 2(xy+yz+zx) = a2

Darirearrangement equality kita tahu bahwax2_+y2_+z2 _{≥xy+yz+zx. Dengan demikian}

a2 =b+ 2(xy+yz +zx)_≤b+ 2(x2 +y2 +z2) = 3b

Sehingga pasangan bilangan (a, b) yang mungkin yaitu (1,1),(1,2),(2,2),(1,3),(2,3),(3,3), (1,4),(2,4),(3,4),(1,5),(2,5),(3,5),(1,6),(2,6),(3,6),(4,6) ada 16 kemungkinan. Jadi, peluangnya adalah 16

36 = 4 9.

14. Misalkan ∆1,∆2,∆3, adalah barisan segitiga sama sisi dengan panjang sisi ∆1 adalah 1.

Untuk n _≥ 1, segitiga ∆n+1 didefinisikan dengan cara sebagai berikut: pertama

didefin-isikan Pn sebagai persegi yang titik-titik sudutnya terletak pada sisi-sisi ∆n, selanjutnya didefinisikan L_n sebagai lingkaran terbesar di dalam P_n , kemudian didefinisikan ∆n+1,

sebagai segitiga sama sisi yang titik-titik sudutnya terletak pada keliling lingkaran. Pan-jang sisi dari ∆2013 adalah ...

Penyelesaian :

Selan-jutnya mari kita lihat ∆n dan mencari hubungannya dengan ∆n+1. Untuk memudahkan

misalkan ∆n diwakili oleh _△ABC dan ∆n+1 diwakili oleh △P QR (seperti gambar di

bawah ini) adalah s dan jari-jari lingkaran r.

Perhatikan _△BF G adalah segitiga siku-siku dengan ∠BF G = 90◦ _{dan ∠F BG = 60}◦_.

Dari sini dapat dilihat bahwa ukuran sisi - sisi segitiga ∆n membentuk barisan geometri

Jadi, panjang sisi dari ∆2013 adalah

6₋3√3 2

!2012 .

15. Suatu barisanx1, x2, x3,· · · , xn,· · · didefinisikan denganx1 = 2, dan

x_n+1 =

1 + 1 n

x_n+ 2 n

untuk setiap bilangan asli n. Nilai x₂₀₁₃ adalah ...

Penyelesaian :

Cek untuk beberapa nilainmaka akan diperoleh bahwa barisan pada soal adalah barisan aritmetika yang berbentuk : 2,6,10,_{· · ·}. Sehingga, xn = 4n−2 dan karenanya x2013 =

8050.

Bukti formal untuk soal ini dapat menggunakan induksi yaitu akan dibuktikan bahwa xn= 4n−2.

• Untuk n= 1 jelas x1 = 4×1−2 = 2 dan untuk n= 2 kita punya

x₂ = 4_×2₋2 = 6 =

1 + 1 1

2 + 2

1

• Untuk n=k _≥2 jika xk = 4k−2 maka

xk+1 =

1 + 1

k

xk+ 2 k

= k+ 1 k

!

(4k₋2) + 2 k

= 1 k

4k2+ 2k₋2 + 2

= 4k+ 2

= 4(k+ 1)₋2

Secara induksi terbukti bahwa xn= 4n−1.

16. Diberikan bujursangkar dengan panjang sisi sama dengan 2√3. Didalam bujursangkar tersebut terdapat dua segitiga sama sisi dengan alas merupakan sisi-sisi bujursangkar yang berhadapan. Perpotongan kedua segitiga sama sisi membentuk rhombus. Luas rhombus sama dengan ...

A B C D

E F

S Q

R

P Y

X

△BEC adalah segitiga samasisi dengan panjang sisi 2√3 maka EQ = F S = 3. Selain itu perlu diperhatikan bahwa

SQ=EQ+F S₋EF _⇔ 2√3 = 3 + 3₋EF _⇔ EF = 6₋2√3

Di sisi lain _△BP X adalah segitiga siku-siku dengan ∠P BX = 30◦_{. Karena BP =} √₃

maka P X = 1. Perlu diingat juga bahwaP X =Y R, jadi kita peroleh

P R=P X+XY +Y R _⇔ 2√3 = 1 +XY + 1 _⇔ XY = 2√3₋2

Luas rhombus EXF Y yaitu 1_{2 ×}EF _×XY = 1₂(6₋2√3)(2√3₋2) = 8√3₋12.

17. Bilangan bulat positifa dan b yang memenuhi F P B(a, b) = 1 dan

a b +

25b 21a

bilangan bulat ada sebanyak ...

Penyelesaian :

Andaikan terdapat bilangan bulat positifa, byang memenuhi kondisi ini. Misalkan a b =x maka x adalah bilangan rasional positif. Misalkan juga

x+ 25

21x =k · · · ∗)

untuk suatu bilangan bulat positifk.

Dari persamaan *) diperoleh persamaan kuadrat dalam x berikut

21x2₋21kx+ 25 = 0

Mengingat x adalah bilangan rasional maka diskriminan dari persamaan kuadrat di atas harus berbentuk bilangan kuadrat sempurna. Dengan demikian diperoleh,

untuk suatu bilangan bulat positifm.

Perhatikan bahwa ruas kiri persamaan **) habis dibagi 21. Oleh karena itu 21 m

2 _=⇒

212 m

2_{. Akibatnya ruas kiri juga harus habis dibagi 21}2_{. Karena 21}2 441k

2 _{maka 2100}

juga habis dibagi 212 _{yang jelas tidak mungkin. Kontradiksi. Jadi, tidak ada bilangan}

bulat positif a, byang memenuhi.

18. Diberikan segitiga ABC, AB= 20, AC = 21 dan BC = 29. Titik D dan E terletak pada segmenBC, sehingga BD= 8 danEC = 9. Besar ∠DAE sama dengan ...

Penyelesaian :

Perhatikan bahwa _△ABC adalah segitiga siku-siku dengan ∠BAC = 90◦_.

A B

C

D E

F

G

Misalkan F dan G berturut - turut titik pada AC dan AB sehingga EF_⊥AC dan DG_⊥AB (seperti terlihat pada gambar). Diperoleh

EF =ECsinC = 9_× 20 29

CF =ECcosC = 9_× 21 29

AF =AC₋CF = 21₋9_× 21

29 = 20× 21 29

DG=BDsinB = 8_× 21 29

BG=BDcosB = 8_× 20 29

AG=AB₋BG= 20₋8_×20

Misal∠GAD=α dan ∠F AE =β, diperoleh

19. Suatu kompetisi diikuti oleh 20 peserta. Pada setiap ronde, dua peserta bertanding. Setiap peserta yang kalah dua kali dikeluarkan dari kompetisi, peserta yang terakhir be-rada di kompetisi adalah pemenangnya. Jika diketahui pemenang kompetisi tidak pernah kalah, banyaknya pertandingan yang dilangsungkan pada kompetisi tersebut adalah ...

Penyelesaian :

Misalkan banyak pertandingan yang berlangsung adalahN. Perhatikan bahwa setelah k

kali pertandingan maka jumlah maksimal peserta yang dikeluarkan adalah $

k 2 %

. Karena

di akhir kompetisi jumlah peserta yang dikeluarkan adalah 19 maka N _≥ 38. Akan tetapi di lain pihak, karena setiap peserta yang kalah dua kali dikeluarkan maka jumlah kekalahan yang terjadi maksimal adalah 2_×19 = 38. Sehingga banyak pertandingan yang terjadi maksimal 38 atau n_≤38. Jadi, diperoleh N = 38.

Jadi, Banyaknya pertandingan yang dilangsungkan pada kompetisi tersebut adalah 38 pertandingan.

20. Jumlah dari semua bilangan bulatxyang memenuhi2_log(x2_{−4x−1) merupakan bilangan}

bulat adalah ...

Penyelesaian :

Agar 2_log(x2 _{−4x−1) merupakan bilangan bulat maka x}2_{−4x−1 = 2}n_{, untuk suatu} bilangan bulat nonnegatif n. Perhatikan bahwa x2 _{−4x−1 = (x−2)}2 _{−5. Sehingga}

diperoleh (x₋2)2 _{= 2}n_{+ 5. Untuk n}

• Jikan = 0 maka diperolehx2₋4x₋1 = 1 _⇔ x2₋4x₋2 = 0 yang tidak memiliki penyelesaian bulat.

• Jikan = 1 maka diperolehx2₋4x₋1 = 2 _⇔ x2₋4x₋3 = 0 yang tidak memiliki penyelesaian bulat.

• Jikan= 2 maka diperolehx2_{−4x−1 = 4 ⇔ x}2_{−4x−5 = 0 ⇔ (x−5)(x+1) =}

0 sehingga x=₋1 atau x= 5.

Pembahasan OSN Matematika SMA Tahun 2013

Seleksi Tingkat Provinsi

Tutur Widodo

Bagian Kedua : Soal Uraian

1. Ada dua gelas, gelasAberisi 5 bola merah, dan gelasB berisi 4 bola merah dan satu bola putih. Satu gelas dipilih secara acak dan kemudian satu bola diambil secara acak dari gelas tersebut. Hal ini dilakukan berulang kali sampai salah satu gelas kosong. Tentukan probabilitas bahwa bola putih tidak terambil.

Penyelesaian :

Karena bola putih tidak terambil maka gelas yang habis adalah gelasA. Agar salah satu gelas habis maka pengambilan dilakukan paling sedikit 5 kali dan paling banyak 9 kali. Untuk itu kita bagi menjadi 5 kasus sebagai berikut :

i. Proses pengambilan bola dilakukan tepat 5 kali.

Untuk kasus ini kelima bola merah berasal dari gelas A semua. Jadi, peluangnya adalah

1 2

5 = 1

32 ii. Proses pengambilan bola dilakukan tepat 6 kali.

Untuk kasus ini kelima bola merah berasal dari gelasA dan satu bola merah berasal dari gelas B. Perhatikan bahwa bola yang berasal dari gelas B tidak boleh diambil pada pengambilan keenam. Jadi, untuk kasus ini peluangnya adalah

1

2 6

×4

5 ×C

5 1 =

1 16

iii. Proses pengambilan bola dilakukan tepat 7 kali.

Untuk kasus ini kelima bola merah berasal dari gelas A dan dua bola merah berasal dari gelas B. Perhatikan bahwa bola yang berasal dari gelas B tidak boleh diambil pada pengambilan ketujuh. Jadi, untuk kasus ini peluangnya adalah

1 2

7

× 4₅× 3₄ ×C₂6 = 9 128

iv. Proses pengambilan bola dilakukan tepat 8 kali.

Untuk kasus ini kelima bola merah berasal dari gelasA dan tiga bola merah berasal dari gelas B. Perhatikan bahwa bola yang berasal dari gelas B tidak boleh diambil pada pengambilan kedelapan. Jadi, untuk kasus ini peluangnya adalah

1 2

8

v. Proses pengambilan bola dilakukan tepat 9 kali.

Untuk kasus ini kelima bola merah berasal dari gelasAdan empat bola merah berasal dari gelas B. Perhatikan bahwa bola yang berasal dari gelas B tidak boleh diambil pada pengambilan kesembilan. Jadi, untuk kasus ini peluangnya adalah

1

Jadi, total peluang bola putih tidak terambil (dengan kata lain semua yang terambil adalah bola merah) yaitu

1

2. Untuk sebarang bilangan real x, didefinisikan _⌊x_⌋ sebagai bilangan bulat terbesar yang kurang dari atau sama denganx. Tentukan banyak bilangan aslin _≤1.000.000 sehingga

√

n₋j√nk< 1 2013

Penyelesaian :

Jikanbilangan kuadrat sempurna diperoleh_⌊√n_⌋=√n, sehingga√n_−⌊√n_⌋= 0< ₂₀₁₃1 . Oleh karena itu semua bilangan kuadrat sempurna memenuhi.

Selanjutnya akan dibuktikan, jika n bukan kuadrat sempurna maka √n_{− ⌊}√n_{⌋ ≥ 2013}1 . Bukti. Karena n bukan kuadrat sempurna maka n = k2 _{+m dengan 1 ≤ m ≤ 2k.}

Sehingga _⌊√n_⌋=k. Perhatikan kita memiliki ketaksamaan berikut

k2+ 1> k2+ 2k+ 1

bilangan aslik.

Karenan _≤1.000.000 maka kita peroleh

√

bilangan kuadrat sempurna yaitu ada 1.000 bilangan.

3. Suatu bilangan aslin dikatakan valid jika 1n_{+ 2}n_{+ 3}n_{+· · ·+m}n _{habis dibagi 1 + 2 +} 3 +_{· · ·}+m untuk setiap bilangan asli m.

a. Tunjukkan bahwa 2013 valid.

b. Buktikan bahwa ada tak hingga banyaknya bilangan yang tidak valid

Penyelesaian :

a. Lemma. Jikan bilangan ganjil makan valid. Bukti. Untuk setiap bilangan ganjil n berlaku

in+ (m₋i)n _≡0 mod m

in+ (m+ 1₋i)n

≡0 mod (m+ 1)

Bagi menjadi dua kasus,

• m bilangan genap, maka berlaku

1n_{+ 2}n_{+ 3}n₊

• m bilangan ganjil, maka berlaku

1n₊₂n₊₃n₊

b. Lemma. Jikan genap maka n tidakvalid. Bukti. Karena n genap diperoleh

1n_{+ 2}n _{= 1 + (3}

−1)n

≡1 + (₋1)n

≡2 mod 3

Jadi, 1n_{+ 2}n _{tidak habis dibagi oleh 1 + 2 = 3. Terbukti n tidak valid.}

Oleh karena itu, semua bilangan asli genap adalah bilangan tidakvalid. Jadi, terbukti ada takhingga bilangan tidak valid.

4. Buktikan bahwa untuk semua bilangan real positif a, b, c dengan a+b+c_≤6 berlaku

a+ 2

5. Diberikan segitiga ABC lancip. Garis tinggi terpanjang adalah dari titik sudutA tegak lurus pada BC, dan panjangnya sama dengan panjang median (garis berat) dari titik sudut B. Buktikan bahwa ∠ABC _≤60◦_.

Penyelesaian :

A B C

D E

F H

G

KarenaAE =EC maka EH = 1

2AD dan EG= 1

2CF. Pada △BEH diperoleh

sin∠HBE = EH BE =

1 2AD

AD =

1 2

sehingga ∠HBE = 30◦_.

Pada _△BEG diperoleh pula

sin∠GBE = EG BE =

1 2CF

AD ≤

1 2AD

AD =

1 2

sehingga ∠GBE _≤30◦_.

Jadi, diperoleh ∠ABC =∠HBE +∠GBE _≤30◦_{+ 30}◦ _{= 60}◦_{. Terbukti.}

Lebih jauh kesamaan terjadi, yaitu ∠ABC = 60◦ _{ketika ABC adalah segitiga samasisi.}

Akan tetapi jika melihat konteks soal bahwa AD adalah garis tinggi terpanjang maka kesamaan tidak mungkin terjadi.

Disusun oleh : Tutur Widodo

Apabila ada saran, kritik maupun masukan silakan kirim via email ke

tutur.w87@gmail.com