BAB II
TINJAUAN PUSTAKA
Pada bab ini akan dijelaskan beberapa konsep dasar tentang teori graf, graf barbel, matriks, determinan yang akan digunakan pada bab berikutnya.
2.1 Teori Graf
Definisi 2.1.1 Graf 𝐺 didefinisikan sebagai pasangan himpunan (𝑉, 𝐸), ditulis 𝐺 = (𝑉, 𝐸), 𝑉 adalah himpunan tidak-kosong dari simpul-simpul (vertices atau node) dan 𝐸 adalah himpunan sisi (edges atau arcs) yang menghubungkan sepasang simpul [4].
Gambar 2.1.1 Contoh Graf 𝐺
Jumlah simpul pada graf disebut sebagai kardinalitas graf dan dinyatakan dengan 𝑛 = |𝑉| dan jumlah sisi dinyatakan dengan 𝑚 = |𝐸| [5]. Sisi pada graf dapat mempunyai orientasi arah. Berdasarkan orientasi arah pada sisi, secara umum graf dibedakan sebagai berikut:
1. Graf Tak-Berarah (Undirected Graph)
Definisi 2.1.2 Graf yang sisinya tidak mempunyai orientasi arah disebut graf tak-berarah [6].
Pada graf tak-berarah, urutan pasangan simpul yang dihubungkan oleh sisi tidak diperhatikan. Jadi, (𝑢, 𝑣) dan (𝑣, 𝑢) adalah sisi yang sama.
2. Graf Berarah (Directed Graph)
Definisi 2.1.3 Graf yang setiap sisinya diberikan orientasi arah disebut sebagai graf berarah [7].
Pada graf berarah, (𝑢, 𝑣) dan (𝑣, 𝑢) menyatakan dua buah sisi yang berbeda, dengan kata lain (𝑢, 𝑣) ≠ (𝑢, 𝑣).
Terdapat beberapa istilah yang biasa digunakan dalam teori graf dan bersesuaian dengan laporan ini di antaranya:
1. Lintasan (Path)
Definisi 2.1.4 Lintasan yang panjangnya 𝑛 dari simpul awal 𝑣0 ke simpul tujuan 𝑣𝑛 di dalam graf 𝐺 ialah barisan berselang-seling simpul-simpul dan
sisi-sisi yang berbentuk 𝑣0, 𝑒1, 𝑣1, 𝑒2, 𝑣2, …, 𝑣𝑛−1, 𝑒𝑛, 𝑣𝑛 sedemikian
sehingga 𝑒1 = (𝑣0, 𝑣1), 𝑒2 = (𝑣1, 𝑣2), …, 𝑒𝑛 = (𝑣𝑛−1, 𝑣𝑛) adalah sisi-sisi dari graf 𝐺 [8].
Gambar 2.1.4 Graf Lintasan 2. Siklus (Cycle) atau Sirkuit (Circuit)
Definisi 2.1.5 Lintasan yang berawal dan berakhir pada simpul yang sama disebut sirkuit atau siklus [9]. Sebuah sirkuit dikatakan sirkuit sederhana (simple circuit) jika setiap rusuk yang dilalui berbeda.
Gambar 2.1.5 Graf Siklus atau Sirkuit 3. Terhubung (Connected)
Definisi 2.1.6 Graf tak berarah 𝐺 disebut graf terhubung (connected graph) jika untuk setiap pasang simpul 𝑢 dan 𝑣 di dalam himpunan 𝑉 terdapat lintasan dari 𝑢 ke 𝑣 (yang juga harus berarti ada lintasan dari 𝑢 ke 𝑣) [10].
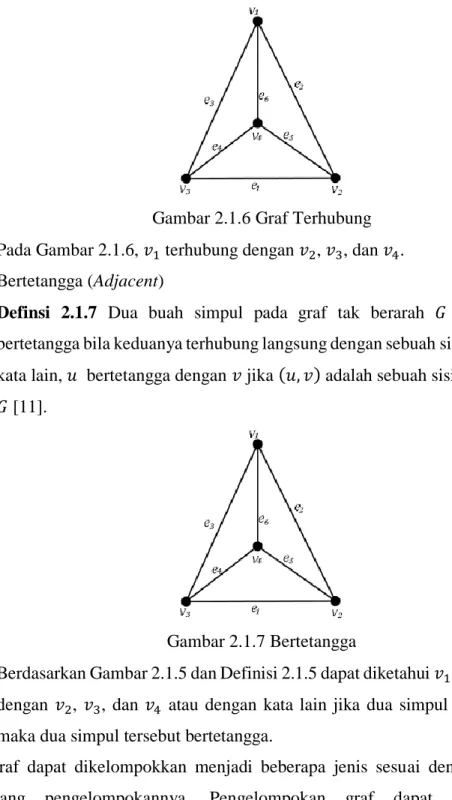
Gambar 2.1.6 Graf Terhubung Pada Gambar 2.1.6, 𝑣1 terhubung dengan 𝑣2, 𝑣3, dan 𝑣4. 4. Bertetangga (Adjacent)
Definsi 2.1.7 Dua buah simpul pada graf tak berarah 𝐺 dikatakan bertetangga bila keduanya terhubung langsung dengan sebuah sisi. Dengan kata lain, 𝑢 bertetangga dengan 𝑣 jika (𝑢, 𝑣) adalah sebuah sisi pada graf 𝐺 [11].
Gambar 2.1.7 Bertetangga
Berdasarkan Gambar 2.1.5 dan Definisi 2.1.5 dapat diketahui 𝑣1 terhubung
dengan 𝑣2, 𝑣3, dan 𝑣4 atau dengan kata lain jika dua simpul terhubung maka dua simpul tersebut bertetangga.
Graf dapat dikelompokkan menjadi beberapa jenis sesuai dengan sudut pandang pengelompokannya. Pengelompokan graf dapat dipandang berdasarkan ada tidaknya rusuk ganda, berdasarkan jumlah simpul, atau berdasarkan orientasi arah pada rusuk [12].
Definisi 2.1.8 Graf yang tidak mengandung gelang maupun sisi-ganda dinamakan graf sederhana [13].
tak-sederhana [14].
Gambar 2.1.9 Graf Tak-Sederhana
Pada Gambar 2.1.9, graf tersebut dikatakan graf tak-sederhana karena terdapat gelang (loop) 𝑒1 yang menghubungkan simpul 𝑣2. Selain itu, contoh gambar
graf di atas juga dikatakan graf tak-sederhana karena terdapat sisi ganda (𝑒4 dan 𝑒5) yang menghubungkan simpul 𝑣1 dengan 𝑣3.
Pada graf sederhana, sisi adalah pasangan tak terurut (unordered pairs). Berikut beberapa jenis graf sederhana antara lain:
1. Graf Lengkap (Complete Graph)
Definisi 2.1.10 Graf lengkap ialah graf sederhana yang setiap simpulnya mempunyai sisi ke semua simpul lainnya [15].
Graf lengkap dengan 𝑛 buah simpul dilambangkan dengan 𝐾𝑛. Setiap simpul 𝐾𝑛 berderajat 𝑛 – 1. Banyaknya rusuk pada graf lengkap yang
terdiri dari 𝑛 buah simpul adalah 𝑛(𝑛 – 1) 2⁄ .
Gambar 2.1.10 Graf Lengkap (Complete Graph) 2. Graf Lingkaran
Definisi 2.1.11 Graf lingkaran adalah graf sederhana yang setiap simpulnya berderajat dua [16].
Graf lingkaran dengan 𝑛 simpul dilambangkan dengan 𝐶𝑛.
Ada berbagai jenis graf yang dapat kita temukan pada teori graf, salah satu di antaranya adalah graf barbel (𝐵𝑛).
Definisi 2.1.12 Graf barbel (𝐵𝑛) adalah graf sederhana yang dibentuk dengan menghubungkan 2 tiruan/jiplakan graf komplit 𝐾𝑛 dengan sebuah jembatan/sisi dengan 𝑛 ≥ 3 dan 𝑛 adalah bilangan asli [3].
Gambar 2.1.12 Graf Barbel (𝐵3, 𝐵4, 𝐵5) 2.2 Matriks
Matriks adalah sekumpulan elemen-elemen 𝑎𝑖𝑗 dengan 𝑖 = 1, 2, 3, … , 𝑚
menyatakan baris dan 𝑗 = 1, 2, 3, … , 𝑛 menyatakan kolom. Secara umum suatu matriks 𝐴 = [𝑎𝑖𝑗] yang memiliki m baris dan n kolom dinyatakan sebagai:
𝐴 = [ 𝑎11 𝑎12 ⋯ 𝑎1𝑛 𝑎21 𝑎22 ⋯ 𝑎2𝑛 ⋮ ⋮ ⋱ ⋮ 𝑎𝑚1 𝑎𝑚2 ⋯ 𝑎𝑚𝑛 ]
Definisi 2.2.1 Suatu matriks adalah susunan elemen-elemen berbentuk persegi. Elemen-elemen tersebut disebut entri-entri pada matriks [17].
Suatu graf dapat direpresentasikan dalam suatu bentuk matriks, salah satunya adalah matriks ketetanggaan.
Definisi 2.2.2 Misalkan 𝐺 = (𝑉, 𝐸) adalah graf dengan n simpul, 𝑛 ≥ 1. Matriks ketetanggan 𝐺 adalah matriks yang berukuran 𝑛 × 𝑛. Bila matriks tersebut dinamakan 𝐴 = [𝑎𝑖𝑗], maka 𝑎𝑖𝑗 = 1 jika simpul 𝑖 dan 𝑗 bertetangga, sebaliknya 𝑎𝑖𝑗 = 0 jika simpul 𝑖 dan 𝑗 tidak bertetangga [18].
2.3 Determinan
𝐴 = [𝑎 𝑏
𝑐 𝑑] ⟹ |𝐴| = |
𝑎 𝑏
𝑐 𝑑| = 𝑎𝑑 – 𝑏𝑐
Suatu matriks dapat diuraikan ke dalam bentuk matriks kofaktor dengan mencari minor dan kofaktor dari matriks tersebut. Hal ini dapat digunakan untuk mencari determinan dari matriks yang berordo 𝑛 × 𝑛.
Definisi 2.3.1. Jika A adalah matriks bujur sangkar, maka minor dari entri 𝑎𝑖𝑗 dilambangkan dengan 𝑀𝑖𝑗 dan didefinisikan sebagai determinan dari submatriks yang tersisa setelah baris ke-𝑖 dan kolom ke-𝑗 dihapus dari 𝐴. Bilangan (−1)𝑖+𝑗𝑀𝑖𝑗 dilambangkan dengan 𝐾𝑖𝑗 dan disebut sebagai kofaktor
dari entri 𝑎𝑖𝑗 [20].
Adapun bentuk matriks pada minor dan kofaktor dari suatu matriks bujur sangkar akan menghasilkan suatu pola sebagai berikut (sesuai dengan penulisan ((−1)𝑖+𝑗𝑀𝑖𝑗) ( + − + − ⋯ − + − + ⋯ + − + − ⋯ − + − + ⋯ ⋮ ⋮ ⋮ ⋮ ⋱ ) Sebagai contoh, 𝐾11 = 𝑀11, 𝐾21 = −𝑀21, 𝐾22 = 𝑀22
Teorema 2.3.1 Jika 𝐴 adalah matriks 𝑛 × 𝑛, maka tanpa memperhatikan baris atau kolom dari 𝐴 yang dipilih, bilangan yang diperoleh dengan mengalikan entri pada baris atau kolom itu dengan kofaktor yang bersesuaian dan menambahkan produk yang dihasilkan selalu sama [21].
Matriks kofaktor dapat digunakan untuk mencari determinan dari suatu matriks.
Definisi 2.3.2 Jika 𝐴 adalah matriks 𝑛 × 𝑛, maka jumlah yang diperoleh dengan mengalikan entri pada setiap baris atau kolom dari matriks 𝐴 dengan kofaktor yang bersesuaian dan menambahkan produk yang dihasilkan disebut sebagai determinan matriks 𝐴, dan penjumlahannya disebut sebagai ekspansi
det(𝐴) = 𝑎1𝑗𝐾1𝑗 + 𝑎2𝑗𝐾2𝑗 + … + 𝑎𝑛𝑗𝐾𝑛𝑗 (ekspansi kofaktor sepanjang kolom
ke-𝑗) dan
det(𝐴) = 𝑎𝑖1𝐾𝑖1 + 𝑎𝑖2𝐾𝑖2 + … + 𝑎𝑖𝑛𝐾𝑖𝑛 (ekspansi kofaktor sepanjang baris ke-𝑖) [21].
Determinan suatu matriks memiliki beberapa sifat, salah satu di antaranya adalah sifat penukaran baris atau kolom pada matriks.
Teorema 2.3.2 Misalkan 𝐴 merupakan matriks. Jika 𝐵 adalah matriks yang dibentuk ketika dua baris atau dua kolom saling bertukar [22].
Teorema 2.3.3 Jika 𝑃 merupakan matriks 𝑛 × 𝑛 dan 𝑃 = [𝐴 𝐵
𝐶 𝐷], maka determinan dari 𝑃 adalah det(𝑃) = det[𝐴 𝐵
𝐶 𝐷] = det(𝐴) det(𝐷 − 𝐶𝐴
−1𝐵) jika