FUNGSI HIPERBOLIK DAN INVERSNYA.

S K R I P S I

Disusun dalam Rangka Menyelesaikan Studi Strata 1 untuk memperoleh Gelar Sarjana Sains

Oleh

Nama : Susanto

Nim : 4150403010

Program Studi : Matematika S1

Jurusan : Matematika

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI SEMARANG

Telah dipertahankan dihadapan Sidang Panitia Ujian Skripsi Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Semarang pada:

Hari : Tanggal :

Panitia Ujian

Ketua, Sekretaris,

Drs. Kasmadi Imam S., M.S Drs. Supriyono, M.Si

NIP. 130781011 NIP. 130815345

Pembimbing Utama, Ketua Penguji,

Drs. Moch. Chotim, M.S Drs. Kartono, M.Si

NIP. 130781008 NIP. 130815346

Pembimbing Pendamping, Anggota Penguji,

Drs. Wuryanto, M.Si Drs. Moch. Chotim, M.S

NIP. 131281225 NIP. 130781008

Anggota Penguji,

Drs. Wuryanto, M.Si

NIP. 131281225

Program Studi Matematika. Jurusan Matematika. Fakultas Matematika dan Ilmu Pengetahuan Alam.

Universitas Negeri Semarang.

Dalam persoalan matematika terapan digunakan banyak sekali kombinasi tertentu fungsi-fungsi eksponen dan . Sehingga fungsi-fungsi yang memuat kombinasi tersebut diberi nama khusus salah satunya adalah fungsi hiperbolik. Telah banyak buku-buku kalkulus yang menulis tentang fungsi hiperbolik, namun tidak banyak yang menulis tentang penurunan rumus atau formula dari fungsi hiperbolik. Permasalahan yang dikaji dalam penelitian ini adalah bagaimana membangun fungsi hiperbolik dan menentukan invers fungsi hiperbolik dan turunan serta anti turunan fungsi hiperbolik dan inversnya. Pertimbangan lebih jauh dari masalah ini adalah bahwa tidak semua fungsi hiperbolik mempunyai invers pada daerah asalnya. Tujuan dari penelitian ini adalah untuk mengetahui rumus atau formula fungsi hiperbolik dan inversnya serta turunan dan anti turunan fungsi hiperbolik dan inversnya.

x

e e−x

Penelitian ini dilakukan melalui tinjauan pustaka terhadap buku-buku atau literatur. Teori-teori yang digunakan sebagai dasar untuk menyelesaikan permasalahan dalam penelitian ini adalah teori tentang fungsi, limit fungsi, turunan dan integral, fungsi invers, fungsi logaritma serta fungsi eksponen. Dari pengertian tersebut, kemudian dibahas materi-materinya secara mendalam.

Hasil dari penelitian ini adalah fungsi hiperbolik dibangun oleh dua fungsi p dan q dengan p :R→R+,

2 ) (

x

e x

p = dan q :R→R+,

2 ) (

x

e x q

−

= .

Selanjutnya dibangun fungsi f dan g yang dinyatakan sebagai jumlah dan selisih dari fungsi p dan q, dengan demikian f(x)= p(x)+q(x) dan

) ( ) ( )

(x p x q x

g = − . Sifat-sifat yang dimiliki oleh fungsi f dan g memiliki kemiripan dengan sifat-sifat fungsi trigonometri, salah satunya adalah kesamaan dasar fungsi yang memiliki kemiripan dengan sifat

pada fungsi trigonometri. Dengan mengacu pada sifat-sifat tersebut, kemudian dikembangkan suatu ide untuk menyatakan fungsi f dan g sebagai fungsi hiperbolik.

1 ) ( )

( 2

2 − =

x g x f 1 sin

cos2 + 2 =

x x

Hasil dari penelitian ini diharapkan dapat bermanfaat sebagai bahan bacaan atau referensi bagi mahasiswa matemetika khususnya dan masyarakat pada umumnya.

Kata Kunci : fungsi eksponen, fungsi hiperbolik, turunan, dan invers.

] With passion, with terminations, and with hard work we can to reach our dream

come true.

] Remember, the problems ahead of you are never as great as the power behind

you.

PERUNTUKAN

Puji syukur kepada Allah swt atas terselesainya skripsi ini.

Kuperuntukan karya ini kepada:

1. Bapak Suyanto dan Ibu Kikis atas doanya

2. Semua Saudara dan Kerabat

3. Guru dan sahabatku

4. All My lovely friends..

petunjuk dan karunia-Nya, sehingga penulis dapat menyelesaikan penulisan skripsi yang berjudul ”Fungsi Hiperbolik dan Inversnya”.

Ucapan terima kasih penulis sampaikan kepada:

1. Drs. Kasmadi Imam S., M.S, Dekan FMIPA Universitas Negeri Semarang. 2. Drs. Supriyono, M.Si, Ketua Jurusan Matematika FMIPA Universitas Negeri

Semarang.

3. Drs. Moch Chotim, M.S, Pembimbing utama yang telah memberikan bimbingan dan arahan kepada penulis dalam menyusun skripsi ini.

4. Drs. Wuryanto, M.Si, Pembimbing pendamping yang telah memberikan bimbingan dan arahan kepada penulis dalam menyusun skripsi ini.

5. Bapak dan ibu yang senantiasa mendoakan serta memberikan dorongan baik secara moral maupun spiritual dan segala yang tak ternilai.

6. Semua keluarga yang telah memberikan dukungan dan semangat serta doa hingga terselesaikanya skripsi ini.

7. Teman-temanku Gandhi, Iwan, Bambang, dan semua angkatan 2003, terima kasih atas semuanya.

8. Kelurga Besar ” Pandawa Kost ” Bapak Sodri sekeluarga, Rudi, Eko Budi, dan Mas Arief yang tiada henti memotivasi penulis agar segera menyelesaikan skripsi ini.

Semarang, Agustus 2007 Penulis,

HALAMAN PENGESAHAN... ii

ABSTRAK ... iii

MOTTO DAN PERUNTUKAN ... iv

KATA PENGANTAR... v

DAFTAR ISI... vii

DAFTAR GAMBAR... ix

BAB I PENDAHULUAN... 1

A. Latar belakang ... 1

B. Permasalahan... 2

C. Tujuan penelitian... 2

D. Manfaat penelitian... 2

E. Sistematika penulisn skripsi ... 3

BAB II LANDASAN TEORI ... 5

A. Fungsi ... 5

B. Limit Fungsi ... 6

C. Kekontinuan Fungsi ... 7

D. Turunan ... 9

E. Integral... 14

F. Fungsi Invers, Logaritma, dan Eksponen... 20

BAB III METODE PENELITIAN ... 32

A. Menentukan masalah... 32

B. Merumuskan masalah... 32

C. Studi pustaka ... 32

D. Analisis dan pemecahan masalah ... 33

E. Penarikan simpulan ... 33

D. Turunan Invers Fungsi Hiperbolik ... 59

E. Anti Turunan Invers Fungsi Hiperbolik ... 63

BAB V PENUTUP... 64

A. Simpulan... 64

B. Saran... 66

DAFTAR PUSTAKA ... 67

Gambar 2 Grafik fungsi f kontinu di titik a... 8

Gambar 3 Grafik fungsi p :R→R+, 2 ) ( x e x p = ... 34

Gambar 4 Grafik fungsi q :R→R+, 2 ) ( x e x q − = ... 35

Gambar 5 Grafik fungsi f :R→[0,∞), f(x)= p(x)+q(x) ... 35

Gambar 6 Grafik fungsi g:R→ R, g(x)= p(x)−q(x)... 36

Gambar 7 Grafik fungsi f :R→(−1,1), f(x)=tanhx ... 41

Gambar 8 Grafik fungsi f :R→(−∞,−1)∪(1,∞), f(x)=cothx... 41

Gambar 9 Grafik fungsi f :R→(0,1], f(x)=sechx... 42

Gambar 10 Grafik fungsi f :R→ R, f(x)=sinh−1x... 48

Gambar 11 Grafik fungsi f :[0,∞)→[1,∞), f(x)=coshx ... 49

Gambar 12 Grafik fungsi f :[1,∞)→[0,∞), f(x)=cosh−1x ... 50

Gambar 13 Grafik fungsi f :(−1,1)→(−∞,∞), f(x)=tanh−1x... 53

Gambar 14 Grafik fungsi f :(−∞,−1)∪(1,∞)→(−∞,∞), x x f( )=coth−1 ... 55

Gambar 15 Grafik fungsi f :[0,∞)→(0,1], f(x)=sechx... 56

Gambar 16 Grafik fungsi f :(0,1]→[0,∞), f(x)=sech−1x... 58

A. LATAR BELAKANG MASALAH

Kalkulus sebagai salah satu cabang ilmu matematika merupakan ilmu yang berintikan teori tentang diferensiasi dan integrasi yang telah dikembangkan secara terpisah oleh matematikawan asal Inggris Issac Newton pada abad ke 17 dan matematikawan Jerman Gottfried Wilhelm Leibniz. Diferensiasi dan integrasi merupakan dua operasi matematis yang saling berkebalikan. Pada intinya, diferensial (teori diferensiasi ) berkenaan dengan penentuan tingkat perubahan suatu fungsi, sedangkan integral (teori integrasi) berkenaan dengan pembentukan suatu fungsi apabila tingkat perubahan fungsi yang bersangkutan diketahui.

Keampuhan Kalkulus, baik berupa turunan maupun integral tak perlu diragukan lagi sebagai sarana ampuh untuk memecahkan berbagai permasalahan yang dihadapi dalam kehidupan nyata. Fungsi logaritma dan fungsi eksponen sebagai bagian dari kalkulus telah memberi pengaruh yang besar dalam perkembangan Kalkulus. Dalam persoalan matematika terapan

banyak sekali digunakan kombinasi-kombinasi tertentu fungsi eksponen e x

dan e−x sehingga kombinasi fungsi-fungsi tersebut diberi nama khusus, salah satunya adalah fungsi hiperbolik. Namun bagaimana membangun fungsi hiperbolik merupakan suatu permasalahan yang menarik untuk kita kaji secara mendalam untuk kemudian ditemukan solusinya.

Dalam penelitian ini juga akan dikaji mengenai invers fungsi hiperbolik. Fungsi invers pada dasarnya ditentukan untuk memperluas dan memperkaya fungsi-fungsi. Invers merupakan salah satu cara yang dapat ditempuh untuk memproduksi fungsi baru yakni dengan mengambil fungsi-fungsi lama kemudian membalikan atau menginverskan fungsi-fungsi-fungsi-fungsi tersebut. Dengan mengacu pada konsep invers pada fungsi biasa tersebut, kemudian akan dikembangkan untuk menentukan invers pada fungsi hiperbolik. Selanjutnya konsep diferensi dan integrasi yang merupakan inti dari Kalkulus akan diterapkan untuk menentukan turunan dan anti turunan fungsi hiperbolik dan inversnya.

Dari uraian di atas maka penulis ingin mengangkat judul “Fungsi Hiperbolik dan Inversnya”, sebagai judul skripsi.

B. PERMASALAHAN

Permasalahan yang akan dikaji dalam penulisan ini adalah: 1.Bagaimana membangun fungsi hiperbolik?

2.Bagaimana menentukan invers fungsi hiperbolik dan turunan serta anti turunan fungsi hiperbolik dan inversnya?

C. TUJUAN PENELITIAN

D. MANFAAT PENELITIAN

Mendapatkan suatu wawasan dan pengetahuan tentang fungsi hiperbolik dan inversnya.

E. SISTEMATIKA PENULISAN SKRIPSI

Penulisan skripsi nantinya akan dibagi menjadi tiga bagian, yakni bagian awal, bagian isi, dan bagian akhir.

Bagian awal, memuat halaman judul, abstrak, halaman pengesahan, halaman motto, halaman peruntukan, kata pengantar, dan daftar isi.

Bagian isi terbagi atas 5 bab, yakni: BAB I PENDAHULUAN

Membahas tentang alasan pemilihan judul, permasalahan yang diangkat, tujuan penelitian, manfaat penelitian, dan sistematika penulisan skripsi.

BAB II LANDASAN TEORI

Mencakup pembahasan materi-materi pendukung yang digunakan dalam pemecahan masalah.

BAB III METODE PENELITIAN

BAB IV PEMBAHASAN

Dalam bab ini berisikan pembahasan dan analisis dari penelitian. BAB V PENUTUP

Berisi tentang kesimpulan dari hasil pembahasan dan saran yang ditujukan untuk pembaca umumnya dan bagi penulis sendiri khususnya.

A. FUNGSI Definisi 1.

Dipunyai D dan R dua himpunan dengan elemen real. Sebuah fungsi f adalah padanan yang mengawankan setiap elemen x di D dengan tepat satu elemen

f(x) di R ditulis dengan simbol f: D →R. Dengan kata lain jika a∈D, b, b’∈R dan (a, b), (a, b’)∈ f maka b = b’.

Himpunan D dinamakan daerah asal (domain) f, dan himpunan R dinamakan daerah hasil atau jelajah (range) f, dan himpunan semua peta unsur di D oleh f

disebut daerah hasil f. Contoh fungsi deberikan pada Gambar 1.

Gambar 1: Diagram fungsi f : D →R Contoh 1

Dipunyai f: D →R, D⊂R, f(x) = x2+ 5. Tujukan f suatu fungsi.

Penyelesaian:

Ambil sembarang a, b∈Ddengan a = b. Jelas f(a) – f(b) = a2 + 5 – b2 - 5

= a2-b2

= 0.

Jadi ∀a,b∈D,a=b,f(a)= f(b). Jadi f suatu fungsi.

Contoh 2

Dipunyai f: D →R, D⊂R2, f(x, y) = x2 + 2y. Tunjukan f suatu fungsi.

Penyelesaian:

Ambil sembarang (x₁,y₁),(x₂,y₂)∈D, (x₁,y₁)=(x₂,y₂). Jelas x₁ =x₂ dan y₁ = y₂

Jelas )f(x₁,y₁)− f(x₂,y₂)=(x₁2 +2y₁)−(x₂2 +2y₂

) 2 ( ) 2

(x₁2 + y₁ − x₁2 + y₁ =

= 0.

Jadi ∀(x₁,y₁),(x₂,y₂)∈D,(x₁,y₁)=(x₂,y₂), f(x₁,y₁)= f(x₂,y₂). Jadi f suatu fungsi.

B. LIMIT FUNGSI Definisi 2.

Milsalkan f sebuah fungsi yang terdefinisi pada suatu selang buka I, yang memuat a, kecuali mungkin pada a itu sendiri. Maka limit f(x) untuk x

L x f

a

x→ ( )=

lim ⇔∀ε >0∃δ >0∋ f(x)−L <εapabila0< x−a <δ . Contoh 3

Buktikan 22lim(4 2) 5 + =

→ x

x .

Bukti:

Tulis f(x) = 4x+2. Ambil sebarang ε >0. Pilih

4

ε δ = .

Dipunyai 0< x−5 <δ

Jelas f(x)−22 = 4x+2−22 = 4x−20

= 4x−5 < 4δ

< 4 4

ε

= ε.

Jadi ∀ε >0∃δ >0∋ f(x)−22 <εapabila0< x−5 <δ

Jadi lim(4 2) 22 5 + =

→ x

x .

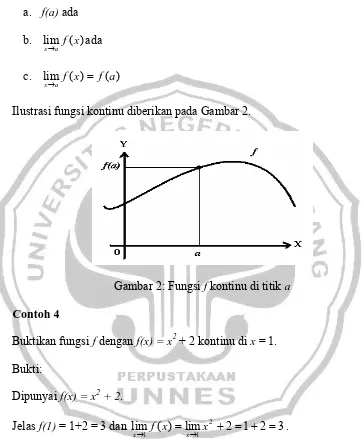
C. KEKONTINUAN FUNGSI Definisi 3.

Misalkan f terdefinisi pada selang buka I yang memuat a. Fungsi f dikatakan kontinu di a jika lim f(x) f(a)

a

Definisi tersebut menysaratkan tiga hal berikut yang harus dipenuhi agar suatu fungsi f kontinu di a, yakni:

a. f(a) ada b. lim f(x)

a

x→ ada c. lim f(x) f(a)

a

x→ =

Ilustrasi fungsi kontinu diberikan pada Gambar 2.

Gambar 2: Fungsi f kontinu di titik a

Contoh 4

Buktikan fungsi f dengan f(x) = x2+2 kontinu di x = 1. Bukti:

Dipunyai f(x) = x2 + 2.

Jelas f(1) = 1+2 = 3 dan lim ( ) lim 2 2 1 2 3

1

1 = → + = + =

→ f x x x

x .

Jadi 3lim ( ) (1)

1 = =

→ f x f

x .

D. TURUNAN (DIFERENSIAL) Definisi 4.

Turunan fungsi f pada bilangan x dinyatakan dengan f’(x) adalah

f’(x) = 0 lim

→

h _h

x f h x

f( + )− ( )

, jika limitnya ada.

Jika f’ ada maka dikatakan f terdiferensial di x. Contoh 5

Carilah turunan fungsi f(x)=x2 −8x+9 pada bilangan a. Penyelesaian:

Dipunyai 9f(x)=x2 −8x+ .

Jelas

h a f h a f a

f

h

) ( ) ( lim ) ( '

0

− + = _→

h

a a h

a h

a

h

] 9 8 [ ] 9 ) ( 8 ) [( lim

2 2

0

+ − − + + − +

= _→

h

a a h

a h ah a

h

9 8 9

8 8 2

lim

2 2

2

0

− + − + − − + + = _→

h h h ah

h

8 2

lim

2

0

− + = _→

) 8 2

( lim

0 + −

= _→ a h

h

8 2 −

= a .

Konsep Turunan (Derivative Formulas) a. Aturan Perpangkatan (Power of x Rule)

Jika f(x) = c, dimana c adalah konstanta, maka f’(x) = 0.

c. Aturan Koefisien (Coefficient Rule)

Jika f terdiferensial pada x, c konstanta, maka cf terdiferensial pada x dan )

( ' ) ( )'

(cf x =cf x .

d. Aturan Jumlah (Sum Rule)

Jika f dan g terdiferensialkan pada x maka (f + g) terdiferensialkan pada x

dan )(f +g)'(x)= f'(x)+g'(x . e. Aturan Selisih (Difference Rule)

Jika f dan g terdiferensialkan pada x maka (f + g) terdiferensialkan pada x

dan )(f −g)'(x)= f'(x)−g'(x . f. Aturan Perkalian (Product Rule)

Jika f dan g terdiferensialkan pada x maka (f. g) terdiferensialkan pada x

dan )(f.g)'(x)= f(x)g'(x)+g(x)f'(x . g. Aturan Hasil Bagi (Quotient Rule)

Jika f dan g terdiferensialkan pada x, g(x)≠0 maka

g f

terdiferensialkan

pada x dan

( )

2 )] ( [

) ( ' ) ( ) ( ' ) (

x g

x g x f x f x g x g

f −

= ⎟⎟⎠ ⎞ ⎜⎜⎝

⎛ _.

h. Aturan Rantai (Chain Rule)

Jika f dan g fungsi yang terdiferensial dengan y = f(u) dan u = g(x), maka

y fungsi yang terddiferensial pada x, dan )

( ). ( g x

dx d u f du

d dx dy

= , atau dapat dituliskan

dx du du dy dx dy

.

Bukti:

(a) Dipunyai f(x) = xn. Jelas h x f h x f x f h ) ( ) ( lim ) ( ' 0 − + = _→ h x h

x n n

h

− + =lim_→ ( )

0 h x h nxh h x n n h nx

xn n n n n n

h − ⎥⎦ ⎤ ⎢⎣ ⎡ _{+ +} − _{+ + +} = − − − → 1 2 2 1 0 ... ! 2 ) 1 ( lim h h nxh h x n n h

nxn n n n

h + + + − + = − − − → 1 2 2 1 0 ... ! 2 ) 1 ( lim 1 2 2 1

0 _2! ...

) 1 (

lim − − − −

→ + + +

− +

= n n n n

h x h nxh h

n n nx 1 − = n nx .

Jadi terbukti bahwa f'(x)=nxn−1. (b) Dipunyai f fungsi konstan, f(x) = c.

Jelas h x f h x f x f h ) ( ) ( lim ) ( ' 0 − + = _→ h c c h − = _→ 0 lim h h 0 lim 0 → = 0 0 lim 0 =

= _h→ .

(c) Dipunyai c konstanta dan f dan cf terdiferensial. Jelas h x cf h x cf x cf h ) )( ( ) )( ( lim ) ( )' ( 0 − + = _→ h x cf h x cf h ) ( ) ( lim 0 − + = _→ ⎥⎦ ⎤ ⎢⎣ ⎡ + − = _→ h x f h x f c h ) ( ) ( lim 0 h x f h x f c h ) ( ) ( lim 0 − + = _→ ) ( ' x cf = .

Jadi terbukti bahwa (cf)'(x)=cf'(x). (d) Dipunyai f,g, dan f + g terdiferensial.

Jelas (f + g)’(x) =

h x g x f x x g x x f h )) ( ) ( ( )) ( ) ( ( lim 0 + − + + + → = h x g h x g x f h x f h ) ( ) ( ) ( ) ( lim 0 − + + − + → = h x g h x g h x f h x f h h ) ( ) ( lim ) ( ) ( lim 0 0 − + + − + → →

= f’(x) + g’(x).

Jadi terbukti bahwa (f + g)’(x) = f’(x) + g’(x). (f) Dipunyai f,g, dan f g terdiferensial.

Jelas (fg)’(x) =

= h x g h x g x f h x g h x f h x f h h h x h ) ( ) ( lim ) ( lim ) ( lim ) ( ) ( lim 0 0 0 − + + + − + → → → →

= f’(x)g(x) + f(x)g’(x)

Jadi terbukti bahwa (fg)’(x) = f’(x)g(x) + f(x)g’(x). (g) Dipunyai f,g, dan

g f

terdiferensial.

Jelas ( )'(x)

g f = h x g x f h x g h x f h ) ( ) ( ) ( ) ( lim 0 − ++ → = h x g h x g h x g x f x g h x f h ) ( ) ( ) ( ) ( ) ( ) ( lim 0 +− + + → = h x g h x g h x g x f x g h x f

h _{[ ( ) ( )]}

) ( ) ( ) ( ) ( lim 0 + + − + → = h h x g x f x g h x f x g h x g h h ) ( ) ( ) ( ) ( lim )] ( ) ( [ 1 lim 0 0 + − + + → →

= {lim ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )} )] ( [ 1 0 2 _h h x g x f x g x f x g x f x g h x f x g h + − + − + →

= {lim ( ( ) ( )) ( ) ( )( ( ) ( )) } )] ( [ 1 0 2 ⎥⎦ ⎤ ⎢⎣ ⎡ + − ₋ + − → _h x g h x g x f x g h x f h x f x g h = )} ) ( ) ( ( lim ) ( lim ) ( lim ) ) ( ) ( ( lim { )] ( [ 1 0 0 0 0 2 h x g h x g x f x g h x f h x f x

g h h h h

− + − − + → → → → = { '( ) ( ) ( ) '( )} )] ( [ 1

2 f x g x f x g x

Jadi terbukti bahwa 2 )] ( [ ) ( ' ) ( ) ( ) ( ' ) ( )' ( x g x g x f x g x f x g f − = .

Berikut diberikan beberapa contoh penggunaan dari konsep diatas. Contoh 6

Diberikan fungsi-fungsi f(x)=5, g(x)=4x2 dan h(x)=x+1. Tentukan )f'(x , )g'(x dan )(g+h)'(x .

Penyelesaian: Jelas 0f'(x)= . Jelas g'(x)=8x.

Jelas )(g+h)'(x)= g'(x)+h'(x

1 8 +

= x . E. INTEGRAL

Definisi 5.

Fungsi F dinamakkan anti turunan dari fungsi f jika turunan dari F adalah f. Contoh 7

Dipunyai f(x)= x2, ₁ 3 3 1 ) (x x

F = , 5

3 1 )

( 3

2 x = x +

F dan F x = x−π

3 1 ) (

3 .

Tunjukan bahwa F₁(x),F₂(x)dan )F₃(x merupakan anti turunan dari f(x). Penyelesaian:

Jelas 2 2

3 3 1 3 . 3 1 ) ( 3 1 3 1 )] ( [ x x dx x d dx x d dx x F d = = = ⎥⎦ ⎤ ⎢⎣ ⎡ = .

Jelas 2 2

3 3

3

2 _.3

Jelas 2 2 3

3 3

2 _.3

3 1 0 ) ( 3 1 ) ( 3

1 3

1 )] ( [

x x dx

x d dx

d x d

dx x d

dx x F d

= =

− =

− ⎥⎦ ⎤ ⎢⎣ ⎡ = ⎥⎦ ⎤ ⎢⎣

⎡ ₋

= π π

Jadi F₁(x),F₂(x)dan )F₃(x semuanya merupakan anti turunan dari f(x). Definisi 6.

Jika )F(x pada selang buka I merupakan anti turunan darif(x)dan C

sembarang konstanta, maka F(x)+C juga merupakan anti turunan dari f(x).

) ( 0 ) ( ) ( )] ( [ ] ) ( [

x f x

f dx

C d dx

x F d dx

C x F d

= + =

+ =

+ _.

Definisi 7.

Dipunyai fungsi f terdefinisi pada selang buka I dan F suatu anti turunan f

pada selang I. Proses menentukan anti turunan dari fungsi f dinamakan imtegral tak tentu f pada I, dinyatakan dengan

∫

f(x)dx=F(x)+C

dengan C sembarang konstanta dan di baca integral tak tentu dai f terhadap variabel x.

Contoh 8

Tentukan

∫

cosxdx. Penyelesaian:

Tulis f(x)=cosx dan F(x)=sinx

Jelas '( ) [ ( )] (sin ) cosx f(x)

dx x d dx

x F d x

F = = = = .

Teorema 2.1

Jika n adalah sebarang bilangan rasional, n≠−1, maka

C n

x dx x

n

n +

+

= +

∫

1 1

.

Bukti:

Tulis F suatu anti turunan dari f. Jelas

∫

f(x)dx=F(x)+C.

Jadi '( ) ( ) [ ( )] f(x)

dx x F d x f x

F = ⇔ = .

dx C n

x d

n

⎥ ⎦ ⎤ ⎢

⎣

⎡ ₊

+ ⇔

+

1 1

dx x d n

n ) ( 1 1 +1

+ ⇔

) ( )

1 ( 1 1

x f x x n n

n n

= = + +

⇔ .

Teorema 2.2

(1)

∫

cf(x)dx=c

∫

f(x)dx, c suatu konstanta. (2)

∫

[f(x)+g(x)]dx=

∫

f(x)dx+

∫

g(x)dx

(3)

∫

[f(x)−g(x)]dx=

∫

f(x)dx−

∫

g(x)dx. Bukti:

(1) Tulis Fsuatu anti turunan dari f .

Jadi '( ) ( ) [ ( )] f(x)

dx x F d x f x

) ( . )] ( [

. c f x dx

x F d

c =

⇔

) ( . )] ( . [

x f c dx

x F c d

=

⇔ .

Jadi cF(x)suatu anti turunan dari cf(x). Jadi

∫

c.f(x)dx=c.F(x)=c

∫

f(x)dx.

(2) Tulis Fdan Gsuatu anti turunan dari f dan g. JadiF'(x)= f(x) dan G'(x)= g(x).

Jadi

∫

f(x)dx=F(x)+C dan

∫

g(x)dx=G(x)+C. Jadi )(F+G)'(x)=(f +g)(x .

Jadi )(F+G suatu anti turunan dari (f +g). Jadi

∫

(f +g)(x)dx=(F+G)(x)+C

] ) ( [ ] ) (

[F x +C₁ + G x +C₂ =

∫

+

∫

= f(x)dx g(x)dx.

(3) Tulis Fdan Gsuatu anti turunan dari f dan g. JadiF'(x)= f(x) dan G'(x)= g(x).

Jadi

∫

f(x)dx=F(x)+C dan

∫

g(x)dx=G(x)+C. Jadi )(F−G)'(x)=(f −g)(x .

Jadi )(F−G suatu anti turunan dari (f −g). Jadi

∫

(f −g)(x)dx=(F−G)(x)+C

] ) ( [ ] ) (

∫

−

∫

= f(x)dx g(x)dx.

Contoh 9

Tentukan: (a)

∫

4cosxdx dan (b)

∫

(x+x2)dx. Penyelesaian:

(a) Jelas

∫

4cosxdx=4

∫

cosxdx

) (sin 4 x+C =

C x 4 sin

4 +

=

K x+

=4sin , K =4C. (b) Jelas

∫

(x+x2)dx=

∫

xdx+

∫

x2dx

2 3 1 2

3 1 2

1

C x C

x + + +

=

2 1 3 2

3 1 2 1

C C x

x + + +

=

C x

x + +

= 2 3

3 1 2 1

, C=C₁+C₂.

Teorema 2.3

Dipunyai g suatu fungsi yang terdiferensialkan pada selang buka I dan F anti turunan dari f. Jika u= g(x),

∫

f[g(x)]g'(x)dx=

∫

f(u)du= F(u)+C =F[g(x)]+C. Bukti:

Dipunyai Rg ⊂ I.

Jadi '[ ( )] [ ( )]

(

[ ( )]

)

f[g(x)]

dx x g F d x

g f x g

Jadi

∫

f[g(x)]d[g(x)]= F[g(x)]+C

∫

= +

⇔ f[g(x)]g'(x)dx F[g(x)] C.

Contoh 10

Tentukan: (a)

∫

(x2 +1)10.2xdx dan (b)

∫

sin2 xcosxdx. Penyelesaian:

(a) Tulis 1u= x2 + .

Jelas x du xdx dx

du

2 2 ⇒ =

=

Jelas

∫

(x2 +1)10.2xdx=

∫

u10.du

C

u +

= 11

11 1

C

x + +

= ( 1)

11 1 ₂

.

(b) Tulis u=sinx.

Jelas x du xdx dx

du

cos cos ⇒ =

= .

Jelas

∫

sin2 xcosxdx=

∫

u2du

C

u +

= 3

3 1

C x+

= 3

sin 3 1

Teorema 2.4

Jika )U =U(x dan V =V(x) fungsi-fungsi yang memiliki turunan pada selang buka I, maka

∫

UdV =U.V −

∫

V.dU. Bukti:

Dipunyai d(U.V)=U.dV +V.dU . Jadi

∫

d(U.V)=

∫

(U.dV +V.dU)

∫

∫

+ =

⇔U.V U.dV V.dU

∫

∫

= −

⇔ U.dV U.V V.dU .

Contoh 11

Tentukan

∫

x.cosxdx. Penyelesaian:

Jelas

∫

x.cosxdx=

∫

xd(sinx)

∫

−

=x.sinx sinx.dx

C x x

x + +

= .sin sin .

F. FUNGSI INVERS, LOGARITMA, DAN EKSPONEN 1. Fungsi Invers

Definisi 8.

Dipunyai f fungsi dengan daerah definisi D. invers fungsi f , ditulis 1

− = f

g , adalah fungsi yang didefinisikan sebagai

x x f

Contoh 12

Dipunyai f(x)=2x, )x∈(−∞,∞ . Tunjukan bahwa inversnya adalah

x x g

2 1 )

( = .

Penyelesaian: Tulis )y= f(x

Jelas y=2x.

Jelas g y = y= .2x= x

2 1 2 1 )

( .

Jelas g f x = f x = .2x= x

2 1 ) ( 2 1 )) (

( , x∈(−∞,∞).

Contoh 13

Dipunyai f(x)= x, x≥0. Tujukan bahwa inversnya adalah g(x)=x2. Penyelesaian:

Tulis )y= f(x

Jelas y= x

Jelas g(y)=

( )

x 2 =x.

Jelas g(f(x))=[f(x)]2 =

( )

x 2 =x, x≥0. Deinisi 9.

Dipunyai f fungsi, f disebut fungsi satu-satu jika untuk setiap x₁,x₂ di domain f, x₁ ≠ x₂ maka f(x₁)≠ f(x₂).

Contoh 14

Tunjukan f fungsi satu-satu. Penyelesaian:

Ambil sembarang (x₁,y₁),(x₂,y₂)∈D, (x₁,y₁)≠(x₂,y₂). Jelas x₁ ≠ x₂ dan y₁ ≠ y₂.

Jelas )f(x₁,y₁)− f(x₂,y₂)=(2x₁2 +y₁)−(2x₂2 + y₂

) (

) 2 2

( x₁2 − x₂2 + y₁ −y₂ =

0

≠ .

Jadi ∀(x₁,y₁),(x₂,y₂)∈D,(x₁,y₁)≠(x₂,y₂), f(x₁,y₁)≠ f(x₂,y₂). Jadi f fungsi satu-satu.

Teorema 2.5

Dipunyai f suatu fungsi yang didefinisikan f :D→R. Jika f fungsi satu-satu maka

(i) f−1ada, dan

(ii) daerah definisi f−1adalah range f. Bukti:

Definisikan pemadanan f

f D

R

g: →

dengan g(y)= x,∀x∈R_f dan y= f(x). Ditunjukan g suatu fungsi.

Ambil y₁,y₂∈R_f dengan y₁ = y₂.

Karena y₁ = y₂, maka f(x₁)= f(x₂). Dipunyai f satu-satu.

Jadi x₁ = x₂. Jadi g suatu fungsi.

Jelas g(f(x))= g(y)= x, ∀x∈D_f .

Jadi terdapat fungsi invers g untuk f. Tulis = −1

f

g .

Jelas D_f−1 =Dg =Rf. Contoh 15

Tentukan invers dari fungsi f(x)=2x−4, x∈(−∞,∞). Penyelesaian:

Dipunyai f(x)=2x−4. Tulis y= f(x).

Jelas y=2x−4 4 2 = +

⇔ x y

2 2 2

4

+ = + =

⇔ x y y .

Jadi 2

2 ) (

1 = +

− _y y

f .

Jelas f− y = (2x−4)+2= x

2 1 ) ( 1

, )x∈(−∞,∞ .

Jadi 2 2 ) (

1 = +

− _x x

2. Fungsi Logaritma Asli Definisi 10.

Fungsi logaritma asli adalah fungsi yang didefinisikan oleh

dt t x=

∫

x

1 1

ln x > 0.

Definisi 11.

Dipunyai f suatu fungsi yang terdiferensialkan pada selang

( )

0,∞ , dengan

x x

f( )=ln , turunan dari f didefinisikan sebagai

, 1 ) (ln

x dx

x d

= x > 0.

Definisi 12.

Dipunyai u fungsi yang terdiferensialkan pada x pada selang buka I, dengan u=lnu, maka turunanya didefinisikan sebagai

, . 1 ) (ln

dx du u dx

u d

= u >0.

Contoh 16

Tentukan turunan dari: (a) f(x)=ln(x+x2) dan (b) f(x)=xln(1+x2). Penyelesaian:

(a) Jelas

dx x x d x

f'( ) [ln( )]

2

+ =

dx x x d x x d

x x

d ( )

. ) (

)]

[ln( 2

2

2 +

++ =

) 2 1 .( ) (

1

2 x

x

x+ +

) ( ) 2 1 ( 2 x x x + + = . (b) Jelas dx x f d x

f'( )= [ ( )]

dx x x

d[ ln(1+ 2)]

= dx x d x dx x d

x ). ( ) . [ln(1 )]

1 ln(

2

2 + +

+ = dx x d x d x d x

x . (1 )

) 1 ( )] 1 [ln( . ) 1 ln( 2 2 2 2 + ++ + + = x x x

x .2

) 1 ( 1 . ) 1 ln( 2 2 + + + = ) 1 ( 2 ) 1 ln( ₂ 2 2 x x x + + + = . Teorema 2.6

Jika a,b∈R, a>0, b>0, dan r rasional maka: (1) ln(ab)=lna+lnb

(2) a b b

a

ln ln ln ⎟= −

⎠ ⎞ ⎜ ⎝

⎛ _,

(3) ln(ar)=rlna. Bukti:

(1) Ambil sembarang x>0.

Pilih f(x)=lnax dan g(x)=lnx.

Jelas x a ax dx ax d ax d ax d dx x f d 1 . 1 ) ( ) ( ) (ln )] ( [ = =

x dx

x d dx

x g

d[ ( )] (ln ) 1

=

= .

Jadi f(x)= g(x)+C untuk suatu konstanta C. Jelas f(1)=g(1)+C ⇔lna=C.

Jadi f(x)= g(x)+lna

a x

ax ln ln

ln = +

⇔ .

Pilih x=b.

Jelas lnab=lna+lnb. (2) Dipunyai lnab=lna+lnb.

Pilih

b a= 1.

Jelas ln1 ln ln 1. ⎟=ln1=0

⎠ ⎞ ⎜ ⎝ ⎛ =

+ b

b b

b .

Jadi b b b

b ln1 ln 0 ln ln

1

ln = − = − =− .

Jadi a b

b a b

a b

a

ln ln 1 ln ln 1 . ln

ln ⎟= + = −

⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝

⎛ _.

(3) Dipunyai ax =ex.lna, ∀x∈R. Pilih r bilangan rasional. Jelas r∈R.

Jadi ar =er.lna. Jadi r r a

e

a ln .ln

ln =

e a r

ar .ln .ln ln =

⇔

a r ar .ln ln =

⇔ .

Jadi 0lnar =r.lna,∀a∈R,a> dan r bilangan rasional. Definisi 13.

Bilangan e adalah bilangan yang didefinisikan oleh persamaan lne=1. Telah ditunjukan e merupakan bilangan irasional dengan ketelitian sampai 12 desimal yakni e≈2,718281828459.

Berdasarkan teorema 2.6 point (3) diperoleh lnen =nlne=n.1=n. Teorema 2.7

Logaritma asli sebagai anti turunan dinyatakan

∫

dx= x +C

x ln

1

, x≠0.

Bukti:

Ambil sembarang x∈R, x≠0. Kasus x>0.

Jelas x = x

Jadi

x x

dx x d x d

x d dx

x d dx

x

d 1

) 1 .( 1 ) ( . ) (

)) (ln( )

(ln( )

(ln

= =

=

= .

Kasus x<0. Jelas x =−x.

Jelas

x x

dx x d x d

x d dx

x d dx

x

d ₁

) 1 .( 1 ) ( . ) (

)) (ln( )

(ln( )

(ln

= − − = − −−

= −

= .

Contoh 17 Tentukan

∫

+

+ _dx

x x

x

sin cos 1

Penyelesaian: Tulis u= x+sinx Jelas du =(1+cosx)dx.

Jelas

∫

=

∫

+ +

u du dx x x

x

sin cos 1

C u + =ln

C x

x+ +

=ln sin .

3. Fungsi Eksponen Definisi 14.

Fungsi eksponen asli merupakan fungsi yang didefinisikan sebagai )

exp(x

y= jika dan hanya jika x=lny. Definisi 15.

)

exp(x adalah fungsi yang didefinisikan sebagai exp(x)=ex, dengan x

bilangan rasional dan e adalah bilangan yang didefinisikan oleh persamaan

1 lne= . Teorema 2.8

Dipunyai x₁,x₂, dan r di R, r rasional maka: (i) _ex1_.ex2 =_ex1+x2_,

(ii) 1 2 2

1

x x x x

e e

e ₋

= , dan

(iii) _[ex1_]r =_erx1_. Bukti:

(i) Tulis 1 1

x

e

y = dan 2 2

x

e

Jelas _y1 =_ex1 ⇔ _x1 =ln_{y1 dan}

2 2

2 ln

2 _{x y}

e

y = x ⇔ = .

Jadi x₁+x₂ =lny₁ +lny₂

) . ln( _{1 2}

2

1 x y y

x + =

⇔

2 1. 2

1 _{y y}

ex x =

⇔ +

2 1 2 1.

x x

e y

y = +

⇔

2 1 2

1 x x x x

e e

e = +

⇔ .

(ii) Tulis 1 1

x

e

y = dan 2 2

x

e

y = .

Jelas _y1 =_ex1 ⇔ _x1 =ln_{y1 dan}

2 2

2 ln

2 _{x y}

e

y = x ⇔ = .

Jadi x₁−x₂ =lny₁ −lny₂

⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ = − ⇔

2 1 2

1 ln y y x

x

2 1 2

1 x x e y

y ₋

= ⇔

2 1 2 1

x x x x

e e

e ₋

=

⇔ .

(iii) Dipunyai lnar =r.lna. Tulis y=(ex1)r_.

Jadi ln_y=ln(_ex1)r =_r.ln_ex1 =_r._x1ln_e=_r._x1.1=_rx1. Jadi _y=_erx1_.

Teorema 2.9 x x

e dx

e d

=

) (

, ∀x∈R.

Bukti:

Ambil sembarang x∈R. Dipunyai lnex =x.

Jelas

dx x d dx

e

d x

) ( ) (ln

=

1 ) ( . ) (

) (ln

= ⇔

dx e d e d

e

d x

x x

1 ) ( . 1

= ⇔

dx e d e

x x

x x

e dx

e d

=

⇔ ( ) .

Jadi x x

e dx

e d

=

) (

untuk setiap x∈R.

Contoh 18

Tentukan turunan dari fungsi f(x)=exsinx. Penyelesaian:

Jelas

dx x f d x

f'( )= [ ( )]

dx e d( xsinx)

=

dx x x d x x d

e

d x x ( sin ) .

) sin (

) ( sin

=

] cos [sin

sin

x x x

ex x +

Teorema 2.10

Teorema 2.9 diatas memberikan formula integrasi sebagai berikut

∫

exdx=ex+C. Bukti:

Dipunyai

∫

exdx=ex +C.

Jelas

( )

dx C x F d dx

dx e

d x _{[ ( )+ ]}

=

∫

dx C e

d( x + )

=

dx C d dx

e

d( x) ( )

+ =

) (x f ex =

= .

Jadi F(x)+C suatu anti turunan dari f. Contoh 19

Tentukan

∫

e−3xdx. Penyelesaian: Tulis u=−3x. Jelas du =−3dx.

Jelas

∫

e− xdx=

∫

eu − )du

3 1 ( 3

∫

−

= eudu

3 1

C eu + − =

3 1

C

e x +

−

= −3

3 1

Pada penelitian ini metode yang digunakan penulis adalah studi pustaka. Langkah-langkah yang dilakukan adalah sebagai berikut:

A. Menentukan Masalah

Dalam tahap ini dilakukan pencarian sumber pustaka dan memilih bagian dalam sumber pustaka tersebut yang dapat dijadikan sebagai permasalahan.

B. Merumuskan Masalah

Tahap ini dimaksudkan untuk memperjelas permasalahan yang telah ditemukan yakni

1.Bagaimana membangun fungsi hiperbolik?

2.Bagaimana menentukan invers fungsi hiperbolik dan turunan serta anti turunan fungsi hiperbolik dan inversnya?

C. Studi Pustaka

Dalam tahap ini dilakukan kajian sumber-sumber pustaka dengan cara mengumpulakan data atau informasi yang berkaitan dengan permasalahan, mengumpulakan konsep pendukung seperti definisi dan teorema serta membuktikan teorema-teorema yang diperlukan untuk menyelesaikan permasalahan. Sehingga didapat suatu ide mengenai bahan dasar pengembangan upaya pemecahan masalah.

D. Analisis dan Pemecahan Masalah

Analisis dan pemecahan masalah dilakuan dengan langkah-langkah sebagai berikut:

1. Mempelajari dan mengkaji menggunakan referensi yang ada tentang bagaimana menurunkan model matematikanya.

2. Mengetahui secara jelas tentang sifat-sifat fungsi hiperbolik.

3. Mencari penurunan rumus fungsi hiperbolik dan invers serta turunan dan anti turunan fungsi hiperbolik dan inversnya.

E. Penarikan Simpulan

BAB IV PEMBAHASAN

A. FUNGSI HIPERBOLIK

Dalam masalah matematika terapan sering kita jumpai

kombinasi-kombinasi tertentu dari fungsi eksponen e dan x e−x sehingga kombinasi fungsi-fungsi tersebut diberi nama khusus. Untuk itu pada bagian ini akan dibahas secara khusus suatu fungsi yang memuat kombinasi dari kedua fungsi tersebut yakni fungsi hiperbolik. Untuk keperluan tersebut, dibangun fungsi-fungsi p dan q sebagai berikut.

+

→R

R

p : ,

2 ) (

x

e x

p = dan q :R→R+,

2 ) (

x

e x q

−

= .

Grafik fungsi p dan q diberikan pada Gambar 3 dan Gambar 4.

Gambar 3. Grafik fungsi p naik

Gambar 4. Grafik fungsi q turun

Selanjutnya dibangun fungsi f dan g yang didefinisikan sebagai jumlah dan selisih fungsi-fungsi p dan q. Dengan demikian

) ( ) ( )

(x p x q x

f = + dan g(x)= p(x)−q(x).

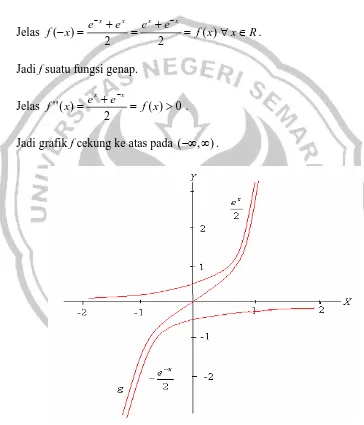
Grafik fungsi f dan g disajikan pada Gambar 5 dan Gambar 6.

Gambar 5. Grafik fungsi f :R→[1,∞)

) ( ) ( )

(x p x q x

Dipunyai )f :R→[1,∞ ,

2 )

(

x x

e e x f

− +

= .

Jelas 0 0

2 )

(

' = − > ∀ >

−

x e

e x f

x x

dan 0 0

2 )

(

' = − < ∀ <

−

x e

e x f

x x

.

Jadi grafik f naik pada [0,∞) dan turun pada (−∞,0].

Jelas f x e e e e f x x R

x x x x

∈ ∀ =

+ = + =

− − − ( )

2 2

)

( .

Jadi f suatu fungsi genap.

Jelas ( ) 0

2 )

(

'' = + = >

−

x f e e x f

x x

.

Jadi grafik f cekung ke atas pada (−∞,∞).

Gambar 6. Grafik fungsi g:R→R

) ( ) ( )

(x p x q x

g = −

Dipunyai g:R→R,

2 )

(

x x

e e x g

− −

Jelas g x e e x R x x ∈ ∀ > +

= − 0

2 )

(

' .

Jadi grafik fungsi g naik pada daerah asalnya.

Jelas g x e e e e g x x R

x x x x ∈ ∀ − = − − = − = − − − ( ) 2 2 ) ( .

Jadi f suatu fungsi ganjil.

Jelas ⎩ ⎨ ⎧ < − > + = − = − 0 , 0 , ) ( 2 ) ( '' x x x g e e x g x x .

Jadi grafik g cekung ke bawah pada (−∞,0] dan cekung ke atas pada [0,∞).

Berikut disajikan beberapa sifat fungsi f dan g. Sifat 4.1

(1) 1f(0)= dan g(0)=0,

(2) f'(x)= g(x)∀x∈R,

(3) g'(x)= f(x)∀x∈R,

(4) 1f2(x)−g2(x)= ,

(5) )f(x+ y)= f(x).f(y)+g(x).g(y ,

(6) )g(x+y)= f(x).g(y)+g(x).f(y ,

(7) ) ( 1 ) ( ) ( 1 ₂ 2 x g x g x f − = ⎥⎦ ⎤ ⎢⎣ ⎡

− , dan

(8) ) ( 1 ) ( ) ( 1 ₂ 2 x f x f x g = ⎥⎦ ⎤ ⎢⎣ ⎡ − . Bukti: Dipunyai 2 ) ( x x e e x f − +

= dan

(1) Jelas 1 2 2 2 ) 0 ( 0 0 = = +

= e e

f dan 0

2 0 2 ) 0 ( 0 0 = = −

=e e

g .

(2) Jelas ( )

2 )

(

' x e e g x

f x x = − = − .

(3) Jelas ( )

2 )

(

' x e e f x

g x x = + = − . (4) Jelas 2 2 2 2 2 2 ) ( ) ( ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ − − ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ + =

−g x ex e−x ex e−x x

f

4 2 4

2 2 2 2

2x x x x

e e

e

e − − − −

− + + = 1 4 4 = = . (5) Jelas 2 ) ( ) (x y y x e e y x f + − + ₊ = + 2 y x y x e e e

e + − −

=

[

x y x y

]

e e e

e + − −

= 2 1

[

( ( ) ( ))( ( ) ( )) ( ( ) ( ))( ( ) ( ))

]

2 1 y g y f x g x f y g y f x g x

f + + + − −

= ⎥⎦ ⎤ ⎢⎣ ⎡ + − − + + + + = ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 1 y g x g y f x g y g x f y f x f x g y g y f x g y g x f y f x f

[

2 ( ) ( ) 2 ( ) ( )

]

2 1 y g x g y f x f + = ) ( ). ( ) ( ).

(x f y g x g y

f +

(6) Jelas

2 )

(

) (x y y x e e y x g + − + ₋ = + 2 y x y x e e e

e − − −

=

[

x y x y

]

e e e

e − − −

= 2 1

[

( ( ) ( ))( ( ) ( )) ( ( ) ( ))( ( ) ( ))

]

2 1 y g y f x g x f y g y f x g x

f + + − − −

= ⎥⎦ ⎤ ⎢⎣ ⎡ − + + − + + + = ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 1 y g x g y f x g y g x f y f x f x g y g y f x g y g x f y f x f

[

2 ( ) ( ) 2 ( ) ( )

]

2 1 y f x g y g x f + = ) ( ). ( ) ( ).

(x g y g x f y

) ( 1 2

x f

= .

Sifat-sifat dari fungsi f dan g yang diberikan pada sifat 4.1 memperlihatkan adanya kemiripan dengan sifat-sifat yang dimiliki oleh fungsi trigonometri. Hal ini memberikan suatu ide untuk mendefinisikan fungsi f dan

g sebagai fungsi hiperbolik sebagai berikut.

Sifat 4.2

(1) Dipunyai f :R→R, fungsi sinus hiperbolik didefinisikan sebagai

2 sinh

x x

e e x

− −

= ,

(2) Dipunyai f :R→[1,∞), fungsi cosinus hiperbolik didefinisikan sebagai

2 cosh

x x

e e x

− +

= ,

(3) Dipunyai f :R→(−1,1), fungsi tangen hiperbolik didefinisikan sebagai

x x

x x

e e

e e x x

x ₋

− + − = =

cosh sinh

tanh ,

(4) Dipunyai f :R→(−∞,−1) ∪(1,∞), fungsi cotangen hiperbolik

didefinisikan sebagai

x x

x x

e e

e e x

x

x ₋

− − + = =

sinh cosh

coth , dan

(5) Dipunyai f :R→(0,1], fungsi secan hiperbolik didefinisikan sebagai

x x

e e x

hx ₋

+ =

= 2

cosh 1

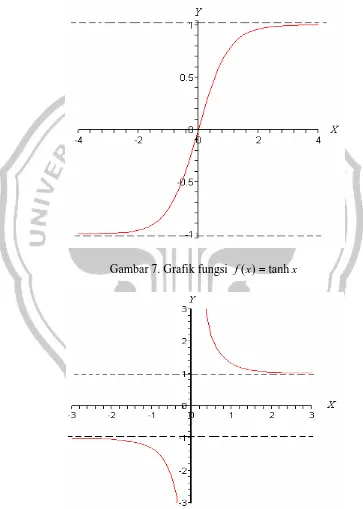
Gambar grafik fungsi tangen hiperbolik, cotangen hiperbolik, dan secan hiperbolik masing-masing diberikan pada Gambar 7, Gambar 8, dan Gambar 9.

Gambar 7. Grafik fungsi f(x)=tanhx

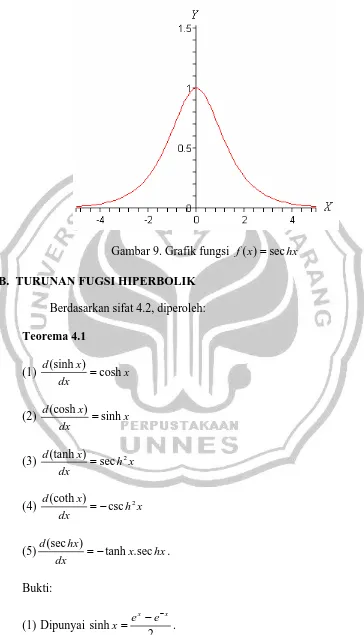
Gambar 9. Grafik fungsi f(x)=sechx

B. TURUNAN FUGSI HIPERBOLIK Berdasarkan sifat 4.2, diperoleh: Teorema 4.1

(1) x

dx x d

cosh )

(sinh

=

(2) x

dx x d

sinh ) (cosh

=

(3) h x

dx x

d 2

sec ) (tanh

=

(4) h x

dx x

d 2

csc )

(coth

− =

(5) x hx

dx hx d

sec . tanh )

(sec

−

= .

Bukti:

(1) Dipunyai

2 sinh

x x

e e x

− −

Jelas

dx e e d

dx x d

x x

⎟⎟⎠ ⎞ ⎜⎜⎝

⎛ − =

−

2 )

(sinh

dx e e

d( x x)

2

1 − −

=

) (

2

1 x x

e

e + −

=

x

cosh

= .

Jadi x

dx x d

cosh )

(sinh

= .

(2) Dipunyai

2 cosh

x x

e

e + −

= .

Jelas

dx e e d

dx x d

x x

⎟⎟⎠ ⎞ ⎜⎜⎝

⎛ + =

−

2 )

(cosh

dx e e

d( x x)

2

1 + −

=

) (

2

1 x x

e

e − −

=

x

sinh

= .

Jadi x

dx x d

sinh ) (cosh

= .

(3) Dipunyai

2 sinh

x x

e e x

− −

= dan

2 cosh

x x

e

e + −

= .

Jelas

dx x x d

dx x

d ⎟⎠

⎞ ⎜

⎝ ⎛

= cosh

sinh )

dx e e

e e

d _{x x}

x x ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ + − = − − 2 ) ( ) ( ) ( ) ( ) ( x x x x x x x x x x e e dx e e d e e dx e e d e e − − − − − + + − − − + = 2 ) ( ) )( ( ) )( ( x x x x x x x x x x e e e e e e e e e e − − − − − +− − − + + = 2 2 2 ) ( ) ( ) ( x x x x x x e e e e e e − − − +− − + = 2 2 ) ( ) (

1 _{x x}

x x e e e e − − + − − = 2 1 ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ + − −

= x −₋x

x x e e e e x 2 tanh 1− = x h2 sec = .

Jadi h x

dx x d 2 sec ) (tanh = . (4) Dipunyai 2 sinh x x e e x − −

= dan

2 cosh

x x

e

e + −

= . Jelas dx x x d dx x

d ⎟⎠

⎞ ⎜ ⎝ ⎛ = sinh cosh ) (coth dx e e e e

d _{x x}

2 ) ( ) ( ) ( ) ( ) ( x x x x x x x x x x e e dx e e d e e dx e e d e e − − − − − − − + − + − = 2 ) ( ) )( ( ) )( ( x x x x x x x x x x e e e e e e e e e e − − − − − −− + + − − = 2 2 2 ) ( ) ( ) ( x x x x x x e e e e e e − − − −− + − = 2 2 ) ( ) (

1 _{x x}

x x e e e e − − − + − = 2 1 ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ − + −

= x ₋−x

x x e e e e x 2 coth 1− = x h2 csc − = .

Jadi h x

dx x d 2 csc ) (coth − = . (5) Dipunyai 2 cosh x x e

e + −

= . Jelas dx x d dx hx

d ⎟⎠

⎞ ⎜ ⎝ ⎛ = cosh 1 ) (sec dx e e

d _{x x}⎟

) (

2 ) (

) (

x x x x

x x

e e e e

e e

− −

−

+ +

− − =

hx x sec. tanh

−

= .

Jadi x hx

dx hx d

sec . tanh )

(sec

−

= .

C. INVERS FUNGSI HIPERBOLIK

Fungsi invers sinus hiperbolik, cosinus hiperbolik, tangen hiperbolik, cotangen hiperbolik, dan secan hiperbolik, masing-masing dinyatakan dengan

1

sinh− , cosh−1, tanh−1, coth−1, dan sech , didefinisikan sebagai −1

(1) y=sinh−1x⇔ x=sinhy,

(2) y=cosh−1x⇔ x=coshy,

(3) y=tanh−1x⇔ x=tanhy,

(4) y=coth−1x⇔ x=cothy, dan

(5) y=sech−1x⇔x=sechy.

Lebih jauhnya tentang invers fungsi hiperbolik disajikan dalam uraian berikut.

(1) Invers Fungsi Sinus Hiperbolik Dipunyai f :R→R, f(x)=sinhx.

Ambil sembarang x₁,x₂∈R,x₁ ≠x₂. Jelas f(x₁)− f(x₂)=sinhx₁−sinhx₂

2 2

2 2 1

1 x x x

x

e e e

e − − −

0 2

) (

)

( 1 2 2 1

≠ −

+ −

= ex ex e−x e−x .

Jadi fungsi f satu-satu.

Berikutnya ditunjukan f fungsi pada. Ambil sembarang x∈R.

Tulis x=sinhy, untuk suatu y∈R.

Jelas

2 y y

e e x

− − =

y y

e e

x= − −

⇔2

) (

2xey =ey ey −e−y ⇔

1

2 = 2 −

⇔ y y

e xe

0 1 2

2 − − =

⇔e y eyx

[

( )2 −2 + 2

]

−(1+ 2)=0

⇔ ey eyx x x

( )

1 0

) (

2 2

2 − + =

−

⇔ ey x x

2 2

1

1 x e x x

x

ey = − + ∨ y = + +

⇔ .

Jelas ey =x+ 1+x2 ⇔ y=ln(x+ 1+x2).

Jadi ln( 1 2) ( )

y f x R x x

y R

x∈ ∃ = + + ∈ ∋ =

∀ .

Jadi f suatu fungsi pada.

Jadi f :R→R, f(x)=sinhx memiliki invers.

Jelas y=sinh−1x⇔ x=sinhy

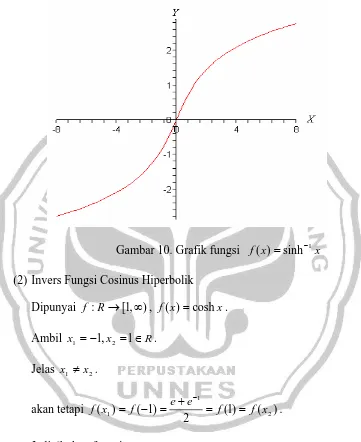
Gambar grafik fungsi f :R→R, f(x)=sinh−1x diberikan pada

Gambar 10.

Gambar 10. Grafik fungsi f(x)=sinh−1x

(2) Invers Fungsi Cosinus Hiperbolik

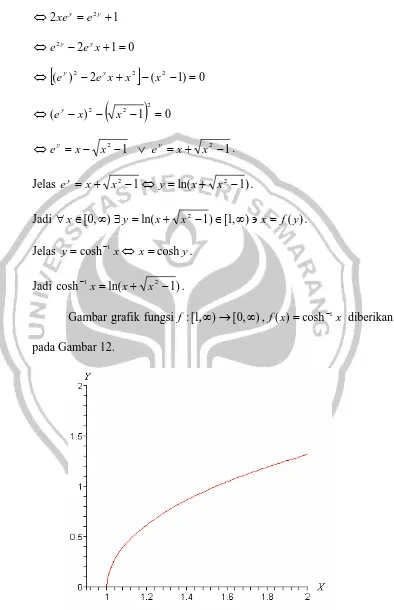
Dipunyai )f :R→[1,∞ , f(x)=coshx.

Ambil x₁ =−1,x₂ =1∈R. Jelas x1 ≠ x2.

akan tetapi (1) ( )

2 ) 1 ( )

( ₂

1

1 f f x

e e f

x

f = − = + = =

−

.

Jadi f bukan fungsi satu-satu.

Jadi fungsi f :R→[1,∞), f(x)=coshx tidak memiliki invers.

Agar f memiliki invers maka kita definis