Informasi Dokumen
- Penulis:
- Didik Nurhadiyanto
- Sekolah: Penerbit K-Media
- Mata Pelajaran: Getaran Struktur
- Topik: Getaran Struktur
- Tipe: buku
- Tahun: 2015
- Kota: Yogyakarta
Ringkasan Dokumen
I. DASAR-DASAR GETARAN
Bab ini membahas konsep dasar getaran, yang merupakan gerakan bolak-balik suatu benda dari posisi keseimbangan. Getaran dapat dibedakan menjadi getaran bebas dan paksa, tergantung pada adanya gaya luar. Pemahaman tentang getaran sangat penting dalam rekayasa, terutama dalam mendesain struktur yang tahan terhadap getaran. Konsep dasar meliputi energi kinetik dan potensial, serta analisis parameter seperti frekuensi dan amplitudo yang menjadi dasar untuk memahami perilaku sistem bergetar.
1.1 Konsep Dasar Getaran
Konsep dasar getaran menjelaskan bahwa sistem yang bergetar mengubah energi potensial menjadi energi kinetik, dan sebaliknya. Contoh yang sering digunakan adalah pendulum sederhana, di mana energi potensial maksimum terjadi pada posisi tertinggi dan energi kinetik maksimum pada posisi terendah. Pemahaman ini penting untuk menganalisis sistem dinamik dan merancang struktur yang dapat menahan gaya getaran.
1.2 Derajat Kebebasan
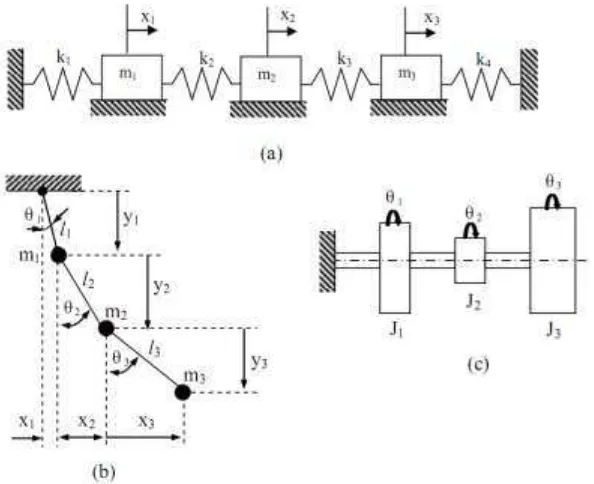
Derajat kebebasan (DOF) menunjukkan jumlah koordinat independen yang diperlukan untuk mendeskripsikan posisi sistem. Sebuah partikel dalam ruang memiliki tiga DOF, sedangkan benda kaku memiliki enam DOF. Pemahaman tentang DOF penting dalam analisis sistem dinamik, karena menentukan kompleksitas perhitungan dan model yang diperlukan untuk analisis.
1.3 Sistem Diskrit dan Kontinu
Sistem getaran dapat dibedakan menjadi sistem diskrit, di mana massa terpusat pada titik tertentu, dan sistem kontinu, di mana massa terdistribusi secara merata. Analisis sistem kontinu lebih kompleks, sering kali memerlukan metode numerik seperti elemen hingga. Pemahaman kedua sistem ini penting untuk merancang dan menganalisis struktur yang berbeda dalam rekayasa.
1.4 Klasifikasi Getaran
Getaran dapat diklasifikasikan berdasarkan beberapa kriteria, termasuk getaran bebas dan paksa, linier dan non-linier, serta teredam dan tanpa redaman. Klasifikasi ini membantu insinyur dalam menentukan metode analisis yang tepat dan memahami perilaku sistem di bawah kondisi yang berbeda.
1.5 Prosedur Menganalisa Getaran
Prosedur analisis getaran melibatkan pemodelan matematika, penyusunan persamaan gerak, penyelesaian persamaan, dan interpretasi hasil. Proses ini penting untuk meramalkan respon sistem terhadap eksitasi dan untuk merancang struktur yang aman dan efektif.
1.6 Elemen Pegas
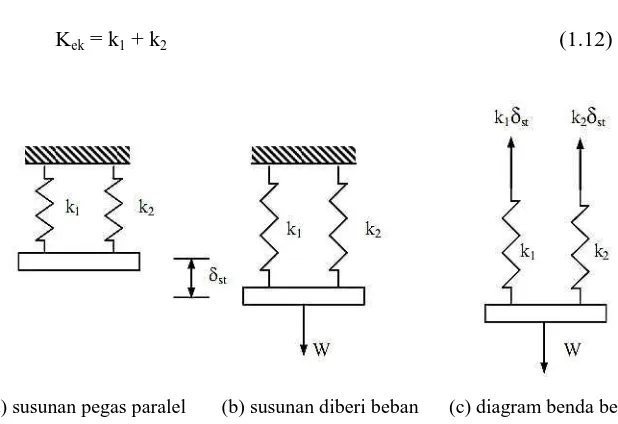
Elemen pegas berfungsi untuk menyimpan energi dan memberikan gaya pemulihan saat sistem bergetar. Dalam analisis, hubungan antara gaya dan defleksi pegas dinyatakan dalam hukum Hooke. Pemahaman tentang elemen pegas sangat penting dalam desain sistem mekanik yang melibatkan komponen elastis.
1.7 Massa atau Inersia Elemen
Massa dalam sistem bergetar berfungsi sebagai elemen inersia yang mempengaruhi gerakan sistem. Analisis massa penting untuk memahami bagaimana sistem bereaksi terhadap gaya dan untuk merancang elemen struktural yang aman.
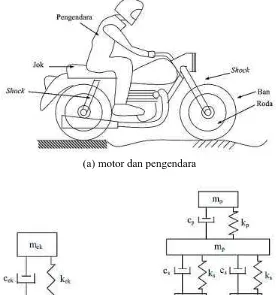
1.8 Elemen Redaman (Damping Element)
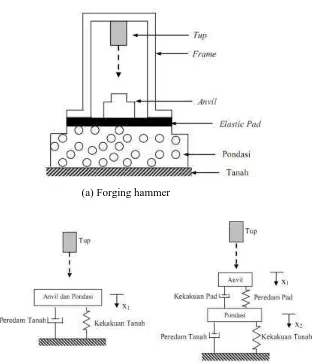
Redaman dalam sistem bergetar berfungsi untuk mengurangi amplitudo osilasi dan menyerap energi. Tipe redaman yang umum termasuk redaman viskos dan Coulomb. Memahami elemen redaman sangat penting untuk merancang struktur yang dapat mengatasi getaran berbahaya.
1.9 Gerak Harmonik
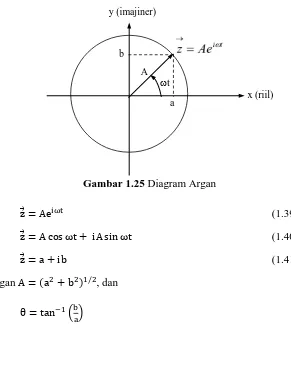
Gerak harmonik adalah gerakan osilasi yang teratur dan dapat dijelaskan melalui fungsi sinusoidal. Pemahaman tentang gerak harmonik sangat penting dalam analisis sistem bergetar dan dalam aplikasi rekayasa seperti perancangan pegas dan sistem suspensi.
1.10 Gerak Periodik
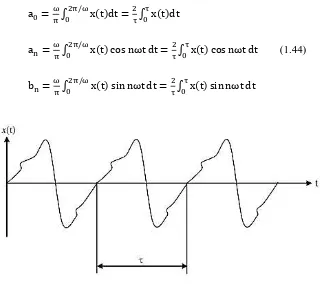
Gerak periodik melibatkan variasi yang berulang pada interval tertentu. Konsep ini penting dalam analisis gelombang dan getaran, serta dalam aplikasi teknik seperti analisis getaran pada struktur dan mesin.
II. GETARAN BEBAS SISTEM SATU DERAJAD KEBEBASAN
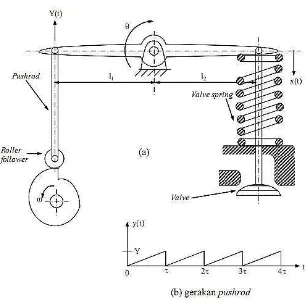
Bab ini membahas getaran bebas pada sistem satu derajat kebebasan, di mana sistem bergetar tanpa pengaruh gaya luar setelah diberi gangguan awal. Fokus utama adalah pada penentuan frekuensi natural dan persamaan gerak sistem, yang merupakan fungsi dari massa dan kekakuan sistem. Memahami getaran bebas sangat penting dalam merancang struktur yang tahan terhadap getaran.
2.1 Persamaan Gerak dan Frekuensi Getaran Translasi
Persamaan gerak untuk sistem pegas-massa didasarkan pada hukum Newton dan memberikan informasi tentang frekuensi natural sistem. Frekuensi natural adalah parameter kunci dalam analisis getaran, karena menentukan respons sistem terhadap eksitasi luar.
2.2 Getaran Bebas untuk Sistem Torsional tanpa Redaman
Getaran torsional melibatkan rotasi benda kaku dan analisis momen torsional. Memahami getaran torsional penting untuk aplikasi seperti desain poros dan sistem rotasi lainnya.
2.3 Metode Energi (Metode Lagrange)
Metode Lagrange memungkinkan analisis gerakan sistem berdasarkan prinsip kekekalan energi. Metode ini sangat berguna untuk sistem yang lebih kompleks, di mana pendekatan tradisional mungkin tidak efektif.
2.4 Kondisi Stabilitas
Kondisi stabilitas sistem bergetar sangat penting untuk memastikan bahwa sistem tidak mengalami osilasi yang berlebihan atau ketidakstabilan. Analisis stabilitas membantu dalam desain sistem yang aman dan efektif.
2.5 Metode Energi Rayleigh
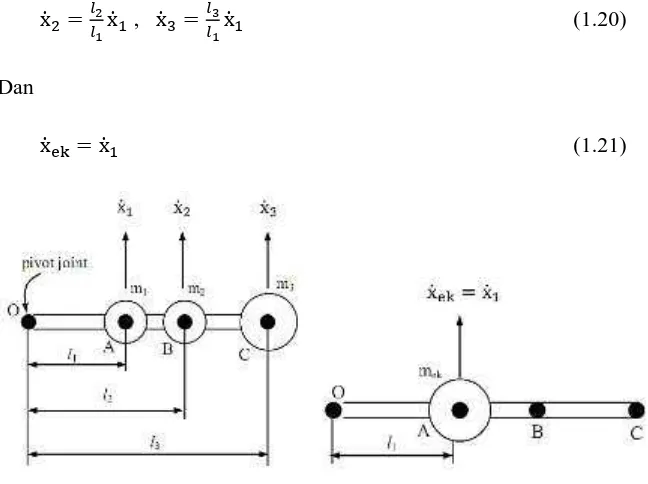
Metode Rayleigh digunakan untuk memperkirakan frekuensi natural sistem dengan massa terdistribusi. Metode ini memberikan pendekatan yang lebih baik dalam analisis sistem kompleks, dengan mempertimbangkan kontribusi massa yang biasanya diabaikan.
Referensi Dokumen
- Elements of Vibration Analysis ( Meirovitch, L. )
- Vibration and Sound ( Morse, M. )
- Mechanical Vibration ( Rao. S., S. )
- Theory of Vibration with Application ( Thompson, W.T. )