Efektivitas pipa berprofil segiempat dengan sirip di bagian dalam pada kasus 2 dimensi keadaan tak tunak - USD Repository

Tugas Akhir

Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Teknik

Program Studi Teknik Mesin

Disusun oleh : Yohanes Johan Cahyadi

NIM 055214002

PROGRAM STUDI TEKNIK MESIN

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

ii Final Project

Presented As Partial Fulfillment Of The Requirement As To Obtain The Sarjana Teknik Degree

in Mechanical Engineering

Disusun oleh : Yohanes Johan Cahyadi Student Number: 055214030

MECHANICAL ENGINEERING STUDY PROGRAM

SCIENCE AND TECHNOLOGY FACULTY

SANATA DHARMA UNIVERSITY

YOGYAKARTA

v "Efektivitas Pipa Berprofil Segiempat Dengan Sirip Di Bagian Dalam Pada Kasus 2 Dimensi Keadaan Tak Tunak" tidak terdapat karya yang pernah diajukan dan dibuat di perguruan tinggi manapun. Sepanjang pengetahuan penulis tidak terdapat pula karya atau pendapat yang pernah diterbitkan, ditulis, atau cara publikasi lain, kecuali mengambil atau mengutip data yang disebutkan di dalam daftar pustaka.

Yogyakarta, 8 Juni 2009

Penulis

vi permukaan pipa. Penelitian ini bertujuan membandingkan panas yang dilepas keluar saluran pada pipa segiempat bersirip di bagian dalamnya dengan pipa segiempat tanpa sirip dari waktu ke waktu, serta mengetahui pengaruh harga koefisien konveksi dalam saluran hDterhadap efektivitas saluran.

Benda uji pertama adalah model pipa segiempat bersirip dalam dengan dimensi 40 mm  40 mm, ketebalan 4 mm, sepanjang 1 meter. Sirip berdimensi 4 mm  10 mm terletak pada tiap sisi dalam saluran. Benda uji kedua adalah pipa dengan dimensi yang sama namun tanpa sirip di dalamnya. Dengan x = 1 mm. Saluran berbahan aluminium, fluida panas mengalir di dalam saluran dengan hD = 200 W/m2oC, fluida dingin di luar saluran dengan hL = 200 W/m2 oC. Mula-mula pipa bersuhu = Ti, secara tiba-tiba dikondisikan dalam lingkungan dengan suhu fluida dalam = Tf dan suhu fluida luar = T. Sifat-sifat bahan seperti massa jenis massa jenis (ρ), panas jenis (c) dan konduktivitas termal (k) diasumsikan seragam (tidak merupakan fungsi posisi) dan tetap (tidak berubah terhadap waktu). Benda tidak mengalami perubahan bentuk dan volume selama proses berlangsung. Perpindahan panas konduksi yang terjadi di dalam sirip berlangsung dalam 2 arah yaitu x dan y. Tidak terdapat pembangkitan energi pada pipa. Nilai hDdan hL tetap dan merata. Suhu fluida di dalam dan di luar saluran nilainya tetap (Tf dan T∞ tetap) dan seragam. Metode yang digunakan adalah metode beda hingga cara eksplisit, yang dipermudah perhitungan dengan membagi benda uji menjadi 1/8

bagian. Penyelesaian dengan membandingkan panas yang dilepas saluran bersirip terhadap saluran tanpa sirip dari waktu ke waktu dengan variasi pengkondisian harga hDsaja, hL saja, dan bahan saja terhadap kondisi standar, juga membuktikan pengaruh variasi harga hD terhadap efektivitas saluran.

Diperoleh kesimpulan bahwa besar laju perpindahan panas pada saluran bersirip lebih besar harganya daripada saluran tanpa sirip. Pada saat tunak untuk

kondisi awal, hD = 50 W/m2 oC, hD = 500 W/m2oC, hL = 50 W/m2 oC, hL = 500

W/m2 oC, pipa bahan besi murni, pipa bahan tembaga, n fin

viii menyelesaikan Tugas Akhir yang berjudul “Efektivitas Pipa Berprofil Segiempat

Dengan Sirip Di Bagian Dalam Pada Kasus 2 Dimensi Keadaan Tak Tunak”.

Banyak suka dan duka yang penulis alami selama penulisan Tugas Akhir

ini dan semuanya memunculkan kesan berharga. Betapa waktu itu berharga,

betapa peran orang tua itu berharga, dan betapa kehadiran teman serta saudara

berharga dalam pembentukan pribadi. Karenanya penulis ingin mengucapkan

terima kasih kepada :

1. Yosef Agung Cahyanta S.T., M.T., selaku Dekan Fakultas Sains dan

Teknologi Universitas Sanata Dharma.

2. Budi Sugiharto S.T, M.T., selaku Ketua Program Studi Teknik Mesin dan

Dosen Pembimbing Akademik.

3. Ir. P. K. Purwadi, M.T., selaku Dosen Pembimbing Tugas Akhir yang telah

memberikan bimbingan, motivasi, dan pandangan hidup yang positif kepada

penulis sehingga dapat menyelesaikan Tugas Akhir ini dengan baik.

4. Ayahku, Stefanus Bandono; dan Ibuku, Lie Fong Ing; dan kakak perempuanku

yang tercinta, Christie Maria; yang selalu mendoakan, memberi semangat, dan

dorongan untuk selalu menjadi yang terbaik.

Penulis menyadari akan adanya kekurangan dalam penyusunan karya

ix Yogyakarta, 8 Juni 2009

x

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

HALAMAN PERNYATAAN KEASLIAN KARYA ... v

INTISARI ... vi

HALAMAN PERNYATAAN PERSETUJUAN ... vii

KATA PENGANTAR ...viii

DAFTAR ISI ... x

DAFTAR TABEL ... xiv

DAFTAR GAMBAR DAN GRAFIK ... xv

BAB I. PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Batasan Masalah ... 5

1.2.1 Bentuk Geometri ... 5

1.2.2 Model Matematik ... 6

1.2.3 Kondisi Awal ... 6

1.2.4 Kondisi Batas ... 6

1.2.5 Asumsi ... 6

1.3 Tujuan ... 7

1.4 Manfaat ... 7

xi

2.2.2 Difusivitas Termal ... 13

2.3 Perpindahan Panas Konveksi ... 14

2.3.1 Angka Reynolds ... 15

2.3.1.1 Angka Reynolds untuk Kondisi Plat Datar ... 15

2.3.1.2 Angka Reynolds untuk Kondisi Aliran Dalam Saluran ... 17

2.3.1.3 Angka Reynolds untuk Kondisi Aliran di Luar Saluran ... 18

2.3.2 Angka Prandtl ... 19

2.3.3 Konveksi Bebas ... 20

2.3.4 Konveksi Paksa ... 22

2.3.5 Angka Nusselt ... 22

2.3.5.1 Angka Nusselt pada Kasus Plat Datar ... 24

2.3.5.2 Angka Nusselt pada Aliran Dalam Saluran ... 25

2.3.5.3 Diameter Hidraulik ... 27

2.3.5.4 Angka Nusselt pada Aliran Silang Silinder ... 29

2.3.5.5 Angka Nusselt pada Aliran Silang Silinder Tak Bundar ... 31

2.3.5.6 Konveksi Bebas dari Silinder Horizontal ... 32

2.3.5.7 Konveksi Bebas dari Plat Horizontal ... 33

2.3.5.8 Konveksi Bebas dari Plat Rata Vertikal ... 34

2.3.5.9 Konveksi Bebas dari Permukaan Miring ... 34

xii

3.2 Kesetimbangan Energi ... 39

3.3 Penurunan Model Matematik Pada Benda Bersirip ... 40

3.4 Persamaan Numerik Node Utama ... 43

3.4.1 Node Dalam (Node a pada Gambar 3.3)... 44

3.4.2 Node Rusuk (Node b pada Gambar 3.3) ... 46

3.4.3 Node Sudut Luar (Node c pada Gambar 3.3) ... 48

3.4.4 Node Sudut Dalam (Node d pada Gambar 3.3) ... 50

3.5 Laju Perpindahan Panas Pada Keadaan Tak Tunak ... 52

3.5.1 Pada Pipa Bersirip ... 53

3.5.2 Pada Pipa Tanpa Sirip ... 54

3.6 Efektivitas Saluran ... 55

BAB IV. METODOLOGI PENELITIAN ... 57

4.1 Benda Uji ... 57

4.2 Variasi Pengujian ... 59

4.3 Metode Penelitian... 60

4.4 Peralatan Pendukung ... 60

4.5 Cara Pengambilan Data ... 60

4.6 Cara Pengolahan Data ... 62

BAB V. PERHITUNGAN DAN PEMBAHASAN... 64

xiii

5.1.2.2 Variasi Terhadap hL ... 70

5.1.2.3 Variasi TerhadapBahan Pipa ... 73

5.2 Efektivitas Saluran Terhadap Berbagai Besaran hD ... 77

5.3 Pembahasan Laju Perpindahan Panas ... 80

5.4 Pembahasan Efektivitas Saluran ... 84

BAB VI. KESIMPULAN DAN SARAN ... 87

6.1 Kesimpulan ... 87

6.2 Saran ... 88

DAFTAR PUSTAKA ... 89

xiv Tabel 2.2. Perpindahan Panas dan Gesekan Fluida untuk Aliran Laminaryang

Berkembang Penuh dalam Saluran dengan Berbagai Penampang. ... 28

Tabel 2.3. Konstanta C dan n Aliran Silang ... 30

Tabel2.4. Konstanta untuk Perpindahan Panas dari Silinder Tak Bundar ... 32

Tabel 5.1. Tabel Laju Perpindahan Panas Untuk Berbagai Pengkondisian ... 80

L.1. Tabel Sifat-sifat Air / Zat Cair Jenuh (Holman, 1997, hal 593) ... 91

L.2. Tabel Sifat-sifat Logam (Holman, 1997, 581) ... 92

L.3. Tabel Sifat-sifat Logam, Lanjutan (Holman, 1997, 582)... 93

L.4. Tabel Sifat-sifat Logam, Lanjutan (Holman, 1997, 583)... 94

xv

Gambar 1.2. Berbagai Profil Sirip ... 3

Gambar 1.3. Aplikasi Sirip Pada Blok Mesin dan Perangkat Komputer ... 3

Gambar 1.4. Model Pipa: a) Bersirip b) Tak Bersirip ... 5

Gambar 2.1. Perpindahan Panas Konduksi ... 11

Gambar 2.2. Perpindahan Panas Konveksi ... 14

Gambar 2.3. Berbagai Daerah Aliran Lapisan Batas di Atas Plat Rata ... 16

Gambar 2.4. Profil Kecepatan Aliran Dalam Tabung... 17

Gambar 2.5. Konveksi Bebas Pada Lapisan Batas Di Atas Plat Rata Vertikal ... 21

Gambar 2.6. Aliran Fluida pada Bidang Datar ... 22

Gambar 2.7. Potongan Penampang Pipa Yang Melepas Panas ke Lingkungan Luar Secara Konveksi ... 36

Gambar 3.1. Kesetimbangan Energi Dalam Volume Kontrol... 40

Gambar 3.2. Kesetimbangan Energi Pada Volume Kontrol Benda 2 Dimensi ... 40

Gambar 3.3. Posisi Node Pada Penampang Pipa 2 Dimensi ... 44

Gambar 3.4. Node Dalam Pada Penampang Pipa 2 Dimensi ... 44

Gambar 3.5. Node Rusuk Pada Penampang Pipa 2 Dimensi ... 46

Gambar 3.6. Node Sudut Luar Pada Penampang Pipa 2 Dimensi ... 48

Gambar 3.7. Node Sudut Dalam Pada Penampang Pipa 2 Dimensi ... 50

Gambar 3.8. Perpindahan Panas Pada Sisi Luar Pipa Bersirip ... 53

xvi Gambar 5.1. Grafik Q berbahan Aluminium dengan hD = hL = 200 W/m2 oC ... 65

Gambar 5.2. Grafik Q berbahan Aluminium dengan hD = hL = 200 W/m2 oC ... 66 Gambar 5.3. Grafik Q pada Aluminium dengan hD = 50 W/m2 oC

dan hL = 200 W/m2 oC ... 67

Gambar 5.4. Grafik Q pada Aluminium dengan hD = 500 W/m2 oC

dan hL = 200 W/m2 oC ... 68

Gambar 5.5. Grafik Q pada Aluminium dengan hD = 50 W/m2 oC

dan hL = 200 W/m2 oC ... 69

Gambar 5.6. Grafik Q pada Aluminium dengan hD = 500 W/m2 oC

dan hL = 200 W/m2 oC ... 69

Gambar 5.7. Grafik Q pada Aluminium dengan hD = 200 W/m2 oC

dan hL = 50 W/m2 oC ... 70

Gambar 5.8. Grafik Q pada Aluminium dengan hD = 200 W/m2 oC

dan hL = 50 W/m2 oC ... 71

Gambar 5.9. Grafik Q pada Aluminium dengan hD = 200 W/m2 oC

dan hL = 500 W/m2 oC ... 72

Gambar 5.10. Grafik Q pada Aluminium dengan hD = 200 W/m2 oC

dan hL = 500 W/m2 oC ... 73

Gambar 5.11. Grafik Q pada Kondisi Standar Dengan Bahan Besi Murni ... 74

1 1.1 Latar Belakang

Dewasa ini peran teknologi sangat berpengaruh dalam kehidupan kita.

Sebagian besar benda di sekitar kita adalah hasil perkembangan teknologi dan

sudah manjadi bagian dari kehidupan kita sehari-hari. Dengan kata lain kita tidak

dapat hidup tanpa teknologi itu sendiri.

Beberapa benda hasil teknologi yang dapat kita jumpai diantaranya sistem

pengkondisian udara (AC), kendaraan bermotor, dan komputer. Ketiga benda ini

memiliki persamaan yaitu perkembangannya diarahkan untuk efisiensi yang lebih

tinggi dengan kapasitas yang makin besar.

Tuntutan ini memiliki konsekuensi terutama berkaitan dengan panas yang

dipindahkan. Pada sistem AC terjadi proses pengkondisian udara yang

menukarkan panas ruangan dengan freon, pada kendaraan bermotor terjadi

pelepasan panas oleh blok mesin ke lingkungan sekitar akibat panas berlebih,

sedangkan pada komputer terjadi proses meningkatnya suhu prosesor akibat

aplikasi yang dijalankan. Apabila pada ketiga sistem di atas proses perpindahan

panas yang terjadi tidak mencukupi, maka kinerja dan efisiensinya akan menurun,

bahkan dimungkinkan terjadi kerusakan.

Beberapa upaya dilakukan untuk mendapatkan perpindahan panas yang

mencukupi, diantaranya mengganti beberapa bagian sistem dengan bahan yang

(fin) pada bagian yang berfungsi sebagai penukar panas (heat exchanger). Dengan

bahan yang konduktivitas termalnya lebih tinggi, laju aliran kalor yang melewati

benda tersebut juga makin besar, begitu juga penggunaan sirip akan menambah

luas permukaan pelepas panas sehingga aliran panas makin besar.

Sebagai media penukar panas, aplikasi sirip meluas hingga mencakup

sebagian besar rancang bangun sistem termal. Kelebihan sirip ini adalah laju

perpindahan panas dapat dicapai setinggi-tingginya dengan harga konstruksi yang

rendah dan dimensi yang kecil.

Walaupun penambahan sirip nampak menguntungkan karena

meningkatkan laju aliran panas, tetapi bersamaan dengan hal itu akan timbul

tahanan konduksi pada bagian permukaan suatu benda dimana sirip tersebut

dipasang, sehingga penambahan sirip pada suatu permukaan benda padat tidak

selalu meningkatkan laju perpindahan panas (Holman, 1997). Oleh karena itu

bentuk dan konfigurasi dari sirip harus dirancang secara khusus demi

mendapatkan laju perpindahan panas yang optimal.

Berikut berbagai model profil sirip yang biasa digunakan dalam

meningkatkan laju aliran panas.

Gambar 1.2. Berbagai Profil Sirip: (a) Balok, (b) Segitiga, (c) Radial, (d) Kerucut

Gambar 1.3. Aplikasi Sirip Pada Blok Mesin dan Perangkat Komputer

Berbagai penelitian tentang sirip telah dilakukan oleh beberapa orang.

Salah satunya oleh Acadêmico Hélio Ramos dan Prof. Luiz Freire. Dalam

jurnalnya ini dijelaskan penelitian yang bertujuan tentang penggunaan Finite

Volume Methods (FVM) dalam menggantikan cara perhitungan konvensional

pada berbagai profil sirip dua dimensi. Dalam kasimpulannya dituliskan bahwa

metode FVM ini dapat digunakan untuk menyelesaikan problem perpindahan

bahkan dengan cara yang sama dapat digunakan pada benda tiga dimensi.

(www.scielo.br ; 3 Februari 2009, 08:57 WIB)

Penelitian yang lain dilakukan oleh Joko Winarno. Penelitiannya ini

bertujuan mengkaji karakteristik dari sirip radial berprofil segiempat dalam suatu

proses perpindahan panas satu dimensi melalui pemodelan numerik. Studi

dilakukan dengan menggunakan seperangkat komputer dan bahasa pemrograman

Fortran. Validasi dilakukan dengan membandingkan hasil kajian numerik dengan

hasil kajian analitis. Dalam penelitian ini didapatkan kesimpulan bahwa

pendekatan yang dihasilkan melalui model komputasi yang didasarkan pada

metode numerik sangat layak digunakan untuk menggambarkan mekanisme

perpindahan panas pada siri radial berprofil segiempat. Kesimpulan yang lain

bahwa untuk mendapatkan laju aliran kalor yang maksimum dari sirip radial

berprofil segiempat, maka harus diupayakan sedemikian sehingga nilai koefisien

perpindahan panas konveksi yang setinggi mungkin.

Hal lain yang berkaitan dengan penelitian ini adalah pengembangan

teknologi terbaru dari PT. LG Innotek, yaitu model pipa penukar panas yang

dibentuk sedemikian rupa sehingga memiliki bentuk profil sirip pada sisi dalam

pipa.

Dalam penelitian ini penulis ingin membahas perpindahan panas dan

efektivitas yang dipengaruhi adanya sirip pada bagian dalam pipa berprofil

segiempat. Metode yang digunakan dalam menghitung perpindahan panas adalah

dan memungkinkan untuk dilakukan banyak variasi sehingga dapat

mempersingkat waktu pengerjaan.

1.2 Batasan Masalah

Pipa segiempat dengan sirip pada sisi dalamnya, bersuhu awal yang

seragam sebesar Ti kemudian dialiri fluida di dalamnya bersuhu Tf dengan

koefisien perpindahan panas konveksi sebesar hD. Perpindahan panas yang terjadi

dari fluida di dalam pipa ke arah fluida di sekeliling luar pipa. Perhitungan panas

yang dilepas didasarkan pada luasan permukaan dinding luar saluran yang

bersentuhan dengan fluida di luar saluran. Fluida di luar saluran memiliki

koefisien perpindahan panas konveksi sebesar hL. Penyelesaian persoalan dengan

membandingkan panas yang dilepas pipa bersirip dengan pipa tanpa sirip.

1.2.1 Bentuk Geometri

a) b)

1.2.2 Model Matematika

Model matematika yang diperlukan untuk menghitung distribusi suhu pada

setiap posisi x dan y untuk benda dua dimensi keadaan tak tunak dengan t ≥ 0

dituliskan dalam persamaan (1.1)













t t y x T y

t y x T x

t y x T

   

  

 , , , , 1 , ,

2 2

2 2

 ………... (1.1)

Dengan T(x,y,t) adalah suhu di posisi x dan y pada waktu t.

1.2.3 Kondisi Awal

Suhu pipa pada kondisi awal t = 0 adalah seragam, yaitu T = Ti, secara

matematis dinyatakan dalam persamaan (1.2)

T(x,y,0) = Ti, berlaku untuk setiap posisi x dan y ………... (1.2)

1.2.4 Kondisi Batas

Seluruh permukaan sisi dalam pipa bersentuhan dengan fluida yang

mengalir di dalam pipa, sedangkan seluruh permukaan luar pipa bersentuhan

dengan fluida di luar saluran. Suhu fluida dalam Tf dengan koefisien perpindahan

panas konveksi hD. Suhu fluida di luar saluran T∞ dengan koefisien perpindahan

panas konveksi hL.

1.2.5 Asumsi

a. Sifat benda (massa jenis, panas jenis, konduktivitas termal) adalah seragam

dan tidak dipengaruhi perubahan suhu, dengan kata lain nilai α tetap.

c. Suhu fluida yang mengalir dalam pipa (Tf) dan suhu fluida yang mengalir di

luar pipa (T) dianggap tetap dan merata.

d. Harga koefisien konveksi untuk fluida di luar pipa (hL) dan fluida di dalam

pipa (hD) adalah tetap dan merata.

e. Bentuk dan volume pipa tidak berubah terhadap waktu dan tidak terpengaruh

perubahan suhu.

f. Tidak ada pembangkitan energi pada pipa.

1.3 Tujuan

Analisis perpindahan panas yang dilakukan bertujuan untuk:

a. Membuat program komputasi dengan metode beda hingga cara eksplisit

untuk menghitung laju perpindahan panas dan efektivitas sirip yang terjadi

pada pipa segiempat bersirip dan tidak bersirip.

b. Membandingkan besar laju perpindahan panas yang dilepas antara pipa

segiempat bersirip dengan pipa segiempat tanpa sirip.

c. Mencari hubungan dari perubahan harga koefisien konveksi dalam saluran

(hD) terhadap efektivitas saluran.

1.4 Manfaat

Penelitian ini diharapkan dapat memberi manfaat, antara lain:

a. Dapat merancang dan membuat sirip secara mandiri sesuai dengan keinginan

b. Dapat mengetahui besarnya distribusi suhu dan laju perpindahan panas yang

dilepas pipa bersirip.

c. Dapat mengetahui pengaruh adanya sirip pada sisi dalam pipa terhadap

efektivitas perpindahan panas pada pipa.

d. Dapat dijadikan referensi serta pertimbangan untuk penelitian lain yang lebih

9 2.1 Perpindahan Panas

Perpindahan panas merupakan peristiwa mengalirnya energi berupa panas

akibat adanya perbedaan suhu di antara benda atau material. Ilmu perpindahan

panas mencoba menjelaskan bagaimana energi panas itu berpindah dari satu

benda ke benda yang lain, sehingga laju perpindahan energi panas yang terjadi

pada kondisi-kondisi tertentu dapat diramalkan. Ilmu ini melengkapi hukum

pertama dan kedua Termodinamika yang berisikan tentang kekekalan energi dan

arah perpindahan panas yang berlangsung pada arah tertentu.

Proses perpindahan energi panas terbagi menjadi tiga macam: konduksi

(conduction) atau hantaran, konveksi (convection) atau rambatan, dan radiasi

(radiation) atau pancaran. Pada konduksi perpindahan energinya tanpa disertai

perpindahan materi benda penghantarnya. Perpindahan panas konveksi

merupakan perpindahan panas yang disertai aliran massa penghantarnya,

sedangkan perpindahan panas radiasi merupakan perpindahan energi panas yang

memancar dan dalam perpindahannya tidak diperlukan zat penghantar. Energi

panas radiasi berupa energi elektromagnetik. Contoh radiasi adalah panas

matahari sampai ke bumi.

Secara alami, energi panas yang mengalir pada suatu medium tidak hanya

dalam satu cara saja akan tetapi dengan beberapa sekaligus secara bersamaan.

diperhatikan sebab setiap kondisi perpindahan panas akan saling mempengaruhi

dalam menentukan proses perpindahan panas yang terjadi. Apabila dalam suatu

mekanisme perpindahan panas ada satu proses yang mendominasi secara

kuantitatif maka akan diperoleh penyeleasaian secara prediksi (approximate

solution) yang bermanfaat dengan mengabaikan semua proses kecuali yang

mendominasi.

2.2 Perpindahan Panas Konduksi

Proses perpindahan panas konduksi (conduction) atau hantaran adalah

proses perpindahan energi dari bagian yang bersuhu tinggi ke bagian yang

bersuhu rendah di dalam suatu medium (padat, cair, atau gas) atau antara

medium-medium lain yang bersinggungan secara langsung disebabkan karena adanya

gradien suhu (temperature gradient). Proses perpindahan panas secara konduksi

bila dilihat secara atomik merupakan pertukaran energi kinetik antar molekul

(atom), dimana partikel yang energinya rendah dapat meningkat dengan

menumbuk partikel dengan energi yang lebih tinggi. (Shirleen, 2007)

Dalam aliran panas konduksi, perpindahan energi panas terjadi karena

hubungan molekul secara langsung tanpa adanya perpindahan molekul yang

cukup besar, sehingga perpindahan molekul yang terjadi sering diabaikan.

Persamaan perpindahan panas konduksi sesuai Hukum Fourier dapat dilihat pada

persamaan (2.1) :

x T T k.A. x

T T k.A. x

T k.A. q

Δ Δ

1 2 2

1  

    

Keterangan :

q = Laju perpindahan panas (Watt)

k = Konduktivitas/hantaran termal (Thermal Conductivity) medium (W/moC)

A = Luas permukaan benda yang mengalami perpindahan panas tegak lurus

arah perpindahan panas (m2)

x T

 

=Gradien suhu ke arah perpindahan panas

Tanda minus disisipkan agar memenuhi hukum kedua termodinamika,

yaitu arah aliran panas yang akan mengalir dari tempat yang bersuhu tinggi ke

tempat yang bersuhu lebih rendah. Perpindahan panas konduksi terjadi pada

medium yang bersifat diam.

x

Gambar 2.1. Perpindahan Panas Konduksi

2.2.1 Konduktivitas Termal

Dengan persamaan (2.1) kita dapat melaksanakan pengukuran dalam

pada suhu yang agak rendah, pengolahan analisis teori kinetik gas dapat

dipergunakan untuk meramalkan secara teliti nilai-nilai yang diamati dalam

percobaan.

Nilai konduktivitas beberapa bahan dapat dilihat dalam (Tabel 2.1). Pada

umumnya konduktivitas termal itu sangat bergantung pada suhu. Jika aliran panas

dinyatakan dalam Watt per derajat Celcius. Laju panas dan nilai konduktivitas

termal itu menunjukkan berapa cepat panas mengalir dalam bahan tertentu.

Tabel 2.1. Nilai Konduktivitas Termal Beberapa Bahan

Bahan

Konduktivitas termal

Panas spesifik

k Cp

W/moC J/kgoC

Logam

Perak (murni) 410 234

Tembaga (murni) 385 383,1

Al (murni) 202 896

Nikel (murni) 93 445,9

Besi (murni) 73 452

Baja karbon 1%C 43 473

Bukan logam

Kuarsa 41,6 820

Magnesit 4,15 1130

Batu pasir 1,83 710

Kaca 0,78 880

Kayu mapel 0,17 240

zat cair Air raksa 8,21 1430

Air 0,556 4225

Gas

H 0,175 14314

He 0,141 5200

Udara 0,024 1005

2.2.2 Difusivitas Termal

Difusivitas termal atau kebauran termal merupakan sebuah parameter yang

cukup penting dalam perpindahan panas konduksi. Makin besar angka difusivitas

termal dalam sebuah medium maka makin cepat panas membaur dalam medium

tersebut.

c k

. 

  ………...…...(2.2)

Dimana :

α = difusivitas termal bahan (m2/s)

k = konduktivitas termal bahan (W/m.°C)

ρ = densitas (kg/m3)

c = panas jenis medium (J/kg.°C)

Nilai α yang besar dapat berarti 2 hal : pertama, nilai konduktivitas termal

yang tinggi menunjukkan laju perpindahan panas yang pesat; atau yang kedua,

nilai kapasitas panas termal (thermal heat capacity) ρc yang rendah. Nilai

kapasitas panas termal yang rendah berarti energi yang berpindah melalui bahan

tersebut yang digunakan untuk menaikkan suhu jumlahnya lebih sedikit, sehingga

2.3 Perpindahan Panas Konveksi

Perpindahan panas konveksi merupakan transpor energi dengan kerja

gabungan dari konduksi panas, penyimpanan energi, dan gerakan campuran.1

Konveksi sangat penting sebagai mekanisme perpindahan energi antara

permukaan benda padat, cair, atau gas. Perpindahan panas konveksi dapat dilihat

seperti pada gambar (2.2). Persamaan perpindahan panas konveksi dapat dilihat

dari persamaan (2.2), persamaan ini merupakan persamaan umum untuk setiap

kondisi perpindahan panas konveksi.



 



h.A.T T

q _w ...………...……….……….……..……...(2.3)

Keterangan :

q = Laju perpindahan panas (Watt)

h = Koefisien perpindahan panas konveksi (W/m2 oC)

A = Luasan permukaan benda yang bersentuhan dengan fluida (m2)

T∞ = Suhu fluida (oC)

Tw = Suhu permukaan benda (oC)

Gambar 2.2. Perpindahan Panas Konveksi

1

Perpindahan panas konveksi dapat terjadi apabila ada medium yang

bersifat bergerak, misal: angin, air, minyak, dan lain-lain. Suatu peristiwa

perpindahan panas konveksi akan menjadi bervariasi, tergantung dari beberapa

faktor antara lain kecepatan aliran fluida, jenis fluida yang mengalir, dan kondisi

aliran (bebas atau paksa), serta bentuk dari benda yang bersinggungan dengan

fluida.

2.3.1 Angka Reynolds

Angka Reynolds merupakan suatu bilangan tak berdimensi yang mewakili

karakteristik fluida yang terlibat perpindahan panas konveksi. Dalam berbagai

kasus konveksi paksa, angka Reynolds ini digunakan sebagai penentu jenis aliran

yang terjadi, apakah laminar atau turbulen.

2.3.1.1 Angka Reynolds untuk Kondisi Plat Datar

Penggambaran sederhana peristiwa konveksi dapat diambil contoh pada

aliran konveksi plat datar. Daerah aliran yang terbentuk dari tepi depan plat itu,

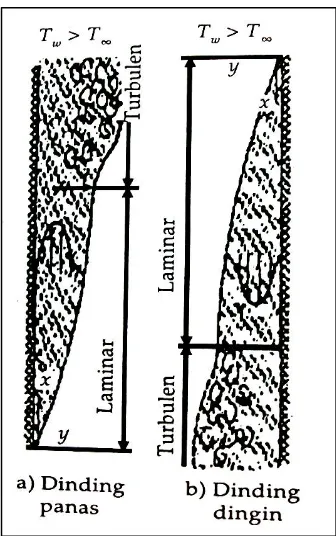
dimana terlihat pengaruh viskositas, disebut lapisan batas (boundary layer). Pada

permulaan, pembentukan lapisan batas itu laminar, tetapi pada suatu jarak kritis

dari tepi depan, bergantung dari medan aliran dan sifat-sifat fluida,

gangguan-gangguan kecil tersebut membesar dan mulailah terjadi proses transisi hingga

aliran menjadi turbulen. Daerah aliran turbulen dapat digambarkan sebagai

kocokan rambang di mana gumpalan fluida bergerak ke sana ke mari di segala

Gambar 2.3. Berbagai Daerah Aliran Lapisan Batas di Atas Plat Rata

Dalam kondisi umum, aliran fluida bertransisi dari laminar menjadi

turbulen terjadi apabila :

5

10 5 .

    

 u x

υ

x u

………..…….(2.4)

Dimana

u∞ = kecepatan aliran bebas (m/s)

x = jarak dari tepi depan (m)

υ = µ/ρ = viskositas kinematik (m2/s)

Pengelompokan khas di atas disebut angka Reynolds, dan angka ini tak

berdimensi apabila untuk semua sifat-sifat di atas digunakan perangkat satuan

yang konsisten.

υ

x u

x 



Re ………...(2.5)

2.3.1.2 Angka Reynolds untuk Kondisi Aliran Dalam Saluran

Pada beberapa kasus perpindahan panas konveksi melibatkan aliran fluida

dalam saluran pipa, misalnya pada alat penukar panas. Pada kondisi aliran fluida

dalam saluran parameter jarak yang berpengaruh terhadap perhitungan adalah

diameter saluran.

υ

d u

d 



Re ………..……….(2.6)

Dimana :

Red = Angka Reynolds pada aliran dalam saluran

u_∞ = kecepatan aliran bebas (m/s)

d = diameter saluran (m)

υ = µ/ρ = viskositas kinematik (m2/s)

Pada gambar tampak suatu model aliran dalam tabung. Terlihat pada

waktu masuk, terbentuk suatu lapisan batas. Lama-kelamaan, lapisan batas ini

memenuhi seluruh tabung, dan kita katakan aliran itu sudah berkembang penuh.

Jika aliran itu laminar, profil kecepatan itu terbentuk parabola, bila aliran turbulen

maka profil aliran berbentuk tumpul.

Angka Reynolds ini digunakan sebagai kriteria untuk menunjukkan apakah

aliran dalam tabung atau pipa itu laminar atau turbulen. Pada :

2300

Re   

υ

d u

d ………..(2.7)

aliran itu biasanya turbulen (Holman, 1997, hal. 195).

2.3.1.3 Angka Reynolds untuk Kondisi Aliran di Luar Saluran

Pada beberapa kasus, aliran fluida terdapat di luar benda (pipa saluran,

tabung, atau silinder). Kasus ini tidak beda jauh dengan kasus aliran dalam pipa

saluran, perhitungan angka Reynolds serupa.

υ

d u

df 



Re ………..……(2.8)

Dimana :

Redf = Angka Reynolds pada aliran di luar saluran

u_∞ = kecepatan aliran bebas (m/s)

d = diameter saluran (m)

2.3.2 Angka Prandtl

Angka Prandtl merupakan perbandingan antara besar viskositas dinamik

fluida dengan konstanta α. Angka ini muncul dari penerapan kondisi batas δt = 0

dan x = 0 pada persamaan diferensial linear orde pertama dari ζ. ζ adalah rasio

ketebalan lapisan batas termal terhadap ketebalan lapisan batas hidrodinamik.

Teori lapisan batas ini diperkenalkan oleh Ludwig Prandtl, seorang ahli

kebangsaan Jerman. Angka Prandtl adalah besaran tak berdimensi apabila kita

menggunakan perangkat satuan yang konsisten.

f

f k

µ

ρ

k

μ/ρ α

υ Cp.

Cp . /

Pr   ………(2.9)

Dengan :

Pr = angka Prandtl

υ = viskositas kinematik (m2/s)

α = difusivitas termal bahan (m2/s)

kf = konduktivitas termal fluida (W/m.°C)

µ = viskositas dinamik (kg/m.s)

ρ = densitas fluida (kg/m3)

Cp = panas jenis fluida pada tekanan konstan ( kJ/kg.°C)

Angka Prandtl ini juga merupakan parameter yang menghubungkan

ketebalan relatif antara lapisan batas hidrodinamik dan lapisan batas termal.

Viskositas kinematik fluida memberikan informasi tentang laju difusi momentum

dalam fluida karena gerakan molekul. Difusivitas termal bahan memberi petunjuk

antara keduanya menunjukkan besaran relatif antara difusi momentum dan difusi

panas dalam fluida.

2.3.3 Konveksi Bebas

Konveksi bebas atau konveksi alamiah adalah konveksi yang terjadi

karena fluida yang mengalami proses pemanasan atau pendinginan berubah

densitasnya (kerapatannya). Perbedaan kerapatan mengakibatkan fluida yang

berat akan mengalir ke bawah dan fluida yang ringan mengalir ke atas. Gerakan

fluida dalam konveksi bebas terjadi akibat gaya apung (buoyancy force) yang

dialaminya, apabila kerapatan fluida di dekat permukaan perpindahan panas

berkurang sebagai akibat proses pemanasan. Gaya apung itu tidak akan terjadi

apabila fluida tersebut tidak mengalami suatu gaya dari luar, misalnya gaya

gravitasi, walaupun gravitasi bukanlah satu-satunya medan gaya luar yang dapat

menghasilkan arus konveksi bebas. Gaya apung yang menyebabkan arus konveksi

bebas disebut gaya badan (body force).2

2

Gambar 2.5. Konveksi Bebas Pada Lapisan Batas Di Atas Plat Rata Vertikal

Pada sistem konveksi bebas kita akan sering bertemu dengan bilangan tak

berdimensi yang disebut angka Grashof (Gr). Bilangan ini merupakan penurunan

angka Prandtl yang didefinisikan sebagai :





2 3

υ

L T T gβ

Gr w  _{………...(2.10)}

Dengan :

g = percepatan gravitasi (m/s2)

L = dimensi karakteristik (m)

υ = viskositas kinematik (m2/s)

β = koefisien ekspansi volume (K-1)

=

µ l

υ υ 

   

 

1

=

T

Angka Grashof (Gr) dapat ditafsirkan secara fisis sebagai suatu gugus tak

berdimensi yang menggambarkan perbandingan antara gaya apung dengan gaya

viskos di dalam sistem aliran konveksi bebas. Peranannya sama dengan angka

Reynolds dalam sistem konveksi paksa dan merupakan variabel utama yang

digunakan sebagai kriteria transisi dari aliran batas laminar menjadi turbulen.

2.3.4 Konveksi Paksa

Proses perpindahan panas konveksi paksa ditandai dengan adanya fluida

yang bergerak dikarenakan adanya alat bantu. Alat bantu tersebut dapat berupa

kipas angin, fan, blower, pompa, dll. Dalam praktiknya konveksi paksa ini

diaplikasikan untuk mempercepat aliran fluida (U∞).

Gambar 2.6. Aliran Fluida pada Bidang Datar

2.3.5 Angka Nusselt

Seorang ilmuwan bernama Wilhelm Nusselt, yang memberikan banyak

sumbangan dalam teori perpindahan panas konveksi, menemukan sebuah

dipakai dalam pencarian harga koefisien konveksi untuk setiap kasus tertentu,

sebab setiap kasus mempunyai bilangan Nusselt tersendiri.

f k

x h.

Nu  ………..(2.11)

Dimana :

h = koefisien perpindahan panas konveksi (W/m2.°C)

x = parameter jarak (m)

kf = konduktivitas termal fluida (W/m.°C)

Pada konveksi bebas, aliran fluida terjadi karena berubah densitasnya

akibat mengalami pemanasan atau pendinginan. Angka Nusselt pada kasus aliran

konveksi merupakan fungsi dari bilangan Reynolds dan Grashof.





m

f f

f C Gr Pr

Nu  ……….(2.12)

Dimana :

f

Nu = harga Nusselt rata-rata untuk berbagai situasi konveksi bebas

C & m = konstanta yang ditentukan dari data percobaan

Subskrip f menunjukkan bahwa sifat-sifat untuk gugus tak berdimensi dievaluasi

pada suhu film.

2

w f

T T

T    ………(2.13)

Dimana :

T∞ = suhu fluida sekitar benda (°C)

Tw = suhu benda yang bersinggungan dengan fluida (°C)

Produk perkalian antara angka Grashof dan angka Prandtl disebut angka Rayleigh.

Ra = Gr Pr ………(2.14)

Pada konveksi paksa, aliran fluida yang terjadi adalah akibat dari adanya

alat bantu. Pada konveksi paksa, angka Nusselt merupakan fungsi dari angka

Reynold dan Prandtl.

n m

CRe Pr

Nu  ………..(2.15)

Dimana C, m, dan n adalah konstanta yang ditentuan dari percobaan.

2.3.5.1 Angka Nusselt pada Kasus Plat Datar

Pada teori perpindahan panas konveksi plat datar, Wilhelm Nusselt

memberikan rumus berikut :

3 1 4 3 0 3 1 2 1 1 Pr Re 332 , 0 Nu                  x x x x ………..(2.16)

Atau, untuk kondisi plat yang dipanaskan pada keseluruhan panjangnya,

x0 = 0

3 1 2 1 Pr Re 332 , 0

Nu_x  _x ………...(2.17)

Dimana :

Nux = angka Nusselt untuk kondisi aliran konveksi plat datar

Rex = angka Reynolds pada aliran konveksi plat datar

Pr = angka Prandtl

hx = koefisien konveksi rata-rata pada plat datar (W/m2.°C)

x = posisi aliran (m)

kf = konduktivitas termal fluida (W/m.°C)

2.3.5.2 Angka Nusselt pada Aliran Dalam Saluran

Aliran dalam saluran tertutup melibatkan suhu limbak (bulk temperature),

yaitu suhu fluida yang dirata-ratakan energinya di seluruh penampang tabung.

Dalam aliran tabung, koefisien perpindahan panas konveksi biasanya

didefinisikan sebagai fluks panas lokal.



T_w T_b



h

q"  



lokal panas

Fluks ………(2.19)

Dimana :

Tw = suhu dinding (°C)

Tb = suhu limbak (°C)

Suhu limbak ini digunakan dalam perumusan koefisien perpindahan panas

konveksi dalam aliran tabung dengan alasan dalam aliran tabung tidak terdapat

kondisi aliran bebas yang jelas seperti pada aliran di atas plat rata. Untuk

kebanyakan soal perpindahan panas pada aliran tabung atau aliran saluran,

fluida, baik dalam panjang unsuran saluran tabung maupun panjang keseluruhan

saluran. Namun pada dasarnya suhu limbak dapat dicapai saat dibiarkan mencapai

keseimbangan.

Untuk aliran turbulen yang sudah jadi atau berkembang penuh (fully

developed turbulent flow) dalam tabung licin, oleh Dittus dan Boelter disarankan

persamaan berikut :

n d d 0,023Re .Pr

Nu  0.8 _{……….(2.20)}

Untuk persamaan ini sifat-sifat ditentukan pada suhu fluida limbak dan nilai

eksponen n adalah sebagai berikut.



n , untuk pemanasan

dinginan untuk pen

,

4 0

3 0

Untuk kondisi aliran dalam saluran, angka Nusselt dapat dinyatakan dalam

persamaan koefisien konveksi.

f d

k d h. ₀

Nu  ………..(2.21)

Sehingga

n d f

k d h

Pr . Re 023 , 0

. 0  0.8 _{……….(2.22)}

Dimana :

Nud = angka Nusselt pada aliran dalam saluran

h = koefisien konveksi rata-rata (W/m2.°C)

kf = konduktivitas termal fluida (W/m.°C)

2.3.5.3 Diameter Hidraulik

Penampang dalam saluran tidak selalu berbentuk lingkaran, oleh sebab itu

korelasi perpindahan panas tersebut didasarkan atas diameter hidraulik DH, yang

didefinisikan sebagai :

P A

D_H  4 ………..(2.23)

Dengan :

A = luas penampang aliran (m2, mm2)

P = perimeter basah/keliling penampang saluran saluran (m, mm)

Pengelompokan ini dilakukan karena menghasilkan diameter fisis yang

sebenarnya apabila diterapkan pada penampang berbentuk lingkaran. Diameter

hidraulik harus digunakan dalam menghitung angka Nusselt dan angka Reynolds,

dan dalam menentukan koefisien gesek yang akan dipergunakan dalam analogi

Reynolds. Dengan adanya perhitungan diameter hidraulik ini maka perbedaan

profil penampang saluran dapat disesuaikan.

Dalam kasus aliran dalam saluran yang turbulen pada saluran non-silindris,

rumus Nusselt menjadi :

f H d

k D h.

Nu  ……….(2.24)

Sedang untuk kasus aliran dalam saluran yang laminer pada saluran

non-silindris perhitungan angka Nusselt telah disederhanakan oleh Shah dan London.

Mereka telah menghimpun informasi tentang gesekan fluida dan perpindahan

panas untuk aliran laminar berkembang penuh di dalam saluran dengan berbagai

bentuk penampang. Berikut daftar berbagai bentuk penampang tersebut.

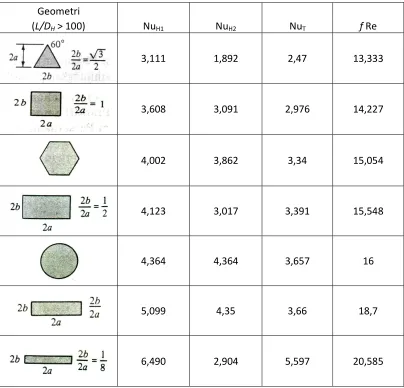
Tabel 2.2. Perpindahan Panas dan Gesekan Fluida untuk Aliran Laminar yang Berkembang Penuh dalam Saluran dengan Berbagai Penampang.

Geometri

(L/DH> 100) NuH1 NuH2 NuT f Re

3,111 1,892 2,47 13,333

3,608 3,091 2,976 14,227

4,002 3,862 3,34 15,054

4,123 3,017 3,391 15,548

4,364 4,364 3,657 16

5,099 4,35 3,66 18,7

Geometri

(L/DH> 100) NuH1 NuH2 NuT f Re

8,235 8,235 7,541 24

5,385 - 4,861 24

(J.P. Holman, 1997, hal.258) Dengan :

NuH1 = angka Nusselt rata-rata untuk fluks panas seragam dalam arah aliran

dan suhu dinding seragam pada penampang aliran tertentu.

NuH2 = angka Nusselt rata-rata untuk fluks panas seragam baik pada arah aliran

maupun sekeliling saluran.

NuT = angka Nusselt rata-rata untuk suhu dinding seragam.

f Re = produk perkalian faktor gesek dengan angka Reynolds.

2.3.5.4 Angka Nusselt pada Aliran Silang Silinder

Pada model aliran konveksi pada silinder, kasus aliran silang adalah yang

paling sering ditemui. Pada kasus ini proses pemisahan aliran bersifat rumit, maka

perhitungan koefisien perpindahan panas rata-rata tidak mungkin didapatkan dari

cara analitis. Namun data eksperimental Hilpert untuk gas dan dari Knudsen –

Katz untuk zat cair menunjukkan bahwa koefisien perpindahan panas rata-rata

dapat dihitung dari :

3 1

Pr .

. n

f

f υ

d u C k

d h

       

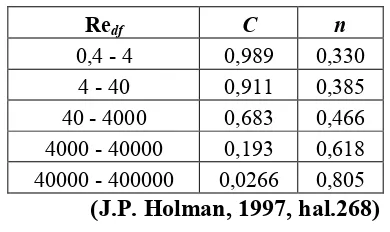
Dimana konstanta C dan n sesuai dengan (Tabel 2.3.) berikut.

Tabel 2.3. Konstanta C dan n Aliran Silang

Redf C n

0,4 - 4 0,989 0,330

4 - 40 0,911 0,385

40 - 4000 0,683 0,466

4000 - 40000 0,193 0,618

40000 - 400000 0,0266 0,805 (J.P. Holman, 1997, hal.268)

Berbagai variasi persamaan Nusselt untuk kasus aliran menyilang silinder

kemudian dirancang untuk rentang angka Reynolds yang berbeda. Ini berarti ada

persamaan-persamaan tertentu yang disesuaikan pemakaiannya pada kondisi

kecepatan aliran fluida tertentu, diameter silinder tertentu, atau viskositas tertentu,

sesuai dengan parameter angka Reynolds. Misal :

 Persamaan Nusselt untuk kondisi perpindahan panas dari zat cair ke silinder pada aliran silang oleh Fand, berlaku untuk rentang 10-1 < Ref < 105.



0,52



0,3

Pr . Re 56 , 0 35 , 0

Nu_f   _{f f} ………..(2.26)

 Perhitungan dengan komputer digunakan rumus yang lebih rumit untuk rentang angka Reynolds yang lebih luas. Eckert dan Drake menyarankan rumus berikut

untuk perpindahan panas dari tabung dalam aliran silang.



0,5



0,38 0,25

Pr Pr Pr . Re 50 , 0 43 , 0 Nu _        w f

untuk 1 < Re < 103 ...(2.27)

25 , 0 38 , 0 6 , 0 Pr Pr Pr . Re 25 , 0 Nu _       w f

 Churchill dan Bernstein menemukan rumus yang lebih komprehensif dan berlaku untuk seluruh rentang data yang ada, berlaku untuk rentang 102 < Red < 107 ; Ped

> 0,2. 5 4 8 5 4 3 3 2 3 1 2 1 000 . 282 Re 1 Pr 4 , 0 1 Pr Re 62 , 0 3 , 0 Nu                                 d ………...(2.29)

Dimana Pe = angka Peclet = Re.Pr

Pilihan mengenai persamaan mana yang akan digunakan untuk

aliran-aliran melintas silinder ditentukan dengan terkaan saja. Persamaan Hilpert dan

Knudsen – Katz merupakan yang termudah dipakai dilihat dari segi

perhitungannya. Persamaan Churchill – Bernstein yang lebih komprehensif lebih

cocok untuk perhitungan dengan komputer karena persamaan demikian meliputi

jenis fluida dan angka Reynolds yang lebih luas. Namun pada kasus fluida udara,

persamaan manapun antara keduanya dapat dipakai (Holman, 1997, hal. 271).

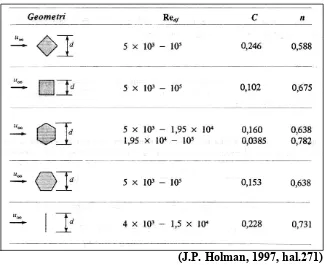
2.3.5.5 Angka Nusselt pada Aliran Silang Silinder Tak Bundar

Pada persoalan aliran silang pada silinder tak bundar, Jakob

merangkumkan hasil-hasil percobaan mengenai perpindahan panas dari silinder

yang tak bundar. Tabel yang dibawah ini merupakan ringkasan yang dipadukan

Tabel 2.4. Konstanta untuk Perpindahan Panas dari Silinder Tak Bundar

(J.P. Holman, 1997, hal.271)

2.3.5.6 Konveksi Bebas dari Silinder Horizontal

Konveksi bebas melibatkan perhitungan angka Grashof dalam persamaan

Nusselt. Churchill dan Chu memberikan rumus Nusselt dengan rentang angka

Rayleigh yang cukup luas.









6 1

9 16 16 9

0,559/Pr 1

Pr . Gr 387

, 0 60 , 0 Nu

    

  

 

 untuk 01-5 < Gr Pr < 1012.(2.30)

Besar nilai koefisien konveksi kemudian dihitung sebagai koefisien

konveksi rata-rata.

f

k d h. ₀

Dimana :

Nu = Angka Nusselt rata-rata

h = koefisien konveksi rata-rata (W/m2.°C)

d0 = diameter silinder, pada profil non-silinder dengan pendekatan diameter

hidraulik

2.3.5.7 Konveksi Bebas dari Plat Horizontal

Untuk kondisi fluks panas tetap, harga Nusselt pada plat horizontal

disesuaikan dengan kea rah mana aliran panas itu menghadap. Untuk muka yang

dipanaskan menghadap ke atas, maka :



_{Gr Pr}



13

13 , 0

NuL  _L untuk GrL Pr < 2108 ……… (2.32)

dan



_{Gr Pr}



13

16 , 0

NuL  _L untuk 2108 < GrL Pr < 1011 …….….(2.33)

Untuk muka yang dipanaskan menghadap ke bawah adalah :



_{Gr Pr}



15

58 , 0

NuL  _L untuk 106 < GrL Pr < 1011 ………(2.34)

Harga koefisien konveksi dinyatakan dalam koefisien konveksi rata-rata.

f L

k L h.

Nu  ………....(2.35)

dengan

P A

Dimana :

L = dimensi karakteristik

A = luas permukaan (m2)

P = perimeter basah (m)

2.3.5.8 Konveksi Bebas dari Plat Rata Vertikal

Konveksi bebas pada plat vertikal ini memiliki perumusan yang lebih

sederhana, tidak terdapat rentang untuk parameter dari angka Nusselt-nya.

Persamaan tak berdimensi untuk koefisien perpindahan panasnya adalah :





14 14

2 1

.Gr Pr

952 , 0 Pr 508 , 0

Nu_x    _x ………...(2.37)

Persamaan ini menunjukkan perubahan koefisien perpindahan panas local

sepanjang plat vertikal. Untuk perubahan ini maka koefisien konveksi dinyatakan

sebagai :

L x

h

h _

3 4

……….(2.38)

Dimana hx=L adalah koefisien konveksi pada ujung plat vertikal (W/m2.°C).

2.3.5.9 Konveksi Bebas dari Permukaan Miring

Sebuah penelitian dilakukan oleh Fujii dan Imura dengan plat yang

dipanaskan di dalam air pada berbagai sudut kemiringan. Sudut yang dibuat plat

itu dengan bidang vertikal ditandai dengan θ, dengan tanda positif untuk

positif berlawanan arah jarum jam / counterclockwise). Untuk plat miring

menghadap ke bawah dengan fluks panas hamper tetap, didapatkan korelasi

berikut untuk angka Nusselt rata-rata.



_{Gr Pr cos}



14

56 , 0

Nue  _{e e}  ……….(2.39)

Batasan rumus ini adalah θ < 88° dan 105 < Gre Pre cos θ < 1011.

Untuk plat hamper horizontal yang menghadap ke bawah (88° < θ < 90°), didapat sebuah rumus tambahan.



_{Gr Pr}



15

58 , 0

Nue  _{e e} untuk 106 < Gre Pre < 1011 ………..……(2.40)

2.4 Laju Perpindahan Panas

Laju perpindahan panas atau laju aliran panas merupakan banyaknya

jumlah panas yang dapat dilepas oleh sirip ke lingkungan atau sebaliknya dalam

bentuk konveksi pada setiap volume kontrol yang bersentuhan dengan fluida.

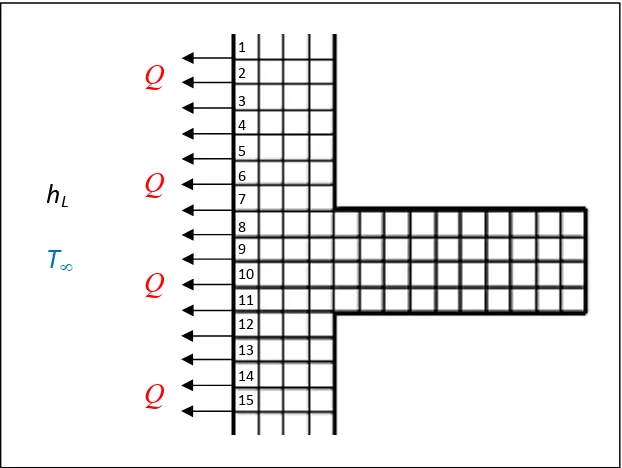
Tampak pada gambar potongan penampang sebuah dinding pipa yang diwakili 15

Gambar 2.7. Potongan Penampang Pipa Saluran Yang Melepas Panas Ke Lingkungan Luar Secara Konveksi

Dari gambar di atas laju perpindahan panas pada pipa saluran secara

matematis dapat dirumuskan sebagai berikut :



 







 



 



 



     T T h.As ... T T h.As T T h.As Q q ... q q Q n n n 15 15 2 2 1 1 14 2 1        fluida dengan gan bersinggun yang sirip permukaan dari node tiap dilepas yang panas Total Q …..(2.41)

Dengan As adalah luasan node yang bersinggungan dengan fluida luar.

2.5 Efektivitas Saluran (

ε

)

Efektivitas saluran merupakan perbandingan antara panas yang dilepas

Efektivitas (

ε)

=

=

sirip tanpa Q

sirip dengan Q_aktual

38 3.1 Pengertian Persamaan Numerik

Persamaan numerik merupakan teknik perhitungan pendekatan (Bejan,

2003, hal. 216). Metode persamaan numerik digunakan untuk menghitung

perpindahan panas pada benda yang memiliki bentuk geometri yang rumit atau

kondisi batas yang kompleks, sehingga tidak memungkinkan diselesaikan dengan

metode analitis-matematis.

Dalam penggunaannya metode numerik ini memanfaatkan persamaan

aljabar untuk mengganti perhitungan diferensial. Persamaan aljabar ini digunakan

untuk mencari suhu yang belum diketahui pada suatu medium. Penyelesaian

menggunakan metode numerik dilakukan secara serentak (simultaneous) dan

terpisah (discrete) untuk tiap node (Cengel, 2002, hal. 265).

Ada dua metode persamaan numerik yang umumnya dilakukan dalam

penyelesaian kasus perpindahan panas : beda hingga cara eksplisit dan beda

hingga cara implisit. Penyelesaian dengan cara eksplisit menggunakan node-node

sekitar atau volume kontrol yang lebih dahulu ditentukan, sedangkan cara implisit

menggunakan metode perhitungan komputasi dengan iterasi langsung. Baik

eksplisit maupun implisit memperhitungkan prinsip kesetimbangan energi

(Hukum Pertama Termodinamika). Pada penelitian ini digunakan metode

Volume kontrol adalah ruang yang dibatasi oleh kontrol permukaan,

namun energi dapat lewat (Yohana, 2007, hal. 18). Metode beda hingga cara

eksplisit menggunakan suhu pada saat n, untuk mencari suhu pada saat n+1

(mencari suhu Tn+1 oC dari suhu TnoC) pada suatu volume kontrol.

3.2 Kesetimbangan Energi

Persamaan numerik yang melibatkan volume kontrol haruslah memenuhi

prinsip kekekalan energi, yaitu Hukum Pertama Termodinamika. Energi tidak

dapat diciptakan atau dimusnahkan, namun hanya berubah bentuk (Cengel, 2002,

hal. 11). Ilustrasi hukum ini dapat dilihat pada Gambar 3.1. Prinsip kesetimbangan

energi pada volume kontrol sirip dapat dilihat pada persamaan umum (3.1).

Ein+Egen-Eout = ΔEsistem ………...(3.1)

Dimana :

Ein = Energi yang masuk ke dalam volume kontrol

Egen = Energi yang dibangkitkan dalam volume kontrol

Eout = Energi yang keluar dari volume kontrol

Gambar 3.1. Kesetimbangan Energi Dalam Volume Kontrol

3.3 Penurunan Model Matematik Pada Benda Bersirip

Penurunan model matematik ini didapatkan dari penurunan prinsip

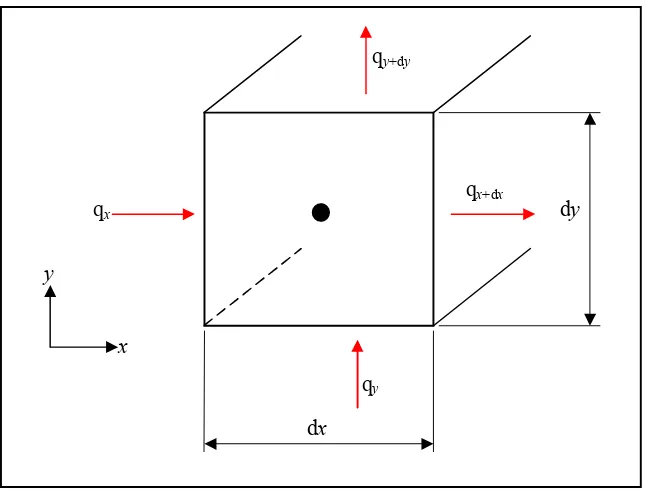
kesetimbangan energi. Pada benda 2 dimensi, laju aliran panas dianalisis terhadap

sumbu x dan y. Digambarkan sebagai berikut.

Gambar 3.2. Kesetimbangan Energi Pada Volume Kontrol Benda 2 Dimensi

Ein

Volume kontrol

Eout

Egen

ΔEsistem

+ −

=

dy

dx qx

qx+dx

qy

qy+dy

Dari persamaan (3.1) dan Gambar 3.2 dapat diketahui bahwa :

Ein = qx+qy

Eout = qx+dx+qy+dy

Sehingga persamaan (3.1) dapat dijabarkan sebagai berikut:

Ein+Egen-Eout= ΔEsistem

(qx+qy) + 0 – (qx+dx+qy+dy) = ΔEsistem ………(3.2)

Pada benda 2 Dimensi analisis volume kontrol diasumsikan memiliki

ketebalan d yang tipis untuk setiap nodenya. Ketebalan ini diberikan untuk

menyederhanakan perhitungan luas perpindahan panas untuk tiap node.

ΔEsistem diasumsikan sebagai volume kontrol untuk closed system, sehingga

persamaan (3.2) dituliskan sebagai berikut:

(qx+qy)– (qx+dx+qy+dy) =

t T ρ.c.V   ………..…(3.3)

qx- qx+dx+ qy- qy+dy=

t T ρ.c.V   Dengan :

qx

 

x T dy d k -         

; qx+dx .dx .



dy t



x T k . . x x T

k. _{ b}

                              

qy = -

 

y T dx d

k _

      

;qy+dy .dy .



dx t



y T k . . y y T

k. _{ b}

Maka diperoleh :

















t

T

ρ.c.V

dx . t . .dy y T k . . y y T k. y T dx d k dy. t . .dx x T k . . x x T k. x T dy d k b b                                                                                                                

















t T ρ.c.V .dx.dy .t y T k . . y y T dx d k. y T dx d k .dx.dy .t x T k . . x x T dy d k. x T dy d k b b                                                                                      



. .



t T t dy dx ρ.c. .dx.dy.t y T k . . y .dx.dy .d x T k . .

x b b 

                                          Dikalikan . . 1 b t dy

dx , maka diperoleh :

t T . y T k . . y x T k . .

x ρ.c 

                                         ………...(3.4)

Untuk harga konduktivitas termal bahan saluran (k) konstan dan k

.c

1 

  , persamaan (3.4) di atas menjadi:

Sehingga model matematis untuk penelitian, pada sirip kasus 2 dimensi ini adalah:

t T

α

y T

x T

       

    

 

 ₁

2 2 2 2

; x0 < x < x0+dx, y0 < y < y0+dy, t0 …………(3.6)

Pada persamaan (3.6):

T = T (x,y, t) = Suhu pada posisi x dan y saat t (oC)

x = menyatakan posisi pada arah sumbu x (m)

y = menyatakan posisi pada arah sumbu y (m)

tb = kedalaman volume kontrol per satuan panjang (m)

t = menyatakan waktu (detik)

α = difusivitas termal bahan (m2/s)

3.4 Persamaan Numerik Node Utama

Persamaannumerik untuk tiap node pada pipa baik bersirip maupun tidak

bersirip memiliki kesamaan, yaitu node dalam, node samping/rusuk, dan node

sudut/ujung. Namun pada profil pipa bersirip memiliki satu tambahan persamaan

numerik, yaitu node sudut dalam. Setiap node dikondisikan dalam jarak xy

Gambar 3.3. Posisi Node Pada Penampang Pipa 2 Dimensi

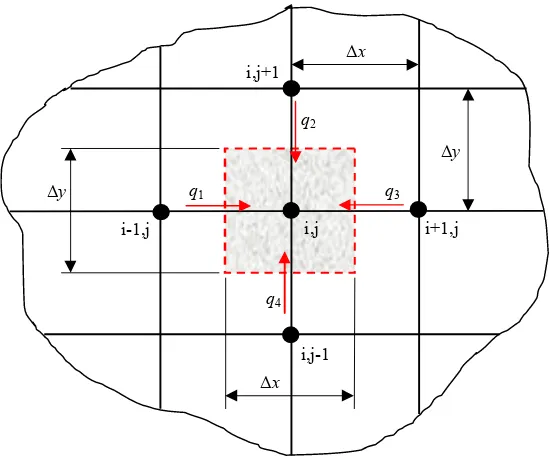
3.4.1 Node Dalam (Node a pada Gambar 3.3)

Gambar 3.4. Node Dalam Pada Penampang Pipa 2 Dimensi Keterangan :

a. Node dalam b. Node rusuk c. Node sudut luar d. Node sudut dalam c

b d

a

Δy

Δx

Δx

i,j i,j+1

i+1,j

i,j-1 i-1,j

q3

q4

q1

q2

Persamaan numerik pada node dalam melibatkan perpindahan panas

konduksi. Jarak antar node Δx= Δy.

q1, q2, q3, dan q4 masing-masing adalah rumus perpindahan panas

konduksi yang mengarah ke sebuah volume kontrol i,j. Dengan mengasumsikan

sebuah node dalam i,j menerima energi panas dari keempat node di sekitarnya

maka berlaku prinsip kesetimbangan energi untuk keadaan tak tunak (1.1).



 

 

 



 

t T T x c T t k T T T T k t T T y x c T T k T T k T T k T T k t T T cV q q q q n j i n j i n j i b n j i n j i n j i n j i n j i n j i n j i n j i n j i n j i n j i n j i n j i n j i n j i n j i                                                    , 1 , 2 , 1 , , 1 1 , , 1 , 1 , , 1 , , , 1 , 1 , , , 1 , 1 , 4 3 2 1 . . 4 1 . .   

Persamaan kemudian disederhanakan dengan mengalikan kedua ruas dengan k 1

 



n



j i n j i n j i n j i n j i n j i n j

i T T

t k x c T T T T

T _, 1 _,

2 , 1 , , 1 1 , , 1 . 4                      Dengan

 

x Fo c t k _   2 .

 , maka

Dari persamaan di atas suhu node dalam i,j pada saat n+1 dapat ditentukan.

   

     

 

 

 

 _{     }

T_i,n_j1 FoT_in_1,j T_i,n_{j 1} T_in_1,j T_i,n_{j 1} T_i,n_j 1 4Fo ……… (3.7)

Persamaan ini memenuhi untuk kondisi batas angka Fourier (Fo) tertentu,

yang dinyatakan dalam syarat stabilitas. Syarat stabilitas untuk persamaan

numerik node dalam :

0 4 1 Fo

Fo 4

1 

4 1 

Fo ………..…(3.8)

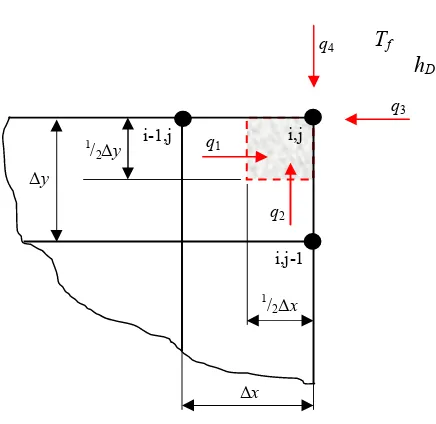
3.4.2 Node Rusuk (Node b pada Gambar 3.3)

Gambar 3.5. Node Rusuk Pada Penampang Pipa 2 Dimensi

Persamaan numerik pada node rusuk ini melibatkan perpindahan panas

konduksi dan konveksi. Jarak antar node Δx= Δy.

i,j i+1,j

i,j-1 i-1,j

q3

q2

q1 Δx

q4

Δx

1

/2Δy

Tf hD

q1, q2, dan q3 masing-masing adalah persamaan perpindahan panas

konduksi, sedangkan q4 adalah persamaan perpindahan panas konveksi yang

mengarah ke sebuah volume kontrol i,j. Dengan mengasumsikan sebuah node

rusuk i,j menerima energi panas dari ketiga node dan fluida di sekitarnya maka

berlaku prinsip kesetimbangan energi untuk keadaan tak tunak (1.1).



 

 



 









 

 

 

t T T x c T x h kT T x h T T T k t T T y x c T T x h T T k T T k T T k t T T cV q q q q n j i n j i n j i D n j i f D n j i n j i n j i n j i n j i n j i f D n j i n j i n j i n j i n j i n j i n j i n j i                                                , 1 , 2 , , , 1 1 , , 1 , 1 , 2 1 , , , 1 , 1 , , , 1 , 1 , 4 3 2 1 2 1 2 2 2 1 . . 2 2   

Persamaan kemudian disederhanakan dengan mengalikan kedua ruas dengan k 1





 

 

 



n



j i n j i n j i D n j i f D n j i n j i n j

i T T

t k x c T k x h T T k x h T T

T _, 1 _,

2 , , , 1 1 , , 1 . 2 . . 2 . 2 2 1                  Dengan

 

x Fo c t k _   2 .  dan

 

D D _Bi k x h   , maka





n j i n j i n j i D n j i f D n j i n j i n j i n j i n j i n j i D n j i f D n j i n j i n j i T T T FoBi T Fo T FoBi T T T Fo T T Fo T Bi T T Bi T T T , 1 , , , , 1 1 , , 1 , 1 , , , , 1 1 , , 1 . 2 . 4 . 2 2 2 1 . . 2 . 2 2 1                                    











