DISTRIBUSI SUHU, LAJU ALIRAN KALOR, DAN EFEKTIVITAS PADA SIRIP BENDA PUTAR 1 DIMENSI KEADAAN TAK TUNAK DENGAN k = k (T)

(1)

DISTRIBUSI SUHU, LAJU ALIRAN KALOR, DAN

EFEKTIVITAS PADA SIRIP BENDA PUTAR 1

DIMENSI

KEADAAN TAK TUNAK DENGAN k = k (T)

NASKAH TUGAS AKHIR

Diajukan untuk memenuhi salah satu syarat memperoleh gelar Sarjana Teknik

Jurusan Teknik Mesin

Disusun oleh :

Nama : ANTONIUS S. W NIM : 025214114

PROGRAM STUDI TEKNIK MESIN

JURUSAN TEKNIK MESIN

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

(2)

DISTRIBUTION OF TEMPERATURE, HEAT

TRANSFER RATE, AND EFFECTIVITY OF ONE

DIMENTIONAL ROTARY BODY FIN IN UNSTEADY

STATE CONDITION WITH k = k (T)

FINAL PROJECT

Presented as Partial Fulfillment of the Requirements to Obtain the Sarjana Teknik Degree

in Mechanical Engineering

By

ANTONIUS S.W Student Number : 025214114

MECHANICAL ENGINEERING STUDY PROGRAM

MECHANICAL ENGINEERING DEPARTMENT

SCIENCE AND TECHNOLOGY FACULTY

SANATA DHARMA UNIVERSITY

(3)

(4)

PERNYATAAN

Saya menyatakan dengan sesungguhnya bahwa Tugas Akhir yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan di dalam daftar pustaka yang sebagaimana layaknya sebuah karya ilmiah.

Yogyakarta, November 2007 Penulis

(5)

(6)

KATA PENGANTAR

Puji syukur kepada Tuhan atas berkat dan karunia-Nya yang begitu besar sehingga penyusun dapat menyelesaikan Tugas Akhir dengan lancar. Tugas Akhir ini adalah untuk memenuhi salah satu syarat agar dapat menyelesaikan studi di Jurusan Teknik Mesin Universitas Sanata Dharma.

Adapun harapan penyusun agar tulisan ini dapat bermanfaat untuk menambah wawasan bagi mahasiswa.

Dalam kesempatan ini penyusun ingin mengucapkan terima kasih kepada semua pihak yang telah banyak membantu selama penyusunan tugas akhir ini, antara lain :

1. Universitas Sanata Dharma Yogyakarta.

2. Romo Ir. Greg Heliarko, S. J., S. S., B. S. T., M. A., M. Sc., selaku Dekan Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta.

3. Bapak Ir. PK. Purwadi, M. T., selaku Dosen Pembimbing Tugas Akhir yang memotivasi serta mendukung penyusunan Tugas Akhir ini.

4. Bapak Budi Sugiharto, S. T., M. T., selaku Ketua Jurusan Teknik Mesin Universitas Sanata Dharma Yogyakarta.

5. Bapak Yosef Agung Cahyanta, S. T., M. T., selaku Dosen Pembimbing Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta.

6. Dosen – dosen Universitas Sanata Dharma Yogyakarta yang telah memberikan bimbingannya kepada penyusun.

7. Pembantu Rektor II yang telah membantu dan memberi kesempatan Dispensasi bagi penyusun.

(7)

9. Joko, Edi, Endang, Hari, selaku saudara kandung penyusun yang mendukung Tugas Akhir penyusun.

10.Ch. Amalia, Popo, Muka Beruang, Pipo, dan Kyo, selaku keluarga kecil bahagia penyusun yang sangat dicintai penyusun.

11.Mahasiswa Fakultas Sains dan Teknologi Angkatan 2002

12.Semua pihak yang tidak bisa penyusun sebutkan satu per satu yang telah membantu penyusun baik secara langsung maupun tidak langsung.

Penyusun menyadari bahwa penyusunan Tugas Akhir ini masih jauh dari sempurna, oleh karena itu saran dan kritik yang bersifat membangun sangat penyusun harapkan demi kesempurnaan Tugas Akhir ini.

Yogyakarta, November 2007 Penyusun

(8)

DAFTAR ISI

Halaman Judul ... i

Title Page ... ii

Lembar Soal ... iii

Lembar Pernyataan ... iv

Lembar Pengesahan ...v

Kata Pengantar ... vi

Daftar Isi ... vii

Daftar Gambar ... xi

Daftar Tabel ... xiv

Lembar Pernyataan Persetujuan Punlikasi Karya Ilmiah ... xv

Intisari ... xvi

BAB I Pendahuluan 1. 1. Latar Belakang Masalah ...1

1. 2. Tujuan Penelitian ...3

1. 3. Manfaat Peneitian ...3

1. 4. Perumusan Masalah ...4

1. 4. 1. Geometri Benda ...4

1. 4. 2. Model Matematika ...4

1. 4. 3. Kondisi Awal ...5

1. 4. 4. Kondisi Batas ...6

1. 4. 5. Asumsi ...6

(9)

2. 2. Perpindahan Kalor Konduksi ...8

2. 3. Konduktivitas Termal ...9

2. 4. Perpindahan Kalor Konveksi ...12

2. 4. 1. Perpindahan Kalor Konveksi Bebas atau Alamiah ...13

2. 4. 1. 1. Bilangan Rayleigh ( Ra ) ...13

2. 4. 1. 2. Bilangan Nusselt ( Nu ) ...14

2. 4. 2. Perpindahan Kalor Konveksi Paksa ...15

2. 4. 2. 1. Untuk Aliran Laminar ...17

2. 4. 2. 2. Untuk Kombinasi Aliran Laminar dan Turbulen ...17

2. 5. Koefisien Perpindahan Kalor Konveksi ...18

2. 6. Laju Perpindahan Kalor ...20

2. 7. Efektivitas Sirip ...20

BAB III Persamaan Numerik Beda Hingga Di Setiap Node 3. 1. Kesetimbangan Energi ...22

3. 2. Penurunan Model Matematika ...23

3. 3. Persamaan Beda Hingga yang Berlaku Pada Tiap Titik Benda Putar 1 Dimensi ...25

3. 3. 1. Node Batas Kiri atau Dasar Sirip ...26

3. 3. 2. Node di Bagian Badan Sirip dan Syarat Stabilitas ...26

3. 3. 3. Node Pada Ujung Sirip atau Batas Kanan dan Syarat Stabilitas ...31

3. 4. Perhitungan Luas Penampang, Luas Selimut, dan Volume Sirip ..34

3. 4. 1. Node Pada Batas Kiri atau Dasar Sirip ...36

3. 4. 2. Node di Bagian Badan Sirip ...37

(10)

BAB IV Metode Penelitian

4. 1. Kondisi Benda uji pada Lingkungan ...41

4. 2. Peralatan Pendukung Penelitian ...42

4. 3. Metode Penelitian yang digunakan ...42

4. 4. Pengambilan dan Pengolahan Data ...43

BAB V Hasil Perhitungan dan Pembahasan 5. 1. Hasil Perhitungan ...44

5. 1. 1. Distribusi Suhu ...45

5. 1. 2. Laju Perpindahan Kalor ...48

5. 1. 3. Efektivitas ...52

5. 2. Pembahasan ...55

BAB VI Kesimpulan dan Saran 6. 1. Kesimpulan ...60

6. 2. Saran ...60

Daftar Rumus Persamaan di tiap Node pada Sirip...62

(11)

DAFTAR GAMBAR

Gambar 1.1 Berbagai jenis muka bersirip...1

Gambar 1.2 Sirip berbentuk benda putar ...4

Gambar 1.3 Konduktivitas termal pada alumunium ...5

Gambar 2.1 Perpindahan Kalor Konduksi ...9

Gambar 2.2 Grafik nilai konduktivitas termal beberapa bahan dengan k = k (T) ... ...11

Gambar 2.3 Perpindahan kalor konveksi ...12

Gambar 2.4 Silinder dalam arah silang...15

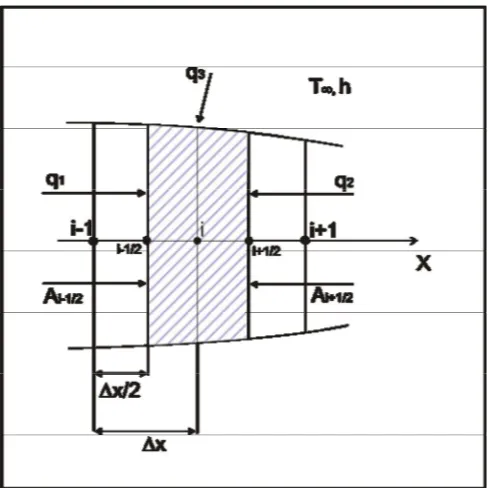
Gambar 3.1 Kesetimbangan energi pada volume kontrol...22

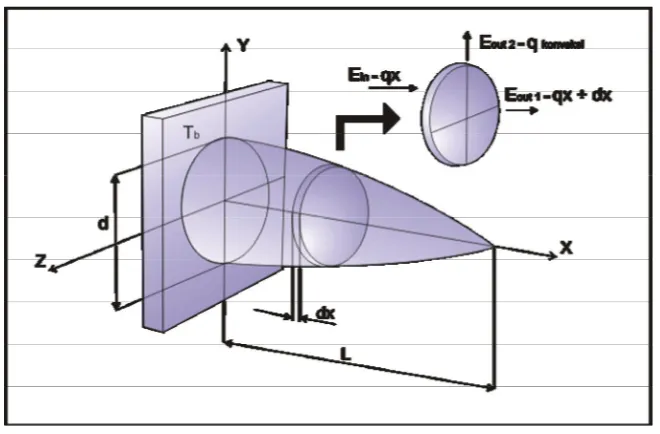
Gambar 3.2 Volume kontrol pada sirip...23

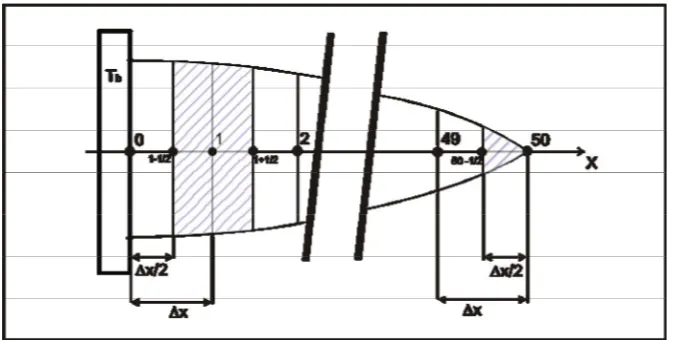
Gambar 3.3. Pembagian volume kontrol pada sirip...26

Gambar 3.4 Volume kontrol pada bagian badan sirip ...27

Gambar 3.5 Volume kontrol pada batas kanan atau ujung sirip ...31

Gambar 3.6 Fungsi sirip...35

Gambar 3.7 Volume kontrol sirip ...35

Gambar 3.8 Luas selimut dan luas permukaan setiap volume kontrol pada sirip ...35

Gambar 3.9 Node datas kiri atau dasar sirip ...36

Gambar 3.10 Node di bagian badan sirip...37

Gambar 3.11 Node pada ujung atau batas kanan ...39

Gambar 4.1 Benda uji dan kondisi lingkungan...41

Gambar 5.1 Distribusi suhu sirip saat t = 0 dtk, dengan variasi h, W/m2.oC ...45

(12)

Gambar 5.8 laju perpindahan kalor saat t = 0 dtk, dengan variasi h, W/m2.oC ...48

Gambar 5.9 laju perpindahan kalor saat t = 5 dtk, dengan variasi h, W/m2.oC ...49

Gambar 5.10 laju perpindahan kalor saat t = 10 dtk, dengan variasi h, W/m2.oC ... ...49

Gambar 5.15 Efektivitas sirip saat t = 0 dtk, dengan variasi h, W/m2.oC ...52

(13)

(14)

DAFTAR TABEL

Tabel 2.1 Nilai Konduktivitas Termal Beberapa Bahan ...10

Tabel 2.2 Beberapa persamaan pendekatan konduktivitas termal k = k (T)...11

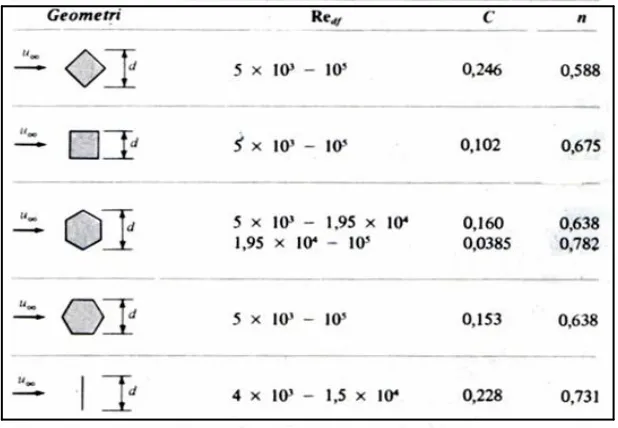
Tabel 2.3 Konstanta Untuk Persamaa 2. 6 ...16

Tabel 2.4 Konsatanta untuk perpindahan kalor dari silinder tak bundar ...16

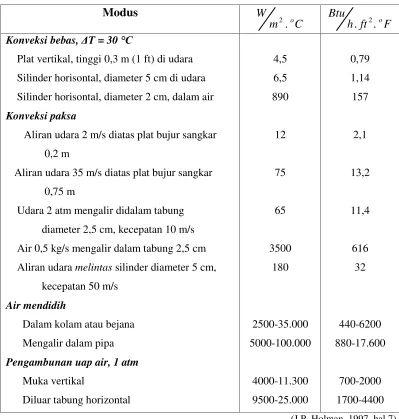
Tabel 2.5 Harga koefisien perpindahan kalor konveksi (h)...19

Tabel 5.1 Laju perpindahan kalor dari waktu ke waktu (Watt) ...57

(15)

LEMBAR PERNYATAAN PERSETUJUAN

PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS

Yang bertanda tangan dibawah ini, saya mahasiswa Universitas Sanata Dharma :

Nama : Antonius Supriadi. W

Nomor Mahasiswa : 025214114

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:

DISTRIBUSI SUHU, LAJU ALIRAN KALOR, DAN EFEKTIVITAS PADA SIRIP BENDA PUTAR 1 DIMENSI KEADAAN TAK TUNAK DENGAN k = k (T)

Beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpas,

mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di Internet atau media lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini yang saya buat dengan sebenarnya. Dibuat di Yogyakarta

Pada tanggal : 8 November 2007

Yang menyatakan

(16)

INTISARI

Penelitian ini bertujuan untuk menentukan besarnya laju aliran kalor q yang dilepas sirip dan efektivitas sirip å pada sirip benda putar dengan fungsi r = -2 (x2)+0,005 keadaan tak tunak dengan berbagai nilai koefisien perpindahan kalor konveksi h dan nilai konduktivitas termal bahan berubah sesuai dengan perubahan suhu dari waktu ke waktu (k=k(T)). Perpindahan kalor konduksi yang terjadi pada sirip ditinjau dalam 1 arah (1 dimensi) yaitu arah x.

Penyelesaian penelitian dilakukan dengan metode komputasi beda-hingga dengan cara eksplisit. Bahan sirip dari alumunium, dengan nilai massa jenis ñ, kalor jenis c. Suhu awal sirip merata pada nilai tertentu, sebesar Ti=100 oC. Suhu dasar sirip dipertahankan tetap sebesar Tb=100. Suhu fluida merata dan tetap

sebesar T_∞=30oC, demikian juga nilai koefisien perpindahan kalor konveksi h bersifat merata dan tetap dari waktu ke waktu. Dipilih nilai koefisien perpindahan kalor konveksi h : 500 W/m2oC, 2500 W/m2oC, 5000, 7500, 10000 W/m2oC. Ukuran dasar sirip yaitu dengan panjang 50 mm dan berdiameter 10 mm.

(17)

BAB I PENDAHULUAN

1.1.Latar Belakang Masalah

Dalam dunia industri, faktor efisiensi dan prestasi kerja mesin yang baik sangat diharapkan. Ada banyak hal yang dapat dilakukan untuk memperolehnya, antara lain dengan cara pendinginan. Untuk menghasilkan proses pendinginan yang cepat pada suatu peralatan dapat digunakan sirip. Sirip digunakan untuk memperluas permukaan suatu benda dengan tujuan mempercepat proses perpindahan kalor, oleh karena itu sirip banyak digunakan pada peralatan yang memiliki suhu kerja yang tinggi.

Contoh penggunaan sirip dalam kehidupan sehari-hari dapat kita lihat pada peralatan elektronika, kendaraan bermotor, rangkaian komputer untuk mendinginkan motherboard, prossesor dan lain-lain. Berbagai jenis permukaan bersirip dengan berbagai variasi bentuk dapat dilihat pada Gambar 1.1.

(18)

Telah banyak penelitian tentang pencarian distribusi suhu keadaan tak tunak pada benda padat dengan berbagai kasus yang sudah dilakukan diantaranya seperti yang telah dilakukan oleh Maxima Estu dengan judul penelitian “Perpindahan Kalor

Pada Sirip Kerucut 1 Dimensi Keadaan Tak Tunak Dengan k = k(T)”. Penelitian

tersebut bertujuan untuk meneliti dan mengetahui kondisi sirip kerucut pada keadaan tak tunak dan keadaan tunak melalui perhitungan laju perpindahan panas, efisiensi sirip dan efektivitas sirip dengan memvariasikan nilai koefisien perpindahan kalor konveksi (h) dan bahan sirip. Hasil yang didapat, semakin besar nilai konduktivitas termal dan difusivitas termal bahan semakin kecil laju perpindahan panas, efisiensi dan efektivitas pada sirip kerucut.

Penelitian lain tentang sirip juga dilakukan oleh Henry Agustinus dengan judul penelitian “Laju Perpindahan Kalor, Efisiensi dan Efektivitas sirip Kerucut

pada Keadaan Tak Tunak 1 Dimensi”. Penelitian dilakukan untuk menghitung laju perpindahan kalor, efisiensi dan efektivitas sirip kerucut dengan diameter sebagai fungsi posisi pada keadaan tak tunak serta memvariasikan nilai koefisien perpindahan kalor konveksi h dan konduktivitas termal bahan k. hasil yang didapat, semakin besar nilai konduktivitas termal bahan dan difusitivitas termal bahan semakin kecil laju perpindahan kalor, efisiensi dan efektivitas sirip kerucut.

(19)

model matematika yang diperlukan untuk menyelesaikan persoalan pada sirip keadaan tak tunak dengan nilai k yang diambil tetap. Hal yang membedakan penelitian ini dari penelitian sebelumnya adalah nilai konduktivitas termal (k) bahan yang merupakan fungsi temperatur, k=k(T) serta dengan bentuk sirip benda putar.

1.2.Tujuan Penelitian Penelitian ini bertujuan untuk:

1. Mengetahui distribusi suhu, laju aliran kalor dan efektivitas pada sirip benda putar dari waktu ke waktu dengan nilai k=k(T) pada keadaan tak tunak.

2. Menentukan nilai koefisien perpindahan kalor konveksi (h) yang memberikan nilai efektivitas sirip yang menguntungkan bagi pemasangan sirip.

1.3. Manfaat Penelitian

Penelitian yang dilakukan diharapkan dapat memberikan manfaat sebagai berikut:

1. Dapat mengerti dan menghitung distribusi suhu dan laju perpindahan kalor pada sirip benda putar dengan sifat bahan yang berubah terhadap suhu k=k(T) dengan metode beda hingga cara eksplisit.

2. Membantu dalam menentukan waktu yang diperlukan sirip benda putar untuk mencapai keadaan tunak.

(20)

1.4. Perumusan Masalah

Sirip berbentuk benda putar mempunyai suhu awal (Ti) yang seragam. Secara tiba-tiba sirip dikondisikan pada fluida lingkungan baru dengan suhu fluida (T_∞) dan nilai koefisien perpindahan kalor konveksi (h). Persoalan yang harus diselesaikan adalah mencari nilai distribusi suhu, laju perpindahan kalor dan efektivitas sirip benda putar dari waktu ke waktu dengan suhu dasar sirip dipertahankan tetap dari waktu ke waktu.

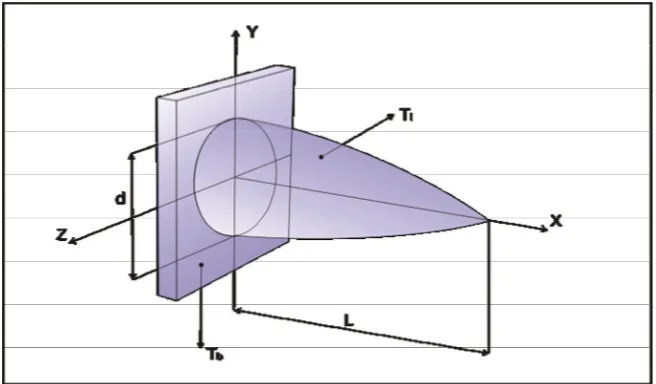
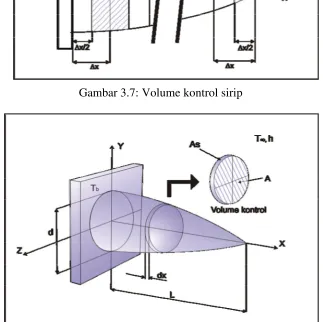
1.4.1. Geometri Benda

Geometri sirip berbentuk benda putar yang berbentuk seperti ujung peluru seperti yang terlihat pada Gambar 1.2.

Gambar 1.2: Sirip berbentuk benda putar

1.4.2. Model Matematika

Model matematika yang sesuai dengan persoalan serta kondisi awal dan kondisi batas dinyatakan dalam persamaan (1.1), (1.2), (1.3) dan (1.4).

(21)

Konduktivitas termal pada alumunium

k = 0,0004(T2)- 0,0371(T) + 205,44

R2 = 0,9862

0 50 100 150 200 250

-100 0 100 200 300 400

Suhu (T), o_C

K

o

n

d

u

k

ti

v

it

a

s

t

e

rm

a

l

(k

),

W

/m

o C

Konduktivitas pada alumunium





t t x T dx

V d c T

T dx dA h x

t x T A T k

x x

s c

  

 

  



  





) , ( . . . .

) , ( ).

( 

; 0 < x < L, t0……….. (1.1)

Untuk menentukan funsi k=k(T) dapat dilihat dari Gambar 1.3, harga konduktivitas termal bahan alumunium dengan harga k=k(T) yang didapat persamaan garis fungsi linier k=0,0004(T2)-0,037(T) +205,44 dengan nilai R2= 0,9862 (mendekati valid).

Gambar 1.3: Konduktivitas termal pada alumunium

1.4.3. Kondisi Awal

Keadaan awal benda yang merupakan kondisi awal benda mempunyai suhu yang seragam atau merata. Secara matematis dinyatakan dengan persamaan:

 

x t T

 

x Ti

(22)

1.4.4. Kondisi Batas

Pada persoalan yang ditinjau semua permukaan sirip bersentuhan dengan fluida lingkungan yang mempunyai suhu T=T_∞ yang dipertahankan tetap dari waktu ke waktu dan merata. Nilai koefisien perpindahan panas konveksi (h) dari fluida lingkungan juga merata dan dipertahankan tetap dari waktu ke waktu.

 Kondisi dasar sirip

b

T t

T(0, ) ; x = 0, t0………..…………..… (1.3)

 Kondisi ujung sirip





t T V c x T A k T T A

h s i c

  

   

 . . . .

.  ; x = L, t0………..…… (1.4)

1.4.5. Asumsi

Asumsi yang didapat adalah sebagai berikut:

 Sifat benda (ñ atau c) tetap dan merata.

 Nilai konduktivitas termal berubah terhadap suhu, k=k(T).

 Selama proses, perubahan volume dan bentuk pada sirip diabaikan.

 Tidak ada energi pembangkitan di dalam sirip.

 Suhu fluida tetap dari waktu ke waktu dan merata.

 Nilai koefisien perpindahan panas konveksi (h) dari fluida tetap dari waktu ke waktu dan merata.

 Arah perpindahan kalor konduksi hanya satu dimensi yaitu hanya dalam satu arah, arah x.

Keterangan:

(23)

T_∞ = suhu fluida, oC

Ti = suhu awal benda sirip pada node I, oC Tb = suhu dasar sirip, oC

Ai = luas penampang volume kontrol, m2 As = luas permukaan volume kontrol, m2 V = besar volume kontrol, m3

D = diameter, m t = waktu, s x = posisi node, m

ñ = massa jenis sirip, kg/ m3 c = kalor spesifik sirip, J/kg oC

h = koefisien perpindahan kalor konveksi, W/m2. oC

(24)

BAB II

LANDASAN TEORI

2.1. Perpindahan Kalor

Perpindahan kalor (heat transfer) adalah proses perpindahan kalor yang terjadi karena adanya perbedaan suhu antara daerah-daerah atau material tersebut. Jika dua benda bersinggungan maka akan terjadi perpindahan kalor dari benda bersuhu tinggi ke benda bersuhu rendah hingga dicapai suhu akhir yang disebut suhu kesetimbangan. Ilmu tentang perpindahan kalor tidak hanya mencoba menjelaskan bagaimana energi kalor dapat berpindah dari satu daerah ke daerah lain tetapi juga meramalkan atau memprediksikan laju perpindahan panas yang terjadi pada kondisi-kondisi tertentu.

Perpindahan kalor yang terjadi pada sirip meliputi perpindahan kalor konduksi, perpindahan kalor konveksi dan perpindahan kalor radiasi tetapi karena perpindahan kalor radiasi yang terjadi sangat kecil maka dapat diabaikan.

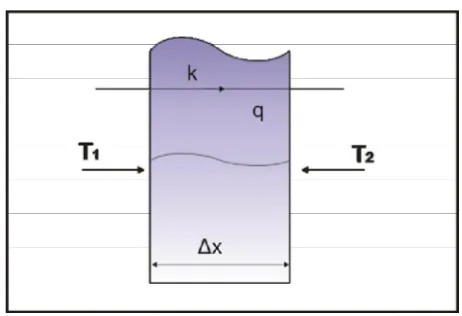
2.2. Perpindahan Kalor Konduksi

Proses perpindahan kalor konduksi adalah perpindahan kalor yang terjadi pada benda tanpa adanya perpindahan bagian dari benda tersebut, biasanya terjadi pada media benda padat. Dalam perhitungan perpindahan kalor konduksi dipakai rumusan umum:

x T A k q

  

 . . ……….…... (2.1)

Keterangan:

(25)

k = konduktivitas termal bahan, W/m.oC A = luas permukaan benda, m2

x T

 

= gradien suhu ke arah perpindahan kalor, _

    

m C

o

Gambar 2.1: Perpindahan kalor konduksi

Tanda - (minus) yang terdapat dalam persamaan (2.1) tersebut dimaksudkan agar persamaan diatas memenuhi hukum kedua termodinamika, yaitu kalor akan mengalir dari suhu tinggi ke suhu rendah atau disebut hukum Fourier tentang konduksi kalor.

2.3. Konduktivitas Termal

(26)

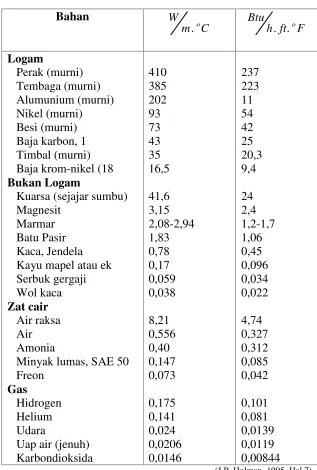
Aliran kalor dinyatakan dalam satuan Watt, sedangkan satuan untuk konduktivitas termal adalah Watt per meter derajat Celsius (W/m.oC). Perhatikan dalam Table 2.1, terlihat nilai konduktivitas termal itu menunjukkan seberapa cepat laju perpindahan kalor ke dalam bahan tertentu. Dapat disimpulkan pula jika makin cepat molekul bergerak maka makin cepat pula energi yang berpindah.

Table 2.1: Nilai Konduktivitas Termal Beberapa Bahan Bahan

C m W

o

. h ft F

Btu

o

. . Logam

Perak (murni) Tembaga (murni) Alumunium (murni) Nikel (murni) Besi (murni) Baja karbon, 1 Timbal (murni) Baja krom-nikel (18 Bukan Logam

Kuarsa (sejajar sumbu) Magnesit

Marmar Batu Pasir Kaca, Jendela Kayu mapel atau ek Serbuk gergaji Wol kaca Zat cair Air raksa Air Amonia

Minyak lumas, SAE 50 Freon

Gas

Hidrogen Helium Udara

Uap air (jenuh) Karbondioksida

410 385 202 93 73 43 35 16,5 41,6 3,15 2,08-2,94 1,83 0,78 0,17 0,059 0,038 8,21 0,556 0,40 0,147 0,073 0,175 0,141 0,024 0,0206 0,0146

(27)

Konduktivitas Termal beberapa bahan

k = 0,0004(T2_{)- 0,0371(T) + 205,44}

k = 0,00002(T2)- 0,0454(T) + 55,786

k = 0,00004(T2_{)- 0,0848(T) + 75,644}

k =0,00006(T2_{)- 0,1103(T) + 92,602}

0 50 100 150 200 250

-100 100 300 500 700 900 1100

Suhu (T), o_C

k

o

n

d

u

k

ti

v

it

a

s

t

e

rm

a

l

(k

),

w

/m

o c

alumunium murni baja karbon (C: 0,5 %) besi murni nikel murni

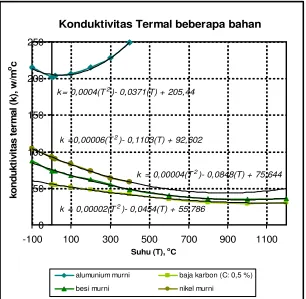
Gambar 2.2: Grafik nilai konduktivitas termal beberapa bahan dengan k= k(T)

Dalam kasus ini konduktivitas termal bahan berubah sesuai dengan perubahan suhu dari waktu ke waktu terlihat pada Gambar 2.2. Nilai konduktivitas termal bahan didapat dari persamaan pendekatan konduktivitas termal k=k(T), seperti pada Tabel 2.2:

Tabel 2.2: Beberapa persamaan pendekatan konduktivitas termal k=k(T)

Bahan

Massa jenis, Kg/m3

Daerah suhu,

o

C

k fungsi dari suhu atau k=k(T), W/m.oC

Alumunium murni Besi murni

Baja karbon (C: 0,5%) Nikel murni

2707 7897 7822 8906

0-400 0-1200 0-1200 0-400

(28)

2.4. Perpindahan Kalor Konveksi

Perpindahan kalor konveksi adalah perpindahan kalor yang terjadi pada benda yang disertai adanya perpindahan bagian atau aliran dari benda tersebut, biasanya terjadi pada benda cair atau gas.

Gambar 2.3: Perpindahan kalor konveksi

Dalam perhitungan perpindahan kalor konveksi dipakai rumusan umum:



 





 h b

q . . ………...………..… (2.2)

Keterangan:

q = perpindahan kalor, Watt

h = koefisien perpindahan kalor konveksi, W/m2 .oC A = luas benda, m2

Tb = suhu permukaan benda, oC T_∞ = suhu fluida, oC

(29)

2.4.1. Perpindahan Kalor Konveksi Bebas atau Alamiah

Perpindahan kalor konveksi secara alamiah atau bebas terjadi karena adanya perbedaan suhu benda dan suhu fluida sehingga mengakibatkan kalor mengalir diantara benda dan fluida serta adanya perubahan kerapatan lapisan-lapisan fluida di dekat permukaan. Perbedaan kerapatan menyebabkan fluida yang lebih berat mengalir ke bawah dan fluida yang ringan akan mengalir ke atas. Perbedaan kerapatan gradien suhu mengakibatkan terjadinya gerakan fluida atau gerakan fluida karena terjadinya beda massa jenis, terjadi tanpa adanya bentuan alat seperti pompa atau kipas. Mekanisme perpindahan kalor ini dikenal dengan konveksi alamiah atau bebas.

Contoh paling sederhana pada perpindahan kalor konveksi alamiah atau bebas ditemui pada kasus memasak air. Semua air yang ada dalam tangki dapat mendidih secara merata karena terjadi pergerakan air yang disebabkan adanya perbedaan massa jenis. Fluida yang mengalami pemanasan akan mengembang sehingga massa jenisnya lebih kecil dari fluida dingin.

2.4.1.1. Bilangan Rayleigh (Ra)

Untuk menghitung besarnya perpindahan kalor konveksi bebas harus diketahui nilai koefisien perpindahan kalor konveksi (h) terlebih dahulu. Nilai h

dapat dicari dari Bilangan Nusselt karena Bilangan Nusselt merupakan fungsi dari bilangan Rayleigh (Ra) maka bilangan Ra harus dicari terlebih dahulu.

Untuk silinder horizontal, bilangan Rayleigh dinyatakan dengan persamaan (2.3).





Pr v

ä T T â g Pr Gr

Ra ₂

3

b   _

   

(30)

Dengan

f

T 1

â dan





2 T T

T b

f



 

Keterangan:

Pr = bilangan Prandtl Gr = bilangan Grashof

g = percepatan gravitasi (g=9,81), m/s2

ä = panjang karakteristik, untuk silinder horizontal ä = L, m

Tb = suhu dinding, °K T_∞ = suhu fluida, °K

Tf = suhu film, °K

v = viskositas kinematik, m2/s

2.4.1.2. Bilangan Nusselt (Nu)

Untuk silinder horizontal, bilangan Nusselt dinyatakan dengan persamaan berikut:

Untuk 10-5 < Gr Pr < 1012, digunakan persamaan (2.4)









6 1

9 16 16 9 2

1

Pr 559 0 1

Pr . 387

, 0 60 , 0

  

 

  

 

 



, Gr

Nu ... (2.4)

Untuk 10-6 < Grd Pr < 109, tetapi berlaku hanya pada aliran laminer digunakan persamaan (2.5):

















 

  

 



  

9 4 16 9

4 1

Pr 559 0 1

Pr 518

, 0 36 , 0

, Gr

(31)

2.4.2. Perpindahan Kalor Konveksi Paksa

Proses perpindahan kalor konveksi paksa ditandai dengan adanya fluida yang bergerak yang dikarenakan adanya peralatan bantu. Alat bantu untuk menggerakkan fluida dapat berupa fan, blower, pompa dll. Akibat dari perbedaan suhu antara benda dan fluida mengakibatkan panas mengalir dari antara benda dan fluida serta mengakibatkan perubahan kerapatan lapisan-lapisan fluida yang ada di dekat permukaan. Perbedaan kerapatan menyebabkan fluida yang berat akan mengalir ke arah bawah dan fluida yang ringan akan bergerak ke atas. Gerakan fluida yang terjadi ini karena adanya bantuan alat seperti fan atau pompa. Mekanisme perpindahan kalor terjadi karena adanya fluida yang bergerak karena adanya alat bantu disebut perpindahan kalor konveksi paksa. Pada kasus sirip diasumsikan konveksi paksa terjadi dalam aliran menyilang silinder dan bola seperti pada Gambar 2.4

Gambar 2.4: Silinder dalam arah silang

(32)

Untuk berbagai bentuk geometri benda, koefisien perpindahan panas rata-rata dapat dihitung dari persamaan (2.6):

3 . 1 ~

Pr .

.

n

f

f v

d u C k

d h

        

 ………...……….. (2.6)

Dengan besarnya konstanta C dan n sesuai dengan Tabel 2.3

Tabel 2.3: Konstanta untuk Persamaan 2.6

Redf C n

0,4 - 4 0,989 0,33

4 - 40 0,911 0,385

40 - 4000 0,683 0,466

40 - 40000 0,193 0,618

40000 - 400000 0,0266 0,805

(J.P.Holman, 1995, hal 268)

perpindahan kalor dari silinder yang tak bundar nilai C dan n dapat ditentukan berdasarkan Tabel 2.4

Tabel 2.4: Konstanta untuk perpindahan kalor dari silinder tak bundar

(33)

2.4.2.1. Untuk Aliran Laminar

Pada aliran menyilang silinder dengan syarat aliran Laminar: Rex < 100.000, Bilangan Reynold dirumuskan sebagai berikut:

ì

x U

ñ

x

. .

Re  ~

... (2.7)

Persamaan Nusselt yang berlaku adalah : Untuk 10-1 < Ref < 105



0,52



0,.3

Pr Re 56 , 0 35 ,

0 f f

f

Nu   ... (2.8) Untuk 1 < Re < 103



0,5



0,38 0,25

Pr Pr Pr

Re 50 , 0 43 ,

0 _

     



w f

Nu ... (2.9)

Untuk 103 < Re < 2 × 105

25 , 0 38

, 0 6 , 0

Pr Pr Pr

. Re . 25 ,

0 _

     

w f

Nu ... (2.10)

2.4.2.2. Untuk Kombinasi Aliran Laminar dan Turbulen

Pada aliran menyilang silinder dengan syarat aliran sudah turbulen: 500.000 < Re < 10 , berlaku persamaan Nusselt:

5 4 8 5

4 3 3 2

3 1 2 1

282000 Re 1

Pr 4 , 0 1

Pr . Re . 62 , 0 3 ,

0 _

  

  

   

  

    

  

        

Nu ... (2.11)

Keterangan :

Re = Bilangan Reynold Nu = Bilangan Nusselt

(34)

T_∞ = Suhu fluida, oC

A = Luas permukaan dinding, m2 g = percepatan gravitasi (g= 9,81), m/s2

ä = panjang karakteristik, untuk dinding vertikal ä = L, m Tf = suhu film, oC

v = viskositas kinematik, m2/s (dapat dilihat pada tabel) k = koefisien perpindahan panas konduksi dari fluida, W/m.oC ñ = Massa jenis fluida, kg/m3

u_∞ = Kecepatan fluida, m/s ì = viskositas dinamik, kg/m.s

kf = koefisien perpindahan panas konduksi fluida, W/mo.C h = koefisien perpindahan panas konveksi, W/m2.oC Pr = Bilangan Prandtl

L = Panjang dinding, m

2.5. Koefisien Perpindahan Kalor Konveksi

(35)

Tabel 2.4: Harga koefisien perpindahan konveksi (h) Modus

C m W

o

.

2

F ft h Btu

o

. . 2 Konveksi bebas, ÄT = 30 °C

Plat vertikal, tinggi 0,3 m (1 ft) di udara

Silinder horisontal, diameter 5 cm di udara

Silinder horisontal, diameter 2 cm, dalam air

Konveksi paksa

Aliran udara 2 m/s diatas plat bujur sangkar

0,2 m

Aliran udara 35 m/s diatas plat bujur sangkar

0,75 m

Udara 2 atm mengalir didalam tabung

diameter 2,5 cm, kecepatan 10 m/s

Air 0,5 kg/s mengalir dalam tabung 2,5 cm

Aliran udara melintas silinder diameter 5 cm,

kecepatan 50 m/s

Air mendidih

Dalam kolam atau bejana

Mengalir dalam pipa

Pengambunan uap air, 1 atm

Muka vertikal

Diluar tabung horizontal

4,5

6,5

890

12

75

65

3500

180

2500-35.000

5000-100.000

4000-11.300

9500-25.000

0,79

1,14

157

2,1

13,2

11,4

616

32

440-6200

880-17.600

700-2000

1700-4400

(J.P. Holman, 1997, hal 7)

Dari bilangan Nusselt (Nu) dapat diperoleh bilai koefsien perpindahan kalor konveksi:

f

k ä h

Nu   atau

ä k Nu

h _  f _………

..…... (2.12)

Keterangan:

Nu = Bilangan Nusselt

h = Koefisien perpindahan kalor konveksi, W/m2.oC

(36)

ä = Panjang karakteristik, untuk dinding vertikal ä = L, m

2.6. Laju Perpindahan Kalor

Laju perpindahan kalor atau laju aliran kalor merupakan jumlah kalor yang dilepas oleh seluruh volume kontrol dari sirip ke lingkungan dengan cara konveksi yang dinyatakan dengan persamaan (2.14)

n

q ... q q q q

Q  ₀  ₁  ₂  ₃   ………..………. (2.13)











  



 _





 

n

i

i si T T

A h

Q

0

………..……… (2.14)

Keterangan:

Q = Laju perpindahan kalor, Watt

h = Koefisien perpindahan kalor konveksi, W/m2 .oC q = Perpindahan kalor di setiap volume kontrol, Watt n = Jumlah volume kontrol

Asi = luas permukaan volume kontrol di posisi i yang bersentuhan fluida, m2 Ti = Suhu volume kontrol pada posisi i, oC

2.7. Efektivitas Sirip

Efektivitas sirip merupakan perbandingan antara kalor yang dilepas sesungguhnya dengan kalor yang dilepas seandainya tidak ada sirip atau tanpa sirip, dinyatakan dengan persamaan (2.16).















 

    



 _





T T A h

î

b c n

i

i si

0 0

(37)

Keterangan:

 = Efektivitas sirip

h = Koefisien perpindahan kalor konveksi, W/m2 .oC

Asi = Luas permukaan volume kontrol di posisi i yang bersentuhan fluida, m2 Ac0 = Luas penampang dasar sirip, m2

Ti = Suhu volume kontrol pada posisi i, oC Tb = Suhu dasar sirip, oC

(38)

BAB III

PERSAMAAN NUMERIK BEDA HINGGA DI SETIAP NODE

3.1. Kesetimbangan Energi

Kesetimbangan energi pada volume kontrol dapat dinyatakan dengan persamaan sebagai berikut:

   

 

   

 

 

   

 

   

 

 

       

 

       

 

       

 

       

 

 

       

 

       

 



t waktu selang

selama kontrol

volume dalam

di

erergi perubahan

t waktu selang

selama kontrol

volume

dalam di an dibangkitk

yang energi besar

t waktu

selang selama

kontrol volume

dari

keluar yang

energi seluruh

t waktu

selang selama

kontrol volume

dalam ke

masuk yang

energi seluruh

Gambar 3.1: Kesetimbangan energi pada volume kontrol

Maka : _  _OUT  _g  _ST ……….…..………... (3.1) Keterangan:

EIN = Energi yang masuk ke dalam volume kontrol persatuan waktu, Watt Est = Energi tersimpan atau perubahan energi dalam volume kontrol persatuan

waktu, Watt

(39)

Dalam hal ini EIN dan Eout terkait dengan proses-proses yang terjadi pada

control surface sehingga merupakan fungsi luas permukaan, sedangkan Est dan Eg merupakan fungsi volume kontrol pada keadaan steady state, tidak terjadi perubahan energi dalam.

3.2. Penurunan Model Matematik dari Sirip

Untuk mendapatkan persamaan model matematika yang sesuai dengan persoalan pada penelitian, peninjauan dilakukan terhadap elemen kecil setebal Äx yang disamakan dengan volume kontrol seperti ditunjukkan pada Gambar 3.2

Gambar 3.2: Volume kontrol pada sirip

(40)

kondisi sirip pada keadaan tak tunak (unsteady state). Sehingga dapat dinyatakan sebagai berikut:                                                                                            t waktu selang selama kontrol volume dalam di erergi perubahan t waktu selang selama kontrol volume dalam di an dibangkitk yang energi besar t waktu selang selama kontrol volume dari keluar yang energi seluruh t waktu selang selama kontrol volume dalam ke masuk yang energi seluruh



Ein Eout



Eg Est ; E g = 0, karena tidak ada energi yang dibangkitkan

Dengan : Ein = qx

Eout = qx+dx + qconv

Est =

t T dV c   . . 

Bila dituliskan dengan notasi matematika maka di dapat persamaan (3.2) :





t T dV c q q

q_x _x _dx _conv

  



 _ . . ... (3.2)

t T dV c q q

q_x _x _dx _conv

  



 _ . . , untuk k = k(T)……….…... (3.3)

dengan : dx x q q q x x dx x      



 





h dAs T T

q_conv _x

maka diperoleh :





t T d.V . c ñ. T T dAs h dx x q q

q x _x

x x             _   

 _ ... (3.4)





t T d.V . c ñ. T T dAs h dx x q x x         

(41)

Persamaan (3.4) dikalikan dengan dx

1

diperoleh Persamaan (3.6) :





t T dx dV c ñ T T dx dAs h x q

x x

  

 

  

 _ ………….………... (3.6)

Persamaan (3.6) disubtitusikan ke dalam Persamaan (2.1) sehingga diperoleh:





t T dx dV c T

T dx dAs h x

x T Ac k

x

  

 

   

 

   

 

   



   

 _  ... (3.7)





t T dx dV c T

T dx dAs h x T Ac k

x x 

 

 

  

   



  ... (3.8)

Model matematika untuk sirip dapat dinyatakan Persamaan (3.9) sebagai berikut:

 





 

t t x T dx dV c T

T dx dAs h x

t x T Ac T k

x x 

 

 

  



  





,

, _

; 0<x<L1, t > 0……….……… (3.9)

3.3. Persamaan Beda Hingga Yang Berlaku Pada Tiap Titik Benda Padat 1 Dimensi

(42)

Gambar 3.3: Pembagian volume kontrol pada sirip

Dalam penelitian ini, besarnya suhu pada batas kiri benda atau pada kondisi dasar (Tb) diasumsikan tetap. Terdapat 3 persamaan pokok yang dipergunakan dalam perhitungan suhu pada keadaan tak tunak pada sirip, yaitu pada node batas kiri atau pada dasar sirip (node 0), pada bagian badan sirip (node 1 s/d node 49) dan pada batas kanan atau pada ujung sirip (node 50).

3.3.1. Node Batas Kiri atau Dasar Sirip

Suhu pada dasar sirip dipertahankan tetap dari waktu ke waktu sebesar T . Secara matematis dinyatakan sebagai berikut:

 

x,t T

 

0,t Tb Ti

T    , maka n _b

T

T1 1  ………..…… (3.10)

Berlaku untuk node: 0 (node di dasar sirip)

3.3.2. Node Yang Terletak Di Bagian Badan Sirip dan Syarat Stabilitas

(43)

Gambar 3.4: Volume kontrol pada bagian badan sirip

Secara umum kesetimbangan energi yang berlaku pada volume kontrol dinyatakan sebagai berikut:

                                                                                           t waktu selang selama kontrol volume dalam di erergi perubahan t waktu selang selama kontrol volume dalam di an dibangkitk yang energi besar t waktu selang selama kontrol volume dari keluar yang energi seluruh t waktu selang selama kontrol volume dalam ke masuk yang energi seluruh



  

_ _       t V c q q

q₁ ₂ ₃ 0 . . . ………...…….……... (3.11)

Untuk:

1. Perpindahan kalor konduksi dari node i-1 ke node i





x T T A k q n i n i i n i       1 2 1 2 1

1 . . ………....…... … (3.12)

2. Perpindahan kalor konduksi dari node i+1 ke node i





x T T A k q n i n i i n i       1 2 1 2 1

(44)

3. Perpindahan kalor konveksi pada node i



n



i si

A h

q₃ . . _  ……….………...……. (3.14)

Dengan prinsip persamaan (3.11) maka diperoleh persamaan (3.15):









                                            n i si n i n i n i n i n i i n

i A _x k A _x h A

k . . . . 1 . .

2 1 1 2 1 1 2 1 2 1        t V c. . .

 ……….….... (3.15)

Sehingga diperoleh persamaan (3.16):









                                            n i si n i n i n i n i n i i n

i A _x k A _x h A

k . . . . 1 . .

2 1 1 2 1 1 2 1 2 1             t V c n i n i i 1 . .

 …...……….. (3.16)

Jika persamaan (3.16) dikalikan dengan Äx, maka akan didapat persamaan (3.17):













                  _ _      n i si n i n i n i n i n i i n i x A h A k A

k . . . . ₁ . . .

2 1 1 2 1 1 2 1 2 1              t x V c n i n i i 1 . . . .

 …...……….………..….. (3.17)

Persamaan (3.17) dapat dijabarkan dan disederhanakan menjadi:













                           n i si n i n i i n i n i n i i n i i x A h A k A k x V c t . . . . . . . . .

. ₂1 ₂1 1 ₂1 1₂ 1





n



i n i 



 1

(45)



  n



 i n i 1













                           n i si n i n i i n i n i n i i n i i x A h A k A k x V c t . . . . . . . . .

. ₂1 ₂1 1 ₂1 1₂ 1



……….………(3.19)

 n1

i 

                           . . . . . .

.cV x k 1₂ A ₂1 1 k 1₂ A ₂1 1 h A x t si n i i n i n i i n i i                        

 A k A h A x

k x V c t T si i n i i n i i n

i . . . .

. . . 1 2 1 2 1 2 1 2 1

 ……….. (3.20)

Syarat stabilitas untuk persamaan (3.20) adalah:

0 . . . . . . . 1 2 1 2 1 2 1 2

1 

                    

 A k A h A x

k x V c t si i n i i n i i

 ………. (3.21)

1 . . . . . .

. ₂1 ₂1 ₂1 ₂1 _

           

 A k A h A x

k x V c t si i n i i n i i

 ………....…… (3.22)

Sehingga, x A h A k A k x V c t si i n i i n i i           . . . . . . . 2 1 2 1 2 1 2 1 

……….…...…….(3.23)

(46)

besar perubahan waktu pada setiap siklus perhitungan, semakin kecil syarat stabilitas yang diambil maka semakin akurat data yang dihasilkan.

Keterangan:

q1 dan 2 = Perpindahan kalor konduksi, Watt. q3 = Perpindahan kalor konveksi, Watt.

1



n i

T = Suhu pada node i, saat n+1, oC

n i

T = Suhu pada node i, saat n, oC

n i

T_₁ = Suhu pada node i-1, saat n, oC

n i

T_₁ = Suhu pada node i+1, saat n, oC



T = Suhu fluida, oC

Vi = Volume kontrol sirip, m3 Ät = Selang waktu, detik

ñ = Massa jenis bahan sirip, Kg/ m3 c = Kalor spesifik bahan sirip, J/kg. oC

h = Koefisien perpindahan kalor konveksi fluida, W/m2 .oC Äx = Panjang volume kontrol, m

2 1



i

A = Luas penampang volume kontrol pada node i-12, m 2

2 1



i

A = Luas penampang volume kontrol pada node i+12, m 2

si

A = Luas selimut volume kontrol pada node i, m2

n i

k

2 1

 = Konduktivitas termal bahan sirip pada posisi i-12saat n, W/m. o

C



  

   



 

 

  

2 2

1

1 ni ni ni

i n

T T

k T k T

(47)

n i

k

2 1

 = Konduktivitas termal bahan sirip pada posisi i+12saat n, W/m.oC



  

            2 2 1

1 ni ni ni

i n T T k T k T k

3.3.2. Node Pada Ujung Sirip atau Batas Kanan dan Syarat Stabilitas Berlaku untuk titik (node): 50

Gambar 3.5: Volume kontrol pada batas kanan atau ujung sirip

Secara umum kesetimbangan energi yang berlaku pada volume kontrol dinyatakan sebagai berikut:

                                                                                           t waktu selang selama kontrol volume dalam di erergi perubahan t waktu selang selama kontrol volume dalam di an dibangkitk yang energi besar t waktu selang selama kontrol volume dari keluar yang energi seluruh t waktu selang selama kontrol volume dalam ke masuk yang energi seluruh



  

_ _      t V c q

(48)

Untuk:

1. Perpindahan kalor konduksi dari nodei-1 ke node i





x T T A k q n i n i i n i       1 2 1 2 1

1 . . ………...…...….… (3.25)

2. Perpindahan kalor konveksi pada node i



n



i si

A h

q2  . .   ………. (3.26)

Dengan prinsip persamaan (3.24) maka diperoleh persamaan (3.27):









                            n i si n i n i i n i A h x A

k . . 1 . .

2 1 2 1        t V c. . .

 ………...…….. (3.27)

Sehingga diperoleh persamaan (3.28):









                            n i si n i n i i n i A h x A

k . . 1 . .

2 1 2 1             t V c n i n i i 1 . .

 …...…... (3.28)

Jika persamaan (3.28) dikalikan dengan Äx, maka akan didapat persamaan (3.29):









             _ _   n i si n i n i i n

i A h A x

k . . ₁ . . .

2 1 2 1              t x V c n i n i i 1 . . . .

 …...……….……….….….. (3.29)

Persamaan (3.29) dapat dijabarkan dan disederhanakan menjadi:









                    n i si n i n i i n i i x A h A k x V c t . . . . . . .

. ₂1 ₂1 1





n



i n i 



 1

(49)



  n



 i n i 1









                    n i si n i n i i n i i x A h A k x V c t . . . . . . .

. ₂1 ₂1 1

 ………..….(3.31)

Sehingga,

 n1

i 

                      . . . . . . .

.cV x k ₂1 A 1₂ 1 h A x t si n i i n i i                     

 A h A x

k x V c t T _si i n i i n

i . . .

. . . 1 2 1 2 1

 ……….…….….. (3.32)

Syarat stabilitas untuk persamaan (3.33) adalah:

0 . . . . . . 1 2 1 2

1 

                 

 A h A x

k x V c t si i n i i

 ……….…….…. (3.33)

1 . . . . .

. ₂1 ₂1 _

        

 A h A x

k x V c t si i n i i

 ……….………..…...…… (3.34)

Sehingga, x A h A k x V c t si i n i i        . . . . . . 2 1 2 1 

………...…...…….(3.35)

(50)

Keterangan:

q1 = Perpindahan kalor konduksi, Watt. q2 = Perpindahan kalor konveksi, Watt.

1



n i

T = Suhu pada node i, saat n+1, oC

n i

T = Suhu pada node i, saat n, oC

n i

T_₁ = Suhu pada node i-1, saat n, oC



T = Suhu fluida, oC

Vi = Volume kontrol sirip, m3 Ät = Selang waktu, detik

ñ = Massa jenis bahan sirip, Kg/ m3 c = Kalor spesifik bahan sirip, J/kg. oC

h = Koefisien perpindahan kalor konveksi fluida, W/m2 .oC Äx = Panjang volume kontrol, m

2 1



i

si

A = Luas selimut volume kontrol pada node i, m2

n i

k

2 1

 = Konduktivitas termal bahan sirip pada posisi i-12saat n, W/m. o

C



  

   



 

 

  

2 2

1

1 ni ni ni

i n

T T

k T k T

k

3.4. Perhitungan Luas Penampang, Luas Selimut, dan Volume sirip

(51)

Sirip Benda Putar

r = -2(x2_)+0,005

0 0,001 0,002 0,003 0,004 0,005 0,006

0 0,005 0,01 0,015 0,02 0,025 0,03 0,035 0,04 0,045 0,05

panjang (m eter)

ja

ri

-j

a

ri

(

m

e

te

r)

permukaan setiap volume kontrol berbeda-beda dan untuk perhitungan luas selimut dan volume untuk sirip benda putar ini dilakukan dengan menggunakan pendekatan.

Gambar 3.6: Fungsi sirip

Gambar 3.7: Volume kontrol sirip

(52)

3.4.1. Node Batas Kiri atau Dasar Sirip Berikut untuk titik (node): 0

Gambar 3.9: Node batas kiri atau dasar sirip

a. Luas penampang, m2

Pada batas kiri atau pada dasar sirip ini mempunyai tebal Äx/2 dan

terdapat 2 bagian luas permukaan lingkaran yang keduanya mempunyai luas permukaan yang berbeda yaitu permukaan pada node i dan i+12

seperti yang terlihat pada Gambar 3.9.

 Luas permukaan pada node i,

 

A_i , m2

Ai = ð.r2 = ð.ri2

 Luas penampang pada node i+12,       



2 1

i

A , m2

2 1



i

A = ð.r2

= ð. _

     



2 1

i

(53)

b. Luas selimut (A_si) volume kontrol pada node i, m2

Pada batas kiri atau pada dasar sirip ini dengan tebal Äx/2 mempunyai

luas selimut yang dalam perhitungannya didekati dengan luas selimut silinder seperti yang terlihat pada Gambar 3.9.

si

A = 2.(ð.r2). 2

x



= 2.(ð.ri2). 2

x



c. Volume kontrol sirip (Vi), m3

Pada batas kiri sirip ini dengan tebal Äx/2 mempunyai volume kontrol

yang dalam perhitungannya didekati dengan volume silinder seperti yang terlihat pada Gambar 3.9.

Vi = ð.r2. 2

x



= ð.ri2. 2

x



3.4.2. Node Di Bagian Badan Sirip

Berikut berlaku untuk titik (node): 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, , …47, 48, 49.

(54)

a. Luas penampang, m2

Pada bagian badan sirip ini mempunyai tebal Äx dan terdapat 2 bagian

luas permukaan lingkaran yang keduanya mempunyai luas permukaan yang berbeda yaitu permukaan pada node i-12 dan i+12 seperti yang

terlihat pada Gambar 3.10.

 Luas penampang pada node i-12,,       



2 1

i

A , m2

Ai = ð.r2

= ð.

2 1



i

r 2

 Luas penampang pada node i+12,       



2 1

i

A , m2

2 1



i

A = ð.r2

= ð. _

     



2 1

i

r 2

b. Luas selimut (A_si) volume kontrol pada node i, m2

Pada bagian badan sirip ini dengan tebal Äx mempunyai luas selimut

yang dalam perhitungannya didekati dengan luas selimut silinder seperti yang terlihat pada Gambar 3.10.

si

A = 2.(ð.r2). Äx = 2.(ð.ri2). Äx c. Volume kontrol sirip (Vi), m3

(55)

Vi = ð.r2. Äx = ð.ri2. Äx

3.4.3. Node Pada Ujung Sirip atau Batas Kanan Berikut untuk titik (node): 50

Gambar 3.11: Node pada ujung sirip atau batas kanan a. Luas penampang, m2

Pada batas kanan atau pada ujung sirip ini mempunyai tebal Äx/2 dan

terdapat 1 bagian luas permukaan lingkaran yaitu pada permukaan node i-12 seperti yang terlihat pada Gambar 3.11.

 Luas penampang pada node i-12,       



2 1

i

A , m2

       



2 1

i

A = ð.r2

= ð.

2 1



i

r 2

 Luas penampang pada node i,

 

Ai , m

2

i

A = ð.r2

= ð.

2 1



i

(56)

= 0 (tidak mempunyai luas permukaan) b. Luas selimut (Asi) volume kontrol pada node i, m

2

Pada batas kanan atau pada ujung sirip ini dengan tebal Äx/2

mempunyai luas selimut yang dalam perhitungannya didekati dengan luas selimut kerucut seperti yang terlihat pada Gambar 3.11.

si

A = ð.r.

 

2 2

2      

 x

r_i

= ð.r.

 

2 2

2      

 x

r_i

c. Volume kontrol sirip (Vi), m3

Pada batas kanan atau ujung sirip ini dengan tebal Äx/2 mempunyai

volume kontrol yang dalam perhitungannya didekati dengan volume kerucut seperti yang terlihat pada Gambar 3.11.

Vi =

3 1

. ð.ri2. 2

x



Keterangan:

r = Jari-jari volume kontrol, m Vi = Volume kontrol sirip, m3 Ät = Selang waktu, detik

Äx = Panjang volume kontrol, m

2 1



i

A = Luas penampang volume kontrol pada node i+12, m 2

2 1



i

si

(57)

BAB IV

METODE PENELITIAN

4.1. Kondisi Benda Uji Pada Lingkungan.

Benda uji terbuat dari alumunium dengan sirip berbentuk benda putar, dengan panjang 50 mm dan berdiameter 10 mm. Benda uji dibagi menjadi 50 elemen kecil, dengan tebal elemen 1/50 dari panjang benda uji (L). Setiap elemen kecil diwakili oleh satu titik node, sehingga terdapat 51 titik node.

Gambar 4.1: Benda uji dan kondisi lingkungan

Keterangan benda uji:

Bahan : Alumunium

Node : 0 – 50

(58)

Elemen (Äx) : L

50 1

, meter

Suhu awal (Ti) = 100 °C

Suhu dasar (Tb) = 100 °C

Di kondisikan pada lingkungan : Suhu fluida (T) = 30 °C

Koefisien perpindahan kalor konveksi (h) = di variasikan (W/m². °C)

: 500 (W/m². °C) ; 2500 (W/m². °C) ; 5000 (W/m². °C) ;

7500 (W/m². °C) ; 10.000 (W/m². °C)

4.2. Peralatan Pendukung Penelitian.

Peralatan pendukung dalam penelitian ini adalah perangkat keras dan perangkat lunak. Terdiri dari:

a) Perangkat keras :

 PC Intel Celeron 1,80 GHz dengan RAM 128 MB

 Printer HP Deskjet 3535 b) Perangkat lunak :

 Microsoft Word 2003

 Microsoft Excel 2003

 Corel Draw 12

4.2. Metode Penelitian Yang Digunakan.

(59)

menjadi elemen-elemen kecil setebal Äx. Banyaknya elemen-elemen kecil ini dapat ditentukan secara sembarang, pada penelitian ini node dimulai dari 0 sampai 50 (51 node). Penyelesaian ini dilakukan dengan mengubah persamaan matematika kedalam bentuk persamaan beda hingga cara eksplisit, dengan cara memanfaatkan deret Taylor atau dengan prinsip kesetimbangan energi. Terdapat banyak model matematika dari persoalan perpindahan panas yang berupa persamaan diferensial parsial dapat diselesaikan dengan mudah dengan metode komputasi numerik.

Berdasarkan prinsip kesetimbangan energi, didapatkan persamaan numerik pada setiap node dengan metode beda hingga cara eksplisit, kemudian dibuat program sesuai dengan bahasa pemrograman yang diperlukan dengan Microsoft Excel setelah itu data-data yang dibutuhkan dimasukan lalu didapat hasil perhitungan yang diinginkan.

4.4. Pengambilan Dan Pengolahan Data.

(60)

BAB V

HASIL PERHITUNGAN DAN PEMBAHASAN

Perhitungan distribusi suhu pada sirip benda putar berbahan alumunium ini dilakukan dengan menggunakan metode beda hingga cara eksplisit yang telah dirumuskan dalam program Microsoft Excel dengan memvariasikan nilai koefisien perpindahan kalor konveksi (h) serta dengan konduktivitas termal bahan yang berubah sesuai dengan perubahan suhu dari waktu ke waktu. Nilai konduktivitas termal bahan alumunium didapat dari persamaan pendekatan konduktivitas termal k=k(T), seperti pada Gambar 1.dan pada Tabel 2.2. Suhu dasar sirip dipertahankan tetap Tb = 100 oC dan suhu fluida disekitar sirip T∞= 30

o C.

Hal yang perlu diperhatikan dalam pencarian distribusi suhu adalah adanya persyaratan yang harus dipenuhi untuk mendapatkan keadaan yang stabil yaitu jika digambarkan dalam bentuk grafik maka garis perjalanan suhu dari waktu ke waktu pada posisi titik tertentu dari benda akan tampak akan mulus (smooth) dan pada akhirnya akan menuju suhu tunak. Pemilihan nilai Äx dan Ät harus diperhatikan dengan baik dan tepat agar diperoleh keadaan yang stabil atau dapat memberikan jawaban yang dapat dipertanggungjawabkan.