PENERAPAN MODEL PEMBELAJARAN VAN HIELE DENGAN BANTUAN MEDIA SOFTWARE GEOGEBRA UNTUK MENINGKATKAN KEMAMPUAN
PEMAHAMAN GEOMETRI SISWA SMP
(Studi Eksperimen terhadap Siswa Kelas VII pada Salah Satu SMPN di Bandung)
SKRIPSI
Diajukan untuk Memenuhi Sebagian dari Syarat untuk Memperoleh Gelar Sarjana Pendidikan
Jurusan Pendidikan Matematika Program Studi Pendidikan Matematika
Oleh
DESLYN EVERINA SIMATUPANG 0700291
JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS PENDIDIKAN INDONESIA
PENERAPAN MODEL PEMBELAJARAN VAN HIELE DENGAN BANTUAN
MEDIA SOFTWARE GEOGEBRA UNTUK MENINGKATKAN KEMAMPUAN
PEMAHAMAN GEOMETRI SISWA SMP
Oleh
Deslyn Everina Simatupang
Sebuah skripsi yang diajukan untuk memenuhi sebagian dari syarat untuk memperoleh gelar Sarjana Pendidikan pada Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam
© Deslyn Everina Simatupang 2014 Universitas Pendidikan Indonesia
Januari 2014
Hak Cipta dilindungi undang-undang.
LEMBAR PENGESAHAN
PENERAPAN MODEL PEMBELAJARAN VAN HIELE DENGAN BANTUAN MEDIA SOFTWARE GEOGEBRA UNTUK MENINGKATKAN KEMAMPUAN
PEMAHAMAN GEOMETRI SISWA SMP
(Studi Eksperimen terhadap Siswa Kelas VII pada Salah Satu SMPN di Bandung)
Oleh
DESLYN EVERINA SIMATUPANG 0700291
Menyetujui: Pembimbing I
Prof. Jozua Sabandar, MA., Ph.D. NIP. 194705241981031001
Pembimbing II
Dr. Hj. Aan Hasanah, M.Pd. NIP. 197006162005012001
Mengetahui,
Ketua Jurusan Pendidikan Matematika
ABSTRAK
Deslyn Everina Simatupang (0700291). Penerapan Model Pembelajaran Van Hiele dengan Bantuan Media Software GeoGebra untuk Meningkatkan Kemampuan Pemahaman Geometri Siswa SMP.
Penelitian ini berlatarbelakang tentang rendahnya kemampuan pemahaman geometri siswa sehingga diperlukan suatu model pembelajaran yang inovatif, salah satunya dengan menerapkan pembelajaran Van Hiele dengan memanfaatkan teknologi berupa software GeoGebra. Tujuan dari penelitian ini untuk mengetahui apakah peningkatan kemampuan pemahaman geometri siswa yang mendapatkan model pembelajaran Van Hiele dengan bantuan media software GeoGebra lebih tinggi dibandingkan dengan siswa yang memperoleh pembelajaran konvensional.
Metode yang digunakan dalam penelitian ini adalah metode kuasi eksperimen dengan desain kelompok kontrol tidak ekuivalen (nonequivalent control group design). Populasi pada penelitian adalah seluruh siswa kelas VII pada salah satu SMP Negeri di Bandung dengan sampelnya dua kelas dari kelas VII, kelas VII B sebagai kelas eksperimen yang diberikan perlakuan, dan kelas VII A sebagai kelas kontrol. Instrumen yang digunakan dalam penelitian ini terdiri dari dua jenis, yaitu instrumen tes (tes kemampuan pemahaman geometri) dan instrumen non-tes (angket sikap siswa dan lembar observasi).
Berdasarkan hasil pengolahan data yang diperoleh, penelitian ini menunjukkan bahwa peningkatan kemampuan pemahaman geometri siswa yang mendapatkan model pembelajaran Van Hiele berbantuan GeoGebra lebih tinggi daripada siswa yang mendapatkan pembelajaran konvensional. Dalam penelitian ini, secara keseluruhan sikap siswa memberikan respon yang positif terhadap model pembelajaran Van Hiele dengan bantuan media software GeoGebra.
ABSTRACT
Deslyn Everina Simatupang (0700291). Penerapan Model Pembelajaran Van Hiele dengan Bantuan Media Software GeoGebra untuk Meningkatkan Kemampuan Pemahaman Geometri Siswa SMP.
The background of research based on the lack of understanding ability toward geometry, so that we need to take account innovative learning models. One of them is Van Hiele learning model assisted GeoGebra. The aim of research is knowing whether the enhancement of understanding ability of students who have Van Hiele’s model assisted by GeoGebra greater than students who have conventional.
The research method is quasi-experimental design with nonequivalent control group design. The population in this research is all students of grade in one of Junior High School in Bandung. The research involved two classes of grade, namely VII B as an experiment class, and VII A as a control class. The instruments of this research include: (1) the written test (geometric understanding ability test); (2) non-test (opinion scale and observation sheet).
The result of research showed that: a) the enhancement of geometry students’ understanding ability who have Van Hiele’s model assisted GeoGebra is greater than students’s who have conventional; b) Generally, students show positive attitude toward Van Hiele’s model assisted GeoGebra.
DAFTAR ISI
KATA PENGANTAR ... i
UCAPAN TERIMA KASIH ... ii
ABSTRAK ... iii
DAFTAR ISI ... iv
DAFTAR TABEL ... vi
DAFTAR LAMPIRAN ... viii
BAB I PENDAHULUAN A. Latar Belakang Masalah ... 1
B. Rumusan Masalah ... 4
C. Batasan Masalah ... 4
D. Tujuan Penelitian ... 5
E. Manfaat Penelitian ... 5
F. Definisi Operasional ... 5
BAB II LANDASAN TEORI A. Model Pembelajaran Van Hiele ... 7
B. GeoGebra ... 11
C. Kemampuan Pemahaman Geometri ... 12
D. Keterkaitan antara Pembelajaran Van Hiele Berbantuan GeoGebra dan Pemahaman Geometri ………. ... 14
E. Hipotesis………. ... 16
BAB III METODE PENELITIAN A. Desain Penelitian ... 17
B. Populasi dan Sampel ... 18
C. Variabel Penelitian ... 18
D. Instrumen Penelitian ... ... 18
1. Instrumen Tes……….. ... 18
2. Angket Skala Sikap ... 19
3. Lembar Observasi ... 19
2. Teknik Analisis Data Kualitatif ... 32
BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. Hasil Penelitian ... 35
1. Hasil Analisis Data Pretest Kemampuan Pemahaman Geometri ... 35
2. Hasil Analisis Data Posttest Kemampuan Pemahaman Geometri ... 38
3. Hasil Analisis Data Indeks Gain Kemampuan Pemahaman Geometri Siswa ... 41
4. Hasil Analisis Data Angket Skala Sikap ... 43
5. Hasil Analisis Data Hasil Observasi ... 45
B. Pembahasan ... 46
1. Kemampuan Pemahaman Geometri ... 46
2. Hasil Angket Sikap Siswa terhadap Model Pembelajaraan Van Hiele dengan Bantuan Software GeoGebra ... 47
3. Deskripsi Pelaksanaan Model Pembelajaraan Van Hiele dengan Bantuan Media Software GeoGebra ... 48
BAB V KESIMPULAN DAN SARAN A. Kesimpulan ... 50
B. Saran ... 50
DAFTAR PUSTAKA ... 52
BAB I PENDAHULUAN
A. LATAR BELAKANG
Geometri merupakan salah satu cabang matematika yang sangat bermanfaat dalam kehidupan, karena itu, geometri perlu diajarkan di sekolah. Adapun tujuan pembelajaran geometri, siswa diharapkan dapat memperoleh rasa percaya diri mengenai kemampuan matematika siswa, menjadi pemecah masalah yang baik, berkomunikasi secara matematik, dan bernalar secara matematik. Menurut Budiarto, pembelajaran geometri bertujuan untuk mengembangkan kemampuan berpikir logis, mengembangkan intuisi keruangan, menanamkan pengetahuan untuk menunjang materi yang lain, dan dapat membaca serta menginterpretasikan argumen-argumen matematik (Abdussakir, 2010).
Salah satu kemampuan yang harus dimiliki oleh siswa agar siswa dapat mencapai tujuan pembelajaran geometri adalah kemampuan pemahaman geometri. Untuk melihat sejauh mana kemampuan siswa dapat memahami materi geometri, maka ditetapkanlah suatu hal yang menjadi tolak ukur yaitu indikator kemampuan pemahaman geometri. Adapun indikator kemampuan pemahaman geometri yang akan digunakan dalam penelitian ini yang diadopsi berdasarkan pernyataan Killpatrick dan Findell (Nurokhmatillah, 2010:16-17), diantaranya sebagai berikut:
a) Dapat menyatakan ulang konsep geometri yang telah dipelajari. b) Dapat mengklasifikasikan objek-objek berdasarkan dipenuhi atau
tidaknya persyaratan yang membentuk konsep geometri tersebut; c) Dapat menerapkan konsep geometri secara algoritma;
d) Dapat memberikan contoh dan contoh penyangkal/bukan contoh (counter example) dari konsep geometri yang telah dipelajari; e) Dapat menyajikan konsep geometri dalam berbagai macam bentuk
representasi matematika;
Fakta yang ada menyatakan bahwa kemampuan pemahaman geometri siswa belum mencapai tujuan pembelajaran geometri yang diharapkan. Geometri merupakan materi yang dianggap sulit oleh kebanyakan siswa. Ini tentunya berdampak pada rendahnya kemampuan pemahaman geometri siswa. Kenyataan ini dapat dilihat dari hasil survey yang dilakukan oleh Ngadiyono (Rahmah, 2010:4) tentang minat siswa terhadap mata pelajaran geometri
“...dalam ujian nasional tahun 2008, pokok bahasan yang paling rendah daya serapnya adalah pokok bahasan yang terkait dengan konsep geometri, khususnya mengenai luas dan keliling bangun datar, yaitu sebesar 25,37% untuk tingkat kabupaten Sragen.”
Lebih lanjut, menurut Sudarman, berbagai penelitian menunjukkan bahwa kemampuan pemahaman geometri siswa masih rendah. Masih banyak siswa SMP yang belum dapat memahami konsep geometri secara benar. Hal ini sejalan dengan penelitian Sunardi, dimana ditemukan banyak siswa SMP yang masih salah dalam menyelesaikan soal-soal garis sejajar dan masih banyak siswa yang menyatakan bahwa belah ketupat bukan jajargenjang (Abdussakir, 2010).
Berkaitan dengan hal tersebut, Rizal (Nurhasanah, 2010:4) mengungkapkan bahwa geometri merupakan cabang matematika yang paling memprihatinkan. Kesulitan siswa dalam mempelajari materi geometri tentunya berdampak pada kemampuan pemahaman geometri siswa yang kurang sempurna sehingga dapat menghambat pembelajaran geometri selanjutnya.
3
Dalam Van Hiele, tingkatan berpikir geometri siswa dapat berkembang atau maju dengan memperhatikan karakteristik-karakteristik sebagai berikut (Crowley dalam Nur’aeni, 2010):
a) Tingkatan Van Hiele bersifat rangkaian yang berurutan; b)Tiap tingkatan memiliki simbol dan bahasa tersendiri;
c) A pa yang implisit pada satu tingkatan akan menjadi eksplisit pada tingkatan berikutnya;
d)Bahan yang diajarkan pada siswa di atas tingkatan pemikiran mereka akan dianggap sebagai reduksi tingkatan;
e) K emajuan dari satu tingkatan ke tingkatan berikutnya lebih tergantung pada pengalaman pembelajaran; bukan pada kematangan atau usia;
f) S eseorang melangkah melalui berbagai tahapan dari satu tingkatan ke tingkatan berikutnya;
g)Pembelajar tidak dapat memiliki pemahaman pada satu tingkatan tanpa melalui tingkatan sebelumnya;
h)Peranan guru dan bahasa dalam konstruksi pengetahuan siswa sebagai sesuatu yang krusial.
Untuk membantu siswa dalam mengembangkan tingkatan berpikir geometri, diperlukanlah suatu tahap-tahap pembelajaran geometri. Tahap-tahap pembelajaran inilah yang menjadi model pembelajaran Van Hiele yang akan digunakan dalam penelitian ini. Model Van Hiele terdiri dari lima tahap pembelajaran, yaitu informasi (information), orientasi terarah/terpandu (guided orientation), eksplisitasi (explicitation), orientasi bebas (free orientation), dan
integrasi (integration). Model pembelajaran Van Hiele dipilih dalam rangka meningkatkan kemampuan pemahaman geometri siswa, karena di dalam model ini ada tingkatan/level berpikir siswa dalam pembelajaran geometri (Nur’aeni, 2010).
Menurut Putz, siswa yang menggunakan GeoGebra akan memahami geometri lebih mendalam karena adanya representasi visual yang jelas pada objek geometri dan keterlibatan siswa untuk mengkonstruksi sehingga pemahaman geometri siswa lebih mendalam (Siregar, 2012:9).
Berdasarkan uraian di atas maka diduga pembelajaran geometri dengan menggunakan model Van Hiele yang berbantuan software GeoGebra dapat meningkatkan kemampuan pemahaman geometri siswa. Oleh karena itu, penulis bermaksud untuk melakukan penelitian mengenai “Penerapan Model Pembelajaran Van Hiele dengan Bantuan Media Software GeoGebra untuk Meningkatkan Kemampuan Pemahaman Geometri Siswa SMP”.
B. RUMUSAN MASALAH
Adanya rumusan masalah adalah untuk memperjelas permasalahan yang akan diteliti. Adapun rumusan masalah dalam penelitian ini adalah :
1. Apakah peningkatan kemampuan pemahaman geometri siswa yang mendapatkan model pembelajaran Van Hiele berbantuan GeoGebra lebih tinggi dibandingkan dengan siswa yang mendapatkan pembelajaran konvensional?
2. Bagaimana respon siswa terhadap model pembelajaran Van Hiele dengan bantuan media software GeoGebra?
C. BATASAN MASALAH
Batasan masalah pada penelitian ini, yaitu :
1. Penelitian dilakukan terhadap siswa SMP kelas VII semester genap pada tahun ajaran 2012/2013;
2. Media yang digunakan dalam penelitian ini adalah media software GeoGebra sebagai alat atau medium yang digunakan sebagai perantara dalam proses pembelajaran matematika;
5
D. TUJUAN PENELITIAN
Berdasarkan permasalahan yang telah dikemukakan di atas, maka tujuan dari penelitian ini adalah sebagai berikut.
1. Mengetahui apakah peningkatan kemampuan pemahaman geometri siswa yang mendapatkan model pembelajaran Van Hiele dengan bantuan media software GeoGebra lebih tinggi dibandingkan dengan siswa yang mendapatkan pembelajaran konvensional.
2. Mengetahui respon siswa terhadap model pembelajaran Van Hiele dengan bantuan media software GeoGebra.
E. MANFAAT PENELITIAN
Penelitian ini diharapkan dapat bermanfaat sebagai berikut.
1) Bagi sekolah, penelitian ini diharapkan dapat memberikan sumbangan yang berarti guna meningkatkan mutu pembelajaran matematika di sekolah.
2) Bagi guru, sebagai salah satu alternatif untuk menerapkan berbagai variasi model pembelajaran geometri khususnya dan memberikan motivasi dalam memanfaatkan teknologi berupa penggunaan GeoGebra sebagai media pembelajaran di sekolah.
3) Bagi siswa, dapat menunjang proses pembelajaran yang mendukung berkembangnya kemampuan pemahaman geometri siswa.
4) Bagi peneliti pada khususnya dan pembaca pada umumnya, tulisan ini dapat menambah dan mengembangkan ilmu pengetahuan dan wawasan.
F. DEFINISI OPERASIONAL
1) Model Van Hiele adalah model pembelajaran geometri yang terdiri dari lima tahap pembelajaran, yaitu informasi (information), orientasi terarah/terpandu (guided orientation), eksplisitasi (explicitation), orientasi bebas (free orientation), dan integrasi (integration).
BAB III
METODE PENELITIAN
A. Desain Penelitian
Dalam penelitian ini menggunakan metode penelitian eksperimen (experiment research). Adapun, tujuan dari penelitian eksperimen menurut Nazir (2003) adalah untuk menyelidiki ada-tidaknya hubungan sebab-akibat serta berapa besar hubungan sebab-akibat tersebut dengan cara memberikan perlakuan-perlakuan tertentu pada beberapa kelompok eksperimen dan menyediakan kontrol untuk perbandingan.
Desain eksperimen yang akan digunakan dalam penelitian ini adalah desain kuasi eksperimen yaitu desain kelompok kontrol tidak ekuivalen (nonequivalent control group design). Menurut Ruseffendi (1994), desain penelitian ini melibatkan dua kelompok, yaitu kelompok eksperimen dan kelompok kontrol dengan pemilihan kedua kelompok dilakukan secara tidak acak. Dengan kata lain, peneliti menerima keadaan kedua kelompok seadanya. Siswa pada kelompok eksperimen diberi perlakuan berupa model pembelajaran Van Hiele dengan bantuan media software GeoGebra. Sedangkan, siswa pada kelas kontrol memperoleh pembelajaran konvensional. Gambar desain penelitian tersebut adalah sebagai berikut:
Keterangan:
: Pemberian pre-test dan post-test;
: Perlakuan terhadap kelompok eksperimen (Van Hiele).
B. Populasi Dan Sampel
Populasi dalam penelitian ini yaitu seluruh siswa kelas VII pada salah satu SMP Negeri di Bandung. Sekolah tesebut dipilih sebagai tempat penelitian karena sekolah itu memiliki laboratorium komputer sehingga dapat digunakan untuk menunjang pembelajaran Van Hiele berbantuan GeoGebra. Sekolah yang dipilih sebagai tempat penelitian ini termasuk ke dalam cluster tiga.
Sampel yang akan diteliti dan dianggap menggambarkan populasi dalam penelitian ini, yaitu siswa kelas VII B sebagai kelas eksperimen dengan siswanya mendapatkan model pembelajaran Van Hiele berbantuan GeoGebra dan siswa kelas VII A sebagai kelas kontrol yang pembelajarannya konvensional.
C. Variabel Penelitian
Dalam penelitian ini, yang menjadi variabel bebas adalah model pembelajaran Van Hiele berbantuan GeoGebra dan variabel terikatnya adalah kemampuan pemahaman geometri siswa.
D. Instrumen Penelitian
Untuk memperoleh data mengenai peningkatan kemampuan pemahaman geometri siswa melalui model pembelajaran Van Hiele berbantuan maka diperlukan seperangkat instrumen penelitian. Ada dua jenis instrumen yang digunakan dalam penelitian ini, yaitu instrumen tes dan instrumen non-tes.
Instrumen tes berupa tes kemampuan pemahaman geometri. Sedangkan, instrumen non-tes berupa angket skala sikap dan lembar observasi. Penjelasan mengenai instrumen yang digunakan sebagai berikut.
1. Instrumen Tes
19
mengetahui kemampuan awal pemahaman geometri siswa, sementara tes akhir (post-test) bertujuan untuk mengetahui sejauh mana peningkatan pemahaman geometri siswa setelah mendapatkan model pembelajaran Van Hiele dengan bantuan media software GeoGebra.
2. Angket Skala Sikap
Ruseffendi (1994:107) menjelaskan bahwa angket adalah sekumpulan pertanyaan atau pernyataan yang dilengkapi oleh responden dengan memilih jawaban atau menjawab pertanyaan melalui jawaban yang sudah disediakan atau melengkapi kalimat dengan jalan mengisi.
Dalam penelitian ini angket tentu saja digunakan untuk mengetahui respon siswa terhadap pembelajaran matematika melalui model pembelajaran Van Hiele dengan bantuan media software GeoGebra untuk meningkatkan kemampuan pemahaman geometri siswa.
Angket disusun dengan menggunakan skala sikap model Likert yang terdiri dari empat jawaban pilihan yaitu sangat setuju (SS), setuju (S), tidak setuju (TS), dan sangat tidak setuju (STS).
3. Lembar Observasi
Menurut Sugiyono (2008:203) observasi merupakan salah satu teknik pengumpulan data yang memiliki ciri-ciri yang spesifik bila dibandingkan dengan teknik yang lain, seperti angket. Hal ini dikarenakan observasi tidak terbatas pada orang, tetapi juga pada objek-objek alam lainnya. Observasi dibuat dengan maksud untuk mengetahui apakah siswa atau guru melaksanakan aktivitas yang disebutkan atau tidak.
Penilaian data hasil observasi dilakukan dengan cara menyimpulkan hasil pengamatan observer selama proses pembelajaran berlangsung. Setiap pernyataan dalam lembar observasi memuat dua kategori, Ya dan Tidak.
E. Prosedur Penelitian
1. Tahap Persiapan
a. Mengidentifikasi permasalahan mengenai bahan ajar. Setelah itu, membuat perencanaan pembelajaran berupa bahan ajar (LKS dan RPP) dan media pembelajaran (software GeoGebra).
b. Melakukan perizinan tempat untuk penelitian. c. Membuat instrumen penelitian.
d. Melakukan uji coba instrumen yang telah dibuat guna mengetahui kualitas instrumen. Uji coba instrumen ini diberikan terhadap subyek lain di luar subyek penelitian, tetapi mempunyai kemampuan yang setara dengan subyek dalam penelitian yang akan dilakukan.
e. Menganalisis kualitas/kriteria instrumen. Ada empat langkah yang dilakukan untuk mengetahui kualitas instrumen yang telah diujicobakan, yaitu uji validitas, uji reliabilitas, uji daya pembeda, dan uji indeks kesukaran.
f. Menentukan dan memilih sampel dari populasi yang telah ditentukan. 2. Tahap Pelaksanaan
a. Memberikan pre-test pada kelas kontrol dan kelas eksperimen.
b. Melaksanakan kegiatan pembelajaran di kedua kelas tersebut. Siswa pada kelas kontrol mendapatkan pembelajaran konvensional, dan siswa pada kelas eksperimen mendapatkan model pembelajaran Van Hiele dengan bantuan media software GeoGebra.
c. Memberikan post-test pada kedua kelas.
d. Memberikan angket skala sikap siswa terhadap pembelajaran matematika. 3. Tahap Analisis Data
a) Pengumpulan data kuantitatif dan data kualitatif.
b) Pengolahan dan penganalisisan data kuantitaf berupa pre-test dan post-test kemampuan pemahaman geometri.
21
Kegiatan yang dilakukan pada tahap ini adalah membuat kesimpulan hasil penelitian berdasarkan hipotesis yang telah dirumuskan.
Hasil uji coba instrumen penelitian yang telah dilaksanakan dijelaskan sebagai berikut.
1) Uji validitas
Dalam penelitian ini, untuk menguji validitas tiap butir soal maka langkah-langkah yang dilakukan sebagai berikut (Sundayana, 2010:60-61).
a) menghitung koefisien validitas tes menggunakan rumus korelasi produk momen memakai angka kasar (raw score) atau rumus korelasi Pearson, yaitu:
∑ ∑ ∑
√( ∑ ∑ )( ∑ ∑ )
Keterangan:
= koefisien korelasi antara variabel x dan variabel y; = banyak subjek (testi);
= skor yang diperoleh dari tes; = rata-rata nilai harian.
b) Setelah nilai validitas diperoleh, maka nilai tersebut harus diuji keberartiannya, dengan melakukan perhitungan uji-t. Rumus statistik uji-t:
√
√ ( )
Keterangan:
= koefisien korelasi antara variabel x dan variabel y; = banyak subjek (testi).
Perumusan hipotesis:
: validitas setiap butir soal berarti
Kriteria pengambilan keputusan untuk pengujian itu sebagai berikut:
jika maka ditolak.
jika maka diterima.
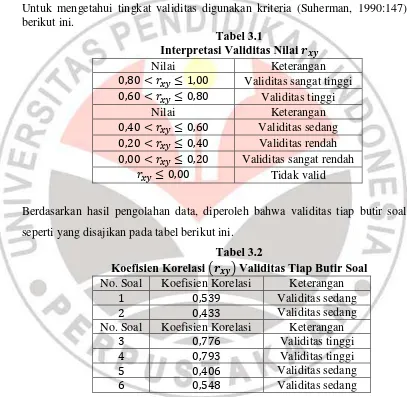
Untuk mengetahui tingkat validitas digunakan kriteria (Suherman, 1990:147) berikut ini.
Tabel 3.1
Interpretasi Validitas Nilai
Nilai Keterangan
Validitas sangat tinggi
Validitas tinggi
Nilai Keterangan
Validitas sedang
Validitas rendah
Validitas sangat rendah
Tidak valid
Berdasarkan hasil pengolahan data, diperoleh bahwa validitas tiap butir soal seperti yang disajikan pada tabel berikut ini.
Tabel 3.2
Koefisien Korelasi ( ) Validitas Tiap Butir Soal No. Soal Koefisien Korelasi Keterangan
Validitas sedang
Validitas sedang
No. Soal Koefisien Korelasi Keterangan
Validitas tinggi
Validitas tinggi
Validitas sedang
Validitas sedang
23
Distribusi t pada dengan derajat kebebasan dan uji dua pihak. Nilai adalah:
Karena nilai tersebut tidak terdapat pada tabel, maka dicari dengan cara interpolasi sehingga diperoleh nilai .
Soal No.1
Perumusan Hipotesisnya sebagai berikut:
: Koefisien validitas butir soal No. 1 tidak berarti : Koefisien validitas butir soal No. 1 berarti Berdasarkan uji statistik t, diperoleh:
√ √ – =
Karena , maka ditolak. Ini berarti bahwa koefisien validitas butir soal No. 1 berarti.
Soal No. 2
Perumusan Hipotesis untuk soal No.2:
: Koefisien validitas butir soal No. 2 tidak berarti : Koefisien validitas butir soal No. 2 berarti Berdasarkan uji statistik t, diperoleh:
√ √ – =
Karena , maka ditolak. Oleh karena itu, dapat disimpulkan bahwa koefisien validitas butir soal No. 2 berarti.
Soal No. 3
Perumusan Hipotesis:
: Koefisien validitas butir soal No. 3 berarti Berdasarkan uji statistik t, diperoleh:
√ √ – =
Nilai . Ini berarti ditolak. Jadi, disimpulkan bahwa koefisien validitas butir soal No. 3 berarti.
Soal No. 4
Perumusan Hipotesis untuk soal No. 4:
: Koefisien validitas butir soal No. 4 tidak berarti : Koefisien validitas butir soal No. 4 berarti Berdasarkan uji statistik t, diperoleh:
√ √ – =
Karena nilai , maka dapat disimpulkan bahwa koefisien validitas butir soal No. 4 berarti.
Soal No. 5
Perumusan Hipotesisnya sebagai berikut:
: Koefisien validitas butir soal No. 5 tidak berarti : Koefisien validitas butir soal No. 5 berarti Berdasarkan uji statistik t, diperoleh:
√ √ – =
Karena , maka dapat disimpulkan bahwa koefisien validitas butir soal No. 5 berarti.
25
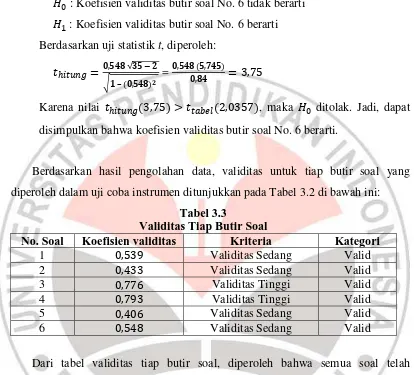
Perumusan Hipotesis:
: Koefisien validitas butir soal No. 6 tidak berarti : Koefisien validitas butir soal No. 6 berarti Berdasarkan uji statistik t, diperoleh:
√ √ – =
Karena nilai , maka ditolak. Jadi, dapat disimpulkan bahwa koefisien validitas butir soal No. 6 berarti.
Berdasarkan hasil pengolahan data, validitas untuk tiap butir soal yang diperoleh dalam uji coba instrumen ditunjukkan pada Tabel 3.2 di bawah ini:
Tabel 3.3
Validitas Tiap Butir Soal
No. Soal Koefisien validitas Kriteria Kategori
1 Validitas Sedang Valid
2 Validitas Sedang Valid
3 Validitas Tinggi Valid
4 Validitas Tinggi Valid
5 Validitas Sedang Valid
6 Validitas Sedang Valid
Dari tabel validitas tiap butir soal, diperoleh bahwa semua soal telah memenuhi kriteria dengan rincian sebanyak empat soal memiliki validitas sedang, yaitu no. 1, 2, 4, dan 6. Selain itu, dua soal memilik validitas tinggi, yaitu no. 3 dan no. 4. Setelah mengetahui bahwa keenam soal valid maka tahap selanjutnya melakukan uji reliabilitas tiap butir soal.
2) Uji reliabilitas
reliabilitas bentuk uraian dikenal dengan rumus Alpha, yaitu sebagai berikut (Suherman, 1990:194).
∑
Keterangan:
= banyak butir soal;
∑ = jumlah varians skor setiap soal;
= varians skor total.
Tolak ukur untuk menginterpretasikan derajat reliabilitas alat evaluasi yang dapat digunakan dibuat oleh Guilford (Suherman, 1990:177) adalah sebagai berikut.
Tabel 3.4
Interpretasi Derajat Reliabilitas
Nilai Keterangan
Sangat rendah
Rendah
Sedang
Tinggi
Sangat tinggi
Berdasarkan hasil pengolahan data, diperoleh reliabilitas sebesar 0,609. Kriteria yang diperoleh termasuk ke dalam kriteria tinggi.
3) Uji daya pembeda
Daya pembeda soal dapat dihitung dengan menggunakan rumus
̅̅̅ ̅̅̅
Keterangan:
= Daya Pembeda;
̅̅̅ = Rata-rata skor kelompok atas;
̅̅̅ = Rata-rata skor kelompok bawah;
27
Klasifikasi interpretasi daya pembeda (Suherman, 1990:202) dapat dilihat pada tabel di bawah ini.
Tabel 3.5
Interpretasi Indeks Daya Pembeda
Nilai Keterangan
Sangat jelek
Jelek
Cukup
Baik
Sangat baik
Berdasarkan hasil pengolahan data, diperoleh daya pembeda tiap butir soal pada Tabel berikut ini:
Tabel 3.6
Daya Pembeda Tiap Butir Soal
No. Soal Nilai Interpretasi
1 0,30 Cukup
2 0,28 Cukup
3 0,90 Sangat Baik
4 0,79 Sangat Baik
5 0,22 Cukup
6 0,30 Cukup
Dari tabel daya pembeda tiap butir soal, dapat dilihat bahwa instrumen yang diberikan terdapat empat soal yang memiliki daya pembeda cukup dan dua soal memiliki daya pembeda yang sangat baik.
4) Uji indeks kesukaran
Rumus untuk mencari indeks kesukaran tiap soal, yaitu:
̅
Keterangan:
= Indeks Kesukaran;
̅ = Rata-rata skor tiap butir soal;
Klasifikasi IK yang paling banyak digunakan (Suherman, 1990: 213) adalah Tabel 3.7
Interpretasi Indeks Kesukaran
Nilai Keterangan
Soal terlalu sukar
Soal sukar
Soal sedang
Soal mudah
Soal terlalu mudah
Berdasarkan hasil pengolahan data, diperoleh indeks kesukaran tiap butir soal pada Tabel berikut ini:
Tabel 3.8
Indeks Kesukaran Tiap Butir Soal
No. Soal Nilai Interpretasi
1 0,25 Sukar
2 0,74 Mudah
3 0,56 Sedang
4 0,41 Sedang
5 0,15 Sukar
6 0,54 Sedang
Dari tabel indeks kesukaran tiap butir soal, dapat dilihat bahwa instrumen kemampuan pemahaman geometri yang terdiri dari enam soal, tiga soal yang memiliki tingkat kesukaran sedang, yaitu no. 3, 4, dan 6. Selain itu, ada satu soal memiliki tingkat kesukaran yang mudah no.2. Sedangkan untuk no.1 dan no. 5 soalnya sukar.
Berdasarkan hasil pengolahan data uji instrumen, maka kesimpulan dari semua hasil pengolahan data uji instrumen kemampuan pemahaman geometri dapat dilihat pada tabel di bawah ini.
Tabel 3.9
Rekapitulasi Hasil Uji Instrumen Kemampuan Pemahaman Geometri No. Soal Validitas Daya Pembeda Indeks Kesukaran Reliabilitas
1 Sedang Cukup Sukar
Tinggi
29
3 Tinggi Sangat Baik Sedang
4 Tinggi Sangat Baik Sedang
5 Sedang Cukup Sukar
6 Sedang Cukup Sedang
F. Teknik Pengolahan Data
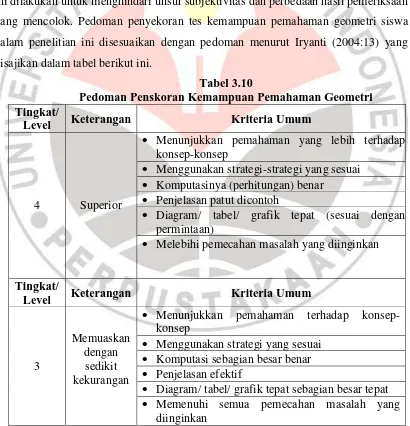
Pengambilan data dalam penelitian ini dilakukan dengan beberapa cara yaitu dengan memberikan seperangkat soal pre-test dan post-test, pengisian angket, dan lembar observasi. Langkah selanjutnya adalah membuat pedoman penyekoran. Hal ini dilakukan untuk menghindari unsur subjektivitas dan perbedaan hasil pemeriksaan yang mencolok. Pedoman penyekoran tes kemampuan pemahaman geometri siswa dalam penelitian ini disesuaikan dengan pedoman menurut Iryanti (2004:13) yang disajikan dalam tabel berikut ini.
Tabel 3.10
Pedoman Penskoran Kemampuan Pemahaman Geometri Tingkat/
Level Keterangan Kriteria Umum
4 Superior
Menunjukkan pemahaman yang lebih terhadap konsep-konsep
Menggunakan strategi-strategi yang sesuai Komputasinya (perhitungan) benar
Penjelasan patut dicontoh
Diagram/ tabel/ grafik tepat (sesuai dengan permintaan)
Melebihi pemecahan masalah yang diinginkan
Tingkat/
Level Keterangan Kriteria Umum
3
Memuaskan dengan
sedikit kekurangan
Menunjukkan pemahaman terhadap konsep-konsep
Menggunakan strategi yang sesuai Komputasi sebagian besar benar Penjelasan efektif
Diagram/ tabel/ grafik tepat sebagian besar tepat Memenuhi semua pemecahan masalah yang
2
Cukup memuaskan
dengan banyak kekurangan
Menunjukkan pemahaman terhadap sebagian besar konsep-konsep
Tidak menggunakan strategi yang sesuai Komputasi sebagian besar benar
Penjelasan memuaskan
Diagram/ tabel/ grafik tepat sebagian besar tepat Memenuhi sebagian besar pemecahan masalah
yang diinginkan
1 Tidak
memuaskan
Menunjukkan sedikit atau tidak ada pemahaman terhadap konsep-konsep
Tidak menggunakan strategi yang sesuai Komputasi tidak benar
Penjelasan tidak memuaskan
Diagram/ tabel/ grafik tepat tidak tepat
Setelah data diperoleh, kemudian dianalisis dengan langkah-langkah sebagai berikut.
1. Teknik Analisis Data Kuantitatif
Setelah mempeoleh data kuantitatif berupa hasil pre-test dan post-test, maka dilakukan analisis data kuantitatif. Hal ini dilakukan untuk melihat seberapa besar peningkatan kemampuan pemahaman geometri siswa pada kedua kelas. Pengolahan data kuantitatif dilakukan dengan menggunakan uji statistik terhadap data pre-test, post-test, dan Indeks Gain Ternormalisasi. Analisis data Gain ternormalisasi dilakukan untuk melihat perbedaan kemampuan pemahaman geometri siswa yang diberi perlakuan pada kelompok eksperimen (menggunakan model pembelajaran Van Hiele dengan bantuan media software GeoGebra) dan siswa yang tidak diberi perlakuan pada kelas kontrol (menggunakan pembelajaran konvensional). Data Gain diperoleh dari hasil pre-test dan post-test kedua kelas tersebut. Rumus untuk normalized Gain (Gain ternormalisasi) menurut Hake (Rahmah, 2010:46) adalah
31
Indeks Gain ternormalisasi diinterpretasikan dengan menggunakan kriteria seperti dalam tabel berikut Hake.
Tabel 3.11 Kriteria Indeks Gain Indeks Gain Kriteria
Tinggi
Sedang
Rendah
Dalam membantu analisis data kuantitatif, digunakan bantuan software SPSS 18.0 for Windows. Langkah-langkah pengujian hipotesis yang dilakukan untuk data pre-test, post-test dan Indeks Gain antara lain sebagai berikut.
1) Uji Normalitas
Uji normalitas dilakukan untuk mengetahui apakah data kedua kelompok berdistribusi normal atau tidak. Apabila hasil pengujian menunjukkan bahwa data berdistribusi normal maka pengujian dilanjutkan dengan uji homogenitas. Uji normalitas dilakukan dengan menggunakan uji Shapiro-Wilk dengan taraf signifikansi . Sedangkan jika hasil pengujian menunjukkan bahwa data tidak berdistribusi normal maka digunakan uji non-parametrik, yaitu Mann-Whitney. 2) Uji Homogenitas Varians
Uji homogenitas varians digunakan untuk mengetahui apakah kedua kelompok sampel mempunyai varians yang sama atau tidak. Apabila kedua kelompok (sampel) mempunyai varians yang sama maka kedua kelompok tersebut homogen. Uji homogenitas dilakukan dengan uji Levene’s test.
3) Uji Perbedaan Dua Rata-rata
berbeda. Untuk data yang tidak normal maka pengujiannya menggunakan uji Mann-Whitney.
2. Teknik Analisis Data Kualitatif
Setelah memperoleh data kualitatif berupa angket skala sikap siswa dan lembar observasi, maka dilakukan analisis data kualitatif. Hal ini dilakukan untuk mengetahui respon siswa terhadap pembelajaran melalui model pembelajaran Van Hiele berbantuan software GeoGebra. Hasil analisis data kualitatif yang diperoleh, diuraikan sebagai berikut.
a. Teknik Analisis Data Angket
Untuk mengolah data angket, ubah data kualitatif hasil angket menjadi data kuantitatif. Skala penilaian sikap yang digunakan adalah skala Likert. Setiap jawaban diberikan bobot skor tertentu sesuai dengan jawabannya, yaitu 1 (STS), 2 (TS), 4 (S), dan 5 (SS) untuk pernyataan positif. Sebaliknya, 1 (SS), 2(S), 4 (TS), dan 5 (STS) untuk pernyataan negatif. Pengolahan dapat dilakukan dengan membandingkan rerata skor subjek dengan rerata skor alternatif jawaban netral dari semua butir pertanyaan (Suherman dalam Pardomuan, 2012: 55). Jika rerata skor subyek lebih besar daripada 3 (rerata skor untuk jawaban netral) maka ia bersikap positif, sebaliknya jika reratanya kurang dari 3 maka ia bersikap negatif.
Seberapa besar perolehan persentasenya dalam angket diketahui dengan perhitungan
Keterangan:
= Persentase jawaban; = Frekuensi jawaban;
33
[image:30.612.120.530.150.557.2]Penafsiran data angket dilakukan dengn menggunakan kategori persentase yang disajikan dalam tabel berikut
Tabel 3.12 Tafsiran Data Angket Persentase Data Interpretasi
Tak seorang pun
Hampir setengahnya
Setengahnya
Sebagian besar
Hampir seluruhnya
Seluruhnya
Selanjutnya, skor hasil skala sikap ini dapat dihitung dengan menggunakan rumus berikut (Suherman dalam Pardomuan, 2012: 55)
Keterangan:
= Skor Pernyataan Item; = Frekuensi jawaban;
= Banyaknya siswa (responden);
= Skor Pernyataan.
b. Data Hasil Observasi
BAB V
KESIMPULAN DAN SARAN
A. Kesimpulan
Berdasarkan hasil analisis dan pembahasan pada keseluruhan tahapan penelitian, diperoleh beberapa kesimpulan berkaitan dengan model pembelajaran Van Hiele dengan bantuan media software GeoGebra terhadap kemampuan pemahaman geometri siswa. Selain itu, dalam kesimpulan ini diungkapkan pula hasil temuan lainnya yang diperoleh dalam penelitian.
1. Peningkatan kemampuan pemahaman geometri siswa yang mendapatkan model pembelajaran Van Hiele dengan bantuan media software GeoGebra lebih tinggi daripada siswa yang mendapat pembelajaran konvensional.
2. Secara keseluruhan, sikap siswa memberikan respon yang positif terhadap model pembelajaran Van Hiele berbantuan software GeoGebra. Hal ini dapat dilihat dari angket skala sikap siswa dimana sebagian besar siswa memberikan respon yang positif untuk setiap tahap pembelajaran Van Hiele dengan bantuan media software GeoGebra.
B. Saran
Berdasarkan hasil penelitian dan kesimpulan mengenai model pembelajaran Van Hiele dengan bantuan media software GeoGebra, maka dapat disarankan beberapa hal berikut ini:
1. Penelitian mengenai model pembelajaran Van Hiele berbantuan GeoGebra direkomendasikan untuk dilanjutkan baik pada aspek penelitian lainnya dengan kajian yang lebih luas, seperti pada materi pembelajaran, subjek penelitian, ataupun kemampuan-kemampuan matematika lainnya.
2. Dapat dikembangkan untuk meneliti tingkatan/level berpikir geometri siswa. 3. Meski rata-rata peningkatan kemampuan pemahaman geometri kelas
51
tidak hanya menggunakan software tetapi juga ada baiknya diselingi dengan menggambar secara manual (penggunaan jangka, busur, dan penggaris). Hal ini dimaksudkan agar hasil yang diperoleh nantinya siswa dapat melukis bangun geometri menggunakan kedua cara tesebut (manual dan software). Selain itu, adanya pemberian waktu tambahan agar siswa dapat mengeksplorasi lebih banyak lagi terkait software GeoGebra.
Abdussakir (2010). Pembelajaran Geometri Sesuai Teori van Hiele. El-Hikmah: Jurnal Kependidikan dan Keagamaan, Vol VII Nomor 2, Januari 2010, ISSN 1693-1499. Fakultas Tarbiyah UIN Maliki Malang. [Online]. Tersedia: http://abdussakir.wordpress.com/2011/02/09/ [14 Februari 2013].
Alip. (2011). Perkenalan dengan Geogebra Software Matematika Gratis. [Online]. Tersedia: http://www.roomantik.com/2011/11/perkenalan-dengan-geogebra-software.html [18 Maret 2013].
Departemen Pendidikan dan Kebudayaan/Pusat Bahasa. 2001. Kamus Besar Bahasa Indonesia (Edisi ke-3). Jakarta: Balai Pustaka.
Ian. (2010). Pengertian kemampuan. [Online]. Tersedia: http://ian43.wordpress.com/2010/12/23/pengertian-kemampuan/ [18 Maret 2013].
Iryanti, P. (2004) Paket Pembinaan Penataran. Yogyakarta: Departemen Pendidikan nasional Direktorat Jendral Pendidikan Dasar dan Menengah Pusat Pengembangan Penataran Guru Matematika.
Kudus, N. (2012). Belajar Matematika Bersama GeoGebra. [Online]. Tersedia: http://blog.unsri.ac.id/nurdinawatikudus/media-pembelajaran/belajar-matematika-bersama-geogebra/mrdetail/55236 [18 Maret 2013]. Nazir, M. (2003). Metode Penelitian. Jakarta: Ghalia Indonesia.
Nur’aeni, E. (2010). “Pengembangan Kemampuan Komunikasi Geometris Siswa Sekolah Dasar Melalui Pembelajaran Berbasis Teori Van Hiele”. Jurnal Saung Guru. 1, (2), 28-34.
Nurhasanah, F. (2010). Penerapan Model Van Hiele Dan Geometers' Sketchpad (Junior High School Students' Abstraction In Learning Geometry Through Van Hiele's Model And Geometers' Sketchpad). Tesis Magister PPS UPI Bandung. Tidak diterbitkan.
Nurokhmatillah, I. (2010). Peningkatan Pemahaman Geometri pada Siswa SMP dengan Menggunakan Model Pembelajaran SAVI.. Skripsi FPMIPA UPI Bandung. Tidak diterbitkan.
53
Ruseffendi, ET. (1994). Dasar-Dasar Penelitian Pendidikan dan Bidang Non-Eksekta Lainnya. Semarang: IKIP Semarang Press.
Siregar, A.S. (2012). Pembelajaran Geometri Melalui Model van Hiele Berbantuan Geogebra Sebagai Upaya Meningkatkan Kemampuan Penalaran Matematis Siswa SMP. Skripsi FPMIPA UPI Bandung. Tidak diterbitkan.
Suherman, dkk. (1990). Petunjuk Praktis untuk Melaksanakan Evaluasi Pendidikan Matematika. Bandung: Wijayakusumah 157.
Suliyanto. (2012). Analisis Statistik-Pendekatan Praktis dengan Microsoft Excel. Yogyakarta: CV ANDI OFFSET.