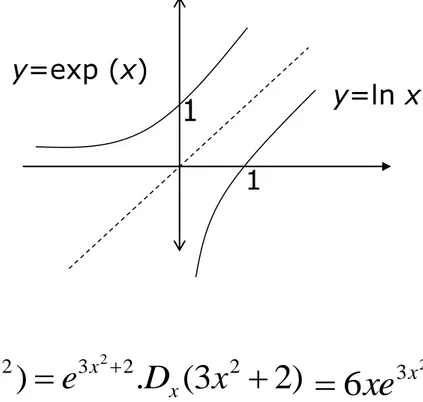8. FUNGSI TRANSENDEN 1

1

8. FUNGSI

8.1 Fungsi Invers

Misalkan denganf : D_f  R_f

)

(x

f

y

x





v

u



f (u)  f (v)

Definisi 8.1 Fungsi y = f(x) disebut satu-satu jika f(u) = f(v) maka u = v atau jika maka

x y 

x y  

fungsi y=-x satu-satu

2

x y 

u v

3 Secara geometri grafik fungsi satu-satu dan garis yang sejajar dengan

sumbu x berpotongan di satu titik.

Teorema : Jika fungsi f satu-satu maka f mempunyai invers notasi 1 f f f

D

R

f

1

:



 

y

f

x

y





1 Berlaku hubungan

x

x

f

f

1

(

(

))



y y f f ( 1( ))  f f f f

R

R

D

D

1



,

1



Df Rf f x y=f(x) R R 1  f ) ( 1 y f x  

Teorema : jika f monoton murni(selalu naik/selalu turun) maka f mempunyai invers x x f ( )  x x f ( )   2 ) (x x f  u v f(x)=x R x x f '( ) 1 0,  f selalu naik f(x)=-x R x x f '( )  1 0,  f selalu turun          0 , 0 0 , 0 2 ) ( ' x x x x f f naik untuk x>0 turun untuk x <0 1  f 1  f 1 

5 Contoh : Diketahui

f x

x

x

( )







1

2

a. Periksa apakah f mempunyai invers b. Jika ada, tentukan inversnya

Jawab: a. 2

)

2

(

)

1

.(

1

)

2

.(

1

)

(

'











x

x

x

x

f

x

Df

x











0

,

)

2

(

3

2

Karena f selalu naik(monoton murni) maka f mempunyai invers b. Misal 2 1    x x y

1

2







y

x

xy

1

1

2

1

2



















y

y

x

y

x

y

x

1

1

2

)

(

1

1

2

)

(

1 1



















 

x

x

x

f

y

y

y

f

Suatu fungsi yang tidak mempunyai invers pada daerah asalnya dapat dibuat mempunyai invers dengan cara membatasi daerah asalnya. 2 ) (x x f  u v 1  f tidak ada

R

x



Untuk 2 ) (x x f  Untuk x>0 ada 1 f 2 ) (x x f 

7

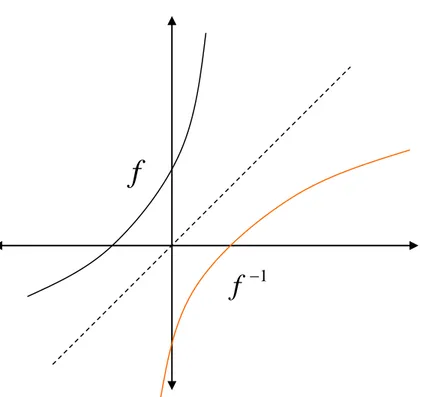
Grafik fungsi invers

Titik (x,y) terletak

pada grafik f Titik (y,x) terletak _{pada grafik} 1

f

Titik (x,y) dan (y,x) simetri terhadap garis y=x Grafik f dan semetri terhadap garis y=x 1

f

f

1



Soal Latihan f x x x ( )    1 1 2 3 2 ) (    x x x f

Tentukan fungsi invers ( bila ada ) dari 1.

9

8.2 Fungsi Logaritma Asli

 Fungsi Logaritma asli ( ln ) didefinisikan sebagai :

 Dengan Teorema Dasar Kalkulus II, diperoleh :

 Secara umum, jika u = u(x) maka

ln

x

,

t

dt

x

x



_

1



0

1

 

x

dt

t

D

x

D

x x x

1

1

ln

1



















 

dx

du

u

dt

t

D

u

D

x u x x

1

1

ln

) ( 1























.

Contoh : Diberikan

maka Jika

Jadi,

Dari sini diperoleh :

Sifat-sifat Ln :

1. ln 1 = 0 2. ln(ab) = ln a + ln b 3. ln(a/b)=ln(a) – ln(b)

)

2

4

ln(

)

(

x



x



f

)

2

4

(

)

2

4

(

1

)

(

'







D

x

x

x

f

_x

2

4

4





x

0

,

|

|

ln





x

x

y

       0 , ) ln( 0 , ln x x x x x y x y  ln  ' 1 x x y x y ln( ) ' 1  1      

.

0

,

1

|)

|

(ln



x



x

x

dx

d



dx



ln

|

x

|



C

x

1

a

r

a

r

ln

ln

.

4



11

dx

x

x



4

_

0 2

2

x

du

dx

xdx

du

x

u

2

2

2

2













Contoh: Hitung Jawab: Misal

x

du

u

x

dx

x

x

2

2

2













u

du



2

ln

|

u

|



c

1

1

2

1

c

x







ln

|

2

|

2

1

₂



0

4

|

2

|

ln

2

1

2

2 4 0 2









dx

x

x

x

.

9

ln

2

1

)

2

ln

18

(ln

2

1







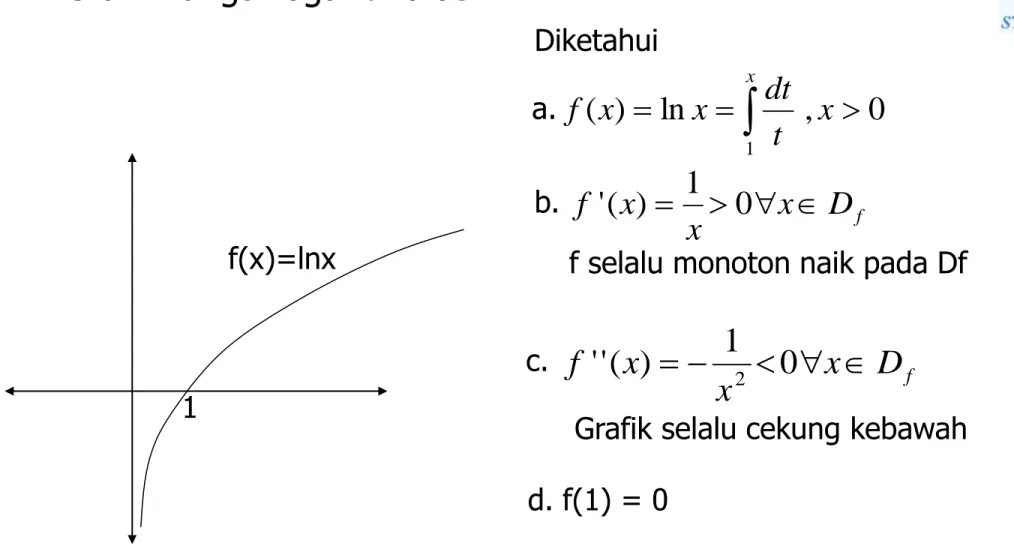
sehingga

Grafik fungsi logaritma asli

0

,

ln

)

(

1









x

t

dt

x

x

f

x f

D

x

x

x

f

'

(

)



1



0





f selalu monoton naik pada Df

f

D

x

x

x

f

'

'

(

)





1

₂



0





Diketahui a. b. c.

Grafik selalu cekung kebawah d. f(1) = 0

1

MA1114 KALKULUS I 13

8.3 Fungsi Eksponen Asli



Karena maka fungsi logaritma asli

monoton murni, sehingga mempunyai invers. Invers dari fungsi

logaritma asli disebut

fungsi eksponen asli,

notasi exp

. Jadi

berlaku hubungan



Dari sini didapat : y = exp(ln y) dan x =ln(exp(x))



Definisi 8.2 Bilangan e adalah bilangan Real positif yang

bersifat ln e = 1.

Dari sifat (iv) fungsi logaritma diperoleh

 

ln



1



0

untuk

x



0

,

x

x

D

_x

y

x

x

y



exp(

)





ln

r

e

r

e

e

r



exp(ln

r

)



exp

ln



exp

x

e

x

)



(

x

e

y

dy

dx

dx

dy







/

1

x x x

e

e

D

(

)



,

Jadi

y

x

e

y



x





ln

Turunan dan integral fungsi eksponen asli Dengan menggunakan turunan fungsi invers Dari hubungan

y

dy

dx

1



'

.

)

(

e

( )

e

u

D

_x u x



u Secara umum Sehingga



e

x

dx



e

x



C

15 1 y=ln x y=exp (x)

Grafik fungsi eksponen asli

Karena fungsi ekponen asli merupakan invers dari fungsi logaritma asli maka grafik fungsi eksponen asli diperoleh dengan cara mencerminkan grafik fungsi logaritma asli terhadap garis y=x

1 Contoh:

)

2

3

(

.

)

(

e

3 22



e

3 22

D

x

2



D

_x x x _x



₆

3x22

_.

xe

.

4

1

4

1

4

4 4

C

e

C

e

du

e

dx

e

x





u



u





x





Contoh :Hitung

dx

e

x



4 Jawab :

4

4

4

x

du

dx

dx

du

u











Misalkan Sehingga

17 ) (

))

(

(

)

(

x

g

x

h x

f



Penggunaan fungsi logaritma dan eksponen asli

Menghitung turunan fungsi berpangkat fungsi Diketahui

))

(

ln(

)

(

))

(

ln(

f

x



h

x

g

x

)))

(

ln(

)

(

(

)))

(

(ln(

f

x

D

h

x

g

x

D

_x



_x

)

(

'

)

(

)

(

))

(

ln(

)

(

'

)

(

)

(

'

x

g

x

g

x

h

x

g

x

h

x

f

x

f





) ( ) ( ' ) ( ) ( )) ( ln( ) ( ' ) ( ' g x f x x g x h x g x h x f _       

?

)

(

'

,

f

x



Contoh :

Tentukan turunan fungsi x

x

x

f

(

)



(

)

4

)

ln(

4

)

ln(

)

(

ln

f

x



x

4x



x

x

Jawab:

))

ln(

4

(

))

(

(ln

f

x

D

x

x

D

_x



_x

x

x

x

x

f

x

f

4

1

)

ln(

4

)

(

)

(

'





Ubah bentuk fungsi pangkat fungsi menjadi perkalian fungsi dengan menggunakan fungsi logaritma asli

Turunkan kedua ruas



4

ln(

)

4



(

)

)

(

'

x

x

f

x

f









x

x

x

x

f

'

(

)



4

ln(

)



4

(

)

4

19 Soal latihan

'

y

x x

e

e

y



2



2sin x

e

x

y



5 3 x x

e

e

y



tan(

2

)



tan ) 3 ln(x3 y ey   1 3 2 2   xy e y x A.Tentukan dari

1

3 2





xy

ye

x



5 6



ln 2    x x y

x

y



ln

cos

3

y

x

x



ln

2





y



ln sin

x

)) 1 2 sin(ln(   x y 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. x

x

y



(sin

)

2

B. Selesaikan integral tak tentu berikut 4 2x 1 dx





_ dx x x 1 3 2 (x  )ex  xdx



3 2 6

(cos )

x e

sin x

dx





x2e2x3dx 1. 2. 3. 4. 5. 6. 7. 8.



 dx e x2 x3



dx x x cos sin



dx x x sin cos

21 C. Selesaikan integral tentu berikut

3 1 2 1 4 



x dx e2x 3dx 0 1 



dx e x



2  ln 0 3



2  0 4 2

dx

xe

x 1. 2. 3. 4.

8.5 Fungsi Eksponen Umum

Fungsi , a > 0 disebut fungsi eksponen umum

Untuk a > 0 dan x  R, definisikan Turunan dan integral

Jika u = u(x), maka

Dari sini diperoleh :

: x

a

x

f

(

)



a

x



e

x ln a

a

a

a

e

e

D

a

D

_x

(

x

)



_x

(

xlna

)



xlna

ln



x

ln

a

u

a

u

a

e

e

D

a

D

_x

(

u

)



_x

(

ulna

)



ulna

ln

.

'



u

'

ln





a



C

a

dx

a

x x

ln

1

23

Sifat–sifat fungsi eksponen umum

Untuk a > 0, b > 0, x, y bilangan riil berlaku

y x y x

a

a

a



 y x y x

a

a

a

_



xy y x

a

a

)



(

x x x

b

a

b

a

_













1. 2. 3. 4.

(

ab

)

x



a

x

b

x 5.



4

x2

.

xdx

C C du u x u    



4 1 4 4 2 x x

x

f

(

)



3

2 1



2

sin2

2

ln

2

cos

2

.

2

3

ln

3

.

2

)

(

'

x

2 1 sin2

x

f



x



x Contoh:

Hitung turunan pertama dari

Jawab : 2. Hitung Jawab :

du

dx

xdx

du

x

u



2





₂





₂1_x Misal 



4x2.xdx

25

Grafik fungsi eksponen umum

0

,

)

(

x



a

a



f

x

)

,

(







Df

a. b.

f

'

(

x

)



a

x

ln

a

         1 , 0 ln 1 0 , 0 ln a a a a a a x x

f monoton naik jika a > 1

monoton turun jika 0 < a < 1

f x

D

x

a

a

x

f

''

(

)



(ln

)

2



0





c.

Grafik f selalu cekung keatas d. f(0) = 1 Diketahui 1 , ) (x  a a  f x 1 0 , ) (x a a  f x

8.6 Fungsi Logaritma Umum

Karena fungsi eksponen umum monoton murni maka ada Inversnya. Invers dari fungsi eksponen umum disebut fungsi Logaritma Umum

( logaritma dengan bilangan pokok a ), notasi , sehingga berlaku :

Dari hubungan ini, didapat

Sehingga

Jika u=u(x), maka

x

a

log

y

a

x





x

y



a

log

a

x

x

a

x

y

a

y

a

x

y a

ln

ln

log

ln

ln

ln

ln

ln













a x a x D x D_x a _x ln 1 ) ln ln ( ) log (  

a

u

u

a

u

D

u

D

_x a _x

ln

'

)

ln

ln

(

)

log

(





27 Contoh: Tentukan turunan pertama dari

)

1

log(

)

(

x



3

x

2



f

Jawab : 3 ln ) 1 ln( ) 1 log( ) ( 2 2 3     x x x f

3

ln

1

1

2

)

(

'

₂





x

x

x

f

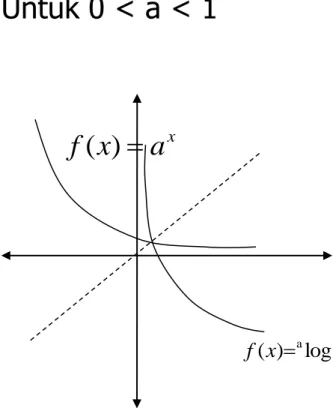
Grafik fungsi logaritma umum

Untuk a > 1 x

a

x

f

(

)



Untuk 0 < a < 1 x a x f ( ) 

Grafik fungsi logaritma umum diperoleh dengan mencerminkan grafik fungsi eksponen umum terhadap garis y=x

x x f ( )alog x x f( )alog

29

y



3

2x 4x 4



9



log

2 10





x

y

Soal Latihan A. Tentukan dari

_y

_'

1. 2.

8.7 Fungsi Invers Trigonometri

Fungsi trigonometri adalah fungsi yang periodik sehingga tidak satu-satu, jika daerah asalnya dibatasi, fungsi trigonometri bisa dibuat menjadi satu- satu sehingga mempunyai invers.

a. Invers fungsi sinus

Diketahui f(x) = sinx , ₂



_x



₂

Karena pada f(x)=sinx monoton murni maka inversnya ada. Invers dari fungsi sinus disebut arcus sinus, notasi arcsin(x),atau _sin 1_{( )}

x  2 2  

_

_



_x

Sehingga berlaku

y

x

x

y



sin

1





sin

2   2 

31

Turunan

Dari hubungan _y _sin1 _x _x _siny

y dy dx dx dy cos 1 / 1 _  2 2 , 1 1       _x  _y

dan rumus turunan fungsi invers diperoleh

1 | | , 1 1 sin 1 1 2 2      x x y 2 1 1 1 ) (sin x x D_x    atau Jika u=u(x) 2 1 1 ' ) (sin u u u D_x   

Dari rumus turunan diperoleh



    C x x dx ₁ 2 sin 1

b. Invers fungsi cosinus

Fungsi f(x) = cosx ,0  x 



x x f ( ) cos

monoton murni(selalu monoton turun), sehingga mempunyai invers

Definisi : Invers fungsi cosx disebut arcuscosx, notasi arc cosx atau _cos 1_{( )}

x  Berlaku hubungan

y

x

x

y



cos

1





cos

Turunan

Dari

_y



_cos

1

_x



_x



_cos

_y

dy

1



1

















1

x

1

,

0

y

,

1 | | , 1 1      x diperoleh

33 atau 2 1 1 1 ) (cos x x D_x     2 1 1 ' ) (cos u u u D_x     Jika u= u(x)

Dari rumus turunan diatas diperoleh



    C x x dx ₁ 2 cos 1 Contoh:





))

(

(sin

1

x

2

D

_x ( ) ) ( 1 1 ₂ 2 2 D x x x  4 1 2 x x  

Contoh: Hitung



_

dx

x

2

4

1

Jawab : Gunakan rumus



    C u du u ) ( sin 1 1 ₁ 2



  dx x ) 4 1 ( 4 1 2



_ dx x2 4 1



  dx x ₂ ) 2 ( 1 ( 1 2 1 Misal

_u

x

_du

_dx

_dx

₂

_du

2

2 1













_ dx x2 4 1



     C u du u 1 2 sin 1 ( 2 2 1

C

x







)

(

sin

1 ₂

35

c. Invers fungsi tangen

Fungsi f(x) = tanx, 2 2  

_

_



_x

2   2  f(x)=tanx

Monoton murni (selalu naik) sehingga mempunyai invers.

Definisi Invers dari tan x disebut fungsi arcus tanx, notasi arc tanx atau

tan

1

(

x

)

Berlaku hubungan

y

x

x

y



tan

1





tan

y

x

x

y



tan

1





tan

y

dy

dx

dx

dy

2

sec

1

/

1

_



Turunan Dari 2 2

,





y



 dan turunan fungsi invers diperoleh

2 2

1

1

tan

1

1

x

y









2 1 1 1 ) (tan x x D_x    2 1 1 ' ) (tan u u u D_x   











C

x

x

dx

₁ 2

tan

1

atau Jika u=u(x)

d. Invers fungsi cotangen

Fungsi f(x)= cot x

_,

₀

_

_x

_

_



f(x)=cotx

selalu monoton turun(monoton murni) sehingga mempunyai invers

Definisi Invers dari fungsi cot x disebut Arcus cotx, notasi arc cotx atau cot1 x

Berlaku hubungan

y

x

x

y



cot

1





cot

Turunan

y

dy

dx

dx

dy

2

csc

1

/

1

_

_



_{2 2}

1

1

cot

1

1

x

y













37 atau 2 1 1 1 ) (cot x x D_x    



_ 2 4 x dx













C

x

x

dx

₁ 2

cot

1

2 1 1 ' ) (cot u u u D_x     Jika u=u(x) Contoh :

)

1

(

(tan

1

x

2



D

_x ( 1) ) 1 ( 1 1 ₂ 2 2     Dx x x

1

(

2

1

)

2

2







x

x

Contoh: Hitung





   x dx x dx ) 4 1 ( 4 1 4 1 2 2 Jawab :



  dx x 2 ) 2 ( 1 1 4 1

du

dx

dx

du

x

u

2

2

2 1



























C

u

du

u

dx

x

1 2 2

tan

2

1

1

2

4

1

4

1

C

x







)

2

(

tan

2

1

₁ Gunakan rumus



    C u du u tan ( ) 1 1 ₁ 2

39

e. Invers fungsi secan

Diberikan f(x) = sec x 2 , 0 ,  x 



x   2

,

0

,

0

tan

sec

)

(

'

x



x

x





x





x





f

f(x) = sec x monoton murni Ada inversnya

Definisi Invers dari fungsi sec x disebut arcus secx, notasi arc secx atau 1 _x sec Sehingga

y

x

x

y



sec

1





sec

Turunan

Dari

_y



_sec

1

_x



_x



_sec

_y

x

y

1

cos



 

x

y



_cos

1 1

 

_x

x

1 1 1

cos

sec





 Sehingga

 

_x x x

x

D

D

_(sec

1

₎



_(cos

1 1 2 2 1

1

)

(

1

1

x

x









1

|

|

2 2





x

x

x

1 | | 1 2   x x Jika u = u(x) 1 | | ' ) (sec 2 1    u u u u D_x











c

x

dx

x

x

|

|

sec

1

1

₁ 2

41

e. Invers fungsi cosecan

Diberikan f(x) = csc x _{, , 0} 2 2     _x  _x

0

,

,

0

cot

csc

)

(

'

x





x

x



₂



x



₂

x



f

 

f(x) = sec x monoton murni Ada inversnya

Definisi Invers dari fungsi csc x disebut arcus csc x, notasi arc cscx atau 1 _x csc Sehingga

y

x

x

y



csc

1





csc

Turunan

Dari

_y



_csc

1

_x



_x



_csc

_y

x

y

1

sin



 

x

y



_sin

1 1

 

_x

x

1 1 1

sin

csc





 Sehingga

 

_x x x

x

D

D

_(csc

1

₎



_(sin

1 1 2 2 1

1

)

(

1

1

x

x







1

|

|

2 2







x

x

x

1 | | 1 2    x x Jika u = u(x) 1 | | ' ) (sec 2 1     u u u u D_x













c

x

dx

x

x

|

|

csc

1

1

₁ 2

43 Contoh:

A. Hitung turunan pertama dari

)

(

sec

)

(

x

1

x

2

f





1

2

)

(

1

)

(

|

|

1

)

(

'

4 2 2 2 2 2









x

x

x

x

Dx

x

x

x

f

1

2

4





x

x

Jawab:

B. Hitung



_ dx x x 4 1 2





   x dx x dx x x ) 1 4 ( 4 1 4 1 2 2



        dx x x 1 2 1 2 1 2 Jawab: Misal

_u

x

_du

_dx

_dx

₂

_du

2

2 1

















 _    u u du du u u dx x x 1 1 2 1 2 1 2 1 2 1 4 1 2 2 2

C

x

C

u









 

|

|

sec

1

|

|

sec

1

_{1 1}

45 Soal Latihan 2 1

)

(sin

x

y





)

(

tan

1

e

x

y





x

x

y



2

tan

1

A. Tentukan turunan pertama fungsi berikut, sederhanakan jika mungkin 1.

2. 3.

B. Hitung



₉

2

_

₁₆

x

dx



_ 16 4x x2 dx



/2

_

 1 0 2 1

1

sin

dx

x

x

1. 2. 3.