BAB 2
LANDASAN TEORI
2.1 Pengertian Regresi
Regresi pertama kali dipergunakan sebagai konsep statistika oleh Sir Francis Galton
(1822 – 1911). Beliau memperkenalkan model peramalan, penaksiran, atau
pendugaan, yang selanjutnya dinamakan regresi, sehubungan dengan penelitiannya
terhadap tinggi badan manusia. Galton melakukan suatu penelitian di mana
penelitian tersebut membandingkan antara tinggi anak laki-laki dan tinggi badan
ayahnya. Galton menunjukkan bahwa tinggi badan anak laki-laki dari ayah yang
tinggi setelah beberapa generasi cenderung mundur (regressed) mendekati nilai
tengah populasi. Dengan kata lain, anak laki-laki dari ayah yang badannya sangat
tinggi cenderung lebih pendek dari pada ayahnya, sedangkan anak laki-laki dari ayah
yang badannya sangat pendek cenderung lebih tinggi dari ayahnya, jadi
seolah-seolah semua anak laki-laki yang tinggi dan anak laki-laki yang pendek bergerak
menuju kerata-rata tinggi dari seluruh anak laki-laki yang menurut istilah Galton
disebut dengan “regression to mediocrity”. Dari uraian tersebut dapat disimpulkan
bahwa pada umumnya tinggi anak mengikuti tinggi orangtuanya (Sudjana, 1996).
Istilah “ regresi” pada mulanya bertujuan untuk membuat perkiraan nilai satu
variabel (tinggi badan anak) terhadap satu variabel yang lain (tinggi badan orang
tua). Pada perkembangan selanjutnya analisis regresi dapat digunakan sebagai alat
untuk membuat perkiraan nilai suatu variabel dengan menggunakan beberapa
variabel lain yang berhubungan dengan variabel tersebut (Algafari, 2000).
Jadi prinsip dasar yang harus dipenuhi dalam membangun suatu persamaan
variabel-variabel bebas (independent variable) lainnya memiliki sifat hubungan sebab akibat (hubungan kausalitas), baik didasarkan pada teori, hasil penelitian
sebelumnya, maupun yang didasarkan pada penjelasan logis tertentu (Algafari,
2000).
2.1.1 Analisis Regresi Linier
Perubahan nilai suatu variabel tidak selalu terjadi dengan sendirinya, namun
perubahan nilai variabel itu dapat disebabkan oleh berubahnya variabel lain yang
berhubungan dengan variabel tersebut. Untuk mengetahui pola perubahan nilai suatu
variabel yang disebabkan oleh variabel lain diperlukan alat analisis yang
memungkinkan untuk membuat perkiraan (prediction) nilai variabel tersebut pada
nilai tertentu variabel yang mempengaruhinya (Algafari, 2000).
Teknik yang umum digunakan untuk menganalisis hubungan antara dua atau
lebih variabel adalah analisis regresi. Analisis regresi (regression analisis)
merupakan suatu teknik untuk membangun persamaan garis lurus dan menggunakan
persamaan tersebut untuk membuat perkiraan (Algafari, 2000). Analisis regresi
merupakan teknik yang digunakan dalam persamaan matematik yang menyatakan
hubungan fungsional antara variabel-variabel. Analisis regresi linier atau regresi
garis lurus digunakan untuk :
1. Menentukan hubungan fungsional antar variabel dependen dengan
independen. Hubungan fungsional ini dapat disebut sebagai persamaan garis
regresi yang berbentuk linier.
2. Meramalkan atau menduga nilai dari satu variabel dalam hubungannya
dengan variabel yang lain yang diketahui melalui persamaan garis regresinya.
Analisis regresi tediri dari dua bentuk yaitu :
1. Analisis Regresi Linear Sederhana
Analisis regresi sederhana adalah bentuk regresi dengan model yang
bertujuan untuk mempelajari hubungan antara dua variabel, yakni variabel dependent
(terikat) dan variabel independent (bebas). Sedangkan analisis regresi berganda
adalah bentuk regresi dengan model yang memiliki hubungan antara satu variabel
dependent dengan dua atau lebih variabel independent (Sudjana, 1996).
Variabel independent adalah variabel yang nilainya tidak tergantung dengan
variabel lainnya, sedangkan variabel dependent adalah variabel yang nilainya
tergantung dari variabel yang lainnya (Algafari, 2000).
Analisis regresi linear dipergunakan untuk menelaah hubungan antara dua
variabel atau lebih, terutama untuk menelusuri pola hubungan yang modelnya belum
diketahui dengan baik, atau untuk mengetahui bagaimana variasi dari beberapa
variabel independen mempengaruhi variabel dependen dalam suatu fenomena yang
komplek. Jika, X1, X2, . . ., Xkadalah variabel-variabel independent dan Y adalah
variabel dependent, maka terdapat hubungan fungsional antara X dan Y, dimana
variasi dari X akan diiringi pula oleh variasi dari Y. (Sujana, 1996). Jika dibuat
secara matematis hubungan itu dapat dijabarkan sebagai berikut:
Dimana : Y = f (X1, X2, . . . , Xk, e)
Y adalah variabel dependen (tak bebas)
X adalah variabel independen (bebas)
e adalah variabel residu (disturbace term)
2.1.2 Analisis Regresi Linier Sederhana
Secara umum regresi linear terdiri dari dua, yaitu regresi linear sederhana yaitu
dengan satu buah variabel bebas dan satu buah variabel terikat; dan regresi linear
berganda dengan beberapa variabel bebas dan satu buah variabel terikat. Analisis
regresi linear merupakan metode statistik yang paling jamak dipergunakan dalam
penelitian-penelitian sosial, terutama penelitian ekonomi. Program komputer yang
dipergunakan untuk mengetahui pengaruh antara satu buah variabel bebas terhadap
satu buah variabel terikat.
Regresi linier sederhana digunakan untuk memperkirakan hubungan antara dua
variabel di mana hanya terdapat satu variabel/peubah bebas X dan satu peubah tak
bebas Y (Drapper & Smith, 1992). Dalam bentuk persamaan, model regresi
sederhana adalah :
Yi = 0 + 1Xi + i (2.1)
dimana : Yi = variabel terikat/tak bebas (dependent)
Xi = variabel bebas (independent)
𝛽𝛽0 = jarak titik pangkal dengan titik potong garis regresi pada sumbu
Y (intercept)
𝛽𝛽1 = kemiringan (slope) garis regresi
𝜀𝜀i = kesalahan (error)
Parameter 𝛽𝛽0 dan 𝛽𝛽1 diduga dengan menggunakan garis regresi. Bentuk persamaan
garis regresi adalah sebagai berikut :
Y
�i = b0 + b1Xi (2.2)
dimana : Y� merupakan penduga titik bagi Yi
b0merupakan penduga titik bagi 𝛽𝛽0
b1 merupakan penduga titik bagi 𝛽𝛽1
dari persamaan
S = � ε2
n
i=1
= �(Yi−Y�i)2 n
i=1
S = � ε2
n
i=1
= �(Yi− 𝛽𝛽0− 𝛽𝛽1𝑋𝑋1)2 n
i=1
(2.3)
Kemudian didiferensialkan terhadap 𝛽𝛽0, 𝛽𝛽1
∂S
∂𝛽𝛽0
=−2�(Yi− 𝛽𝛽0− 𝛽𝛽1𝑋𝑋1) n
i=1
∂S
∂𝛽𝛽1
=−2� 𝑋𝑋1(Yi− 𝛽𝛽0− 𝛽𝛽1𝑋𝑋1) n
i=1
(2.4)
�(Yi−b0−b1Xi) = 0
nol maka diperoleh persamaan
�Yi−nb0−b1�Xi = 0
Dari persamaan (2.6) diperoleh persamaan normal
2.1.3 Analisis Regresi Linier Berganda
Untuk memperkirakan nilai variabel tak bebas Y, akan lebih baik apabila kita ikut
memperhitungkan variabel-variabel bebas lain yang ikut mempengaruhi nilai Y.
dengan demikian dimiliki hubungan antara satu variabel tidak bebas Y dengan
beberapa variabel lain yang bebas X1, X2, dan X3, . . . , Xk. Untuk itulah digunakan
regresi linear berganda. Dalam pembahasan mengenai regresi sederhana, simbol
yang digunakan untuk variabel bebasnya adalah X. Dalam regresi berganda,
persamaan regresinya memiliki lebih dari satu variabel bebas maka perlu menambah
tanda bilangan pada setiap variabel tersebut, dalam hal ini X1, X2, . . . , Xk
(Sudjana, 1996).
Model regresi linier berganda atas X1, X2, . . . , Xk dibentuk dalam persamaan :
Y
�i = b0 + b1 X1+ b2X2i + . . . + bkXki + εi (2.9)
Koefisien-koefisien b0, b1, b2, . . . , bk ditentukan dengan menggunakan metode
kuadrat terkecil seperti halnya menentukan koeisien b0, b1, untuk regresi Y�i = b0 +
b1Xi + ei. Oleh karena Rumus (2.9) berisikan (k+1) buah koefisien, maka b0, b1, b2, . .
. , bk didapat dengan jalan menyelesaikan sistem persamaan yang terdiri atas (k+1)
buah persamaan. Dapat dibayangkan bahwa untuk ini diperlukan metode
penyelesaian yang lebih baik dan karenanya memerlukan matematika yang lebih
tinggi pula, lebih-lebih kalau harga k yang menyatakan variabel bebas, cukup besar.
Oleh karena itu untuk menyelesaikan persamaan regresi linier berganda dengan
variabel bebas X lebih dari dua variabel dapat diselesaikan dengan metode matriks.
Dalam model persamaan regresi dengan k buah variabel prediktor X yang
indevenden dan satu variabel dependen Y, maka model peresamaan statistikanya
dapat ditulis dengan:
Yi = β0 + β1 X1i + β2 X2i + β3 X3i + … + βk Xki + εi i = 1,2, ,n (2.10)
Keterangan:
i = 1,2, ,n
Yi = Variabel terikat
β0,β1,β2,β3,…βk = Parameter regresi yang belum diketahui nilainya
εi = Nilai kesalahan
Persamaan umum model regresi linier berganda populasi dengan jumlah
variabel bebas X sebanyak k buah
Y1 = β0 + β1 X11 + β2 X21 + β3 X31 + … + βk Xk1 + ε1
Y2 = β0 + β1 X12 + β2 X22 + β3 X32 + … + βk Xk2 + ε2
Y3 = β0 + β1 X13 + β2 X23 + β3 X33 + … + βk Xk3 + ε3 (2.11)
. . .
. . .
. . .
Yn = β0 + β0 X1n + β2 X2n + β3 X3n + … + β k Xkn + εn
Persamaan regresi populasi dinyatakan dengan notasi matriks akan menjadi:
Y = B [X] + ε. (2.12)
Apabila terdapat sejumlah n pengamatan dan k variabel bebas X maka untuk
setiap observasi atau responden mempunyai persamaannya seperti berikut:
Ŷi = b0 + b1 X1i + b2 X2i + b3 X3i + … + bk Xki + εi (2.13)
Keterangan
i = 1, 2, . . . , n
Ŷi = Variabel terikat
X1i, X2i, X3i,... Xki = Variabel bebas
b0,b1,b2,b3,…bk = Parameter regresi yang belum diketahui nilainya
εi = Nilai kesalahan
Persamaan umum model regresi linier berganda untuk setiap obsevasi atau
responden dengan jumlah variabel bebas X sebanyak k buah
Y1 = b0 + b1X11 + b2X21 + . . . + bkXk1
Y2 = b0 + b1X12 + b2X22 + . . . + bkXk2
.
. (2.14)
.
Dalam hal ini:
Ŷ merupakan penduga titik bagi Y
Dengan menggunakan matriks
Y = b [X] + e (2.15)
Rumus (2.15) inilah yang akan kita gunakan untuk menghitung koefisien-koefisien
b0 , b1, …bk. Untuk itu, terhadap Rumus (2.15) kita kalikan sebelah kiri dan kanan
dengan X'sehingga diperoleh X' Y = X' X b (2.17)
Dan selanjutnya hasil ini dari sebelah kiri kita kalikan dengan inversnya X' X ialah
(X' X )-1 sehingga diperoleh b = ( X' X )-1 X' Y (2.18)
Inilah rumus untuk mencari koefisien regresi linear ganda b0,b1,b2, . . . .bk
dalam bentuk matriks yang elemen-elementnya terdiri atas data pengamatan. Dalam
bentuk jumlah kuadrat dan produk silang data pengamatan Xij,elemen-elemen
matriks '
X X adalah seperti berikut
Sedangkan 𝑋𝑋′Y merupakan vektor kolom dengan elemen-elemen
Sebagai ketentuan dalam melakukan penelitian yang berhubungan dengan
pengambilan data adalah harus diketahui ukuran sampel yang memenuhi untuk
dianalisa. Untuk menentukan ukuran sampel yang memenuhi untuk dianalisa, maka
dilakukan uji kecukupan sampel dengan taraf signifikan yang dipilih 𝛼𝛼= 0,05
Hipotesa :
𝐻𝐻0 : ukuran sampel telah memenuhi syarat
𝐻𝐻1 : ukuran sampel tidak memenuhi syarat
Dengan statistik penguji:
kriteria pengujian : 𝐻𝐻0 diterima jika 𝑁𝑁′≤𝑁𝑁.
𝐻𝐻0 ditolak jika 𝑁𝑁′>𝑁𝑁
2.3 Prosedur Regresi dengan Menggunakan Metode Backward
Metode backward merupakan langkah mundur, mulai dengan regresi terbesar dengan
menggunakan semua variabel bebas 𝑋𝑋𝑖𝑖dan secara bertahap mengurangi banyaknya
variabel didalam persamaan sampai satu keputusan dicapai untuk menggunakan
persamaan yang diperoleh dengan jumlah variabel tertentu dimana semua variabel 𝑋𝑋
diregresikan dengan variabel dependen 𝑌𝑌. Pengeleminasian variabel 𝑋𝑋 didasarkan
pada nilai 𝐹𝐹𝑝𝑝𝑝𝑝𝑝𝑝 dari masing-masing variabel 𝑋𝑋 yaitu variabel yang mempunyai nilai
𝐹𝐹𝑝𝑝𝑝𝑝𝑝𝑝 terkecil dan turut tidaknya variabel 𝑋𝑋 pada model juga ditentukan oleh nilai
𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡.
Langkah 1 : Membentuk persamaan regresi linier berganda lengkap
Menentukan persamaan yang membuat semua variabel bebas dengan koefisien
regresi 𝑡𝑡0,𝑡𝑡1,𝑡𝑡2,𝑡𝑡3,𝑡𝑡4. Dapat diselesaikaan dengan metode matriks seperti yang
dijelaskan sebelumnya.
Langkah 2: Menentukan nilai F parsial dari masing-masing variabel 𝑋𝑋𝑖𝑖.
Bila sebuah model regresi mempunyai beberapa suku maka dapat dipandang
masing-masing suku itu sebagai “memasuki” persamaan regresi dalam urutan apa saja.
Besaran 𝐽𝐽𝐽𝐽(𝑡𝑡𝑖𝑖 ∣∣ 𝑡𝑡0, …𝑡𝑡𝑖𝑖−1,𝑡𝑡𝑖𝑖+1, … ,𝑡𝑡𝑘𝑘)𝑖𝑖 = 1,2, …𝑘𝑘
Merupakan jumlah kuadrat yang berderajat bebas satu yang mengukur sumbangan
koefisien 𝑡𝑡𝑖𝑖 pada jumah kuadrat regresi bila semua suku yang tidak mengandung 𝛽𝛽𝑖𝑖
telah ada di dalam model. Dengan kata lain, bila dimiliki suatu ukuran manfaat
penambahan suku 𝛽𝛽𝑖𝑖 pada model yang sebelumnya tidak mencakup suku tersebut.
Cara lain menyatakan ini adalah dimiliki suatu ukuran manfaat 𝛽𝛽𝑖𝑖 seolah-olah suku
ini dimasukkan kedalam model yang terakhir kali. Kuadrat tengahnya yang sama
dengan jumlah kuadratnya karena ia mempunyai satu derajat bebas dapat
dibandingkan dengan 𝑠𝑠2 melalui suatu uji F. Uji F semacam ini disebut uji F parsial
kita dapat berbicara tentang uji F parsial terhadap peubah X, meskipun kita
menyadari bahwa uji itu sesungguhnya ditujukan pada koefisien 𝛽𝛽𝑡𝑡.
Bila suatu model yang sesuai sedang ’dibangun’, Uji F parsial merupakan
kriterium yang sangat berguna untu memasukkan atau mengeluarkan suku dari model
tersebut. Penagruh suatu peubah X (Xq misalnya) dalam menentukan suatu respon
mungkin besar bila persamaan regresinya hanya mencakup Xq. Akan tetapi bila
peubah yang sama dimasukkan ke dalam persamaan regresi setelah peubah-peubah
yang lain, pengaruhnya terhadap respons mungkin menjadi sangat kecil. Ini
disebabkan oleh tingginya korelasi antara Xq dengan peubah-peubah yang sudah ada
dalam persamaan regresi, Uji F parsial dapat dilakukan terhadap semua koefisien
regresi seolah-olah peubah bersangkutan masuk ke dalam persamaan paling akhir.
Informasi ini dapat digabungkan dengan informasi lain bila pemilihan peubah perlu
dilakukan. Misalkan, 𝑋𝑋1 atau 𝑋𝑋2 saja dapat digunakan untuk menghasilkan
persamaan regresi bagi respon 𝑌𝑌. Misalnya penggunaan 𝑋𝑋1 menghasilkan galat
peramalan yang lebih kecil daripada penggunaan 𝑋𝑋2. Maka bila ketelitian ramalan
yang dikehendaki. 𝑋𝑋1 mungkin yang akan digunakan dimasa-masa mendatang. Akan
tetapi, kalau 𝑋𝑋2 adalah peubah yang memungkinkan pengendalian terhadap respons
(sedangkan 𝑋𝑋1 adalah peubah yang terukur namun bukan pengendali) dan bila
kendali atau control lebih dianggap penting dibandingkan dengan peramalan, maka
mungkin lebih baik menggunakan 𝑋𝑋2 daripada 𝑋𝑋1 sebagai peubah bebas di
masa-masa mendatang.
(Penggunaan istilah Uji F parsial hanya menekankan bahwa itu hanyalah nama yang
ringkas dan memudahkan bagi uji-uji F khusus yang secara teoritis benar dalam
beberapa program paket statistika uji F parsial sering disebut sebagai F untuk
mengeluarkan (F to remove) atau F untuk memasukkan (F to enter) )
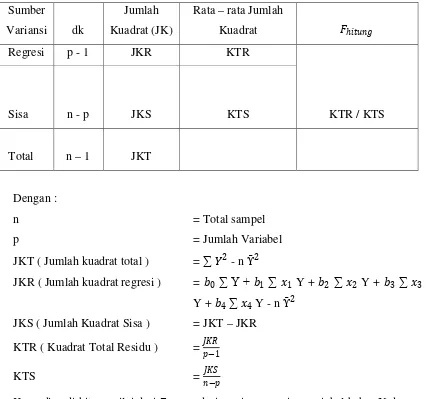
Untuk menentukan nilai F parsial dari masing-masing variabel 𝑋𝑋𝑖𝑖 diperlukan
Tabel 2.1 Analisa Variansi
Sumber
Variansi dk
Jumlah
Kuadrat (JK)
Rata – rata Jumlah
Kuadrat 𝐹𝐹ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖
Regresi p - 1 JKR KTR
KTR / KTS
Sisa n - p JKS KTS
Total n – 1 JKT
Dengan :
n = Total sampel
p = Jumlah Variabel
JKT ( Jumlah kuadrat total ) = ∑ 𝑌𝑌2 - n Ῡ2
JKR ( Jumlah kuadrat regresi ) = 𝑡𝑡0 ∑ Y + 𝑡𝑡1 ∑ 𝑥𝑥1 Y + 𝑡𝑡2 ∑ 𝑥𝑥2 Y + 𝑡𝑡3 ∑ 𝑥𝑥3
Y + 𝑡𝑡4 ∑ 𝑥𝑥4 Y - n Ῡ2
JKS ( Jumlah Kuadrat Sisa ) = JKT – JKR
KTR ( Kuadrat Total Residu ) = 𝐽𝐽𝐽𝐽𝐽𝐽
𝑝𝑝−1
KTS = 𝐽𝐽𝐽𝐽𝐽𝐽
𝑛𝑛−𝑝𝑝
Kemudian di hitung nilai dari 𝐹𝐹𝑝𝑝𝑝𝑝𝑝𝑝𝑠𝑠𝑖𝑖𝑝𝑝𝑝𝑝 dari masing – masing variabel bebas X dengan
menggunakan tabel sebagai berikut ini :
Tabel 2.2 Uji Korelasi Parsial
No
Koefisien
Regresi Galat baku 𝑭𝑭𝒑𝒑𝒑𝒑𝒑𝒑
1 𝑡𝑡1 𝑠𝑠1 𝑡𝑡1 2/ 𝑠𝑠1 2
2 𝑡𝑡2 𝑠𝑠2 𝑡𝑡2 2/ 𝑠𝑠2 2
3 𝑡𝑡3 𝑠𝑠3 𝑡𝑡3 2/ 𝑠𝑠3 2
Dengan :
𝑡𝑡1 ,𝑡𝑡2,𝑡𝑡3,𝑡𝑡4,: Koefisien regresi
𝑠𝑠1 , 𝑠𝑠2, 𝑠𝑠3, 𝑠𝑠4 : Galat taksiran Y atas X, untuk 𝑋𝑋1,2,3,4 Dengan :
𝑠𝑠𝑖𝑖 = �𝐽𝐽𝐽𝐽𝐽𝐽𝑝𝑝𝑒𝑒𝑠𝑠.𝐵𝐵𝑖𝑖𝑖𝑖
𝐽𝐽𝐽𝐽𝐽𝐽𝑝𝑝𝑒𝑒𝑠𝑠 : Rata – rata Jumlah Kuadrat Residu
𝐵𝐵𝑖𝑖𝑖𝑖 : Elemen matrik 𝐵𝐵−1 pada baris ke – 1 kolom ke – j
Langkah 3 : Pemilihan Variabel yang Pertama Keluar dari Model.
Variabel yang pertama di uji apakah terpilih keluar dari model atau tidak adalah
variabel yang memiliki nilai 𝐹𝐹𝑝𝑝𝑝𝑝𝑝𝑝𝑠𝑠𝑖𝑖𝑝𝑝𝑝𝑝 terkecil pada tabel 2.2 , misalnya nilai dari
variabel 𝑋𝑋1. Untuk menentukan apakah 𝑋𝑋1 keluar atau tidak, maka nilai 𝐹𝐹𝑝𝑝𝑝𝑝𝑝𝑝 dari
nilai variabel 𝑋𝑋1 di bandingkan dengan nilai 𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝, dengan hipotesa sebagai berikut :
Uji Hipotesa
𝐻𝐻0 : regresi antara Y dan 𝑋𝑋𝑖𝑖 tidak signifikan
𝐻𝐻1 : regresi antara Y dan 𝑋𝑋𝑖𝑖 signifikan
Keputusan :
Bila 𝐹𝐹𝑝𝑝𝑝𝑝𝑝𝑝𝑠𝑠𝑖𝑖𝑝𝑝𝑝𝑝 < 𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡 maka terima 𝐻𝐻𝑂𝑂
Bila 𝐹𝐹𝑝𝑝𝑝𝑝𝑝𝑝𝑠𝑠𝑖𝑖𝑝𝑝𝑝𝑝 ≥ 𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡 maka tolak 𝐻𝐻𝑂𝑂
Dengan taraf nyata yang dipilih α = 0,05
𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝= 𝐹𝐹(𝑝𝑝−1,𝑛𝑛−𝑝𝑝,0,5)
Langkah 4 : Membentuk Persamaan Regresi Linier Berganda yang kedua.
Bila pada langkah 3, 𝐻𝐻0 ditolak maka proses berakhir dan penduga yang di gunakan
adalah persamaan regresi linier berganda lengkap. Sebaliknya jika 𝐻𝐻0 di terima maka
langkah selanjutnya adalah membentuk persamaan regresi linier berganda yang
memuat semua variabel 𝑋𝑋𝑖𝑖. Untuk itu prosedur yang di lakukan adalah seperti pada
Langkah 5 : Pemilihan Variabel yang Kedua Keluar dari Model.
Untuk memilih variabel yang keluar dari model didasarkan pada nilai 𝐹𝐹𝑝𝑝𝑝𝑝𝑝𝑝 dari
variabel bebas yang termuat pada persamaan regresi linier berganda yang ke dua
seperti langkah 4.
Proses ini diulang secara berurutan sampai pada akhirnya nilai 𝐹𝐹𝑝𝑝𝑝𝑝𝑝𝑝 terkecil
dari variabel bebas akan lebih besar dari 𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡
2.4 Prosedur Regresi dengan Menggunakan Metode Forward
Metode forward adalah langkah maju, menurut metode ini variabel bebas
dimasukkan satu demi satu menurut urutan besar pengaruhnya terhadap model, dan
berhenti bila yang semua memenuhi syarat telah masuk. Dimulai dengan memeriksa
matriks korelasi dan kemudian mengambil variabel bebas yang menghasilkan 𝑝𝑝𝑋𝑋2𝑖𝑖𝑌𝑌
maksimum 𝑖𝑖= 1,2, … ,𝑘𝑘. Korelasi positif atau negatif tidak dipersoalkan karena
yang diperhatikan hanyalah eratnya hubungan antara suatu variabel bebas dengan 𝑌𝑌.
Sedangkan arah hubungan tidak menjadi persoalan.
Langkah 1 : Membentuk Matriks Koefisien Korelasi.
Koefisien korelasi yang dicari adalah koefisien korelasi linier sederhana 𝑌𝑌 dengan 𝑋𝑋𝑖𝑖,
dengan rumus:
(2.21)
Bentuk matriks koefisien korelasi linier sederhana antara 𝑌𝑌 dan 𝑋𝑋𝑖𝑖:
Langkah 2: Membentuk Regresi Pertama (Persamaan Regresi Linier)
Variabel yang pertama diregresikan adalah variabel yang mempunyai harga mutlak
koefisien korelasi yang terbesar antara 𝑌𝑌 dan 𝑋𝑋𝑖𝑖 , misalnya 𝑋𝑋1. Dari variabel ini
Keberartian regresi diuji dengan tabel analisa variansi. Perhitungan untuk membuat
anava adalah sebagai berikut:
MSE = SSE
𝑛𝑛−𝑝𝑝 (2.26)
sehingga didapat harga standard error dari 𝑡𝑡, dengan rumus:
𝐽𝐽2(𝛽𝛽) = MSE (𝑋𝑋𝑇𝑇𝑋𝑋)−1 (2.27)
𝐽𝐽(𝑡𝑡0) =�𝐽𝐽2(𝑡𝑡0)
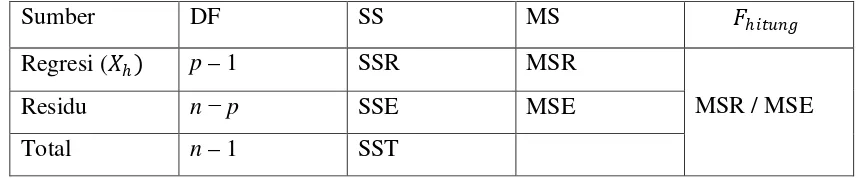
Tabel 2.3 Analisa Variansi untuk Uji Keberartian Regresi
Sumber DF SS MS 𝐹𝐹ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖
Regresi (𝑋𝑋ℎ) p – 1 SSR MSR
MSR / MSE
Residu n −p SSE MSE
Total n – 1 SST
Uji hipotesa:
𝐻𝐻0 : Regresi antara 𝑌𝑌 dengan 𝑋𝑋ℎ tidak signifikan.
𝐻𝐻1 : Regresi 𝑌𝑌 dengan 𝑋𝑋ℎ signifikan. Keputusan:
Bila𝐹𝐹ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖 < 𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝, maka terima 𝐻𝐻0.
Bila 𝐹𝐹ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖 ≥ 𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝, maka tolak 𝐻𝐻0.
Dengan:𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝 = 𝐹𝐹(𝑝𝑝−1,𝑛𝑛−𝑝𝑝,0,05)
Dengan nilai 𝛼𝛼 yang dipilih = 0,05
Langkah 3 : Seleksi Variabel Kedua Diregresikan
Cara menyeleksi variabel yang kedua diregresikan adalah memilih parsial korelasi
variabel sisa yang terbesar. Untuk menghitung harga masing-masing parsial korelasi
sisa digunakan rumus:
𝑝𝑝
𝑌𝑌𝑋𝑋ℎ.𝑋𝑋𝑘𝑘=
𝑝𝑝𝑌𝑌𝑋𝑋ℎ−𝑝𝑝𝑌𝑌𝑋𝑋𝑘𝑘𝑝𝑝𝑋𝑋ℎ𝑋𝑋𝑘𝑘
��1−𝑝𝑝𝑌𝑌𝑋𝑋𝑘𝑘2 ���1−𝑝𝑝𝑋𝑋ℎ 𝑋𝑋𝑘𝑘2 �
(2.28)
Langkah 4 : Membentuk Regresi Kedua (Persamaan Regresi Ganda)
Dengan memilih parsial korelasi variabel sisa terbesar untuk variabel tersebut masuk
dalam regresi, persamaan regresi kedua dibuat 𝑌𝑌=𝑡𝑡0+𝑡𝑡ℎ𝑋𝑋ℎ +𝑡𝑡𝑘𝑘𝑋𝑋𝑘𝑘 +𝜀𝜀𝑖𝑖
Dengan cara sebagai berikut:
𝑋𝑋=
⎝ ⎛
1 1
⋮
1
𝑋𝑋ℎ1
𝑋𝑋ℎ2
⋮ 𝑋𝑋ℎ𝑛𝑛
𝑋𝑋𝑘𝑘1
𝑋𝑋𝑘𝑘2
⋮ 𝑋𝑋𝑘𝑘𝑛𝑛⎠
⎞
(𝑋𝑋𝑇𝑇𝑋𝑋)−1 =�
𝑛𝑛 ∑ 𝑋𝑋ℎ ∑ 𝑋𝑋𝑘𝑘
∑ 𝑋𝑋ℎ ∑ 𝑋𝑋ℎ2 ∑ 𝑋𝑋ℎ𝑋𝑋𝑘𝑘
∑ 𝑋𝑋𝑘𝑘 ∑ 𝑋𝑋ℎ𝑋𝑋𝑘𝑘 ∑ 𝑋𝑋ℎ2
�
𝑌𝑌= �
𝑌𝑌1
𝑌𝑌2
⋮ 𝑌𝑌𝑛𝑛
� 𝑋𝑋𝑇𝑇𝑌𝑌 =�∑ 𝑋𝑋∑ 𝑌𝑌
ℎ𝑌𝑌
∑ 𝑋𝑋𝑘𝑘𝑌𝑌
�
𝛽𝛽 = (𝑋𝑋𝑇𝑇𝑋𝑋)−1 .𝑋𝑋𝑇𝑇𝑌𝑌= �
𝑡𝑡0
𝑡𝑡ℎ
𝑡𝑡𝑘𝑘
� (2.29)
Uji keberartian regresi dengan tabel anava (sama dengan langkah kedua yaitu dengan
menggunakan Tabel 2.2), kemudian dicek apakah koefisien regresi 𝑡𝑡𝑘𝑘 signifikan,
dengan hipotesa:
𝐻𝐻0:𝑡𝑡ℎ = 0
𝐻𝐻1:𝑡𝑡ℎ ≠0
𝐹𝐹
ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖=
�
𝐽𝐽(𝑡𝑡𝑡𝑡ℎℎ)�
2(2.30)
sedangkan,
Keputusan: bila 𝐹𝐹ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖 <𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝 terima 𝐻𝐻0 artinya 𝑡𝑡𝑘𝑘 dianggap sama dengan nol,
maka proses dihentikan dan persamaan terbaik 𝑌𝑌 = 𝑡𝑡0+𝑡𝑡ℎ𝑋𝑋ℎ. Bila 𝐹𝐹ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖 ≥
𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝 tolak 𝐻𝐻0 artinya 𝑡𝑡𝑘𝑘 tidak sama dengan nol, maka variabel 𝑋𝑋𝑘𝑘 tetap didalam
penduga.
Langkah 5 : Seleksi Variabel Ketiga Diregresikan
Dipilih kembali harga parsial korelasi variabel sisa terbesar. Menghitung harga
masing-masing parsial korelasi variabel sisa dengan Langkah 3, dengan rumus:
𝑝𝑝
𝑌𝑌𝑋𝑋1 .𝑋𝑋ℎ𝑋𝑋𝑘𝑘=
𝑝𝑝𝑌𝑌𝑋𝑋1 .𝑋𝑋ℎ−𝑝𝑝𝑌𝑌𝑋𝑋𝑘𝑘.𝑋𝑋ℎ𝑝𝑝𝑋𝑋1𝑋𝑋𝑘𝑘𝑋𝑋ℎ
��1−𝑝𝑝𝑌𝑌𝑋𝑋𝑘𝑘2 .𝑋𝑋ℎ���1−𝑝𝑝𝑋𝑋21𝑋𝑋𝑘𝑘.𝑋𝑋ℎ�
(2.31)
Langkah 6 : Membentuk Persamaan Regresi Ketiga (Regresi Ganda) Dengan memilih parsial korelasi terbesar, persamaan regresi yang dibuat:
𝑌𝑌= 𝑡𝑡0+𝑡𝑡ℎ𝑋𝑋ℎ +𝑡𝑡𝑘𝑘𝑋𝑋𝑘𝑘 +𝑡𝑡1𝑋𝑋1 (2.32)
dengan𝑋𝑋1 adalah variabel sisa yang mempunyai parsial korelasi terbesar, dengan
cara sebagai berikut:
𝑋𝑋=
⎝ ⎛
1 1
⋮
1
𝑋𝑋ℎ1
𝑋𝑋ℎ2
⋮ 𝑋𝑋ℎ𝑛𝑛
𝑋𝑋𝑘𝑘1
𝑋𝑋𝑘𝑘2
⋮ 𝑋𝑋𝑘𝑘𝑛𝑛
𝑋𝑋11
𝑋𝑋12
⋮ 𝑋𝑋1𝑛𝑛⎠
⎞
(𝑋𝑋𝑇𝑇𝑋𝑋)−1 =
⎝ ⎛
𝑛𝑛 ∑ 𝑋𝑋ℎ
∑ 𝑋𝑋𝑘𝑘
∑ 𝑋𝑋1
∑ 𝑋𝑋ℎ
∑ 𝑋𝑋ℎ2
∑ 𝑋𝑋ℎ𝑋𝑋𝑘𝑘
∑ 𝑋𝑋ℎ𝑋𝑋1
∑ 𝑋𝑋𝑘𝑘
∑ 𝑋𝑋ℎ𝑋𝑋𝑘𝑘
∑ 𝑋𝑋𝑘𝑘2
∑ 𝑋𝑋𝑘𝑘𝑋𝑋1
∑ 𝑋𝑋1
∑ 𝑋𝑋ℎ𝑋𝑋1
∑ 𝑋𝑋𝑘𝑘𝑋𝑋1
∑ 𝑋𝑋12 ⎠
⎞
−1
𝑋𝑋𝑇𝑇𝑌𝑌 = �
∑ 𝑌𝑌 ∑ 𝑋𝑋ℎ𝑌𝑌
∑ 𝑋𝑋𝑘𝑘𝑌𝑌
∑ 𝑋𝑋1𝑌𝑌
diperoleh = (𝑋𝑋𝑇𝑇𝑋𝑋)−1 . 𝑋𝑋𝑇𝑇𝑌𝑌 untuk membuat tabel anava uji keberartian regresi,
menghitung masing-masing harga-harga yang diperlukan, dilakukan dengan cara
yang sama seperti diatas. Begitu juga untuk pengujiannya. Bila hasil pengujian
menyatakan koefisien regresi tidak signifikan maka proses dihentikan berarti
persamaannya adalah:
𝑌𝑌= 𝑡𝑡0+𝑡𝑡ℎ𝑋𝑋ℎ +𝑡𝑡𝑘𝑘𝑋𝑋𝑘𝑘 (2.34)
Jika signifikan maka proses dilanjutkan sama dengan cara yang diatas. Demikian
seterusnya sampai tidak ada lagi variabel yang masuk dalam model. Uji keberartian
keseluruhan koefisien regresi yang masuk ke dalam persamaan penduga. Dalam
pengujiannya, masing-masing koefisien regresi diuji dengan uji hipotesa:
𝐻𝐻0:𝑡𝑡𝑞𝑞 = 0
𝐻𝐻1:𝑡𝑡𝑞𝑞 ≠0 untuk
𝐹𝐹
ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖=
�
𝐽𝐽(𝑡𝑡𝑡𝑡𝑞𝑞𝑞𝑞)�
2(2.35)
dimana q adalah masing-masing nomor urutan variabel yang diterima masuk ke
dalam persamaan penduga. Sedangkan 𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝 =𝐹𝐹(𝑝𝑝−1,𝑛𝑛−𝑝𝑝,0,05). Bila diantara harga
𝐹𝐹ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖 < 𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝, maka teorema 𝐻𝐻0 artinya variabel tersebut keluar dari regresi. Bila
semua harga 𝐹𝐹ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖 <𝐹𝐹𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝, maka tolak 𝐻𝐻0 artinya semua variabel tetap dalam
regresi.
2.5 Membentuk Model Penduga
Apabila proses pengeluaran variabel bebas dari persamaan regresi telah selesai, maka
ditetapkan persamaan regresi yang menjadi penduga linier yang diinginkan.
2.5.1 Persamaan Penduga Pada Metode Backward
Bentuk Penduga ditetapkan adalah: 𝑌𝑌�=𝑡𝑡0 +∑ 𝑡𝑡𝑝𝑝𝑋𝑋𝑝𝑝 dimana 𝑋𝑋𝑝𝑝 adalah semua
2.5.2 Persamaan Penduga Pada Metode Forward
Persamaan penduga 𝑌𝑌�=𝑡𝑡0 +𝑡𝑡1𝑋𝑋1, dimana 𝑋𝑋1 adalah semua variabel 𝑋𝑋 yang
masuk kedalam penduga (faktor penduga) dan 𝑡𝑡1 adalah koefisien regresi untuk 𝑋𝑋1.
2.6 Koefisien Korelasi Berganda (Koefisien Determinasi).
Uji koefisien determinasi (R2) dilakukan untuk mengetahui ketetapan yang paling
baik dari garis regresi. Uji ini dilakukan dengan melihat besarnya nilai koefisien
determinasi (R2) merupakan nilai besaran non negatif.
Besarnya nilai koefisien determinasi adalah antara nol sampai dengan satu
( 1 ≥ R2 ≥ 0 ). Koefisien determinasi bernilai nol berarti tidak adahbungan antara
variabel independent dengan variabel dependent, sebaliknya nilai koefisien
determinasi satu berart suatu kecocokan sempurna. Maka R2 akan dituliskan dengan
rumus, yaitu :
R2 = 𝐽𝐽𝐽𝐽𝑝𝑝𝑒𝑒𝑖𝑖
⅀𝑦𝑦𝑖𝑖2 (2.36)
2.7 Pertimbangan Terhadap Penduga
Sebagai pembahasan suatu penduga, untuk mengomentari atau menanggapi
kecocokan penduga yang diperoleh ada dua hal yang dipertimbangkan yakni:
a. Pertimbangan berdasarkan Koefisien Determinasi (𝐽𝐽2)
Suatu penduga sangat baik digunakan apabila persentase variasi yang
dijelaskan sangat besar atau bila 𝐽𝐽2 mendekati 1.
b. Analisa Residu (sisa)
Suatu regresi adalah berarti dan model regresinya cocok (sesuai berdasarkan
data observasi) apabila kedua asumsi pada 2.1 dipenuhi. Kedua asumsi ini
dibuktikan dengan analisa residu. Untuk langkah ini awalnya dihitung residu
oleh penduga berdasarkan prediktor observasi. Dengan rumus: 𝑒𝑒𝑖𝑖 =𝑌𝑌𝑖𝑖 − 𝑌𝑌�𝑖𝑖 ,
ditunjukkan pada tabel 2.4;
Tabel 2.4 Residu
No Residu Respon (𝑌𝑌𝑖𝑖) Penduga (𝑌𝑌�𝑖𝑖) Residu (𝑒𝑒𝑖𝑖)
1 𝑌𝑌1 𝑌𝑌�1 𝑌𝑌1− 𝑌𝑌�1
2 𝑌𝑌2 𝑌𝑌�2 𝑌𝑌2− 𝑌𝑌�2
3 𝑌𝑌3 𝑌𝑌�3 𝑌𝑌3− 𝑌𝑌�3
.
.
.
.
.
.
.
.
.
.
.
.
N 𝑌𝑌𝑛𝑛 𝑌𝑌�𝑛𝑛 𝑌𝑌𝑛𝑛 − 𝑌𝑌�𝑛𝑛
Jumlah � 𝑒𝑒
𝑖𝑖
Rata-rata �𝑒𝑒𝑖𝑖
𝑛𝑛
i. Pembuktian Asumsi
Asumsi :
a. Rata-rata residu sama dengan nol (𝑒𝑒̅= 0). Kebenaran keadaan ini akan
terlihat pada tabel 2.4.
b. Varian (𝑒𝑒𝑖𝑖) = varian (𝑒𝑒𝑘𝑘) = 𝜎𝜎2.
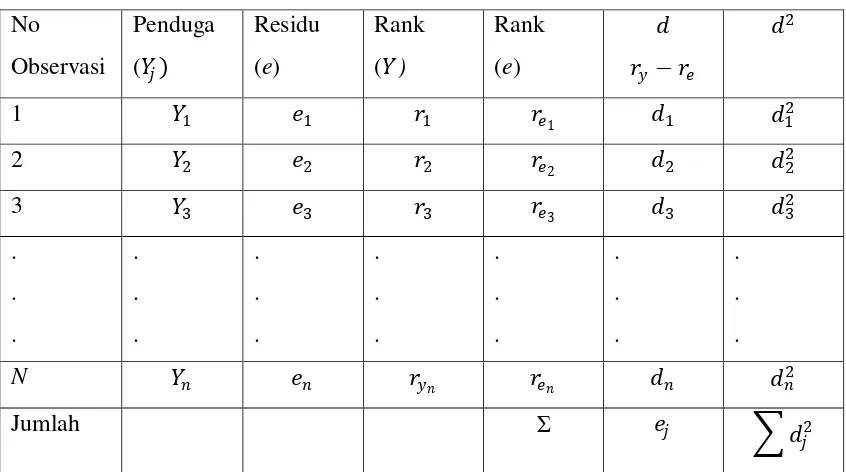
Keadaan ini dibuktikan dengan uji statistik dengan menggunakan uji Korelasi
Rank Spearman (Spearman’s Rank Correlation Test). Untuk uji ini, data yang
diperlukan adalah Rank (𝑒𝑒𝑖𝑖) dan Rank (𝑌𝑌𝑖𝑖), dimana:
𝑑𝑑𝑖𝑖 = Rank (𝑌𝑌𝑖𝑖)− Rank (𝑒𝑒𝑖𝑖).
Tabel 2.5 Rank Spearman
No
Observasi
Penduga
(𝑌𝑌𝑖𝑖)
Residu
(e)
Rank
(𝑌𝑌)
Rank
(e)
𝑑𝑑 𝑝𝑝𝑦𝑦 − 𝑝𝑝𝑒𝑒
𝑑𝑑2
1 𝑌𝑌1 𝑒𝑒1 𝑝𝑝1 𝑝𝑝𝑒𝑒
1 𝑑𝑑1 𝑑𝑑1
2
2 𝑌𝑌2 𝑒𝑒2 𝑝𝑝2 𝑝𝑝𝑒𝑒
2 𝑑𝑑2 𝑑𝑑2
2
3 𝑌𝑌3 𝑒𝑒3 𝑝𝑝3 𝑝𝑝𝑒𝑒
3 𝑑𝑑3 𝑑𝑑3
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
N 𝑌𝑌𝑛𝑛 𝑒𝑒𝑛𝑛 𝑝𝑝𝑦𝑦𝑛𝑛 𝑝𝑝𝑒𝑒𝑛𝑛 𝑑𝑑𝑛𝑛 𝑑𝑑𝑛𝑛2
Jumlah Σ 𝑒𝑒𝑖𝑖 � 𝑑𝑑
𝑖𝑖2
Koefisien Korelasi Rank Spearman (𝑝𝑝𝑠𝑠):
𝑝𝑝𝑠𝑠 = 1−6� ∑𝑑𝑑𝑖𝑖
2
𝑛𝑛(𝑛𝑛2−1)�
Pengujian menggunakan uji t dimana:
𝑡𝑡ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖 =𝑝𝑝𝑠𝑠√𝑛𝑛−2 �1−𝑝𝑝𝑠𝑠2
𝑡𝑡𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝 = 𝑡𝑡(𝑛𝑛−2,1−𝛼𝛼)
dimana 𝑛𝑛 −2 adalah derajat kebebasan dan 𝛼𝛼 adalah taraf signifikan hipotesa.
Dengan membandingkan 𝑡𝑡ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖 < 𝑡𝑡𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝, maka varian (𝑒𝑒𝑖𝑖) = varian (𝑒𝑒𝑘𝑘) dengan
kata lain bila 𝑡𝑡ℎ𝑖𝑖𝑡𝑡𝑖𝑖𝑛𝑛𝑖𝑖 <𝑡𝑡𝑡𝑡𝑝𝑝𝑡𝑡𝑒𝑒𝑝𝑝, maka varian seluruh residu adalah sama. Bila terbukti