VARIABEL RANDOM DAN DISTRIBUSI PELUANG

(1)

VARIABEL RANDOM DAN DISTRIBUSI PELUANG

'Variabel Random dan Distribusi Peluang' - Sipil Geoteknik 2013 1

(2)

Definisi Variabel Random

2

Variabel random ialah

Suatu fungsi yang mengaitkan suatu bilangan real pada setiap unsur dalam ruang sampel.

Variabel random dinyatakan dengan huruf besar : X

Sedangkan nilainya dinyatakan dengan huruf kecil : x

(3)

Contoh 1

3

Dua bola diambil satu demi satu tanpa dikembalikan dari suatu kantong berisi 4 bola merah dan 3 bola hitam.

Bila Y menyatakan jumlah bola merah yang diambil maka nilai y yang mungkin dari variabel random Y adalah:

Solusi:

Y = jumlah bola merah yang diambil S = {Y|y = 0,1,2}

MM 2 MH, HM 1

R u a n g

s a

(4)

Type Variabel Random

4

1. Ruang sampel Diskrit

Jika suatu ruang sampel mengandung titik yang berhingga banyaknya atau sederatan anggota yang banyaknya sebanyaknya

bilangan bulat.

2. Ruang sampel Kontinou

Bila ruang sampel mengandung titik sampel yang tak berhingga banyaknya dan

banyaknya sebanyak titik pada sepotong

garis.

(5)

f(x) = p(x) = P(X = x) = fgs dist peluang

= fungsi padat peluang

= pdf = probability density function F(X = x) = P(X ≤ x)

= cdf = cumulative distribution function

 

^dF

 

^x

x f 

5

(6)

Sifat Distribusi peluang variabel random

1.

2.

3.

Variabel random

4.

Diskrit

5. Variabel random

6.

^Kontinou

1 )

(

0  f x_i 



_i



i

P X x

x

f ( )  



^







i

xi

f ( ) 1











x t

t f x

X P x

F( ) ( ) ( )

 

^¹







 i

xi

f

 ^t ^dt

f x

X P x

F



x





 ( )

) (

6

(7)

Contoh 2

7

Sebuah kontraktor mempunyai 4 mesin yang digunakan pada suatu proses produksi.

Diramalkan mesin mempunyai rata-rata usia pakai 10 tahun.

Tentukan ruang sampel dari variabel random x.

Misal: X menyatakan jumlah mesin dalam keadaan baik.

(8)

Solusi

8

X: jumlah mesin dalam keadaan baik setelah 10 th S: {X|x = 0,1,2,3,4}

Kondisi mesin bil real (x)

BBBB 4 BBBR, BBRB, BRBB, RBBB 3 BBRR, BRRB, RRBB, RBRB, RBBR, RBRB 2 BRRR, RBRR, RRBR, RRRB 1

RRRR 0

(9)

Distribusi Peluang

9

Distribusi peluang suatu variabel random X adalah himpunan nilai peluang variabel

random X yang ditampilkan dalam bentuk tabel dan atau gambar.

X X₁ X₂ ... X_k

Peluang f(x₁) f(x₂) ... f(x_k)

(10)

Distribusi peluang keadaan mesin baik setelah 10 tahun

BBRR BRBR RBBRRBRB RRBB BRRB RRRR

BRRR RBRRRRBR RRRB

BBBR BBRBBRBB RBBB

BBBB

10

X 4 3 2 1 0

P(X) 1/16 4/16 6/16 4/16 1/16

(11)

Berdasarkan Contoh 2:

a. Tentukan peluang lebih dari 2 mesin yang baik dengan usia lebih dari 10 tahun:

b. Tentukan peluang paling banyak 1 mesin baik dengan usia lebih dari 10 tahun:

c. Tentukan peluang antara 1 sampai 2 mesin baik dengan

4 1 5

( 2)

16 16 16 P X    

16 5 16

4 16

) 1 1

(X     P

11

(12)

Contoh 3

Sebuah pengiriman 8 komputer pc yang sama ke suatu toko mengandung 3 yang cacat. Bila suatu sekolah membeli 2 komputer secara random,

Tentukan distribusi peluang banyaknya komputer yg cacat.

X = banyaknya komputer yang cacat = {0, 1, 2}

f(0) = P(X = 0) f(1) = P(X = 1) f(2) = P(X = 2)

12

(13)

13

;

Distribusi Probabilitas

3 5

0 2

8 2

(0) ( 0) 10

28 f P X C C

   C  ¹³ ¹⁵

8 2

(1) ( 1) 15

28 f P X C C

   C 

3 5

2 0

8 2

(2) ( 2) 3

28 f P X C C

   C 

X = 0 X = 1 X = 2

(14)

Contoh 4:

Misalkan bahwa galat suhu reaksi, dalam ⁰C pada percobaan laboratorium, merupakan variabel

random X yang mempunyai fungsi padat peluang:

a. Tunjukkan bahwa

b. Cari

 

2

, 1 2

3

0 ,

x x

f x

lainnya

   

 



 

¹

f x dx











⁰ ¹



P  X 

(15)

Solusi:

a.

b.

2 2 3 2

1 1

8 1

3 9 9 9 1

x x

dx

 

   



 

¹ ² ³ ¹

0 0

0 1 1

3 9 9

x x

P  X  



dx  

(16)

c. Untuk -1 < x < 2

jadi:

   

² ³ ³

1 1

1

3 9 9

x x x

t t x

F x f t dt dt

  









  

 

³

0 1

1 1 2

9 1 2

x

F x x x

x

  

 

    

 



(17)

Beberapa distribusi peluang Diskrit a.l:

1. Distribusi Uniform

ialah suatu kejadian yang mempunyai probabilitas yang sama.

misal:

Probabilitas mata dadu keluar angka 5:

Probabilitas mata uang keluar muka:

 

x k

f 1



6 1

1

17

(18)

2. Distribusi Binomial

- Peristiwa terjadi n kali percobaan/kejadian.

- Tiap peristiwa menghasilkan 2 kemungkinan,

‘sukses’ (p) or ‘gagal’ (q).

- Tiap peristiwa terjadi saling independen.

x = 0, 1, 2, … , n



^X ^x



^C_xⁿ^P^x



^P



ⁿ ^x

P   1 ^

18

(19)

Contoh 5:

Suatu suku cadang dapat menahan uji goncangan tertentu dengan peluang ¾. Hitunglah

a. Peluang bahwa tepat 2 dari 4 suku cadang yang diuji tidak akan rusak.

b. Peluang paling banyak 1 yang rusak dari 4 suku cadang yang diujikan.

c. Peluang terdapat paling sedikit 3 suku cadang yang baik dari 4 suku cadang yang diujikan.

19

(20)

Solusi:

X : Suku cadang yang baik a. P( X = 2) = ?

b. P( X ≥ 3) = P(X = 3) + P(X = 4) c. P( X ≥ 3) = P(X = 3) + P(X = 4)



; ,



2⁴ ² (1 )^{4 2} B x n p  C p  p ^

20

2 4 2

4 2

3 3 3

2; 4, 1

4 4 4

B C

        

     

     

(21)

3. Distribusi Binomial Negatif

Percobaan seperti kejadian pada Binomial,

dengan usaha diulang sampai tercapai sejumlah

sukses tertentu.

Jadi banyaknya usaha X untuk

menghasilkan k sukses pada n kejadian

adalah Variabel random Binomial Negatif.

Distribusi peluangnya disebut distribusi Binomial Negatif.

21

(22)

Berapa peluang sukses ke-k akan terjadi pada kejadian ke-n.

Contoh 6:

Peluang cacat pembuatan tiang pancang sebesar 0.1. Pada pemeriksaan kualitas dilakukan

pengambilan sampel sebanyak 5 item.

 ^X

_k

ⁿ  ^C

_kⁿ

^p

^k

^q

ⁿ ^k

P  

_^₁¹ ^

22

(23)

Berapa peluang pengambilan tiang pancang yang ke-5, adalah pengambilan tiang pancang cacat

yang ke-2 ? Solusi:

Kemungkinan yang terjadi:

1. BBBCC P(BBBCC) = (0.9)(0.9) (0.9)(0.1)(0.1) 2. BBCBC P(BBCBC) = (0.9) (0.9)(0.1)(0.9)(0.1)

23

(24)

Fungsi dist Binomial Negatif



Jadi peluang pengambilan tiang pancang yang ke-4 adalah pengambilan tiang pancang cacat yang

kedua sebesar 2.43 %



2 5



2 1^{5 1} ² ^{5 2}

P X   C _^ p q ^



₂ ⁵



₁⁴

   

^0.1 ² ^0.9 ³ ^0.02916

P X   C 

24

(25)

4. Distribusi Geometrik

Sukses pertama pada kejadian ke-n

Contoh 7:

Pada saat sibuk di suatu sentral telepon mencapai batas daya sambungnya, sehingga orang tidak

mendapat sambungan. Andaikan peluang mendapat sambungan selama waktu sibuk adalah 0.05. Berapa peluang diperlukan 6 kali usaha agar sambungan



^X₁ ^ ⁿ



^ ^pqⁿ^¹

P

25

(26)

X = kejadian sambungan berhasil

Diperlukan 6 kali usaha agar sambungan berhasil:

GGGGGS

Jadi peluang yang diperlukan agar 6 kali usaha

dalam melakukan sambungan akan berhasil sebesar 3.6 %



^X₁ ^

⁶  

^

⁰ ^. ⁰⁵  ⁰ ^. ⁹⁵ 

⁵ ^

⁰ ^. ⁰³⁶

P

26

(27)

5. Distribusi Hypergeometrik

Banyaknya sukses dalam variabel random ukuran n sampel yang diambil dari N populasi, yang

mengandung k sifat tertentu dari populasi.

x = 0, 1, 2, …, n



 







 







 



 







 ^^

n N

x n

k N

x k

C C k C

n N x

h _N

n k N

x n k

) x

, ,

; (

27

(28)

Contoh 8:

Suatu kotak berisi 40 suku cadang, dikatakan

memenuhi syarat penerimaan bila berisi tidak lebih dari 3 yang cacat. Cara sampling kotak ialah

dengan memilih 5 suku cadang secara random.

Berapa peluang mendapatkan tepat satu yang cacat dalam sampel berukuran 5?

3011 .

40 0 4 37 1

3 )

3 , 5 , 40

; 1

( 







 







 





 h

28

(29)

6. Distribusi Poisson

Banyaknya sukses yang terjadi dalam suatu selang waktu atau daerah tertentu.

x = 0, 1, 2, … e = 2.71828

Sebagai pendekatan untuk distribusi binomial bila n cukup besar dan p kecil (n > 20 dan p < 0.05)

) !

( x

x e f

x



 

29

(30)

Contoh 9:

Dari pengalaman masa lalu selama 20 tahun terakhir, rata-rata terjadi hujan lebat 4 kali per tahun.

Berapa peluang tidak terjadi hujan lebat tahun depan?

018 .

! 0 0 ) 4

0 (

4

0 



 e^

X P _t

30

(31)

Soal-soal

1. Seorang petani jeruk mengeluh karena

dari panen jeruknya terserang suatu virus. Cari peluangnya bahwa diantara 4 buah jeruk yang diperiksa dari hasil panen ini:

a. Semuanya terserang virus tersebut.

b. Antara 1 sampai 3 yang terserang virus tersebut.

c. Cari distribusi peluangnya

3 2

31

(32)

2. Dalam pengujian sejenis ban truk melalui jalan yang kasar ditemukan bahwa 25 % truk mengalami

kegagalan karena ban pecah. Carilah peluangnya dari 15 truk yang diuji, jika:

a. 3 sampai 6 mengalami ban pecah

b. kurang dari 4 yang mengalami ban pecah c. lebih dari 5 yang mengalami ban pecah

32

(33)

3. Dari kotak berisi 10 peluru, diambil 4 secara acak dan kemudian ditembakkan. Bila kotak itu

mengandung 3 peluru yang cacat yang tidak akan meledak, berapakah peluang bahwa:

a. keempatnya meledak

b. paling banyak 2 yang tidak akan meledak

33

(34)

Rata-rata dan varians dari distribusi peluang

Jika X adalah variabel random diskrit dengan distribusi peluang f(x), maka nilai rata-rata X dinyatakan:

E(X) = ekspektasi X

Varians X dinyatakan dgn Var(X) =

 

_i

 

_i

i

E X   x f x  



2

     

   

2 2

2

i i

i

E X X f x

  ^   ^ 



  

34

(35)

Ekspektasi dari Distribusi peluang

Diskrit

Kontinou

 

 ^g ^x  ^g     ^x ^f ^x ^dx

E ^ 

  ^X ^x ^f   ^x ^dx

E ^ ^ ^ 

 

 ^g ^x  ^g     ^x ^f ^x

E ^ 

  ^X ^x ^f   ^x

E ^ ^ ^ 

35

(36)

Sifat-sifat ekspektasi:

1. E(ax) = a E(x)

2. E(a + bx

²

) = a + b E(x

²

) 3. E(xy) = E(x) E(y)

36

(37)

Standart Deviation

Var (X) = E( X – μ)

²

= E(X

²

) – μ

²

, dimana; μ = E(X)

= E(X

²

) – (E(X))

²

) (

tandart Deviasi X Varians X

S 

37

(38)

Sifat-sifat varians:

1. Varians tidak negatif 2. Var (x + a) = Var (x) 3. Var (bx) = b

²

Var (x)

4. Var (a + bx) = b

²

Var (x)

38

(39)

Distribusi Binomial (x; n, p)

 Nilai Harapan (expected value)

 Varians X

 

i

 

i i

E X   x f x    np

 

( )

2

1

Var X 



 np  p

(40)

Distribusi Binomial Negatif (x; k, p)

 Varians X

 

i

 

i

¹

i

E X x f x k p

 ^ p

   

2

(1 )

( ) p

Var X k

 p ^

 

(41)

Distribusi Geometrik (x; p)

 Varians X

 

i

 

i

¹

i

E X x f x

 p

   

2

(1 )

( ) p

Var X

 p ^

 

(42)

Distribusi Hipergeometrik (x; N, n, k)

 Varians X

 

i

 

i i

E X x f x n k

 N

   

( ) 2 1

1

N n k k

Var X n

N N N

 ^ ^ ^

     

(43)

Distribusi Poisson (x; )

 Varians X

 

E X ^ 

 

Var X 



(44)

contoh 10

Seorang kontraktor memasukkan penawaran tender untuk 3 pekerjaan A, B dan C. Jumlah pesaing untuk mendapatkan pekerjaan A, B dan C masing-masing 4, 3 dan 2. Andaikan peristiwa A, B dan C bebas secara statistik dan X menyatakan jumlah total pekerjaan yang akan dimenangkan kontraktor:

a. Tentukan distribusi peluang X b. Tentukan rata-rata X

c. Tentukan varians X

44

(45)

Peluang sukses mendapatkan pekerjaan A:

Peluang sukses mendapatkan pekerjaan B:

Peluang sukses mendapatkan pekerjaan C:

X = jumlah total pekerjaan yang akan dimenangkan seorang kontraktor.

15

14

13

 

⁰^.⁴

3 2 4

3 5

0 4  



 







 







 



 

 X P

45

(46)

 

⁰^.¹⁴⁹

3 1 4

1 5

4 3

1 4

3 5

1 3

2 4

1 5

2 1  



 







 







 







 







 







 







 







 







 





 X P

 

⁰^.⁰¹⁶⁷

3 1 4

1 5

3 1  



 







 







 



 

 X P

X 0 1 2 3

f(x) 0.4 0.43 0.149 0.016

E(x) = x f(x) 0 0.43 0.298 0.348

(47)

Jadi rata-rata hanya satu pekerjaan yang akan dimenangkan oleh seorang kontraktor.

  

^ ^



i

i f x

x

x 1.076 1

X 0 1 2 3

f(x) 0.40 0.43 0.149 0.016

X² f(x) 0 0.43 0.596 1.044

(48)

Var (X) = E(X²) – μ²

= E(X²) – (E(X))²

= 2.07 - (1.076)²

= 0.91

 

^

_ ^{ }

^

i

i f x

x X

E ² ² 2.07

48

(49)

Koefisien Variasi ( δ

_x

)

Kemencengan (θ)

x x

x



  

 

3

x

X x

E





 ^



49

(50)

Distribusi Kontinou

1. Distribusi NORMAL

KARL FRIEDRICH GAUSS

-



< x <  Simetris

Bell shape

X  N ( , 2 )

2

2 1

2

) 1 (



 



  



^





x

e x

f

50

(51)

51

f(x)

x

(52)

Transformasi Normal Standart

52

(Transformasi)

 menggunakan tabel normal standart



²



~ ,

X N  

 

~ 0, 1 Z N

Z X 



 

(53)

Contoh 11:

Pendapatan mingguan seorang karyawan di

industri kaca berdistribusi normal dengan mean $ 1.000 dan standart deviasi $ 100.

1. Berapa probabilitas karyawan yang

berpendapatan paling banyak $ 900 per minggu.

berpendapatan paling sedikit $ 1.250 per minggu.

berpendapatan antara $ 900 dan $ 1.100 per

53

(54)

Solusi :

X = pendapatan mingguan,  = $ 1.000 dan  = $ 100 a. P( x < 900) =

= = 0.1587 b. P( x > 1.250) =

=

= =



 



   

10

000 .

1 900 100

000 .

1 P x



 



 

 100 Z 100

P ^P



^Z ^ ^¹





 



   

100

000 . 1 250 . 1 100

000 . 1 P x



 

 

100 Z 250

P ^P



^Z ^ ²^.⁵





²^.⁵



1 P Z  ¹^ ⁰^.⁹⁹³⁸

54

(55)

c. P(900 < x < 1.100) =

= =

=



 



 

 

100

000 . 1 100 . 1 100

000 . 1 100

000 . 1

900 x

P

100 100

P  Z  ^P



^¹ ^ ^Z ^ ¹





^Z ^¹

 

^ ^P ^Z ^ ^¹



P = 0.8413 - 0.1587

= 0.6826 = 68.26 %

55

(56)

Soal

1. Diketahui distribusi normal : dgn  = 40 dan  = 5 Tentukan :

a. P(x < 35) b. P(x > 45)

c. P(20 < x < 50) d. P(x < k) = 0.05 e. P(x > k) = 0.2578

56

(57)

2. Diberikan distribusi normal dengan  = 40 dan

 = 6, dapatkan luasan : a). Di bawah 32

b). Di atas 27

c). Antara 42 dan 51

d). Cari suatu nilai k sedemikian hingga luasan di bawah k = 45%

e). Cari suatu nilai k sedemikian hingga luasan di

57

(58)

3. Sebuah perusahaan alat listrik memproduksi bolam yang umurnya berdistribusi normal dengan mean 800 jam dan standart deviasinya 40 jam. Hitung

probabilitas sebuah bolam hasil produksinya akan berumur antara 778 dan 834 jam.

58

(59)

4. Kekuatan batang baja yang dibuat dengan proses tertentu diketahui kira-kira mendekati distribusi normal dengan mean 24 dan deviasi standart 3.

Para konsumen menghendaki bahwa paling sedikit 95% batang tersebut mempunyai kekuatan lebih 20.

Apakah kualitas batang baja tersebut sesuai dengan ketetapan konsumen.

59

(60)

5. Ukuran mata bor untuk komponen tertentu yang digunakan dalam proses perakitan (assembly) merupakan dimensi (karakteristik) kualitas yang penting. Dari pengamatan tiap jam berukuran 4 sampel selama 25 jam diperoleh : = 4,3 mm, s = 0,243 mm. Batas spesifikasi mata bor 4,4  0,2 mm. Biaya scrap dan rework tiap unit masing-masing $ 2,40 dan $ 0,75. Produksi 1200 unit.

a). Taksir parameter produk yang discrap & rework?

b). Taksir biaya total scrap dan rework tiap hari?

c). Jika rata-rata proses digeser 4,5 mm, jelaskan

dampaknya pada persentase produk yang discrap dan rework serta biayanya?

60

x

(61)

61

6. Tinjau proses pembuatan coil. Diambil sampel berukuran 5 buah tiap jam dan dicatat tingkat resistensinya (ohm)nya.

Data diberikan pada Tabel 1.

Andaikan spesifikasi proses 21  3 ohm

a. Tentukan persentase produk cacat (tidak memenuhi) spesifikasi bila tingkat resistensi berdistribusi normal.

b. Andaikan tiap hari diproduksi 10000 coil dan coil dengan

(62)

62

Tabel 1 Sampel

ke

Data Sampel

ke

Data

1 2 3 4 5 6 7 8 9 10

11

20,22,21,23,22 19,18,20,20,22 25,18,20,17,22 20,21,22,21,21 19,24,23,22,20 22,20,18,18,19 18,20,19,18,20 20,18,23,20,21 21,20,24,23,22 21,19,20,20,20 20,20,23,22,20

21,6 19,8 20,4 21,0 21,6 19,4 19,0 20,4 22,0 20,0 21,0

14 15 16 17 18 19 20 21 22 23 24

20,21,22,21,22 20,24,24,23,23 21,20,24,20,21 20,18,18,20,20 20,24,22,23,23 20,19,23,20,19 21,21,21,24,22 23,22,22,20,22 21,18,18,17,19 21,24,24,23,23 20,22,21,21,20

21,2 22,8 21,2 19,2 22,4 20,2 22,0 21,8 18,6 23,0 20,8

x x

(63)

63

Tabel 1



mean = 20,816



Standar deviasi = 1,188725

(64)

64

Tabel 2

Mean = 37,175

Standar deviasi = 1,678933

(65)

65

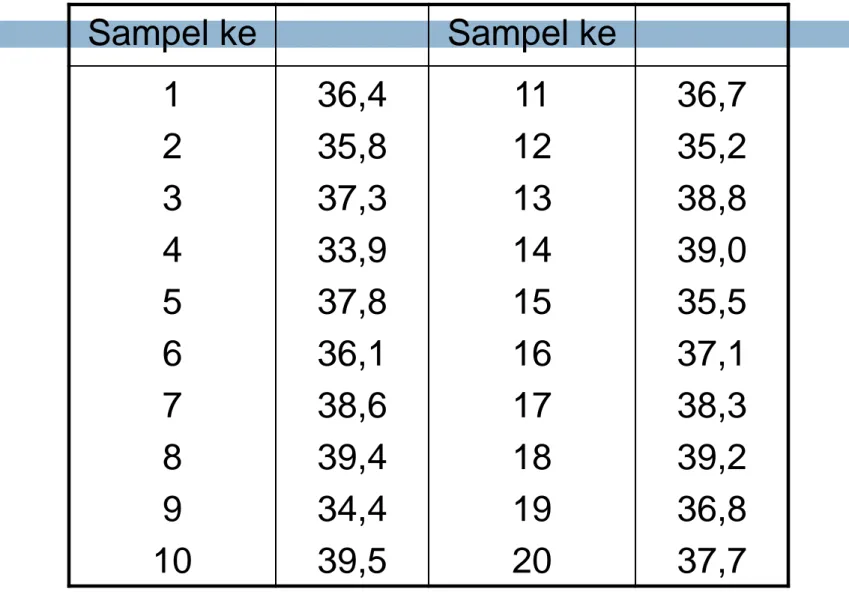
7. Tingkat ketebalan magnetic coating pada proses pem- buatan audio tape merupakan karakteristik kualitas penting. Suatu sampel berukuran 4 unit dipilih tiap jam dan tingkat ketebalannya diukur dengan instrument optik (Tabel 2). Batas-batas spesifikasi proses 38  4,5.

Jika tingkat ketebalan proses coating kurang dari batas spesifikasi maka digunakan untuk produk lain dengan melalui proses lain.

a). Berapa persen produk tidak memenuhi batas spesifikasi?

b). Jika rata-rata proses bergeser menjadi 37,8 berapa persen produk akan diterima?

(66)

Tabel 2

66 Sampel ke Sampel ke

1 2 3 4 5 6 7 8 9

36,4 35,8 37,3 33,9 37,8 36,1 38,6 39,4 34,4

11 12 13 14 15 16 17 18 19

36,7 35,2 38,8 39,0 35,5 37,1 38,3 39,2 36,8

(67)

THE GOLDEN TRIANGEL