Nining Iswahyuni Dosen Pembimbing : Drs. M. Setijo Winarko, M.Si Drs. I Gst Ngr Rai Usadha, M.Si

(1)

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT TEKNOLOGI SEPULUH NOPEMBER SURABAYA

2013

Nining Iswahyuni 1209 100 092

Dosen Pembimbing : Drs. M. Setijo Winarko, M.Si Drs. I Gst Ngr Rai Usadha, M.Si

(2)

(3)

LATAR BELAKANG

Pemodelan

matematika

Penyakit

menular pada

masyarakat

Model

epidemik SIS

Analisa

kualitatif pada

model

Bifurkasi mundur yang

dianalisa dengan fungsi

matematis yaitu fungsi

(4)

Lanjutan…

LATAR BELAKANG

Penelitian sebelumnya :



Eksistensi Bifurkasi Mundur pada Model

Penyebaran Penyakit Makroparasitis (Djasuli,

2009).

(5)

RUMUSAN MASALAH

Bagaimana perubahan titik kesetimbangan dan

kestabilan populasi pada sistem epidemik apabila

diberikan tindakan pengobatan.

(6)

BATASAN MASALAH



Model epidemik yang dianalisis merupakan model tipe SIS

yang bersifat deterministik atau model kompartemen.



Model epidemik SIS dianalisis dengan tindakan

pengobatan yang dinyatakan sebagai fungsi pengobatan

yaitu T(I).



Populasi antara S dan I adalah populasi yang tertutup (laju

kelahiran dan kematian sama).



Individu yang baru lahir dikelompokkan dalam kelompok

(7)

TUJUAN

Mengetahui perilaku dinamik dari sistem

epidemik dengan tindakan pengobatan.

MANFAAT



Adanya pengetahuan bagi peneliti mengenai sifat-sifat

kualitatif dari model epidemik dengan tipe SIS,



Sebagai rujukan untuk melakukan penelitian yang sejenis,

serta



Sebagai bahan pertimbangan bagi pihak terkait dalam

menangani penyebaran penyakit menular bertipe SIS

dengan tindakan pengobatan.

(8)

(9)

Penelitian Terkait



(Lestari, 2012) dalam Tugas Akhir yang berjudul

“Eksistensi Bifurkasi Mundur pada Model Penyebaran

Penyakit Menular dengan Vaksinasi”, menganalisis

terjadinya bifurkasi mundur dari model epidemik SIS

dengan vaksinasi.



Artikel oleh (Xue, Wang, 2012) dengan model penyebaran

penyakit bertipe SIR, menganalisis terjadinya bifurkasi

mundur pada model epidemik dengan daya penularan

pada individu yang terinfeksi (infected) dan masa

kekebalan dan pengobatan.

(10)

Model Epidemik SIS dengan Pengobatan

Model penyebaran penyakit menular tipe SIS dengan pengobatan : 𝑑𝑑

𝑑𝑑 = Λ − 𝜇𝑑 − 𝛽𝑑𝛽 + 𝛾𝛽 + 𝑇(𝛽) 𝑑𝛽

𝑑𝑑 = 𝛽𝑑𝛽 − 𝜇 + 𝛼 + 𝛾 𝛽 − 𝑇(𝛽) dengan

S : populasi yang rentan terhadap penyakit menular (susceptible). I : populasi pengidap penyakit menular (infected).

Λ : laju rekruitmen dari populasi (laju kelahiran dan laju imigrasi). 𝜇 : laju kematian alami dari populasi.

𝛼 : laju kematian yang berhubungan dengan penyakit dengan 𝛼 > 0.

𝛽 : koefisien yang menyatakan tingkat penyakit (dipengaruhi musim, besar kecilnya kontak antara S dan I, tingkat mobilisasi pengidap penyakit).

𝛾 : laju kesembuhan alami dari individu yang terinfeksi. 𝑇(𝛽) : fungsi matematis dari pengobatan.

(11)

Fungsi Matematis dari Pengobatan

Diberikan fungsi pengobatan : 𝑇 𝛽 = �𝑟𝛽,_𝑘, 0 ≤ 𝛽 ≤ 𝛽_{𝛽 > 𝛽} 0

0

dengan 𝑘 = 𝑟𝛽₀

r : konstanta positif

𝛽₀ : tingkat infektif pada sistem pelayanan kesehatan yang mencapai kapasitas tertentu.

Diasumsikan bahwa besarnya pengobatan berbanding lurus dengan jumlah individu yang sakit. Dengan catatan bahwa jumlah individu yang sakit tidak melebihi jumlah maksimal dari pengobatan 𝛽₀. Jumlah maksimal dari pengobatan adalah nol. Tetapi ketika jumlah individu yang sakit lebih besar dari jumlah maksimal dari pengobatan 𝛽₀ maka besarnya pengobatan berupa suatu konstanta.

(12)

Bilangan Reproduksi Dasar (

_𝑅

₀

)

Definisi :

Bilangan reproduksi dasar ( 𝑅0 ) merupakan bilangan yang

menyatakan banyaknya rata-rata individu infektif sekunder akibat tertular individu infektif primer yang berlangsung di dalam populasi susceptible.

Titik kesetimbangan pada model epidemik berpengaruh pada kondisi 𝑅0 antara lain :

 Jika 𝑅₀ < 1 maka tidak terjadi penyebaran penyakit menular atau

penyakit akan menghilang.

 Jika 𝑅₀ > 1 maka terjadi penyebaran penyakit menular atau

penyakit akan meningkat menjadi wabah.

(13)

Bifurkasi

Definisi :

Perubahan kualitatif yang meliputi perubahan stabilitas dan perubahan banyaknya titik kesetimbangan karena perubahan nilai-nilai parameter.

Ada dua jenis bifurkasi dalam model penyebaran penyakit menular yaitu :

 Bifurkasi Maju

Fenomena bifurkasi maju terjadi pada saat 𝑅0 > 1 dimana hanya

ada satu titik kesetimbangan endemik.

 Bifurkasi Mundur

Fenomena bifurkasi mundur terjadi pada saat 𝑅₀ < 1 mempunyai dua titik kesetimbangan endemik.

(14)

Diagram Bifurkasi

Garis

putus-putus

menunjukkan

titik

kesetimbangan endemik yang tidak stabil dan garis

yang padat menunjukkan titik kesetimbangan

endemik lokal yang stabil.

(15)

Titik Kesetimbangan

Diberikan sistem persamaan diferensial non linear di bawah ini : 𝑑𝑑

𝑑𝑑 = 𝑓(𝑑, 𝑦) 𝑑𝑦

𝑑𝑑 = 𝑔 𝑑, 𝑦

Sebuah titik (𝑑̅₀, 𝑦�₀)merupakan titik kesetimbangan dari persamaan di atas jika memenuhi :

𝑓(𝑑̅0, 𝑦�0) = 0 dan 𝑔(𝑑̅0, 𝑦�0) = 0

Turunan suatu konstanta sama dengan nol, sehingga sepasang fungsi konstan 𝑑 𝑑 ≡ 𝑑̅₀ dan 𝑦 𝑑 ≡ 𝑦�₀ merupakan penyelesaian titik kesetimbangan dari persamaan di atas.

(16)

Kestabilan di sekitar Titik Kesetimbangan

Diberikan sistem persamaan diferensial autonomous di bawah ini : 𝑑𝑑

𝑑𝑑 = 𝑑̇ = 𝑓 𝑑 ∀𝑑 ∈ ℝ𝑛

Titik 𝑑̅ 𝑑 = 𝑑0 disebut titik kesetimbangan jika 𝑓 𝑑0 = 0.

Kestabilan asimtotis lokal pada titik kesetimbangan ditentukan oleh tanda pada bagian real dari akar-akar kharakteristik sistem pada matriks Jacobian yang dihitung di sekitar titik kesetimbangan.

(17)

Definisi

Diberikan matriks koefisien konstan J berukuran n x n dan sistem persamaan diferensial biasa homogen 𝑑̇ = 𝐽𝑑, 𝑑 0 = 𝑑₀, 𝑑 ∈ ℝ𝑛 . Suatu vektor tak nol x di dalam ℝ𝑛_{disebut vektor eigen dari J jika}

untuk suatu skalar 𝜆 berlaku :

𝐽𝑑 = 𝜆𝑑

Nilai skalar λ dinamakan nilai eigen dari J.

Untuk mencari nilai λ dari J, maka sistem persamaan dapat ditulis sebagai berikut :

𝐽 − 𝜆𝛽 𝑑 = 0

dengan I adalah matriks identitas. Sistem persamaan mempunyai solusi nontrivial jika dan hanya jika

𝑃 𝜆 = 𝐽 − 𝜆𝛽 = 0

(18)

Teorema

Diberikan matriks Jacobian :

𝐽 = 𝜕𝑓 𝜕𝑑 𝑑𝑜, 𝑦0 𝜕𝑓 𝜕𝑦 𝑑𝑜, 𝑦0 𝜕𝑔 𝜕𝑑 𝑑𝑜, 𝑦0 𝜕𝑔 𝜕𝑦 𝑑𝑜, 𝑦0

Titik kesetimbangan (x�0, y�0) stabil asimtotis jika dan hanya jika nilai

kharakteristik dari matriks Jacobian mempunyai tanda negatif pada bagian realnya. Titik kesetimbangan (x�0, y�0) tidak stabil jika sedikitnya

satu dari nilai kharakteristik dari matriks Jacobian mempunyai tanda positif pada bagian realnya.

(19)

METODE PENELITIAN

Identifikasi dan Studi Literatur

Mengkaji Model Epidemik SIS dengan Pengobatan

Melakukan Analisa Kualitatif pada Model Epidemik

Melakukan Simulasi Numerik

(20)

(21)

Model Epidemik SIS dengan Pengobatan

Model epidemik tipe SIS dengan pengobatan mempunyai asumsi-asumsi sebagai berikut :

 Populasi dibagi menjadi dua kelompok yaitu :

S adalah populasi susceptible dan I adalah populasi infected.

 Diasumsikan Λ adalah laju kelahiran yang sama dengan laju kematian.

Jumlah populasi yang lahir dalam populasi tiap satuan waktu selalu konstan. Jumlah populasi yang lahir tersebut akan memasuki kelompok S (susceptible).

 𝛽𝑑𝛽 adalah laju besarnya populasi yang terinfeksi dimana 𝛽 adalah

koefisien transmisi yang menunjukkan tingkat kontak antara kelompok S dan I sehingga terjadi penularan penyakit.

 Populasi infected sembuh dan kembali menjadi kelompok susceptible

dengan laju 𝛾.

 𝛼𝛽 adalah laju kematian yang berhubungan dengan penyakit pada

(22)

 Laju kematian pada setiap populasi adalah sama, yaitu 𝜇 . Jadi

banyaknya kematian pada populasi 𝑑 dan 𝛽 masing - masing sebesar 𝜇𝑑 dan 𝜇𝛽.

 𝑇(𝛽) adalah suatu fungsi matematis untuk menyatakan tingkat

pengobatan pada populasi infected.

Dari asumsi-asumsi tersebut didapatkan diagram kompartemen sebagai berikut :

(23)

Dari diagram kompartemen diperoleh model epidemik tipe SIS dengan pengobatan 𝑑𝑑 𝑑𝑑 = Λ − 𝜇𝑑 − 𝛽𝑑𝛽 + 𝛾𝛽 + 𝑇 𝛽 (1) 𝑑𝑑 𝑑𝑑 = 𝛽𝑑𝛽 − 𝜇 + 𝛼 + 𝛾 𝛽 − 𝑇 𝛽 (2)

(24)

Daerah Penyelesaian

Misalkan daerah penyelesaian Ω didefinisikan sebagai berikut :

Ω = {(𝑑, 𝛽) ∈ 𝑅₊2|𝑑 + 𝛽 = 𝑁, 𝑑 ≥ 0, 𝛽 ≥ 0} dan 𝑁 0 = 𝑁₀ > 0.

Dari persamaan (1) dan (2) diperoleh

𝑑𝑁 𝑑𝑑 = 𝑑𝑑 𝑑𝑑 + 𝑑𝛽 𝑑𝑑 _{= Λ − 𝜇𝑁 − 𝛼𝛽} (3) Penyelesaian dari persamaan (3) adalah

𝑁(𝑑) = Λ_{𝜇 −} 𝐶_{𝜇 𝑒}−𝜇𝑑 Sehingga _lim 𝑑⟶∞𝑁 𝑑 = lim𝑑⟶∞ Λ 𝜇 − 𝐶 𝜇 𝑒−𝜇𝑑 = Λ 𝜇

(25)

Titik Kesetimbangan Model Epidemik SIS

Titik kesetimbangan diperoleh dengan mengambil 𝑑𝑑

𝑑𝑑 = 0 dan 𝑑𝑑

𝑑𝑑 = 0.

Dengan mensubstitusi fungsi pengobatan ke dalam persamaan (1) dan (2) sehingga diperoleh Jika 0 < 𝛽 ≤ 𝛽₀ Λ − 𝜇𝑑 − 𝛽𝑑𝛽 + 𝛾𝛽 + 𝑟𝛽 = 0 (4) 𝛽𝑑𝛽 − 𝜇 + 𝛼 + 𝛾 + 𝑟 𝛽 = 0 (5) Jika 𝛽 > 𝛽₀ Λ − 𝜇𝑑 − 𝛽𝑑𝛽 + 𝛾𝛽 + 𝑘 = 0 (6) 𝛽𝑑𝛽 − 𝜇 + 𝛼 + 𝛾 𝛽 − 𝑘 = 0 (7)

(26)

Titik Kesetimbangan Bebas Penyakit

Titik kesetimbangan bebas penyakit diperoleh pada saat 𝛽 = 0, yang artinya tidak ada individu pada kelompok I yang dapat menyebarkan penyakit.

Dari persamaan (4) diperoleh Λ − 𝜇𝑑 − 𝛽𝑑𝛽 + 𝛾𝛽 + 𝑟𝛽 = 0 Λ − 𝜇𝑑 = 0

𝑑 = Λ_𝜇

(27)

Titik Kesetimbangan Endemik

Titik kesetimbangan endemik adalah suatu keadaan dimana 𝛽∗ _{≠ 0 yang} menunjukkan bahwa terdapat individu pada kelompok I yang dapat menyebarluaskan penyakit dan menyebabkan endemik.

Dari persamaan (4) diperoleh 𝛽𝑑𝛽 − 𝜇 + 𝛼 + 𝛾 + 𝑟 𝛽 = 0 𝛽 = 0 atau 𝑑∗ ₌ 𝜇+𝛼+𝛾+𝑟

𝛽

Dari persamaan (5) diperoleh

Λ − 𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟_𝛽 − 𝛽 𝜇 + 𝛼 + 𝛾 + 𝑟_𝛽 𝛽 + 𝛾𝛽 + 𝑟𝛽 = 0 𝛽∗ = 𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟 (𝑅_{𝛽 𝜇 + 𝛼} 0 − 1)

Jadi titik kesetimbangan endemik adalah

𝐸∗ = 𝑑∗, 𝛽∗ = 𝜇 + 𝛼 + 𝛾 + 𝑟_𝛽 ,𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟 𝑅_{𝛽 𝜇 + 𝛼} 0 − 1

(28)

Bilangan Reproduksi Dasar

Bilangan reproduksi dasar merupakan bilangan yang menyatakan besar kecilnya populasi pengidap penyakit. Pada model epidemik SIS ini diperoleh nilai 𝑅₀ dari persamaan (5)

𝛽∗ = 𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟

Λ𝛽

𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟 − 1 𝛽 𝜇 + 𝛼

Maka bilangan reproduksi dasar untuk model epidemik SIS adalah

𝑅₀ = Λ𝛽

(29)

Jika 𝑅₀ > 1, maka persamaan (4) dan (5) memuat penyelesaian positif tunggal. Sekarang, ditinjau persamaan (6) dan (7). Dari persamaan (6) diperoleh

_{Λ − 𝜇𝑑 − 𝛽𝑑𝛽 + 𝛾𝛽 + 𝑘 = 0}

𝑑 = Λ+𝛾𝑑+𝑘_{(𝜇+𝛽𝑑)} (8)

Persamaan (8) disubstitusikan ke persamaan (7) diperoleh 𝛽𝑑𝛽 − 𝜇 + 𝛼 + 𝛾 𝛽 − 𝑘 = 0 𝐴𝛽2 + 𝐵𝛽 + 𝐶 = 0 (9) dengan 𝐴 = 𝛽 𝜇 + 𝛼 𝐵 = 𝜇2 + 𝜇𝛼 + 𝜇𝛾 − 𝛽Λ 𝐶 = 𝑘𝜇

(30)

Agar persamaan (6) dan (7) mempunyai penyelesaian positif, yaitu S, I > 0 , maka persamaan (9) haruslah definit positif, yaitu A > 0 dan ∆ < 0. Jika 𝐵 ≥ 0, maka persamaan (9) tidak mempunyai penyelesaian positif.

Diskriminan dari persamaan (9) yaitu

∆= −𝑅₀𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟 + 𝜇 𝜇 + 𝛼 + 𝛾 2 − 4𝑘𝜇𝛽 𝜇 + 𝛼 Jika ∆ ≥ 0, maka diperoleh

𝑅₀ ≤ 1 − _{𝜇 𝜇+𝛼+𝛾+𝑟}𝜇𝑟 − 2_{𝜇 𝜇+𝛼+𝛾+𝑟}𝑘𝜇𝛽 𝜇+𝛼 (10) atau

𝑅₀ ≥ 1 − _{𝜇 𝜇+𝛼+𝛾+𝑟}𝜇𝑟 + 2_{𝜇 𝜇+𝛼+𝛾+𝑟}𝑘𝜇𝛽 𝜇+𝛼 =: 𝑝₀ (11)

Jika B < 0, maka diperoleh

(31)

�𝐵 < 0_{∆ ≥ 0 ⇔ 𝑅}₀ ≥ 1 − _{𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟 + 2}𝜇𝑟 _{𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟 =: 𝑝}𝑘𝜇𝛽 𝜇 + 𝛼 ₀

Jadi persamaan (9) mempunyai dua penyelesaian positif jika B < 0 𝛽₁ = _{2𝛽 𝜇+𝛼}−𝐵− ∆ dan 𝛽₂ = _{2𝛽 𝜇+𝛼}−𝐵+ ∆

Tetapkan himpunan 𝑑𝑖 = Λ+k+𝛾𝑑_{(𝜇+𝛽𝑑}_𝑖₎𝑖 dan 𝐸𝑖 = (𝑑𝑖, 𝛽𝑖) untuk i = 1, 2. Jika

𝛽1 ≥ 𝛽0, maka diperoleh

_{2𝛽 𝜇+𝛼}−𝐵− ∆ > 𝛽₀ (13) −𝐵 − ∆ > 2𝛽 𝜇 + 𝛼 𝛽₀ (14) 𝐵 + 2𝛽 𝜇 + 𝛼 𝛽₀ < 0, karena ∆ ≥ 0 (15)

(32)

(𝐵 + 2𝛽 𝜇 + 𝛼 𝛽₀)2> ∆

(17)

Dengan mensubstitusi nilai ∆ dan B, maka diperoleh

𝑅₀ < 1 + 𝛽 𝜇+𝛼 𝑑0

𝜇 𝜇+𝛼+𝛾+𝑟 =: 𝑝2 (18)

Oleh karena itu, 𝛽₁ > 𝛽₀ ada jika dan hanya jika persamaan (16) dan (18) berlaku. Jika 𝑝₂ ≤ 𝑅₀ ≤ 𝑝₁ maka diperoleh 𝛽₁ ≤ 𝛽₀. Untuk pernyataan yang sama bahwa 𝛽₂ > 𝛽₀ berlaku atau 𝑝₂ < 𝑅₀ ≤ 𝑝₁. Sehingga 𝛽₂ ≤ 𝛽₀ jika 𝑅₀ ≤ min {𝑝₁, 𝑝₂}.

(33)

Kestabilan Lokal Titik Kesetimbangan

Kestabilan model ditentukan oleh nilai eigen matriks Jacobian dari sistem (4) dan (5).

𝐽 = −𝜇 − 𝛽𝛽_𝛽𝛽 _{𝛽𝑑 − 𝜇 + 𝛼 + 𝛾 + 𝑟}−𝛽𝑑 + 𝛾 + 𝑟

 Kestabilan Lokal Titik Kesetimbangan Bebas Penyakit (𝐸₀)

_𝐽(𝐸₀_{) =} −𝜇 −𝛽

Λ

𝜇 + 𝛾 + 𝑟

0 𝛽Λ_𝜇 − 𝜇 + 𝛼 + 𝛾 + 𝑟

diperoleh nilai eigen sebagai berikut

_𝜆₁ _{= −𝜇 , 𝜆}₁ _{< 0}

𝜆₂ = 𝛽 Λ_𝜇 − 𝜇 + 𝛼 + 𝛾 + 𝑟

Untuk 𝜆₂ = 𝛽Λ_𝜇 − 𝜇 + 𝛼 + 𝛾 + 𝑟 belum dapat ditentukan tandanya (dapat bernilai positif atau negatif).

(34)

Berdasarkan nilai eigen dapat dianalisa sebagai berikut :

_𝜆₂_{akan bernilai negatif jika}

𝛽 Λ_{𝜇 − 𝜇 + 𝛼 + 𝛾 + 𝑟 < 0} atau 𝛽Λ 𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟 < 1 dengan 𝛽Λ 𝜇 𝜇+𝛼+𝛾+𝑟 = 𝑅0

Dari nilai 𝑅₀, maka didapatkan kestabilan untuk titik kesetimbangan bebas penyakit sebagai berikut :

 Jika 𝑅₀ < 1, maka didapatkan nilai eigen 𝜆₁ < 0 dan 𝜆₂ < 0 sehingga titik

kesetimbangan bebas penyakit stabil asimtotik.

 Jika 𝑅₀ > 1, maka didapatkan nilai eigen 𝜆₁ < 0 dan 𝜆₂ > 0 sehingga titik

(35)

 Kestabilan Lokal Titik Kesetimbangan Endemik (𝐸∗) 𝐽(𝐸∗_{) =} −𝜇 − 𝛽 𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟 𝑅0− 1 𝛽 𝜇 + 𝛼 −𝛽 𝜇 + 𝛼 + 𝛾 + 𝑟 𝛽 + 𝛾 + 𝑟 𝛽 𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟 𝑅_{𝛽 𝜇 + 𝛼} 0− 1 𝛽 𝜇 + 𝛼 + 𝛾 + 𝑟_𝛽 − 𝜇 + 𝛼 + 𝛾 + 𝑟

diperoleh nilai eigen sebagai berikut 𝜆₁ = − 𝜇 + 𝜇 𝜇+𝛼+𝛾+𝑟 𝑅0−1

𝜇+𝛼

𝜆₂ = 𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟 𝑅₀ − 1

Dengan menggunakan tabel Routh-Hurwitz diperoleh

untuk 1 > 0, 𝑎₁ > 0, 𝑏₁ > 0 menyebabkan titik kesetimbangan endemik stabil karena kolom pertama pada tabel mempunyai tanda yang sama (bernilai positif).

(36)

Kestabilan model untuk titik kesetimbangan 𝐸1 dan 𝐸2 ditentukan oleh nilai eigen dari

sistem (1) dan (2).

𝐽 = −𝜇 − 𝛽𝛽_𝛽𝛽 𝑖 −𝛽𝑑𝑖 + 𝛾

𝑖 𝛽𝑑𝑖 − 𝜇 + 𝛼 + 𝛾 dengan i = 1, 2

 Kestabilan Lokal Titik Kesetimbangan (𝐸₁)

𝐽 𝐸1 = −𝜇 − 𝛽𝛽_𝛽𝛽 1 −𝛽𝑑1 + 𝛾 1 𝛽𝑑1− 𝜇 + 𝛼 + 𝛾

𝜆₁ = − 𝜇 + 𝛽𝛽₁ − 𝛽𝑑₁ + 𝜇 + 𝛼 + 𝛾

𝜆2 = −𝜇𝛽𝑑1 + 𝜇 𝜇 + 𝛼 + 𝛾 + 𝛽𝛽1 𝜇 + 𝛼

Selanjutnya determinan dari matriks 𝐽 𝐸₁ adalah _{det 𝐽 𝐸}₁ _{= − ∆}.

Titik kesetimbangan _𝐸₁ _{= 𝑑}₁_{, 𝛽}₁ merupakan titik pelana (saddle point) karena mempunyai nilai eigen real yang berbeda tanda, _{det 𝐽 𝐸}₁ _{< 0}, dan titik kesetimbangan ini bersifat tidak stabil.

(37)

 Kestabilan Lokal Titik Kesetimbangan (𝐸₂)

_{𝐽 𝐸}₂ ₌ −𝜇 − 𝛽𝛽2 −𝛽𝑑2 + 𝛾

𝛽𝛽2 𝛽𝑑2 − 𝜇 + 𝛼 + 𝛾

𝜆₁ = − 𝜇 + 𝛽𝛽₂ − 𝛽𝑑₂ + 𝜇 + 𝛼 + 𝛾

𝜆₂ = −𝜇𝛽𝑑₂ + 𝜇 𝜇 + 𝛼 + 𝛾 + 𝛽𝛽₂ 𝜇 + 𝛼

Selanjutnya determinan dari matriks det 𝐽 𝐸₂ adalah det 𝐽 𝐸₂ = ∆. Titik Kesetimbangan 𝐸₂ = 𝑑₂, 𝛽₂ adalah focus, simpul (node point), atau

pusat (center) karena mempunyai nilai eigen real yang berbeda tanda dan det 𝐽 𝐸₂ > 0.

_{𝑑𝑟𝑎𝑡𝑒 𝐽 𝐸}₂ = − _{2𝜇 𝜇+𝛼}2𝜇+𝛼 ( ∆ − 𝐷)

(38)

Misalkan ∆ = 𝐷 diperoleh 𝑘 = _{4𝛽𝜇 𝜇+𝛼}𝐵2−𝐷2 . Kestabilan dari titik kesetimbangan 𝐸₂ yaitu

i. _𝐸₂ stabil jika salah satu memenuhi D < 0 atau �_{𝑘 <}𝐷 > 0𝐵2−𝐷2

4𝛽𝜇(𝜇+𝛼)

ii. _𝐸₂ tidak stabil jika

�_{𝑘 >}𝐷 > 0𝐵2−𝐷2 4𝛽𝜇(𝜇+𝛼)

(39)

Kurva Bifurkasi

Untuk menggambar kurva bifurkasi diasumsikan 𝛽 sebagai parameter dengan _{𝜇, 𝛾, 𝛼, 𝑟, 𝛽}₀ _{konstan. 𝛽 dipandang sebagai} parameter untuk bifurkasi karena 𝛽 menentukan besar kecilnya penyebaran penyakit.

Diferensial implisit dari persamaan (9) terhadap 𝛽 adalah 𝑑𝛽

𝑑𝛽 =

𝛽 Λ − 𝛽 𝜇 + 𝛼 2𝐴𝛽 + 𝐵

Kemiringan kurva bifurkasi didapatkan sebagai berikut :

i. Jika 𝑑𝑑

𝑑𝛽 > 0, maka kurva bifurkasi mempunyai kemiringan

positif. Hal ini menyebabkan titik kesetimbangan endemik stabil asimtotik dan terjadi bifurkasi maju.

ii. Jika _𝑑𝛽𝑑𝑑 < 0, maka kurva bifurkasi mempunyai kemiringan

negatif. Hal ini menyebabkan ada titik kesetimbangan endemik tidak stabil dan stabil serta terjadi bifurkasi mundur.

(40)

Didapatkan diagram bifurkasi pada model eidemik SIS dengan pengobatan sebagai berikut :

(41)

Simulasi dan Interpretasi

Dari persamaan (4) didapatkan persamaan _𝑅₀ yang mengandung I 𝛽𝛽2 + 𝛾+𝑟−𝛽𝛽_Λ 𝛽 + 1 = _𝑅1

0 (19) dengan _{𝑋 = 𝛽 ; 𝑌 =} 𝛾+𝑟−𝛽𝛽

Λ ; 𝑍 = 1

Diagram Bifurkasi Mundur Diagram Bifurkasi Maju

(42)

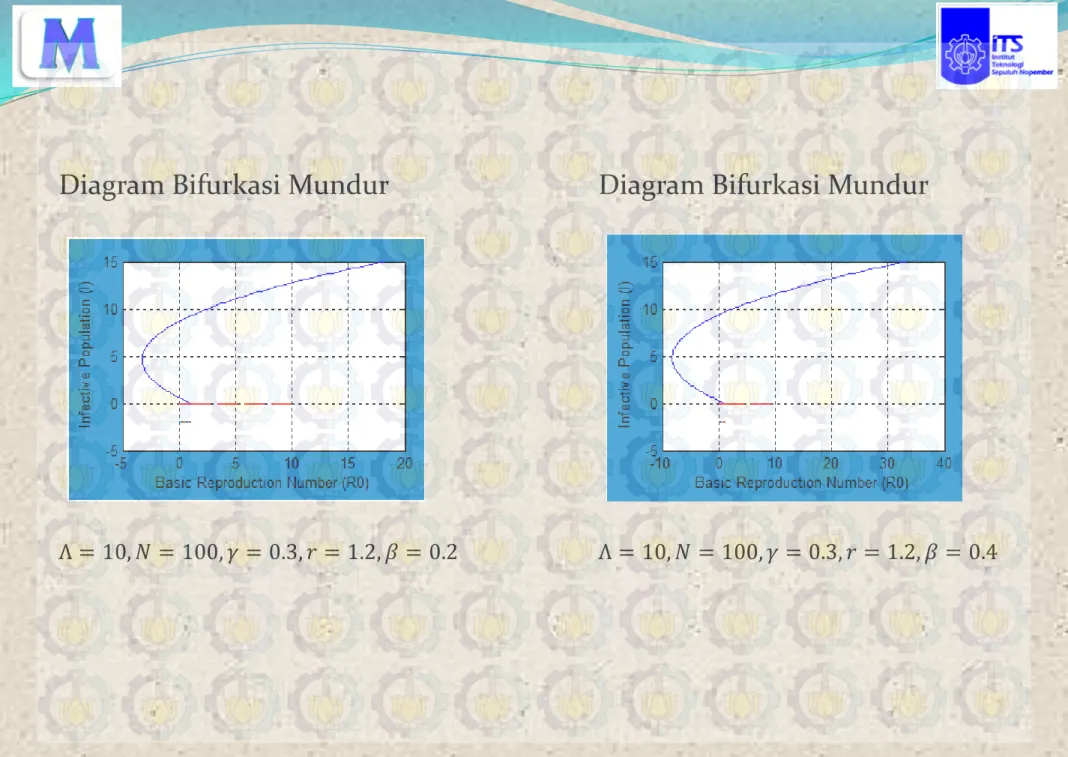
Diagram Bifurkasi Mundur Diagram Bifurkasi Mundur

(43)

KESIMPULAN

1. Bilangan reproduksi dasar dari model penyebaran penyakit menular bertipe SIS dengan tindakan pengobatan adalah

𝑅0 = _{𝜇 𝜇 + 𝛼 + 𝛾 + 𝑟}Λ𝛽

Titik kesetimbangan bebas penyakit adalah stabil asimtotik jika

R₀ < 1 dan tidak stabil jika R₀ > 1. Hal ini menunjukkan bahwa tidak terjadi infeksi ketika R₀ < 1 .

2. Bifurkasi mundur terjadi pada saat R₀ = 1 dimana terdapat dua titik kesetimbangan endemik jika R₀ < 1. Fenomena terjadinya bifurkasi mundur menunjukkan bahwa pada saat R₀ < 1 kapasitas pengobatan yang diberikan kurang efektif sehingga menyebabkan masih ada individu yang terinfeksi dan penyakit akan menjadi endemik.

(44)

SARAN

Dalam Tugas Akhir ini dianalisa eksistensi bifurkasi

mundur pada model penyebaran penyakit menular SIS

dengan memberikan tindakan pengobatan. Penelitian

selanjutnya disarankan untuk menganalisa terjadinya

bifurkasi pada model penyebaran penyakit menular

dengan menambahkan kompartemen pada populasi.

(45)

DAFTAR PUSTAKA

[1] Zhou, Yicang. (2003). “Stability Of Periodic Solutions For An SIS Model With Pulse Vaccination”. Mathematical and Computer Modelling Vol. 38. Hal. 299 - 308.

[2] Wang, Xueying. (2010). “SAMSI Undergraduate Workshop Spring 2010”.

[3] Djasuli, M. (2009). “Eksistensi Bifurkasi Mundur pada Model

Penyebaran Penyakit Makroparasitis”. Institut Teknologi Sepuluh Nopember Surabaya, Thesis S2 Jurusan Matematika.

[4] Li, Xue-Zhi, Li, Wen-Sheng, Ghosh, Mini. (2009). “Stability And Bifurcation Of An SIS Epidemic Model With Treatment”. Chaos, Solitons, and Fractals Vol. 42. Hal. 2822 - 2832.

[5] Wang, Wendi. (2006). “Backward Bifurcation Of An Epidemic

Model With Treatment”. Mathematical Biosciences Vol. 201. Hal.

(46)