A. Integral Tak Tentu

(1)

Materi SMK Kelas XII

15. INTEGRAL (ANTI DIVERENSIAL)

1) Rumus-Rumus Integral Tak Tentu Fungsi Aljabar dan Trigonometri 1.  dx = x + c

2.  a dx = a  dx = ax + c 3.  xn dx = _n1_₁

x

n1+ c 4.  sin ax dx = – _a1 cos ax + c 5.  cos ax dx = _a1 sin ax + c 6.  sec2ax dx = _a1tan ax + c

7.  [ f(x)  g(x) ] dx =  f(x) dx  g(x) dx

Catatan

1. Identitas trigonometri yang biasa digunakan a. 2sinAcosB = sin(A + B) + sin(A – B) b. –2sinAsinB = cos(A + B) – cos(A – B) c. sin2A =₂1

{

1



cos

2

A

}

d. cos2A =1₂

{

1



cos

2

A

}

e. sin 2A = 2sin A  cos A

2. Teknik Penyelesain Bentuk Integran

Misalkan u(x) dan v(x) masing-masing adalah fungsi dalam variabel x, maka metode pengintegralan yang bisa digunakan adalah:

a. Metode substitusi

Jika bentuk integran :  u v dx , dengan u dan v memiliki hubungan, yaitu v dx = du b. Metode Parsial dengan TANZALIN

(2)

SOAL PENYELESAIAN 1. UN 2011 PAKET 12

Hasil



 



dx x x

x 1 9 3

3 2

2 = …

a. 2 3x2 9x1c b. 1₃ 3x2 9x1c c. ₃2 3x2 9x1c d. ₂1 3x2 9x1c e. ₂3 3x2 9x1c Jawab : c

2. UN 2011 PAKET 46 Hasil



6x 3x2 5dx = … a. (6x2 5) 6x2 5c

3 2

b. ₃2(3x25) 3x2 5c c. ₃2(x2 5) x25c d. ₂3(x2 5) x25c e. ₂3(3x25) 3x2 5c Jawab : b

3. UN 2009 PAKET A/B

Hasil

dx

x





4

2

3

2

= …

(3)

SOAL PENYELESAIAN 4. UN 2006

Hasil dari (x – 3)(x2– 6x + 1)–3dx = …

a.

(

x

2

6

x

1

)

4

c

8

1







b. (x2 6x 1) 4 c

4

1 _ _ _

 

c.

(

x

2

6

x

1

)

4

c

2

1







d. (x2 6x 1) 2 c

4

1 _ _ _

 

e. (x2 6x 1) 2 c

2

1 _ _ _

 

Jawab : d 5. UAN 2003

Hasil x x1dx= …

a. (x 1) x 1 (x 1)2 x 1 c 3

2 5

2 _ _ _ _ _ _

b.

(

3

x

2

x

2

)

x

1

c

15

2







c. (3x2 x 4) x 1 c

15

2 _ _ _ _

d.

(

3

x

2

x

2

)

x

1

c

15

2





e.

(

x

2

x

2

)

x

1

c

5

2







Jawab : b

6. UN 2011 PAKET 12

Hasil dari cos42x sin 2x dx = … a.



sin

5

2

x



c

101

b.



₁₀1

cos

5

2

x



c

c.



₅1

cos

5

2

x



c

d. ₅1

cos

5

2

x



c

e. ₁₀1

sin

5

2

x



c

Jawab : b

7. UN 2011 PAKET 46 Hasil sin33x cos 3x dx = … a. ₄1sin43xc

(4)

SOAL PENYELESAIAN 8. UN 2010 PAKET A

Hasil  (sin2 x – cos2x) dx adalah … a. ₂1 cos 2x + C

b. –2 cos 2x + C c. – 2 sin 2x + C d. ₂1 sin 2x + C e. –₂1 sin 2x + C Jawab : c

9. UN 2010 PAKET B

Hasil dari (3 – 6 sin2x) dx = … a. ₂3sin2 2x + C

b. ₂3cos2 2x + C c. ₄3sin 2x + C d. 3 sin x cos x + C e. ₂3sin 2x cos 2x + C Jawab : d

10. UN 2009 PAKET A/B Hasil 4sin 5x cos 3x dx = …

a. –2 cos 8x – 2 cos 2x + C b.



₄1

cos

8

x



cos

2

x

+ C c. ₄1

cos

8

x



cos

2

x

+ C d.



₂1

cos

8

x



cos

2

x

+ C e. ₂1

cos

8

x



cos

2

x

+ C Jawab : b

11. UN 2008 PAKET A/B Hasil dari sin2x cos x dx = … a. 1₃cos3 x + C

b.



₃1 cos3 x + C c.



₃1 sin3 x + C d. 1₃ sin3 x + C e. 3 sin3 x + C Jawab : d 12. UN 2006

(5)

SOAL PENYELESAIAN 13. UN 2005

Hasil dari



(

x

2



1

)

cos

x

dx

= …

a. x2 sin x + 2x cos x + c b. (x2– 1) sin x + 2x cos x + c c. (x2 + 3) sin x – 2x cos x + c d. 2x2 cos x + 2x2 sin x + c e. 2x sin x – (x2– 1)cos x + c Jawab : b

14. UN 2004

Hasil dari



x

2

sin

2

x

dx

= …

a. –

2 1 _x2

cos 2x –

2

1_{x sin 2x +} 4

1 _{cos 2x + c}

b. –

2 1 _x2

cos 2x +

2

1_{x sin 2x}_– 4

1 _{cos 2x + c}

c. –

2 1 _x2

cos 2x +

2

1_{x sin 2x +} 4

1_{cos 2x + c}

d.

2 1 _x2

cos 2x –

2

1 _{x sin 2x}_– 4

1 _{cos 2x + c}

e.

2 1 _x2

cos 2x –

2

1 _{x sin 2x +} 4

1 _{cos 2x + c}

(6)

2) Penggunaan Integral Tak Tentu

Integral tak tentu di gunakan untuk mencari persamaan suatu kurva y = f(x) apabila

diketahui turunan pertama dan sebuah titik pada kurva tersebut yaitu:

f(x) =



f’(x) dx, dengan f’(x)

adalah turunan pertama dari f(x) atau:

y =



dx

dx dy

, dengan

_dxdy

adalah turunan pertama y

SOAL PENYELESAIAN

1. UN 2004

Gradien garis singgung suatu kurva adalah m =

dx dy

= 2x – 3. kurva itu melalui titik (3,2).

Persamaan kurva tersebut adalah …

a. y = x2– 3x – 2 b.

y = x

2

–

3x + 2

c. y = x2 + 3x – 2 d.

y = x

2

+ 3x + 2

e.

y = x

2

+ 3x

–

1

Jawab : b

2. UAN 2003

Jika grafik y = f(x) melalui titik (1, 2) dan

turunannya f’(x) = x2

+ 1, maka grafiknya

y = f(x) memotong sumbu Y di titik …

(7)

Menghitung integral tak tentu fungsi aljabar dan fungsi trigonometri. 1. Hasil dari (x – 3)(x2– 6x + 1)–3dx = …

a. 1₈(x26x1)4c b.  x2 x 4c

4

1₍ ₆ ₁₎

c. 1₂(x26x1)4c d. 1₄(x26x1)2c e.  x2 x 2c

2

1₍ ₆ ₁₎

2. Hasil dari



x  x  x 3 dx

5 ) 5 3 )( 1

( 2 3 = ...

a. 1₃_(x3

+ 3x + 5) 3₍_x3_₃_x_₅₎2 _{+ C} b. 1₃(x3 + 3x + 5) 3 x33x5+ C c. 1₈(x3 + 3x + 5)2 3₍_x3_₃_x_₅₎2 _{+ C} d. ₈1(x3 + 3x + 5)2 3x33x5+ C e. ₈1(x3 + 3x + 5)2 + C

3. Hasil dari ....

5 6 2 ) 2 3 (

2_ _  



dx

x x

x

a. 2 2x26x5c b.  2x26x5c c. 2x 6x5c

2

1 2

d. 2x26x5c e. 2x 6x5c

2

3 2

4. Hasil dx

x x



_ 4 2 3 3 2 = …

a. 4 2x34 + C b. 2 2x34 + C c. 2x34 + C d. 1₂ 2x34 + C e. 1₄ 2x34 + C 5. Hasil dari



 dx x x 8 6 3 2 = ...

a. x38+ C d. 3 x38+ C b. ₂3 3_₈

x + C e. 4 x38+ C

c. 2 x38+ C

6. Hasil dari







 



5 3 3

2 1 2 4 6 x x x

dx = ...

a. ₅2 5



x32x1



2 _{+ C} b. ₂5 5



_x3_₂_x_₁



2 _{+ C} c. 55



x32x1



2 + C d. 55



x32x1



3 + C e. 55



x32x1



4 + C 7. Hasil dari







 



5 3 2

2 1 2 6 9 x x x

dx = ...

a. ₅25



x32x1



2 _{+ C} b. ₂55



x32x1



2 _{+ C} c. 55



x32x1



2 + C

d. 55



x32x1



3 + C e. 55



x32x1



4 + C 8. Hasil



   dx x x x 1 9 3 3 2

2 = …

a. 2 3x2 9x1c b. 3x2 9x1c

3 1

c. ₃2 3x2 9x1c d. ₂1 3x29x1c e. ₂3 3x2 9x1c 9. Hasil



6x 3x2 5dx = …

a. (6x25) 6x25c

3 2

(8)

10. Hasil dari cos42x sin 2x dx = … a.



₁₀1

sin

5

2

x



c

b.



₁₀1

cos

5

2

x



c

c.



₅1

cos

5

2

x



c

d. ₅1

cos

5

2

x



c

e. ₁₀1

sin

5

2

x



c

11. Hasil sin33x cos 3x dx = … a. ₄1sin43xc

b. ₄3sin43xc c. 4sin43xc d. 1₃sin43xc e. ₁₂1 sin43xc

12. Hasil dari sin2x cos x dx = … a. 1₃cos3 x + C

b.



₃1 cos3 x + C c.



₃1 sin3 x + C d. 1₃ sin3 x + C e. 3 sin3 x + C 13. Hasil



x x1dx= …

a. ₅2(x1) x12₃(x1)2 x1c b. ₁₅2(3x2x2) x1c c. ₁₅2(3x2x4) x1c d. ₁₅2(3x2x2) x1c e. ₅2(x2x2) x1c 14. Hasil 4sin 5x cos 3x dx = …

a. –2 cos 8x – 2 cos 2x + C b. ₄1cos8xcos2x + C c. 1₄cos8xcos2x + C d. ₂1cos8xcos2x + C e. 1₂cos8xcos2x + C

15. Hasil dari



sin3x.cosxdx= ... . a. 1₈ sin 4x – ₄1 sin 2x + C b. 1₈ cos 4x – ₄1 cos 2x + C c. ₄1 cos 4x – ₂1_{cos 2x + C} d. 1₈ cos 4x – ₈1 cos 2x + C e. ₄1 cos 4x – 1₂ cos 2x + C

16. Hasil dari





cos2x2sin2 x



dx = ... a. 2 sin 2x + x + C

b. sin 2x + x + C c. sin 2x – x + C d. 2 sin 2x + x + C e. cos 2x + x + C

17. Hasil dari





₂1cos2xcos2x



dx = ... a. ₈5_{sin 2x +}

4 1 _{x + C}

b. 5₈ sin 2x + 1₈x + C c. ₈5_{cos 2x +}

4 1 _{x + C}

d. 5₈ sin 2x + ₄1 x + C e. ₈5_{cos 2x +}

4 1 _{x + C}

18. Hasil dari





x 2 x



dx 2

1_sin 2

cos = ...

a. ₈5sin 2x – ₄1 _{x + C}

b. 5₈sin 2x – 1₈x + C c. ₈5cos 2x – ₄1_{x + C}

d. 5₈cos 2x – ₄1x + C e. ₈5sin 2x – ₄1 _{x + C}

19. Hasil  (sin2 x – cos2x) dx adalah … a. ₂1 cos 2x + C

(9)

20. Hasil dari (3 – 6 sin x) dx = … a. ₂3sin2 2x + C

b. ₂3cos2 2x + C c. ₄3sin 2x + C d. 3 sin x cos x + C e. ₂3sin 2x cos 2x + C

21. Hasil dari (x2–3x + 1) sin x dx = … a. (–x2 + 3x + 1) cos x + (2x – 3) sin x + c b. (–x2 + 3x – 1) cos x + (2x – 3) sin x + c c. (x2– 3x + 1) sin x + (2x – 3) cos x + c d. (x2– 3x + 1) cos x + (2x – 3) sin x + c e. (x2– 3x + 3) cos x + (2x – 3) sin x + c

22. Hasil dari



(x21)cosxdx= … a. x2 sin x + 2x cos x + c

b. (x – 1) sin x + 2x cos x + c c. (x2 + 3) sin x – 2x cos x + c d. 2x2 cos x + 2x2 sin x + c e. 2x sin x – (x2– 1)cos x + c 23. Hasil dari



x2sin2xdx= …

a. –

2 1 _x2

cos 2x –

2

1 _{x sin 2x +} 4

1_{cos 2x +}

c

b. –

2 1 _x2

cos 2x +

2

1 _{x sin 2x}_– 4

1_{cos 2x +}

c

c. –₂1 x2 cos 2x +1₂x sin 2x +₄1cos 2x + c

d. ₂1x2 cos 2x –₂1 x sin 2x –₄1 cos 2x + c e. ₂1x2 cos 2x –₂1 x sin 2x +₄1 cos 2x +

(10)

B. INTEGRAL TENTU

Misalkan kurva y = f(x) kontinu pada interval tertutup [a, b], maka luas daerah L yang dibatasi oleh kurva y = f(x), sumbu X, garis x = a, dan garis x = b, ditentukan dengan rumus:

L =



  

b

a

b

a F b F a x

F dx x

f( ) [ ( )] ( ) ( ), dengan F(x) adalah integral (antidiferensial) dari f(x) 1) Integral Tentu Fungsi Aljabar dan Trigonometri

SOAL PENYELESAIAN



  

4

2

2 ₆ ₈₎

( x x dx = …

a. 38₃ b. 26₃ c. 20₃ d. 16₃ e. ₃4 Jawab : e





3

1

6 1

2 ₎

(x dx = …

a. 9₃1 b. 9 c. 8 d. 10₃ e. 3 Jawab : b

3. UN 2010 PAKET A

Hasil dari

dx

x

















2

1 2

2

1

_{= …}

(11)

4. UN 2010 PAKET B

Hasil dari







2

0

)

6

)(

1

(

3

x

dx

= …

a. –58 b. –56 c. –28 d. –16 e. –14 Jawab : a

Nilai a yang memenuhi persamaan





1

2 2

1

)

(

12

a

dx

x

= 14 adalah …

a. –2

b. –1

c. 0

d. ₂1

e. 1

Jawab : c

6. UN 2008 PAKET A/B Hasil dari







0

1

5 3

2

(

x

2

)

dx

x

= …

a. 85₃ b. 75₃ c. ₁₈63 d. ₁₈58 e. ₁₈31 Jawab : e

7. UN 2007 PAKET A Diketahui





p

1 3

2

)

dx

x

(

x

3

= 78.

Nilai (–2p) = …

a. 8

b. 4

c. 0

d. –4

e. –8

(12)

SOAL PENYELESAIAN 8. UN 2007 PAKET B

Diketahui







p

1

2

6

t

2

)

dt

t

3

(

= 14.

Nilai (–4p) = …

a. –6

b. –8

c. –16

d. –24

e. –32

Jawab : b

9. EBTANAS 2002 Hasil dari





1

2

(

x

6

)

dx

x

= …

a. –4 b.



1₂ c. 0 d. ₂1 e.

4

₂1 Jawab : a

10. EBTANAS 2002

 

a

2 2

dx ) 1 x

4

( =

a

1

. Nilai a2 = … a. –5

b. –3 c. 1 d. 3 e. 5 Jawab : e

11. UN 2011 PAKET 12

Hasil







0

) cos 3

(sin x x dx = …

a. 10₃ b.

3 8 c. ₃4 d.

(13)

12. UN 2011 PAKET 46

Hasil





2

0

) 2 cos sin 2 ( 

dx x

x = …

a. ₂5 b.

2 3 c. 1 d. 2 e. ₂5 Jawab : d

13. UN 2010 PAKET A

Nilai dari



6  0

) 3 cos 3 (sin 

dx x

x = …

a. ₃2 b. 1₃ c. 0 d. –₃1 e. –₃2 Jawab : a

14. UN 2010 PAKET B Hasil dari







 3

2

2 1

) 3

cos( x dx = …

a. –1 b. –₃1 c. 0 d. 1₃ e. 1 Jawab : b 15. UN 2004

Nilai dari



2  

3

) 3 sin( ) 3 cos( 



 x dx

x =

a. –₆1 b. –₁₂1

c. 0

d.

12 1

e.

6 1

(14)

SOAL PENYELESAIAN 16. UAN 2003





0

dx

x

cos

x

= …

a. –2

b. –1

c. 0

d. 1

e. 2

Jawab : a 17. UAN 2003



 4

0

dx

x

sin

x

5

sin

= …

a. –

2

1 _d.

8 1

b. –

6

1 _e.

12 5

c.

12

1 _{Jawab : c}

18. EBTANAS 2002







 

6

0 3 3

dx

)

x

cos(

)

x

sin(

= …

a. –

4

1 _d.

4 1

b. –

8

1 _e.

8 3

c.

8

1 _{Jawab c}

19. EBTANAS 2002





1

0

2 2

x

cos

x

dx

sin

= …

a. 0 d.

8 1_

b.

8

1 _e.

4 1 _

c.

4

1 _{Jawab : b}

20. EBTANAS 2002





 2

dx

x

sin

x

= …

a.  + 1 b. – 1 c. – 1

d. 

(15)

a) Untuk Menghitung Luas Daerah

a. Luas daerah L pada gb. 1 L =



b

a dx x f( ) , untuk f(x)  0

b. Luas daerah L pada gb. 2 L = –



b

a dx x

f( ) , atau

L =



b

a dx x

f( ) untuk f(x)  0

c. Luas daerah L pada gb. 3 L = b





a

dx x g x

f( ) ( )}

{ ,

dengan f(x)  g(x)

SOAL PENYELESAIAN

1. UN 2011 PAKET 12

Luas daerah yang dibatasi kurva

y = 4 – x2_{, y = -}_{x + 2 dan 0 ≤ x ≤ 2 adalah}

…

a. 8₃satuan luas b. 10₃ satuan luas c. 14₃ satuan luas d. 16₃ satuan luas e. 26₃ satuan luas Jawab : b

2. UN 2011 PAKET 46

Luas daerah yang dibatasi kurva y = x2 , y = x + 2, sumbu Y dikuadran I

adalah …

(16)

SOAL PENYELESAIAN 3. UN 2010 PAKET A

Luas daerah yang dibatasi parabola y = x2– x – 2 dengan garis y = x + 1 pada

interval 0 ≤ x ≤ 3 adalah …

a. 5 satuan luas b. 7 satuan luas c. 9 satuan luas d. 10₃1 satuan luas e. 10₃2 satuan luas Jawab : c

4. UN 2010 PAKET B

Luas daerah di kuadran I yang dibatasi kurva y = x3, y = x, x = 0, dan garis x = 2

adalah …

(17)

5. UN 2009 PAKET A/B

Luas daerah yang dibatasi oleh parabola y = x2– 6x + 8, garis y = x – 2 dan sumbu

X dapat dinyatakan dengan …

a.



 x  x dx

4

2 2

) 8 6

( +



   

4

3

2

)) 8 6 ( ) 2

((x x x

b.



 x  x dx

4

2

2 ₆ ₈₎ (

c.





x  x  x



dx

4

3

2 3

1₍ ₃₎ ₍ ₆ ₈₎

d.



 x  x dx

4

3

2 ₆ ₈₎

( +



x x x



dx



   

5

4

2

) 8 6 ( ) 3 (

e.



x dx

4

2 ) 2

( +



x x x



dx



   

5

4

2 ₆ ₈₎ (

(18)

SOAL PENYELESAIAN 6. UN 2008 PAKET A/B

Luas daerah yang dibatasi oleh kurva y = x1, sumbu X dan 0 ≤ x ≤ 8 adalah …

a. 6 satuan luas b. 6₃2 satuan luas c. 17₃1satuan luas d. 18 satuan luas e. 18₃2 satuan luas Jawab : c

7. UN 2007 PAKET A

Luas daerah tertutup yang dibatasi oleh kurva x = y2 dan garis y = x –2 adalah …

a. 0 satuan luas b. 1 satuan luas c. 4₂1satuan luas d. 6 satuan luas e. 16 satuan luas Jawab : c

8. UN 2006

Luas daerah tertutup yang dibatasi oleh kurva y = 6x – x2 dan y = x2– 2x pada

interval 0 ≤ x ≤ 5 sama dengan …

a. 30 satuan luas b. 26 satuan luas c. 64₃ satuan luas d. 50₃ satuan luas e. 14₃ satuan luas Jawab : b

9. UAN 2003

Luas daerah pada kuadran I yang dibatasi oleh kurva y = x2, sumbu Y, dan garis

x + y = 12 adalah …

(19)

10. UAN 2003

Luas daerah yang dibatasi oleh kurva y = x2– 9x + 15 dan y = –x2 + 7x – 15

adalah …

a. 2

3

2 _{satuan luas}

b. 2

5

2 _{satuan luas}

c. 2

3

1_{satuan luas}

d. 3

3

2 _{satuan luas}

e. 4

3

1_{satuan luas}

Jawab : a

11. EBTANAS 2002

Luas daerah yang dibatasi parabola y = 8 – x2dan garis y = 2x adalah …

a. 36 satuan luas b. 41

3

1_{satuan luas}

c. 41

3

2_{satuan luas}

d. 46 satuan luas e. 46

3

2_{satuan luas}

(20)

b) Untuk Menghitung Volume Benda Putar

V =



b

a

dx x f( ))2 (

 atau V =



b

a dx y2

 V =



d

c

dy y g( ))2 (

 atau V =



d

c dy x2 

V =





b

a

dx x g x

f ( ) ( )}

{( 2 2

 atau V =





b

a

dx y

y )

( ₁2 ₂2

 V =





d

c

dy y g y

f ( ) ( )}

{ 2 2

 atau V

=





d

c

dy x

x )

(21)

1. UN 2011 PAKET 12

Volum benda putar yang terjadi jika daerah yang dibatasi oleh kurva y = x2, garis y =2x dikuadran I diputar 360 terhadap sumbu X

adalah …

a.  15

20 _{satuan volum} b. ₁₅30satuan volum c. 

1554 satuan volum d. ₁₅64 satuan volum e. 144₁₅  satuan volum Jawab : d

2. UN 2010 PAKET A

Volum benda putar yang terjadi jika daerah yang dibatasi oleh kurva y = 2x – x2 dan y = 2 – x diputar mengelilingi sumbu X sejauh 360

adalah …

(22)

SOAL PENYELESAIAN 3. UN 2010 PAKET B

Volum benda putar yang terjadi bila daerah yang dibatasi oleh kurva

y = x2 dan y = x diputar mengelilingi sumbu X sejauh 360adalah …

a. ₁₀3  satuan volum b. ₁₀5  satuan volum c. 1₃ satuan volum d. 10₃  satuan volum e. 2 satuan volum Jawab : a

4. UN 2009 PAKET A/B

Perhatikan gambar di bawah ini: Jika daerah yang diarsir pada gambar diputar mengelilingi sumbu X sejauh 360 maka volume benda putar yang terjadi

adalah … satuan volume

(23)

Daerah yang dibatasi oleh kurva y = 4 – x, x = 1, x = 3, dan sumbu X diputar

mengelilingi sumbu X sejauh 360, maka

volume benda putar yang terjadi adalah …

a. 4₃2 satuan volume b. 6₃1 satuan volume c. 8₃2 satuan volume d. 10₃2 satuan volume e. 12₃1 satuan volume Jawab : c

6. UN 2007 PAKET A

Volum benda putar yang terjadi jika daerah yang dibatasi oleh kurva y = 2x dan

parabola y = x2 diputar sejauh 360º

mengelilingi sumbu X adalah …

a. 32₅  satuan volume b. ₁₅64 satuan volume c. ₁₅52  satuan volume d. ₁₅48 satuan volume e. ₁₅32  satuan volume Jawab : b

7. UN 2007 PAKET A

Volum benda putar yang terjadi jika daerah yang dibatasi oleh kurva y = x2 + 1 dan y = 3 diputar mengelilingi sumbu Y sejauh

360º adalah …

(24)

SOAL PENYELESAIAN 8. UN 2005

Volum benda putar yang terjadi karena daerah yang dibatasi oleh parabola y = x2 dan y2 = 8x diputar 360º mengelilingi

sumbu Y adalah ….

a. 2

5

4 __{satuan volum}

b. 3

5

c. 4

5

d. 5

5

e. 9

5

Jawab : c

9. UAN 2003

Volum benda putar yang terjadi karena daerah yang dibatasi oleh sumbu X, sumbu Y, dan kurva y =

4



x

diputar terhadap sumbu Y sejauh 360º, dapat dinyatakan

dengan …

a.



 

2

0

2 2

)

y

4

(

dy satuan volume

b.







2

0

2

y

4

dy satuan volume

c.



 

2

0

2

)

y

4

(

dy satuan volume

d.



 

2

0

2 2

)

y

4

(

2

dy satuan volume

e.



 

2

0

2

)

y

4

(

2

dy satuan volume

(25)

10. EBTANAS 2002

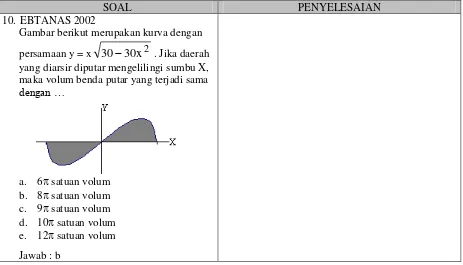
Gambar berikut merupakan kurva dengan persamaan y = x 3030x2 . Jika daerah yang diarsir diputar mengelilingi sumbu X, maka volum benda putar yang terjadi sama

dengan …

(26)

KUMPULAN SOAL INDIKATOR 26 (ii) UN 2011

Menghitung integral tentu fungsi aljabar dan fungsi trigonometri. 1. Hasil



  

4

2

2 ₆ ₈₎

( x x dx = …

a. 3 38 _c. 3 20 _e. 3 4 b. 26₃ d. 16₃

2. Hasil



 3

1

6 1

2 ₎

(x dx = …

a. 9₃1 c. 8 e. 3

b. 9 d. 10₃

3. Hasil dari dx

x x



_  _ 2

1 2

2 1 _{= …}

a. ₅9 c. 11₆ e. 19₆ b. ₆9 d. 17₆

4. Hasil dari



  2 0 ) 6 )( 1 (

3 x x dx = …

a. –58 c. –28 e. –14 b. –56 d. –16

5. Hasil dari





 1

1

2₍_x ₆₎_dx

x = …

a. –4 c. 0 e.

4

₂1

b.



₂1 d. ₂1

6. Nilai a yang memenuhi persamaan



 1 2 2 ) 1 ( 12 a dx x

x = 14 adalah …

a. –2 c. 0 e. 1

b. –1 d. ₂1

7. Hasil dari



  0 1 5 3

2₍_x ₂₎ _dx

x = …

a. 85₃ c. ₁₈63 e. ₁₈31 b. 75₃ d. ₁₈58

8. Hasil







0

) cos 3

(sin x x dx = …

a. 3

10 _c.

3

4 _e.

3 1 b. ₃8 d. ₃2

9. Hasil





2 0 ) 2 cos sin 2 (  dx x

x = …

a.  ₂5 c. 1 e. ₂5

b. ₂3 d. 2

10. Nilai dari



6  0 ) 3 cos 3 (sin  dx x

x = …

a. 3

2 _{c. 0} _e._–

3 2 b. 1₃ d. –₃1

11. Hasil dari



    3 2 2 1 ) 3

cos( x dx = …

a. –1 c. 0 e. 1

b. – 3 1 _d. 3 1 12.



 0

cosxdx

x = …

a. –2 c. 0 e. 2

b. –1 d. 1

13.





 2

sinxdx

x = …

a.  + 1 c. – 1 e.  + 1 b. – 1 d. 

14.



4 0 sin 5 sin  dx x

x = …

a. –

2 1 _c. 12 1 _e. 12 5

b. –

6

1 _d.

(27)

15.



6  

0 3 3

) cos( )

sin(x  x  dx= …

a. –

4 1 _c. 8 1 _e. 8 3

b. –

8

1 _d.

4 1

16. Nilai dari



 

2 3 ) 3 sin( ) 3 cos(   

 x dx

x =

a. –

6

1 _{c. 0} _e.

6 1

b. –

12 1 _d. 12 1 17.



1 0 2 2 _cos

sin x xdx= …

a. 0 c.

4 1 _e. 4 1 _ b. 8 1 _d. 8 1_

18. Hasil dari



 

 4 1 0 4 4 .... ) cos sin

2 x xdx

a. -1 c. 1 e. ½ 3

b. 0 d. ½ 2

19. Diberikan









 3

1

2 ₂ ₄₄

2ax x dx . Nilai a = ...

a. 1 c. 3 e. 6

b. 2 d. 4

20. Di berikan



3 2



20 1

2_ _





dx x

x .

Nilai a2 + a = ... .

a. 2 c. 6 e. 24

b. 3 d. 12

21. Diketahui



 p 1

2

dx 2x)

(3x = 78.

Nilai p 2 3

= ...

a. 4 c. 8 e. 12

b. 6 d. 9

22. Diketahui





p dx x x 1 3 2₎ (

3 = 78.

Nilai (–2p) = …

a. 8 c. 0 e. –8

b. 4 d. –4

23. Diketahui



 

p dt t t 1 2 ) 2 6 3

( = 14.

Nilai (–4p) = …

a. –6 c. –16 e. –32 b. –8 d. –24

24.





a dx x 2 2 ) 1 4 ( = a 1

. Nilai a2 = …

a. –5 c. 1 e. 5

(28)

KUMPULAN SOAL INDIKATOR 27 UN 2011

Menghitung luas daerah dan volume benda putar dengan menggunakan integral.

1. Luas daerah yang dibatasi parabola y = x2–_x–_{2 dengan garis y = x + 1 pada} interval 0 ≤ x ≤ 3 adalah … satuan luas

a. 5 c. 9 e. 10₃2 b. 7 d. 10

3 1

2. Luas daerah yang dibatasi kurva

y = 4 – x2_{, y = -}x + 2 dan 0 ≤ x ≤ 2 adalah …

satuan luas a. 3 8 _c. 3 14 _e. 3 26 b. 3 10 _d. 3 16

3. Luas daerah yang dibatasi kurva

y = x2_{, y = x + 2, sumbu Y dikuadran I adalah} … a. 3 2 _c. 3 6 _e. 3 10 b. 3 4 _d. 3 8

4. Luas daerah di kuadran I yang dibatasi kurva y = x3, y = x, x = 0, dan garis x = 2 adalah …

satuan luas

a. 2₄1 c. 3₄1 e. 4₄1 b. 2₂1 d. 3₂1

5. Luas daerah yang dibatasi oleh kurva y = x1, sumbu X dan 0 ≤ x ≤ 8 adalah …

satuan luas

a. 6 c. 17₃1 e. 18₃2 b. 6

3

2 _{d. 18}

6. Luas yang dibatasi oleh kurva y = 2x2–_{8, dan}

sumbu X, pada 0 ≤ x ≤ 3 adalah .... satuan luas a. 10

3

2 _{c. 15}

3 1 e. 17 3 1 b. 13 3

1 _{d. 16}

3

2

7. Luas daerah tertutup yang dibatasi oleh kurva x = y2_{dan garis y = x}–2 adalah … satuan luas

a. 0 c. 41₂ e. 16

b. 1 d. 6

8. Luas daerah tertutup yang dibatasi oleh kurva y = 6x – x2_{dan y = x}2–2x pada interval 0 ≤ x ≤ 5 sama dengan … satuan luas

a. 30 c. 64₃ e. 14₃ b. 26 d. 50₃

9. Luas daerah yang dibatasi oleh kurva y = x2–_{9x + 15 dan y =}–_x2_{+ 7x}–_{15 adalah} … satuan luas

a. 2

3

2 _{c. 2}

3

1 _{e. 4}

3 1

b. 2

5

2 _{d. 3}

3 2

10. Luas daerah pada kuadran I yang dibatasi oleh kurva y = x2_{, sumbu Y, dan garis}

x + y = 12 adalah … satuan luas

a. 57,5 c. 49,5 e. 22,5 b. 51,5 d. 25,5 11. Luas daerah yang dibatasi parabola

y = 8 – x2dan garis y = 2x adalah … satuan

luas

a. 36 c. 41

3

2 _{e. 46}

3 2

b. 41

3

1 _{d. 46}

12. Luas daerah yang dibatasi oleh kurva y = 9 – x2_{dan garis y = x + 3 adalah.... satuan}

luas a. 2 6 5 c. 19 6 5 e. 21 6 5 b. 3 6 5 d. 20 6 5

13. Volum benda putar yang terjadi jika daerah yang dibatasi oleh kurva y = 2x – x2_dan

y = 2 – x diputar mengelilingi sumbu X sejauh 360adalah … satuan volum

a.

5

1_ _c.

5

3_ _e._

b.

5

2_ _d.

5 4_

14. Volum benda putar yang terjadi bila daerah yang dibatasi oleh kurva y = x2_{dan y =} _x

diputar mengelilingi sumbu X sejauh 360

adalah … satuan volum

a. ₁₀3  c.

3

1_ _{e. 2}_

b. ₁₀5  d. 10₃ 

15. Daerah yang dibatasi oleh kurva y = 4 – x, x = 1, x = 3, dan sumbu X diputar mengelilingi sumbu X sejauh 360, maka volume benda

putar yang terjadi adalah … satuan volum

a. 4

3

2_ _{c. 8}

3

2_ _{e. 12} 3 1_

(29)

yang dibatasi oleh kurva y = 2x dan parabola y = x2_{diputar sejauh 360º mengelilingi sumbu X} adalah … satuan volum

a.

5

32 _ _c. 15

52 _ _e.

15 32_

b.

15

64 _ _d. 15 48_

17. Volum benda yang terjadi, jika daerah yang dibatasi oleh kurva y9x2 dan garis

7  x

y diputar mengelilingi sumbu X sejauh 360oadalah … _{satuan volum}

a.

15 14

178  c.

5 4

53  e.

5 4 35 

b. 66₅3  d. 51₅4 

18. Volum benda putar yang terjadi jika daerah yang dibatasi oleh kurva y = x2_{+ 1 dan}

y = 3 diputar mengelilingi sumbu Y sejauh 360º

adalah … satuan volum

a. 2 c. 3 e. 5 b. 2₂1 d. 4

3 1_

19. Volum benda putar yang terjadi karena daerah yang dibatasi oleh parabola y = x2_{dan y}2_{= 8x}

diputar 360º mengelilingi sumbu Y adalah …. satuan volum

a. 2

5

4 _ _{c. 4} 5

4 _ _{e. 9}

5 4 _

b. 3

5

4 _ _{d. 5} 5 4 _

20. Volum benda yang terjadi, jika daerah yang dibatasi oleh kurva y x2 dan garis

0 2

2yx  diputar mengelilingi sumbuY sejauh 360oadalah … _{satuan volum}

a.

3 1

1  c. 5  e.

5 3

9 

b. 2  d. 9 

21. Gambar berikut merupakan kurva dengan persamaan y = x 3030x2 . Jika daerah yang diarsir diputar mengelilingi sumbu X, maka volum benda putar yang terjadi sama

dengan … satuan volum

a. 6 c. 9 e. 12 b. 8 d. 10

yang dibatasi oleh sumbu X, sumbu Y, dan kurva y = 4xdiputar terhadap sumbu Y

sejauh 360º, dapat dinyatakan dengan …

a.





2 0 2 2₎ 4 ( y

 dy satuan volum

b.





2

0

2 4 y

 dy satuan volum

c.





2

0

2₎ 4

( y

 dy satuan volum

d.





2 0 2 2₎ 4 (

2 y dy satuan volum

e.





2

0

2₎ 4 (

2 y dy satuan volum

23. Perhatikan gambar di bawah ini:

Jika daerah yang diarsir pada gambar diputar mengelilingi sumbu X sejauh 360 maka

volume benda putar yang terjadi adalah …

satuan volum

a. 

15

123 _c. _

1577 e. 1535

b. 

15

83 _d. _

1543

24. Volume benda putar yang terjadi jika daerah yang dibatasi oleh sumbu Y, kurva y = x2, garis y = 2, dan y =5 diputar mengelilingi

sumbu Y ádalah … satuan volum

(30)

25. Perhatikan gambar berikut!

Jika daerah yang diarsir diputar mengelilingi sumbu-X sejauh 360, maka volume benda putar yang terjadi adalah ... satuan volum a.

15

88_ _c.

15

184_ _e.

15 280_

b.

15

96 _ _d.

15 186_

Jika daerah yang diarsir diputar mengelilingi sumbu-X sejauh 360, maka volume benda putar yang terjadi adalah ... satuan volum a. 16 c.

5

32_ _e.

15 32_

b.

3

32_ _d. 10 32 _

Jika daerah yang diarsir diputar mengelilingi sumbu-Y sejauh 360, maka volume benda putar yang terjadi adalah ...

a.

48

6 _ _c.

48

9 _ _e.

48 11_

b.

48

8 _ _d.

48 10_

16. PROGRAM LINEAR

A. Persamaan Garis Lurus

0 b

a

(b, 0) X Y

(0, a)

0 x2

y2

(x1, y1) X Y

(x2, y2)

x1 y1

0 x1 y1 (x1, y1)

(31)

bergradien m dan melalui titik (x1, y1) adalah:

y – y1 = m(x – x1)

melalui dua titik (x1, y1) dan (x2, y2) adalah :

)

x

(

x

y

₁

1 2

1







memotong sumbu X di (b, 0) dan memotong sumbu Y di (0, a) adalah:

ax + by = ab

B. Himpunan penyelesaian dari pertidaksamaan linear

Untuk menentukan daerah HP pertidaksamaan liniear ax + by ≤ c dengan metode grafik dan uji titik, langkah-langkahnya adalah sebagai berikut :

1. Gambarkan garis ax + by = c

2. Lakukan uji titik, yaitu mengambil sembarang titik (x, y) yang ada di luar garis ax + by = c, kemudian substitusikan ke pertidaksamaan ax + by ≤ c

3. Jika pertidaksamaan itu bernilai benar, maka HPnya adalah daerah yang memuat titik tersebut dengan batas garis ax + by = c

4. Jika pertidaksamaan itu bernilai salah, maka HPnya adalah daerah yang tidak memuat titik tersebut dengan batas garis ax + by = c

C. Fungsi Tujuan (Obyektif / Sasaran), Nilai Maksimum, dan Nilai Minimum

1) Fungsi tujuan adalah nilai f untuk x dan y tertentu dari suatu program linear, dan dinyatakan f(x, y) 2) Nilai fungsi sasaran yang dikehendaki adalah kondisi x dan y yang menyebabkan maksimum

atau minimum

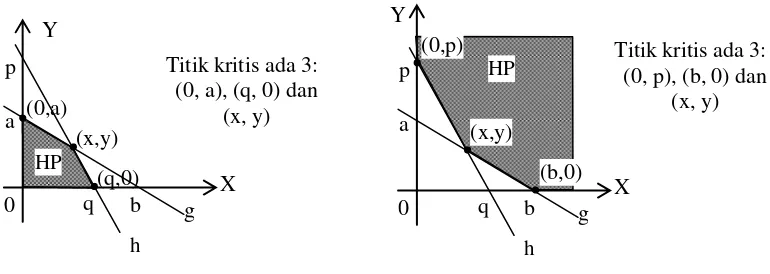
3) Pada gambar HP program linear, titik-titik sudut merupakan titik-titik kritis, dimana nilai minimum atau maksimum berada. Apabila sistem pertidaksamaannya terdiri dari dari dua pertidaksamaan, maka titik-titik kritisnya bisa ditentukan tanpa harus digambar grafiknya.

O

ax + by = c Y

X a

b (0, a)

(b, 0)

(x, y)

(32)

Grafik HP untuk fungsi tujuan maksimum Grafik HP untuk fungsi tujuan minimum Berdasarkan kedua grafik di atas dapat disimpulkan cara penentuan titik kritis sebagai berikut: 1. Pilih titik potong kurva dengan sumbu Y atau sumbu X yang terkecil (0, a) dan (q, 0) jika tujuannya maksimumkan atau yang terbesar (0, p), (b, 0) jika tujuannya minimumkan 2. Titik potong antara kedua kurva (x, y)

SOAL PENYELESAIAN

1. UN 2011 PAKET 12

Seorang anak diharuskan minum dua jenis tablet setiap hari. Tablet jenis I mengandung 5 unit vitamin A dan 3 unit vitamin B. Teblet jenis II mengandung 10 unit vitamin A dan 1 unit vitamin B. Dalam 1 hari anak tersebut memerlukan 25 unit vitamin A dan 5 unit

0 a

X Y

b _g

HP p

q h (x,y) (0,p)

(b,0)

Titik kritis ada 3: (0, p), (b, 0) dan

(x, y)

0 a

X Y

b _g

HP p

q h (x,y) (0,a)

(q,0)

Titik kritis ada 3: (0, a), (q, 0) dan

(33)

biji dan tablet II Rp8.000,00 per biji, pengeluaran minimum untuk pembelian tablet

per hari adalah …

a. Rp12.000,00 b. Rp14.000,00 c. Rp16.000,00 d. Rp18.000,00 e. Rp20.000,00 Jawab : e

2. UN 2011 PAKET 46

Di atas tanah seluas 1 hektar akan dibangun dua tipe rumah, yaitu tipe A dan tipe B. Tiap unit rumah tipe A luasnya 100 m2, sedangkan tipe B luasnya 75m2. Jumlah rumah yang akan dibangun paling banyak 125 unit. Harga jual rumah tipe A adalah Rp100.000.000,00 dan rumah tipe B adalah Rp60.000.000. Supaya pendapatan dari hasil penjulana seluruh rumah maksimum, maka harus

dibangun rumah sebanyak…

a. 100 rumah tipe A saja b. 125 rumah tipe A saja c. 100 rumah tipe B saja

d. 100 rumah tipe A dan 25 tipe B e. 25 rumah tipe A dan 100 tipe B Jawab : c

SOAL PENYELESAIAN

3. UN 2010 PAKET A

(34)

250.000,00 per unit dan barang jenis II dijual seharga Rp 400.000,00 perunit, maka agar penjualannya mencapai maksimum, berapa banyak masing-masing barang harus di buat? a. 6 jenis I

b. 12 jenis II

c. 6 jenis I dan jenis II d. 3 jenis I dan 9 jenis II e. 9 jenis I dan 3 jenis II Jawab : e

4. UN 2010 PAKET B

Luas daerah parkir 1.760m2 luas rata-rata untuk mobil kecil 4m2 dan mobil besar 20m2. Daya tampung maksimum hanya 200

kendaraan, biaya parkir mobil kecil

Rp1.000,00/jam dan mobil besar Rp2.000,00/ jam. Jika dalam satu jam terisi penuh dan tidak ada kendaran yang pergi dan dating, penghasilan maksimum tempat parkir adalah

…

a. Rp 176.000,00 b. Rp 200.000,00 c. Rp 260.000,00 d. Rp 300.000,00 e. Rp 340.000,00 Jawab : c

SOAL PENYELESAIAN

(35)

yang diperoleh dari penjualan toko tersebut

adalah …

a. Rp 575.000.000,00 b. Rp 675.000.000,00 c. Rp 700.000.000,00 d. Rp 750.000.000,00 e. Rp 800.000.000,00 Jawab : c

Pada tanah seluas 24.000 m2 dibangun perumahan dengan dua tipe. Tipe A dengan luas 150m2 dan tipe B dengan luas 100 m2. Jumlah rumah yang dibangun tidak lebih dari 200 unit. Jika laba untuk setiap rumah tipe A Rp4.000.000,00 dan tiap rumah tipe B Rp3.000.000,00, maka laba maksimum yang

dapat diperoleh adalah …

SOAL PENYELESAIAN

7. UN 2007 PAKET A

(36)

B, dan 1 kg bahan C. Bahan baku yang tersedia 480 kg bahan A, 720 kg bahan B, dan 360 kg bahan C. Harga barang jenis I adalah Rp 40.000,00 dan harga barang jenis II adalah Rp 60.000,00. Pendapatan maksimum yang

diperoleh adalah …

a. Rp 7.200.000,00 b. Rp 9.600.000,00 c. Rp 10.080.000,00 d. Rp 10.560.000,00 e. Rp 12.000.000,00 Jawab : d

8. UN 2007 PAKET B

Perusahaan tas dan sepatu mendapat pasokan 8 unsur P dan 12 unsur K setiap minggu untuk produksinya. Setiap tas memerlukan 1 unsur P dan 2 unsur K dan setiap sepatu memerlukan 2 unsur P dan 2 unsur K. Laba untuk setiap tas adalah Rp18.000,00 dan setiap sepatu adalah Rp12.000,00. keuntungan maksimum

perusahaan yang diperoleh adalah …

a. Rp 120.000,00 b. Rp 108.000,00 c. Rp 96.000,00 d. Rp 84.000,00 e. Rp 72.000,00 Jawab : b

SOAL PENYELESAIAN

9. UN 2006

(37)

upah untuk membungkus kado jenis A Rp2.500,00/buah dan kado jenis B Rp2.000,00/buah, maka upah maksimum yang

dapat diterima karyawati tersebut adalah …

a. Rp 40.000,00 b. Rp 45.000,00 c. Rp 50.000,00 d. Rp 55.000,00 e. Rp 60.000,00 Jawab : b

10. UN 2005

Suatu pesawat udara mempunyai 60 tempat duduk. Setiap penumpang kelas utama boleh membawa barang hingga 50 kg, sedangkan untuk setiap penumpang kelas ekonomi diperkenankan paling banyak membawa 20 kg barang. Bagasi pesawat itu hanya mampu menapung 1.500 kg barang. Jika harga tiket kelas utama Rp 500.000,00, dan untuk kelas ekonomi Rp 300.000,00, pendapatan

maksimum untuk sekali penerbangan adalah …

SOAL PENYELESAIAN

11. UN 2004

(38)

dapat dibuat adalah …

a. 10 potong b. 11 potong c. 12 potong d. 14 potong e. 16 potong Jawab : c

12. UAN 2003

Nilai maksimum fungsi sasaran Z = 6x + 8y dari sistem pertidaksamaan

    

 

 

0 , 0

48 4 2

60 2 4

y x

adalah …

a. 120 b. 118 c. 116 d. 114 e. 112

Jawab : a

SOAL PENYELESAIAN

13. EBTANAS 2002

(39)

harinya Rp 100.000,00 dan paling banyak hanya dapat memproduksi 400 kue, maka keuntungan terbesar yang dapat dicapai ibu

tersebut dari modalnya adalah …

a. 30%

b. 32%

c. 34%

d. 36%

e. 40%

Jawab : c

KUMPULAN SOAL INDIKATOR 11 UN 2011

Menyelesaikan masalah program linear

1. Seorang anak diharuskan minum dua jenis tablet setiap hari. Tablet jenis I mengandung 5

(40)

vitamin B. Dalam 1 hari anak tersebut memerlukan 25 unit vitamin A dan 5 unit vitamin B. Jika harga tablet I Rp4.000,00 per biji dan tablet II Rp8.000,00 per biji,

pengeluaran minimum untuk pembelian tablet

per hari adalah …

a. Rp12.000,00 d. Rp18.000,00 b. Rp14.000,00 e. Rp20.000,00 c. Rp16.000,00

2. Sebuah toko bangunan akan mengirim sekurang-kurangnya 2.400 batang besi dan 1.200 sak semen. Sebuah truk kecil dapat mengangkut 150 batang besi dan 100 sak semen dengan ongkos sekali angkut Rp 80.000. Truk besar dapat mengangkut 300 batang besi dan 100 sak semen dengan onkos sekali jalan Rp 110.000. maka besar biaya minimum yang dikeluarkan untuk pengiriman tersebut adalah

a. Rp 1.000.000,00 d. Rp 1.070.000,00 b. Rp 1.050.000,00 e. Rp 1.080.000,00 c. Rp 1.060.000,00

3. Sebuah rombongan wisata yang terdiri dari 240 orang akan menyewa kamar-kamar hotel untuk satu malam. Kamar yang tersedia di hotel itu adalah kamar untuk 2 orang dan untuk 3 orang. Rombongan itu akan menyewa kamar hotel sekurang-kurangnya 100 kamar. Besar sewa kamar untuk 2 orang dan kamar untuk 3 orang per malam berturut-turut adalah Rp 200.000,00 dan Rp 250.000,00. Besar sewa kamar minimal per malam untuk seluruh rombongan adalah ....

4. Di atas tanah seluas 1 hektar akan dibangun dua tipe rumah, yaitu tipe A dan tipe B. Tiap unit rumah tipe A luasnya 100 m2, sedangkan tipe B luasnya 75m2. Jumlah rumah yang akan dibangun paling banyak 125 unit. Harga jual rumah tipe A adalah Rp100.000.000,00 dan rumah tipe B adalah Rp60.000.000. Supaya pendapatan dari hasil penjulana seluruh rumah maksimum, maka harus dibangun rumah

sebanyak…

a. 100 rumah tipe A saja b. 125 rumah tipe A saja c. 100 rumah tipe B saja

d. 100 rumah tipe A dan 25 tipe B e. 25 rumah tipe A dan 100 tipe B 5. Luas daerah parkir 1.760m2_{luas rata-rata}

untuk mobil kecil 4m2_{dan mobil besar 20m}2_.

Daya tampung maksimum hanya 200 kendaraan, biaya parkir mobil kecil

Rp1.000,00/jam dan mobil besar Rp2.000,00/ jam. Jika dalam satu jam terisi penuh dan tidak ada kendaran yang pergi dan dating,

penghasilan maksimum tempat parkir adalah

…

a. Rp 176.000,00 d. Rp 300.000,00 b. Rp 200.000,00 e. Rp 340.000,00 c. Rp 260.000,00

6. Tanah seluas 10.000 m2_{akan dibangun toko 2}

tipe. Untuk toko tipe A diperlukan tanah seluas 100 m2_{dan tipe B diperlukan 75 m}2_{. Jumlah}

toko yang dibangun paling banyak 125 unit. Keuntungan tiap tipe A sebesar

Rp7.000.000,00 dan tiap tipe B sebesar Rp4.000.000,00. Keuntungan maksimum yang diperoleh dari penjualan toko tersebut adalah

…

a. Rp 575.000.000,00 b. Rp 675.000.000,00 c. Rp 700.000.000,00 d. Rp 750.000.000,00 e. Rp 800.000.000,00

7. Suatu perusahaan meubel memerlukan 18 unsur A dan 24 unsur B per hari. Untuk membuat barang jenis I dibutuhkan 1 unsur A dan 2 unsur B, sedangkan untuk membuat barang jenis II dibutuhkan 3 unsur A dan 2 unsur B. Jika barang jenis I dijual seharga Rp 250.000,00 per unit dan barang jenis II dijual seharga Rp 400.000,00 perunit, maka agar penjualannya mencapai maksimum, berapa banyak masing-masing barang harus di buat? a. 6 jenis I

b. 12 jenis II

c. 6 jenis I dan jenis II d. 3 jenis I dan 9 jenis II e. 9 jenis I dan 3 jenis II

(41)

diperoleh adalah …

9. Perusahaan tas dan sepatu mendapat pasokan 8 unsur P dan 12 unsur K setiap minggu untuk produksinya. Setiap tas memerlukan 1 unsur P dan 2 unsur K dan setiap sepatu memerlukan 2 unsur P dan 2 unsur K. Laba untuk setiap tas adalah Rp18.000,00 dan setiap sepatu adalah Rp12.000,00. keuntungan maksimum

perusahaan yang diperoleh adalah …

a. Rp 120.000,00 d. Rp 84.000,00 b. Rp 108.000,00 e. Rp 72.000,00 c. Rp 96.000,00

10. Pada sebuah toko, seorang karyawati

menyediakan jasa membungkus kado. Sebuah kado jenis A membutuhkan 2 lembar kertas pembungkus dan 2 meter pita, Sebuah kado jenis B membutuhkan 2 lembar kertas

pembungkus dan 1 meter pita. Tersedia kertas pembungkus 40 lembar dan pita 30 meter. Jika upah untuk membungkus kado jenis A

Rp2.500,00/buah dan kado jenis B

Rp2.000,00/buah, maka upah maksimum yang

dapat diterima karyawati tersebut adalah …

b. Rp 45.000,00 e. Rp 60.000,00 c. Rp 50.000,00

11. Suatu pesawat udara mempunyai 60 tempat duduk. Setiap penumpang kelas utama boleh membawa barang hingga 50 kg, sedangkan untuk setiap penumpang kelas ekonomi diperkenankan paling banyak membawa 20 kg barang. Bagasi pesawat itu hanya mampu menapung 1.500 kg barang. Jika harga tiket kelas utama Rp 500.000,00, dan untuk kelas ekonomi Rp 300.000,00, pendapatan

maksimum untuk sekali penerbangan adalah …

12. Seorang penjahit membuat 2 model pakaian. Model pertama memerlukan 1 m kain polos dan 1, 5 kain corak. Model kedua memerlukan 2 m kain polos dan 0,5 m kain bercorak. Dia hanya mempunyai 20 m kain polos dan 10 m kain bercorak. Jumlah maksimum pakaian yang

dapat dibuat adalah … potong

a. 10 c. 12 e. 16

b. 11 d. 14

17. MATRIKS

A. Transpose Matriks

Jika A = _      d c b a

, maka transpose matriks A adalah AT = _      d b c a

B. Penjumlahan dan Pengurangan Matriks

Dua matriks dapat dijumlahkan bila kedua matriks tersebut berordo sama. Penjumlahan dilakukan dengan menjumlahkan elemen–elemen yang seletak

Jika A = _

     d c b a

, dan B = _      n m l k

, maka A + B = _      d c b a + _      n m l k = _          n d m c l b k a

(42)

LATIH UN_{Prog. IPA Edisi 2011}

http://www.soalmatematik.com

INFORMASI PENDIDIKAN

http://ibnufajar75.blogspot.com

196

Jika A = _      d c b a

, maka nA = n _      d c b a = _      dn cn bn an

D. Perkalian Dua Buah Matriks

 Perkalian matriks A dan B dapat dilakukan bila jumlah kolom matriks A sama dengan jumlah baris matriks B (Am×n × Bp×q, jika n = p) dan hasil perkaliannya adalah matriks berordo m × q.

 Hasil perkalian merupakan jumlah perkalian elemen–elemen baris A dengan kolom B.

Jika A = _

     d c b a

, dan B = _

     p o n m l k , maka

A × B = _

     d c b a × _      p o n m l k = _            dp cm do cl dn ck bp am bo al bn ak

E. Matriks Identitas (I)

 I = _

     1 0 0 1

 Dalam perkalian dua matriks terdapat matriks identitas (I), sedemikian sehingga I×A = A×I = A F. Determinan Matriks berordo 2×2

Jika A = _      d c b a

, maka determinan dari matriks A dinyatakan Det(A) = d c

b a

= ad – bc Sifat–sifat determinan matriks bujursangkar

1. det (A ± B) = det(A) ± det(B) 2. det(AB) = det(A)  det(B) 3. det(AT) = det(A)

4. det (A–1) =

)

det(

1

A

G. Invers Matriks

 Dua matriks A dan B dikatakan saling invers bila A×B = B×A = I, dengan demikian A adalah invers matriks B atau B adalah invers matriks A.

Bila matriks A = _      d c b a

, maka invers A adalah:

            a c b d bc ad 1 ) A ( Adj ) A ( Det 1

A 1 , ad –bc ≠ 0

 Sifat–sifat invers dan determinan matriks

(43)

INFORMASI PENDIDIKAN

197

2) (B×A)–1 = A–1 ×B–1 H. Matriks Singular

matriks singular adalah matriks yang tidak mempunyai invers, karena nilai determinannya sama dengan nol

I. Persamaan Matriks

Bentuk–bentuk persamaan matriks sebagai berikut: 1) A × X = B  X = A–1 × B

2) X × A = B  X = B × A–1

SOAL PENYELESAIAN

1. UN 2010 PAKET A

Diketahui matriks A =















9

3

5

3

1

6

4

8

4

c

b

a

dan B =















9

5

3

1

6

4

8

12

b

a

Jika A = B, maka a + b + c = …

a. –7 b. –5 c. –1 d. 5 e. 7 Jawab : e

SOAL PENYELESAIAN

2. UN 2010 PAKET B

Diketahui matriks–matriks A = _   

 

0 1

2

c ,

B = _

  

 

 5 6 4

b

a

, C = _

  

 

2 0

3 1

, dan

D = _

  

 

2 3

4 b

.

Jika 2A –B = CD, maka nilai a + b + c = … a. –6

(44)

LATIH UN_{Prog. IPA Edisi 2011} http://www.soalmatematik.com

INFORMASI PENDIDIKAN

198

e. 8 Jawab : c

3. UN 2009

Diketahui 3 matriks, A = _

     b a 1 2 ,

B = _

     1 2 1 4

b

, C =

_

      2 2 b a b

Jika A×Bt –_{C =}

      4 5 2 0

dengan Bt_adalah

transpose matriks B, maka nilai a dan b masing–

masing adalah …

a. –1 dan 2 b. 1 dan –2 c. –1 dan –2 d. 2 dan –1 e. –2 dan 1 Jawab : a

4. UN 2008 PAKET A/B

Diketahui matriks P = _

     11 0 4 12 ,

Q = _

  

 

3 4 2y x

, dan R = _

       44 66 20 96 .

Jika PQT_{= R (Q}T_{transpose matriks Q), maka nilai} 2x + y = …

a. 3 b. 4 c. 7 d. 13 e. 17 Jawab : e

SOAL PENYELESAIAN

5. UN 2008 PAKET A/B Diketahui matriks P = _

     3 1 5 2 dan

Q = _

     1 1 4 5

. Jika P–1 adalah invers matriks P dan Q–1 adalah invers matriks Q, maka determinan matriks Q–1 P–1adalah …

(45)

INFORMASI PENDIDIKAN

199

6. UN 2007 PAKET A

Diketahui persamaan matriks A = 2BT (BT adalah transpose matriks B), dengan

A = _

     c 3 b 2 4 a

dan B = _

        7 b a 1 a 2 b 3 c 2 .

Nilai a + b + c = …

a. 6 b. 10 c. 13 d. 15 e. 16 Jawab d

7. UN 2007 PAKET B

Diketahui matriks A = _

       y x y x y x ,

B = _

        3 y 2 x

1 ₂1

, dan AT = B dengan AT menyatakan transpose dari A.

Nilai x + 2y adalah …

a. –2 d. 1 b. –1 e. 2 c. 0 Jawab : c 8. UN 2006

Diketahui matriks A = _         2 1 x 10

x6 _dan

B = _

     3 5 2 x

. Jika AT = B–1 dengan

AT= transpose matrik A, maka nilai 2x = …

a. –8 d. 4

b. –4 e. 8

c. ₄1 Jawab : e

SOAL PENYELESAIAN

9. UN 2005

Diketahui matriks A = _        0 1 3 2 ,

B = _

     2 1 2 4

, dan C = _

       1 1 0 1 . Hasil dari A+(B×C) = …

a. _        2 0 5 8

d. _

     2 0 0 6 b. _        1 0 9 8

e. _

(46)

LATIH UN_{Prog. IPA Edisi 2011} http://www.soalmatematik.com

INFORMASI PENDIDIKAN

200

c. _      2 0 0 2

Jawab : a 10. UN 2004

Diketahui persamaan matriks

                            1 1 2 3 2 1 2 1 3 4 5 2 3 1 b b a

Nilai a dan b adalah …

a. a = 1, b = 2 b. a = 2, b =1 c. a = 5, b = –2 d. a = –2 , b = 5 e. a = 4, b = –1 Jawab : b 11. UAN 2003

Nilai x2 + 2xy + y2 yang memenuhi

persamaan : _

                    5 2 3 1 6 2 y x adalah … a. 1 b. 3 c. 5 d. 7 e. 9 Jawab : a

12. UN 2011 PAKET 12

Diketahui persamaan matriks                        1 0 0 1 1 2 4 9 2 5 y x x .

Nilai x –y = …

a. ₂5 d. 22₂

b. 15₂ e. 23₂

c. 19₂ Jawab : e

SOAL PENYELESAIAN

13. UN 2011 PAKET 46 Diketahui persamaan                      9 23 8 21 2 1 4 1 3 2 z y x x . Nilai x + y –z = …

(47)

INFORMASI PENDIDIKAN

201

14. UN 2011 PAKET 12

Diketahui matriks A = _     

5 0

2 3

dan

B = _

  

  

 

0 17

1 3

. Jika AT = transpose matriks A dan AX = B + AT, maka

determinan matriks X = …

a. –5 b. –1 c. 1 d. 5 e. 8 Jawab : b

15. UN 2011 PAKET 46

Diketahui matriks A = _     

5 3

2 1

dan

B = _

  

  

4 1

2 3

. Jika At adalah transpose dari matriks A dan AX = B + At, maka determinan matriks X = …

(48)

LATIH UN_{Prog. IPA Edisi 2011}

INFORMASI PENDIDIKAN

202

KUMPULAN SOAL INDIKATOR 12 UN 2011

Menyelesaikan operasi matriks

1. Diketahui matriks A =

            9 3 5 3 1 6 4 8 4 c b a

dan B =

            9 5 3 1 6 4 8 12 b a

Jika A = B, maka a + b + c = …

a. –7 c. –1 e. 7 b. –5 d. 5

2. Diketahui matriks-matriks A = _

     0 1 2 c ,

B = _

     

5 6

4 b

a

, C = _

     2 0 3 1 , dan

D = _

    

2 3

4 b

. Jika 2A – B = CD,

maka nilai a + b + c = …

a. –6 c. 0 e. 8

b. –2 d. 1 3. Diketahui 3 matriks, A = _

     b a 1 2 ,

B = _

     1 2 1 4

b , C = _       2 2 b a b .

Jika A×Bt–_{C =}

      4 5 2 0

dengan Bt_{adalah transpose matriks B, maka nilai a dan b masing-}masing adalah …

a. –1 dan 2 d. 2 dan –1 b. 1 dan –2 e. –2 dan 1 c. –1 dan –2

4. Diketahui matriks P = _

     11 0 4 12 ,

Q = _

  

 

3 4 2y x

, dan R = _

       44 66 20 96 .

Jika PQT_{= R (Q}Ttranspose matriks Q), maka nilai 2x + y = …

a. 3 c. 7 e. 17

b. 4 d. 13

5. Diketahui persamaan matriks A = 2BT

(BT_{adalah transpose matriks B), dengan}

A = _

     c b a 3 2 4

dan B = _

        7 1 2 3 2 b a a b c .

Nilai a + b + c = …

a. 6 c. 13 e. 16

b. 10 d. 15

6. diketahui matriks A = _

       y x y x y x ,

B = _

        3 2 1 ₂1

y x

(49)

INFORMASI PENDIDIKAN

204

a. –2 c. 0 e. 2

b. –1 d. 1

7. Diketahui matriks A = _

        2 1 10 6 x x _dan

B = _

     3 5 2 x

. Jika AT_{= B}–1_dengan

AT= transpose matrik A, maka nilai 2x = …

a. –8 c. 1₄ e. 8

b. –4 d. 4

8. Diketahui matriks-matriks A = _

     

1 2

5 3

dan B = _

       1 1 5 4

, jika (AB)– 1_{adalah invers dari matriks AB maka}

(AB)– 1_{= ...}

a. _

         17 6 20 7

d. _

       17 6 20 7

b. _

     17 6 20 7

e. _

     7 6 20 17

c. _

�