Numerik
2.1 Rasionalisasi
Dalam penyelesaian masalah matematika yang terkait dengan integral, diferensial dan lainnya dari fungsi f(x) = x2 + 2x + 6 secara anlitik umumnya dengan mudah dapat kita selesaikan. Akan tetapi dalam upaya menyelesaikan dx
x x
10 sin
secara analitik menjadi bukan pekerjaan yang gampang. Butuh pengetahuan yang luas dengan penguasaan analisis yang tinggi. Sementara fungsi
x x x
f( ) sin sangat banyak
digunakan dalam kehidupan karena fungsi tersebut merupakan model dari gelombang suara yang dibutuhkan dalam kehidupan sehari-hari.
-15 -10 -5 0 5 10 15
-0. 2 0 0.2 0.4 0.6 0.8 1
x s in(x)/x
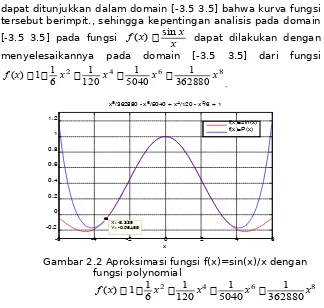
Gambar 2.1 Grafk fungsi f(x) = sin (x)/x Mengubah bentuk fungsi
x x x
f( ) sin menjadi fungsi
polynomial lainnya yang bersesuaian dalam domain tertentu menjadi alternatif solusi yang cepat dalam penyelesaian integrasi tersebut. Suatu hampiran yang digunakan untuk mendapatkan model yang berbeda dari suatu model matematika atau fakta alam yang ada disebut dengan Aproksimasi. Suatu hampiran yang baik dari
x x x
f( ) sin
adalah 2 4 6 8
362880 1 5040
1 120
1 6
1 1 )
(x x x x x
f . Hal ini
BAB
Numerik
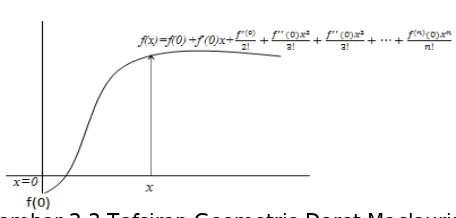
dapat ditunjukkan dalam domain [-3.5 3.5] bahwa kurva fungsi tersebut berimpit., sehingga kepentingan analisis pada domain [-3.5 3.5] pada fungsi
x x x
f( )sin dapat dilakukan dengan
menyelesaikannya pada domain [-3.5 3.5] dari fungsi 8
6 4
2
362880 1 5040
1 120
1 6
1 1 )
(x x x x x
f
.
-6 -4 -2 0 2 4 6
-0.2 0 0.2 0.4 0.6 0.8 1 1.2
x
x8/ 362880 - x6/ 5040 + x4/120 - x2/ 6 + 1
X: -3.339 Y : -0.05485
f(x )=s in(x ) f(x )=P (x )
Gambar 2.2 Aproksimasi fungsi f(x)=sin(x)/x dengan fungsi polynomial
8 6
4 2
362880 1 5040
1 120
1 6
1 1 )
(x x x x x
f
Lebih lanjut, dalam upaya mendapatkan mendapatkan nilai f(75) dari f(x) = x2+2x+2 dengan sangat mudah kita lakukan, yakni f(75) = 752 + 2(75) + 2 = 5777. Akan tetapi menjadi sulit jika akan dicari nilai f(75) dari sekumpulan data pemetaan seperti:
x 50 100 150 200 250 300
f(x) 45 60 78 73 57 41
Numerik
interpolasi yang sebentar ajan di bahas, diperoleh persamaan pendekatan analitik yang dapat digunakan pada f(x) tersebut adalah f(x) = 135.9999999998 - 4107666666667 x + 0.062416666667x2-0.000382333333x3 +0.000001033333x4 -0.00000000104x5
.
Dapat diperiksa bahwa pemetaan x ke f(x) dapat dirumuskan dengan fungsi tersebut di atas sehingga dapat dengan mudah dihitung nilai dari f(75).
2.2 Aproksimasi
2.2.1 Metode Deret Maclaurin
Persamaan umum fungsi polynomial f(x) = a0 + a1x+ a2x2 + a3x3 + a4x4 + ... + anxn
Turunan fungsi polynomial tersebut hingga turunan ke-n adalah sebagai berikut:
f(x) = a0 + a1x+ a2x2 + a3x3 + a4x4 + ... + anxn f'(x) = (1)a1+ 2a2x+ 3a3x2 + 4a4x3 + ... + nanxn-1
f"(x) = (1)(2)a2+ (2)(3)a3x+ (3)(4)a4x2 + ... + (n-1)(n)anxn-2 f'"(x) = (1)(2)(3)a3+ (2)(3)(4)a4x+ ... + (n-2)(n-1)(n)anxn-3 fiv(x) = (1)(2)(3)(4)a
4 + ….+ (n-3)(n-2)(n-1)(n)anxn-4 f(n)(x) =(1) (2)(3) ... (n-2)(n-1)(n)a
n = n!an untuk x = 0 →f(0) = a0 → a0 = f(0)
f'(0) = a1 → a1 = f'(0) f"(0) = 2a2 = 2!a2 → a2 =
! 2
) 0 (
f
f"'(0) = (2)(3)a3 = 3!a3 → a3 = ! 3
) 0 (
f
fiV(0) = 4!a
4 a4= fiv(0)/4! f(n) (0) = (2)(3)...(n-2)(n-1(n)a
n = n!an → an =
! ) 0 ( ) (
n f n
n n
x n f x
f x f x f f
x f
! ) 0 ( !
3 ) 0 ( !
2 ) 0 ( !
1 ) 0 ( ! 0
) 0 ( )
( 2 3 ( )
Selanjutnya deret tersebut didefnisikan sebagai deret Maclaurin.
Numerik
Gambar 2.3 Tafsiran Geometris Deret Maclaurin Teladan 2.1
Diketahui: f(x)= sin x
Tuliskan f(x)dalam bentuk fungsi polinomial!
Solusi:
f(x) = sin x → f(0) = 0
f'(x) = cos x → f'(0) = 1 f''(x) = -sin x → f''(0) = 0
f'"(x) = -cos x → f'"(0) = -1 f'"'(x) = sin x → f'"'(0) = 0
f'"''(x) = cos x → f'"''(0) = 1
sehingga diperoleh
f(x) = f(0)+f'(0)x+
= 0 +(1)x +(0)x2 + + ...
=x -
Jadi, bentuk pebdekatan polinomial dari f(x)=sin x adalah
Numerik
-6 -4 -2 0 2 4 6
-2. 5 -2 -1. 5 -1 -0. 5 0 0.5 1 1.5 2 2.5
x x -1/ 6 x3
+ 1/120 x5
-1/ 5040 x7
+1/ 362880 x9
f(x )= s in(x )
Gambar 2.4 Aproksimasi Deret Macalurin hingga derajat ke-10 2.1.2 Metode Deret Taylor
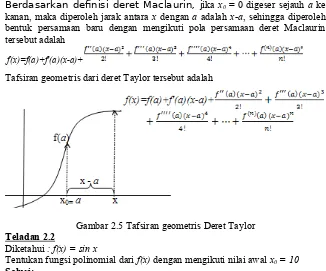
Berdasarkan defnisi deret Maclaurin, jika x0 = 0 digeser sejauh a ke kanan, maka diperoleh jarak antara x dengan a adalah x-a, sehingga diperoleh bentuk persamaan baru dengan mengikuti pola persamaan deret Maclaurin tersebut adalah
f(x)=f(a)+f'(a)(x-a)+
Tafsiran geometris dari deret Taylor tersebut adalah
Gambar 2.5 Tafsiran geometris Deret Taylor Teladan 2.2
Diketahui : f(x) = sin x
Tentukan fungsi polinomial dari f(x) dengan mengikuti nilai awal x0 = 10 Solusi:
f(x) = sin x → f(10) = sin(10) = -0.5440
Numerik
Untuk a = 10, maka diperoleh
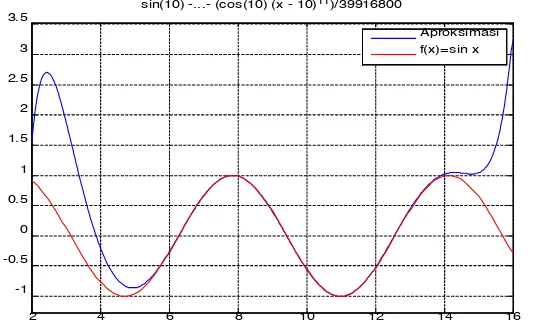
Komputer program yang dapat digunakan unutk mengevaluasi deret taylor ini dan sketsa grafiknya adalah
syms x
plot(d,subs(f,d),'r')
legend('Aproksimasi','f(x)=sin x') grid on
)/ 39916800
Aprok s imasi f(x)= sin x
Numerik
Aproksimasi fungsi dari f(x) = sin x dengan fungsi polynomial berderajat 11 (sebelas ) adalah
2.3 Interpolasi
Interpolasi adalah suatu cara untuk mencari nilai di antara beberapa titik data yang telah diketahui. Dalam kehidupan sehari- hari ,interpolasi dapat digunakan untuk memperkirakan suatu fungsi dimana fungsi tersebut tidak terdefinisi dengan suatu formula, tetapi didefinisikan hanya dengan data
2.3.1 Interpolasi Polinomial
Interpolasi polynomial merupakan suatu metode untuk mendapatkan nilai suatu titik data yang terletak diantara data-data yang diketahui mengunakan persamaan polynomial. Tinjauan kembali persamaan umum polinimial sebagai berikut: f(x) = a0 + a1x+ a2x2 dengan n bilangan Asli
Numerik
berderajat n. Pemilihan jenis interpolasi polynomial tersebut didasari atas banyaknya data dan pola data yang diketahui. 2.3.1.1 Interpolasi Linier
Sebagaimana dalam pembahasan sebelumnya, bahwa interpolasi linier merupakan interpolasi yang mengunakan persamaan polynomial berderajat n=1 dengan persamaan linier, f(x) = a0 + a1x. Misalkan dimiliki dua buah titik (x1, f(x1)) dan (x2, f(x2)), maka persamaan linier yang melalui kedua titik tersebut adalah:
f(x1) = ao + a1x1 f(x2) = a0 + a1x2 ____________
-f(x2) – f(x1) = a1(x2 – x1)
1 2
1 2
1
) ( ) (
x x
x f x f a
f(x1) = ao + a1x1 a0 = f(x1) – a1x1 = f(x1) -
1 2
1
2) ( )
( x x
x f x f
x1
f(x) = a0 + a1x = f(x1) -
1 2
1
2) ( )
( x x
x f x f
x1 +
1 2
1
2) ( )
( x x
x f x f
x
f(x) =
1 2
1
2) ( )
( x x
x f x f
(x-x1)+f(x1)
Persamaan terakhir disebut sebagai persamaan untuk interpolasi linier yang digunakan untuk mendpatkan nilai f(x) berdasarkan data (x1,f(x1)) dan (x2, f(x2)).
Teladan 2.3
Dua buah warung makan sama-sama menjual nasi bungkus dengan harga yang sama, pada hari penjualan yang sama, warung A mendapat untung Rp. 130.000 perhari dengan modal awal Rp. 500.000 dan warung B mendapat untung sebesar Rp. 50.000 dengan modal Rp. 300.000. karena melihat warung A dan B memperoleh keuntungan yang cukup menjanjikan, pak Ahmad berkeinginan untuk menjual nasi bungkus seperti yang dijual oleh kedua warung tersebut. Dengan melihat perbandingan hasil atau keuntungan yang didapatkan oleh toko A dan B, berapakah keuntungan yang akan didapatkan pak Ahmad dengan menggunakan modal sebesar Rp. 350.000
Solusi:
Numerik
x1 = 200.000,- dan f(x1) = 50.000,-x2 = 500.000,- dan f(x2) = 130.000,-x = 350.000,- dan f(130.000,-x) = ….?
f(x) =
1 2
1
2) ( )
( x x
x f x f
(x-x1)+f(x1)
= (350.000 200.000) 50.000 000
. 200 000 . 500
000 . 50 130000
=
90.000,-Jadi perkiraan keuntungan penjualan dengan modal Rp. 350.000,- adalah Rp.
90.000,-Teladan 2.4
Berapakah perkiraan jumlah penduduk Indonesia pada tahun 1990 berdasarkan data hasil sensus pada tabel dibawah ini:
Tahun 1986 1994
Jumlah penduduk
(juta) 133.4 143.5
Variable tahun kita sebut sebagai x, (x1= 1996, x2=1994) dan variable jumlah penduduk sebagi y, (y1= 133.4, y2=143.5). dengan menggunakan persamaan interpolasi linier diperoleh nilai untuk jumlah penduduk tahun 1990
Jadi perkiraan banyaknya penduduk Indonesia pada tahun 1990 adalah 129.35 juat jiwa.
Teladan 2.5
Aliefa akan menentuka nilai ttabel pada taraf siginifkan 5% untuk uji satu pihak dengan dk = 47. Pada table tersebut nilai yang dicari tidak termuat. Akan tetapi nilai yang termuat adalah ttabel= 2.68 untuk dk = 40 dengan ttabel = 1.67dan dk =
60. Tentukan nilai pendekatan ttabel pada dk 47 tersebut dengan mengunakan interpolasi linier.
Solusi:
Numerik
x1 = 40, f(x1) = 2.68 x2 = 60, f(x2) = 1.68 x = 47, f(x) = ..?
f(x) =
( 2) ( 1)
1 2
1 f x f x
x x
x x
+f(x1)
f(x) =
1.68 2.68
40 60
40 47
+2.68 = 2.33
Jadi nilai ttabel = 2.33 pada taraf signifkan 5% dengan dk = 47. Teladan 2.6
Hasil pengukuran kedalam sungai yang memiliki lebar 3m pada interval tiap 50cm dari suatu pinggir sungai adalah sebagai berikut:
Jarak (cm) 50 100 150 200 250 300 Kedalaman
cm 45 60 78 73 57 41
Tentukan pendekatan secara linier kedalam sungai tiap 10 cm dan sketsa grafk perkiraan pola dasar sungai.
Solusi:
Penyelesaian masalah tersebut dengan metode interpolasi linier dilakukan dengan menentukan nilai pada tiap 10 cm pada selang [50 100], [100 150], [150 200],[200 250] dan [250 300] dengan cara sebagai berikut:
Interval (x)
Formula Interpolasi x f(x)
[50 100] f(x) =
60 45
45 50100 50
x
= (3*x)/10 + 30
50.00 60.00 70.00 80.00 90.00 100.00
45.00 48.00 51.00 54.00 57.00 60.00
[100 150] f(x) =
78 60
60 100150 100
x
= (9*x)/25 + 24
110.00 120.00 130.00 140.00 150.00
63.60 67.20 74.40 70.80 78.00
[150 200] f(x) =
73 78
78 150200 150
x
= 93 - x/10
160.00 170.00 180.00 190.00
Numerik
Interval
(x) Formula Interpolasi x f(x)
200.00 73.00
[200 250] f(x) =
57 73
73 200250 200
x
= 137 - (8*x)/25
210.00 220.00 230.00 240.00 250.00
69.80 66.60 63.40 60.20 57.00
[250 300] f(x) =
41 57
57 250300 250
x
= 137 - (8*x)/25
260.00 270.00 280.00 290.00 300.00
53.80 50.60 47.40 44.20 41.00
Evaluasi nilai di atas dilakukan dengan kode program berikut:
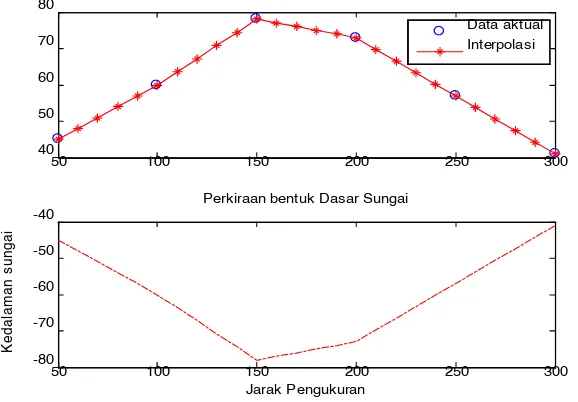
x=[50 100 150 200 250 300]; y=[45 60 78 73 57 41]; xi=[50:10:300];
yi=interp1(x,y,xi,'linear'); [xi yi];
subplot(2,1,1) plot(x,y,'o') hold on
plot(xi,yi,'-*r')
legend('Data aktual','Interpolasi') subplot(2,1,2)
plot(xi,-yi,'-.r')
title('Perkiraan bentuk Dasar Sungai') xlabel('Jarak Pengukuran')
ylabel('Kedalaman sungai')
Numerik
Data ak tual
Interpolasi
Perkiraan bentuk Das ar Sungai
Jarak Pengukuran
K
Gambar 2.7 Model dasar sungai dengan interpolasi linier 2.3.1.2 Interpolasi Kudrat
Interpolasi kuadrat erupakan metode untuk mendapatkan nilai diantara titik-titik data yang diketahui menggunakan persamaan kuadrat atau polynomial berderajat 2, yaitu f(x) = a0 + a1x + a2x2. persamaan linier 3 (tiga) variable sebagai berikut:
(x1, y1) a0 + x1a1 +x12 a2= y1 (x2, y2) a0 + x2a1 + x22 a2= y2 (x3, y3) a0 + x3a1 + x33a2 = y3
Augmented matriks dari SPL tersebut adalah
Numerik
Jadi persamaan interpolasi kuadrat yang dapat dilakukan adalah
f(x) = a0 + a1x + a2x2 dengan
Teladan 2.7
Selesaikanteladan 3.6 di atas dengan mengunakan interpolasi kuadrat
Solusi:
Prosedur penyelesaian yang dapat diterapkan adalah dengan membangun partisi domain interpolasi kuadrat sebagai berikut:
(1) Untuk titik (50,45), (100, 60) dan (150,78) diperoleh bentuk augmented matriks koefesien polynomial kuadrat adalah
Dengan komputasi sederhana dapat diperoleh persamaan kuadrat sebagai berikut:
A1=[1 50 50^2;1 100 100^2;1 150 150^2]; B1=[45;60;78];
k1=inv(A1)*B1 k1 =
33.000000000000000 0.210000000000000 0.000600000000000
Hasil komputasi tersebut memberikan persamaan kuadrat 2
pada interval [50 150].
Numerik
A2=[1 150 150^2;1 200 200^2;1 250 250^2]; B2=[78;73;57];
k2=inv(A2)*B2 k2 =
27.000000000000000 0.670000000000000 -0.002200000000000
Hasil komputasi tersebut memberikan persamaan kuadrat 2
pada interval [150 250].
(3) Untuk titik (250, 57) dan (300, 41) tidak cukup untuk melakukan interpolasi kuadrat, pendekatan yang dilakukan dengan interpolasi linier dengan bentuk persamaan sebelumnya f(x) = 137 - (8*x)/25.
Berdasarkan analisis di atas, maka persamaan interpolasi yang dapat digunakan adalah sebagai berikut:
program komputasi berikut:
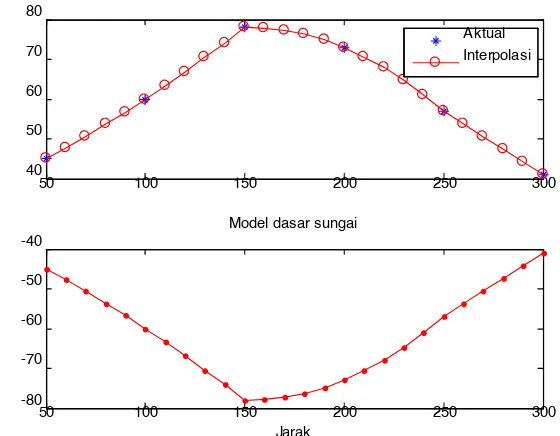
xa=[50 100 150 200 250 300]; ya=[45 60 78 73 57 41];
yi=[subs(f1,x1) subs(f2,x2) subs(f3,x3)]; subplot(2,1,1)
Numerik
hold on
plot(xi,yi,'-or')
legend('Aktual','Interpolasi') subplot(2,1,2)
plot(xi,-yi,'.-r') xlabel('Jarak'); ylabel('Kedalaman')
title('Model dasar sungai')
Hasil komputasi dengan kode program di atas diperoleh sebagai berikut:
Jarak
Kedalam an
Jara k
Kedalam an
Jara k
Kedalam an
50 45 150 78 250 57
60 47.76 160 77.88 260 53.8
70 50.64 170 77.32 270 50.6
80 53.64 180 76.32 280 47.4
90 56.76 190 74.88 290 44.2
100 60 200 73 300 41
110 63.36 210 70.68
120 66.84 220 67.92
130 70.44 230 64.72
Numerik
50 100 150 200 250 300
40 50 60 70 80
Aktual
Interpolasi
50 100 150 200 250 300
-80 -70 -60 -50 -40
Jarak
K
e
d
a
la
m
a
n
Model dasar sungai
Gambar 2.8 Model dasar sunagi dengan interpolasi kuadrat 2.3.1.3 Interpolasi Kubik
Interpolasi kubik merupakan metode untuk mendapatkan nilai diantara titik-titik data yang diketahui menggunakan persamaan polynomial berderajat 3 dengan persamaan umum f(x) = a0 + a1x + a2x2 + a3x3.
Metode ini digunakan apabila diketahui minimal data pengamatan ada 4 titik. Misalkan titik-titik yang diketahui adalah (x1,y1), (x2, y2), (x3, y3) dan (x4, y4), maka nilai yang terdapat diantara titik-titik tersebut akan memeuhi fungsi kubik dengan a0, a1, a2 dan a3 adalah solusi dari system persamaan linier 4 (empat) variable sebagai berikut:
(x1, y1) a0 + a1x1 +a2x12+ a3x13 = y1 (x2, y2) a0 + a1x2 + a2x22+ a3x23= y2 (x3, y3) a0 + a1x3 + a2x33 + a3x33= y3 (x4,y4) a0 + a1x4 + a2x43 + a3x43= y3
Numerik
Teladan 2.8
Penyelesaian permasalahn teladan 2.6 di atas dapat dilakukan dengan interpolasi kubik dengan partisi titik-titik data pengukuran sebagai berikut:
(1) Partisi pertama adalah titik {(50,40),(100,60),(150,78),(200,73)} sehingga diperoleh Augmented matriks koefesien SPL adalah sebagai berikut:
Penyelesaian dengan computer program diperoleh sebagai berikut:
format long k=inv(A)*B k =
38.999999999999986 -0.310000000000003 0.008000000000000 -0.000028000000000
Dari hasil komputasi tersebut diperoleh fungsi interpolasi kubik yaitu f(x) =
38.999999999999986–0.31x + 0.008x2 – 0.000028x3.
Numerik
derajat 3 yaitu titik {(200,73),(250,57), (300,41)}. Aumented mPenyelesaian dengan computer program sebagai berikut:
A=[1 200 200^2;1 250 250^2;1 300 300^2]; B=[73;57;41];
format long k=inv(A)*B;
poly2sym([k(3) k(2) k(1)]) ans =
137 - (8*x)/25
Hasil komputasi tersebut memberikan fungsi polynomial yang dapat digunakan adalah linier f(x) = 137 - (8*x)/25. Hal ini menunjukkan ketiga titik (200,73),(250,57), (300,41) cendrung membentuk suatu garis lurus ketimbang kuadrat. Fungsi polynomial yang digunakan untuk melakukan interpolasi adalah
200 300
25 8 137
200 x 50 0.000028x3
-0.008x2 +
0.31x -99999986 38.9999999
)
(x x x
f
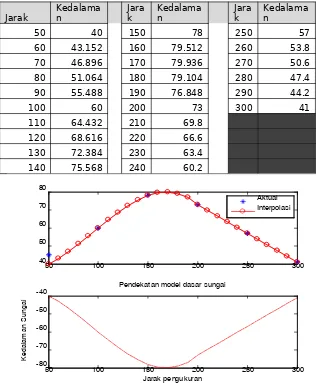
Perhitungan dengan computer sebagimana kode program di bawah ini menghasilkan nilai pendekatan kedalaman sungai dan grafik model dasar sungai sebagai berikut:
syms x
xa=[50 100 150 200 250 300]; ya=[45 60 78 73 57 41]; d1=[50:10:200];
d2=[210:10:300];
f1=38.999999999999986-0.31*x + 0.008*x*x-0.000028*x*x*x; f2=137-(8/25)*x;
xi=[d1 d2];
yi=[subs(f1,d1) subs(f2,d2)]; [xi;yi]'
subplot (2,1,1) plot(xa,ya,'*') hold on plot(xi,yi,'-or')
Numerik
subplot(2,1,2) plot(xi,-yi,'-.r')
xlabel('Jarak pengukuran') ylabel('Kedalaman Sungai')
title('Pendekatan model dasar sungai')
Jarak Kedalaman Jarak Kedalaman Jarak Kedalaman
50 40 150 78 250 57
60 43.152 160 79.512 260 53.8
70 46.896 170 79.936 270 50.6
80 51.064 180 79.104 280 47.4
90 55.488 190 76.848 290 44.2
100 60 200 73 300 41
110 64.432 210 69.8
120 68.616 220 66.6
130 72.384 230 63.4
140 75.568 240 60.2
50 100 150 200 250 300
40 50 60 70 80
50 100 150 200 250 300
-80 -70 -60 -50 -40
Jarak pengukuran
K
e
d
a
la
m
a
n
S
u
n
g
a
i
Pendekatan model dasar sungai
Aktual
Interpolasi
Numerik
2.3.1.4 Interpolasi Polinomial Derajat n
Interpolasi polynomial nerajan n merupakan metode untuk maka akan diperoleh Sistem persamaan Linier untuk koefesien polynomial sebagai berikut:
(x1, y1) a0 + a1x1 + a2x12 + a3x12 + … + anx1n-1 = y1 (x2, y2) a0 + a1x2 + a2x22 + a3x22 + … + anx2n-1 = y2 (x3, y3) a0 + a1x3+ a2x32 + a3x32 + … + anx3n-1 = y3
(xn, yn) a0 + a1xn + a2xn2 + a3xn2 + … + anxnn-1 = yn Augmented matriks dari koefesien SPL adalah
Sehingga solusi dari koefesien SPL tersebut adalah
Teladan 2.9
Tinjau kembali data pengukuran kedalaman sungai pada teladan 2.6 di atas.
Jarak (cm) 50 100 150 200 250 300 Kedalaman
Numerik
Karena banyaknya data ada 6 titik, maka interpolasi polynomial yang dapat dikontruksi adalah polynomial berderajat 5. Augmented matriks koefesien yang dapat diperoleh adalah sebagai berikut:
Dengan komputasi sebagaimana kode di bawah ini diperoleh penyelesaian sebagai berikut:
A=[1 50 50^2 50^3 50^4 50^5;...
1.35999999999998 -0.04107666666667 0.00062416666667 -0.00000382333333 0.00000001033333 -0.00000000001040
Hasil komputasi tersebut diperoleh nilai untuk a0 = 1.35999999999998 x 102
Numerik
f(x) = 135.9999999998 - 4107666666667 x + 0.062416666667x2
-0.000382333333x3 +0.000001033333x4 -0.00000000104x5
f=poly2sym([k(6) k(5) k(4) k(3) k(2) k(1)]); pretty(f)
Evaluasi nilai f(x) pada data interpolasi pada domain [50 300] dengan Δx = 10
Jarak Kedalaman Jarak Kedalaman Jarak Kedalaman
50 45 150 78 250 57
60 44.239296 160 78.756096 260 53.904896
70 46.227072 170 78.519872 270 50.908672
80 50.016128 180 77.388928 280 47.905728
90 54.819904 190 75.496704 290 44.701504
100 60 200 73 300 41
Numerik
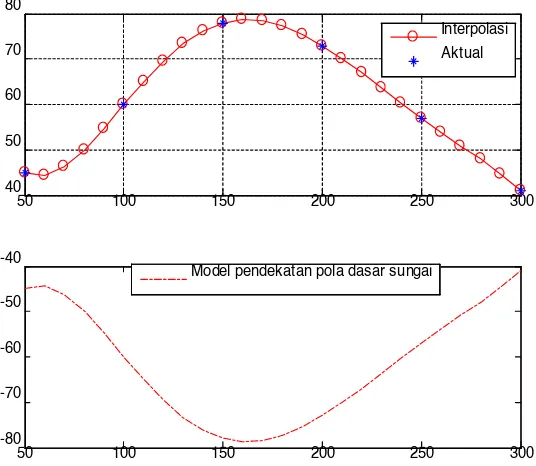
50 100 150 200 250 300 40
50 60 70 80
Interpolasi Aktual
50 100 150 200 250 300 -80
-70 -60 -50 -40
Model pendekatan pola dasar sungai
Gambar 2.10 Model dasar sunagi dengan interpolasi derajat 5 Kode komputasi unutk mengambar grafk fungsi tersebut:
d=[50:10:300]; subplot(2,1,1) plot(d,subs(f,d),'-or') hold on
plot([50:50:300],[45 60 78 73 57 41],'*') legend('Interpolasi','Aktual')
grid on
subplot(2,1,2) plot(d,subs(f,d),'-.r') plot(d,-subs(f,d),'-.r')
legend('Model pendekatan pola dasar sungai')
Teladan 2.9
Numerik
angkatan dengan banyaknya mahasiswa berdasarkan data actual pada jurusan pendidikan matematika IAIN MAtaram dari tahun 2003 sampai dengan 2010 sebagai berikut:
Tahun 200
3 2004 2005 2006 2007 2008 2009 2010
Karena ada 8 data yang diketahui maka interpolasi polinomila yang dapat diterapkan adalah polynomial derajat 7 dengan persamaan umum
h
Dan berdasarkan data yang diketahui, maka bentuk SPL simultannya adalah
Dan augmented matriks koefesien SPL adalah
.
Evaluasi nilai koefesien SPL dengan kode program komputer sebagai berikut:
A=[2003^7 2003^6 2003^5 2003^4 2003^3 2003^2 2003 1;...
2004^7 2004^6 2004^5 2004^4 2004^3 2004^2 2004 1;... 2005^7 2005^6 2005^5 2005^4 2005^3 2005^2 2005 1;... 2006^7 2006^6 2006^5 2006^4 2006^3 2006^2 2006 1;... 2007^7 2007^6 2007^5 2007^4 2007^3 2007^2 2007 1;... 2008^7 2008^6 2008^5 2008^4 2008^3 2008^2 2008 1;... 2009^7 2009^6 2009^5 2009^4 2009^3 2009^2 2009 1;... 2010^7 2010^6 2010^5 2010^4 2010^3 2010^2 2010 1]; B=[43;40;80;114;177;98;147;146];
Numerik
k =
1.0e+017 *
0.00000000000000 -0.00000000000000 0.00000000000000 -0.00000000000035 -0.00000000203975 0.00000588520083 -0.00631513379020 2.51648371579466
Berdasarkan hasil komputasi nilai koefesien SPL tersebut, dapat dikontruksi fungsi polinomial pendekatan yang diperoleh dengan kode program berikut:
Kode komputasi unutk kontruksi fungsi
syms x
f=k(1)*x^7+k(2)*x^6+k(3)*x^5+k(4)*x^4+k(5)*x^3+k(6)*x ^2+k(7)*x+k(8); pretty(f)
Hasil evaluasi fungsi tersebut terhadap data aktual menunjukkan bahwa nilai yang diberikan tidak tepat dengan data aktual (lihat tabel di bawah). Hal ini menunjukkan bahwa fungsi pendekatan tersebut tidak valid, sehingga perlu dilakukan analisis ulang. Suatu analisis yang memungkinkan dilakukan adalah dengan melakukan normalisasi data x (tahun angkatan). Pemilihan cara ini didasri atas kenyataan nilai variabel x yang memuat bilangan ribuan sedangkan y bilangan ratusan yang memiliki penyimpangan sangat besar antara data x dan data y. Persamann normalisasi yang digunakan adalah
) (t std
t t x
Dimana :
Numerik
t rata-rata dari t = 2006.5
Stdv (t) = standar deviasi dari t = 2.45
Sehingga diperoleh data transpormasi untuk tahun angkatan adalah
No Tahun Masuk(t)
) (t std
t t x
y
1 2003 -1.428869016623 52
43
2 2004
-1.020620726159 66
40
3 2005
-0.612372435695 79
80
4 2006
-0.204124145231 93
11 4
5 2007 0.204124145231 93
17 7
6 2008 0.612372435695 79
98
7 2009 1.020620726159 66
14 7
8 2010
1.428869016623 52
14 6
Dengan menerapkan cara yang sama sebagaimana
Numerik
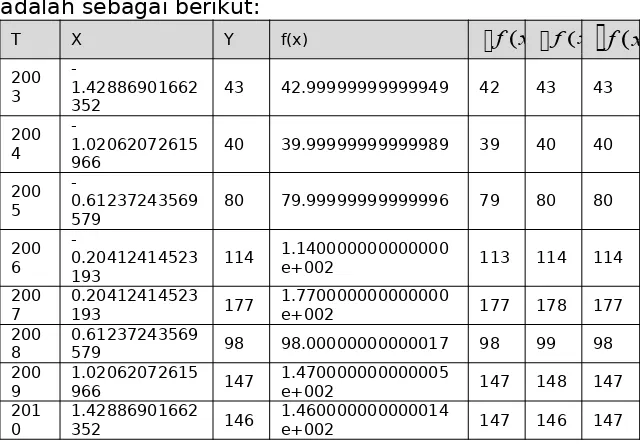
Evaluasi nilai dari persamaan tersebut terhadap data actual adalah sebagai berikut:
T X Y f(x)
f(x)
f(x)
f(x)
200 3
-1.42886901662
352 43 42.99999999999949 42 43 43
200 4
-1.02062072615
966 40 39.99999999999989 39 40 40
200 5
-0.61237243569
579 80 79.99999999999996 79 80 80
200 6
-0.20412414523
193 114
1.140000000000000
e+002 113 114 114
200
7 0.20412414523193 177 1.770000000000000e+002 177 178 177 200
8 0.61237243569579 98 98.00000000000017 98 99 98 200
9 1.02062072615966 147 1.470000000000005e+002 147 148 147 201
0 1.42886901662352 146 1.460000000000014e+002 147 146 147
Numerik
Dan grafk model matematis berdasarkan interpolasi polynomial berderajat 7 dari banyaknya mahasiswa tiap tahun angkatan adalah
Gambar 2.11 Model pendekatan dengan interpolasi polynomial berderajat 7.
Teladan 2.10:
Numerik
berdasarkan sketsa gambar di bawah. Dilakukan pengukuran tinggi tebing pada gambar pada tiap satuan jarak pada sumbu horizontal. Gambar grid pengukuran dan hasil pengukuran diberikan sebagai berikut:
Gambar 2.12 Model pelukis sebuah bukit
i 0 1 2 3 4 5 6 7 8 9 10 11
x 1 2 3 4 5 6 7 8 9 10 11 12
f 0. 5
1. 1
1. 6
2. 7
5. 3
6. 3
7. 8
10 10. 3
10. 5
10. 6
10. 7 Tentukan kemiringan tebing pada tiap titik untuk ∆x = 0.1. Solusi:
Untuk mendapatkan kemiringan tiap titik dengan ∆x = 0.1, maka perlu diketahui nilai f(x) pada tiap ∆x = 0.25. Untuk itu perlu dilakukan interpolasi nilai tiap titik yang belum diketahui. Mencermati gambar di atas, berdasarkan bentuk pola gambar, maka ditentukan beberapa jenis interpolasi yang dipilih sebagai berikut:
Numerik
l Interpo
lasi
. Berdasarkan evaluasi nilai a dan b dapat didefnisikan sebagai f(x) = 0.6x -0.1.
b. Domain 2 ≤ x ≤ 3 f(x) = ax + b sehingga diperoleh fungsi interpolasi adalah f(x) = 0.5x + 0.1. Hasil komputasi ketinggian tebing pada interval 2 ≤ x ≤ 3 adalah
diperoleh fungsi interpolasi adalah
f(x) = -0.5167x3 + 6.95x2 -28.4333x + 38.3 d. Domain 5 ≤ x ≤ 8 f(x) = ax3 + bx2 + cx + d
Numerik
, sehingga
diperoleh fungsi interpolasi adalah
f(x) = 0.0333 x3 -0.35x2 + 1.8167x + 0.8
sehingga diperoleh fungsi interpolasi adalah f(x) = -0.05x2+1.15x+4
sehingga diperoleh fungsi interpolasi adalah
f(x) = -0.000000000000001x2 + 0.09999999999999x +
9.5
Grafk pendekatan model bukit berdasarkan hasil interpolasi.
k1=inv([1 1;2 1])*[0.5;1.1] p1=poly2sym(k1);
d1=[1:0.1:2]; f1=subs(p1,d1);
Numerik
k5=inv([64 8 1;81 9 1;100 10 1])*[10;10.3;10.5] p5=poly2sym(k5);
d5=[8:0.1:10]; f5=subs(p5,d5);
k6=inv([100 10 1;121 11 1;144 12 1])*[10.5;10.6;10.7]
Persamaan fungsi yang memenuhi model bukit tersebut adalah
Numerik
Pendekatan model t ebing
Dasar
Gambar 2.13 Grafk interpolasi model pelukis bukitbukit pada gambar 2.13
Sedangkan persamaan kemiringan tiap titik diberikan oleh turunan pertama dari f(x) sebagai berikut:
Numerik
0 2 4 6 8 10 12
-1 -0. 5 0 0.5 1 1.5 2 2.5 3
Jarak
T
i
n
g
k
a
t
K
e
c
u
r
a
m
a
n
Grafik turunan pada interval yang diberikan
Gambar 2.14 Gradien setiap titik dipermukaan bukit pada gambar 2.13
Kode program yang digunakan unutk menghitung
d1=[1:0.1:2]; n1=length(d1); df1=ones(1,n1)*0.6;
d2=[2:0.1:3]; n2=length(d2); df2=ones(1,n2)*0.5;
d3=[3:0.1:5]; syms x
dp3=-1.5501*x^2+13.9*x-28.4333; df3=subs(dp3,d3);
d4=[5:0.1:8];
dp4=0.0999*x^2-0.7*x+1.8167; df4=subs(dp4,d4);
d5=[8:0.1:10]; dp5=-0.1*x+1.15; df5=subs(dp5,d5);
d6=[10:0.1:12];
Numerik
plot(d1,df1,'.-',d2,df2,'.-',d3,df3,'.-',d4,df4,'.-', d5,df5,'.-',d6,df6,'.-')
xlabel('Jarak')
ylabel('Tingkat Kecuraman')
title('Grafik turunan pada interval yang diberikan')
2.3.2 Interpolasi Newton Gregori
Interpolasi Newton Gregori merupakan interpolasi yang dikontruksi dari aproksimasi dengan Deret Taylor menggunakan perhitungan beda hingga. Beda hingga terdiri dari beda maju, beda mundur dan beda tengah.
2.3.2.1 Beda Hingga
Beda dapat dipandang sebagai selisih sedangkan berhingga berarti nilainya dapat dinyatakan dengan jelas, sehingga beda hingga memiliki pengertian selisih yang dapat ditentukan. Beda dalam matematika disimbolkan dengan lambang ∆ (baca delta) untuk beda maju dan (baca nabla) untuk beda mundur . Perhatikan ilustrasi berikut:
Gambar 2.15 Tafsiran geometris beda hingga
Pada gambar 2.15.a di atas, merupakan bentuk analitik dari beda hingga. Mula-mula dimiliki titik x dan f(x) . Dari titik x ditentukan titik berikutnya sejauh h, yaitu titik x+h dan diperoleh pemetaanya di f(x+h). selisih nilai dari (x+h) – x dan selisih pemetaanya f(x+h) – f(x) disebut sebagai beda maju dengan formula analitiknya adalah ∆x = (x+h) – x dan ∆f = f(x+h) – f(x)
Pada gambar 2.15b di atas, titik x bersesuian dengan xi, sehingga x berikutnya yang ditentukan sejauh h keknana dari titik xi disebut xi+1 dan titik sebelumnya yang ditentukan sejauh
Numerik
Beda maju dari xi dan fi ditentukan dengan formula numerik beda maju adalah ∆xi = xi+1 – xi dan ∆fi = fi+1 – fi.
Defnisi beda Maju
i i
i x x
x x h x h
x
( ) 1
i i i f f f
x f h x f
f ( ) ( ) 1
Lebih lanjut beda mundur secara analitik ditentukan dengan nilai selisih dari x – (x-h) dan f(x) – f(x-h) untuk bentuk analitik dan xi – xi-1 dan fi - fi-1 untuk bentuk numeriknya.
Defnisi beda Mundur
i i
i x x
x h x x h
x
( ) 1
i i
i f f
f h x f x f
f
( ) ( ) 1
Tinjau kembali gambar 2.15 di atas. Jika dari titik x+h dan x-h ditentukan bedanya maka nilai bedanya tersebut dinyatakan sebagai beda tengah, karena x berada ditengah-tengah x+h dan x-h. Sejalan dengan itu, selisih dari nilai pemetaanya juga, yaitu f(x+h)-f(x-h) disebut sebagai beda tengah. Sedangkan selisih secara numeriknya adalah xi+1 – xi-1 dan fi+1 – fi-1 disebut formula beda beda tengah.
2 2
) ( )
( 1 1
x h x h xi xi
h
1 1 ) ( )
(xh f xh fi fi f
Beda tingkat ke-n dari x dan f(x) secara matematis didefnisikan sebagai berikut:
)
( n 1 i
i
nx x
dan nxi (n1xi) )
( n 1 i
i
n f f
dan nfi (n1fi)
Berdasarkan defnisi tersebut maka bentuk-bentuk sebagai berikut:
Menurut beda maju i = 0 ==> ∆f0 = f1 – f0
Numerik
dst
Menurut beda mundur
1 1 0 0
0
f f f f
i
0 1
1 2
1 2 1 01 0 0
0
2 ( ) ( )
f f f
f f
f
f f f
f f
f
dst
Secara sederhana formula ini dapat dikontruksi kedalam bentuk tabel beda hingga sebagai berikut:
Suatu kenyataan yang dapat diaplikasikan dari beda hingga tersebut adalah untuk memeriksa apakah suatu data terkontruksi dari polynomial berderajat n. Apabila beda ke-n memberikan nilai 0 (nol), maka data tersebut terkontruksi dari polynomial berderajat (n-1).
Teladan 2.11
Tunjukkan bahwa fungsi f(x) = x3 memiliki beda yang ke-4 bernilai 0 (nol).
Numerik
x f(x) f 2f 3f 4f
0 0
1
1 1 6
7 6
2 8 12 0
19 6
3 27 18 0
37 6
4 64 24 0
61 6
5 125 30
91
6 216
Berdasarkan tabel di atas, dapat diketahui bahwa beda ke-4 dari f(x) bernilao 0 (nol). Hal ini disebabkan karena fungsi f(x) berderajat 3 (tiga) dimana apabila sudah di turunkan derajatnya hingga tingkat 4, akan bernilai 0 (nol).
Teladan 2.12
Numerik
Har i
0 1 2 3 4 5 6 7
Lab a
-8
-6.333
3
-4.666
7
-3 6 31 57.
5 8 4
17 7
32 2
53 1
Ket. Laba dalam satuan ratusan ribu.
Solusi:
Untuk dapat menyelesaikan permasalahan tersebut, dianalisis model hubungan yang terjadi. Analisis pertama untuk mengetahui apakah data tersebut terkontruksi oleh suatu fungsi polynomial atau tidak. Dengan menerapkan table beda hingga diperoleh sebagai berikut:
x f(x) f 2f 3f 4f
0 -8
5
1 -3 4
9 12
2 6 16 0
25 12
3 31 28 0
53 12
4 84 40 0
93 12
5 65 52 0
145 12
6 322 64 0
Numerik
x f(x) f 2f 3f 4f
7 531 76
Berdasarkan table beda hingga di atas, diketahui bahwa pada beda ke-4, nilai bedanya 0 (nol). Hal ini mnunjukkan bahwa data tersebut terkontruksi dengan fungsi polynomial berderajat 3 dengan bentuk persamaan umum f(x) = a3x3 + a2x2 + a1x + a0. Dengan mengambil sembarang 4 (empat) buah titik dari 8 (delapan) titik yang ada, maka diperoleh augmented matriks koefesien polynomial berderajat 4 adalah sebagai berikut: Titik yang dipilih (0,-8), (1,-3), (2,6) dan (3,31)
(x,f(x)) f(x) = a3x3 + a2x2 + a1x + a0 (0,-8) -8 = a0
(1,-3) -3 = a3 + a2 + a1 - 8 a3 + a2 + a1 = 5 (2,6) 6 = 8a3 + 4a2 + 2a1 – 8 8a3 + 4a2 + 2a1 = 14 (3,31) 31 = 27a3 + 9a2 + 3a1 -8 27a3 + 9a2 + 3a1 = 39 Sehingga ougmented matriks koefesien SPL tersebut adalah
dan a0 = -8 sehingga persamaan dari data laba penjualan itu adalah
f(x) = 2x3 – 4x2 + 7x -8.
Evaluasi nilai f(x) untuk 0 ≤ x ≤ 7 dengan ∆x = 1 diperoleh sebagai berikut:
X 0 1 2 3 4 5 6 7
Numerik
X 8 9 10 11 12 13 14 15
f(x) 81 6
1189 166 2
224 7
295 6
380 1
479 4
5947
0 5 10 15
-1000 0 1000 2000 3000 4000 5000 6000
Hari
L
a
b
a
Hubungan hari dengan laba
Dat a ak t ual Int erpolasi P 3 Ek s t rapolasi P 3
Gambar 2.16 Grafk pemetaan hari terhadap laba
Memperhatikan bahwa interpolasi derajat tiga yang diterapkan dapat dengan tepat melalui semua titik yang ada, maka fungsi f(x) = 2x3 – 4x2 + 7x -8 dapat diterapkan unutk melakukan ektrapolasi, yaitu penentuan nilai yang berada diluar titik data yang ada. Hasil yang diperoleh sebagaimana pada table di atas. Laba yang diperoleh setelah 15 hari penjualan adalah dengan menjumlahkan nilai laba dari hari awal hingga hari ke-15 yaitu Rp.
2.455.200.000,-Beberapa sifat beda hingga adalah sebagai berikut: 1.
1 2 3
! 3
) 2 )( 1 ( !
2 ) 1 (
n i n
i n
i n i i
nf f nf n n f n n n f
2. Jika h = 1, maka ∆nxn = n(n-1)(n-2)…(3)(2)(1) = n!
Numerik
2.3.2.2 Metode Newton Gregori Maju
Metode Newton Gregori Maju merupakan metode interpolasi mengunakan polinomial yang direkontruksi dari Deret Taylor.
Dengan
h x x
s 0
Numerik
Selesaikan teladan di atas dengan mengunakan interpolasi polynomial newton gregori maju.
Solusi
Tinjau kembali table beda hingga pada teladan di atas. Jika mengambil nilai awal x0 = 0, maka diperoleh koefesien beda hingga untuk polynomial newton gregori maju sebagaimana yang terlingkari berikut:
xi
x f(x
)
f
2 f
3f
4f
x
0
0 -8
5 x
1
1 -3 4
9 12
x
2
2 6 16 0
25 12
x
3
3 31 28 0
53 12
x
4
4 84 40 0
93 12
x
5
5 17
7
52 0
145 12
x
6
6 32
2
64
209 x
7
7 53
Numerik
Dari table di atas, diperoleh nilai x0 = 0, f0 = -8, ∆f0 = 5, ∆2f0 = 4 dan ∆3f
0 = 12. h = x1 – x0 = 1 – 0 = 1 dan s = (x – x0)/h = x. Drin ilia tersebut maka diperoleh pendekatan dengan polynomial newton gregori maju sebagai berikut:
! 3
) 2 )( 1 ( !
2 ) 1 ( ! 1 ! 0 )
(x f0 s f0 s s 2f0 s s s 3f0
Pn
6
) 2 )( 1 ( 12 2
) 1 ( 4 5
8
x x x x x x
6
) 2 3 ( 12 2
4 4 5
8 2 2
x x x x x x
6 24 36
12 6
12 12 6 30 8
2 3
2 x x x x
x
x
8 7 4 2 6
12 24 42
8 2 3 3 2
x x x x x x
8 7 4 2 )
( 3 2
P x x x x
Hasil ini sesuai dengan hasil fungsi .
Sebagai pembanding hasil persamaan yang diperoleh tersebut, misalkan diambil nilai awal x0 = 3, maka diperoleh nilai beda hingga yang digunakan unutk interpolasi adalah sebagaimana yang dilingkari.
xi
x f(x) f 2 f 3f 4f
x-3
0 -8
5
x-2
1 -3 4
9 12
x-1
2 6 16 0
25 12
x0 3 31 28 0
53 12
x1
4 84 40 0
93 12
x2
Numerik polynomial adalah
! berbeda akan tetapi tetap memberikan persamaan interpolasi yang sama.
2.3.2.3 Defnisi Polinomial Newton Gregori Mundur
Dengan
h x x
s 0
Numerik
-3 = 12, sehingga diperoleh polynomial newton Gregory Mundur adalah sebagai berikut:
Numerik
Jadi dengan polynomial Newton Mundur dan x0 = 7
diperoleh fungsi polynomial ( ) 2 3 4 2 7 8
3 x x x x
P .
Hasil ini sama dengan nilai dari polynomial newton maju sebelumnya.
Selanjutnya dilakukan pemeriksaan apakah perhitungan polynomial newton gregori mundur dengan nilai awal x0
= 5 akan memberikan nilai yang sama dengan hasil sebelumnya.
Untuk x0 = 3, maka s= x-3, f0=31, ∆f-1=25, ∆2f-2=16 dan
∆3f
-3 = 12
! 3
) 2 )( 1 ( !
2 ) 1 ( ! 1 ! 0 ) ( )
( 2
3 1
2 1
0
3
P x f s f s s f s s s f
x f
6
12 ) 1 )( 2 )( 3 ( 2
16 ) 2 )( 3 ( 25 ) 3 (
31
x x x x x x
2 ) 6 5 6
5 ( 8 ) 6 5 ( 75 25
31 2 3 2 2
x x x x x x x x
12 10 2
12 10
2 48 40 8
75 25
31 2 3 2 2
x x x x x x x x
3 2 2
4 7
8 x x x
Hasil akhir ini menunjukkan polynomial yang diberikan selalu sama meskipun dilakukan dengan metode invers matriks, polynomial newton maju, dengan nilai awal yang berbeda dan polynomial newton mundur dengan nilai awal yang berbeda. Teladan.
Evaluasi nilai f(0.73) dari data f(x)=tan (x) pada interval [0 1] dengan ∆x = 0.2 mengunakan polynomial newton maju dan munur.
Solusi:
Tabel beda hingga perolehan data dari fungsi f(x)=tan x pada domain interval [0 1] dengan ∆x = 0.2 adalah:
S X f(x) ∆f(x
) ∆
2f(
x) ∆
3f(
x) ∆
4f(x )
x-2 0 0
0.20 3 x-1 0.2 0.20
3
Numerik
Penyelesaian menggunakan interpolasi Newton-Gregory Maju
Diketahui: h = 0.2
Ambil x0 = 0.4 , bias juga x0 = 0.6 ( karena sebelum 0.73 (jika gunakan polynomial Newton Maju)
65
S gunakan f(0.73)
Jadi:
Perhitungan nilai f(0.73) menggunakan interpolasi polynomial newton gregori maju diperoleh tingkat error = |0.893-0.897| =
Numerik 2.4 Rangkuman
1. Suatu hampiran yang digunakan untuk mendapatkan model yang berbeda dari suatu model matematika atau fakta alam yang ada disebut dengan Aproksimasi
2. Metode aproksimasi dengan Deret Maclaurin adalah n
3. Metode aproksimasi Deret Taylor adalah
4. Interpolasi adalah menentukan nilai suatu objek atau titik yang terletak di antara titik titik yang ada.
5. Interpolasi Linier adalah menentukan nilai yang terletak diatara dua titik dengan persamaan garis f(x) = ax + b. 6. Interpolasi kuadrat adalah menentukan nilai yang terletak
diantara tiga titik dengan persamaan kuadrat f(x) = ax2 + bx +c.
7. Interpolasi Kubik adalah menentukan nilai yang terletak diantara empat titik dengan persamaan polinomial derajat tiga f(x) = ax3 + bx2 + cx + d
8. Interpolasi polinomial berderajat n adalah menentukan nilai diantara n data dengan polinomial berderajat n-1 dengan persamaan
f(x) = an-1xn-1 + an-2 xn-2 + an-3 xn-3 + … + a1 x +a0
Numerik
! 4
) 3 )( 2 )( 1 ( !
3 ) 2 )( 1 ( !
2 ) 1 ( ! 1 ! 0 )
(x f0 s f0 s s 2f0 s s s 3f0 s s s s 4f0 Pn
dengan
h x x
s 0 .
10. Interpolasi Newton Gergori Mundur adalah menentukan nilai di antara data yang diketahui dengan persamaan
! 4
) 3 )( 2 )( 1 ( !
3 ) 2 )( 1 ( !
2 ) 1 ( ! 1 ! 0 )
(x f0 s f 1 s s 2f 1 s s s 3f 2 s s s s 4f 3 Pn
Dengan
h x x
Numerik
2.5 Latihan
Selesaikan soal di bawah ini dengan benar!
1. Dapatkan persamaan yang memenuhi dari data
Kemudian tentukan nilai y bila x = 0.4
2. Lakukan interolasi polinomial untuk merekontruksi model garis pelukis bukit pada gambar di bawah ini, kemudian tentukan ketingian bukit pada jarak h = ¼ dan tingkat kecuramanya.
Gambar 2.17 Model gritosasi pola sebuah bukit 3. Lakukan aproksimasi untuk mendapatkan bentuk fungsi
Numerik
x x
x x
xe x e
x
xe e
x x f
4 sin ln
) ln(
tan ) cos( 2 ) (
3 2 sin 2
sin 3
pada domain 1 < x < 1.5. kemudian tentukan nilai dari f’(1.2).
4. Lakukan gritisasi dan rekontruksi fungsi yang tepat melalui kurva daerah rawan banjir (warna merah) di kecamatan Sandubaya Kota Mataram berikut, kemudian hitung luasnya.
Suber: Peta tata ruang 2011-2031 kota Mataram Gambar 2.18 Peta daerah rawan banjir di Kecamatan
Sandubaya Kota Mataram NTB
5. Lengkapi tabel berikut dan Sketsa grafk fungsi y = f(x) . x y ∆y ∆2y ∆3y ∆4y ∆5y
0 ………
….
……… …
5 ………
…. 0.0013
0.088
8 …………..
1
Numerik
……… …..
……… …..
-0.000 2 1
5 ………... ………….. ………….
………
…. 0.0017
2
0 …………. ………….. ………
… 2
5
0.466 3
6. Lakukan aproksimasi dengan deret Maclaurinatau Deret Taylor untuk menghampiri fungsi berikut sehingga bernilai sama pada domain yang diberikan:
a. f(x) = ex pada domain [-5 5];
b. f(x) = sin x / x pada domain [10 13];
7. Dengan metode Newton Gregory Maju dan Mundur, tentukan nilai awal yang tepat untuk menentukan nilai f(0.158) dan f(0.636) dari data sebagaimana tabel beda hingga berrikut :
x f(x) ∆f ∆2f ∆3f ∆4f
0.125 0.7916 8
-0.0183 4 0.250 0.7733
4 -0.0112
9
-0.0296 3
0.0013 4 0.375 0.7437
1 -0.0099
5
-0.00038
-0.0395 8
0.0017 2
Numerik
3 0.0082
3
-0.0478 1
0.0020 0 0.625 0.6563
2 -0.0062
3
-0.0540 4 0.750 0.6022
8
8. Tentukan nilai dari y untuk x = 0.58 dengan interpolasi kubik pada domain [0.3 0.9] dari data berikut:
x y ∆y ∆2y ∆3y
0.1 0.003
0.064
0.3 0.067 0.017
0.081 0.002
0.5 0.148 0.019
0.100 0.003
0.7 0.248 0.022
0.122 0.004
0.9 0.370 0.026
0.148 0.005
1.1 0.518 0.031
0.179