3. H
u
b
u
ng
a
n g
a
r
i
s d
e
ng
a
n
l
i
ngk
a
r
a
n
Oleh Aska Muta Yuliani
Misalnya diminta untuk menentukan sebuah titik sembarang di luar lingkaran, misalnya titik P. Melalui titik P diminta untuk menggambar garis yang memotong lingkaran di dua titik, yaitu di titik A dan titik B, garis yang memotong lingkaran di satu titik saja, yaitu titik C dan garis yang tidak memotong lingkaran.
Misalnya diminta untuk menentukan sebuah titik sembarang di luar lingkaran, misalnya titik P. Melalui titik P diminta untuk menggambar garis yang memotong lingkaran di dua titik, yaitu di titik A dan titik B, garis yang memotong lingkaran di satu titik saja, yaitu titik C dan garis yang tidak memotong lingkaran.
jadi posisi garis terhadap lingkaran
ada 3 macam, yaitu
1. garis memotong lingkaran pada
dua titik berbeda.
jadi posisi garis terhadap lingkaran
ada 3 macam, yaitu
1. garis memotong lingkaran pada
dua titik berbeda.
A
2. garis memotong lingkaran pada satu
titik saja, dan ini disebut garis
menyinggung lingkaran
Untuk menenentukan posisi garis
terhadap lingkaran dapat dilihat dari
nilai diskriminanya (D)
Jika
maka
D < 0
tidak memotong
D= 0 memotong pada satu titik
(menyinggung)
:Tentukan posisi garis Penyeleaian
y = subsitusi pada
:Tentukan posisi garis Penyeleaian
y = subsitusi pada
D =
= 944 D>0 ,
Maka garis memotong pada dua titik yang berbeda
Contoh
4. Hubungan
antar
• Pada gambar a lngkaran dan berpotongan di dua titik yang
berlainan
Jika pusat lingkaran berada di lingkaran , atau sebaliknya dikatakan dan berpotongan didalam. Perhatikan gambar a(i) Jika pusat lingkaran di luar lingkaran atau sebaliknya
,dikatakan dan berpotongan di luar. Perhatikan gambar a(ii)
• Pada gambar a lngkaran dan berpotongan di dua titik yang
berlainan
Jika pusat lingkaran berada di lingkaran , atau sebaliknya dikatakan dan berpotongan didalam. Perhatikan gambar a(i) Jika pusat lingkaran di luar lingkaran atau sebaliknya
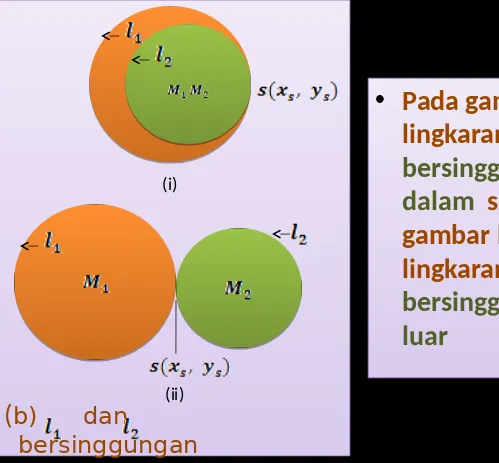
(
b) dan bersinggungan(
b) dan bersinggungan•
Pada gambar b (i)
lingkaran dan
bersinggung di
dalam sedangkan
gambar b(ii),
lingkaran dan
bersinggung di
luar
•
Pada gambar b (i)
lingkaran dan
bersinggung di
dalam
sedangkan
gambar b(ii),
lingkaran dan
bersinggung di
luar
(i)
[image:9.720.58.557.42.505.2]Pada gambar c(i), lingkaran dan tidak berpotongan maupun bersinggung didalam
Pada gambar c(ii), lingkaran dan tidak berpotongan maupun bersinggung diluar
Jika lingkaran dan tidak berpotongan maupun bersinggungan di kataka dan saling lepas.
Pada gambar c(i), lingkaran dan tidak berpotongan maupun bersinggung didalam
Pada gambar c(ii), lingkaran dan tidak berpotongan maupun bersinggung diluar
Jika lingkaran dan tidak berpotongan maupun bersinggungan di kataka dan saling lepas.
(ii) (c). dan Tidak
•
Tentukan posisi dua lingkaran berikut ini.
•
Jawab :
•
Tentukan posisi dua lingkaran berikut ini.
•
Jawab :
•
Substitusi ke
diperoleh
•