SKRIPSI. Diajukan untuk Memenuhi Salah Satu Syarat. Memperoleh Gelar Sarjana Pendidikan. Program Studi Pendidikan Matematika

(1)

SELING (𝑨_𝒏), GRUP DIHEDRAL (𝑫_𝟐𝒏), DAN GRUP QUATERNION (𝑸_𝟖)

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Disusun oleh :

Anastasia Melissa Raharjo NIM : 171414053

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA 2021

(2)

i

GRAF KEMBAR NON-KOMUTING DARI GRUP SIMETRI (𝑺_𝒏), GRUP SELANG- SELING (𝑨_𝒏), GRUP DIHEDRAL (𝑫_𝟐𝒏), DAN GRUP QUATERNION (𝑸_𝟖)

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Disusun oleh :

Anastasia Melissa Raharjo NIM : 171414053

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA 2021

(3)

ii

(4)

iii

(5)

iv

HALAMAN PERSEMBAHAN

Dengan mengucap syukur kepada Tuhan, skripsi ini penulis persembahkan untuk : 1. Tuhan Yesus Kristus yang senantiasa melimpahkan berkat-Nya sehingga

saya dapat menyelesaikan skripsi ini.

2. Orang tua dan adik saya terkasih yang selalu memberikan dukungan dalam bentuk apapun baik secara langsung maupun tidak langsung.

3. Program Studi Pendidikan Matematika Universitas Sanata Dharma yang telah memberikan saya pengalaman belajar selama 4 tahun.

4. Para pembaca maupun siapapun yang tertarik dengan aljabar abstrak.

Semoga apa yang saya tuliskan dalam skripsi ini dapat berguna bagi anda semua.

(6)

v MOTTO

“Jangan takut untuk menerima tantangan walaupun awalnya kamu tidak tahu apa-apa”

“Abstact is beautiful”

(7)

vi

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa yang skripsi yang saya tulis ini tidak memuat karya atau bagian karya dari orang lain kecuali yang telah disebutkan dalam kutipan dan daftar pustaka sebagaimana layaknya karya ilmiah.

Yogyakarta, 26 April 2021

Anastasia Melissa Raharjo

(8)

vii

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma :

Nama : Anastasia Melissa Raharjo

Nomor Induk Mahasiswa : 171414053

Demi perkembangan ilmu pengetahuan, saya memberikan kepada perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul :

“GRAF KEMBAR NON-KOMUTING DARI GRUP SIMETRI (𝑺_𝒏), GRUP SELANG-SELING (𝑨_𝒏), GRUP DIHEDRAL (𝑫_𝟐𝒏), DAN GRUP QUATERNION (𝑸_𝟖)”

Dengan demikian, saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengolahnya dalam pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu meminta izin kepada saya maupun memberikan royalti pada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini saya buat dengan sebenarnya.

Yogyakarta, 26 April 2021 Yang menyatakan

Anastasia Melissa Raharjo

(9)

viii ABSTRAK

Anastasia Melissa Raharjo. 2021. Graf Kembar Non-Komuting dari Grup Simetri (𝑺_𝒏), Grup Selang-seling (𝑨_𝒏), Grup Dihedral (𝑫_𝟐𝒏), dan Grup Quaternion (𝑸_𝟖). Skripsi. Program Studi Pendidikan Matematika. Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam. Fakultas Keguruan dan Ilmu Pendidikan. Universitas Sanata Dharma.

Representasi graf dari suatu grup merupakan salah satu kajian matematika yang belakangan ini sedang berkembang, salah satunya adalah mengenai graf non-komuting. Graf non-komuting dari suatu grup pertama kali diperkenalkan oleh Paul Erdos pada tahun 1975 melalui sebuah permasalahan menganai batasan kardinalitas pada graf non-komuting dari sebuah grup 𝐺 yang tidak memiliki subgraf lengkap tak terhingga. Permasalahan tersebut kemudian dijawab oleh B.H Newman. Abdollahi (2006) melanjutkan kajian mengenai graf non-komuting dari suatu grup. Berkaitan dengan graf non-komuting, dua tahun belakangan ini berkembang kajian mengenai graf kembar non-komuting dari suatu grup yang dilakukan oleh Tolue (2019). Tujuan penelitian ini adalah (1) untuk mengetahui definisi graf non-komuting dan graf kembar non-komuting dari suatu grup dan (2) untuk mengetahui sifat-sifat graf kembar non-komuting dari grup simetri, grup selang-seling, grup dihedral dan grup quaternion.

Graf non-komuting dari grup 𝐺 (Γ_𝐺) adalah graf sederhana yang himpunan simpulnya adalah 𝑉(Γ_𝐺) = 𝐺 − 𝑍(𝐺) dan untuk setiap 𝑥, 𝑦 ∈ 𝑉(Γ_𝐺), (𝑥, 𝑦) ∈ 𝐸(Γ_𝐺) jika dan hanya jika 𝑥𝑦 ≠ 𝑦𝑥. Selanjutnya, graf kembar non- komuting dari suatu grup 𝐺 (Γ_𝐺^∗) adalah graf yang dibentuk dengan mempartisi simpul-simpul dari dari graf non-komuting Γ(𝐺) berdasarkan sifat simpul kembar sehingga himpunan simpul dari graf kembar non-komuting adalah 𝑉(𝛤_𝐺^∗) = {𝑣₁^∗, 𝑣₂^∗, 𝑣₃^∗, … , 𝑣_𝑘^∗} dengan 𝑣_𝑖^∗ adalah anggota himpunan semua simpul yang kembar dengan 𝑣_𝑖 pada Γ_𝐺. Selanjutnya, 𝑣_𝑖^∗𝑣_𝑗^∗ ∈ 𝐸 (𝛤_𝐺^∗) jika dan hanya jika 𝑣_𝑖𝑣_𝑗 ∈ 𝐸(𝛤_𝐺). Beberapa sifat graf non-komuting dan graf kembar non-komuting dari suatu grup telah dibahas oleh Abdollahi (2006) dan Tolue (2019). Hasil penelitian ini menunjukkan bahwa graf non-komuting dari grup selang-seling (Γ_𝐴_𝑛) merupakan subgraf dari graf non-komuting dari grup simetri (Γ_𝑆_𝑛) dan graf kembar non-komuting dari grup selang-seling (Γ_𝐴^∗_𝑛) merupakan subgraf dari graf kembar non-komuting dari grup simetri (Γ_𝑆^∗_𝑛). Selain itu, pada grup dihedral (𝐷_2𝑛), Γ_𝐷^∗_2𝑛≅ 𝐾₂ untuk 𝑛 bilangan ganjil dan Γ_𝐷^∗_2𝑛 ≅ 𝐾^𝑛

2+1 untuk 𝑛 bilangan genap. Untuk grup quaternion (𝑄₈), Γ_𝑄₈ ≅ Γ_𝐷₈ dan Γ_𝑄^∗₈ ≅ Γ_𝐷^∗₈ meskipun 𝑄₈ tidak isomorfis dengan 𝐷₈.

Kata kunci : grup, graf non-komuting, graf kembar non-komuting.

(10)

ix ABSTRACT

Anastasia Melissa Raharjo. 2021. Twin Non-commuting Graph of Symmetric Group (𝑺_𝒏), Alternating Group (𝑨_𝒏), Dihedral Group (𝑫_𝟐𝒏), and Quaternion Group (𝑸_𝟖). Undergraduate Thesis. Mathematic Education Study Program.

Department of Mathematics and Science Education. Facukty of Education and Teacher Training. Sanata Dharma University.

Graph representation of a group is a mathematical study that is currently being developed. One of them is about non-commuting graphs. The non- commuting graph of a group was first introduced by Paul Erdos in 1975 through the following problem. Let G be a group whose non-commuting graph has no inﬁnite complete subgraph. Is it true that there is a ﬁnite bound on the cardinalities of complete subgraphs of 𝛤_𝐺?The problem was answered by B.H Newman. Abdollahi (2006) continued the study of non-commuting graphs of a group. Then, a study about twin non-commuting graph of a group has been conducted by Tolue in 2019. The objectives of this study are (1) to see the definition of non-commuting and twin non-commuting graph of a group and (2) to see the properties of non-commuting and non-commuting twin graph of symmetric group, alternating group, dihedral group and quaternion group.

The non-commuting graph of a group 𝐺,denoted by 𝛤_𝐺, is a simple graph which the vertices 𝑉(𝛤_𝐺) = 𝐺 − 𝑍(𝐺) and for each 𝑥, 𝑦 ∈ 𝑉(𝛤_𝐺), 𝑥𝑦 ∈ 𝐸(𝛤_𝐺) if and only if 𝑥𝑦 ≠ 𝑦𝑥. Then, the twin non-commuting graph of a group 𝐺, denoted by 𝛤_𝐺^∗, is a graph formed by partitioning the vertices of the non-commuting graph 𝛤_𝐺 where the vertices of the twin non-commuting graph is 𝑉(𝛤_𝐺^∗) = {𝑣₁^∗, 𝑣₂^∗, 𝑣₃^∗, … , 𝑣_𝑘^∗} where 𝑣_𝑖^∗ is an element of set of all vertices that are twins with 𝑣_𝑖. Furthermore,𝑣_𝑖^∗𝑣_𝑗^∗is adjacent, that is 𝑣_𝑖^∗𝑣_𝑗^∗ ∈ 𝐸 (𝛤_𝐺^∗), if and only if 𝑣_𝑖𝑣_𝑗 ∈ 𝐸(𝛤_𝐺). Some properties on the non-commuting graph and the twin non- commuting graph has been disscussed by Abdollahi (2006) and Tolue (2019). This study show that the non-commuting group of alternating group (𝛤_𝐴_𝑛) is a subgraph of the non-commuting graph of symmetric group (𝛤_𝑆_𝑛) and the twin non- commuting group of alternating group (𝛤_𝐴^∗_𝑛) is a subgraph of the twin non- commuting graph of symmetric group (𝛤_𝑆^∗_𝑛). Furthermore, the twin non- commuting graph of dihedral group (𝛤_𝐷^∗_2𝑛) is isomorphic to 𝐾₂ if 𝑛 is odd and isomorphic to 𝐾^𝑛

2+1 if 𝑛 is even. For quaternion group (𝑄₈), Γ_𝑄₈ ≅ Γ_𝐷₈ and Γ_𝑄^∗₈ ≅ Γ_𝐷^∗₈ although 𝑄₈ is not isomorphic to 𝐷₈.

Keywords : group, non-commuting graph, twin non-commuting graph.

(11)

x

KATA PENGANTAR

Puji syukur ke-Hadirat Tuhan Yang Maha Esa atas rahmat dan kasih karunia-Nya, peneliti dapat menyelesaikan skripsi berjudul “Graf Kembar Non- Komuting dari Grup Simetri (𝑆_𝑛), Grup Selang-seling (𝐴_𝑛), Grup Dihedral (𝐷_2𝑛), dan Grup Quaternion (𝑄₈)” dengan baik dan lancar. Dalam proses penyusunan skripsi ini, peneliti mendapatkan banyak pengalaman dan juga hambatan. Namun, peneliti dapat menyelesaikan penulisan skripsi ini dengan baik atas bantuan, dukungan, semangat, dan motivasi dari berbagai pihak. Oleh sebab itu, penulis mengucapkan banyak terima kasih kepada :

1. Bapak Dr. Yohanes Harsoyo S.Pd, M.Si., selaku Dekan Fakultas Keguruan dan Ilmu Pendidikan.

2. Bapak Beni Utomo, M.Sc selaku Ketua Program Studi Pendidikan Matermatika sekaligus sebagai Dosen Pembimbing Akademik Peneliti selama menempuh pendidikan di Universitas Sanata Dharma.

3. Rm. Eko Budi Santoso, S.J., S.Pd, Ph.D selaku dosen pembimbing skripsi yang telah meluangkan waktu, tenaga, dan pikiran untuk membimbing peneliti dalam menyelesaikan tugas akhir ini.

4. Segenap dosen Program Studi Pendidikan Matematika Universitas Sanata Dharma yang senantiasa membimbing dan memberikan ilmu yang berguna bagi peneliti selama perkuliahan.

5. Segenap staff Sekertariat JPMIPA yang telah banyak membantu peneliti dalam mengurus administrasi selama berkuliah di Program Studi Pendidikan Matematika.

(12)

xi

6. Keluarga dan teman-teman peneliti yang senantiasa memberikan dukungan dan semangat kepada peneliti sehingga peneliti dapat menyelesaikan skripsi ini.

Terlepas dari hal tersebut, peneliti menyadari bahwa penulisan skripsi ini masih terdapat berbagai bentuk kekurangan. Oleh karena itu, peneliti berharap hasil penelitian ini, selain dapat menambah wawasan pembaca, juga dapat dijadikan acuan atau referensi penelitian lain. Semoga skripsi ini dapat berguna bagi pembaca terlebih dalam rangka perkembangan aljabar abstrak selanjutnya.

Yogyakarta, 21 April 2021 Peneliti

(13)

xii DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN ... ii

HALAMAN PENGESAHAN ... iii

HALAMAN PERSEMBAHAN ... iv

HALAMAN MOTTO ... v

PERNYATAAN KEASLIAN KARYA ... vi

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ... vii

ABSTRAK ... viii

ABSTRACT ... ix

KATA PENGANTAR ... x

DAFTAR ISI ... xii

DAFTAR TABEL ... xv

DAFTAR GAMBAR ... xvi

DAFTAR NOTASI ... xviii

BAB I PENDAHULUAN ... 1

A. Latar Belakang ... 1

B. Rumusan Masalah ... 5

C. Batasan Masalah ... 6

D. Tujuan dan Manfaat Penelitian ... 6

(14)

xiii

E. Metode Penulisan ... 6

F. Sistematika Penulisan ... 7

BAB II KAJIAN PUSTAKA ... 9

A. Fungsi ... 9

B. Grup ... 25

C. Jenis-jenis Grup ... 41

D. Graf ... 56

BAB III GRAF NON-KOMUTING DARI SUATU GRUP ... 73

A. Graf Non-Komuting dari Suatu Grup ... 73

B. Bentuk-bentuk Graf Non-Komuting dari Grup Simetri (𝑆_𝑛) ... 73

C. Bentuk-bentuk Graf Non-Komuting dari Grup Selang-seling (𝐴_𝑛) ... 76

D. Bentuk-bentuk Graf Non-Komuting dari Grup Dihedral (𝐷_2𝑛) ... 78

E. Bentuk Graf Non-Komuting dari Grup Quaternion (𝑄₈) ... 82

F. Sifat-sifat Graf Non-Komuting dari Suatu Grup ... 83

BAB IV PEMBAHASAN ... 90

A. Graf Kembar Non-Komuting ... 90

B. Bentuk-bentuk Graf Kembar Non-Komuting dari Grup Simetri (𝑆_𝑛) ... 94

C. Bentuk-bentuk Graf Kembar Non-Komuting dari Grup Selang-seling (𝐴_𝑛) ... 97

D. Bentuk-bentuk Graf Kembar Non-Komuting dari Grup Dihedral (𝐷_2𝑛) ... 98

E. Bentuk Graf Kembar Non-Komuting dari Grup Quaternion (𝑄₈) ... 100

F. Sifat-sifat Graf Kembar Non-Komuting dari Suatu Grup ... 101

BAB V PENUTUP ... 107

(15)

xiv

A. Kesimpulan ... 107

B. Saran ... 109

DAFTAR PUSTAKA ... 110

LAMPIRAN : Publikasi ... 112

LAMPIRAN : Bukti Penerimaan Abstrak ... 119

LAMPIRAN : Sertifikat Peserta Seminar ... 120

(16)

xv

DAFTAR TABEL

Halaman

Tabel 2.1 Tabel Cayley ℤ/4ℤ ... 41

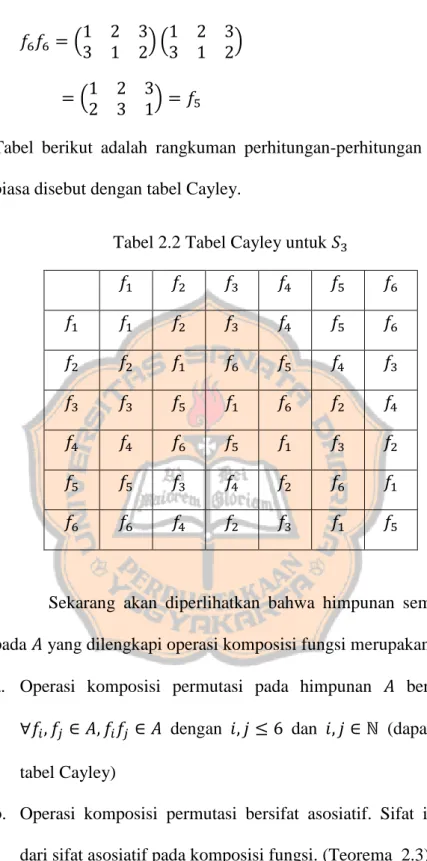
Tabel 2.2 Tabel Cayley untuk Grup 𝑆₃ ... 46

Tabel 2.3 Tabel Cayley Himpunan 𝐵 ... 51

Tabel 2.4 Tabel Hasil Rotasi dan Refleksi Persegi PWGB ... 54

Tabel 2.5 Tabel Cayley Grup 𝑄₈... 57

Tabel 3.1 Tabel Cayley Grup 𝐷₆ ... 79

Tabel 3.2 Tabel Cayley Grup 𝐷₈ ... 80

Tabel 3.3 Tabel Cayley Grup 𝐷₁₀ ... 81

(17)

xvi

DAFTAR GAMBAR

Halaman

Gambar 1.1 Jembatan Koeningberg ... 1

Gambar 1. 2 Salah satu solusi Knight Tour Problem ... 2

Gambar 2.1 Relasi dari A ke B ... 10

Gambar 2.5 Fungsi Injektif ... 12

Gambar 2.6 Fungsi Surjektif ... 13

Gambar 2.7 Fungsi Bijektif ... 14

Gambar 2.8 Permutasi dan Bukan Permutasi ... 15

Gambar 2.9 Komposisi Dua Fungsi ... 22

Gambar 2.10 Isomorfisme ... 35

Gambar 2.11 Persegi PWGB ... 53

Gambar 2.12 Graf 𝐺 ... 56

Gambar 2.13 Graf 𝐻 ... 59

Gambar 2.14 Graf 𝐺 dan Graf 𝐻 ... 61

Gambar 2.15 Graf Lengkap 𝐾₄ ... 62

Gambar 2.17 Graf 𝐼 ... 64

(18)

xvii

Gambar 2.20 Lintasan 𝑃... 68

Gambar 2.21 Graf Planar 𝑃 ... 70

Gambar 3.1 Graf Non-Komuting dari Grup 𝑆₂ ... 74

Gambar 3.2 Graf Non-Komuting dari Grup 𝑆₃ ... 75

Gambar 3.3 Graf Non-Komuting dari Grup 𝑆₄ ... 76

Gambar 3.4 Graf Non-Komuting dari Grup 𝐴₃ ... 77

Gambar 3.5 Graf Non-Komuting dari Grup 𝐴₄ ... 78

Gambar 3.6 Graf Non-Komuting dari Grup 𝐷₆ ... 80

Gambar 3.7 Graf Non-Komuting dari Grup 𝐷₈ ... 81

Gambar 3.8 Graf Non-Komuting dari Grup 𝐷₁₀ ... 82

Gambar 3.9 Graf Non-Komuting dari Grup 𝑄₈ ... 83

Gambar 4.2 Graf 𝐺^∗ ... 93

Gambar 4.3 Graf Kembar Non-Komuting dari Grup 𝑆₃ ... 95

Gambar 4.4 Graf Kembar Non-Komuting dari Grup 𝑆₄ ... 96

Gambar 4.5 Graf Kembar Non-Komuting dari Grup 𝐴₄ ... 98

Gambar 4.6 Graf Kembar Non-Komuting dari Grup 𝐷₆ ... 99

Gambar 4.7 Graf Kembar Non-Komuting dari Grup 𝐷₈ ... 99

Gambar 4.8 Graf Kembar Non-Komuting dari Grup 𝐷₁₀ ... 100

Gambar 4.9 Graf Kembar Non-Komuting dari Grup 𝑄₈ ... 101

(19)

xviii

DAFTAR NOTASI

𝑆_𝑛 : Grup simetri dari permutasi 𝑛 elemen

𝐴_𝑛 : Grup selang-seling dari permutasi genap 𝑛 elemen

𝐷_2𝑛 : Grup dihedral yang dibentuk dari komposisi perputaran atau pencerminan pada bangun segi 𝑛

𝑄₈ : grup quaternion dengan 8 elemen

|𝐺| : Order dari grup 𝐺 𝑍(𝐺) : Center dari grup 𝐺 𝐶(𝑥) : Centralizer dari 𝑥 ∈ 𝐺 𝑎𝐻 : Koset kiri dari 𝐻 𝐻𝑎 : Koset kanan dari 𝐻 𝐻 ⊲ 𝐺 : 𝐻 subgrup normal dari 𝐺 𝐺/𝐻 : Grup faktor

𝑉(𝐺) : Himpunan simpul dari graf 𝐺 𝐸(𝐺) : Himpunan sisi dari graf 𝐺 deg (𝑣) : Derajat simpul 𝑣

𝑑(𝑢, 𝑣) : Jarak simpul 𝑢 dan 𝑣

𝑁(𝑢) : Himpunan semua simpul yang bertetangga dengan 𝑢

𝑁[𝑢] : Gabungan 𝑢 dan himpunan semua simpul yang bertetangga dengan 𝑢 𝑒(𝑣) : Essentrisitas simpul 𝑣

𝑔(𝐺) : girth dari graf 𝐺

𝜔(𝐺) : bilangan clique dari graf 𝐺

(20)

xix 𝑑𝑖𝑎𝑚(𝐺) : Diameter graf 𝐺.

𝑢^∗ : Himpunan semua simpul yang memiliki tetangga sama dengan 𝑢 𝛤_𝐺 : Graf non-komuting dari grup 𝐺

𝛤_𝐺^∗ : Graf kembar non-komuting dari grup 𝐺

(21)

1 BAB I PENDAHULUAN

A. Latar Belakang

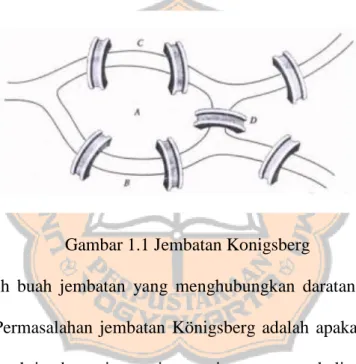
Teori graf merupakan salah satu cabang ilmu dalam matematika. Teori graf pada mulanya digunakan untuk permasalahan yang berkaitan dengan jaringan. Sejarah teori graf bermula dari permasalahan jembatan Konigsberg.

Gambar 1.1 Jembatan Konigsberg

Ada tujuh buah jembatan yang menghubungkan daratan yang dibelah oleh sungai. Permasalahan jembatan Königsberg adalah apakah mungkin melalui ketujuh buah jembatan itu masing-masing tepat satu kali, dan kembali lagi ke tempat semula? Permasalahan tersebut berhasil dipecahkan pada tahun 1736 oleh matematikawan asal Swiss yaitu Leonard Euler dengan memodelkan masalah tersebut dalam bentuk graf. Daratan dinyatakan sebagai titik yang dalam teori graf disebut simpul (vertex) dan jembatan dinyatakan sebagai garis yang disebut sisi (edge). Setiap titik diberi label huruf A, B, C, dan D.

Selanjutnya, teori graf juga digunakan pada permasalahan jarak terpendek. Contohnya adalah pada abad ke-19, seorang matematikawan

(22)

Irlandia W.R. Hamilton dan matematikawan Inggris Thomas Kirkman mempublikasikan sebuah permasalahan yang dikenal dengan persoalan perjalanan salesman (Traveling Salesman Problem). Seorang salesman akan mengunjungi beberapa tempat atau kota maka salesman tersebut harus menentukan rute yang paling pendek untuk mengunjungi semua kota tersebut.

Pertanyaannya adalah manakah jalur terpendek yang harus dilalui oleh salesman untuk mengunjungi semua kota yang dilalui dan kembali ke tempat asal. Permasalahan ini dikenal dengan Masalah Jalur Terpendek atau Traveling Salesman Problem.

Teori graf juga berkembang untuk menyelesaikan permasalahan- permasalahan dalam permainan. Salah satunya adalah pada abad ke 18, Moivre dan Euler memunculkan permasalahan berkaitan dengan permainan catur yang disebut Knight Tour Problem. Permasalahannya adalah bagaimana rute bidak kuda untuk mengunjungi setiap petak papan catur tepat satu kali.

Permasalahan ini selanjutnya memotivasi penelitian dalam teori graf yang dikenal dengan lintasan Hamilton (Palberry, 1997).

Gambar 1. 2 Salah satu solusi Knight Tour Problem

(23)

Selain penelitian tentang graf yang sudah disebutkan di atas, belakangan ini muncul perkembangan baru penelitian teori graf yang mengkaitkan graf dengan grup. Grup merupakan suatu kajian yang abstrak sehingga akan lebih mudah memahami sifat-sifat grup jika grup tersebut direpresentasikan dalam bentuk graf. Salah satu representasi graf dari suatu grup adalah graf non-komuting. Kajian mengenai graf non-komuting dari suatu grup diawali oleh masalah yang diajukan Paul Erdos pada tahun 1975 (Abdollahi, 2006). Erdos mengajukan permasalahan sebagai berikut

“Misalkan 𝐺 adalah suatu grup yang graf non-komutingnya tidak memiliki subgraf lengkap tak terhingga. Apakah benar ada batasan pada kardinalitas subgraf lengkap dari ΓG?”. Permasalahan itu kemudian dijawab oleh B.H.

Newmann pada tahun 1975 dalam sebuah tulisan yang berjudul “A Problem of Paul Erdos on Groups”. Dalam artikel tersebut, Newmann menjawab

permasalahan tersebut dengan membuktikan bahwa grup Paul Erdos (PE- groups) merupakan FC-group. Adapun FC-group adalah suatu grup yang

setiap kelas konjugasi dari elemennya memiliki kardinalitas yang terbatas (Scott, 1987).

Kajian mengenai graf non-komuting dilanjutkan oleh Abdollahi pada tahun 2006 yang melakukan eksplorasi sifat-sifat graf non-komuting 𝛤_𝐺 sehingga Abdollahi sering disebut sebagai seseorang yang memperkenalkan graf non-komuting dari suatu grup. Pada artikel tersebut, definisi graf non- komuting adalah sebagai berikut :

“Let 𝑍(𝐺) be the center of 𝐺. Associate a graph 𝛤_𝐺 with 𝐺 as follows: Take 𝐺\𝑍(𝐺) as the vertices of 𝛤_𝐺 and join two

(24)

distinct vertices 𝑥 and 𝑦 whenever 𝑥𝑦 ≠ 𝑦𝑥. Note that if 𝐺 is abelian, then 𝛤_𝐺 is the null graph.” (Abdollahi,2006)

Selain itu, juga ditunjukkan bahwa jika 𝐺 adalah grup nilpoten non-abelian berhingga dan 𝐻 adalah suatu grup sedemikian sehingga 𝛤_𝐺≅ 𝛤_𝐻 dan |𝐺| =

|𝐻|, maka 𝐻 adalah nilpoten.

Graf non-komuting bukanlah satu-satunya representasi graf dari grup.

Jenis graf lain yang didapat dari suatu grup yang pertama adalah graf identitas yaitu graf dengan simpul yang terdiri dari semua elemen dari 𝐺 dengan dua simpul berbeda 𝑥 dan 𝑦 dikatakan bertetangga apabila 𝑥𝑦=𝑒. Hal tersebut mengimplikasikan bahwa elemen identitas dari suatu grup selalu bertetangga dengan elemen yang lain (Kandasamy, 2009). Yang kedua adalah graf komuting yaitu graf dengan simpul yang terdiri dari semua elemen dari G dengan dua simpul berbeda 𝑥 dan 𝑦 dikatakan bertetangga apabila 𝑥𝑦=𝑦𝑥 (Vahidi, 2010). Selanjutnya ada graf koprima yaitu graf dengan simpul yang terdiri dari semua elemen dari 𝐺 dengan dua simpul berbeda 𝑥 dan 𝑦 dari Γ_𝐺 dikatakan bertetangga apabila (|𝑥|,|𝑦|)=1 (Ma, 2014). Dari pemaparan diatas, sejauh ini representasi graf dari suatu grup ada empat jenis.

Graf non-komuting dapat terlihat sangat kompleks. Maka dari itu, dua tahun belakangan ini berkembang suatu kajian mengenai graf kembar non- komuting dari suatu grup. Graf kembar (𝐺^∗) adalah suatu graf yang dibentuk dengan mempartisi simpul-simpul dari suatu graf berdasarkan sifat simpul kembar sehingga 𝑉(𝐺^∗) = {𝑣₁^∗, 𝑣₂^∗ , … , 𝑣_𝑛^∗} 𝑣_𝑖^∗ adalah himpunan semua simpul yang kembar dengan 𝑣_𝑖 dan (𝑣_𝑖^∗, 𝑣_𝑗^∗) ∈ 𝐸(𝐺^∗) jika dan hanya jika

(25)

(𝑣_𝑖, 𝑣_𝑗) ∈ 𝐸(𝐺). Dengan demikian, graf tersebut menjadi terlihat lebih sederhana.

Salah satu penelitian mengenai graf kembar non-komuting dari suatu grup adalah penelitian yang dilakuakan oleh Benhaz Tolue pada tahun 2019 yang berjudul “Twin Non-Commuting Graph of A Group”. Tolue memperkenalkan graf kembar non-komuting dari suatu grup. Salah satu hasil penelitiannya adalah dimensi metrik dari graf kembar non-komuting dari suatu grup adalah 3 jika dan hanya jika graf tersebut terkait dengan grup 𝑆₃ , 𝐷₈ , dan 𝑄₈.

Berdasarkan hasil dari penelitian-penelitian atau kajian-kajian sebelumnya, masih sangat jarang ditemui bentuk-bentuk graf kembar non- komuting dari suatu grup. Maka dari itu, penulis ingin melanjutkan penelitian tentang twin non-commuting graph of a group. Adapun jenis grup yang dipilih dalam penelitian ini meliputi grup simetri (𝑆_𝑛), grup selang-seling (𝐴_𝑛), grup dihedral (𝐷_2𝑛), dan grup quaternion (𝑄_𝑛).

B. Rumusan Masalah

1. Apa yang dimaksud dengan graf non-komuting dari suatu grup (non- commuting graph of a group)?

2. Apa yang dimaksud dengan graf kembar non-komuting (twin non- commuting graph of a group)?

(26)

3. Apa saja sifat-sifat graf non komuting dan graf kembar non-komuting dari grup simetri (𝑆_𝑛), grup selang-seling (𝐴_𝑛), grup dihedral (𝐷_2𝑛) dan grup quaternion (𝑄_𝑛).?

C. Batasan Masalah

Pada penelitian ini, penulis membatasi penelitian grup simetri (𝑆_𝑛), grup selang-seling (𝐴_𝑛), grup dihedral (𝐷_2𝑛) dan grup quaternion (𝑄_𝑛).

D. Tujuan dan Manfaat Penelitian

1. Untuk mengetahui definisi graf non-komuting dari suatu grup

2. Untuk mengetahui definisi graf kembar non-komuting dari suatu grup 3. Untuk mengetahui sifat-sifat graf non-komuting dan graf kembar non-

komuting dari grup simetri (𝑆_𝑛), grup selang-seling (𝐴_𝑛), grup dihedral (𝐷_2𝑛) dan grup quaternion (𝑄_𝑛).

E. Metode Penelitian

Metode penelitian yang digunakan dalam penelitian ini adalah penelitian pustaka (Library Research). Secara garis besar tahapan-tahapan yang akan dilakukan dalam penelitian ini, antara lain:

1. Mengumpulkan beberapa literatur mengenai topik graf kembar non- komuting dari suatu grup dan berbagai macam grup.

2. Mempelajari literatur yang telah dikumpulkan

(27)

4. Membuat dugaan-dugaan awal terkait dengan bentuk graf kembar tidak komuting dari grup simetri (𝑆_𝑛), grup selang-seling (𝐴_𝑛), grup dihedral (𝐷_2𝑛) dan grup quaternion (𝑄_𝑛).

5. Membuktikan dugaan-dugaan yang telah dibuat.

F. Sistematika Penulisan

Untuk mempermudah penulis dan pembaca dalam mengkaji skripsi ini, maka skripsi dibagi menjadi 5 bagian, yaitu:

BAB I PENDAHULUAN

Bab ini berisi paparan mengenai latar belakang, rumusan masalah, batasan masalah, tujuan dan manfaat penelitian, metode penelitian, dan sistematika penulisan

BAB II KAJIAN PUSTAKA

Bab ini berisi paparan konsep-konsep dasar dalam Teori Graf dan Grup yang dipergunakan dalam penelitian ini.

BAB III GRAF NON-KOMUTING DARI SUATU GRUP

Bab ini berisi paparan mengenai definisi graf non-komuting dari suatu grup beserta ilustrasinya dan hasil-hasil penelitian mengenai topik tersebut beserta teorema dan pembuktiannya.

(28)

BAB IV GRAF KEMBAR NON-KOMUTING DARI SUATU GRUP Bab ini berisi paparan mengenai definisi graf kembar non-komuting dari suatu grup beserta ilustrasinya dan hasil-hasil penelitian mengenai topik tersebut beserta teorema dan pembuktiannya.

BAB V PENUTUP

Bab ini berisi kesimpulan dari pembahasan pada BAB III dan BAB IV serta saran-saran untuk penelitian lanjut.

(29)

9 BAB II

KAJIAN PUSTAKA

A. Fungsi

Penelitian ini membahas grup-grup yang elemennya berupa fungsi. Maka dari itu, berikut adalah definisi-definisi dan istilah-istilah terkait fungsi yang perlu dipahami dalam penelitian ini.

Definisi 2.1. Fungsi (Susilo, 2012)

Diberikan himpunan X dan Y. Suatu fungsi adalah relasi khusus dari X ke Y, dinotasikan 𝑓: 𝑋 → 𝑌, yang memetakan setiap elemen 𝑋 dengan tepat satu elemen 𝑌. Dengan kata lain, suatu relasi dari X ke Y dikatakan fungsi jika dan hanya jika setiap elemen X berelasi dengan suatu elemen Y dan elemen dari himpunan Y yang berelasi dengan elemen di himpunan X adalah tunggal atau jika dituliskan dalan notasi adalah (∀𝑥₁, 𝑥₂ ∈ 𝑋) jika 𝑥₁ = 𝑥₂ maka 𝑓(𝑥₁) = 𝑓(𝑥₂).

Conton 2.1

Diberikan himpunan 𝐴 = {1,2,3} dan 𝐵 = {𝑎, 𝑏, 𝑐}. Gambar 2.1, 2.2, 2.3. dan 2.4 berikut adalah relasi-relasi dari himpunan A ke himpunan B.

(30)

Relasi di atas merupakan fungsi karena setiap elemen di A berelasi dengan elemen di B dan elemen di B tersebut tunggal.

Relasi yang diperlihatkan pada Gambar 2.2 merupakan fungsi karena setiap elemen di A berelasi secara tunggal dengan elemen di B.

Gambar 2.1. Relasi dari A ke B

𝐴 𝐵

𝑓

1 2 3

𝑎 𝑏 𝑐

𝐴 𝐵

𝑓

1 2 3

𝑎 𝑏 𝑐

(31)

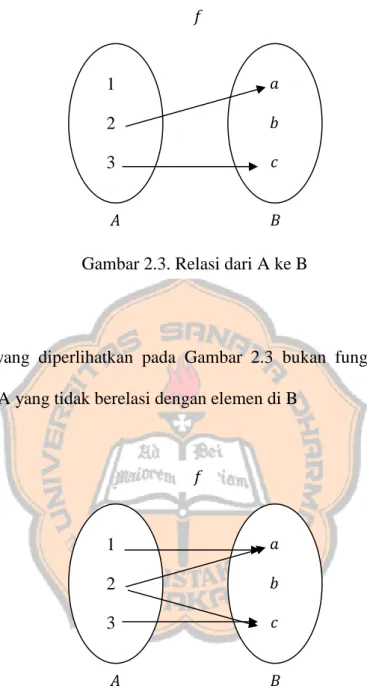
Relasi yang diperlihatkan pada Gambar 2.3 bukan fungsi karena terdapat elemen A yang tidak berelasi dengan elemen di B

Relasi yang diperlihatkan pada Gambar 2.4 bukan fungsi karena terdapat elemen di A yang berelasi dengan lebih dari satu elemen di B.

𝐴 𝐵

𝑓

1 2 3

𝑎 𝑏 𝑐

𝐴 𝐵

𝑓

1 2 3

𝑎 𝑏 𝑐

(32)

Fungsi-fungsi Khusus

Berikut adalah pembahasan mengenai beberapa fungsi khusus yang digunakan dalam penelitian ini.

1. Fungsi Injektif

Suatu fungsi dikatakan fungsi injektif apabila dua elemen dalam domain memiliki peta yang sama maka kedua elemen tersebut juga sama. Maka dari itu fungsi injektif dapat didefinisikan sebagai beikut.

Definisi 2.2. Fungsi Injektif (Susilo, 2012)

Suatu fungsi 𝑓: 𝑋 → 𝑌 dikatakan fungsi injektif jika dan hanya jika untuk setiap 𝑥₁, 𝑥₂ ∈ 𝑋, Jika 𝑓(𝑥₁) = 𝑓(𝑥₂) maka 𝑥₁ = 𝑥₂.

2. Fungsi Surjektif

Suatu fungsi dikatakan fungsi surjektif jika setiap elemen di kodomain memiliki pasangan di domain. Maka, fungsi surjektif dapat didefinisikan sebagai berikut.

𝑋 𝑌

2 1 3

𝑎 𝑏 𝑐 𝑑

Gambar 2.5. Fungsi Injektif

(33)

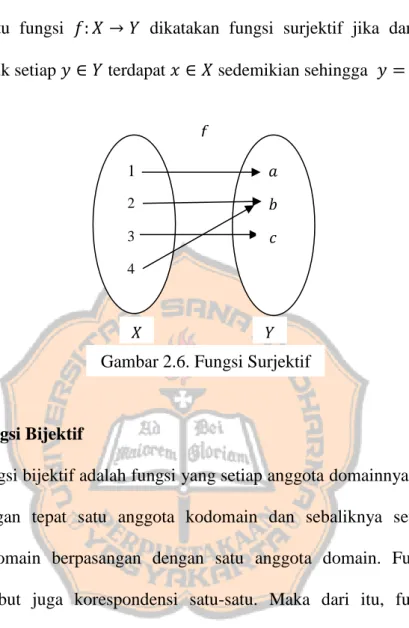
Definisi 2.3 Fungsi Surjektif (Susilo, 2012)

Suatu fungsi 𝑓: 𝑋 → 𝑌 dikatakan fungsi surjektif jika dan hanya jika untuk setiap 𝑦 ∈ 𝑌 terdapat 𝑥 ∈ 𝑋 sedemikian sehingga 𝑦 = 𝑓(𝑥)

3. Fungsi Bijektif

Fungsi bijektif adalah fungsi yang setiap anggota domainnya berpasangan dengan tepat satu anggota kodomain dan sebaliknya setiap anggota kodomain berpasangan dengan satu anggota domain. Fungsi bijektif disebut juga korespondensi satu-satu. Maka dari itu, fungsi bijektif didefinisikan sebagai berikut.

Definisi 2.4 Fungsi Bijektif (Susilo, 2012)

Suatu fungsi dikatakan fungsi bijektif jika dan hanya jika fungsi tersebut injektif dan surjektif.

𝑋 𝑌

1 2 3

𝑎 𝑏 𝑐 4

𝑓

Gambar 2.6. Fungsi Surjektif

(34)

4. Fungsi Invers

Jika 𝑓 merupakan fungsi yang memetakan himpunan 𝑋 ke himpunan 𝑌 maka invers dari fungsi 𝑓, dinotasikan dengan 𝑓⁻¹merupakan suatu relasi dari himpunan Y ke himpunan X sedemikian sehingga untuk 𝑦 ∈ 𝑌 dan 𝑥 ∈ 𝑋, (𝑦, 𝑥) ∈ 𝑓⁻¹↔ 𝑦 = 𝑓(𝑥). Maka dari itu 𝑓⁻¹ belum tentu merupakan fungsi.

Teorema 2.1 berikut menjelaskan syarat cukup dan syarat perlu sehingga 𝑓⁻¹ merupakan fungsi.

Teorema 2.1 (Susilo, 2012)

Diberikan fungsi 𝑓: 𝑋 → 𝑌 dan 𝑓⁻¹ adalah invers dari 𝑓. 𝑓⁻¹ merupakan fungsi jika dan hanya jika 𝑓 adalah fungsi bijektif. Selanjutnya 𝑓⁻¹ juga merupakan fungsi bijektif

Bukti :

a. Diketahui : 𝑓⁻¹ merupakan fungsi 𝑓

𝑋 𝑌

1 2 3

𝑎 𝑏 𝑐

4 𝑑

Gambar 2.7. Fungsi Bijektif

(35)

Akan dibuktikan : 𝑓 adalah fungsi bijektif maka harus ditunjukkan bahwa 𝑓 injektif dan surjektif

Bukti :

1) Pembuktian Surjektif

𝑓⁻¹: 𝑌 → 𝑋 merupakan fungsi maka setiap 𝑦 ∈ 𝑌 terdapat 𝑥 ∈ 𝑋 sedemikian sehingga 𝑥 = 𝑓⁻¹(𝑦). Dengan kata lain, setiap 𝑦 ∈ 𝑌 terdapat 𝑥 ∈ 𝑋 sedemikian sehingga 𝑦 = 𝑓(𝑥) sehingga 𝑓 merupakan fungsi surjektif

2) Pembuktian Injektif

Ambil sebarang 𝑥₁, 𝑥₂ ∈ 𝑋 dengan 𝑓(𝑥₁) = 𝑓(𝑥₂) = 𝑦 ∈ 𝑌.

Dengan kata lain 𝑥₁ = 𝑓⁻¹(𝑦) dan 𝑥₂ = 𝑓⁻¹(𝑦). Karena diketahui bahwa 𝑓⁻¹: 𝑌 → 𝑋 merupakan fungsi maka 𝑓⁻¹(𝑦) ∈ 𝑋 adalah tunggal akibatnya jika 𝑥₁ = 𝑓⁻¹(𝑦) dan 𝑥₂ = 𝑓⁻¹(𝑦) maka 𝑥₁ = 𝑥₂. Dengan kata lain 𝑓 merupakan fungsi injektif.

Karena terbukti bahwa 𝑓 injektif dan surjektif maka 𝑓 merupakan fungsi bijektif.

b. Diketahui : 𝑓 adalah fungsi bijektif Akan dibuktikan : 𝑓⁻¹ merupakan fungsi Bukti :

Diketahui bahwa 𝑓: 𝑋 → 𝑌 adalah fungsi bijektif artinya 𝑓 adalah fungsi injektif dan surjektif. Karena 𝑓 fungsi surjektif maka setiap 𝑦 ∈ 𝑌 terdapat 𝑥 ∈ 𝑋 sedemikian sehingga 𝑦 = 𝑓(𝑥) artinya

(36)

setiap elemen di 𝑌 berelasi dengan elemen di 𝑋 dengan relasi 𝑓⁻¹ sedemikian sehingga 𝑥 = 𝑓⁻¹(𝑦).

Selanjutnya, untuk membuktikan ketunggalan elemen di 𝑋 yang berpasangan dengan setiap elemen di 𝑌, diambil sebarang 𝑦₁, 𝑦₂ ∈ 𝑌 dengan 𝑦₁ = 𝑦₂. Akan ditunjukkan bahwa 𝑓⁻¹(𝑦₁) = 𝑓⁻¹(𝑦₂). Misalkan 𝑦₁ = 𝑓(𝑥₁) dan 𝑦₂ = 𝑓(𝑥₂) sehingga 𝑓⁻¹(𝑦₁) = 𝑥₁ dan 𝑓⁻¹(𝑦₂) = 𝑥₂. Jika 𝑦₁ = 𝑦₂ maka 𝑓(𝑥₁) = 𝑓(𝑥₂). Karena 𝑓 adalah fungsi injektif maka jika 𝑓(𝑥₁) = 𝑓(𝑥₂) maka 𝑥₁ = 𝑥₂ dengan kata lain 𝑓⁻¹(𝑦₁) = 𝑓⁻¹(𝑦₂). Jadi, terbukti bahwa setiap elemen di 𝑌 berelasi dengan tepat satu elemen di 𝑋 sehingga 𝑓⁻¹ merupakan fungsi.

Berdasarkan bukti pada a dan b maka terbukti bahwa 𝑓⁻¹ merupakan fungsi jika dan hanya jika 𝑓 adalah fungsi bijektif. Selanjutnya akan ditunjukkan bahwa 𝑓⁻¹ juga merupakan fungsi bijektif. 𝑓: 𝑋 → 𝑌 merupakan fungsi, maka untuk setiap 𝑥 ∈ 𝑋 terdapat 𝑦 ∈ 𝑌 sedemikian sehingga 𝑦 = 𝑓(𝑥) akibatnya 𝑥 = 𝑓⁻¹(𝑦). Maka, jika 𝑓⁻¹: 𝑌 → 𝑋 maka untuk setiap 𝑥 ∈ 𝑋 terdapat 𝑦 ∈ 𝑌 sedemikian sehingga 𝑥 = 𝑓⁻¹(𝑦). Dengan kata lain, 𝑓⁻¹ merupakan fungsi surjektif. Selanjutnya diambil sebarang 𝑦₁, 𝑦₂ ∈ 𝑌 dengan 𝑓⁻¹(𝑦₁) = 𝑓⁻¹(𝑦₂). Untuk menunjukkan fungsi tersebut injektif maka harus ditunjukkan 𝑦₁ = 𝑦₂. Misalkan 𝑓⁻¹(𝑦₁) = 𝑥₁ dan 𝑓⁻¹(𝑦₂) = 𝑥₂ sehingga 𝑦₁ = 𝑓(𝑥₁) dan 𝑦₂ = 𝑓(𝑥₂). Jika 𝑓⁻¹(𝑦₁) = 𝑓⁻¹(𝑦₂) maka

(37)

𝑥₁ = 𝑥₂. Karena 𝑓: 𝑋 → 𝑌 merupakan fungsi maka untuk setiap 𝑥₁, 𝑥₂ ∈ 𝑋, 𝑓(𝑥₁) = 𝑓(𝑥₂) dengan kata lain 𝑦₁ = 𝑦₂ sehingga 𝑓⁻¹ merupakan fungsi injektif. Karena 𝑓⁻¹ merupakan fungsi surjektif dan injektif, maka 𝑓⁻¹ merupakan fungsi bijektif. 

5. Komposisi Fungsi

Sebarang dua fungsi dapat dioperasikan sehingga menghasilkan fungsi baru. Salah satu operasi tersebut disebut dengan komposisi fungsi.

Definisi 2.5 Komposisi Fungsi (Susilo, 2012)

Diberikan fungsi 𝑓: 𝑋 → 𝑌 dan 𝑔: 𝑌 → 𝑍. Komposisi dari kedua fungsi tersebut didefinisikan sebagai fungsi 𝑔 ∘ 𝑓: 𝑋 → 𝑍 dengan 𝑔 ∘ 𝑓 = 𝑔(𝑓(𝑥)) untuk setiap 𝑥 ∈ 𝑋.

Contoh 2.2

Misalkan 𝑋 = {1,2,3,4}, 𝑌 = {𝑎, 𝑏, 𝑐}, dan 𝑍 = {1,3,5,7}. Diberikan dua buah fungsi 𝑓: 𝑋 → 𝑌 dan 𝑔: 𝑌 → 𝑍 dengan 𝑓 = {(1, 𝑎), (2, 𝑐), (3, 𝑏), (4, 𝑎)} dan 𝑔 = {(𝑎, 1), (𝑏, 3), (𝑐, 5)}.

Maka komposisi dari kedua fungsi tersebut adalah 𝑔 ∘ 𝑓 = {(1,1), (2,5), (3,3), (4,1)} seperti disajikan dalam Gambar 2.8

(38)

Sifat-sifat Komposisi Fungsi

Beberapa sifat komposisi fungsi yang digunakan di penelitian ini akan dibahas dalam beberapa teorema di bawah ini.

Jika 𝑓, 𝑔, dan ℎ adalah tiga buah fungsi yang dapat dikomposisikan, maka (𝑓 ∘ 𝑔) ∘ ℎ = 𝑓 ∘ (𝑔 ∘ ℎ). Dengan kata lain, komposisi fungsi bersifat asosiatif.

Bukti :

Untuk setiap 𝑥 anggota domain (𝑓 ∘ 𝑔) ∘ ℎ berlaku 1 3 5 7 1

2 3 4

𝑍 1 3 5 7 𝑎

𝑏 𝑐 1

2 3 4

𝑔

𝑋 𝑌

𝑓

𝑋

𝑔 ∘ 𝑓

𝑍 Gambar 2.8. Komposisi Dua Fungsi

(39)

((𝑓 ∘ 𝑔) ∘ ℎ)(𝑥) = ((𝑓 ∘ 𝑔)(ℎ(𝑥)))

= 𝑓 (𝑔(ℎ(𝑥)))

= 𝑓(𝑔 ∘ ℎ)(𝑥)

= 𝑓 ∘ (𝑔 ∘ ℎ)(𝑥)

Jadi diperoleh (𝑓 ∘ 𝑔) ∘ ℎ = 𝑓 ∘ (𝑔 ∘ ℎ) sehingga terbukti bahwa

komposisi fungsi bersifat asosiatif. 

a. Komposisi dua fungsi injektif menghasilkan fungsi injektif b. Komposisi dua fungsi surjektif menghasilkan fungsi surjektif c. Komposisi dua fungsi bijektif menghasilkan fungsi bijektif

Bukti :

a. Diberikan dua buah fungsi injektif misalnya 𝑓: 𝑋 → 𝑌 dan 𝑔: 𝑌 → 𝑍.

Akan dibuktikan 𝑔 ∘ 𝑓 ∶ 𝑋 → 𝑍 merupakan fungsi injektif. Ambil sebarang 𝑥₁, 𝑥₂ ∈ 𝑋 sedemikian sehingga 𝑔 ∘ 𝑓(𝑥₁) = 𝑔 ∘ 𝑓(𝑥₂) artinya 𝑔(𝑓(𝑥₁)) = 𝑔(𝑓(𝑥₂)) dan akan ditunjukkan 𝑥₁ = 𝑥₂. Karena 𝑔 merupakan fungsi injektif maka 𝑓(𝑥₁) = 𝑓(𝑥₂). Karena 𝑓 juga fungsi injektif maka 𝑥₁ = 𝑥₂. Jadi terbukti bahwa 𝑔 ∘ 𝑓 merupakan fungsi injektif.

b. Diberikan dua buah fungsi surjektif misalnya 𝑓: 𝑋 → 𝑌 dan 𝑔: 𝑌 → 𝑍.

Akan dibuktikan 𝑔 ∘ 𝑓 ∶ 𝑋 → 𝑍 merupakan fungsi surjektif. Ambil sebarang 𝑧 ∈ 𝑍, akan ditunjukkan bahwa terdapat 𝑥 ∈ 𝑋 sedemikian

(40)

sehingga (𝑔 ∘ 𝑓)(𝑥) = 𝑧. Karena 𝑔 merupakan fungsi surjektif maka terdapat 𝑦 ∈ 𝑌 sedemikian sehingga 𝑔(𝑦) = 𝑧. Karena 𝑓 juga merupakan fungsi surjektif maka terdapat 𝑥 ∈ 𝑋 sedemikian sehingga 𝑓(𝑥) = 𝑦. Berdasarkan hal-hal tersebut maka (𝑔 ∘ 𝑓)(𝑥) = 𝑔(𝑓(𝑥)) = 𝑔(𝑦) = 𝑧 sehingga diperoleh (𝑔 ∘ 𝑓)(𝑥) = 𝑧. Jadi terbukti bahwa 𝑔 ∘ 𝑓 merupakan fungsi surjektif.

c. Diberikan dua buah fungsi bijektif misalnya 𝑓: 𝑋 → 𝑌 dan 𝑔: 𝑌 → 𝑍 artinya baik 𝑓 maupun 𝑔, keduanya adalah fungsi yang injektif seklaigus surjektif. Akan dibuktikan 𝑔 ∘ 𝑓 ∶ 𝑋 → 𝑍 adalah fungsi bijektif. Karena 𝑓 dan 𝑔 injektif, maka berdasarkan (a), 𝑔 ∘ 𝑓 merupakan fungsi injektif. Karena 𝑓 dan 𝑔 surjektif, maka berdasarkan (b), 𝑔 ∘ 𝑓 merupakan fungsi surjektif. Diperoleh 𝑔 ∘ 𝑓 injektif dan surjektif, dengan kata lain 𝑔 ∘ 𝑓 merupakan fungsi yang bijektif. Jadi terbukti bahwa 𝑔 ∘ 𝑓 merupakan fungsi bijektif. 

6. Permutasi

Permutasi adalah salah satu fungsi khusus. Permutasi inilah yang nantinya akan membentuk suatu grup permutasi dengan operasi komposisi fungsi.

Definisi 2.6. Permutasi (Gallian, 2010)

Permutasi pada himpunan 𝐴 adalah suatu fungsi bijektif dari 𝐴 ke 𝐴.

Ilustrasi fungsi pada sebuah himpunan yang merupakan permutasi dibahas dalam Contoh 2.3 berikut.

(41)

Contoh 2.3

Diberikan himpunan 𝐴 = {1, 2, 3}. Fungsi 𝑓: 𝐴 → 𝐴 yang didefinisikan dengan 𝑓(1) = 3, 𝑓(2) = 1, 𝑓(3) = 2 merupakan sebuah permutasi.

Fungsi 𝑔: 𝐴 → 𝐴 yang didefinisikan dengan 𝑔(1) = 3, 𝑔(2) = 3, 𝑔(3) = 1 bukan merupakan sebuah permutasi. Dari ilustrasi yang diperlihatkan dalam Gambar 2.9, tampak bahwa fungsi 𝑓 merupakan sebuah fungsi bijektif pada 𝐴, sedangkan fungsi 𝑔 bukan merupakan fungsi bijektif.

(a) (b)

Gambar 2.9. (a) Permutasi dan (b) Bukan Permutasi

Dalam Contoh 2.3, fungsi dinyatakan dengan menyebutkan satu per satu nilai fungsi tersebut dan dengan menggunakan diagram panah.

Fungsi juga dapat disajikan dengan menggunakan matriks. Misalkan 𝐴 = {1,2,3}, maka fungsi 𝑓 seperti didefinisikan dalam Contoh 2.3 dapat dinyatakan dalam bentuk matriks berikut.

𝐴 𝐴

𝑓

1 2 3

𝐴 𝐴

𝑔

1 2 3

(42)

𝑓 = (1 2 3 3 1 2)

Baris pertama dalam matriks tersebut menyatakan anggota-anggota himpunan 𝐴, sedangkan baris kedua menyatakan nilai-nilai fungsi yang untuk setiap anggota himpunan 𝐴, 1 dipetakan oleh 𝑓 ke 3, 2 dipetakan ke 1, dan 3 dipetakan ke 2. Cara lain yang lebih singkat untuk menyajikan sebuah fungsi adalah dengan notasi sikal. Teorema berikut mendiskusikan bahwa suatu permutasi permutasi dapat ditulis sebagai sikal terpisah (disjoint cycle)

Operasi komposisi fungsi juga berlaku pada permutasi. Contoh berikut adalah komposisi pada permutasi.

Contoh 2.4

Pada contoh 2.3 diberikan himpunan 𝐴 = {1, 2, 3} dan 𝑓: 𝐴 → 𝐴 merupakan suatu permutasi dengan 𝑓 = (1 2 3

3 1 2). Misalkan 𝑔: 𝐴 → 𝐴 juga merupakan permutasi dengan 𝑔 = (1 2 3

1 3 2), maka 𝑔 ∘ 𝑓 = (1 2 3

1 3 2) (1 2 3

3 1 2) = (1 2 3

2 1 3). Komposisi 𝑔 ∘ 𝑓 artinya 𝑓(𝑔(𝑥)) sehingga 𝑓 dikerjakan lebih dahulu maka 1 oleh 𝑓 dipetakan ke 3 lalu 3 dipetakan oleh 𝑔 ke 2, maka 1 dipetakan oleh 𝑔 ∘ 𝑓 ke 2. Demikian pula elemen 𝑋 yang lain.

(43)

Teorema 2.4 (Gallian, 2010)

Setiap permutasi dari himpunan berhingga dapat ditulis sebagai sikal atau sebagai hasil operasi dari sikal terpisah (disjoint cycle).

Bukti :

Misalkan 𝛼 adalah permutasi dari 𝐴 = {1,2,3, … , 𝑛}. Untuk menuliskan 𝛼 sebagai hasil operasi dua buah sikal, dipilih 𝑎₁ ∈ 𝐴 sedemikian sehingga 𝑎₂ = 𝛼(𝑎₁), 𝑎₃ = 𝛼(𝑎₂) = 𝛼(𝛼(𝑎₁)) = 𝛼²(𝑎₁), 𝑎₄ = 𝛼³(𝑎₁), dan seterusnya sampai dengan 𝑎₁ = 𝛼^𝑚(𝑎₁) untuk suatu 𝑚. Nilai 𝑚 selalu ada karena banyaknya anggota 𝐴 berhingga sehingga barisan 𝑎₁, 𝛼(𝑎₁), 𝛼²(𝑎₁), … merupakan barisan yang berhingga. Maka, akan ada perulangan sedemikian sehingga 𝛼^𝑖(𝑎₁) = 𝛼^𝑗(𝑎₁) untuk suatu 𝑖 dan 𝑗 dengan 𝑖 < 𝑗. Jika 𝑎₁ = 𝛼^𝑚(𝑎₁) maka 𝑚 = 𝑗 − 𝑖. Jadi dapat ditulis 𝛼 = (𝑎₁ 𝑎₂ 𝑎₃… 𝑎_𝑚) … . Akan tetapi, terdapat kemungkinan bahwa ada anggota 𝐴 yang belum terdaftar pada sikal (𝑎₁ 𝑎₂ 𝑎₃… 𝑎_𝑚) sehingga diambil lagi 𝑏₁ ∈ 𝐴 yang mana 𝑏₁ belum muncul pada sikal yang telah dibuat sebelumnya. Misalkan 𝑏₂ = 𝛼(𝑏₁), 𝑏₃ = 𝛼(𝑏₂) = 𝛼(𝛼(𝑏₁)) = 𝛼²(𝑏₁), 𝑎₄ = 𝛼³(𝑏₁), dan seterusnya sampai dengan 𝑏₁ = 𝛼^𝑘(𝑏₁) untuk suatu 𝑘 sehingga dapat dibentuk sikal baru yaitu (𝑏₁ 𝑏₂ 𝑏₃… 𝑏_𝑘).Sikal baru ini tidak akan memiliki elemen yang sama dengan sikal yang dibangun sebelumnya. Sebab, jika demikian maka 𝛼^𝑖(𝑎₁) = 𝛼^𝑗(𝑏₁) untuk suatu 𝑖 dan 𝑗 dengan 𝑖 < 𝑗 sehingga 𝛼^𝑗−𝑖(𝑎₁) = 𝑏₁ akibatnya 𝑏₁ = 𝑎_𝑡 untuk suatu 𝑡. Hal tersebut kontradiksi dengan cara pemilihan 𝑏₁. Dengan melanjutkan proses membuat sikal hingga seluruh anggota 𝐴 ada

(44)

didalam sikal, maka permutasi dari 𝐴 dapat ditulis 𝛼 = (𝑎₁ 𝑎₂ 𝑎₃… 𝑎_𝑚)(𝑏₁ 𝑏₂ 𝑏₃… 𝑏_𝑘) … (𝑐₁ 𝑐₂ 𝑐₃… 𝑐_𝑝). Jadi terbutkti bahwa permutasi dapat ditulis dalam bentuk sikal maupun hasil operasi dari sikal terpisah.

Contoh 2.5

Diberikan 𝐴 = {1,2,3,4,5,6,7} dan 𝛼 = (1 3 2 5). Dipilih 𝑎₁ = 7. Maka 𝛼(7) = 7. Tetapi pemilihan tersebut belum memuat semua anggota A sebagai satu sikal. Oleh karena itu dipilih elemen 𝐴 yang lain, misalnya 𝑏₁ = 5. Diperoleh 𝛼(𝑏₁) = 1, 𝛼²(5) = 3, 𝛼³(5) = 2, 𝛼⁴(5) = 5, dan 𝛼⁵(5) = 1. Karena 𝛼(𝑏₁) = 𝛼⁵(𝑏₁), maka diperoleh 𝑚 = 5 − 1 = 4.

Fungsi 𝑓 = (1 2 3

3 1 2), jika disajikan dalam notasi sikal, dapat ditulis menjadi 𝑓 = (1 3 2). Notasi tersebut juga berarti, 1 dipetakan ke 3, 3 dipetakan ke 2, dan 2 dipetakan ke 1. Contoh lain notasi sikal untuk permutasi pada 𝐴 = {1, 2, 3} adalah

ℎ = (1 2 3

3 2 1) = (1 3)(2) = (1 3).

Notasi tersebut berarti fungsi ℎ memetakan 1 ke 3, 3 ke 1, dan 2 ke 2.

Untuk lebih mempersingkat penulisan, pemetaan ke dirinya sendiri tidak perlu dituliskan dalam notasi.

Teorema 2.1 menyatakan bahwa suatu fungsi memiliki invers (invertibel) jika dan hanya jika fungsi tersebut bijektif. Maka, permutasi

(45)

juga merupakan fungsi yang meiliki invers. Hal tersebut dinyatakan dalam akibat berikut ini.

Akibat 2.1

Diberikan 𝑓: 𝑋 → 𝑋 merupakan suatu permutasi dari himpunan 𝑋. Invers dari permutasi tersebut, 𝑓⁻¹: 𝑋 → 𝑋, adalah juga permutasi pada himpunan 𝑋.

Bukti :

Permutasi dari himpunan 𝑋 merupakan suatu fungsi bijektif, maka berdasarkan Teorema 2.1 permutasi memiliki invers. Invers dari fungsi bijektif juga merupakan fungsi bijektif sehingga invers dari permutasi dari himmpunan 𝑋 juga merupakan suatu permutasi pada himpunan tersebut.

 Contoh 2.6

Pada Contoh 2.3 diberikan himpunan 𝐴 = {1, 2, 3}. Fungsi 𝑓: 𝐴 → 𝐴 yang didefinisikan dengan 𝑓(1) = 3, 𝑓(2) = 1, 𝑓(3) = 2. Permutasi dari himpunan 𝐴 dapat dilihat pada Gambar 2.8 sebelah kiri. Fungsi invers dari 𝑓 yaitu 𝑓⁻¹: 𝐴 → 𝐴 yaitu 𝑓⁻¹(1) = 2, 𝑓⁻¹(2) = 3, 𝑓⁻¹(3) = 1 maka 𝑓⁻¹ = (1 2 3

2 3 1) atau jika ditulis dengan notasi sikal yaitu 𝑓⁻¹= (1 2 3).

(46)

B. Grup

Berikut ini adalah definisi-definisi dan istilah-istilah terkait grup yang digunakan dalam penelitian ini.

Definisi 2.7. Grup (Gallian, 2010)

Diberikan sebuah himpunan 𝐺 yang dilengkapi dengan operasi biner “*” yang didefinisikan pada 𝐺. (𝐺,∗) dikatakan grup jika memenuhi tiga aksioma dibawah ini :

1. Sifat asosiatif. Setiap 𝑎, 𝑏, 𝑐 ∈ 𝐺, (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)

2. Terdapat elemen identitas 𝑒 pada 𝐺 sedemikian sehingga 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 untuk setiap 𝑎 ∈ 𝐺.

3. Setiap elemen di 𝐺 memiliki invers. (∀𝑎 ∈ 𝐺), (∃𝑏 ∈ 𝐺) (𝑏 disebut invers dari 𝑎) sedemikian sehingga 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎 = 𝑒

Contoh 2.7

Diberikan himpunan bilangan bulat ℤ dan operasi “+” didefinisikan seperti operasi penjumlahan biasa pada bilangan bulat.

Berdasarkan hal tersebut dapat diperoleh informasi sebagai berikut :

i. Operasi pada penjumlahan bilangan bulat merupakan operasi biner atau tertutup karena setiap 𝑎, 𝑏 ∈ ℤ, 𝑎 + 𝑏 ∈ ℤ.

ii. Operasi penjumlahan pada bilangan bulat bersifat asosiatif.

iii. Dalam himpunan bilangan bulat, terdapat 0 ∈ ℤ sedemikian sehingga setiap 𝑎 ∈ ℤ, 𝑎 + 0 = 0 + 𝑎 = 𝑎 sehingga 0 disebut sebagai identitas penjumlahan.

(47)

iv. Setiap 𝑎 ∈ ℤ terdapat 𝑏 = −𝑎 ∈ ℤ sedemikian sehingga 𝑎 + 𝑏 = 𝑎 + (−𝑎) = −𝑎 + 𝑎 = 0

Berdasarkan (i) sampai (iv) dan definisi 2.1 maka dapat disimpulkan bahwa (ℤ, +) merupakan grup.

Operasi antar elemen pada suatu grup mempunya beberapa sifat. Teorema- teorema berikut menjelaskan sifat-sifat operasi antar elemen dalan grup.

Teorema 2.5 (Dummit dan Foote, 2004) Diberikan grup 𝐺, maka :

1. Untuk setiap 𝑎, 𝑏 ∈ 𝐺, (𝑎𝑏)⁻¹= 𝑏⁻¹𝑎⁻¹. 2. Untuk setiap 𝑎 ∈ 𝐺, (𝑎⁻¹)⁻¹= 𝑎

Bukti :

1. Ambil sebarang 𝑎, 𝑏 ∈ 𝐺 maka 𝑎𝑏 ∈ 𝐺 dan 𝑎𝑏(𝑎𝑏)⁻¹= 𝑒 sehingga 𝑎𝑏(𝑎𝑏)⁻¹ = 𝑒

𝑎⁻¹𝑎𝑏(𝑎𝑏)⁻¹ = 𝑎⁻¹𝑒 𝑏(𝑎𝑏)⁻¹= 𝑎⁻¹ 𝑏⁻¹𝑏(𝑎𝑏)⁻¹= 𝑏⁻¹𝑎⁻¹

(𝑎𝑏)⁻¹= 𝑏⁻¹𝑎⁻¹ Diperoleh (𝑎𝑏)⁻¹= 𝑏⁻¹𝑎⁻¹

2. Ambil sebarang 𝑎 ∈ 𝐺, maka berlaku 𝑒 = 𝑎⁻¹𝑎. Selain itu, juga terdapat 𝑎⁻¹∈ 𝐺 sedemikian sehingga 𝑎⁻¹(𝑎⁻¹)⁻¹= 𝑒 sehingga

𝑒 = 𝑎⁻¹𝑎 𝑎⁻¹(𝑎⁻¹)⁻¹= 𝑎⁻¹𝑎

(𝑎⁻¹)⁻¹(𝑎⁻¹(𝑎⁻¹)⁻¹) = (𝑎⁻¹)⁻¹(𝑎⁻¹𝑎)

(48)

((𝑎⁻¹)⁻¹𝑎⁻¹)(𝑎⁻¹)⁻¹= ((𝑎⁻¹)⁻¹𝑎⁻¹)𝑎 (𝑎⁻¹)⁻¹= 𝑎

Diperoleh (𝑎⁻¹)⁻¹= 𝑎 

Definisi 2.7 menjelaskan tentang grup secara umum, namun ada pula grup yang lebih khusus yaitu grup abelian. Definisi 2.8 berikut menjelaskan tentang grup abelian.

Definisi 2.8 Grup Abelian (Gallian, 2010)

Diberikan suatu grup 𝐺, jika grup tersebut memiliki sifat 𝑎𝑏 = 𝑏𝑎 untuk setiap 𝑎, 𝑏 ∈ 𝐺 maka grup tersebut disebut grup abelian. Sebaliknya jika ada pasangan (𝑎, 𝑏) di 𝐺 yang tidak memenuhi 𝑎𝑏 = 𝑏𝑎 maka grup tersebut disebut grup non-abelian.

Contoh 2.8

Pada grup (ℤ, +) seperti pada Contoh 2.7. Operasi penjumlahan pada bilangan bulat bersifat komutatif. Dengan kata lain, setiap 𝑎, 𝑏 ∈ ℤ, 𝑎𝑏 = 𝑏𝑎.

Jadi berdasarkan Definisi 2.8, (ℤ, +) merupakan grup abelian.

Berikut adalah teorema yang berkaitan dengan grup abelian.

Teorema 2.6

Jika 𝐺 merupakan sebuah grup dan untuk setiap 𝑥 ∈ 𝐺 berlaku 𝑥² = 1 maka 𝐺 merupakan grup abelian.

Bukti :

Ambil sebarang 𝑥, 𝑦 ∈ 𝐺 maka berlaku 𝑥² = 1 artinya 𝑥𝑥 = 1 sehingga 𝑥 = 𝑥⁻¹. Demikian pula 𝑦 = 𝑦⁻¹. Karena 𝑥, 𝑦 ∈ 𝐺 dan 𝐺 merupakan grup maka

(49)

𝑥𝑦 ∈ 𝐺 sehingga pada 𝑥𝑦 juga berlaku (𝑥𝑦)² = 1 ↔ (𝑥𝑦)(𝑥⁻¹𝑦⁻¹) = 1 ↔ 𝑥𝑦 = (𝑥⁻¹𝑦⁻¹)⁻¹↔ 𝑥𝑦 = (𝑦⁻¹)⁻¹(𝑥⁻¹)⁻¹= 𝑦𝑥. Jadi 𝐺 merupakan grup

abelian. 

Berdasarkan banyaknya anggota pada suatu grup. Terdapat dua jenis grup yaitu grup berhingga dan grup tak berhingga. Berikut adalah definisi order dari suatu grup.

Definisi 2.9 Order dari Grup (Gallian,2010)

Diberikan suatu grup 𝐺, order dari grup 𝐺, dinotasikan dengan |𝐺|, merupakan suatu bilangan asli 𝑛 yang menyatakan banyaknya anggota 𝐺.

Contoh 2.9 :

1. Diberikan grup himpunan bilangan bulat dengan notasi penjumlahan.

Order dari grup tersebut adalah tak terhingga.

2. Diberikan grup 𝑈(10) = {1,3,7,9} dengan operasi perkalian pada modulo 10. |𝑈(10)| = 4.

Selain dituliskan dalam himpunan, grup juga dapat dinyatakan sebagai grup siklik. Berikut adalah definisi grup siklik.

Definisi 2.10 Grup Siklik (Gallian, 2010)

Diberikan suatu gurp 𝐺, grup 𝐺 dikatakan sebagai grup siklik jika terdapat 𝑎 ∈ 𝐺 sedemikian sehingga 𝐺 = {𝑎^𝑛|𝑛 ∈ ℕ}. 𝑎 disebut sebagai generator dari grup 𝐺 dan dapat ditulis 𝐺 = 〈𝑎〉.

Contoh 2.10

Diberikan grup ℤ₈ = {0,1,2,3,4,5,6,7} dengan operasi penjumlahan pada modulo 8. Diperlihatkan bahwa 1¹ = 1, 1² = 2, 1³ = 3, 1⁴ = 4, 1⁵ =

(50)

5, 1⁶ = 6, 1⁷ = 7, dan 1⁸ = 0. Karena {1^𝑛|𝑛 ∈ ℕ} = ℤ₈ maka 1 merupakan generator dari ℤ₈ dan ℤ₈ = 〈1〉. Akan tetapi {2^𝑛|𝑛 ∈ ℕ} ≠ ℤ₈ maka 2 bukan generator untuk ℤ₈.

Grup berkaitan dengan himpunan. Jika suatu himpunan merupakan himpunan bagian dari suatu grup maka himpunan tersebut dapat menjadi grup bagian (subgroup) dari grup tersebut jika memenuhi definisi dan teorema berikut.

Definisi 2.11 Subgrup (Gallian, 2010)

Diberikan suatu grup 𝐺. Misalkan 𝐻 adalah himpunan bagian dari 𝐺. Jika 𝐻 merupakan grup dengan operasi yang didefinisikan pada 𝐺 maka 𝐻 subgrup dari 𝐺.

Beberapa teorema dibawah ini dapat digunakan untuk mengidentifikasi apakah suatu himpunan bagian dari grup merupakan grup bagian.

Teorema 2.7 Uji Subgrup dengan Satu Langkah (Gallian, 2010)

Diberikan suatu grup 𝐺 dan 𝐻 ⊂ 𝐺. Jika 𝑎𝑏⁻¹∈ 𝐻 untuk setiap 𝑎, 𝑏 ∈ 𝐻 maka 𝐻 merupakan grup bagian dari 𝐺.

Bukti :

Diketahui : 𝐻 ⊂ 𝐺 dan 𝑎𝑏⁻¹ ∈ 𝐻 Akan dibuktikan : 𝐻 adalah grup bagian 𝐺

(51)

Bukti :

Diketahui 𝐻 ⊂ 𝐺 maka jelas bahwa operasi pada 𝐻 sama dengan operasi pada 𝐺 sehingga sifat asosiatif juga berlaku pada 𝐻. Untuk membuktikan bahwa elemen identitas berada di 𝐻, misalkan 𝑒 = 𝑥𝑥⁻¹. Dipilih 𝑎 = 𝑥 dan 𝑏 = 𝑥 maka 𝑒 = 𝑥𝑥⁻¹ = 𝑎𝑏⁻¹∈ 𝐻. Selanjutnya dibuktikan bahwa untuk setiap 𝑥 ∈ 𝐻 terdapat 𝑥⁻¹ ∈ 𝐻, 𝑥⁻¹= 𝑒𝑥⁻¹, maka dipilih 𝑎 = 𝑒 dan 𝑏 = 𝑥 sehingga 𝑒𝑥⁻¹ = 𝑎𝑏⁻¹∈ 𝐻. Terakhir, akan ditunjukkan bahwa operasi pada 𝐺 juga tertutup pada 𝐻 dengan kata lain harus ditujukkan bahwa untuk setiap 𝑥, 𝑦 ∈ 𝐻 maka 𝑥𝑦 ∈ 𝐻. Sebelumnya, telah ditunjukkan bahwa untuk setiap 𝑦 ∈ 𝐻, terdapat 𝑦⁻¹∈ 𝐻 maka dipilih 𝑎 = 𝑥 dan 𝑏 = 𝑦⁻¹ sehingga 𝑥𝑦 = 𝑥(𝑦⁻¹)⁻¹= 𝑎𝑏⁻¹ ∈ 𝐻. Dengan demikian berdasarkan Definisi 2.7 maka 𝐻 merupakan grup. Karena 𝐻 adalah grup dan 𝐻 ⊂ 𝐺 maka berdasarkan

Definisi 2.11, 𝐻 merupakan subgrup dari 𝐺. 

Selain uji grup bagian dengan satu langkah, teorema berikut membahas uji grup bagian dengan dua langkah.

Teorema 2.8 Uji Subgrup dengan Dua Langkah (Gallian, 2010)

Diberikan suatu grup 𝐺 dan 𝐻 ⊂ 𝐺. Jika 𝑎𝑏 ∈ 𝐻 untuk setiap 𝑎, 𝑏 ∈ 𝐻 (operasi pada 𝐻 bersifat tertutup) dan terdapat 𝑎⁻¹∈ 𝐻 untuk setiap 𝑎 ∈ 𝐻 (setiap elemen di 𝐻 mempunyai invers) maka 𝐻 merupakan subgrup dari 𝐺.