BAB 2 Sistem Bilangan Riil - Bab 2 Sistem Bilangan Riil

BAB 2

Bilangan Riil

 Himpunan bilangan riil adalah himpunan bilangan yang merupakan gabungan dari himpunan bilangan

rasional dan himpunan bilangan irasional

 Himpunan bilangan rasional, Q = {x|x = , p dan

q Z, dengan q 0}

contoh :

 Himpunan-himpunan berikut ada di dalam himpunan bilangan rasional :

* Himpunan bilangan asli, N = {1,2,3,….}

* Himpunan bilangan bulat, Z = {…-2,-1,0,1,2,……}

p q

1 4 57 , , 3 9 1

 Himpunan bilangan irasional,

iR = {x|x tidak dapat dinyatakan dalam bentuk } contoh : , e, log 5,

 Teorema :

“Jumlah bilangan rasional dan irrasional adalah irrasional”

 Representasi desimal bilangan rasional adalah berakhir

atau berulang dengan pola yang sama :

contohnya : 3/8 = 0.375, atau 0.3750000000…. 13/11 =1.1818181818…

 Setiap bilangan rasional dapat ditulis sebagai desimal

berulang dan sebaliknya contoh : x = 0.136136136…. y = 0.271271271…..

Buktikan x dan y merepresentasikan bilangan rasional

 Representasi bilangan irrasional tidak berulang dan

sebaliknya, contoh : 0.101001000100001….

p q

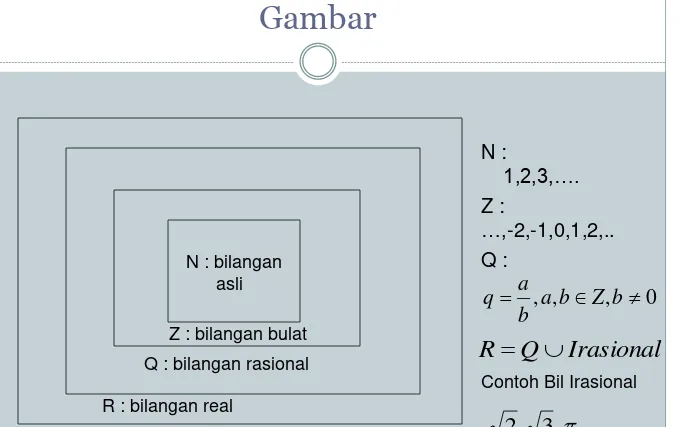
Gambar

N : bilangan asli

Z : bilangan bulat Q : bilangan rasional

R : bilangan real

N :

1,2,3,…. Z :

…,-2,-1,0,1,2,..

0 ,

,

,  

 a b Z b b

a q

Q :

Irasional Q

R  



, 3 , 2

Sifat-Sifat Bilangan Riil

Untuk sebarang R berlaku sifat-sifatnsebagai berikut:

1. Sifat komutatif

2. Sifat asosiatif

3. Sifat distibutif perkalian terhadap penjumlahan

7. Hukum Kanselasi

(i). Jika dan maka (ii). Jika maka

8. Sifat pembagi nol



Sifat-sifat urutan :

 Trikotomi

Jika x dan y adalah suatu bilangan, maka pasti berlaku salah satu dari x < y atau x > y atau x = y

 Ketransitifan

Jika x < y dan y < z → x < z

 Penambahan

Jika x < y ↔ x + z < y + z

 Perkalian

Misalkan z bilangan positif, x < y ↔ xz < yz, sedangkan bila z bilangan negatif, x < y ↔ xz > yz

Latihan 1

Ubahlah masing-masing desimal berulang menjadi hasil bagi dua bilangan bulat.

Selang (Interval)

Pertidaksamaan adalah salah satu bentuk

pernyataan matematika yang mengandung satu

peubah atau lebih yang dihubungkan oleh

tanda-tanda < , > , ≤ atau ≥.

Contoh Pertidaksamaan:

1. 2x

–

7 < 4x

–

2

2.

–5 ≤ 2x + 6 < 4

3. x

2

–

_x

–

_{6 < 0}

4. 3x

2

–

_x

–

_{2 > 0}

Pertidaksamaan

Bentuk umum pertidaksamaan :

dengan A(x), B(x), D(x), E(x) adalah suku

banyak (polinom) dan

B(x) ≠ 0, E(x) ≠ 0

 

 

E

 

 

x

x

D

x

B

x

A

Pertidaksamaan

Menyelesaikan suatu pertidaksamaan

adalah mencari semua himpunan

bilangan real yang membuat

pertidaksamaan berlaku. Himpunan

bilangan real ini disebut juga Himpunan

Penyelesaian (HP)

Cara menentukan HP :

1. Bentuk pertidaksamaan diubah menjadi :

, dengan cara :

₀

) (

) (



x Q

Pertidaksamaan

 Ruas kiri atau ruas kanan dinolkan

 Menyamakan penyebut dan menyederhanakan

bentuk pembilangnya

2.

Dicari titik-titik pemecah dari pembilang dan

penyebut dengan cara P(x) dan Q(x) diuraikan

menjadi faktor-faktor linier dan/ atau kuadrat

3.

Gambarkan titik-titik pemecah tersebut pada

Contoh :

Tentukan Himpunan Penyelesaian

5

3

2

13



x





3

5

2

3

13





x





8

2

16



x



4

8



x



8

4



x



 

4

,

8

Hp =

4

8

8

   



 ,3 2 1

0

3

5

2

x

2



x







2

_x



1



_x



3





0

Titik Pemecah (TP) :

2

1





x

dan

x



3

3

++ -- ++

2 1



3.

Hp =

Contoh :

6

3

7

6

4

2

x







x



x



x

x

4

6

7

2







dan

6



7

_x



3

_x



6

4

6

7

2

x



x





dan



7

x



3

x





6



6

4.

10

9

x



dan



10

x



0

9

10



x

dan

10

x



0

9

10



x

dan

x



0

Contoh :

Hp =



_













 



0

,

9

10

,

0

9 10

Dari gambar tersebut dapat disimpulkan :

Hp =









9

10

,



1



3

1



0

x

Untuk pembilang

₂

2



₂



₃

x

x

mempunyai nilai

Diskriminan (D) < 0, sehingga nilainya selalu

positif, Jadi TP : 2,-3

Pembilang tidak menghasilkan titik pemecah.

-3 2

-- ++ --





,



3

  



2

,



Pertidaksamaan Nilai Mutlak

Nilai mutlak

x

(|

x

|) didefinisikan sebagai jarak

x

dari titik pusat pada garis bilangan, sehingga jarak

selalu bernilai positif.

Definisi nilai mutlak :















0

,

0

,

x

x

x

x

Pertidaksamaan nilai mutlak

Sifat-sifat nilai mutlak:

y

x

y

x



2

x

x



a

x

a

a

a

x



,



0









a

x

a

a

x



,



0





atau

x





a





y

x

x

2



y

2

1. 2.

3.

4.

Contoh: Menentukan Himpunan Penyelesaian

4

1







x

Contoh :

3

5

2

x





Kita bisa menggunakan sifat ke-2.

3

5

2

3











x

5

3

2

3

5











x

8

2

2







x

Hp =

 

1

,

4

1 4

Contoh: Menentukan Himpunan Penyelesaian

Kita bisa juga menggunakan sifat ke-4,

karena ruas kiri maupun kanan keduanya positif.

5

4

3

2

x





x



3.

Kita bisa menggunakan sifat 4



 

2



2

Contoh: Menentukan Himpunan Penyelesaian

Hp =

_[



₄

_/

₃

_,



₁

_]

Jika digambar pada garis bilangan :

-1

3 4



++ --

Contoh: Menentukan Himpunan Penyelesaian

2 7

2  

x

2 7

2  

 x _{7 2}

2   

x

5

2







x

₉

2  

x

10







x

x





18





10

,



 







,



18



4.

atau

atau

atau

Hp =

Soal Latihan

3 7

2x 

Cari himpunan penyelesaian dari pertidaksamaan berikut.

7 3

2  

 x

x

1.

2.

3.

2 4

7

2x  x

4.

4 6 2

5  

 x

5.

2 5

3

 