DWIWARNA PRIMITIF DENGAN n-TITIK GANJIL
SKRIPSI
MARDHA TILLAH 090803044
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
DWIWARNA PRIMITIF DENGAN n-TITIK GANJIL
SKRIPSI
Diajukan untuk melengkapi tugas akhir dan memenuhi syarat mencapai gelar Sarjana Sains
MARDHA TILLAH 090803044
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : EKSPONEN TITIK KELUAR DARI SEBUAH KELAS
DIGRAF DWIWARNA PRIMITIF ATAS n-TITIK GANJIL
Kategori : SKRIPSI
Nama : MARDHA TILLAH
Nomor Induk Mahasiswa : 090803044
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM
(FMIPA) UNIVERSITAS SUMATERA UTARA
Medan, Oktober 2013
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Dra. Mardiningsih, M.Si Prof. Dr. Saib Suwilo, M.Sc
NIP.19630405 198811 2 001 NIP.19640109 198803 1 004
Diketahui oleh :
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
EKSPONEN TITIK KELUAR DARI SEBUAH KELAS DIGRAF DWIWARNA PRIMITIF ATAS n-TITIK GANJIL
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa ku-tipan dan ringkasan penting yang masing-masing disebutkan sumbernya.
Medan, Oktober 2013
PENGHARGAAN
Besar rasa syukur kepada Sang Khaliq dengan limpahan rahmat dan kasih sayang-Nya memberikan keluasan waktu serta kesempatan bagi saya untuk menyele-saikan penelitian ini dengan judul ”EKSPONEN TITIK KELUAR DARI SE-BUAH KELAS DIGRAF DWIWARNA PRIMITIF ATAS n-TITIK GAN-JIL”. Serta salawat dan salam kepada baginda Rasul Muhammad SAW yang sampai detik ini merupakan panutan terbaik bagi setiap manusia.
Serangkai ucapan terima kasih saya hanturkan kepada Ibunda Sabariah, Ibunda Waliyah dan Ayahanda Alm.H.Amiruddin Tholib yang tanpa pernah lelah menyayangi, menjaga, merawat serta mendoakan dalam setiap langkah. Semoga Ibunda dan Aya-handa tercinta selalu berada dalam cinta dan lindungan-Nya. Kepada Bapak Prof.Saib Suwilo,M.Sc selaku dosen pembimbing I dan Ibu Dra.Mardiningsih,M.Si selaku dosen pembimbing II terima kasih atas segala bentuk bimbingan dan motivasi dalam menye-lesaikan penelitian ini sebagai tugas akhir akademik, dan kepada Bapak Prof.Tulus,M.Si dan Bapak Drs.Ariswoyo,M.Si selaku dosen penguji, terima kasih atas segenap saran-nya. Kepada Bapak Prof.Dr.Sutarman,M.Sc, selaku Dekan FMIPA USU, Bapak Prof.Dr.Tulus,M.Si dan Ibu Dra.Mardiningsih,M.Si, selaku Ketua Departemen dan Sekretaris Departemen FMIPA USU serta seluruh Staf Pengajar yang telah mem-berikan pengetahuan-pengetahuan akademik dan seluruh Staf Departemen Matematika yang turut mempermudah jalannya proses penyelesaian tugas akhir ini. Semoga selalu dalam Rahmat dan Karunia-Nya.
Terima kasih kepada seluruh abanganda tercinta Ahmad Aulia,S.Pd, Afzar Aulia, Alfi Syahrin,S.E, dr.Ibnu Hasyim, Ir.Anshor Khawari, dan abanganda Rafiq Kahfi serta adikku tercinta Samanthi Hibbah yang selalu memberikan motivasi, dukungan moral dan materi, serta doa yang tak pernah henti, semoga selalu dalam lindungan dan Rahmat Allah SWT, dan kepada sahabatku Anggita Fathimah Sire-gar yang tak pernah bosan mendenSire-gar segala keluh kesah perjalanan tugas akhir ini serta selalu mengingatkan bahwa pelajaran yang takkan habis dalam hidup ini adalah bab ikhlas, bab adil, dan bab sabar, terima kasih atas segala dukungannya. Semoga segala impianmu dapat terwujud. Kepada sahabat-sahabat Ilham Firdaus Siregar, Dewi Uli Sinulingga, dan teman-teman seperjuangan 1708 di pesantren Ar-Raudhatul yang ikut memberikan dukungan, terima kasih atas segala bantuan, motivasi serta doanya. Semoga visi dan misi hidup kita berjalan dalam Ridho-Nya.
bisa disebutkan namanya satu persatu oleh penulis, terima kasih atas ikatan perte-manan dan silaturrahmi yang dijalani bersama. Semoga tali silaturrahmi ini dapat terjalin tanpa batas waktu.
Sebagai manusia, sudah tentu banyak kekurangan penulis dalam bentuk apapun, baik dalam silaturrahmi ataupun dalam penulisan tugas akhir ini penulis hanturkan segenap permintaan maaf dan harapan dalam menyelesaikan tulisan ini semoga berguna bagi pembaca. Akhir kata, ribuan terima kasih penulis hanturkan atas segala doa dan dukungan pembaca. Wassalam.
Medan, Oktober 2013 Penulis
ABSTRAK
Sebuah digraf dwiwarna D(2) adalah primitif jika terdapat bilangan bulat tak negatif
g dan h sehingga untuk setiap pasang titik u dan v di D(2) terdapat (g, h)-walk dari
u ke v. Bilangan bulat positif g +h terkecil dari semua bilangan bulat tak negatif
g dan h disebut eksponen dari digraf dwiwarna D(2), dinotasikan dengan expD(2)(v). Andaikan v adalah sebuah titik di D(2). Eksponen titik keluar v pada D(2) adalah bilangan bulat positif terkecilg+hsehingga terdapat (g, h)-walk dari titikv ke setiap titik di D(2), dinotasikan dengan expoutD(2)(v). Penelitian ini mempelajari eksponen
titik keluar dari sebuah kelas digraf dwiwarna primitifD(2) atasn≥5 titik ganjil yang terdiri dari n-cycle v1 →vn → vn−1 → · · · → v2 → v1 dan tepat satu arc v1 →vn+1
2 .
Andaikan vk, k = 1,2, ..., n adalah sebuah titik di D(2). Diperlihatkan bahwa jika arc biru berturut-turut terletak pada arc v2 → v1 dan arc v1 → vn di D(2) , maka eksponen titik keluar dari digraf dwiwarnaD(2) adalahexpoutD(2)(vk) =n2−n−2 +k untuk semuak = 1,2, ..., n.Jika arc biru berturut-turut terletak pada arcvn+3
2 →v
n+1
2
dan arc vn+1
2 →v
n
−1
2 , maka eksponen titik keluar dari digraf dwiwarna primitifD
(2) adalah expoutD(2)(vk) = 2
n2−3n−2+2k
2 untuk semua k= 1,2, ..., n.
THE OUTER VERTEX EXPONENTS OF A CLASS OF PRIMITIVE TWO -COLORED DIGRAPHS ON n-ODD VERTEX
ABSTRACT
A two-colored digraph D(2) is primitive provided there are nonnegative integerg and
h such that for each pair of vertices u and v there is a (g, h)-walk from vertex u to vertexv. The smallest positive integerg+htaken over all such nonnegative integers
g and h is the exponent of a two-colored digraph D(2), denoted by exp(D(2)). Let v
be a vertex of D(2). The outer vertex exponentv is the smallest positive integerg+h
there is a (g, h)-walk from v to every vertex in D(2), denoted by expoutD(2)(v). This
study explains about the outer vertex exponent of primitive two colored-digraph D(2)
on n ≥ 5 odd vertices consisting the n-cycle v1 → vn → vn−1 → · · · → v2 → v1 and blue arc v1 →vn+1
2 . Let v
k be a vertex ofD(2). We show that if two consecutive blue arcs lies on arc v2 → v1 and arc v1 → vn in D(2), then the outer vertex exponents is
expoutD(2)(vk) = n2 −n −2 +k for all k = 1,2, ..., n. If two consecutive blue arcs lies on arc vn+3
2 → v
n+1
2 and arc v
n+1
2 → v
n
−1
2 , then the outer vertex exponents is expoutD(2)(vk) = 2
n2−3n−2+2k
2 for all k = 1,2, ..., n.
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK v
ABSTRACT vi
DAFTAR ISI vii
DAFTAR GAMBAR viii
BAB 1 PENDAHULUAN
1.1 Latar Belakang Penelitian 1
1.2 Masalah Penelitian 2
1.3 Tinjauan Pustaka 3
1.4 Tujuan Penelitian 5
1.5 Manfaat Penelitian 6
BAB 2 DIGRAPH DWIWARNA PRIMITIF
2.1 Definisi 7
2.2 Matriks Adjacency 10
2.3 Primitifitas Dari Digraph Dwiwarna Terhubung Kuat 12 2.4 Matriks Tak Negatif dan Eksponen Digraph Dwiwarna 16
2.5 Eksponen Titik Digraph dan Digraph Dwiwarna 24
2.6 Sistem Persamaan Diophantine 26
2.7 Formula Eksponen Titik Digraph Dwiwarna dengan Dua Cycle 28
BAB 3 METODOLOGI PENELITIAN
3.1 Menentukan Eksponen Titik Keluar 31
3.2 Pembuktian Bentuk Umum Eksponen Titik Keluar 31
BAB 4 EKSPONEN TITIK KELUAR 33
BAB 5 KESIMPULAN DAN SARAN
5.1 Kesimpulan 42
5.2 Saran 42
DAFTAR GAMBAR
Gambar Halaman
1.1 Karakter PertamaD(2) 5
1.2 Karakter Kedua D(2) 5
2.1 Digraf dengan 4 titik dan 6 arc 8
2.2 Digraf dwiwarna dengan 6 titik dan 8 arc 9
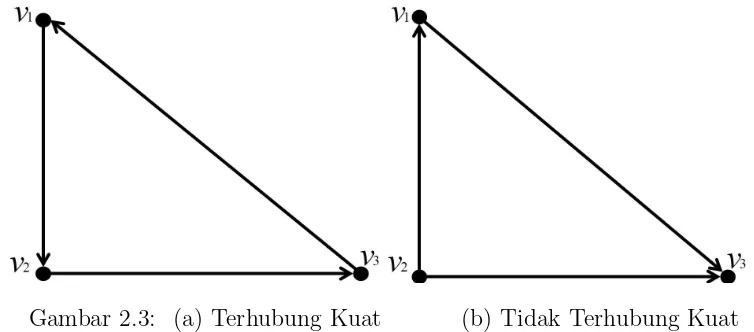
2.3 Digraf terhubung kuat dan tidak terhubung kuat 12
2.4 Digraf terhubung kuat dan primitif 13
2.5 Digraf dwiwarna terhubung kuat dan tidak terhubung kuat 14
2.6 Digraf dwiwarna terhubung kuat dan primitif 15
2.7 Digraf dengan 3 titik dan 4 arc 20
4.1 Digraf dwiwarna D(2) Tipe A 34
ABSTRAK
Sebuah digraf dwiwarna D(2) adalah primitif jika terdapat bilangan bulat tak negatif
g dan h sehingga untuk setiap pasang titik u dan v di D(2) terdapat (g, h)-walk dari
u ke v. Bilangan bulat positif g +h terkecil dari semua bilangan bulat tak negatif
g dan h disebut eksponen dari digraf dwiwarna D(2), dinotasikan dengan expD(2)(v). Andaikan v adalah sebuah titik di D(2). Eksponen titik keluar v pada D(2) adalah bilangan bulat positif terkecilg+hsehingga terdapat (g, h)-walk dari titikv ke setiap titik di D(2), dinotasikan dengan expoutD(2)(v). Penelitian ini mempelajari eksponen
titik keluar dari sebuah kelas digraf dwiwarna primitifD(2) atasn≥5 titik ganjil yang terdiri dari n-cycle v1 →vn → vn−1 → · · · → v2 → v1 dan tepat satu arc v1 →vn+1
2 .
Andaikan vk, k = 1,2, ..., n adalah sebuah titik di D(2). Diperlihatkan bahwa jika arc biru berturut-turut terletak pada arc v2 → v1 dan arc v1 → vn di D(2) , maka eksponen titik keluar dari digraf dwiwarnaD(2) adalahexpoutD(2)(vk) =n2−n−2 +k untuk semuak = 1,2, ..., n.Jika arc biru berturut-turut terletak pada arcvn+3
2 →v
n+1
2
dan arc vn+1
2 →v
n
−1
2 , maka eksponen titik keluar dari digraf dwiwarna primitifD
(2) adalah expoutD(2)(vk) = 2
n2−3n−2+2k
2 untuk semua k= 1,2, ..., n.
THE OUTER VERTEX EXPONENTS OF A CLASS OF PRIMITIVE TWO -COLORED DIGRAPHS ON n-ODD VERTEX
ABSTRACT
A two-colored digraph D(2) is primitive provided there are nonnegative integerg and
h such that for each pair of vertices u and v there is a (g, h)-walk from vertex u to vertexv. The smallest positive integerg+htaken over all such nonnegative integers
g and h is the exponent of a two-colored digraph D(2), denoted by exp(D(2)). Let v
be a vertex of D(2). The outer vertex exponentv is the smallest positive integerg+h
there is a (g, h)-walk from v to every vertex in D(2), denoted by expoutD(2)(v). This
study explains about the outer vertex exponent of primitive two colored-digraph D(2)
on n ≥ 5 odd vertices consisting the n-cycle v1 → vn → vn−1 → · · · → v2 → v1 and blue arc v1 →vn+1
2 . Let v
k be a vertex ofD(2). We show that if two consecutive blue arcs lies on arc v2 → v1 and arc v1 → vn in D(2), then the outer vertex exponents is
expoutD(2)(vk) = n2 −n −2 +k for all k = 1,2, ..., n. If two consecutive blue arcs lies on arc vn+3
2 → v
n+1
2 and arc v
n+1
2 → v
n
−1
2 , then the outer vertex exponents is expoutD(2)(vk) = 2
n2−3n−2+2k
2 for all k = 1,2, ..., n.
PENDAHULUAN
1.1 Latar Belakang Penelitian
Penelitian mengenai eksponen digraf dwiwarna telah banyak dilakukan. Shader dan
Suwilo (2003) adalah yang pertama sekali melakukan penelitian tersebut. Pada tahun
2002 , Wielandt ( Schneizer,H ) melakukan penelitian mengenai eksponen matrik tak
negatif. Andaikan A adalah sebuah matriks tak negatif berordo n×n. Matriks tak
negatif A dikatakan primitif jika dan hanya jika terdapat bilangan bulat positif k
sehingga Ak bernilai positif dan bilangan bulat terkecil k disebut sebagai eksponen
dari A.
Selanjutnya Digraf D(A) adalah sejumlah titik yang terhubung dengan garis
berarah (arc) pada setiap pasang titik (vi, vj) di D(A) jika dan hanya jika entri dari
matriks tak negatif A, yaituai,j >0, untuk i, j = 1,2,· · ·, n. Digraf D(A) dikatakan
terhubung kuat jika untuk setiap pasang titik (vi, vj) di D(A) terdapat walk dari vi
kevj dan darivj kevidengani, j = 1,2,· · ·, n. Suatu digrafD(A) dikatakanprimitif jika dan hanya jika terdapat bilangan bulat positif l sehingga untuk setiap pasangan
titik (vi, vj) terdapat walk dengan panjang l, maka bilangan bulat terkecil l disebut
sebagai eksponen dari digraf D(A) yang dinotasikan sebagai exp(D) (Brualdi dan
Ryser,1991). Eksponen titik dari digraph D(A) adalah jumlahwalk dengan panjang
minimum l′
yang menghubungkan titik vk, k = 1,2,· · ·, n ke setiap titik di D(A),
dinotasikan dengan expD(vk).
Pada tahun 1997, Fornasini dan Valcher mendefinisikan digraf dwiwarna
seba-gai berikut. Digraf dwiwarna D(2) merupakan suatu digraf yang setiaparcnya diberi
jika terdapat suatu bilangan bulat tak negatif m dan n dengan m+n > 0 sehingga
untuk setiap pasang titik (vi, vj) di D(2) terdapat (m, n)-walk dari vi kevj dan walk
dari vj ke vi, dengan m dan n masing-masing merupakan jumlaharc merah dan arc
biru, kemudian bilangan bulat positif terkecil dari m+n disebut sebagai eksponen
digraf dwiwarna D(2) yang dinotasikan dengan exp
D(2) (Shader dan Suwilo,2003).
Eksponen titik dari digraph dwiwarna D(2) adalah jumlah walk dengan panjang
minimumm′+n′ yang menghubungkan titikvk, k= 1,2,· · ·, n ke setiap titik diD(2) , untukm′
dann′
masing-masing adalah jumlaharcmerah danarcbiru, dinotasikan
dengan expD(2)(vk).
Pada tahun 2009 Gao dan Shao mulai memperkenalkan konsep eksponen
lokal. Andaikan D(2)adalah sebuah digraf dwiwarna primitif. Eksponen titik keluar
dari digraf dwiwarna adalah bilangan bulat positif terkecil g +h sehingga terdapat
(g, h)-walk untuk setiap pasang titikvk, k = 1,2,· · ·, n ke setiap titik di D(2),
dino-tasikan dengan expoutD(2)(vk) . Sedangkan eksponen titik masuk dari digraf
dwi-warna adalah bilangan bulat positif terkecil g′
+h′
sehingga terdapat (g′ , h′
)-walk
untuk setiap titik di D(2) ke titikv
k diD(2), dinotasikan dengan expinD(2)(vk) .
Bai dan Shao (2007) melakukan penelitian menentukan eksponen dari kelas
digraf dwiwarna dengan n-titik ganjil dengan batasan eksponen serta karakteristik
ekstermal dari digraf dwiwarna D(2) yang primitif atas n-titik ganjil yang memiliki
dua cycleyaknin-cycledan 1
2(n+ 1)-cycle. Sedangkan penelitian kali ini meneruskan
penelitian yang dilakukan oleh Bai dan Shao untuk menentukan eksponen titik keluar
dari digraf dwiwarna D(2).
1.2 Perumusan Masalah
Andaikan D(2) adalah digraf dwiwarna yang primitif atas n-titik ganjil. Kemudian,
mencari bagaimana pola dari eksponen titik keluar untuk setiap titikvk pada
1.3 Tinjauan Pustaka
Pada digraf dwiwarna, komponen terpenting dari sebuahwalkditentukan oleh jumlah
busur merah dan busur biru. Sebuah (h, k)-walk adalah sebuah walk yang terdiri
dari h buah busur berwarna merah dan k buah busur berwarna biru. Andaikan
w adalah sebuah walk dari digraf dwiwarna, dengan r(w) adalah banyaknya busur
berwarna merah dari w dan b(w) adalah banyaknya busur berwarna biru. Sehingga
vektor
r(w)
b(w)
disebut sebagai komposisi dari w.
Andaikan D(2) adalah sebuah digraf dwiwarna terhubung kuat dan C =
{c1, c2, ...., ct}adalah himpunan semua cycle di D(2). Sebuah matriks cycle dari D(2)
adalah sebuah matriks 2×t dalam bentuk
S =
r(c1) r(c2) ... r(ct)
b(c1) b(c2) ... b(ct)
setiap kolom ke-i dengan i = 1,2, ..., t dari matriks tersebut adalah komposisi dari
cycle ct. Fornansi Valcher (1997) memberikan karakteristik secara aljabar bagi
prim-itifitas digraf dwiwarna. Sebuah digraf dwiwarna terhubung kuat adalah primitif jika
dan hanya jika pembagi persekutuan terbesar dari determinan submatriks 2×2 dari
S adalah 1.
AndaikanD(2) merupakan digraf dwiwarna yang terdiri dari 2 cycle, sehingga
setiap walk pada D(2) dapat didekomposisi kedalam path pi,j dari titik vi ke setiap
titik vj dengan menggunakan sistem persamaan berikut
S
x1
x2
+
r(pi,j)
b(pi,j)
=
g
h ,
i, j = 1,2, ..., n
untuk memperoleh solusi bulat tak negatif x1, x2 ≥0.
Penelitian mengenai eksponen digraf dwiwarna dimulai oleh Shader dan Suwilo
bila D(2) adalah digraf dwiwarna yang primitif atasn-titik, maka eksponen terbesar
D(2) terletak pada interval [1 2(n
3−5n2),1 2(3n
3 −2n2−2n)].
Bai dan Shao (2007) melakukan penelitian menentukan eksponen dari kelas
digraf dwiwarna dengan n-titik ganjil dengan batasan eksponen serta karakteristik
ekstermal dari digraf dwiwarnaD(2) yang primitif atasn-titik ganjil yang memiliki 2
cycle yaknin-cycle dan 12(n+ 1)-cycle.
Gao dan Shao (2009) melakukan penelitian menentukan eksponen lokal keluar
dari titik-titik pada digraf dwiwarna tipe Wiedlant. Gao dan Shao mendefinisikan
eksponen lokal sebagai walk dengan komposisi sama yang berasal dari satu titik
ter-tentu dan menuju kesemua titik lainnya. Suwilo (2011) menentukan eksponen lokal
keluar dari titik-titik pada digraf ministrong ekstermal dwiwarna, sedangkan
Syah-marani dan Suwilo (2012) menentukan eksponen lokal keluar dari digraf Hamilton
dwiwarna dengan eksponen terbesar dan dengan eksponen terkecil.
Bai dan Shao membagi digraf dwiwarnaD(2) berdasarkan warnaarcyang terletak
pada arc v1 →v1
2(n+1) menjadi dua tipe yakni :
1. Tipe pertama, jika arc v1 → v1
2(n+1) berwarna biru maka batasan eksponen terletak pada [1
2(4n
2−n−1),4n2−5n] .
2. Tipe kedua, jika arc v1 → v1
2(n+1) berwarna merah maka batasan eksponen terletak pada [1
2(4n
2−3n+ 1),4n2 −6n].
Penelitian kali ini bertujuan untuk menentukan bentuk umum eksponen titik
keluar dari ekstermal digraf dwiwarna yang primitif atasn-titik ganjil dari tipe kedua
dengan dua arc biru berturut-turut pada penelitian yang dilakukan oleh Bai dan Shao.
Dalam hal ini terdapat dua karakter posisi arc biru berturut-turut yaitu :
Gambar 1.1 : Karakter Pertama D(2)
2. arc biru tepat berada pada posisi arc v1
2(n+1) → v12(n−1) dan arc v12(n+3) →
v1 2(n+1)
Gambar 1.2 : Karakter KeduaD(2)
1.4 Tujuan Penelitian
Tujuan dari penelitian ini adalah menentukan bentuk umum eksponen titik keluar
dari digraf dwiwarna yang primitif dengan n-titik ganjil dan dua arc biru
1.5 Manfaat Penelitian
Penelitian ini dilakukan untuk memperkaya literature dan menambah pengetahuan
DIGRAF DWIWARNA PRIMITIF
Pada bab ini akan dibahas teorema, definisi dan landasan teori pada penelitian ini.
Berikut akan dibahas mengenai digraf, digraf dwiwarna dan hubungan keduanya
dengan primitif itas,terhubung kuat, eksponen dan eksponen titik.
2.1 Definisi
Sub-bab ini akan membahas definisi tentang digraf dan digraf dwiwarna secara
ke-seluruhan.
2.1.1 Digraf
Andaikan V adalah sebuah himpunan berhingga yang tak kosong yang disebut
sebagai titik (vertex) dan E adalah himpunan pasangan berurut dari titik V yang
disebut sebagai edge, maka graf adalah suatu objek yang dibentuk dari himpunan
V,dan himpunan E ⊆V ×V yang unsurnya disebut sebagai edge.
Digraf D adalah objek yang dibentuk dari himpunan V, dan himpunan
A ⊆ V ×V yang unsurnya disebut sebagai arc dari D. Jika (u, v)∈ A merupakan
sebuah arc pada digraf D, maka u sebagai titik awal dan v sebagai titik akhir. Titik
V direpresentasikan dalam bentuk titik atau lingkaran kecil sedangkan arc
direpsen-tasikan dalam bentuk garis berarah.
Barisan sejumlah titikv1, v2, ..., vmsehingga terdapat arc dalamDyang menghubungkan
titik vi ke titik vi+1 untuk setiap i = 1,2,3, ..., m−1 disebut sebagai walk dengan
v1 →v2 →v3 →...→vm
untuk v1 6= vm maka disebut walk terbuka. Suatu walk yang tidak mengalami
pe-rulangan titik disebut sebagai path, sedangkan suatu path tertutup disebut sebagai
cycle dan cycle yang memiliki panjang 1 disebut sebagai loop.
Contoh 2.1.1 Berikut merupakan representasi dari definisi diatas.
Gambar 2.1 : Digraf dengan 4 titik dan 6 arc
Digraf diatas memperlihatkan walk , path, cycle, dan loop sebagai berikut:
a. v1 →v2 →v3 →v4 →v2 adalah walk terbuka
b. v1 →v2 →v3 →v4 →v2 →v3 →v1 adalah walk tertutup namun bukan path
c. v1 →v2 →v3 →v4 adalah path terbuka
d. v1 →v2 →v3 →v1 adalah path tertutup atau disebut cycle
e. v1 →v1 adalah loop
2.1.2 Digraf Dwiwarna
Suatu digraf yang setiap arc-nya berwarna biru atau merah dan tidak keduanya pada
satu arc disebut sebagai digraf dwiwarna. Digraf dwiwarna dibentuk oleh himpunan
vertex V, himpunan R ⊆ V ×V yang unsurnya adalah arc berwarna merah, dan
B ⊆ V ×V yang unsurnya adalah arc berwarna biru. Digraf Dwiwarna dinotasikan
Arc merah (u, v) direpresentasikan dengan u→m v atau dengan tanda panah sedangkan arc biru (u, v) direpresentasikan dengan u→b v atau garis putus-putus.
Contoh 2.1.2 Berikut gambar digraf dwiwarna
Gambar 2.2 : Digraf Dwiwarna dengan 6 titik 8 arc
Digraf dwiwarna diatas memperlihatkan himpunan vertex V = {v1, v2, v3, v4, v5, v6}
dengan uraian sebagai berikut :
a. Himpunan arc biru B ={(v3, v4),(v4, v2),(v6, v1)}
b. Himpunan arc merahR ={(v1, v2),(v2, v3),(v2, v5),(v5, v6),(v1, v1)}
merupakan suatu digraf dwiwarna dengan 6 vertex, 3 arc biru dan 5 arc merah.
Pada digraf dwiwarna juga terdapat walk, path, dan cycle. Suatu (h, k)-walk
dalam digraf dwiwarna adalah sebuah walk denganharc merah dankarc biru
sedan-gkan vektor ((r(w), b(w)) atau
r(w)
b(w)
merupakan komposisi dari walk w, dengan
r(w) adalah notasi dari jumlah arc merah dan b(w) adalah notasi dari jumlah arc
biru dan l(w) =r(w) +b(w) adalah panjang walkwyang merupakan jumlah dari arc
merah dan arc biru.
Seperti halnya digraf,path pada digraf dwiwarna merupakan walk yang tidak
mengalami perulangan titik, namun jika titik awal sama dengan titik akhir maka
satu yang memiliki komposisi 1 0 atau 0 1 .
Contoh 2.1.3 Berikut adalah contoh walk, path, cycle dan loop dari Gambar 2.2.
Digraf dwiwarna diatas memperlihatkan :
1. v1
m →v2
m →v3
b →v4
b
→v2 adalah walk terbuka.
2. v1 →m v2 →m v3 →b v4 adalah path terbuka.
3. v1
m →v2
m →v5
m →v6
b
→v1 adalah cycle.
4. v1
m
→v1 adalah loop dengan komposisi
1 0
2.2 Matriks Adjacency
Matriks adjacency dari digraf dan digraf dwiwarna dengan n-titik adalah suatu
ma-triks berordon×nyang dinotasikan denganAdimana setiap entrinya adalah 1 atau 0.
2.1.2 Matriks Adjacency Digraf
Matriks adjacency pada Digraf D dengan n-titik yang dinotasikan sebagai A(D) =
[aij] dengan entry sebagai berikut:
aij =
(
1, jika terdapat arc darivi kevj di D
0, jika sebaliknya untuk i, j = 1,2,3, ..., n
Contoh 2.2.1 Berikut adalah matriks adjacency pada digrafD yang diperoleh dari
Gambar 2.1
1 1 0 0
0 0 1 0
1 0 0 1
0 1 0 0
2.2.2 Matriks Adjacency Digraf Dwiwarna
Pada digraf dwiwarna matriks adjacency dibagi menjadi 2 bagian berdasarkan warna
arc yakni :
a. Matriks adjacency merah
Matriks adjacency merah yang berordo n ×n dinotasikan sebagai R = [rij]
dengan entri adalah sebagai berikut:
rij =
(
1, jika terdapat arc merah dari vi ke vj diD(2)
0, jika sebaliknya
untuk i, j = 1,2,3, ..., n
Contoh 2.2.2 Berikut adalah matriks adjacency merah dari digraf dwiwarna
yang diperoleh dari Gambar 2.2.
1 1 0 0 0 0
0 0 1 0 1 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 1
0 0 0 0 0 0
b. Matriks adjacency biru
Matriks adjacency biru yang berordon×n dinotasikan sebagai B = [bij]dengan
entri adalah sebagai berikut:
bij =
(
1, jika terdapat arc biru darivi kevj di D(2)
0, jika sebaliknya
untuk i, j = 1,2,3, ..., n.
Contoh 2.2.3 Berikut adalah matriks adjacency biru dari digraf dwiwarna
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 1 0 0
0 1 0 0 0 0
0 0 0 0 0 0
1 0 0 0 0 0
2.3 Primitifitas Digraf dan Digraf Dwiwarna Terhubung Kuat
Pada subbab ini akan dibahas mengenai digraf dan digraf dwiwarna terhubung kuat
dan hubungannya dengan primitifitas.
2.3.1 Primitifas Digraf Terhubung Kuat
Suatu digraf D dikatakan terhubung kuat (strongly connected) jika untuk setiap
pasang titik udan v di D terdapat walk dari uke v dan walk dari v keu.
Contoh 2.3.1Berikut adalah digraf terhubung kuat dan tak terhubung kuat.
Gambar 2.3: (a) Terhubung Kuat (b) Tidak Terhubung Kuat
Gambar 2.3 memperlihatkan bahwa pada (a) terdapat walk dari satu titik ketitik
Lemma 2.3.1 Andaikan D adalah digraf terhubung kuat maka setiap titik u di D
terletak pada cycle.
Bukti : Ambil sebarang titiku diD dan sebarang arc dari titikukev diD. Karena
D adalah digraf terhubung kuat, maka terdapat path dari titiku kev dan path dari
titik v ke u akibatnya terdapat path tertutup atau disebut sebagai cycle untuk
se-tiap titikudiD. Dengan kata lain bahwa setiap titikudiDterletak pada suatu cycle.
Andaikan C = {γ1, γ2, ..., γq} merupakan himpunan semua cycle di D dan
misalkan notasi l(γi) merupakan panjang semua cycle pada digraf D untuk setiap
i= 1,2,· · ·, q. Suatu digrafDterhubung kuat dikatakan primitif jika dan hanya jika pembagi persekutuan terbesar dari setiap panjang cycle di D adalah 1 (Brualdi dan
Ryser,1991).
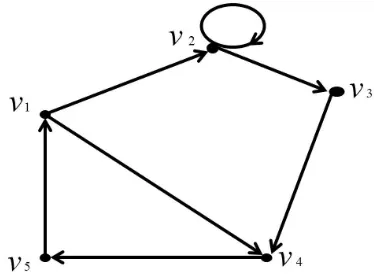
Contoh 2.3.2 Berikut adalah digraf terhubung kuat yang primitif.
Gambar 2.4 : Digraf Terhubung Kuat dan Primitif
Pada gambar 2.4 diperlihatkan bahwa l(γ1) dari cyclev1 →v2 →v3 →v4 →v5 →v1
adalah 5. Kemudian l(γ2) dari cycle v1 → v4 → v5 → v1 adalah 3. Dan l(γ3) dari
cycle tertutup v1 ke v1 adalah 1. Sehingga diketahui bahwa pembagi persekutuan
2.3.2 Primitifitas Digraf Dwiwarna Terhubung Kuat
Suatu digraf D dikatakan terhubung kuat (strongly connected) jika untuk setiap
pasang titik udan v di D terdapat walk dari uke v dan walk dari v ke u.
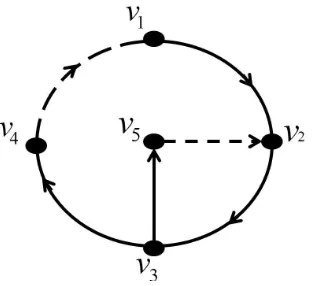
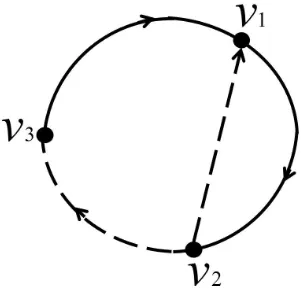
Contoh 2.3.3Berikut adalah digraf dwiwarna terhubung kuat dan tidak terhubung
kuat.
Gambar 2.5: (a)Terhubung Kuat (b)Tidak Terhubung Kuat
Gambar 2.5 memperlihatkan bahwa pada digraf dwiwarna (a) terdapat walk dari satu
titik ketitik lainnya. Sedangkan (b) tidak terdapat walk dari v3 kev1.
Lemma 2.3.2 Andaikan D(2) adalah digraf dwiwarna terhubung kuat maka setiap
titik u di D(2) terletak pada cycle.
Bukti : Ambil sebarang titik u di D(2) dan sebarang arc dari titik u ke v di D(2).
KarenaD(2) adalah digraf dwiwarna terhubung kuat, maka terdapat path dari titiku
kev dan path dari titikv keuakibatnya terdapat path tertutup atau disebut sebagai
cycle untuk setiap titik u di D(2). Dengan kata lain bahwa setiap titik u di D(2)
terletak pada suatu cycle.
Digraf dwiwarna D(2) terhubung kuat dikatakan primitif jika terdapat suatu
titik (u, v) di D(2) terdapat (h, k)-walk dari u ke v dan walk dari v keu.
Andaikan C = {γ1, γ2, ..., γq} merupakan himpunan semua cycle di D(2) dan
misalkan notasi l(γi) merupakan panjang semua cycle pada digraf dwiwarna D(2)
untuk setiap i = 1,2,3,· · ·, q. S disebut sebagai matriks cycle adalah matriks yang berordo 2×q sebagai berikut
S =
r(γ1) r(γ2) · · · r(γq)
b(γ1) b(γ2) · · · b(γq)
Kolom ke-qdari matrik cycleS merupakan komposisi dari cycleγq dan jumlah
baris pada matriksSmenyatakan banyaknya warna padaD(2). Suatu digraf dwiwarna
dikatakan primitif jika dan hanya jika pembagi persekutuan terbesar dari
determinan-determinan matriks minor berordo 2×2 dariSadalah 1 (Fornasini dan Valcher,1997).
Contoh 2.3.4 Berikut adalah digraf dwiwarna terhubung kuat yang primitif.
Gambar 2.6 Digraf Dwiwarna Terhubung Kuat dan Primitif
Dari Gambar 2.6 diatas terdapat 2 cycle yaitu cycle yang pertama v1
m → v2
m →v3
m →
v4
b
→ v1 dengan komposisi S1 =
3
1
dan cycle kedua adalah v5
b → v2
m → v3
m → v5
dengan komposisi S2 =
2
1
, maka matriks cycle dari D(2) adalah S =
3 2
1 1
dengan det(S) = 1. Sehingga Digraf Dwiwarna pada Gambar 2.6 adalah terhubung
2.4 Matriks Tak Negatif dan Digraf Dwiwarna
Suatu matriks A dikatakan matriks tak negatif jika untuk setiap entri dari matriks
A= [aij] bernilai tak negatif atau dapat dinotasikan dengan aij ≥0 .
Contoh 2.4.1Berikut adalah matriks tak negatif.
1 0 0
0 1 0
0 0 1
sedangkan matriksA dikatakan postitif, jika untuk setiap entri dari matriksA= [aij]
bernilai positif atau dapat dinotasikan dengan aij >0 .
Contoh 2.4.2 Berikut adalah matriks positif.
1 4 7
2 5 8
3 6 9
Pada suatu digrafD, terdapat suatu bilangan bulat positiflsehingga untuk setiap
pasangan titik-titikudan v terdapat walk dari uke v dengan panjangl, maka
bilan-gan bulat positif terkecil l disebut sebagai eksponen dari digraf D yang dinotasikan
sebagai exp(D) (Brualdi dan Ryser,1991).
Proposisi 2.4 Andaikan A adalah suatu matriks adjacency dari digraf D. Entri
ak
ij dari Ak menyatakan banyaknya walk dari titik vi ke vj dengan panjang k di D.
Bukti : Andaikan A suatu matriks adjacency dari digraf D, maka setiap entri aij
dari A menyatakan arc dari titikvi kevj diD. Sehingga untukk = 1, terdapat entri
a1
ij dariA1 menyatakan banyaknya walk dari titikvi kevj dengan panjang satu diD.
Asumsikan setiap entri ak
ij dari Ak menyatakan banyaknya walk dari titik vi
entriak+1
ij menyatakan banyaknya walk dari titikvi kevj dengan panjang k+ 1 diD,
untuk setiap k ≥1 .
Perhatikan setiap walk dari titik vi ke vj di D dengan panjang k + 1 yang
terdiri dari walk vi ke vl dengan panjang k dengan l = 1,2,3, .., n dan dilanjutkan
dengan arc dari titikvl kevj. Sehinggaakilalj menyatakan walk dengan panjang k+ 1
dari titik vi ke vj di D untuk k = 1,2,3,· · ·, n. Jika terdapat walk dengan panjang
k dari titik vi ke vj di D, maka akil = 0 sehingga akilalj = 0. Hal ini berarti tidak
terdapat walk dengan panjang k + 1 dari titik vi ke vj yang melalui titik vl di D.
Sehingga diperoleh jumlah walk dengan panjang k+ 1 dari titik vi kevj diD adalah
ak
i1a1j +aki2a2j+...+akinanj = n
X
i=1
ak ilalj
Karena Ak+1 = AkA maka ak ij =
Pn
i=1akilalj . Hal ini berakibat a k+1
ij adalah benar menyatakan banyaknya walk dari titik vi ke vj yang panjangnya k+ 1 di D.
Contoh 2.4.1 Berikut adalah representasi menghitung eksponen dari digrafD.
Dari Gambar 2.1 diatas diperoleh matriks adjacency sebagai berikut.
A=
1 1 0 0
0 0 1 0
1 0 0 1
0 1 0 0
Dari proposisi diatas, dengan mencari banyak walk dari titik vi kevj dengan
panjang k, sehingga bilangan bulat positif terkecil k adalah eksponen dari digraf D.
Perhatikan matriks Ak untuk k:
a. Untukk = 1, diperoleh A=
1 1 0 0
0 0 1 0
1 0 0 1
0 1 0 0
maka k = 1 bukan merupakan eksponen dari digraf karena tidak terdapat walk
b. untuk k = 2, diperolehA2=
1 1 1 0
1 0 0 1
1 2 0 0
0 0 1 0
maka k = 2 bukan merupakan eksponen dari digraf karena tidak terdapat walk
dengan panjang 2 dari titik v1 ke v4, v2 ke v2,v2 kev3,v3 kev4, dst.
c. Untukk = 3 , diperoleh A3 =
2 1 1 1
1 2 0 1
1 1 2 0
1 0 0 1
maka k= 3 bukan merupakan eksponen dari digraf, karena tidak terdapat walk
dengan panjang tiga dari titik v2 kev3,v3 kev4, dst.
d. Untukk = 4, diperoleh A4 =
3 3 1 1
1 1 2 0
3 1 1 2
1 2 0 0
maka k= 4 bukan merupakan eksponen dari digraf, karena tidak terdapat walk
dengan panjang empat dari titik v2 ke v4, v4 ke v3, v4 ke v4, dst.
e. Untukk = 5, diperoleh A5 =
4 4 3 1
3 1 1 2
4 5 1 1
1 1 2 0
maka k= 5 bukan merupakan eksponen dari digraf, karena tidak terdapat walk
dengan panjang lima dari titik v4 kev4.
f. Untukk = 6, diperoleh A6 =
7 5 4 3
4 5 1 1
5 5 5 1
3 1 1 2
merupakan eksponen dari digraf, karena setiap pasang titik (vi, vj) memiliki
Pada digraf dwiwarnaD(2), eksponen dari digraf dwiwarnaD(2), di definisikan
sebagai bilangan bulat positif terkecilh+k yang terdiri dari h arc merah dan k arc
biru sehingga untuk setiap pasang titikudanv terdapat sebuah (h, k)-walk dari uke
v, eksponen dari digraf dwiwarnaD(2) dinotasikan olehexp(D(2))(Shader dan Suwilo,
2003).
Andaikan A dan B adalah suatu matriks tak negatif berordo m ×m. Un-tuk bilangan tak negatif h dan k di definisikan (h, k)-Hurwitz product, (R, B)(h,k)
adalah jumlah keseluruhan matriks dari perkalianR sebanyakh kali danB sebanyak
k kali.
Contoh 2.4.2 :
(R, B)(1,0) =R dan (R, B)(2,2)=R2B2+RBRB+RB2R+BRBR+B2R2
Lemma 2.4.1 Jika (R, B) adalah matriks adjacency dari digraf dwiwarna. Maka
(R, B)(h,k) adalah jumlah (h, k)-walk dari v
i ke vj pada digraf dwiwarna.
Bukti : Pembuktian dilakukan dengan cara induksi, yakni jika h = 0 dan k = 1
maka (R, B)(0,1) =B merupakan walk dari v
i ke vj memiliki komposisi
0
1
pada
digraf dwiwarna . Kemudian jika h= 1 dan k = 0 maka (R, B)(1,0) =R merupakan
walk dari vi kevj memiliki komposisi
1
0
pada digraf dwiwarna.
Kemudian diperlihatkan untuk semua bilangan bulat tak negatif h+k + 1
adalah benar dengan pembuktian sebagai berikut.
(R, B)(h+1,k) =R(R, B)(h,k)+B(R, B)(h+1,k−1)
sehingga R(R, B)(h,k) menyatakan bahwa terdapat walk dariv
i kevj dengan panjang
(h, k) yang diikuti dengan sebuah arc merah, sedangkan B(R, B)(h+1,k−1) menyatakan
bahwa terdapat walk dari vi ke vj dengan panjang (h+ 1, k−1) yang diikuti oleh
dari vi kevj.
[image:32.612.251.403.156.302.2]Contoh 2.4.3 Berikut adalah representasi menghitung eksponen digraf dwiwarna.
Gambar 2.7 : Digraf Dwiwarna dengan 3 titik dan 4 arc
Dari Gambar 2.7 digraf dwiwarna terhubung kuat yang primitif terdapat matriks
ad-jacency merah R =
0 1 0
0 0 0
1 0 0
dan matriks adjacency biru B =
0 0 0
1 0 1
0 0 0
.
Menggunakan Lemma 2.4.1, jika (R, B) adalah matriks adjacendy dari digraf
dwi-warna. Maka (R, B)(h,k)adalah jumlah (h, k)-walk dariv
ikevjpada digraf dwiwarna.
Sehingga h+k merupakan eksponen dari digraf bila matriks (R, B)(h,k) adalah
ma-triks positif.
Dengan demikian perhatikan matriks adjacency merahRdan matriks adjacency biru
B adalah sebagai berikut :
1. Untukh+k = 2 , maka diperoleh
a. (R, B)(2,0) =R2 =
0 0 0
0 0 0
0 1 0
b. (R, B)(1,1) =RB+BR=
0 0 0
0 0 0
0 0 0
c. (R, B)(0,2) =B2 =
1 0 1
1 1 0
0 0 0
2. Untukh+k = 3, maka diperoleh
a. (R, B)(3,0) =R3 =
0 0 0
0 0 0
0 0 0
b. (R, B)(2,1) =R(R, B)(1,1)+BR2 =
1 1 0
0 1 0
1 0 1
c. (R, B)(1,2) =RB2+B(R, B)(1,1)=
0 0 0
1 0 1
0 0 0
d. (R, B)(0,3) =B3 =
0 0 0
0 0 0
0 0 0
3. Untukh+k = 4, maka diperoleh
a. (R, B)(4,0) =R4 =
0 0 0
0 0 0
0 0 0
b. (R, B)(3,1) =R(R, B)(2,1)+BR3 =
0 1 0
0 0 0
1 0 1
c. (R, B)(2,2) =R(R, B)(1,2)+B(R, B)(2,1)=
1 0 1
2 1 1
0 0 0
d. (R, B)(1,3) =RB3+B(R, B)(1,2)=
0 0 0
0 0 0
0 0 0
e. (R, B)(0,4) =B4 =
0 0 0
0 0 0
0 0 0
4. Untukh+k = 6, maka diperoleh
a. (R, B)(6,0) =R6 =
0 0 0
0 0 0
0 0 0
b. (R, B)(1,5) =RB3+B(R, B)(1,4)=
0 0 0
0 0 0
0 0 0
c. (R, B)(2,4) =R(R, B)(1,4)+B(R, B)(2,3)=
0 0 0
0 0 0
0 0 0
d. (R, B)(3,3) =R(R, B)(2,3)+B(R, B)(3,2)=
1 0 1
3 1 2
0 0 0
e. (R, B)(4,2) =R(R, B)(3,2)+B(R, B)(4,1)=
1 2 0
0 1 0
2 1 1
f. (R, B)(5,1) =R(R, B)(4,1)+BR5 =
0 0 0
0 0 0
0 0 0
a. (R, B)(0,6) =B6 =
0 0 0
0 0 0
0 0 0
5. Untukh+k = 10, maka diperoleh
a. (R, B)(10,0)=R10 =
0 0 0
0 0 0
0 0 0
b. (R, B)(1,9) =RB9+B(R, B)(1,8)=
0 0 0
0 0 0
0 0 0
c. (R, B)(2,8) =R(R, B)(1,8)+B(R, B)(2,7)=
0 0 0
0 0 0
0 0 0
d. (R, B)(3,7) =R(R, B)(2,7)+B(R, B)(3,6)=
1 0 1
3 1 2
0 0 0
e. (R, B)(4,6) =R(R, B)(3,6)+B(R, B)(4,5)=
1 2 0
0 1 0
2 1 1
f. (R, B)(5,5) =R(R, B)(4,5)+B(R, B)(5,4)=
1 0 1
5 1 4
0 0 0
a. (R, B)(6,4) =R(R, B)(5,4)+B(R, B)(6,3)=
6 4 3
4 6 1
4 1 3
se-hingga exp(D(2)) = 10 dengan komposisi 6 arc merah dan 4 arc biru yakni
6
4
.
2.5 Eksponen Titik Digraf dan Digraf Dwiwarna
Pada subbab ini akan dibahas definisi dan penentuan eksponen titik digraf dan digraf
dwiwarna.
2.5.1 Eksponen Titik Digraf
Misalkan D adalah sebuah digraf primitif yang terdiri dari himpunan titik V(D) =
{v1, v2, ..., vn}. Eksponen titik dari digraph D didefinisikan sebagai jumlah walk
dengan panjang minimumm yang menghubungkan titikvk ke setiap titik di D
dino-tasikan γD(vk).
Misalkan Dadalah sebuah digraf dwiwarna primitif yang berordo n×n. Jika
titik-titik di D adalah (v1, v2, ...vn) sehingga
γD(v1)≥γD(v2)≥...≥γD(vn)
MakaγD(vk) adalah tipe pertama generalisasi eksponen ke-kdariD, yang dinotasikan
dengan expD(vk).
Contoh 2.5.1Berikut adalah bagaimana mencari eksponen titik dari masing-masing
titik di digraf D, berdasarkan proposisi 2.4 entri aij harus bernilai positif.
Dari Contoh 2.4.1 diperoleh matriks-matriks dari Ak :
1. Untuk k=3, pada baris pertama semua entri bernilai positif, makaexpD(v1) = 3.
2. Untuk k=4, pada baris ke-3 semua entri juga bernilai positif,makaexpD(v3) = 4.
3. Untuk k=5, pada baris ke-2 semua entri bernilai positif, maka expD(v2) = 5.
2.5.2 Eksponen Titik Digraf Dwiwarna
Misalkan D(2) adalah sebuah digraf dwiwarna primitif yang terdiri dari himpunan
titik V(D) = {v1, v2, ..., vn}. Eksponen titik dari digraph dwiwarna D(2)
didefin-isikan sebagai jumlah walk dengan panjang minimumg+hyang menghubungkan titik
vk ke setiap titik di D(2), dengang menyatakan jumlah arc merah danh menyatakan
jumlah arc biru . Kemudian dinotasikan dengan γD(vk).
Misalkan Dadalah sebuah digraf dwiwarna primitif yang berordo n×n. Jika titik-titik di D(2) adalah (v
1, v2, ..., vn), maka
γD(v1)≥γD(v2)≥...≥γD(vn)
sehingga γD(vk) adalah tipe pertama generalisasi eksponen ke-k dariD(2), yang
dino-tasikan dengan expD(2)(vk) .
Dengan menggunakan operasi (g, h)-matriksHurwitz ProductRdanByang
telah didefenisikan pada subbab 2.4. Untuk suatu bilangan positif terkecil g dan h
yang masing-masing merupakan jumlah arc merah dan arc biru, sehinggag+h
meru-pakan eksponen titik digraf dwiwarna untuk setiap baris ke-k dari matriks tersebut
yang seluruh entrinya bernilai positif .
Contoh 2.5.2 Berikut mencari eksponen titik digraf dwiwarna dari masing-masing
titik pada Gambar 2.6.
1. Untuk g+h=4, dengan
(R, B)(2,2) =R(R, B)(1,2)+B(R, B)(2,1)=
1 0 1
2 1 1
0 0 0
pada baris ke-2 semua entri bernilai positif,maka expD(2)(v3) = 4 yang terdiri
dari 2 arc merah dan 2 arc biru yakni
2
2
2. Untuk g+h=5 dengan
(R, B)(3,2) =R(R, B)(2,2)+B(R, B)(3,1)=
2 1 1
1 2 0
1 0 1
pada baris pertama semua entri bernilai positif, maka expD(2)(v1) = 5 yang
terdiri dari 3 arc merah dan 2 arc biru yakni
3
2
.
3. Untuk g+h=6, dengan
(R, B)(4,2) =R(R, B)(3,2)+B(R, B)(4,1)=
1 2 0
0 1 0
2 1 1
pada baris ke-3 semua entri bernilai positif, maka expD(2)(v2) = 6 yang terdiri
dari 4 arc merah dan 2 arc biru yakni
4
2
.
2.6 Sistem Persamaan Diophantine
Bentuk persamaaan Diophantine dapat dituliskan sebagai berikut
a1x1+a2x2 +a3x3+...+anxn=b
memiliki solusi bilangan bulat untuk semua bilangan bulat positif n dan
koefisien-koefisien a1, a2, a3, ..., an tidak semuanya bernilai nol.
Teorema 2.6 Persamaan diophantine
a1x1+a2x2 +a3x3+...+anxn=b
Bukti : Sistem persamaan diophantine adalah himpunan dari m persamaan
dio-phantine dalam n variabel yang sama, untuk m, n > 0. Berikut merupakan sistem
persamaan diophantine.
a11x1+a12x2 +...+a1nxn =b1
a21x1+a22x2 +...+a2nxn =b2
.. .
am1x1+am2x2 +...+amnxn =bm
Sistem persamaan diophantine tersebut dapat pula direpresentasikan dalam bentuk
persamaan matriks Ax=b sebagai berikut
A=
a11 a12 · · · a1n
a21 a22 · · · a2n ..
. ... . .. ...
am1 am2 · · · amn
, x=
x1 x2 .. . xn
dan b =
b1 b2 .. . bm
Sistem persamaan diophantine memiliki solusi bilangan bulat jika dan hanya jika
pembagi persekutuan terbesar dari determinan-determinan submatriks 2×2 dari A adalah ±1.
2.7 Formula Eksponen Titik Digraf Dwiwarna dengan Dua Cycle
Subbab ini dibahas bagaimana menentukan batas atas dan batas bawah eksponen
titik digraf dwiwarna yang primitif yang memuat dua cycle.
Lemma 2.7.1 Andaikan D(2) adalah digraf dwiwarna primitif yang memuat dua
cycle dengan matriks cycle S=
r(γ1) b(γ2)
b(γ1) r(γ2)
. Misalkanvkadalah sembarang titik
dariD(2) dan terdapat sebuah(g, h)-walk dari titikv
kke setiap titikvj, j = 1,2,· · ·, n
di D(2) dengan persamaan berikut
g
h
maka u w
≥ S−1
r(p(k,j)
b(p(k,j)
untuk sembarang bilangan bulat tak negatif u, v dan
untuk suatu path p(k,j) dari vk ke vj.
Bukti : Misalkanp(k,j)adalah path dari titikvkkevj untuk sembarangj = 1,2, ..., n.
KarenaD(2) memuat 2 cycle maka setiap walknya dapat didekomposisi ke dalam path
dan cycle sebagai berikut :
g
h
=S x1 x2 +
r(p(k,j))
b(p(k,j))
(2)
dengan x1, x2 ≥0. Karena D(2) primitif, makaM memiliki invers. Dengan
menggu-nakan persamaan (1) dan (2), maka diperoleh :
S u w
=S x1 x2 +
r(p(k,j))
b(p(k,j))
S x1 x2
=S u w −
r(p(k,j))
b(p(k,j))
x1 x2 = u w
−S−1
r(p(k,j))
b(p(k,j))
≥0
sehingga u w
≥ S−1
r(p(k,j)
b(p(k,j)
dan Lemma 2.7.1 terbukti.
Menggunakan Lemma 2.7.1 diperoleh teorema sebagai berikut.
Teorema 2.7.1 Andaikan D(2) adalah digraf dwiwarna primitif yang terdiri dari
cycle γ1 dan γ2. Misalkan vk adalah titik diD(2). Untuk sembarang titik vi dan vj di
D(2), didefinisikan u
0 =b(γ2)r(pk,j)−r(γ2)b(pk,j) danw0 =r(γ1)b(pk,j)−b(γ1)r(pk,j)
maka g h
≥S
u0
w0
, sehingga expD(2)(vk)≥l(γ1)u0+l(γ2)w0.
g
h
=S
u
w
sehingga diperoleh persamaan
u
w
≥S−1
r(p(k,j))
b(p(k,j))
=
b(γ2)r(pk,j)−r(γ2)b(pk,j)
r(γ1)b(pk,j)−b(γ1)r(pk,j)
(3)
untuk setiap path pk,j dari titikvk ke vj.
Untuk sembarang titikvj, j = 1,2, ..., n, diperoleh
u0 =b(γ2)r(pk,j)−r(γ2)b(pk,j)≥0 (4)
dan untuk sembarang titik vi, i= 1,2, ..., n, diperoleh
w0 =r(γ1)b(pk,i)−b(γ1)r(pk,i)≥0 (5)
sehingga u≥u0 dan w≥w0. Oleh Lemma 2.6.1 diperoleh
g
h
=S
u
w
≥S
u0
w0
(6)
sehinggaexpD(2)(vk) =g+h≥(r(γ1)+b(γ1))u0+(r(γ2)+b(γ2))w0 =l(γ1)u0+l(γ2)w0.
Teorema 2.7.1 menerangkan tentang batas bawah eksponen titik, sedangkan
Proposisi 2.7.1 berikut akan menerangkan batas atas eksponen titik digraf dwiwarna
yang primitif dari suatu titikv, dengan d(v, vk) merupakan jarak dari titikvk ke titik
v sebagai walk terpendek dari vk ke titikv.
Proposisi 2.7.1 Asumsikan D(2) adalah digraf dwiwarna primitif atas n-titik.
Mis-alkan v adalah sebuah titik di D(2) dengan exp(2)
D (vk). Untuk sembarang titik vk, k = 1,2, ..., n di D(2), exp
D(2)(vk)≤expD(2)(v) +d(vk, v).
Bukti : Untuk setiap k = 1,2, ..., n misalkan pk,v adalah (r(pk,v), b(pk,v))-path dari
titik vk ke titik v dengan panjang d(vk, v). Terdapat (g, h)-walk dari titik v ke
se-tiap titik vj, j = 1,2, ..., n di D(2) , sehingga expD(2)(v) = g +h. ini
titik vk ke setiap titik vj. Walk tersebut berjalan dari titik vk ke v dengan melalui
(r(pk,v), b(pk,v))-path selanjutnya menuju ke titik vj melalui (g +h)-walk. Sehingga
diperoleh expD(2)(vk)≤expD(2)(v) +d(vk, v).
Proposisi 2.7.2 Andaikan D(2) adalah digraf dwiwarna yang terdiri atas cycle γ 1
danγ2. Misalkan titik vk adalah titik di D(2) yang terdapat pada cycleγ1 danγ2. Jika
untuk setiap i = 1,2, ..., n dan sembarang bilangan g dan h, terdapat path pk,i dari
titik vk ke titik vi sehingga sistem persamaan
Sx+
r(p(k,i))
b(p(k,i))
=
g
h
(7)
punya solusi bilangan bulat tak negatif, sehingga expD(2)(v)≤g+h.
Bukti : Misalkan bahwa solusi persamaan (7) adalah x = (x1, x2)T. Karena D(2)
adalah digraf dwiwarna primitif, maka S punya invers sehingga x1, x2 6= 0, sehingga
terdapat tiga kemungkinan dalam hal ini.
1. Jika x1, x2 > 0, maka terdapat (g, h)-walk yang bergerak dari titik vk ke titik
vi mengelilingi γ1 sebanyak x1 kali dan mengelilingin γ2 sebanyak x2 kali dan
kembali ke titikvkdan kemudian bergerak menuju titikvi dengan panjang path
pk,i.
2. Jika x1 = 0 dan x2 >0, maka terdapat (g, h)-walk yang bergerak dari titikvk
ke titikvimengelilingiγ2 sebanyakx2kali dan kembali ke titikvkdan kemudian
bergerak menuju titikvi dengan panjang path pk,i.
3. Jika x1 >0 dan x2 = 0, maka terdapat (g, h)-walk yang bergerak dari titikvk
ke titikvimengelilingiγ1 sebanyakx1kali dan kembali ke titikvkdan kemudian
bergerak menuju titikvi dengan panjang path pk,i.
Sehingga untuk setiap titik vi, i= 1,2, ..., n terdapat (g, h)-walk dari titikvk ke titik
METODOLOGI PENELITIAN
Metodologi penelitian yang dilakukan untuk menentukan bentuk umum eksponen
titik keluar dari digraf dwiwarna dengann-titik ganjil dan duaarcbiru berturut-turut
adalah dengan mengumpulkan informasi-informasi yang berkaitan dengan penelitian
ini. Beberapa langkah berikut merupakan sistematis penulisan yang dilakukan.
3.1 Menentukan Eksponen Titik Keluar
Dengan menggunakan program yang ditulis dalam MATLAB diperoleh
bilangan-bilangan bulat tak negatif g dan h sehingga
expoutD(2)(vk) =g+h
untuk semua k = 1,2,· · ·, n.
Cara manual juga dapat dilakukan dengan menghitung hasil kali matriks adjacency
(R, B)(g,h) dengan (g, h) adalah jumlah walk dari v
k ke setiap titik diD(2).
3.2 Pembuktian Bentuk Umum Eksponen Titik Keluar
Setelah memperoleh bilangan-bilangan bulat tak negatif g dan h , langkah
berikut-nya adalah membuktikan bahwaexpoutD(2)(vk) =g+h. Sehingga perlu diperlihatkan
batas bawah dan batas atas eksponen titik keluar yakni expoutD(2)(vk) ≥g +h dan
expoutD(2)(vk)≤g+h untuk semua k= 1,2,· · ·, n.
Langkah pertama ialah memperlihatkan batas bawah eksponen titik keluar
g
h
≥S
u0
w0
dengan u0, w0 >0, sehingga expoutD(2)(vk)≥g+h untuk semua k = 1,2, ..., n.
Kemudian memperlihatkan batas atas eksponen titik keluar expoutD(2)(vk)≤
g+huntuk semuak = 1,2, ..., n, dengan memperlihatkan sistem persamaan berikut
S
x1
x2
+
r(pk,j)
b(pk,j)
=
g
h
j = 1,2, ..., n
mempunyai solusi bulat tak negatif yakni x1, x2 ≥ 0 untuk semua titik di D(2) dan
untuk semua path pk,j dari vk kevj.
Setelah memperlihatkan kedua batas tersebut, maka terbukti bahwa
expoutD(2)(vk) =g+h
EKSPONEN TITIK KELUAR D(2)
Pada bab ini akan dibahas eksponen titik keluar dari kelas digraf dwiwarna yang
primitif. Andaikan D(2) merupakan suatu digraf dwiwarna yang primitif atas n ≥ 5
titik ganjil yang terdiri dari cyclev1 →vn→vn−1 → · · · →v2 →v1 dengan panjang
n dan arc v1 → vn+1
2 . Terdapat 2 cycle pada D
(2) yakni cycle v
1 → vn → vn−1 →
· · · → v2 → v1 dengan panjang n dan cycle v1 → vn+1 2 → v
n−1
2 → · · · → v2 → v1 dengan panjang (n+1)/2. Oleh sifat digraf dwiwarnaD(2), assumsikan bahwa matriks
cycle dari D(2) adalah sebagai berikut.
S1 =
n+1
2 −a n−b
a b
atau S2 =
a b
n+1
2 −a n−b
untuk sebarang bilangan bulat 1≤a≤n dan 1≤b ≤n.
Digraf dwiwarna dikatakan primitif jika dan hanya jika content dari matriks cycle
D(2) adalah 1, sehingga det(S
1) = ±1 atau det(S2) = ±1. Hal tersebut akan
ter-penuhi jika dan hanya jikaa = 1 dan b= 2, sehingga matriks cycle dari D(2) adalah
S1 =
n−1
2 n−2
1 2
atau S2 =
1 2
n−1
2 n−2
dengan cycle γ1 terdiri dari (n−1)/2 arc merah dan tepat 1 arc biru , sedangkan
cycle γ2 terdiri dari n− 2 arc merah dan 2 arc biru . Dalam pembuktian kali ini
digunakan matriks cycle S =
n−1
2 n−2
1 2
.
Penelitian ini juga membagi digraf dwiwarna D(2) atas 2 tipe.
1. Tipe A
panjang n−2 yang terletak pada vn →vn−1 → · · · →vn−1 2 →v
n−3
2 → · · ·v3 →
v2 dan dua arc biru berturut-turut terletak padav2 →v1 dan v1 →vn. Berikut
[image:46.612.223.456.166.346.2]adalah gambar dari Tipe A.
Gambar 4.1 : Digraf Dwiwarna D(2) Tipe A
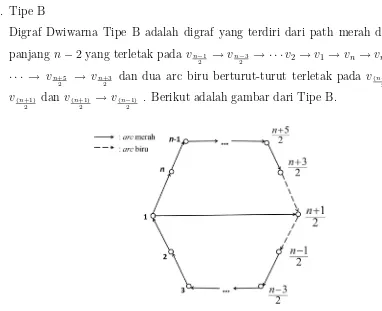
2. Tipe B
Digraf Dwiwarna Tipe B adalah digraf yang terdiri dari path merah dengan
panjang n−2 yang terletak pada vn−1 2 →v
n−3
2 → · · ·v2 →v1 →vn→ vn−1 → · · · → vn+5
2 → v n+3
2 dan dua arc biru berturut-turut terletak pada v( n+3)
2 →
v(n+1) 2 dan v
(n+1) 2 → v
(n−1)
2 . Berikut adalah gambar dari Tipe B.
[image:46.612.131.513.388.699.2]Teorema 4.1 Andaikan D(2) merupakan digraf dwiwarna primitif tipe A, maka
expoutD(2)(vk) = n2−n−2 +k untuk semua k = 1,2,· · ·, n.
Bukti: Langkah awal pembuktian ialah dengan memperlihatkan batas bawah
expoutD(2)(vk) ≥ n2 −n− 2 +k untuk semua k = 1,2,· · ·, n. Pada Gambar 4.1, terlihat jelas bahwa path merah terletak pada vn → vn−1 → · · · → vn−1
2 → v n−3
2 → · · ·v3 →v2. Asumsikan bahwa x∗ =vn dan y∗=v2 sebagai titik awal dan titik akhir
dari path merah. Pembuktian pada tipe A ini akan dibagi menjadi dua kasus sebagai
berikut.
1. Untukk = 1
Untuk k = 1, expoutD(2)(v1) = n2 −n−1. Akan diperlihatkan batas bawah
expoutD(2)(v1) ≥n2−n−1. Dengan memilih y∗ = v2, sehingga terdapat dua
path dari v1 kev2 yakni (n−2,1)-path dan ((n−1)/2,0)-path. Menggunakan
(n−2,1)-path padaTeorema 2.7.1dalam persamaan (4), diperolehu0 sebagai
berikut
u0 =b(γ2)r(p1,2)−r(γ2)b(p1,2) = 2(n−2)−(n−2)(1) =n−2 (8)
dan dengan menggunakan ((n−1)/2,0)-path diperoleh u0 berikut
u0=b(γ2)r(p1,2)−r(γ2)b(p1,2) = 2(
n−1
2 )−(n−2)(0) =n−1 (9)
Nilai u0 yang memenuhi untuk menentukan batas bawah adalah nilai terkecil
dari u0, sehingga nilaiu0 yang dipilih dari persamaan (8) dan (9) adalah u0 =
n−2.
Dipilih x∗ = v
n untuk menentukan w0 dan terdapat path dari v1 ke vn yakni
(0,1)-path. Dengan menggunakan persamaan (5), diperolehw0 sebagai berikut
w0 =r(γ1)b(p1,n)−b(γ1)r(p1,n) = (
n−1
2 )1−1(0) = (n−1)/2 (10)
Dengan menggunakan Teorema 2.7.1 diperoleh
g
h
≥S
u0
w0
=
n−1
2 n−2
1 2
n−2
n−1 2
=
n2−3n+ 2
2n−3
sehingga
expoutD(2)(v1) =g+h≥n2−n−1 =n2−n−2 +k (11)
2. Kasus 2≤k ≤n
Dengan memilihy∗ =v
2, terdapat tepat satu path dari vkkev2 yakni (k−2,
0)-path. Menggunakan (k−2,0)-path padaTeorema 2.7.1dalam persamaan (4), diperoleh u0 sebagai berikut
u0 =b(γ2)r(p1,2)−r(γ2)b(p1,2) = 2(k−2)−(n−2)(0) = 2k−4 (12)
Dipilih x∗ = v
n untuk menentukan w0 dan terdapat path dari vk ke vn yakni
(k − 2,2)-path. Dengan menggunakan persamaan (5), diperoleh w0 sebagai
berikut
w0 =r(γ1)b(p1,n)−b(γ1)r(p1,n) = (
n−1
2 )2−1(k−2) = n+ 1−k (13)
Dengan menggunakan Teorema 2.7.1 diperoleh
g
h
≥S
u0
w0
=
n−1
2 n−2
1 2
2k−4
n+ 1−k
=
n2−3n+k
2n−2
sehingga
expoutD(2)(vk) =g+h ≥n2−n−2 +k (14)
untuk semua k = 2,3,· · ·, n.
Dari persamaan (11) dan (14) dapat disimpulkan bahwa
expoutD(2)(vk) = g+h≥n2−n−2 +k
untuk semua k = 1,2,· · ·, n.
Selanjutnya akan diperlihatkan batas atasexpoutD(2)(vk) =g+h≤n2−n−2+k
untuk semuak = 1,2,· · ·, n. Untukk= 1 diperolehexpoutD(2)(v1) = n2−n−1. Persamaan (11) membuktikanexpoutD(2)(v1)≥n2−n−1 untukk = 1 dan akan
batas atas, perlu diperlihatkan bahwa Lemma 2.7.1 dengan persamaan (2) sebagai berikut S x1 x2 +
r(p(k,j))
b(p(k,j))
=
n2−3n+ 2
2n−3
memiliki solusi bulat tak negatif. Andaikan p1,i merupakan path dari v1 ke vi,
untuk semua i= 1,2,· · ·, n,maka diperoleh
S x1 x2 =
n2 −3n+ 2
2n−3
−
r(p(1,i))
b(p(1,i))
x1 x2 =
2 2−n
−1 n−1 2
n2−3n+ 2−r(p (1,i))
2n−3−b(p(1,i))
(15)
=
n−2 + (n−2)b(p(1,i))−2r(p(1,i))
(n−1 + (1−n)b(p(1,i)) + 2r(p(1,i)))/2
(16)
Jika i = 1, r(p(1,1)) = b(p(1,1)) = 0 maka diperoleh nilai x1 = n −2 > 0 dan
x2 = (n−1)/2>0 sebagai solusi tak negatif, maka terbukti bahwa
expoutD(2)(v1)≤n2−n−1 (17)
untukk = 1. Dengan menggunakan persamaan (11) dan (17),dapat dibuktikan
expoutD(2)(v1) =n2−n−1
untuk k = 1, dan dengan mengetahui d(vk, v1) =k−1, maka diperoleh
expoutD(2)(vk) =n2−n−1 +k−1 =n2 −n−2 +k (18)
untuk semua k = 1,2,· · ·, n.
Teorema 4.2 Andaikan D(2) merupakan digraf dwiwarna primitif tipe B, maka
Bukti: Untuk awal pembuktian, akan diperlihatkan batas bawah expoutD(2)(vk) ≥ (2n2 −3n−3 + 2k)/2 untuk semua k = 1,2,· · ·, n. Pada Gambar 4.2, terlihat jelas
bahwa path merah terletak pada vn−1 2 → v
n−3
2 → · · · → v2 → v1 → vn → vn−1 → · · · → vn+5
2 → v n+3
2 . Asumsikan bahwa x
∗ =vn−1
2 dan y
∗ = vn+3
2 . Pembuktian pada tipe B ini akan dibagi menjadi tiga kasus sebagai berikut.
1. Kasus 1≤k ≤(n−1)/2
Akan diperlihatkanexpoutD(2)(vk)≥(2n2−3n−3+2k)/2 untukk = 1,2,· · ·,(n−
1)/2. Menggunakan y∗ = vn+3
2 untuk memperoleh u0 dan terdapat tepat satu path dari vk ke vn+3
2 yakni ((n−3 + 2k)/2,0)-path. Menggunakan ((n −3 + 2k)/2,0)-path dan Teorema 2.7.1 pada persamaan (4), diperoleh u0 sebagai
berikut
u0 =b(γ2)r(pk,n+3
2 )−r(γ2)b(pk, n+3
2 ) = 2(
n−3 + 2k
2 )−(n−2)(0)
=n−3 + 2k (19)
Menggunakan x∗ =vn−1
2 untuk memperoleh w0 dan terdapat dua path dari vk ke vn−1
2 yakni ((n−3 + 2k)/2,2)-path dan (k,1)-path. Dengan menggunakan ((n−3 + 2k)/2,2)-path dan persamaan (5) , diperoleh w0 sebagai berikut
w0 =r(γ1)b(pk,n−1
2 )−b(γ1)r(pk, n−1
2 ) = (
n−1
2 )2−1(
n−3 + 2k
2 )
= (n+ 1−2k)/2 (20)
kemudian dengan menggunakan (k,1)-path dan persamaan (5) diperoleh w0
sebagai berikut
w0 =r(γ1)b(pk,n−1
2 )−b(γ1)r(pk, n−1
2 ) = (
n−1
2 )1−1(k)
= (n−1−2k)/2 (21)
Nilai w0 yang memenuhi untuk menentukan batas bawah adalah nilai terkecil
(n−1−2k)/2.
Dengan menggunakan Teorema 2.7.1 diperoleh
g
h
≥S u0 w0 =
(n−1)/2 n−2
1 2
n−3 + 2k
(n−1−2k)/2
=
(2n2−7n+ 5 + 2k)/2
2n−4
sehingga
expoutD(2)(vk) =g+h≥(2n2 −3n−3 + 2k)/2 (22)
untuk semua k = 1,2,· · ·,(n−1)/2.
2. Kasus k = (n+ 1)/2
Akan diperlihatkan expoutD(2)(vk) ≥ (2n2 −3n −3 + 2k)/2 untuk k = (n +
1)/2. Dengan memilihy∗ =vn+3
2 dan terdapat tepat satu path dari vk ke v n+3
2 yakni (n−2,1)-path. Menggunakan (n−2,1)-path danTeorema 2.7.1 pada
persamaan (4), diperoleh u0 sebagai berikut
u0 =b(γ2)r(pk,n+3
2 )−r(γ2)b(pk, n+3
2 ) = 2(n−2)−(n−2)(1) =n−2 (23)
Dipilihx∗ =vn−1
2 untuk menentukanw0 dan terdapat pula path dari vk kev n−1
2 yakni (0,1)-path. Dengan menggunakan persamaan (5), diperoleh w0 sebagai
berikut
w0 =r(γ1)b(pk,n−1
2 )−b(γ1)r(pk, n−1
2 ) = (
n−1
2 )1−1(0) = (n−1)/2 (24)
Dengan menggunakan Teorema 2.7.1 diperoleh
g
h
≥S u0 w0 =
(n−1)/2 n−2
1 2
n−2 (n−1)/2
=
n2 −3n+ 2
2n−3
sehingga
expoutD(2)(vk) =g+h ≥n2−n−1 = (2n2−3n−3 + 2k)/2 (25)
untuk k = (n+ 1)/2
3. Kasus (n+ 3)/2≥k ≥n
Akan diperlihatkan expoutD(2)(vk) ≥ (2n2 −3n −3 + 2k)/2 untuk k = (n +
3)/2,(n+ 5)/2,· · ·, n. Dengan memilihy∗ =vn+3
2 dan terdapat tepat satu path darivkkevn+3
2 yakni ((2k−n−3)/2,0)-path. Menggunakan ((2k−n−3)/2, 0)-path dan Teorema 2.7.1 pada persamaan (4), di